Application of Fuzzy Logic and Fractal Modeling Approach for Groundwater Potential Mapping in Semi-Arid Akka Basin, Southeast Morocco
Abstract
:1. Introduction
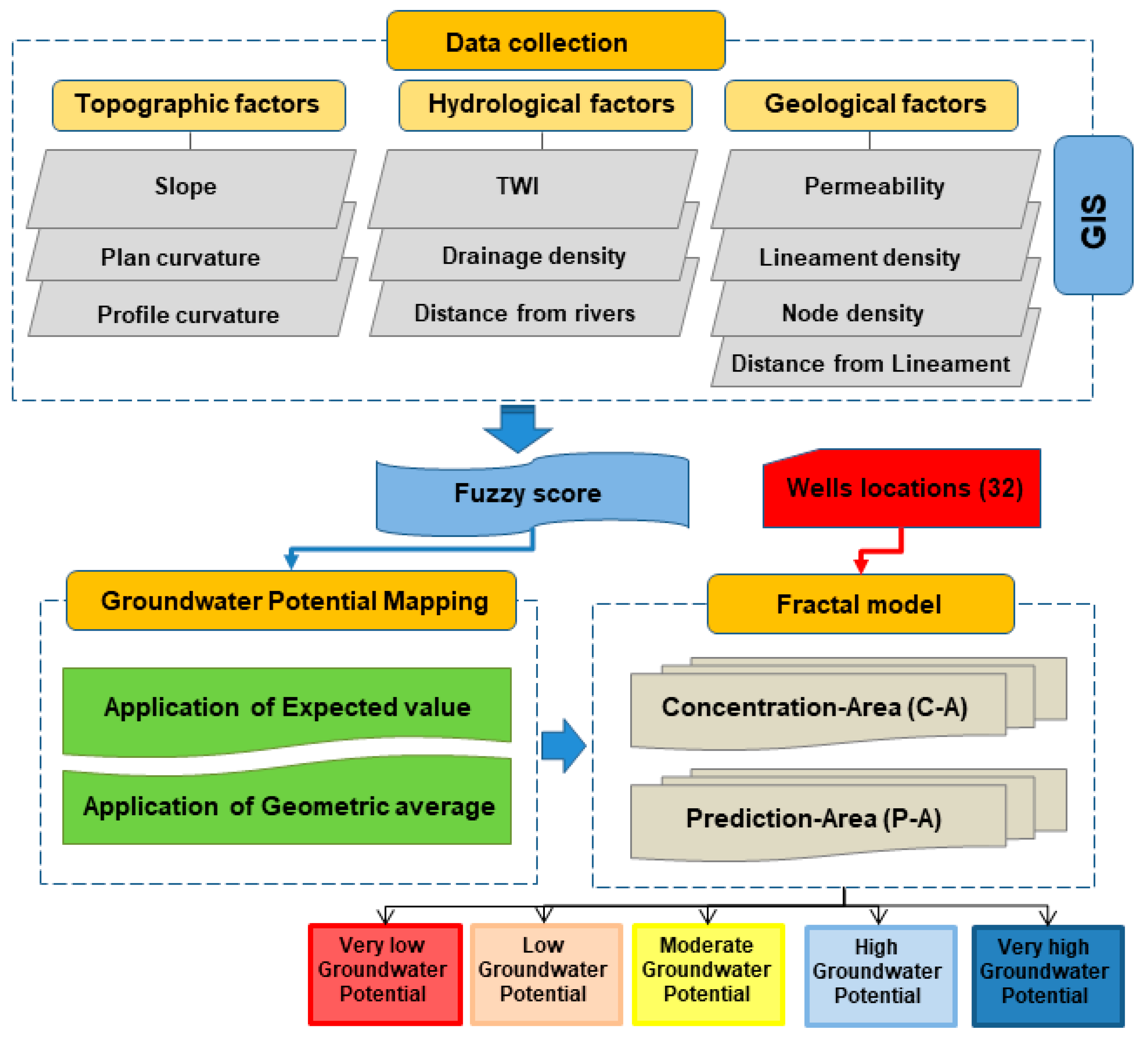
2. Materials and Methods
2.1. Study Area
2.2. Datasets Preparation
2.3. Fuzzy Logic Function
2.4. Factors Influencing Groundwater
2.4.1. Lineament Density
2.4.2. Node Density
2.4.3. Drainage Density
2.4.4. Distance from Rivers
2.4.5. Distance from Lineament
2.4.6. Permeability
2.4.7. Slope
2.4.8. Topographic Witness Index (TWI)
2.4.9. Plan Curvature and Profile Curvature
2.5. Integration of Transformed Factors
2.5.1. Geometric Average Model
2.5.2. Expected Value Model
3. Results and Discussion
3.1. Elaborated Model Assessment
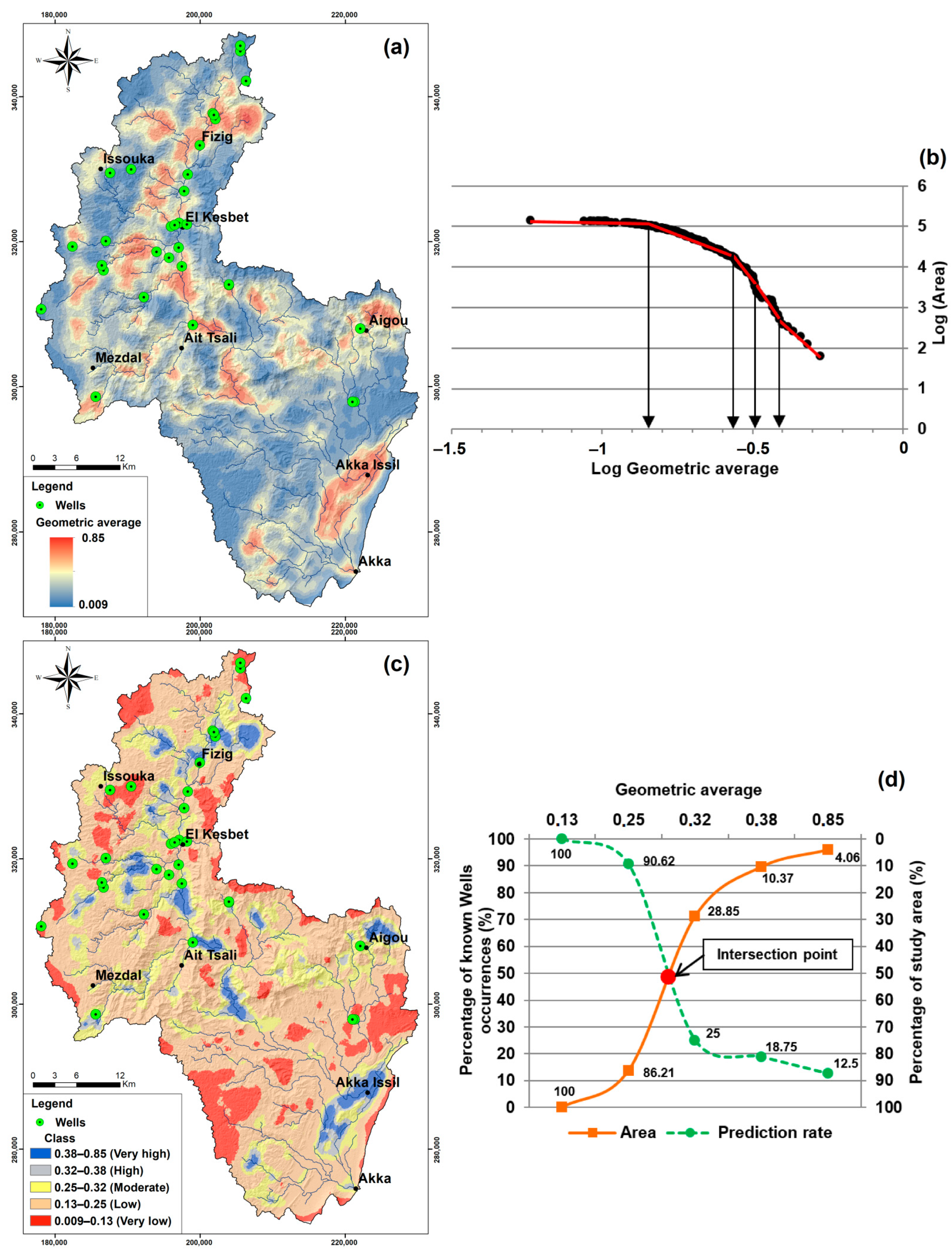
3.2. Groundwater Potential Map
3.3. Validation of Model
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Najafi Saleh, H.; Valipoor, S.; Zarei, A.; Yousefi, M.; Baghal Asghari, F.; Mohammadi, A.A.; Amiri, F.; Ghalehaskar, S.; Mousavi Khaneghah, A. Assessment of groundwater quality around municipal solid waste landfill by using Water Quality Index for groundwater resources and multivariate statistical technique: A case study of the landfill site, Qaem Shahr City, Iran. Environ. Geochem. Health 2020, 42, 1305–1319. [Google Scholar] [CrossRef] [PubMed]
- Ahmed II, J.B.; Pradhan, B. Spatial assessment of termites interaction with groundwater potential conditioning parameters in Keffi, Nigeria. J. Hydrol. 2019, 578, 124012. [Google Scholar] [CrossRef]
- Hoekstra, A.Y.; Chapagain, A.K. The water footprints of Morocco and the Netherlands: Global water use as a result of domestic consumption of agricultural commodities. Ecol. Econ. 2007, 64, 143–151. [Google Scholar] [CrossRef]
- Manap, M.A.; Sulaiman, W.N.A.; Ramli, M.F.; Pradhan, B.; Surip, N.A. knowledge–driven GIS modeling technique for groundwater potential mapping at the Upper Langat Basin, Malaysia. Arab. J. Geosci. 2013, 6, 1621–1637. [Google Scholar] [CrossRef]
- Ait Kadi, M.; Ziyad, A. Integrated water resources management in Morocco. In Global Water Security; World Water Council, Ed.; Springer: Singapore, 2018; pp. 143–163. [Google Scholar] [CrossRef]
- Golkarian, A.; Naghibi, S.A.; Kalantar, B.; Pradhan, B. Groundwater potential mapping using C5. 0, random forest, and multivariate adaptive regression spline models in GIS. Environ. Monit. Assess. 2018, 190, 149. [Google Scholar] [CrossRef]
- Seif-Ennasr, M.; Zaaboul, R.; Hirich, A.; Caroletti, G.N.; Bouchaou, L.; El Morjani, Z.E.A.; Beraaouz, E.H.; McDonnell, R.A.; Choukr-Allah, R. Climate Change and Adaptive Water Management Measures in Chtouka Aït Baha Region (Morocco). Sci. Total Environ. 2016, 573, 862–875. [Google Scholar] [CrossRef]
- Wilby, R.L.; Keenan, R. Adapting to flood risk under climate change. Prog. Phys. Geogr. 2012, 36, 348–378. [Google Scholar] [CrossRef]
- Bahir, M.; Ouhamdouch, S. Groundwater quality in semi–arid environments (Essaouira Basin, Morocco). Carbonates Evaporites 2020, 35, 41. [Google Scholar] [CrossRef]
- Driouech, F.; Rached, S.B.; Hairech, T.E. Climate Variability and Change in North African Countries. In Climate Change and Food Security in West Asia and North Africa; Sivakumar, M.V.K., Lal, R., Selvaraju, R., Hamdan, I., Eds.; Springer: Dordrecht, The Netherlands, 2013; pp. 161–172. [Google Scholar] [CrossRef]
- Razandi, Y.; Pourghasemi, H.R.; Neisani, N.S.; Rahmati, O. Application of analytical hierarchy process, frequency ratio, and certainty factor models for groundwater potential mapping using GIS. Earth Sci. Inform. 2015, 8, 867–883. [Google Scholar] [CrossRef]
- Rahmati, O.; Nazari Samani, A.; Mahdavi, M.; Pourghasemi, H.R.; Zeinivand, H. Groundwater potential mapping at Kurdistan region of Iran using analytic hierarchy process and GIS. Arab. J. Geosci. 2015, 8, 7059–7071. [Google Scholar] [CrossRef]
- Oh, H.J.; Kim, Y.S.; Choi, J.K.; Park, E.; Lee, S. GIS mapping of regional probabilistic groundwater potential in the area of Pohang City, Korea. J. Hydrol. 2011, 399, 158–172. [Google Scholar] [CrossRef]
- Rahmati, O.; Naghibi, S.A.; Shahabi, H.; Bui, D.T.; Pradhan, B.; Azareh, A.; Rafiei–Sardooi, E.; Samani, A.N.; Melesse, A.M. Groundwater spring potential modelling: Comprising the capability and robustness of three different modeling approaches. J. Hydrol. 2018, 565, 248–261. [Google Scholar] [CrossRef]
- Arnous, M.O. Groundwater potentiality mapping of hard–rock terrain in arid regions using geospatial modelling: Example from Wadi Feiran basin, South Sinai, Egypt. Hydrogeol. J. 2016, 24, 1375–1392. [Google Scholar] [CrossRef]
- Naghibi, S.A.; Pourghasemi, H.R.; Dixon, B. GIS–based groundwater potential mapping using boosted regression tree, classification and regression tree, and random forest machine learning models in Iran. Environ. Monit. Assess. 2016, 188, 44. [Google Scholar] [CrossRef]
- Naghibi, S.A.; Ahmadi, K.; Daneshi, A. Application of support vector machine, random forest, and genetic algorithm optimized random forest models in groundwater potential mapping. Water Resour. Manag. 2017, 31, 2761–2775. [Google Scholar] [CrossRef]
- Shao, Z.; Huq, M.E.; Cai, B.; Altan, O.; Li, Y. Integrated remote sensing and GIS approach using Fuzzy–AHP to delineate and identify groundwater potential zones in semi–arid Shanxi Province, China. Environ. Model. Softw. 2020, 134, 104868. [Google Scholar] [CrossRef]
- Pham, B.T.; Jaafari, A.; Prakash, I.; Singh, S.K.; Quoc, N.K.; Bui, D.T. Hybrid computational intelligence models for groundwater potential mapping. Catena 2019, 182, 104101. [Google Scholar] [CrossRef]
- Nykänen, V.; Groves, D.I.; Ojala, V.J.; Eilu, P.; Ardoll, S.J. Reconnaissance–scale conceptual fuzzy–logic prospectivity modelling for iron oxide copper–gold deposits in the northern Fennoscandian Shield, Finland. Aust. J. Earth Sci. 2008, 55, 25–38. [Google Scholar] [CrossRef]
- Yousefi, M.; Carranza, E.J.M. Fuzzification of continuous–value spatial evidence for mineral prospectivity mapping. Comput. Geosci. 2015, 74, 97–109. [Google Scholar] [CrossRef]
- Yousefi, M.; Carranza, E.J.M. Prediction–area (P–A) plot and C–A fractal analysis to classify and evaluate evidential maps for mineral prospectivity modeling. Comput. Geosci. 2015, 79, 69–81. [Google Scholar] [CrossRef]
- Echogdali, F.Z.; Boutaleb, S.; Abia, E.H.; Ouchchen, M.; Dadi, B.; Id–Belqas, M.; Abioui, M.; Pham, L.T.; Abu–Alam, T.; Mickus, K.L. Mineral prospectivity mapping: A potential technique for sustainable mineral exploration and mining activities—A case study using the copper deposits of the Tagmout basin, Morocco. Geocarto. Int. 2021, 1–22. [Google Scholar] [CrossRef]
- Nguyen, P.T.; Ha, D.H.; Avand, M.; Jaafari, A.; Nguyen, H.D.; Al–Ansari, N.; Van Phong, T.; Sharma, R.; Kumar, R.; Le, H.V.; et al. Soft computing ensemble models based on logistic regression for groundwater potential mapping. Appl. Sci. 2020, 10, 2469. [Google Scholar] [CrossRef]
- Chen, W.; Li, Y.; Tsangaratos, P.; Shahabi, H.; Ilia, I.; Xue, W.; Bian, H. Groundwater spring potential mapping using artificial intelligence approach based on kernel logistic regression, random forest, and alternating decision tree models. Appl. Sci. 2020, 10, 425. [Google Scholar] [CrossRef]
- Saravanan, S.; Saranya, T.; Abijith, D. Application of frequency ratio, analytical hierarchy process, and multi–influencing factor methods for delineating groundwater potential zones. Int. J. Environ. Sci. Technol. 2021, 1–24. [Google Scholar] [CrossRef]
- Ghosh, B. Spatial mapping of groundwater potential using data–driven evidential belief function, knowledge–based analytic hierarchy process and an ensemble approach. Environ. Earth Sci. 2021, 80, 625. [Google Scholar] [CrossRef]
- Ghosh, D.; Mandal, M.; Banerjee, M.; Karmakar, M. Impact of hydro–geological environment on availability of groundwater using analytical hierarchy process (AHP) and geospatial techniques: A study from the upper Kangsabati river basin. Groundw. Sustain. Dev. 2020, 11, 100419. [Google Scholar] [CrossRef]
- Abdelouhed, F.; Ahmed, A.; Abdellah, A.; Yassine, B.; Mohammed, I. Using GIS and remote sensing for the mapping of potential groundwater zones in fractured environments in the CHAOUIA–Morocco area. Remote Sens. Appl. Soc. Environ. 2021, 23, 100571. [Google Scholar] [CrossRef]
- Mihalasky, M.J.; Bonham–Carter, G.F. Lithodiversity and its spatial association with metallic mineral sites, Great Basin of Nevada. Nat. Resour. Res. 2001, 10, 209–226. [Google Scholar] [CrossRef]
- Ozdemir, A. GIS–based groundwater spring potential mapping in the Sultan Mountains (Konya, Turkey) using frequency ratio, weights of evidence and logistic regression methods and their comparison. J. Hydrol. 2011, 411, 290–308. [Google Scholar] [CrossRef]
- Chaudhry, A.K.; Kumar, K.; Alam, M.A. Mapping of groundwater potential zones using the fuzzy analytic hierarchy process and geospatial technique. Geocarto Int. 2021, 36, 2323–2344. [Google Scholar] [CrossRef]
- Doke, A.B.; Zolekar, R.B.; Patel, H.; Das, S. Geospatial mapping of groundwater potential zones using multi–criteria decision–making AHP approach in a hard rock basaltic terrain in India. Ecol. Indic. 2021, 127, 107685. [Google Scholar] [CrossRef]
- Echogdali, F.Z.; Boutaleb, S.; Jauregui, J.; Elmouden, A. Cartography of flooding hazard in semi–arid climate: The case of Tata valley (South–East of Morocco). J. Geogr. Nat. Disast. 2018, 8, 214. [Google Scholar] [CrossRef]
- Ouchchen, M.; Boutaleb, S.; El Azzab, D.; Abioui, M.; Mickus, K.L.; Miftah, A.; Echogdali, F.Z.; Dadi, B. Structural interpretation of the Igherm region (Western Anti Atlas, Morocco) from an aeromagnetic analysis: Implications for copper exploration. J. Afr. Earth Sci. 2021, 176, 104140. [Google Scholar] [CrossRef]
- Echogdali, F.Z.; Boutaleb, S.; Taia, S.; Ouchchen, M.; Id–Belqas, M.; Kpan, R.B.; Abioui, M.; Aswathi, J.; Sajinkumar, K.S. Assessment of soil erosion risk in a semi–arid climate watershed using SWAT model: Case of Tata basin, South–East of Morocco. Appl. Water Sci. 2022, 12, 137. [Google Scholar] [CrossRef]
- Choubert, G. Essai de mise au point du problème des “ignimbrites”. Bull. Volc. 1963, 25, 123–140. [Google Scholar] [CrossRef]
- Algouti, A.; Algouti, A.; Chbani, B.; Zaim, M. Sédimentation et volcanisme synsédimentaire de la série de base de l’Adoudounien infra–cambrien à travers deux exemples de l’Anti–Atlas du Maroc. J. Afr. Earth Sci. 2001, 32, 541–556. [Google Scholar] [CrossRef]
- Benssaou, M.; Hamoumi, N. The western Anti–Atlas of Morocco: Sedimentological and palaeogeographical formation studies in the Early Cambrian. J. Afr. Earth Sci. 2001, 32, 351–372. [Google Scholar] [CrossRef]
- Benssaou, M.; Hamoumi, N. Le graben de l’Anti–Atlas occidental (Maroc): Contrôle tectonique de la paléogéographie et des séquences au Cambrien inférieur. C. R. Géosci. 2003, 335, 297–305. [Google Scholar] [CrossRef]
- Choubert, G. L’accident majeur de l’Anti–Atlas. C. R. Acad. Sci. Paris 1947, 224, 1172–1173. [Google Scholar]
- Thomas, R.J.; Chevallier, L.P.; Gresse, P.G.; Harmer, R.E.; Eglington, B.M.; Armstrong, R.A.; De Beer, C.H.; Martini, J.E.J.; De Kock, G.S.; Macey, P.H.; et al. Precambrian evolution of the Sirwa window, Anti–Atlas orogen, Morocco. Precambrian Res. 2002, 118, 1–57. [Google Scholar] [CrossRef]
- Huq, M.E.; Su, C.; Li, J.; Sarven, M.S. Arsenic enrichment and mobilization in the Holocene alluvial aquifers of Prayagpur of Southwestern Bangladesh. Int. Biodeterior. Biodegrad. 2018, 128, 186–194. [Google Scholar] [CrossRef]
- Zabihi, M.; Pourghasemi, H.R.; Pourtaghi, Z.S.; Behzadfar, M. GIS–based multivariate adaptive regression spline and random forest models for groundwater potential mapping in Iran. Environ. Earth Sci. 2016, 75, 665. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Das, S.; Das, S.; Kalashetty, M.; Warghat, S.R. An integrated approach for mapping groundwater potential applying geospatial and MIF techniques in the semiarid region. Environ. Dev. Sustain. 2021, 23, 495–510. [Google Scholar] [CrossRef]
- Haris, K.; Efstratiadis, S.N.; Maglaveras, N.; Katsaggelos, A.K. Hybrid image segmentation using watersheds and fast region merging. IEEE Trans. Image Process. 1998, 7, 1684–1699. [Google Scholar] [CrossRef]
- Boutaleb, S.; Boualoul, M.; Oudra, M.; Bouchaou, L.; Dindane, K. Apports du traitement d’image et de la géophysique à l’étude des ressources en eau en milieu fissuré: Cas de l’Anti–Atlas marocain. Afr. Geosci. Rev. 2008, 15, 129–141. [Google Scholar]
- Boutaleb, S.; Boualoul, M.; Bouchaou, L.; Oudra, M. Application of Remote–Sensing and Surface Geophysics for Groundwater Prospecting in a Hard Rock Terrain. In Applied Groundwater Studies in Africa; Adelana, S.M.A., MacDonald, A.M., Eds.; CRC Press/Balkema: Leiden, The Netherlands, 2008; Volume 13, pp. 215–227. [Google Scholar] [CrossRef]
- Boutaleb, S.; Hammichi, F.; Tabyaoui, H.; Bouchaou, L.; Dindane, K. Détermination des écoulements préférentiels en zone karstique (Tafrata, Maroc), Apport des données satellitaires SAR ERS–1 et Landsat ETM+ et de la prospection géophysique. J. Water Sci. 2009, 22, 407–419. [Google Scholar]
- Hssaisoune, M.; Boutaleb, S.; Bouchaou, L.; Benssaou, M.; Tagma, T. Use of remote sensing and electrical resistivity tomography to determine Tidsi spring recharge and underground drainage. Eur. Water 2017, 57, 429–434. [Google Scholar]
- Ghosh, D.; Mandal, M.; Karmakar, M.; Banerjee, M.; Mandal, D. Application of geospatial technology for delineating groundwater potential zones in the Gandheswari watershed, West Bengal. Sustain. Water Resour. Manag. 2020, 6, 14. [Google Scholar] [CrossRef]
- Berthold, M.; Hand, D.J. Intelligent Data Analysis: An Introduction; Springer: Berlin, Germany, 2003. [Google Scholar]
- Alpaydm, E. Introduction to Machine Learning; MIT Press: London, UK, 2004. [Google Scholar]
- Micheli-Tzanakou, E. Supervised and Unsupervised Pattern Recognition; CRC Press: Boca Raton, FL, USA, 1999. [Google Scholar]
- Yousefi, M.; Nykänen, V. Data–driven logistic–based weighting of geochemical and geological evidence layers in mineral prospectivity mapping. J. Geochem. Explor. 2016, 164, 94–106. [Google Scholar] [CrossRef]
- Haridas, V.R.; Aravindan, S.; Girish, G. Remote sensing and its applications for groundwater favourable area identification. Q. J. GARC 1998, 6, 18–22. [Google Scholar]
- Mahmoud, S.H.; Alazba, A.A. Integrated remote sensing and GIS-based approach for deciphering groundwater potential zones in the central region of Saudi Arabia. Environ. Earth Sci. 2016, 75, 344. [Google Scholar] [CrossRef]
- Huggett, R.J. Fundamentals of Geomorphology, 2nd ed.; Routledge: London, UK, 2007. [Google Scholar]
- Patra, S.; Mishra, P.; Mahapatra, S.C. Delineation of groundwater potential zone for sustainable development: A case study from Ganga Alluvial Plain covering Hooghly district of India using remote sensing, geographic information system and analytic hierarchy process. J. Clean. Prod. 2018, 172, 2485–2502. [Google Scholar] [CrossRef]
- Ayazi, M.H.; Pirasteh, S.; Arvin, A.K.P.; Pradhan, B.; Nikouravan, B.; Mansor, S. Disasters and risk reduction in groundwater: Zagros Mountain Southwest Iran using geoinformatics techniques. Disaster Adv. 2010, 3, 51–57. [Google Scholar]
- Charon, J.E. Hydrogeological applications of ERTS satellite imagery. In Proc UN/FAO Regional Seminar on Remote Sensing of Earth Resources and Environment; Commonwealth Science Council: Cairo, Egypt, 1974; pp. 439–456. [Google Scholar]
- Jaiswal, R.K.; Mukherjee, S.; Krishnamurthy, J.; Saxena, R. Role of remote sensing and GIS techniques for generation of groundwater prospect zones towards rural development––an approach. Int. J. Remote Sens. 2003, 24, 993–1008. [Google Scholar] [CrossRef]
- Naghibi, S.A.; Pourghasemi, H.R.; Pourtaghi, Z.S.; Rezaei, A. Groundwater qanat potential mapping using frequency ratio and Shannon’s entropy models in the Moghan watershed, Iran. Earth Sci. Inform. 2015, 8, 171–186. [Google Scholar] [CrossRef]
- Moore, I.D.; Grayson, R.B.; Ladson, A.R. Digital terrain modelling: A review of hydrological, geomorphological, and biological applications. Hydrol. Process. 1991, 5, 3–30. [Google Scholar] [CrossRef]
- Naghibi, S.A.; Moradi Dashtpagerdi, M. Evaluation of four supervised learning methods for groundwater spring potential mapping in Khalkhal region (Iran) using GIS–based features. Hydrogeol. J. 2017, 25, 169–189. [Google Scholar] [CrossRef]
- Yousefi, M.; Carranza, E.J.M. Geometric average of spatial evidence data layers: A GIS–based multi–criteria decision–making approach to mineral prospectivity mapping. Comput. Geosci. 2015, 83, 72–79. [Google Scholar] [CrossRef]
- Bonham-Carter, G.F. Geographic Information Systems for Geoscientists: Modeling with GIS; Pergamon: Oxford, UK, 1994. [Google Scholar]
- Carranza, E.J.M. Geochemical Anomaly and Mineral Prospectivity Mapping in GIS; Elsevier: Amsterdam, The Netherlands, 2008. [Google Scholar]
- Chen, Y.; Yu, J.; Khan, S. Spatial sensitivity analysis of multi–criteria weights in GIS–based land suitability evaluation. Environ. Model. Softw. 2010, 25, 1582–1591. [Google Scholar] [CrossRef]
- Feizizadeh, B.; Jankowski, P.; Blaschke, T. A GIS based spatially–explicit sensitivity and uncertainty analysis approach for multi–criteria decision analysis. Comput. Geosci. 2014, 64, 81–95. [Google Scholar] [CrossRef]
- Mosher, S.W.; Maučec, M.; Spanier, J.; Badruzzaman, A.; Chedester, C.; Evans, M. Expected–value techniques for Monte Carlo modeling of well logging problems. Nucl. Instrum. Methods Phys. Res. A 2010, 613, 334–341. [Google Scholar] [CrossRef]
- Runge, M.C.; Converse, S.J.; Lyons, J.E. Which uncertainty? Using expert elicitation and expected value of information to design an adaptive program. Biol. Conserv. 2011, 144, 1214–1223. [Google Scholar] [CrossRef]
- Gupta, P.; Mittal, G.; Mehlawat, M.K. Expected value multiobjective portfolio rebalancing model with fuzzy parameters. Insu. Math. Econ. 2013, 52, 190–203. [Google Scholar] [CrossRef]
- Bragg, S.M. Financial Analysis: A Controller’s Guide; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2006. [Google Scholar]
- Cheng, Q. Mapping singularities with stream sediment geochemical data for prediction of undiscovered mineral deposits in Gejiu, Yunnan Province, China. Ore Geol. Rev. 2007, 32, 314–324. [Google Scholar] [CrossRef]
- Wang, G.; Carranza, E.J.M.; Zuo, R.; Hao, Y.; Du, Y.; Pang, Z.; Sun, Y.; Qu, J. Mapping of district–scale potential targets using fractal models. J. Geochem. Explor. 2012, 122, 34–46. [Google Scholar] [CrossRef]
- Ouchchen, M.; Boutaleb, S.; Abia, E.H.; El Azzab, D.; Miftah, A.; Dadi, B.; Echogdali, F.Z.; Mamouch, Y.; Pradhan, B.; Santosh, M.; et al. Exploration targeting of copper deposits using staged factor analysis, geochemical mineralization prospectivity index, and fractal model (Western Anti–Atlas, Morocco). Ore Geol. Rev. 2022, 143, 104762. [Google Scholar] [CrossRef]
- Heidari, S.M.; Afzal, P.; Ghaderi, M.; Sadeghi, B. Detection of mineralization stages using zonality and multifractal modeling based on geological and geochemical data in the Au–(Cu) intrusion–related Gouzal–Bolagh deposit, NW Iran. Ore Geol. Rev. 2021, 139, 104561. [Google Scholar] [CrossRef]
- Zissimos, A.M.; Cohen, D.R.; Christoforou, I.C.; Sadeghi, B.; Rutherford, N.F. Controls on soil geochemistry fractal characteristics in Lemesos (Limassol), Cyprus. J. Geochem. Explor. 2021, 220, 106682. [Google Scholar] [CrossRef]
- Cheng, Q. Singularity theory and methods for mapping geochemical anomalies caused by buried sources and for predicting undiscovered mineral deposits in covered areas. J. Geochem. Explor. 2012, 122, 55–70. [Google Scholar] [CrossRef]
- Afzal, P.; Alghalandis, Y.F.; Khakzad, A.; Moarefvand, P.; Omran, N.R. Delineation of mineralization zones in porphyry Cu deposits by fractal concentration–volume modeling. J. Geochem. Explor. 2011, 108, 220–232. [Google Scholar] [CrossRef]
- Cheng, Q.; Agterberg, F.P.; Ballantyne, S.B. The separation of geochemical anomalies from background by fractal methods. J. Geochem. Explor. 1994, 51, 109–130. [Google Scholar] [CrossRef]
- Parsa, M.; Maghsoudi, A.; Yousefi, M.; Sadeghi, M. Prospectivity modeling of porphyry–Cu deposits by identification and integration of efficient mono–elemental geochemical signatures. J. Afr. Earth Sci. 2016, 114, 228–241. [Google Scholar] [CrossRef]
- Naef, D.; Rickenmann, D.; Rutschmann, P.; McArdell, B.W. Comparison of flow resistance relations for debris flows using a one-dimensional finite element simulation model. Nat. Hazards Earth Syst. Sci. 2006, 6, 155–165. [Google Scholar] [CrossRef]
- Ma, G.; Rezania, M.; Nezhad, M.M. Stochastic Assessment of Landslide Influence Zone by Material Point Method and Generalized Geotechnical Random Field Theory. Int. J. Geomech. 2022, 22, 04022002. [Google Scholar] [CrossRef]
- Ma, G.; Rezania, M.; Mousavi Nezhad, M.; Hu, X. Uncertainty quantification of landslide run out motion considering soil interdependent anisotropy and fabric orientation. Landslides 2022, 19, 1231–1247. [Google Scholar] [CrossRef]



| Model | Pr (%) | Oa (%) | Nd | We |
|---|---|---|---|---|
| Expected value | 65 | 35 | 1.86 | 0.62 |
| Geometric average | 49 | 51 | 0.96 | −0.04 |
| Class | Expected Value | Geometric Average | ||||
|---|---|---|---|---|---|---|
| Area (Km2) | Area % | Number of Wells | Area (Km2) | Area % | Number of Wells | |
| Very high | 450.15 | 21.78 | 13 | 83.93 | 4.06 | 4 |
| High | 381.58 | 18.47 | 9 | 130.36 | 6.31 | 2 |
| Moderate | 439.45 | 21.27 | 3 | 381.95 | 18.48 | 2 |
| Low | 412.95 | 19.98 | 4 | 1185.25 | 57.36 | 21 |
| Very low | 382.23 | 18.50 | 3 | 284.90 | 13.79 | 3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Echogdali, F.Z.; Boutaleb, S.; Kpan, R.B.; Ouchchen, M.; Bendarma, A.; El Ayady, H.; Abdelrahman, K.; Fnais, M.S.; Sajinkumar, K.S.; Abioui, M. Application of Fuzzy Logic and Fractal Modeling Approach for Groundwater Potential Mapping in Semi-Arid Akka Basin, Southeast Morocco. Sustainability 2022, 14, 10205. https://doi.org/10.3390/su141610205
Echogdali FZ, Boutaleb S, Kpan RB, Ouchchen M, Bendarma A, El Ayady H, Abdelrahman K, Fnais MS, Sajinkumar KS, Abioui M. Application of Fuzzy Logic and Fractal Modeling Approach for Groundwater Potential Mapping in Semi-Arid Akka Basin, Southeast Morocco. Sustainability. 2022; 14(16):10205. https://doi.org/10.3390/su141610205
Chicago/Turabian StyleEchogdali, Fatima Zahra, Said Boutaleb, Rosine Basseu Kpan, Mohammed Ouchchen, Amine Bendarma, Hasna El Ayady, Kamal Abdelrahman, Mohammed S. Fnais, Kochappi Sathyan Sajinkumar, and Mohamed Abioui. 2022. "Application of Fuzzy Logic and Fractal Modeling Approach for Groundwater Potential Mapping in Semi-Arid Akka Basin, Southeast Morocco" Sustainability 14, no. 16: 10205. https://doi.org/10.3390/su141610205
APA StyleEchogdali, F. Z., Boutaleb, S., Kpan, R. B., Ouchchen, M., Bendarma, A., El Ayady, H., Abdelrahman, K., Fnais, M. S., Sajinkumar, K. S., & Abioui, M. (2022). Application of Fuzzy Logic and Fractal Modeling Approach for Groundwater Potential Mapping in Semi-Arid Akka Basin, Southeast Morocco. Sustainability, 14(16), 10205. https://doi.org/10.3390/su141610205










