Statistical Analysis of Design Variables in a Chiller Plant and Their Influence on Energy Consumption and Life Cycle Cost

Abstract

An appropriate design of a chiller plant is crucial to guarantee highly performing solutions. However, several design variables, such as type of systems, total cooling capacity, and hydraulic arrangement, need to be considered. On the one hand, at present, different technical criteria for selecting the most suitable design variables are available. Studies that corroborate the influence of the design variables over the operational variables are missing. In order to fill this knowledge gap, this work proposes a statistical analysis of design variables in chiller plants operating in medium- and large-scale applications and evaluates their influence on energy consumption and life cycle cost (LCC) under the same thermal demand conditions. A case study involving 138 chiller plant combinations featuring different arrangements and a Cuban hotel was selected. The results suggested that the total chiller design and cooling capacity distribution among chillers have a significant influence on the energy consumption of the chiller plant with a Spearman’s Rho and Kendall Tau (τ) correlation index value of −0.625 and 0.559, respectively. However, with LCC, only the cooling capacity distribution among the chillers had a certain influence with a Kendall Tau correlation index value of 0.289. As for the considered total cooling capacity, the applied statistical test showed that this design variable does not have any influence on performing the chiller plant.

1. Introduction

Chiller plants are widely used in centralized air-conditioning systems, which are employed in installations requiring medium to large cooling loads. They feature different coupled sub-elements, including the chillers, the condensing system, the hydraulic system, and the ventilation system. In order to implement energy-efficient and affordable chiller plants, different design parameters, such as type of chillers, total installed cooling capacity, the number of chillers, distribution of the cooling capacity among the chillers, hydraulic arrangement of the primary circuit, need to be assessed. As an example, Ref. [1] recommend the adoption of a safety factor (SF), i.e., an increase in the peak demand obtained from the total cooling load calculation owing to the unavoidable uncertainty of climate data, indoor occupants, and internal heat gains, by between 10% and 20%. The magnitude of the safety factor depends on international or local standards. For example, ASHRAE Standard 62.2-2016 [2] establishes a value of SF of 15%, whereas the Cuban standard NC-220:2009 [3] suggests a value of SF of up to 10%. Nall [4] and Ruya and Augenbroe [5] reported values of SF of 15% to 25%. However, according to [6,7,8,9], the adoption of a safety factor is excessive and results in higher investment costs and in malfunctions. In order to overcome these drawbacks, Chen et al. [10] implemented a robust optimal design involving sequential Monte Carlo simulation to optimize the design of the cooling water system. The results showed that the system could decrease 22.7% with respect to the total cost of the optimized as contrasted with the conventional design in a building in Hong Kong. Gang et al. [11] showed that the uncertainties in the indoor condition play a crucial role in the design optimization of district cooling systems. Cheng et al. [12] implemented a probabilistic approach for uncertainty-based optimal design to chiller plants involving uncertainties of weather, occupants, and heat transfer coefficients of building envelopes. Kang et al. [13] implemented a novel approach to size chiller plants based on the scenario parameter uncertainty, the discrete spectrum of the nominal cooling load of chillers, and the difference between chiller cooling capacity under nominal conditions and peak cooling load conditions. The results revealed that the use of this method leads to a decrease in the chiller nominal cooling capacity of up to 22.51% in a three-story office building in Guangzhou, China.

The methods employed by Huang et al. [14], Chai et al. [15], and Liao et al. [16] are not attractive to engineers from outside academia due to the high-risk level, as a practical point of view is not used [17].

The chillers to be installed in a large-scale application need to be at least three, according to [18]. Cheng et al. [10] observed that, on the one hand, a high number of chillers allows reducing the operating costs. On the other hand, this would increase the investment and maintenance costs. Therefore, the selection of the most appropriate number of chillers is crucial for medium and large plants. Chen et al. [19] also showed that there is a relative margin between the increase in the number of chillers and the efficiency of the plant, as it does not behave proportionally, resulting in the need to find an optimal value.

The distribution of the cooling capacity between chillers can be based on two different configurations, i.e., a symmetrical arrangement or an asymmetrical one. Huang et al. [20] and Vasisht et al. [21] observed that asymmetrical plants could perform more efficiently as this configuration allows the thermal demand of the building to adjust to the cooling capacity of the plant.

Designers generally arrange the hydraulic circuit in series, series–parallel, or parallel configurations. Kapoor and Edgar [22] highlighted that parallel configuration features a simple schematic and ease of maintenance and can offer a decrease in energy consumption of 9.62% and an increase in efficiency by 12.26% compared to a series arrangement. However, a series arrangement is recommended to be used as the temperature difference is excessive or the cooling load demand is stable [23].

There are some studies in which statistical correlation analysis was applied to heating, ventilation, and air condition (HVAC) systems. However, they focused on the correlation analysis between parameters associated with the operation of HVAC systems and the thermal comfort parameters. For example, Valentina et al. [24] conducted a statistical study to assess the impact of HVAC systems on indoor air quality parameters and microbiological growth. Hong et al. [25] defined the parameters having the greatest influence on the energy consumption of the HVAC system in office buildings located in Shanghai. They found values of Pearson correlation equal to 0.6056 for the construction year, 0.3075 for the number of floors, 0.2006 for the window/wall ratio, and 0.3684 for the building orientation, respectively.

Other studies involved the implementation of novel methods for the optimal design of HVAC systems. Huang et al. [14] found that the life cycle cost of a plant can be reduced by up to 12.5% as the design parameters, i.e., the number of chillers and the distribution of the cooling capacity between them, are optimized. Furthermore, Lee and Lee [26] developed a simplified statistics-based method to preliminary assess the configuration of multiple-chillers systems. The authors observed an energy saving of up to 9.5% by changing the number of chillers. Gant et al. [27] proposed a new method for the optimal design of building cooling systems considering cooling load uncertainty and HVAC equipment reliability. An annual total cost reduction of about 4–15% was estimated compared to the conventional methodology. Catrini et al. [28] carried out an exergoeconomic analysis aiming at supporting the optimal design and operation of multiple chiller systems in air conditioning applications. The authors evaluated decreases in the exergoeconomic cost of the chilled water by about 7% and 30% as unevenly sized systems were replaced by even ones in both series and parallel configurations. Furthermore, they highlighted that the recent studies by Maasoumy et al. [29] and Bhattacharya et al. [30] encourage the researchers to define the design parameters of a chiller plant from a creative combination of control-simulation of several design options (Co-design) to select the most suitable architecture instead to applying conservative approaches. However, different optimization techniques [31] can be applied in the design phase to implement life cycle cost and energy analyses, among others.

There are several factors, such as goal criteria, standard requirements, and technical and economic criteria that allow engineers to narrow the chiller plant options to be analyzed in the design phase [32]. However, regarding technical and economic criteria, there are certain unofficial rules that constricted the value-engineer options, such as over-sizing of chiller plant leads to deteriorated energy performance, the increment of the number of units improves the energy efficiency, and the asymmetrical arrangement is more highly performing than the symmetrical solution. In particular, the literature review highlights that the comparison of various configurations was carried out with a few viable options. Therefore, these studies do not have sufficient data to determine statistically the influence of the design parameters on the operating parameters of chiller plants operating in medium- and large-scale applications. To bridge this knowledge gap, a statistical analysis of design variables in chiller plants operating in medium- and large-scale applications and assess their effect on energy consumption and life cycle cost under the same thermal demand conditions is proposed in this paper. A case study based on 138 chiller plant combinations presenting different arrangements and a Cuban hotel has been used.

The manuscript is structured: Section 2 describes the methodology used in the paper, while the results are presented and discussed in Section 3. Finally, Section 4 summarizes the conclusions.

2. Materials and Methods

2.1. Research Study: Procedure to Obtain the Optimal Distribution Cooling Capacity of an Air-Condensed Chiller Plant for a Hotel Facility Conceptual Design

Previous research conducted by Diaz et al. [33,34,35] comprised the development of a procedure to select the optimal configuration of a water chiller plant in a hotel facility during the design phase. The selection criterion was based on the LCC analysis, involving three stages:

• Stage 1: The thermal demand values of the building were analyzed through the transfer method, using the technical description of the real estate project, the meteorological conditions of the region, and the statistical information of occupancy and operation patterns of hotels with similar characteristics;
• Stage 2: The generation of chiller plant alternatives was carried out through a statistical–mathematical procedure using the calculated thermal demand values and black box models of the water chillers. This procedure allowed different plant architectures to be established by modifying the design parameters, i.e., installed cooling capacity, number of units, and distribution of cooling capacity between chillers, regarding constraints according to design standards;
• Stage 3: As an initial state, the chiller plant was a decoupled system comprising n air-cooled chillers arranged in parallel, and only the primary circuit was involved in the analysis. The energy verification of the chiller plants generated was carried out by solving a non-linear, multivariable combinatorial optimization problem of optimal chiller loading (OCL) and optimal chiller sequence (OCS) versus building demand profiles. In order to establish the OCS, a baseline decision was made. A genetic algorithm was used for the optimization procedure. For the LCC analysis, economic and financial parameters and criteria of the region where the case study was analyzed were used.

The procedure was implemented for a hotel installation in the construction phase, comprising 187 rooms and various facilities in the public and service areas. Phase 1 identified the maximum demand to be installed (i.e., 489 kW) and 8 thermal demand profiles, and these values allowed the identification of the individual cooling capacities of the chillers in phase 2. Twelve air-cooled screw chillers and their black box model describing their electrical and thermal demands were implemented. At the end of this phase, and with the restriction that the total installed capacity was in a range of 10–20% above the maximum demand, it was found that the plants were composed of 2–5 chillers. A total of 138 chiller plants of different architecture and with a cooling capacity between 537–582 kW were generated. Finally, in phase 3 of the research, the values of annual energy consumption and LCC of each of the chiller plants generated were obtained, which were used for their subsequent selection.

The energy consumption and LCC analyses of the 138 chiller plant were carried out according to Stage 3 of the methodology. The summary of the results obtained is shown in

Table A1. Main characteristics and performance data of the chiller plants relying on 2 and 3 units (obtained from Diaz Torres [33], Diaz et al [34] Diaz et al [35]. Reprinted/adapted with permission from Ref. [34]. 2021, Elsevier and Copyright Clearance Center. Reprinted/adapted with permission from Ref. [35]. 2022, Elsevier and Copyright Clearance Center.

Chiller Plant No.	Chiller Cooling Capacity at STD (kW)			Total Units	Total Cooling Capacity (kW)	Cooling Distribution among Chillers (%)	Energy Consumption (kWh/year)	LCC MMcup
	1	2	3
1	181.3	360.0	-	2	538	33/67	476.3	799.86
2	199.8	360.0	-	2	557	36/ 64	487.1	816.14
3	203.1	360.0	-	2	560	36/64	487.8	817.13
4	229.9	312.2	-	2	540	42/58	483.2	807.17
5	273.0	273.0	-	2	542	50/50	545.1	891.09
6	273.0	312.2	-	2	582	47/53	533.9	882.30
7	98.2	98.2	360.0	3	553	18/18/65	460.8	801.82
8	98.2	119.0	360.0	3	574	17/21/62	432.5	766.46
9	98.2	135.1	312.2	3	543	18/25/57	442.8	778.19
10	98.2	151.2	312.2	3	559	17/27/56	449.3	791.61
11	98.2	161.7	312.2	3	569	17/28/55	446.8	790.34
12	98.2	181.3	273.0	3	549	18/33/49	432.0	765.91
13	98.2	199.8	273.0	3	568	17/35/48	443.7	783.34
14	98.2	203.1	273.0	3	571	17/35/48	444.7	785.09
15	98.2	229.9	229.9	3	556	18/41/41	432.4	764.26
16	119.0	119.0	312.2	3	548	22/22/57	431.8	763.54
17	119.0	135.1	312.2	3	564	21/24/55	435.4	772.64
18	119.0	151.2	273.0	3	540	22/28/50	436.8	774.93
19	119.0	151.2	312.2	3	580	20/26/54	440.3	783.24
20	119.0	161.7	273.0	3	551	22/29/49	427.9	763.51
21	119.0	181.3	273.0	3	570	21/32/48	419.6	753.15
22	119.0	199.8	229.9	3	546	22/36/42	416.0	744.67
23	119.0	203.1	229.9	3	550	22/37/42	417.5	747.27
24	119.0	229.9	229.9	3	577	20/40/40	414.2	745.79
25	135.1	135.1	273.0	3	540	25/25/50	462.1	809.18
26	135.1	135.1	312.2	3	579	23/23/54	460.1	808.53
27	135.1	151.2	273	3	556	24/27/49	447.1	750.89
28	135.1	161.7	273	3	566	24/28/48	436.2	742.44
29	135.1	181.3	229.9	3	543	25/33/42	406.6	777.79
30	135.1	181.3	273	3	585	23/31/46	424.6	737.08
31	135.1	199.8	229.9	3	562	24/35/41	423.1	825.32
32	135.1	203.1	203.1	3	538	25/38/38	471.3	753.34
33	135.1	203.1	229.9	3	565	24/36/41	424.1	828.08
34	151.2	151.2	273	3	572	26/26/47	457.8	778.04
35	151.2	161.7	229.9	3	540	28/30/42	428.5	798.99
36	151.2	161.7	273	3	582	26/28/47	445.3	768.39
37	151.2	181.3	229.9	3	559	27/32/41	424.6	806.38
38	151.2	199.8	199.8	3	548	27/36/36	483.9	757.73
39	151.2	199.8	203.1	3	551	27/36/37	480.5	846.01
40	151.2	199.8	229.9	3	578	26/34/40	437.5	844.73
41	151.2	203.1	203.1	3	554	27/36/36	482	775.57
42	151.2	203.1	229.9	3	581	26/35/39	438.4	846.2
43	161.7	161.7	229.9	3	550	29/29/42	430.7	803.73
44	161.7	181.3	199.8	3	539	30/33/37	458.2	811.80
45	161.7	181.3	203.1	3	543	30/33/37	457.4	805.69
46	161.7	181.3	229.9	3	570	28/32/40	424.3	807.89
47	161.7	199.8	199.8	3	558	29/36/36	483.5	758.89
48	161.7	199.8	203.1	3	561	29/35/36	479.0	846.8
49	161.7	203.1	203.1	3	564	28/36/36	480.1	841.14
50	181.3	181.3	181.3	3	540	33/33/33	475.7	838.53
51	181.3	181.3	199.8	3	559	32/32/36	466.4	831.09
52	181.3	181.3	203.1	3	562	32/32/36	465.4	819.71
53	181.3	199.8	199.8	3	578	31/34/34	491.2	820.22
54	181.3	199.8	203.1	3	581	31/34/35	487.6	859.85
55	181.3	203.1	203.1	3	584	31/35/35	488.4	855.43

for the chiller plants with up to 3 units,

Table A2. Main characteristics and performance data of the chiller plants relying on 4 units (obtained from Diaz Torres [33], Diaz et al [34] Diaz et al [35]. Reprinted/adapted with permission from Ref. [34]. 2021, Elsevier and Copyright Clearance Center. Reprinted/adapted with permission from Ref. [35]. 2022, Elsevier and Copyright Clearance Center.

Chiller Plant No.	Chiller Cooling Capacity at STD (kW)				Total Units	Total Cooling Capacity (kW)	Cooling Distribution among Chillers (%)	Energy Consumption (kWh/year)	LCC MMcup
	1	2	3	4
56	98.2	98.2	98.2	273.0	4	564	17/17/17/48	445.0	809.77
57	98.2	98.2	119.0	229.9	4	543	18/18/22/42	412.6	763.93
58	98.2	98.2	119.0	273.0	4	585	17/17/20/46	416.5	775.88
59	98.2	98.2	135.1	229.9	4	559	17/17/24/41	410.6	763.35
60	98.2	98.2	151.2	199.8	4	545	18/18/28/36	434.5	797.67
61	98.2	98.2	151.2	203.1	4	548	18/18/27/37	434.2	797.41
62	98.2	98.2	151.2	229.9	4	575	17/17/26/40	411.7	767.57
63	98.2	98.2	161.7	181.3	4	536	18/18/30/34	418.6	773.63
64	98.2	98.2	161.7	199.8	4	555	18/18/29/36	432.1	796.08
65	98.2	98.2	161.7	203.1	4	558	18/18/28/36	430.5	794.19
66	98.2	98.2	161.7	229.9	4	585	17/17/27/39	407.7	764.42
67	98.2	98.2	181.3	181.3	4	556	18/18/32/32	423.9	783.34
68	98.2	98.2	181.3	199.8	4	574	17/17/31/35	433.7	799.89
69	98.2	98.2	181.3	203.1	4	577	17/17/31/35	432.5	798.58
70	98.2	119.0	119.0	203.1	4	537	18/22/22/38	399.4	752.36
71	98.2	119.0	119.0	229.9	4	564	17/21/21/41	400.6	750.58
72	98.2	119.0	135.1	199.8	4	549	18/22/24/36	411.4	768.97
73	98.2	119.0	135.1	203.1	4	553	18/21/24/37	413.1	771.65
74	98.2	119.0	135.1	229.9	4	580	17/20/23/39	406.8	757.75
75	98.2	119.0	151.2	181.3	4	547	18/22/28/33	399.3	750.35
76	98.2	119.0	151.2	199.8	4	566	17/21/27/35	407.8	765.13
77	98.2	119.0	151.2	203.1	4	569	17/21/26/35	409.3	767.41
78	98.2	119.0	161.7	161.7	4	538	18/22/30/30	402.1	756.76
79	98.2	119.0	161.7	181.3	4	557	18/21/29/32	407.1	759.09
80	98.2	119.0	161.7	199.8	4	576	17/21/28/35	421.1	781.27
81	98.2	119.0	161.7	203.1	4	579	17/21/28/35	423.0	784.39
82	98.2	119.0	181.3	181.3	4	577	17/21/31/31	418.9	776.52
83	98.2	135.1	135.1	181.3	4	546	18/25/25/33	410.0	765.87
84	98.2	135.1	135.1	199.8	4	565	17/24/24/35	418.0	767.00
85	98.2	135.1	135.1	203.1	4	568	17/24/24/36	418.8	781.43
86	98.2	135.1	151.2	161.7	4	543	18/25/28/30	419.1	777.68
87	98.2	135.1	151.2	181.3	4	562	17/24/27/32	418.6	773.63
88	98.2	135.1	151.2	199.8	4	581	17/23/26/34	432.1	796.08
89	98.2	135.1	151.2	203.1	4	584	17/23/26/35	430.5	794.19
90	98.2	135.1	161.7	161.7	4	553	18/24/29/29	407.7	764.42
91	98.2	135.1	161.7	181.3	4	573	17/23/28/31	405.7	761.68
92	98.2	151.2	151.2	151.2	4	549	18/27/27/27	453.7	825.76
93	98.2	151.2	151.2	161.7	4	559	17/27/27/29	442.2	812.07
94	98.2	151.2	151.2	181.3	4	579	17/26/26/31	429.3	794.90
95	98.2	151.2	161.7	161.7	4	569	17/26/28/28	440.7	810.60
96	98.2	161.7	161.7	161.7	4	579	17/28/28/28	442.5	814.10
97	119.0	119.0	119.0	181.3	4	537	22/22/22/34	392.2	736.27
98	119.0	119.0	119.0	199.8	4	555	21/21/21/36	413.3	767.54
99	119.0	119.0	119.0	203.1	4	558	21/21/21/36	414.8	769.64
100	119.0	119.0	119.0	229.9	4	585	20/20/20/39	411.8	768.95
101	119.0	119.0	135.1	181.3	4	552	22/22/24/33	387.7	718.53
102	119.0	119.0	135.1	199.8	4	571	21/21/24/35	405.5	760.66
103	119.0	119.0	135.1	203.1	4	574	21/21/23/35	407.9	764.44
104	119.0	119.0	151.2	151.2	4	539	22/22/28/28	411.6	765.70
105	119.0	119.0	151.2	161.7	4	549	22/22/27/29	402.3	754.34
106	119.0	119.0	151.2	181.3	4	568	21/21/26/32	394.8	745.03
107	119.0	119.0	161.7	161.7	4	559	21/21/29/29	402.5	755.48
108	119.0	119.0	161.7	181.3	4	578	21/21/28/31	392.9	743.90
109	119.0	135.1	135.1	151.2	4	538	22/25/25/28	421.5	780.67
110	119.0	135.1	135.1	161.7	4	548	22/24/24/29	411.8	767.60
111	119.0	135.1	135.1	181.3	4	567	21/24/24/32	401.6	755.48
112	119.0	135.1	135.1	199.8	4	586	20/23/23/34	415.2	777.81
113	119.0	135.1	151.2	151.2	4	554	21/24/27/27	422.5	783.74
114	119.0	135.1	151.2	161.7	4	564	21/24/27/28	411.7	770.18
115	119.0	135.1	151.2	181.3	4	583	20/23/26/31	403.4	760.75
116	119.0	135.1	161.7	161.7	4	574	21/23/28/28	412.5	772.18
117	119.0	151.2	151.2	151.2	4	570	21/26/26/26	444.5	816.84
118	119.0	151.2	151.2	161.7	4	580	20/26/26/28	432.1	801.51
119	135.1	135.1	135.1	135.1	4	537	25/25/25/25	464.4	841.26
120	135.1	135.1	135.1	151.2	4	553	24/24/24/27	447.8	819.40
121	135.1	135.1	135.1	161.7	4	563	24/24/24/29	437.1	804.99
122	135.1	135.1	135.1	181.3	4	583	23/23/23/31	424.8	790.61
123	135.1	135.1	151.2	151.2	4	569	24/24/26/26	447.3	820.04
124	135.1	135.1	151.2	161.7	4	579	23/23/26/28	435.6	805.29
125	135.1	151.2	151.2	151.2	4	585	23/26/26/26	468.0	851.37

for the chiller plants with up to 4 units, and

Table A3. Main characteristics and performance data of the chiller plants relying on 5 units (obtained from Diaz Torres [33], Diaz et al [34] Diaz et al [35]. Reprinted/adapted with permission from Ref. [34]. 2021, Elsevier and Copyright Clearance Center. Reprinted/adapted with permission from Ref. [35]. 2022, Elsevier and Copyright Clearance Center.

Chiller Plant No.	Chiller Cooling Capacity at STD (kW)					Total Units	Total Cooling Capacity (kW)	Cooling Distribution among Chillers (%)	Energy Consumption (kWh/year)	LCC MM Cup
	1	2	3	4	5
126	98.2	98.2	98.2	98.2	151.2	5	541	18/18/18/18/28	436.8	825.18
127	98.2	98.2	98.2	98.2	161.7	5	551	18/18/18/18/29	435.7	825.45
128	98.2	98.2	98.2	98.2	181.3	5	571	17/17/17/17/32	437.5	830.07
129	98.2	98.2	98.2	119.0	135.1	5	546	18/18/18/22/25	410.2	788.54
130	98.2	98.2	98.2	119.0	151.2	5	562	17/17/17/21/27	411.3	793.40
131	98.2	98.2	98.2	119.0	161.7	5	573	17/17/17/21/28	408.6	791.19
132	98.2	98.2	98.2	135.1	135.1	5	561	17/17/17/24/24	421.6	806.30
133	98.2	98.2	98.2	135.1	151.2	5	578	17/17/17/23/26	418.9	805.36
134	98.2	98.2	119.0	119.0	119.0	5	552	18/18/22/22/22	410.5	787.51
135	98.2	98.2	119.0	119.0	135.1	5	567	17/17/21/21/24	402.6	781.18
136	98.2	98.2	119.0	119.0	151.2	5	583	17/17/20/20/26	400.6	781.26
137	98.2	98.2	119.0	135.1	135.1	5	583	17/17/20/23/23	405.8	788.54
138	98.2	119.0	119.0	119.0	119.0	5	573	17/21/21/21/21	410.5	791.43

for the chiller plants with up to 5 units, respectively. The collected information also shows the key features of each chiller plant architecture (e.g., total cooling capacity, number of units, and the cooling distribution among chillers) and constitutes the database of the current work.

2.2. Methodology

The correlation analysis is a statistical methodology, which aims to assess the relationship between individual differences (cases or subjects) regarding two or more random variables. In order to perform influence statistical analysis of one or several independent variables on the dependent variable, the conditions of parameter setting need to be verified. These are: (a) the study variable (dependent variable) needs to be measured on a scale, such as an interval, or ideally, a ratio. (b) the size of the sample to be analyzed needs to be greater than 30 values; (c) the data set of the dependent variable needs to have a normal distribution; finally (d) the existence of homoscedasticity between the study variable and the independent variables. Non-compliance with these assumptions infers the use of non-parametric tests for bivariate statistical analysis [36].

Normality analyses, also called normality tests, aim to analyze how much the distribution of the observed data differs from what would be expected if they came from a normal distribution with the same mean and standard deviation. The normal distribution, known as Gauss distribution, is defined by the following probability density function shown in Equation (1):

$$f\left(x\right)=\frac{1}{\sigma \sqrt{2\pi }}\exp \left(\frac{-1}{2}{\left(\frac{x-\mu }{\sigma }\right)}^2\right),\hspace{0.5em}\infty <x<\infty \hspace{0.5em}\left(\sigma >0\right)$$

(1)

Here, μ is the mean and σ is the standard deviation. If in Equation (1) the condition of μ = 0 and σ = 1 is fulfilled, then the standard normal distribution function is expressed in Equation (2):

$$f\left(x\right)=\frac{1}{\sigma \sqrt{2\pi }}{e}^{\frac{1}{2}{x}^2}$$

(2)

Different researchers implemented nearly 50 normality tests. The most widely available goodness-of-fit tests provide by statistic web packages are bias and kurtosis test [35], Shapiro–Wilk [37], Anderson–Darling [38,39], Kolmogorov–Smirnov [40,41], Pearson’s chi-square [42], Cramér–von Mises [43,44], Lilliefors [45], Jarque–Bera [46,47,48], D’Agostino–Pearson [49]. The sample size, nature of the data power of the test, and simplicity of performing define the test to be employed.

Different authors carried out comparison studies to determine the best method to determine the normality condition. Hernandez [50] compared through the test’s power, interpreted as the ability to identify a sample upcoming from a non-normal distribution accurately and expressed in terms of probability. According to the results obtained from 20 previous studies, the Shapiro–Wilk (SW) test is the most powerful test for determining normality, followed by the Anderson–Darling (AD) test. Similar results were achieved by Razali and Whal [51].

In case of the SW test, the procedure is based on a linear model between the ordered observations and the expected values of the ordered statistics of the standard normal distribution, and the AD test is how close the points are to the straight line estimated in a probability graphic. The statistic of the SW test and the SD test are shown in Equations (3) and (4), respectively.

$$W=\frac{{\left({\displaystyle \sum a_{i}y\left(i\right)}\right)}^2}{{\displaystyle \sum {\left(y_i-\overline{y}\right)}^2}}$$

(3)

$$A=-n-\frac{1}{n}{\displaystyle \sum \left(2i-1\right)}\left[\log \left(P_{\left(i\right)}+\log \left(1-P_{\left(n-i+1\right)}\right)\right)\right]$$

(4)

in which in Equation (4), a_i represents the best linear unbiased estimator for σ, and P_(i) are given by Equation (5).

$$P_{\left(i\right)}=\Phi \left(\frac{xi-\overline{x}}{8}\right)$$

(5)

Demir [52] concluded that the normality test is not affected by the sample size while the skewness and kurtosis coefficient were equal or close to zero; otherwise, as the sample has over 200 values, the results are affected, and instead histogram or critical values may be used.

Apart from the normality distribution, parametric tests assume data are homoscedasticity or equality of variances. The assumption of homoscedasticity can be seen in Equation (6)

$$H_0:{\sigma }_1^2={\sigma }_2^2=\cdots {\sigma }_k^2$$

(6)

Different numerical tests can test graphically and correct the homoscedasticity, such as Levene’s test [53], Bartlett’s test [54], Cochran’s test [55], and Brown–Forsythe test [56]. The failure of Equation (6) is called heteroscedasticity (see Equation (7)).

$$H_1:\exists 1\le i,l\le k:{\sigma }_i^2\ne {\sigma }_l^2$$

(7)

According to Vorapongsathorn [57], Cochran’s test is one of the most powerful tests, as its results are not affected by the nature of the independent variables, e.g., if one variable has an unequal sample size, it is non-normally distributed, and the variance is larger. Cochran’s test statistic is defined in Equation (8):

$$C=\frac{\max s_i^2}{{\displaystyle {\sum }_{i=1}^k{s}_i^2}}$$

(8)

The hypothesis H0 is rejected on significance level α, as Equation (9) complies the inequality:

$$C>C_{\alpha ,k,n-1}$$

(9)

in which critical value $C_{\alpha ,k,n-1}$ is in special statistical tables.

As the normality and homoscedasticity conditions are verified, the correlation analysis is carried out by using the Pearson correlation coefficient [58]. The coefficient is defined by Equation (10) [59]

$${\rho }_{XY}=\frac{\mathrm{cov}\left(x,y\right)}{{\sigma }_x{\sigma }_y}\hspace{0.5em}-1\le {\rho }_{XY}\le 1$$

(10)

in which if the value of $\rho$ is positive, the relationship between the variables is direct; otherwise, the relationship is inverse. If $\rho$ is equal to 0, the variables are independent. This coefficient can be expressed in terms of its statistic r_XY, as shown in Equation (11).

$$r_{XY}=\frac{{\displaystyle \sum _{i=1}^n\left(Xi-\overline{X}\right)\left(Yi-\overline{Y}\right)}}{\sqrt{\left[{\displaystyle \sum _{i=1}^n{\left(Xi-\overline{X}\right)}^2}\right]\left[{\displaystyle \sum _{i=1}^n{\left(Yi-\overline{Y}\right)}^2}\right]}}\hspace{0.5em}-1\le r_{XY}\le 1$$

(11)

Pearson’s correlation coefficient is an indicator of how strongly two variables are linked. According to Hair et al. [60], if the coefficient varies from ±0.00 to ±0.20, the correlation´s degree is slight (almost negligible). If the coefficient ranges between ±0.20 and ±0.40, a small but definitive relationship coexists. The moderate classifications are between ±0.41 and ±0.70. Values between ±0.71 to ±0.90 indicate a high correlation, and finally, the range ±0.91 to ±1.00 define a very strong relationship between dependent and independent variables.

One of the causes of the non-normality distribution could be the presence of heteroscedasticity. The heteroscedasticity can be corroborated by different tests, e.g., Park test [61], Glejser test [62], Goldfeld–Quandt test [63], Harrison–McCabe test [64], Breusch–Pagan–Godfrey test [65], White test [66], Koenker–Basset (KB) test [67]. Onifade and Olanrewaju [68] observed that for sample sizes below 50, the most powerful tests are the white and Harrison McCabe test; otherwise, Glejser and Park test are recommended to check heteroscedasticity. The Glejser test [62] suggests first obtaining the residuals (û_i) of the regression under the ordinary least squares (OLS) method and regressing (û_i) on the explanatory variable (X) that is supposed to be related to the heteroscedastic variance (${\sigma }_i^2$). After it is found not to be asymptotically valid under asymmetric disturbances, the function used for sample sizes larger than 50 is described in Equations (12)–(15):

$$\left|{\hat{u}}_i\right|={\beta }_1+{\beta }_2{X}_i+{\nu }_i$$

(12)

$$\left|{\hat{u}}_i\right|={\beta }_1+{\beta }_2\sqrt{X_i}+{\nu }_i$$

(13)

$$\left|{\hat{u}}_i\right|={\beta }_1+{\beta }_2\frac{1}{X_i}+{\nu }_i$$

(14)

$$\left|{\hat{u}}_i\right|={\beta }_1+{\beta }_2\frac{1}{\sqrt{X_i}}+{\nu }_i$$

(15)

in which β₁ and β₂ are the regression coefficients, (|û_i|) represents the residuals of the new regression and (υ_i) indicates the error term. Therefore, the Equations from (12)–(15) with the highest value of R² and the lowest value of standard error was selected to represent heteroscedasticity. Finally, a t-test needed to be performed on the selected equation, as ${\beta }_0=0$ and ${\beta }_1\ne 0$ suggested pure heteroscedasticity, whereas ${\beta }_0\ne 0$ and ${\beta }_1\ne 0$ was an indication of mixed heteroscedasticity. If the sample value of the statistic was high enough that the probability of rejecting the null hypothesis being true was less than 1%, the null hypothesis of homoscedasticity was rejected.

The heteroscedasticity can be corrected by mathematically transforming the dependent variable, such as square root, logarithmic, inverse function, and Box–Cox. These transformations can stabilize the variances and also define a trend [69]. However, there is a risk that the transformed variable loses its practical meaning and, in the retransformation of the variable, produces bias [70]. The other way is to use two statistically principal approaches yielding more proper inferences and thus resulting in much lower change in the correlation’s interpretation, i.e., the heteroscedastic consistent standard errors and the bootstrap. The first approach is known as White, Huber–White, or robust standard errors, respectively, and the sandwich estimators [66,71,72]. Essentially, they recognize the presence of heteroskedastic and offer an alternative method for estimating the variance in the sample regression coefficients. The bootstrap aims to compute critical values for the different test statistics, intending to improve upon the critical values derived from the asymptotic null distributions. Authors in [73,74,75,76,77,78] propose an alternative procedure known as the wild bootstrap.

The normality distribution prevails in the way of parametric or no-parametric analysis. If, with the correction of heteroscedasticity, the dependent variable Y rejects the hypothesis of normality, then non-parametric tests need to apply correlation analysis, and Spearman’s correlation coefficient is usually applied [79]. Here, the disadvantage is that these tests are less powerful than parametric tests, and, in this case, the association between the variables is determined. The Spearman’s rho coefficient (r_s) is given in Equation (16), and its calculation is exactly the same as Pearson’s but on ranks rather than absolute values. Its power can be similar or only slightly lower. These are the correlation analysis, and variables are measured on a scale that is at least ordinal.

$$r_s=1-\left[6{\displaystyle \sum \frac{d_i^2}{(n^3-n)}}\right]\hspace{0.5em}-1\le r_s\le 1$$

(16)

In Equation (16), d_i is the difference between ranks of Xi and Yi. Furthermore, n is the number of observations. Another rank coefficient, Kendall’s tau (τ) [80], is used as there are multiple independent variables. As a partial correlation coefficient, it is used as there are data on a third variable that may influence the association between two other variables of interest. It can be considered as the estimated correlation between these two variables with the same value as the third variable. Its conclusions are identical to Spearman’s correlation coefficient, as only two variables are involved. The mathematical expression of τ is presented in Equation (17):

$$\tau =\frac{(Sa-Sb)}{\left[\frac{n(n-1)}{2}\right]}\hspace{0.5em}-1\le \tau \le 1$$

(17)

in which Sa is the sum of higher ranks and Sb is the sum of lower ranks. Although non-parametric tests are used for data with a skewed distribution, a discrete or ranked scale, Spearman and Kendall’s rank correlation test does not make any assumptions about data distribution. The rule of thumb to analyze the results is similar to the Pearson coefficient proposed by Hair et al. [60].

3. Results and Discussion

The main characteristics of the design and performance variables employed for carrying out the statistical analysis to define the influence of the proposed design variable on performing a chiller plant and summarized in Table A1, Table A2 and Table A3 are shown in

Table 1. Main characteristics of the design and performance variables in a chiller plant.

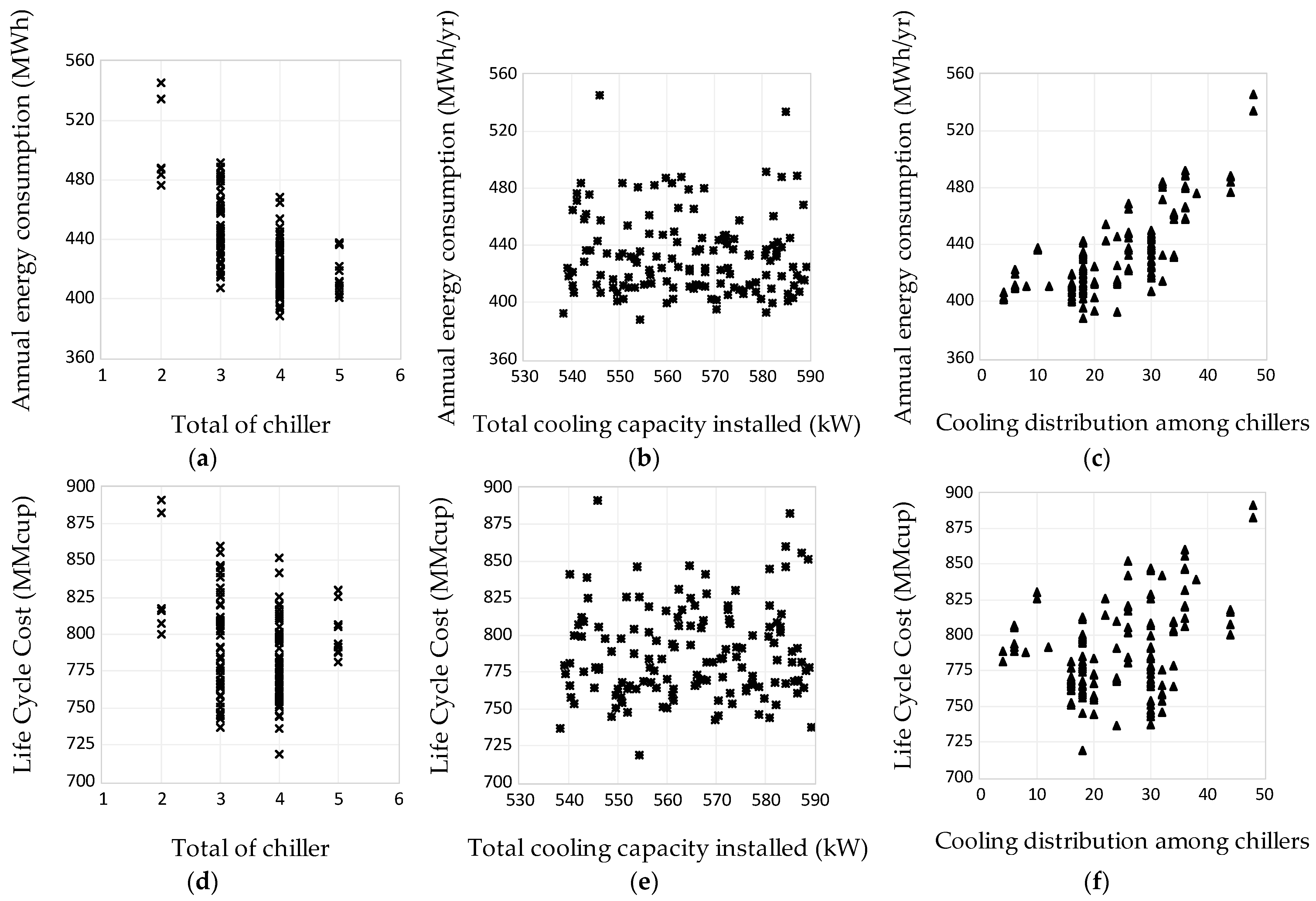
Variable	Symbol	Classification	Characteristic	Total of Values	Unit
Total of chiller	Nch	Independent	Numerical	138	-
Total cooling capacity installed	Qch	Independent	Numerical	138	kW
Cooling distribution among chillers	Cdch	Independent	Ordinal	138	-
Annual energy consumption	AEC	Dependent	Numerical	138	MWh/year
Life Cycle Cost	LCC	Dependent	Numerical	138	MMCup *

* Cup: currency of the country’s study case.

.

The cooling distribution among the chiller was ordinal, and thus it needed to be transformed into a numerical variable. As for the numerical transformation of the cooling distribution among the chillers, the technical criteria described by Equations (18)–(38) were used. The coefficient of variation (CV) was used mainly for defining the arrangements with a similar structure to the symmetrical chiller plant. In this study case, the authors considered that, despite the different chiller capacities, the cooling capacity values were similar, and thus it was possible to gather them in the same group. The range of the classification was based on the statement that each configuration was unique and the number of units had a strong influence, further enriching the technical criterion of whether a configuration was symmetrical or asymmetrical. The procedures of the mathematical transformation are shown in

Table 2. Mathematical transformation criteria for the ordinal variable cooling distribution among chillers.

Total Units	Arrangement Type	Mathematical Expression	Constrains	Equation	Classification	Scale
2	Symmetrical	$c_1=c_2$	-	(18)	S1	48
	Similar	$c_1\approx c_2$	CV ≤ 7	(19)	S2	46
	Asymmetrical type1	$c_1\ne c_2$	CV ≤ 20	(20)	S3	44
	Asymmetrical type2	$c_1\ne c_2$	CV > 20	(21)	S4	42
3	Symmetrical	$c_1=c_2=c_3$	-	(22)	S1	38
	Similar	$c_1=c_2\approx c_3$ $c_1\approx c_2\approx c_3$	CV ≤ 15	(23)	S2	36
	Asymmetrical type1	$c_1=c_2\ne c_3$	$c_1<c_3$	(24)	S3	34
	Asymmetrical type2	$c_1=c_2\ne c_3$	$c_1>c_3$	(25)	S4	32
	Asymmetrical type3	$c_1\ne c_2\ne c_3$	CV ≥ 18	(26)	S5	30
4	Symmetrical (similar)	$c_1=c_2=c_3=c_4$ $c_1=c_2=c_3\approx c_4$$c_1\approx c_2\approx c_3\approx c_4$	CV ≤ 11	(27)	S1	26
	Asymmetrical type1	$c_1=c_2=c_3\ne c_4$	$c_1<c_4$	(28)	S2	24
	Asymmetrical type2	$c_1=c_2=c_3\ne c_4$	c1 > c4	(29)	S3	22
	Asymmetrical type3	$c_1=c_2\ne c_3=c_4$ $c_1=c_2\ne c_3\approx c_4$	-	(30)	S4	20
	Asymmetrical type4	$c_1=c_2\ne c_3\ne c_4$	-	(31)	S5	18
	Asymmetrical type5	$c_1\ne c_2\ne c_3\ne c_4$	CV > 13	(32)	S6	16
5	Symmetrical (similar)	$c_1=c_2=c_3=c_4=c_5$ $c_1=c_2=c_3=c_4\approx c_5$	CV ≤ 9	(33)	S1	12
	Asymmetrical type1	$c_1=c_2=c_3=c_4\ne c_5$	-	(34)	S2	10
	Asymmetrical type2	$c_1=c_2=c_3\ne c_4=c_5$	-	(35)	S3	8
	Asymmetrical type3	$c_1=c_2=c_3\ne c_4\ne c_5$	-	(36)	S4	6
	Asymmetrical type4	$c_1=c_2\ne c_3=c_4\ne c_5$	-	(37)	S5	4
	Asymmetrical type5	$c_1\ne c_2\ne c_3\ne c_4\ne c_5$	-	(38)	S6	2

.

The results of the numerical transformation of the ordinal variable, cooling distribution among chillers, and for the chiller plants are summarized in

Table 3. Numerical transformation of the ordinal variable, cooling distribution among chiller, for the chiller plant.

Chiller Plant No.	Classification	Scale	Chiller Plant No.	Classification	Scale	Chiller Plant No.	Classification	Scale
1	s4	44	47	s4	32	93	s5	18
2	s4	44	48	s2	36	94	s5	18
3	s4	44	49	s4	32	95	s5	18
4	s4	44	50	s1	38	96	s3	22
5	s1	48	51	s2	36	97	s2	24
6	s2	48	52	s2	36	98	s2	24
7	s3	34	53	s2	36	99	s2	24
8	s5	30	54	s2	36	100	s2	24
9	s5	30	55	s2	36	101	s5	18
10	s5	30	56	s2	24	102	s5	18
11	s5	30	57	s5	18	103	s5	18
12	s5	30	58	s5	18	104	s4	20
13	s5	30	59	s5	18	105	s5	18
14	s5	30	60	s5	18	106	s5	18
15	s4	32	61	s5	18	107	s4	20
16	s3	34	62	s5	18	108	s5	18
17	s5	30	63	s5	18	109	s1	26
18	s5	30	64	s5	18	110	s5	18
19	s5	30	65	s5	18	111	s5	18
20	s5	30	66	s5	18	112	s5	18
21	s5	30	67	s4	20	113	s1	26
22	s5	30	68	s5	18	114	s6	16
23	s5	30	69	s5	18	115	s6	16
24	s4	32	70	s5	18	116	s5	18
25	s3	34	71	s5	18	117	s1	26
26	s3	34	72	s6	16	118	s1	26
27	s5	30	73	s6	16	119	s1	26
28	s5	30	74	s6	16	120	s1	26
29	s5	30	75	s6	16	121	s1	26
30	s5	30	76	s6	16	122	s2	24
31	s5	30	77	s5	18	123	s1	26
32	s4	32	78	s5	18	124	s1	26
33	s5	30	79	s6	16	125	s1	26
34	s3	34	80	s6	16	126	s2	10
35	s5	30	81	s6	16	127	s2	10
36	s5	30	82	s5	18	128	s2	10
37	s5	30	83	s5	18	129	s4	6
38	s4	32	84	s5	18	130	s4	6
39	s2	36	85	s5	18	131	s4	6
40	s5	30	86	s6	16	132	s4	6
41	s4	32	87	s6	16	133	s4	6
42	s5	30	88	s6	16	134	s3	8
43	s3	34	89	s6	16	135	s5	4
44	s2	36	90	s5	18	136	s5	4
45	s2	36	91	s6	16	137	s5	4
46	s5	30	92	s3	22	138	s1	12

. In general, 32 symmetrical or similar chiller plant arrangements, 51 arrangements with at least an n + one unit symmetrical in their architecture, and 55 asymmetrical chiller plant arrangements were found. Once all the variables were of a numerical nature, the statistical inference of their relationships could be carried out.

The fulfilment of the parametricity condition of the energy consumption and LCC was analyzed. According to the information obtained in Table A1, Table A2 and Table A3 and

Table 4. Analysis of the normality condition of the dependent variable (p-value).

Statistical Test	AEc (Y)		LCC (Y)
	Statistic	p-Value	Statistic	p-Value
Shapiro–Wilk (SW)	0.904483	1.54798 × 10−12	0.957847	0.00242575
Anderson–Darling (A2)	3.49206	9.01993 × 10−9	1.52435	0.000603096

, the first two requirements were fulfilled. Next, the normality condition was evaluated, and in case of the null hypothesis was not rejected, then the homoscedasticity was analyzed.

In this research, the condition of normality of the dependent variables (i.e., annual energy consumption and LCC) described in Equation (2) was verified in order to define the correlation test to be used. The hypotheses to be tested were:

-

if p-value > α (0.05) Accept H0 = accept that the data were from a normal distribution;

-

if p-value < α (0.05) Accept H1 = reject that the data were from a normal distribution.

Through the STATGRAPFICS-18 platform [81], the Shapiro–Wilk normality test (Equation (3)) and Anderson–Darling test (Equation (4)) were both determined in order to improve the inference study. The results are shown in Table 4.

As can be seen in the results for the dependent variables analyzed, the p-value was lower than that established in the hypothesis test (p ≥ 0.05), and they came from a normal distribution with 95% confidence that could be rejected.

In order to determine heteroscedasticity, the graphical method was first used. Therefore, the regression analysis between the dependent (Y) and independent (X) variables using the OLS method was carried out with the assumption of homoscedasticity. Then the analysis of the regression residuals (û_i) and the independent variable (Ŷi) was performed to assess if they exhibited any systematic pattern. The results of this statistical pre-test are shown in

Table 5. Results of the statistical Pre-test: regression analysis between variable assuming homoscedasticity.

Equation	Bivariate Relationship (Yi = mXi + n)	Coefficients (m; n)	Standard Error (m; n)	t-Statistic (m; n)	Prob. (m; n)	R-Squared
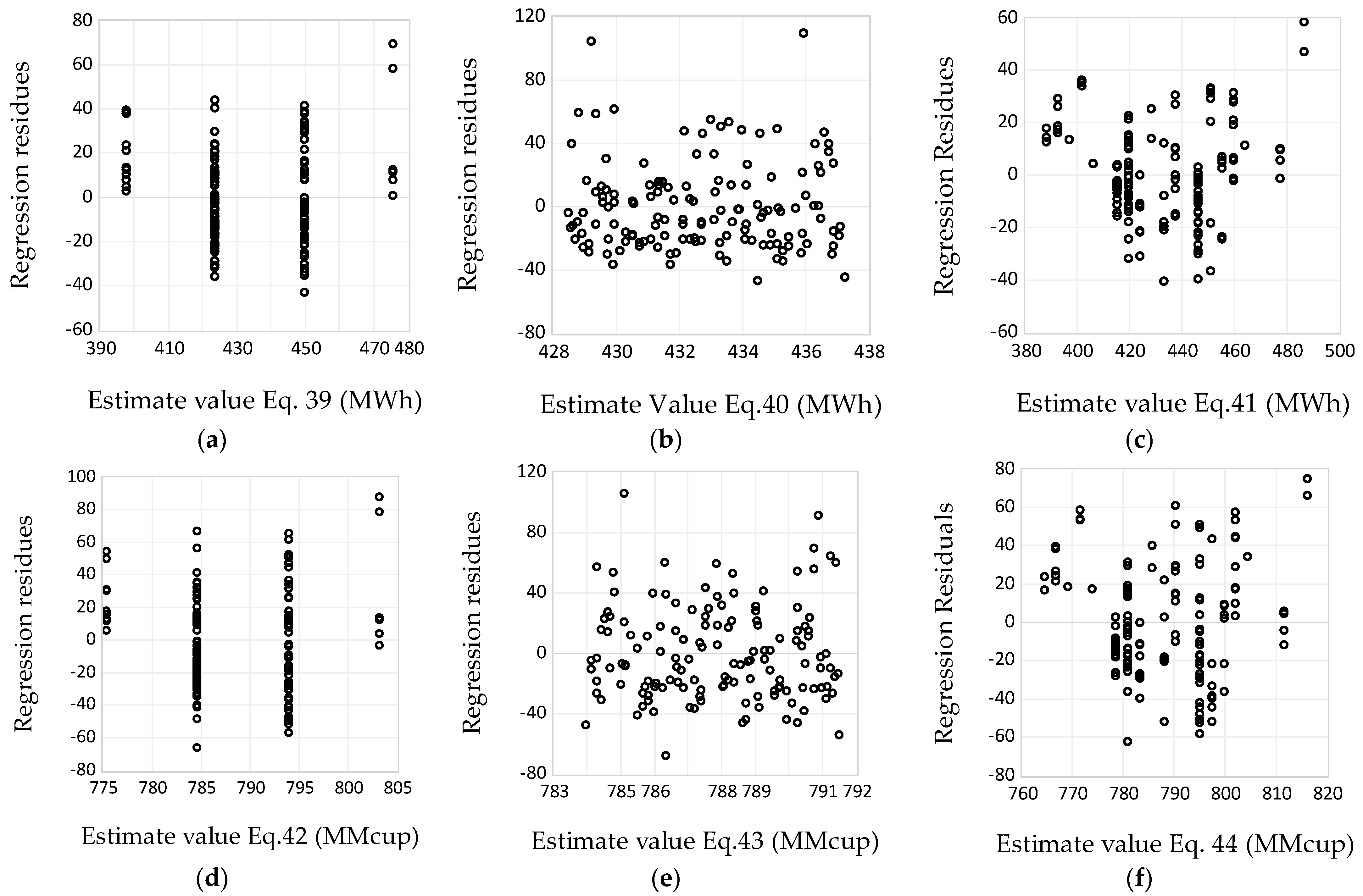
(39)	(AEc) vs. (Nch)	(−25.86455; 527.1655)	(2.56915; 9.5579)	(−10.06736; 55.15443)	(0.0000; 0.0000)	0.427011
(40)	(AEc) vs. (Qch)	(−0.171896; 529.7965)	(0.162240; 91.67009)	(−1.059517; 5.779382)	(0.2912; 0.0000)	0.008187
(41)	(AEc) vs. (Cdch)	(2.238676; 379.1052)	(0.168833; 4.343118)	(13.25968; 87.28871)	(0.0000; 0.0000)	0.563850
(42)	(LCC) vs. (Nch)	(−9.305803; 821.8668)	(3.678271; 13.68425)	(−2.529939; 60.05934)	(0.0125; 0.0000)	0.044948
(43)	(LCC) vs. (Qch)	(0.147560; 704.5334)	(0.180214; 101.8261)	(0.818803; 6.918990)	(0.4143; 0.0000)	0.0.04906
(44)	(LCC) vs. (Cdch)	(1.177679; 759.6843)	(0.264905; 6.814493)	(4.445666; 111.4807)	(0.0000; 0.0000)	0.126884

.

Figure 1 plots (û_i) vs. (Ŷi) using the regression line for each bivariate relationship shown in Table 5 to determine whether the estimated mean value of (Ŷi) is systematically related to the (û_i).

In Figure 1b,e, it can be seen that there was no systematic pattern between the two variables, suggesting that there could be no heteroscedasticity in the data. However, Figure 1a,c,d,f shows defined patterns, showing a quadratic relationship between (û_i) vs. (Ŷi).

The Glejser test was then applied to corroborate these results. The comparison to be analyzed is:

-

Heteroskedasticity Test

-

Hypothesis:

-

If p-value > α (0.05) Accept H0 = Homoscedastic

-

If p-value < α (0.05) Accept H1 = Heteroscedastic

The Glejser test calculates an auxiliary regression of the estimation error (û_i) in absolute value. Using the E-view statistical package [82], it was determined that the function with the highest R² value was the function described in Equation (12). Furthermore, the heteroscedasticity of the models described in Equations (39)–(44) was checked. The results are showed in

Table 6. Results of the Heteroskedasticity Test (Glejser test).

Bivariate Relationship	Equations	p-Value	Heteroscedasticity	Mathematical Model	R-Squared
(AEC) vs. (Nch)	(39)	0.0240	Yes	$\left|{\hat{u}}_i\right|=29.4254018319-3.278402(N_{ch})$	0.036910
(AEC) vs. (Qch)	(40)	0.4138	No	$\left|{\hat{u}}_i\right|=68.87957-0.083524(Q_{ch})$	0.004916
(AEC) vs. (Cdch)	(41)	0.1418	No	$\left|{\hat{u}}_i\right|=11.29616-0.148112(C{d}_{ch})$	0.015805
(LCC) vs. (Nch)	(42)	0.0189	Yes	$\left|{\hat{u}}_i\right|=42.76556-4.850004(N_{ch})$	0.039849
(LCC) vs. (Qch)	(43)	0.6400	No	$\left|{\hat{u}}_i\right|=-2.408414+0.04860(Q_{ch})$	0.001585
(LCC) vs. (Cdch)	(44)	0.0518	No	$\left|{\hat{u}}_i\right|=16.86090+0.292584(C{d}_{ch})$	0.027534

.

The residuals of the regression in Equations (40) and (41) and Equations (43) and (44) did not have a linear dependence on the dependent variable analyzed, so it could be defined with 95% confidence that they did not have problems of heteroscedasticity. However, the models expressed in Equations (39) and (42) could be defined to be heteroskedastic. Next, the Huber–White–Hinkley test [83] of consistent standard errors and covariance was applied to these equations, including Equation (44), since the p-value had a value close to that established in the hypothesis test, to correct for heteroscedasticity and obtain new values for the estimators.

Table 7. Results of the regression analysis between variables with the heteroscedasticity fixed.

Equation	Bivariate Relationship (Yi = mXi + n)	Coefficients (m; n)	Standard Error (m; n)	t-Statistic (m; n)	Prob. (m; n)	R-Squared
(39) *	(AEc) vs. (Nch)	(−25.86455; 527.1655)	(3.210059; 12.35129)	(−8.057346; 42.68102)	(0.0000; 0.0000)	0.427011
(42) *	(LCC) vs. (Nch)	(−9.305803; 821.8668)	(4.344333; 16.79198)	(−2.142055; 48.94401)	(0.0340; 0.0000)	0.044948
(44) *	(LCC) vs. (Cdch)	(1.177679; 759.6843)	(0.313664; 7.307557)	(3.754583; 103.9587)	(0.0030; 0.0000)	0.126884

* Equations with the new estimators values due heteroscedasticity fixed.

shows the new equation results.

As can be seen from the results in Table 7, the coefficients that adjust Equations (39), (42), and (44) were the same as the original equation generated by the ordinary least squares method (Table 5). However, the standard errors and the t-statistic were different, concluding that in these models, these metrics belong to a matrix that was consistent and converged to the true population value as the value of Xi was increased. Under these specifications, one can now proceed to re-run the normality test on the estimated values of Ŷi. 

Table 8. Analysis of the normality condition of the estimate value (Ŷi) of the dependent variable (p-value).

	Statistic	p-Value	Statistic	p-Value	Statistic	p-Value
	AEc (Ŷi) Equation (39) *		AEc (Ŷi) Equation (40)		AEc (Ŷi) Equation (41)
(SW)	0.831547	2.78972 × 10−11	0.954328	0.000153493	0.960179	0.000483601
(A2)	11.5387	<0.01	1.49567	≥0.10	2.44905	≥0.10
	LCC (Ŷi) Equation (42) *		LCC (Ŷi) Equation (43)		LCC (Ŷi) Equation (44) *
(SW)	0.831547	2.78972 × 10−11	0.954328	0.0001534	0.960179	0.000483
(A2)	11.5387	<0.01	1.49567	≥0.10	2.44905	<0.10

* Equations with the new estimators values due heteroscedasticity fixed.

describes the results of this inference.

It can be seen from the results that, despite applying corrective measures to the dependent variables AEC and LCC, it was again corroborated that they did not have a normal distribution. As for the A2 tests performed on Equations (40), (41), and (43), the p-value of the hypothesis test did not reject that this came from a normal distribution. However, although the SW test was more powerful, having two different conclusions, it was applied to the Chi-square distribution test [84], obtaining a p-value of 0.00074255, 0.0, and 0.00074255 by using Equations (40), (41), and (43), respectively. These results define the research with the use of non-parametric tests to establish the level of association between the variables proposed in Table 5.

Due to the design variables, the correlation analysis among variables was tested using Spearman’s Rho index for the total number of chillers and the total installed cooling capacity. As for the cooling distribution among chillers, Kendall’s Tau coefficient was applied. For the analysis, the IBM SPSS software for Windows, version 20.0 [85], was used. The results are shown in

Table 9. Results of the statistical significance test.

Operational Variables (Dependant)		Design Variables (Independent)
		Cooling Distribution among Chillers	Total Chillers	Total Installed Cooling Capacity
Energy consumption	rs	-	−0.625 **	−0.086
	Sig. (bilateral)	-	0.000	0.314
	τ	0.559 **	-	-
	Sig. (bilateral)	0.000	-	-
LCC	rs	-	−0.135	0.063
	Sig. (bilateral)	-	0.113	0.463
	τ	0.289 **	-	-
	Sig. (bilateral)	0.001	-	-

** Correlation at level 0.010 (2-tailed) is significant.

.

The results in Table 9 show that the design variables’ cooling distribution and the total chiller and chiller energy consumption featured 99% bilateral significance. Regarding the LCC, the correlation coefficient (τ) was found to decrease in the cooling distribution among the chiller, although it was still significant. This result was because of the increase in maintenance costs as a function of the symmetry of the cooling capacity arrangement and the decrease in energy consumption as a function of the symmetry of the arrangement. In the number case of chiller and LCC, no statistical association was observed. The number of units installed is probably because the trend of decreasing operating costs was counterbalanced by increasing investment costs. This factor needs to be considered in making the best decision about the optimal total of units. This factor needs to be taken into account to make the best decision about the optimal total of units. Finally, the results of both statistical tests showed that there was no statistical correlation between the total installed capacity within the FS range established in the study and the operating variables of the plant.

Figure 2a allows us to corroborate the results shown in Table 9. The outcomes presented highlighted that the energy consumption decreases with the rise in installed chillers. However, this relation was not found to be categorical, unlike what was claimed by Cheng et al. [12] and Chen et al. [19]. Figure 2a shows a quadratic relationship between (AEC) vs. (N_ch). In the present case study, some chiller plant configurations with four units achieved better performance than a five-unit chiller plant. Regarding the influence of (N_ch) on the (LCC), Figure 2d reveals that these quadratic relationships were more evident, and the trend of increase in the number of installed chillers caused an increase in LCC. Therefore, it could be seen that an optimal configuration of three to four chillers could be found.

Figure 2b,e and results of the Table 9 show that there is no relation between energy consumption and LCC with the total installed cooling capacity in the selected range. This result differs from what was stated by many authors, such as Wang et al. [8], Li et al. [9], and Cheng et al. [12], among others [13,15,20,86], who affirmed that the malfunctioning of the plants was because of their over-sizing.

Finally, Figure 2c,f reveals that the cooling distribution among chillers had a similar influence on performing a chiller plant to that of the total installed units, and the asymmetrical arrangement was found to achieve better results than the symmetrical configuration. The graph shows that the statistical relationship of the variables AEC vs. Cd_ch and LCC vs. Cd_ch tends to be exponential. This phenomenon was also influenced by the increase in the number of chillers, leading to the asymmetrical arrangement being better. This conclusion was not categorical either, as the chiller plant relies on two units and the symmetrical arrangement offered better performance than that with the asymmetrical arrangement. Therefore, the engineers need to analyze the arrangement according to the number of chillers to be installed.

4. Conclusions

This work presents the analysis of the statistical relationship between the energy performance and life cycle costs of a chiller plant composed of multiple units with respect to important design variables, i.e., chiller plant configuration, total installed cooling capacity, the total number of chillers, and distribution of cooling capacity among the chillers. A case study involving a Cuban hotel has been selected. By means of the correlation analysis, it has been possible to define the design variables, which have the greatest influence on the operation of the plant. Therefore, the engineers have been provided with solid criteria to be certain about the variables needing to be modified to achieve significant energy and LCC savings in the HVAC system.

The correlation analysis between the annual energy consumption and LCC with respect to the design variables N_ch, CD, and GV has been carried out using non-parametric methods, as the dependent variables do not have a normal distribution. The results obtained have suggested that the total chiller design and the cooling capacity distribution among chillers have a significant influence on the energy consumption of the chiller plant with a Spearman’s Rho association index and Kendall Tau association index of −0.625 and 0.559, respectively. However, as the LCC has been considered, only the cooling capacity distribution among chillers has a substantial influence on the Kendall Tau association index (value of 0.289). Furthermore, the total installed cooling capacity has been found not to affect the performance of the chiller plant substantially. Likewise, it is proposed to define through non-parametric methods such as kernel and spline smoothing techniques, among others, the estimators that adjust the curves of the significant bivariate relationships

The results have been corroborated with the hypothesis test of the bilateral significance and revealed that the unofficial rules in the HVAC design do not always work properly. An overall analysis of multiple design options has been found to be the wisest methodology for the selected case study. In future work, it is planned to increase the sample size, as large samples tend to normalize the data.