Abstract
Due to the technological advancement in cellular networks, massive data traffic appends to the existing digital technologies. These emerging digital technologies face quality of service (QoS) challenges, particularly when it comes to maintaining the tradeoffs between customers and service providers. The cellular service providers are trying to meet the needs of end users by handling four substantially different types of data, i.e., Real Time, Video, Audio, and Text, with each type having its own requirements. To achieves an efficient QoS, different incentive-based algorithms were proposed. However, these schemes do not ensure a fair distribution of profit among the mobile network operator and access points. Furthermore, these schemes do not provide efficient QoS to the end user and cannot ensure a fair distribution of channels in crowning time. We propose an incentive-based scheme using game theory and two-stage Stackelberg approach for integrated data, offloading the decision-making process in a heterogeneous network. A single mobile base station and some integrated access points in a crowded metropolitan area are modeled in our proposed scheme. This station offers an economic incentive based on traffic types, and access points compete with each other to earn incentives for offload traffic. A mathematical game is derived to analyze the real-world scenario through simulation. The experimental method is applied to validate the numerical outcomes by comparing the results with other models.
1. Introduction
The world has seen an unprecedented data increase in the last two decades due to the realization of both wired and wireless networks. The formation of these small and medium-sized enterprises (SMEs) networks has been considered a significant contribution to the field of science and technology. These networks are being utilized worldwide, experienced by billions of users any time around the world, which frames the world as a global village for efficient decision-making processes. Wireless networking procured more attention from users due to mobility both in personal and corporate computing in different SMEs [1].
Wireless and mobile communication has affected networking enormously in the last two decades due to excessive usage of emerging digital technologies, such as smartphones, tablets, laptops, and other portable gadgets used for convenience in our daily lives. Sufficient wireless communication has been established, especially in terms of cellular networks. These cellular networks have become a fundamental part of our daily lives, and they have served us with a persistent supply of internet services for different SMEs [2].
The Cisco index mentioned in its statistics that there were 18 billion global mobile devices in 2017, out of which 58 percent were smartphones. It has been estimated that in 2022, the ratio of the emerging digital mobile devices will grow to 28.5 billion [3].
The diurnal activities of the emerging digital technology have been influenced by the usage of the latest smart devices utilizing the fastest 4/5G LTE networks. Due to an exponential increase in the emerging digital technology in mobile data traffic, the management of data overload has grown into a challenge for the mobile network operators (MNOs) in these SMEs. Smart devices, social networking, live streaming, and sharing of audio and videos have made an abnormal contribution to the flow of network traffic [4]. According to statistics of the Cisco index, sevenfold global mobile data traffic can be observed from 2017 to 2022, which is twofold the fixed IP traffic for the mentioned period [5].
An exceptional solution is required to address these issues of massive traffic, especially mobile data traffic, which has worsened the smooth provision of data services to the end users of different SMEs. To manage network traffic, mobile network operators (MNOs) may consider scalability, optimization, or data offloading as possible solutions. However, the former two approaches are expensive, may cause an extra burden, and decrease profit, while the third one is adopted by the MNOs all over the world to address the issue of mobile data offloading [6]. Mobile data offloading (MDO) can be achieved through Wi-Fi, femtocells, IP flow mobility, etc. However, due to the easy deployment of Wi-Fi hotspots and the availability of Wi-Fi interface in smartphones, mobile data offloading through Wi-Fi is considered as one of the realistic solutions to the current issue [7].
Statistics show that sixty percent (60%) of global mobile data traffic was offloaded through Wi-Fi up to 2016, and a 63 percent increase was expected in this offloaded traffic up to 2021. Research works revealed that customer experience measured in terms of high data rates and improved quality of service (QoS) is enhanced by mobile data offloading through Wi-Fi [8]. The QoS is the main expectation of a customer from an MNO to maintain the efficient operation of the network [9].
Different existing techniques, including artificial intelligence (AI) techniques, on mobile data offloading are proposed. For example, game-based solutions are used for network resources sharing in device to device communication. To find the optimal solution, the Nash bargaining solution has been used [10]. In Ref [11], the author proposed an optimal pricing method between a service provider and service request based on the Stackelberg approach. Weak aspects of the related literature demonstrate the drawbacks of these approaches, which are related to the need to (i) ensure a fair distribution of profit among the MNO and APs; (ii) provide improved quality of service (QoS) to the end user; (iii) ensure a fair distribution of channels in peak time and off-peak time to eliminate congestion; (iv) obtain maximum throughput by utilizing an optimal number of APs.
To handle these problems, we propose a scheme that is different from these techniques by examining mobile data offloading through Wi-Fi and focusing on designing a fair economic incentive mechanism based on AI techniques to be applied by the MNO to obtain its benefit, as well as to benefit its partner APs. We present an incentive-based scheme with three different traffic types that are considered, including Video, Audio, and Text data. Each traffic type has a different scheme of incentives. When using them, the APs are required to maximize their profit, while, on the other hand, the MNO will obtain the benefit of maximum data to offload in a congested situation, especially during peak times. In off-peak times, the MNO may utilize its resources to maximize its payoff when data offloading is not required due to congestion. The main novelties and contributions of our work are as follows:
- We consider an MNO and multiple APs to model the scenario, and an essential economic incentive mechanism between the MBS and APs for mobile data offloading decision making. Among the different data offloading AI techniques, such as fuzzy logic, neural networks, game theory, etc., we use the game theory based on the Stackelberg approach. The type of game theory used is non-cooperative game theory.
- The two-stage Stackelberg game determines the incentives on a traffic-type basis, which will be awarded to the APs, and the APs will compete with each other by offloading more data to maximize their profit. We consider a single mobile base station (MBS) and multiple access points (APs) in a metropolitan environment to model for optimum results. Two players are involved in the game: one is a leader; that is, MBS, while the other is a follower; that is, APs. The leader offers incentives, while the follower competes for these incentives and offloads more and more data. Our model also optimizes strategies for both players.
- The mathematical game set develops to apply various analytical and experimental procedures to assess the possible outcomes. It further shows that the proposed game achieves the optimal incentives distribution for optimum offloading, attaining a maximum offloading ratio. Peak-time and off-peak-time usage of the channels, the throughput of existing cellular networks, and the designed heterogeneous networks were also studied. The comparisons with other models show the maximum profit achieved by the players, improved throughput, and achievement of a total unique equilibrium.
- The experimental performance is evaluated in MATLAB concerning various QoS parameters and compared with the existing techniques.
This paper addresses how to enhance the QoS in 5G and 6G networks. To achieve high QoS, we use the non-cooperative game algorithm. The non-cooperative game Nash equilibrium proved the maximum net profit for the mobile network operator and the enhancement of QoS for mobile users.
In this manuscript, we study the issue of integrated mobile data offloading (IMDO) via Wi-Fi. Unambiguously, we consider an offloading scenario where multiple mobile users use a primary channel, such as 5/6G networks, to upload and download various types of applications during peak time and off-peak time. When the primary channel faces a congestion issue due to high data traffic, then the mobile network operator transfers the traffic from the primary channel to the secondary channel (Wi-Fi) for offloading. In this scenario, we study the issue of integrated mobile data offloading (IMDO) via Wi-Fi in terms of maintaining the QoS services on the mobile users’ level and maximum revenue on the MNO level. To handle this issue of integrated mobile data offloading (IMDO) via Wi-Fi, we model and analyze the integrated mobile data offloading (IMDO) via Wi-Fi problem by using the non-cooperative game theory model. The proposed game model offers an incentive based on the traffic types, and access points use this incentive to offload the traffic. Additionally, a theoretical investigation establishes the existence of the Nash equilibrium.
The contribution of the model in the field of data offloading is its achievement of a QoS approach to the flow of the network, making traffic flow congestion free by maximizing offloading through a game-theory-based approach. Various results of the proposed model superseded its predecessors by showing the overall best results in this regard. The proposed model provides an efficient way to curb traffic congestion and minimize response delay for a better experience for the end user, and thus provides a state-of-the-art solution for such problems.
2. Related Works
Recently, mobile data offloading has gained great attention regarding proper management of this huge amount of traffic. MDO can be categorized into three technologies, such as small cell, Wi-Fi, and opportunistic communication [12]. In [10], the author takes the issue of degrading QoS due to traffic congestion and no fear mechanism for load balancing. The author designed a game-based algorithm using the NBS scheme. The simulation result shows that the proposed game achieves a high offloading ratio, improves throughput, and shows high fairness in the network compared to other existing techniques.
In [11], the author considers the mobility issue in the offloading scheme. The vehicular ad hoc networks method for offloading was proposed as a solution with which to overcome the overload problem. The author designed an algorithm based on the Stackelberg game. The experimental results show that the proposed game effectively reduced the downloading time with high throughput and reduced delay.
In [13], the author takes the issue of QoS parameter energy efficiency in task offloading. To solve the issue, the author designed a scheme based on Lagrangian Suboptimal Convergent Computation Offloading Algorithm (LSCCOA), which works in cooperative mode. The analytical and experiential results show that the proposed algorithm achieves high QoS performance in terms of reduced delay, high throughput, and better energy efficiency.
In [14], the author studies the 5G architecture for communication service performance and found that traffic delay is the key issue for a requirement of 5G. The author considers game theory as an optimal solution for this issue and developed a game based on the auction model. The utilization of Wi-Fi and cellular network resource simultaneously due to huge traffic is a big issue for MNO, as discussed in [15]. To manage proper utilization, the author designed a scheme based on a bid-based Heterogeneous Resources Allocation (HRA) framework using the auction model. The analytical calculation and experimental results show that the proposed framework achieves maximum profit compared to the existing framework. The reader may be referred to a detailed study of action theory for a computer network in [16].
The resource limitation in a wireless mobile network is a key issue. Mobile data offloading is a novel technique used to overcome this issue. The author designed a distributed optimization-based algorithm that uses the concept of a modified alternating direction method of multipliers (ADMM) algorithm. The experimental result shows high utility achievements [17]. Mobile data offloading is an efficient technology used to alleviate the overload problem in the cellular network. The co-channel interference is a big issue in this process, as discussed in [18].
To allocate resources in an optimal way, the author designed an algorithm based on uplink traffic offloading through joint optimization. The numerical and experimental results show that the proposed scheme reduced computational time up to 90% compared to the existing scheme. The reader may refer to slides game theory for resource allocation [19]. To provide better QoS in the 5G network, unlicensed spectrum sharing between users is a key issue in the 5G network discussed in [20].
To fairly manage the unlicensed spectrum management, the author proposed a scheme that is the combination of a virtual coalition formation game (VCFG) and Q-learning algorithms. The experimental results show good fairness management for Wi-Fi. The MNO faces a great challenge of overload due to huge traffic and media-hungry applications, but the mobility issue in the vehicular ad hoc network wireless channel is a great challenge for MNO, as discussed in [21]. To address this issue, the author developed an algorithm based on the Q learning, reinforcement, and Intelligent Access Network Discovery and Selection Function (I-ANDSF). The simulation results show that the proposed algorithm achieves high QoS performance and optimal network selection.
In [22], the spectral efficiency issue between D2D users and cellular users is discussed. The author proposed an algorithm called dynamic Resource Block (RB) using a repeated game concept. The evolution performance showed remarkable improvement compared to other techniques. This paper presents the security and data tracking in vehicle communication. The issue is solved through the framework Directed Acyclic Graph enabled IoV (DAGIoV) [23]. The reader may refer to a detailed study of cooperative and non-cooperative computational offloading in [24].
Mobile Data offloading uses many technologies for offloading such as Wi-Fi, small cell, and D2D. In [25], the author considers D2D technology for offloading, but interference management is an issue in this offloading, degrading the QoS performance of the users. The face issue is solved through a joint pricing framework based on the Stackelberg model. The experimental results show a win–win situation. A detailed study of game theory for the 5G network may be found in [26]. Offloading through Wi-Fi technology has gained more popularity due to the built-in capability of smartphones. In [27], the author discusses the issue of Wi-Fi offloading with uncertain contact durations. The issue is solved through online offloading based on a multi-armed bandit (MAB). The higher utility is the achievement of the proposed scheme.
The details of 5G requirements for communication are discussed in [28]. In [29], the author discusses the mobile data offloading overview for green wireless networks. The recent advancement and economy of MDO are discussed briefly, and finally, some open issues for discussion are outlined. Due to the rapid increase in traffic ratio, the existing cellular network requires novel network architecture, and the communication model is discussed in [30].
The author designed the bargaining-based solution for MNO and APs. The model achieves good economics and an optimal offloading ratio. Offloading through Wi-Fi and utility through the maximization problem is discussed in detail in [31]. To manage the economics ratio and optimal offloading, the ratio between cellular and Wi-Fi issue is discussed in [32]. Stackelberg’s theory is applied to achieve this, and the results show proper agreement and cooperation between them. For a detailed technical and business overview of mobile data offloading through various technologies, the reader may refer to [33,34].
This study also discusses the details of offloading technology through Wi-Fi, and also future direction [35]. Offloading through Wi-Fi performance quantitative study is conducted in [36]. The simulation result shows that 65% of traffic is offloaded through Wi-Fi, and it saves 55% of the battery power. The technical and economic issue of offloading through Wi-Fi is discussed in [37]. To address this issue, the author uses a famous model of game theory called the double auction mechanism. To ensure the efficiency of the market of offloading, the author uses the iterative double auction mechanism [38]. Comparative analysis of the single and multi-channel for MANETs is discussed in [39,40]. A mathematical model is designed for channel allotment, and the results show fair performance [41]. In this paper, a Stackelberg-based algorithm is designed for channel allocation to primary users and secondary users. The performance results show high data rates and low delay in high traffics [42], and efficient power management and budget allocation issues are resolved through the blotto game (SABG) in this paper [43]. In this paper, the authors review the various previous incentive-based algorithms with merit and demerits. In [44] the author takes the issue of fear of bandwidth utilization for IoT. The author proposes a smart architecture-based framework to utilize bandwidth [45]. Wireless data exchange is the key issue for today’s market. To handle this issue, the author proposed a software-defined network model based on game theory. The performance results show better performance compared to previous techniques. In [46], the author takes the issue of efficient computing resource offloading. The proposed algorithm based on the Stackelberg model calculates the fear resource price. The simulation results show certain superiority in allocation. Security and efficient data efficiency are the key issues in mobile edge computing. To address these issues, the author designed the non-cooperative game. The simulation results were more effective compared to existing algorithms [47].
In this paper [48], the author discusses the issue of offloading between cellular networks and Wi-Fi. To address the arising issue, the author designed an appropriate offloading algorithm based on exponential-learning-based minority game (MG) theory. The simulation results achieve better QoS for different traffic conditions.
The traffic burden issue on the cellular network is discussed in [49]. The author proposed an algorithm based on a Reverse Auction-based Incentive Mechanism, named RAIM. Simulation results show that it outperformed in different offloading rates.
Dynamic bandwidth allocation is a key issue in offloading. The author proposed a Satisfaction-based Dynamic Bandwidth Reallocation (SDBR) scheme that will consider the user ratio and appropriate revenue factor. Simulation results show fear bandwidth allocation performance [50].
The bulk of data transmission is the issue in offloading [51]. The author proposed a data transmission model based on the Manhattan mobility model. The simulation results show that the proposed scheme is better in load and transmission time from the rest of the schemes.
3. Problem Formulation and Proposed Model
Wireless cellular networks have worldwide acceptance due to their mobile nature, and currently, the most inhabited area is cellular communication. With the technological development, the data traffic over cellular networks has also horribly increased. To facilitate customer, and for the convenience of their data demands, MNOs deploy 4/5G LTE, which provides the fastest cellular communication.
The latest technology is being introduced by the network service providers, but the ever-growing traffic still decreases their performance by affecting throughput and response delay, in addition to other Quality of Service (QoS) parameters. Expensive technologies are being proved much less capable of fulfilling the requirements of end users. Increasing data demands of end users, and more bandwidth being utilized for multifarious activities over the networks, especially cellular networks, make the traffic flow very congested, and the response is dropping day by day. The proposed incentive-based scheme provides QoS-level service to end users.
In Figure 1, we deliberate a heaving resident zone where most of the consumers have smart devices, including smartphones and tablets, for different internet services. The provision of QoS downgraded due to excessive uses of data services, and a huge number of users were admitted. An extremely congested environment was established, especially during peak time, while the situation was different during off-peak time. Video streaming demand was high during peak time, which is a high data-consuming type of traffic. Taking these factors into consideration, and implanting offloading over integrated Wi-Fi as a key to the problem, a simulation of a heterogeneous network comprised of an MBS (Mobile Base Station) and some APs (access points) formed to practically experience the scenario.
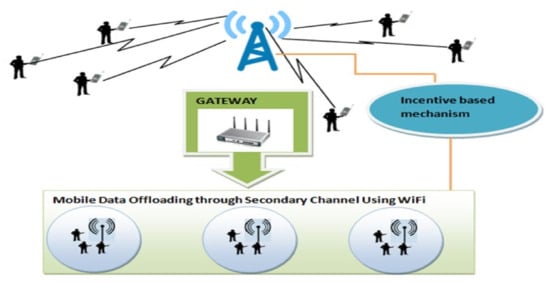
Figure 1.
IDO based on Game Model.
MBS has a larger area of coverage, while APs with a smaller area inside the range of MBS have non-overlapping areas of coverage with each other. In this heterogeneous network, we consider one MBS and multiple APs for this offloading process to model it in its true spirit [12].
where
Area covered by MBS =
Area covered by AP =
The Area of MBS with no offloading option
Physical areas of the above-covered regions can be determined by the following equations [2]:
The above figure shows the 5G and 6G communication model. All the users are connected and are performing uploading and downloading jobs. To avoid the congestion issue, we implement the IDO (Integrated Data Offloading)-based game model.
By putting these values in Equation (1), we obtain the area covered by MBS, which is not reachable by any AP. In Equation (1), represents the area of the MBS with no offloading situation; AMBS represents the area covered by MBS, represents the area covered by APs. Traffic types are differentiated by the following set of types [2]:
In Equation (4), TT represent traffic types, R represents real-time data, V is used for video, A for audio, and T represents text data, while the set of APs is given by [2]:
In Equation (5) [2], P represents a set of players and AP represents the access point from 1 to n. The Cartesian product of both the mentioned sets represents the distinct types of data for each AP:
In Equation (6) [1], shows that in an offloading situation, the access point offloads different types of traffic, such as real, video, audio, and text. The sum of elements of function f where any particular AP is taken in this relation will find the total traffic per AP, which is given as:
In Equation (7) [1], represents the total traffic per AP, where represents the AP involved in the offloading, and where T represents traffic types. The total traffic load on this heterogeneous network is given by:
In Equation (7), shows the total traffic load. Among this, traffic offloaded by a cellular network can be determined as:
In Equation (7), the variables represent traffic offloaded by a cellular network, where shows the downloading position and show the offloading position. Our model is based on a game-theoretic mechanism used to obtain maximum offloading through APs, but the offloading ratio in peak time and off-peak time will be managed through a traffic-wise offloading mechanism. For this, the instantaneous rate of AP is taken as its period which is represented by Ra, where the subscript differentiates AP. By using this instantaneous rate, we can represent the throughput of a given AP as
In Equation (10), show the instantaneous rate of AP, where represents throughput. The total amount of heterogonous network is the sum of both networks
In Equation (11), shows the throughput of MBS, and represents throughput of APs. In game theory, the building of real-world models and their interaction are observed through independent decision-making chosen from a set of strategies. It involves three factors named players, strategies, and payoff. It describes the action in response and decision taken by players along with variance in position and cooperation among players.
The payoff function is given by
The variables in Equation (12) [4] represent the different functions: show the payoff function, show the incentive offered, show the cost paid for the offered incentive. The payoff function is designed to measure the performance of the prototypical founded on spurs offered by MBS and the amount of traffic offloaded by APs. A non-cooperative game is one in which all AP strives with its enemy to maximize its profits. The game set has the subsequent essentials.
In Equation (13), k ∈ P, G represents the game, Pl represents players involved in-game that are MBS and APs and represents the set of strategies to be applied by players to obtain their maximum payoff, and Pk is the payoff or score function that represents the earning of the players.
In Equation (14) [5], show that Traffic load has a four-dimensional space where Q, R, S, T are subspaces; the ordered pair given below is used to represent a particular instance data load:
where
Nash Equilibrium
For the mentioned game set, there is Nash equilibrium if, for every aimed at wholly , somewhere, Pk (lk, l −k) remains the subsequent tender for the k participant, assuming that the additional troupes tender outcomes l − k [6].
Pk is concave in lk, while Sk is convex in given spaces.
The data are offloaded in a type-based mechanism considering well-defined priority; for instance, video data can stream on a priority basis compared to textual data.
Proving its wrap, we see that Utlm continues to l, so we take out the second-order derivative concerning km. The leading derivative is assumed in the next equation:
Equation (16) [7] plays the partial derivative rule to prove its concavity. The variable show partial derivative, show the incentive offered for Wi-Fi, show offloaded traffic, and show the cost paid for that offloading traffic.
For the second derivative with respect to lm, we have
In Equation (15) [8], the second-order derivative shows a negative multiplier, and it transpires that in each case, the result will be negative; therefore, it is proved that Pk is a concave function. We see that Um is concave in lm, while the Sk is convex; therefore, the Nash equilibrium exists in the game. The variables have already been discussed in Equation (15).
Unique Nash Equilibrium
The game has Nash Equilibrium, as it has been substantiated prior to vector lk. To validate its uniqueness, Best Response function R is required to be specified in terms of standardization, for which it needs to comprehend three conditions, which are positivity, monotonicity, and scalability. Here, R(lk) represents the Best Response function.
The optimal solution of the Best Response would be such that the total traffic downloaded by any AP is limited to the total capacity of the AP. In either situation, the former would be less satisfactory and unable to exceed the latter. Therefore, this constraint can be mathematized as shown below [9]:
In Equation (18), the variables are the cost paid for offloading, offers incentive for traffics, and represents the Best Response function. The above relation satisfies the positivity of the game. To maximize profit, the Best Response function would approach the instantaneous rate of AP, comprising the factor mentioned in Equation (15). The Best Response relation can be extended as:
Equation (19) shows [10], which shows a monotonical increase, while to show its scalability, we consider the following situation:
In Equations (20) and (21), the variables show the Best Response function for the cost paid for offloading. show the offloaded traffic. Combining Equations (17) and (18) and simplifying them, we obtain as change parameter, which is always greater than zero; therefore, the Best Response function is also scalable. By satisfying all three criteria, it is ensured that the Best Response function is a standard function and satisfies the Nash equation.
Total Unique Equilibrium
Total unique equilibrium in the traffic type set of the game can be estimated as , where in [10]
where is the Best Response value for in cases when is subject to the satisfaction of the conditions given in Equations (18) and (19) together, and exceeding either side will incline to limits given. This achieves the total unique equilibrium of the game.
The payoff for the MBS can be determined as:
where k ∈ TT, δ is unit spectrum rendered congestion-free by utilizing APs for offloading, and β is an economic incentive for k type traffic. In this non-cooperative game, the MBS will maximize its utility by optimizing the β incentive to the maximum extent.
Substituting Equation (16), we obtain the maximum utility profit as follows:
Subject to .
The MBS utility function is subject to maximization; hence, it is convex in nature. To achieve equity justice offload in between APs, the logarithmic purpose will be effective. Interchangeably, the MBS utility can be computed as [11]:
Substituting Equation (16), we obtain.
By replacing Г and φ, we obtain:
The inference indicates that the MBS function of the app is concave. The total amount of economic benefit is obtained by relating the correct first-order status.
Taking the Lagrangian of the problem with respect λ as Lagrange Multiplier [12], the outcome is:
The mentioned equation has a maximized state subject to the λ ≥ 0 which is the dual function and can be resolved via sub-gradient retrieval of the Lagrange Multiplier, as follows:
Wherever κ(s) is a step-by-step size in repetition s. The step size is always positive of the form, [Y]+ = max{0, Y} [1]. Complete economic stimulus β∗ can be obtained using Karush–Kuhn–Tucker (KKT), given that the first-order derivative of the Lagrangian Function of with respect to β is zero. The complete economic benefit solution has been simplified as follows [13]:
Based on the above inferences, we designed an algorithm for our model, which is as follows:
Nash equilibrium is crucial because it enables to choose the optimum outcome in a circumstance by taking into account their own choices and those of other parties. Our game is a non-cooperative-based game using Nash equilibrium. Nash equilibrium proved analytically shows that the customer achieves high QoS in simulation results. In the simulation maximum, the net profit graph shows the maximum profit of the mobile operators.
All the equations are analyzed in two phases in first phase equation, which finds the Nash equilibrium for primary players and the second for secondary players. All the equations are used step by step to find Nash equilibrium for both parties.
All the variables that are used in the above mathematical model and Algorithm 1 are explained in tabular form in Table 1.

Table 1.
Variables and Their Explanation.
| Algorithm 1 For the IDO using Game Theory |
| Input: {MBS information, APs information, Economic incentives based on traffic types} Output: {maximum payoff, Maximum offloading} 1 Let the Network have N No of APs 2 MBS be the Macro cell for all APs 3 Let γ is Unit Power Cost for offloading of various traffics 4 Let β = {βR, βV, βA, βT} is the Offered Incentives by MBS to APs 5 Let λ be the Unit Spectrum 6 Initialize γ= {[1:1:20],1} //Definition and Initialization of variables 7 function MBS Role (β, λ) //Function show MBS Role, calculate incentive and other properties 8 Initialize Im and Im* //Two different states of an AP 9 Initialize Cost, fm, fm* //Most formulae have two fragments 10 For I = I to N 11 Cost= Cost + γ(I) End for //calculate total cost 12 fm = (N-1)/Cost //Calculate 1st fragment 13 For I= 1 to N 14 fm* = fm*+((1-(N-1)*γ(I)) End For //Cost Calculate 2nd fragment 15 Im = fm* 16 Im* = β*fm*fm* //Economic Incentive 17 η = η+η*fm*fm* //Progressive balance of offloaded traffic 18 Γ = fm*fm* //Calculate proportional fairness of offload MBS = λ*Im*–Power(β,2)*Im*fm End function //Maximum net profit gained 19 function OptimalIncentive(X, λ) //To find out optimal incentive 20 Initialize Im and Im* //Two different states of an AP 21 Initialize Cost,fm,fm* //Two fragments and cost initialization 22 For I = I to X 23 Cost = Cost+γ(I) End for //Calculate total cost Calculate 1st fragment 24 fm = (X−1)/Cost 25 For I = 1 to X 26 fm* = fm* + ((1-(X-1) * γ(I)) End for //Cost Calculate 2nd fragment 27 Im = fm* 28 Γ = fm * fm* 29 β = sqrt ((λ * X) / 2 * Γ //Incentive Calculation Im* = Power (λ, 2) * fm * Im/4 End function // Optimal economic incentive per traffic type 30 functions Cut Off Data (X, β) //This function is used only When MBS only need to check traffic offload status. 31 Initialize Im and Im* //Two different states of an AP 32 Initialize Cost, fm, fm* //Two fragments and cost Initialization 33 For I = I to X 34 Cost=Cost+γ(I) //Calculate total cost 35 fm =(X-1)/Cost End for //Calculate 1st fragment 36 For I = 1 to X fm* = fm* + ((1-(X-1) * γ(I)) End for //Cost Calculate 2nd fragment 37 Im = fm* 38 Im* = β * fm * fm* End function //Economic incentive |
The proposed non-cooperative game distributes incentives to the secondary players based on the traffic category on demand. It will improve the QoS to avoid the congestion issue through integrated data offloading based on Stackelberg’s theory. We have applied a non-cooperative game theory model called the Stackelberg model, which uses integrated data offloading to alleviate the congestion issue of mobile users. The intersection of the Best Response function from all players in the Stackelberg model proved Nash equilibrium.
Algorithm No.1 takes MBS information with predefined economic incentives and input and produces the output of maximum payoff and offloading to benefit the cellular network in an efficient way. Different symbols are used for various factors, i.e., unit spectrum, unit power cost, and incentives of the appropriate type. To simplify larger equations with repetitive parts, some temporary variables such as fm are introduced, and lm is used as the state of AP. Some calculations are performed, such as total cost, fragments, economic incentives, progressive balance, proportional fairness, etc.
Subsequently, net profit gain is calculated for decision-making by MBS. Two functions, optimal incentive and cut-off data, are used to estimate optimal incentives and traffic status, which are frequently used in different formats.
4. Performance Evaluation and Results Discussion
In this section, we evaluate the performance of the proposed algorithm IBS through MATLAB [11]. We conducted detailed parameters, which are given in Table 2.

Table 2.
Simulation Environment Parameters.
The simulation uses QoS parameters such as energy consumption, throughput, delay, congestion control, and peak time and off-peak time as the metrics of performance within wireless cellular networks. Energy consumption shows the consumption of energy with offloading and offloading levels. The delay shows the average amount of time that has to be taken when uploading to and downloading from the service to the provider. The congestion control shows the link overhead ratio. The peak time and off-peak time show the ratio of the user that uses a wireless cellular network with and without offloading. Table 3 shows the mathematical representation of the QoS parameters.

Table 3.
Simulation Parameters.
The proposed algorithm IBS is compared with existing algorithms such as IFPC [14] and IMDO [15].
Results and Discussion
The offload ratio corresponds to the rate of data offloaded per unit time. We take data in 10 MB size chunks and time rate in seconds. The first achievement of our model is maximized offload, which has a high effect on the rest of the factors shown in the figures. The graph given in Figure 2 shows that offloading starts when at least one AP is introduced, and it increases with the introduction of more APs. The proposed model achieved seven units, which denotes 70 MB/s data offload on 20 APs. This shows sufficient improvement compared to existing models, as shown in Figure 2 and Figure 3. The lines shown are differentiated based on the incentive scheme offered by the respective models. Our model performed comparatively well.
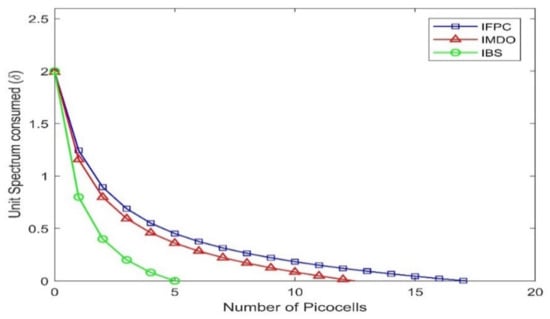
Figure 2.
Spectrum Use Ratio.
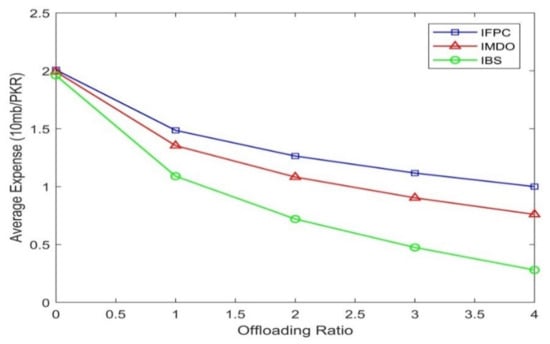
Figure 3.
Offload Ratio.
The QoS decreases due to overload traffic, which leads to network congestion. To handle the issue, our model presents a strategy with the outcome of maximum offloading and unique management of integrated Wi-Fi, due to which five Pico cells are proven sufficient to control the congestion on spectrum value 2, while IMDO and IFPC models do the same job on 12 and 17 Pico cells, respectively. This shows that our model refined the control of congestion compared to other models, as shown in Figure 3. The result of the proposed model is superior to the other models.
Our proposal of an incentive-based scheme based on game theory and a two-stage Stackelberg approach for integrated data offloading has made the decision-making process in a heterogeneous network. A single mobile base station and some integrated access points in a crowded metropolitan area are taken to model our proposed scheme. This station offers an economic incentive based on traffic types, and access points compete with each other to earn incentives for offload traffic. A mathematical game derives analysis of real-world scenarios through simulation.
The data transferred from source to destination in a fixed time interval refer to throughput. The amount of data is represented in bytes form, while time is measured in seconds, but throughput is their benchmark or often taken in percentage. The graph shows throughput performance in association with the spectrum used. The spectrum used is taken from zero to two, and its impact is examined on the throughput of the three models. Zero spectrums mean no throughput, and the addition of spectrum implies refinement of throughput. With congestion, reduction in throughput occurs, but as the models reduce congestion, it is added to the throughput. The proposed model accomplishes one hundred percent throughput, as shown in Figure 2 using spectrum value 2, while the other two models are rendered to attain 48% and 62%, comparatively.
We use the Stackelberg-based game model to derive optimal incentives based on the traffic types. The primary player will pay the optimal incentive to the secondary player, and the secondary player will perform optimal offloading based on the offered incentive. The throughput graph shows that we achieve high throughput in the offloading. The absolute result has been exhibited by the proposed scheme proposed shown in Figure 4.
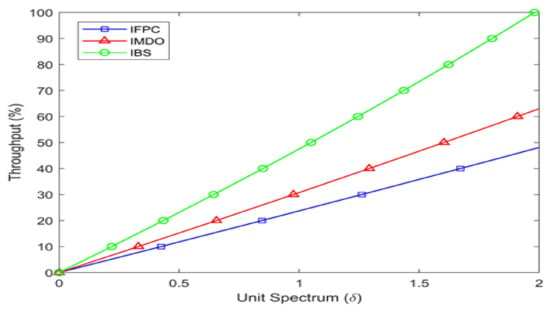
Figure 4.
Throughput Analysis.
The time taken for data to travel travel from host to client is referred to as response delay. In the graph, the delay is represented on the y-axis in milliseconds and with the spectrum used on the x-axis for the data in increasing order to test the response, but despite the effect of growing load on the spectrum, all three models reduced delay due to offloading and making the channel congestion free. IMDO performed the best overall in this result, but our model more rapidly gained its position as shown in Figure 5, which is evident from the end near 1.7, while IFPC approaches near 2.
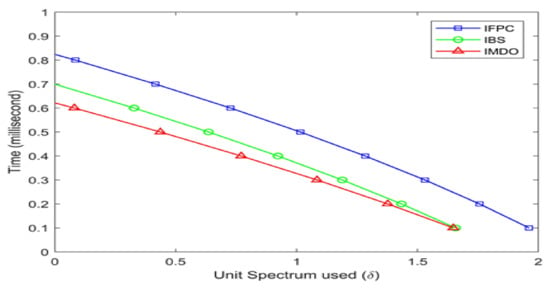
Figure 5.
Response Delay Analysis.
The proposed algorithm uses IDO to alleviate the congestion issue. It will migrate the traffic from the primary channel to the secondary channel based on the traffic category, so the chance of congestion is less, due to which the delay is decreased.
The growing load on the spectrum reduced delay due to offloading and making the channel congestion free. IMDO performed the best overall because it will use a non-cooperative-based game model that will distribute channels fairly to both users. The results of our model are fair, and are shown in Figure 5.
Energy consumption is considered an important factor in mobile devices concerning their QoS. The latest wireless communication technologies focus on improving their energy requirements. Energy consumption is taken in megabytes offload per watts concerning the increasing number of picocells. The IMDO model performed best, but with a slight difference; the proposed model showed its outcome. The proposed scheme is better, but it is not absolute due to the integrated architecture, where much sub-level management is required. The result is satisfactory compared with other schemes, as shown in Figure 6.
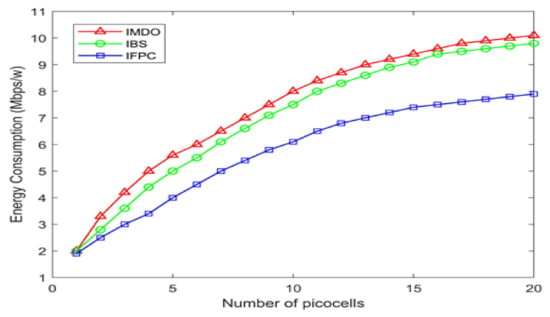
Figure 6.
Energy Consumption Analysis.
Economic feasibility for industrialized technologies is very important, which primarily depends on the cost factor. In this simulation, we tested the Average Expense on the y-axis concerning the offloading ratio on the x-axis. The result is constructed based on 10 MB per Pakistani Rupee as a unit of average expense for the MNO with a different offloading ratio up to four, as shown in Figure 7. The proposed scheme has shown a considerable decrease in expense per 10 MB per PKR and attains 0.4 PKR on four offload ratios, which are the achievements of the proposed model.
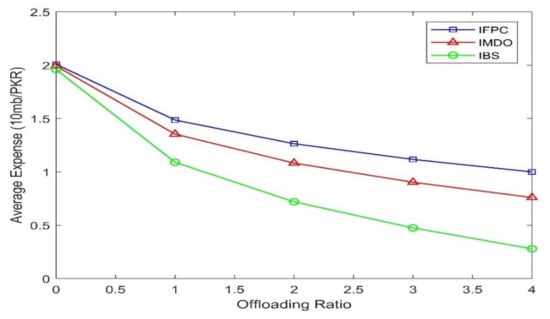
Figure 7.
Average Expense or Cost Factor.
This simulation is constructed to demonstrate the peak and off-peak time offload of the proposed scheme because it is also a considerable factor for MBS to save for itself when there is a much lesser load on the primary channel. The utilization of AP should be fairly controllable to maximize MBS earning, and APs need to be honestly consumed to provide QoS to end users. The performance of picocells in peak time in terms of offload ratio on the y-axis is far better than its performance in off-peak time, which shows better management of picocells, as shown in Figure 8.
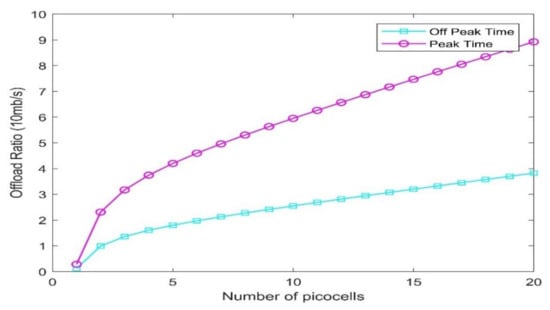
Figure 8.
Peak Time and Off-Peak Time Performance.
We consider a crowded urban environment for our model where excessive data required services are utilized; therefore, there is congestion in a cellular channel, and the APs are used to balance this load. For this, we take the same scenario to examine the load-balancing manner through APs. During peak time, the simulation shows that picocells are grabbing more load than the entire MBS. The graph shows that APs are offloading 12 MB/s, while MBS usage is 7.1 MB/s, which shows that the APs could easily lead the MBS in data management. This shows the utmost consumption of APs with the proposed scheme given in Figure 9.
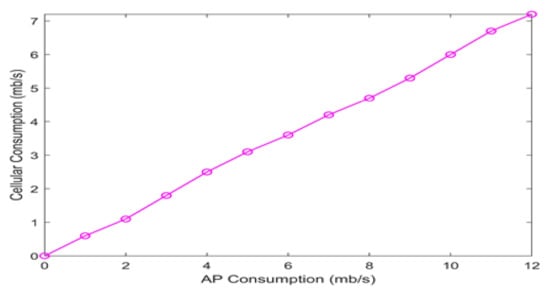
Figure 9.
Cellular vs. AP Consumption.
In this simulation, network throughput is checked with and without Wi-Fi offloading. The simulation shows less than 20% throughput result for spectrum up to two without Wi-Fi, while with Wi-Fi offloading, it establishes the throughput up to 100%. The graph in Figure 10 shows the deep impact of Wi-Fi offloading on the considered network throughput.
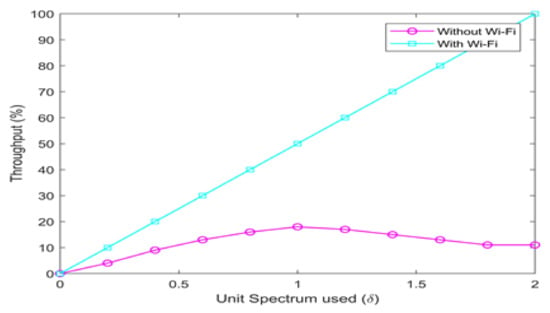
Figure 10.
Impact of Wi-Fi.
5. Conclusions and Future Work
The fast internet connections and the emergence of the latest smart devices everywhere have tremendously increased the data traffic on networks due to the use of data-hungry services. To cope with the situation, Mobile Network Operators (MNO) need to fulfill the high capacity requirement, throughput, coverage, and better QoS to ensure the long life of their relationship with users, in order to earn in a more sophisticated way. Mobile Data Offloading is a cheap solution among all providers, improving QoS by reducing the burden on the network. Different technologies such as Wi-Fi, WiMAX, Femtocells, Opportunistic communication, and IP run movable are used to offload data from the cellular network. However, Wi-Fi offloading is widespread among them because it is economical for both providers and users. We considered offloading through Wi-Fi as a solution and built various scenarios to examine the association of Wi-Fi with cellular networks for offloading. The main target of our work was to accomplish maximum offloading via Wi-Fi using the Stackelberg approach. We studied the outcomes of the Stackelberg approach in the commercial market. We have introduced a two-stage game model. In the first phase, the MBS provides economic stimulus to the APs based on the types of traffic used, while in the next phase, the APs exploit these stimuli, releasing various traffic. The mathematical model is developed to analyze our works, passed through simulation and experimental methods. We have used MATLAB as a simulation tool and presented simulations for different values of incentives to examine their effects on offloading. Furthermore, the QoS parameter performance was analyzed and compared with the existing model. The experiments proved that the proposed model performs better than the previous model, and Nash Equilibria via Best Response potential function was achieved using the proposed scheme. Additionally, the proposed traffic types-based game achieved a total unique equilibrium. Because of these numerical outcomes, it is concluded that the proposed traffic-types-based game is impartially superior in all considerable structures and operations. Based on optimal incentives, maximum offloading and enhanced throughput is the achievement of our model.
The issue of privacy and security is open to exploration in such a two-way offloading process, and the study of the multiple base station and multiple attached APs with parameters of delivery and the speed differences is the open issue for future research.
Author Contributions
Conceptualization, M.A. (Muhammad Asif), and methodology, E.R.; software, T.S., validation, M.A. (Muhammad Abid); formal analysis, M.H.; resources, M.A. (Muhammad Aslam); writing—review and editing, S.F.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data will be available on request.
Acknowledgments
We acknowledged Foundation University Islamabad, Pakistan.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gavrilovska, L.; Valentin, R.; Vladimir, A. Visions towards 5G: Technical requirements and potential enablers. Wireless Personal Comm. 2016, 87, 731–757. [Google Scholar] [CrossRef]
- Alexiou, A. Wireless World 2020: Radio interface challenges and technology enablers. IEEE Veh. Technol. Mag. 2014, 9, 46–53. [Google Scholar] [CrossRef]
- Maxwell, R.; Miller, T. How Green Is Your Smartphone; Polity: Cambridge, UK, 2020. [Google Scholar]
- Cisco. Cisco Visual Networking Index: Forecast and Trends, 2017–2022; Cisco Systems: San Francisco, CA, USA, 2018; pp. 1–7. [Google Scholar]
- Dahlman, E.; Parkvall, S.; Skold, J. 4G: LTE/LTE-Advanced for Mobile Broadband; Academic Press: Cambridge, MA, USA, 2013. [Google Scholar]
- Index, C.V. Global Mobile Data Traffic Forecast Update. Cisco White Paper. 2015. Available online: http://www.cisco.com/en/US/solutions/collateral/ns341/ns525/ns537/ns705/ns827/white_paper_c11-520862.pdf (accessed on 16 June 2022).
- Wang, T.; Li, P.; Wang, X.; Wang, Y.; Guo, T.; Cao, Y. A comprehensive survey on mobile data offloading in heterogeneous network. Wirel. Netw. 2019, 25, 573–584. [Google Scholar] [CrossRef]
- Zhou, H.; Wang, H.; Li, X.; Leung, V. A survey on mobile data offloading technologies. IEEE Access 2018, 30, 5101–5111. [Google Scholar] [CrossRef]
- Markova, E.; Moltchanov, D.; Gudkova, I.; Samouylov, K.; Koucharyavy, Y. Performance assessment of QoS-aware LTE sessions offloading onto LAA/WiFi systems. IEEE Access 2019, 7, 36300–36311. [Google Scholar] [CrossRef]
- Asif, M.; Khan, S.; Ahmad, R.; Sohail, M.; Singh, D. Quality of service of routing protocols in wireless sensor networks: A review. IEEE Access 2017, 5, 1846–1871. [Google Scholar] [CrossRef]
- Thien, H.T.; Vu, V.-H.; Koo, I. Game Theory-Based Smart Mobile-Data Offloading Scheme in 5G Cellular Networks. Appl. Sci. 2020, 10, 2327. [Google Scholar] [CrossRef]
- Yang, F.; Yan, J.; Guo, Y.; Luo, X. Stackelberg-game-based mechanism for opportunistic data offloading using moving vehicles. IEEE Access 2019, 7, 166435–166450. [Google Scholar] [CrossRef]
- Rebecchi, F.; Dias de Amorim, M.; Conan, V.; Passarella, A.; Bruno, R.; Conti, M. Data offloading techniques in cellular networks: A survey. IEEE Commun. Surv. Tutor. 2014, 17, 580–603. [Google Scholar] [CrossRef]
- Anajemba, J.; Yue, T.; Iwendi, C.; Alenezi, M.; Mittal, M. Optimal cooperative offloading scheme for energy efficient multi-access edge computation. IEEE Access 2020, 8, 53931–53941. [Google Scholar] [CrossRef]
- Antoniou, J. Using Game Theory to Address Mobile Data Offloading in 5G. In Game Theory, the Internet of Things and 5G Networks; Springer: Cham, Switzerland, 2020; pp. 43–60. [Google Scholar]
- Zhao, Y.; Xu, K.; Zhong, Y.; Li, X.; Wang, N.; Su, H.; Shen, M.; Li, Z. Incentive mechanisms for mobile data offloading through operator-owned WiFi access points. Comput. Netw. 2020, 174, 107226. [Google Scholar] [CrossRef]
- Niyato, D.; Luong, N.C.; Wang, P.; Han, Z. Auction Theory for Computer Networks; Cambridge University Press: Cambridge, UK, 2020. [Google Scholar]
- Wang, Z.; Feng, X.; Zhu, H.; Liu, C. Optimal data offloading via an ADMM algorithm in mobile ad hoc cloud with malicious resource providers. Comput. Commun. 2020, 158, 10–16. [Google Scholar] [CrossRef]
- Wu, Y.; He, Y.; Qian, L.P.; Huang, J.; Shen, X. Optimal resource allocations for mobile data offloading via dual-connectivity. IEEE Trans. Mob. Comput. 2018, 27, 2349–2365. [Google Scholar] [CrossRef]
- Hamidouche, K. Game Theoretic Approach for Resource Allocation in Small Cell Networks. Ph.D. Thesis, University of Oulu, Oulu, Finland, 2016. [Google Scholar]
- Bairagi, A.; Abedin, S.F.; Tran, N.H.; Niyato, D.; Hong, C.S. QoE-enabled unlicensed spectrum sharing in 5G: A game-theoretic approach. IEEE Access 2018, 6, 50538–50554. [Google Scholar] [CrossRef]
- Raja, G.; Ganapathisubramaniyan, A.; Anbalagan, S.; Baskaran, S.B.; Raja, K.; Bashir, A. Intelligent reward-based data offloading in next-generation vehicular networks. IEEE Internet Things J. 2020, 7, 3747–3758. [Google Scholar] [CrossRef]
- Barik, P.; Shukla, A.; Datta, R.; Singhal, C. A resource sharing scheme for intercell D2D communication in cellular networks: A repeated game theoretic approach. IEEE Trans. Veh. Technol. 2020, 69, 7806–7820. [Google Scholar] [CrossRef]
- Hassija, V.; Chamola, V.; Han, G.; Rodrigues, J.; Guizani, M. DAGIoV: A framework for vehicle to vehicle communication using directed acyclic graph and game theory. IEEE Trans. Veh. Technol. 2020, 69, 4182–4191. [Google Scholar] [CrossRef]
- Chen, X.; Zhou, Z. Noncooperative and Cooperative Computation Offloading. In Fog and Fogonomics: Challenges and Practices of Fog Computing, Communication, Networking, Strategy, and Economics; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2020. [Google Scholar]
- Noreen, S.; Saxena, N.; Roy, A. Incentive and Penalty Mechanism for Power Allocation in Cooperative D2D-Cellular Transmissions. Electron 2020, 9, 408. [Google Scholar] [CrossRef]
- Dong, C.; Li, Z.; Qu, Y.; Wu, Q.; Tang, S.; Qin, Z. Towards near optimal WiFi offloading with uncertain contact duration. IEEE Access 2018, 6, 31117–31128. [Google Scholar] [CrossRef]
- Chih-Lin, I.; Han, S.; Xu, Z.; Sun, Q.; Pan, Z. 5G: Rethink mobile communications for 2020+. Philos. Trans. R. Soc. Math. Phys. Eng. Sci. 2016, 374, 20140432. [Google Scholar] [CrossRef]
- Yu, H.; Cheung, M.; Iosifidis, G.; Gao, L.; Tassiulas, L.; Huang, J. Mobile data offloading for green wireless networks. IEEE Wirel. Commun. 2017, 24, 31–37. [Google Scholar] [CrossRef]
- Gao, L.; Iosifidis, G.; Huang, J.; Tassiulas, L.; Li, D. Bargaining-based mobile data offloading. IEEE J. Sel. Areas Commun. 2014, 2, 1114–1125. [Google Scholar] [CrossRef]
- Kang, X.; Chia, Y.; Sun, S.; Chong, H. Mobile data offloading through a third-party WiFi access point: An operator’s perspective. IEEE Trans. Wirel. Commun. 2014, 13, 5340–5351. [Google Scholar] [CrossRef]
- Ho, T.; Tran, N.; Do, C.; Kazmi, S.; LeAnh, T.; Hong, C. Data offloading in heterogeneous cellular networks: Stackelberg game based approach. In Proceedings of the 17th Asia-Pacific Network Operations and Management Symposium (APNOMS), Busan, Korea, 19 August 2015; pp. 168–173. [Google Scholar]
- Aijaz, A.; Aghvami, H.; Amani, M. A survey on mobile data offloading: Technical and business perspectives. IEEE Wirel. Commun. 2013, 20, 104–112. [Google Scholar] [CrossRef]
- Aijaz, A.; Uddin, N.; Holland, O.; Aghvami, A. On practical aspects of mobile data offloading to wi-fi networks. arXiv 2015, arXiv:1508.01926. [Google Scholar]
- Hinger, D.; Kalbande, D. Review of mobile data offloading through Wi-Fi. In Proceedings of the International Conference on Circuits, Systems, Communication and Information Technology Applications (CSCITA), Mumbai, India, 4–5 April 2014; pp. 425–429. [Google Scholar]
- Lee, K.; Lee, J.; Yi, Y.; Rhee, I.; Chong, S. Mobile data offloading: How much can WiFi deliver? IEEE/ACM Trans. Netw. 2012, 21, 536–550. [Google Scholar] [CrossRef]
- Iosifidis, G.; Gao, L.; Huang, J.; Tassiulas, L. A double-auction auction mechanism for mobile data-offloading markets. IEEE/ACM Trans. Netw. 2014, 23, 1634–1647. [Google Scholar] [CrossRef]
- Iosifidis, G.; Gao, L.; Huang, J.; Tassiulas, L. An iterative double auction auction for mobile data offloading. In Proceedings of the 11th International Symposium and Workshops on Modeling and Optimization in Mobile, Ad Hoc and Wireless Networks (WiOpt), Tsukuba Science City, Japan, 13 May 2013; pp. 154–161. [Google Scholar]
- Shah-Mansouri, H.; Wong, V.; Huang, J. An incentive framework for mobile data offloading market under price competition. IEEE Trans. Mob. Comput. 2017, 16, 2983–2999. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, J.; Gan, X.; Fu, L.; Yu, H.; Wang, X. A contract-based incentive mechanism for delayed traffic offloading in cellular networks. IEEE Trans. Wirel. Commun. 2016, 15, 5314–5327. [Google Scholar] [CrossRef]
- Tan, C.K.; Teong, C.C.; Tan, S.W. Resource allocation for OFDMA-based multicast cognitive radio networks using a Stackelberg pricing game. Comput. Commun. 2016, 88, 57–72. [Google Scholar] [CrossRef]
- Tan, C.K.; Moh, L.S.; Teong, C.C.; Su, W.T. Blotto game-based low-complexity fair multiuser subcarrier allocation for uplink OFDMA networks. EURASIP J. Wirel. Commun. Netw. 2011, 2011, 53. [Google Scholar] [CrossRef]
- Noreen, S.; Navrati, S. A review on game-theoretic incentive mechanisms for mobile data offloading in heterogeneous networks. IETE Tech. Rev. 2017, 34, 15–26. [Google Scholar] [CrossRef]
- Bali, M.S.; Kamali, G.; Deepika, K.; Atef, Z.; Shubham, M.; Amit, K.P. Smart architectural framework for symmetrical data offloading in IoT. Symmetry 2021, 13, 1889. [Google Scholar] [CrossRef]
- Blocher, J.; Frederick, C.H., Jr. An Equilibrium Analysis of a Secondary Mobile Data-Share Market. Information 2021, 12, 434. [Google Scholar] [CrossRef]
- Yuan, X.; Zhidong, X.; Xin, T. Computation Offloading in UAV-Enabled Edge Computing: A Stackelberg Game Approach. Sensors 2022, 22, 3854. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Li, X.; Li, G.; Rui, Z. Non-Cooperative Game Forwarding Leveraging User Trustworthiness in Mobile Edge Networks. Sustainability 2022, 14, 4473. [Google Scholar] [CrossRef]
- Majumder, B.; Venkatesh, T.G. Mobile data offloading based on minority game theoretic framework. Wirel. Netw. 2022, 1–16. [Google Scholar] [CrossRef]
- Zhou, H.; Tong, W.; Xin, C.; Shibo, H.; Jie, W. RAIM: A Reverse Auction-based Incentive Mechanism for Mobile Data Offloading through Opportunistic Mobile Networks. IEEE Trans. Netw. Sci. Eng. 2021. [Google Scholar] [CrossRef]
- Bhooanusas, N.; Sou, S.-I.; Cheng, K.-C. Satisfaction-based Dynamic Bandwidth Reallocation for multipath mobile data offloading. Comput. Netw. 2021, 185, 107594. [Google Scholar] [CrossRef]
- Zhao, M.; Li, J.; Tang, F.; Asif, S.; Zhu, Y. Learning based massive data offloading in the iov: Routing based on pre-RLGA. IEEE Trans. Netw. Sci. Eng. 2022, 9, 2330–2340. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).