Propagation of Nonplanar SH Waves Emanating from a Fault Source around a Lined Tunnel

Abstract

An analytical solution is presented for scattering nonplanar SH waves emanating from a fault source using a lined tunnel. The lined tunnel is assumed to be an annular elastic solid in half-space. A simplified circular arc fault model is employed to represent the wave source. By means of the separation of variables method, all wave fields are given in terms of the wave function series with unknown coefficients. Taking advantage of the method of images, the zero-stress boundary condition on the horizontal ground surface is satisfied automatically. By applying Graf’s addition formula, a system of equations for seeking the unknowns is derived by taking advantage of the boundary conditions. The problem of wave scattering is finally solved after seeking solutions for the system of equations through standard matrix techniques. The effects of fault distance, fault curvature, and fault orientation are revealed with numerical results. It is found that the plane waves provide a good approximation to the fault-induced cylindrical waves when the source-receiver distance or fault radius of curvature is larger enough. Fault-induced topographic effects are strongly affected by source orientation.

1. Introduction

Nowadays, as so many underground structures, such as subways, water-conveyance tunnels, mineral prospecting, and military facilities, have been constructed all around the world, the dynamic response of underground tunnels subjected to seismic waves has attracted more and more attention from geophysicists, seismologists, and civil engineers. Long underground tunnels are more likely to cross faults. Investigations of the water conveyance tunnel of Shih-Gang Dam affected by the Chi-Chi Earthquake (1999) show that tunnels passing through the displaced fault zone suffered catastrophic damage, and the lining was sheared off [1]. Similar damages are found in numerous tunnels during the Wenchuan Earthquake (2008) due to fault displacements, e.g., Longxi tunnel, Shaohuoping tunnel, Longchi tunnel, Chediguan tunnel, and Taoguan tunnel [2]. Therefore, there is an urgent need to study the scattering of nonplanar SH waves emanating from a fault by underground tunnels. The seismic response of tunnels is affected by the incident seismic wave, the reflected wave caused by the ground surface, and the scattered wave caused by the tunnel. Therefore, the wave scattering effect should be considered in the study of the seismic response of tunnels.

There have been a series of analytical studies on the seismic response of tunnels. Pao and Mow [3] first proposed a wave function series solution for the dynamic stress concentration of circular cavities in the whole space under the incidence of elastic SH waves. Then, Lee and Trifunac [4] extended the solution to the half-space case. The wave scattering problem is much more complicated in the case of incident P or SV waves due to the presence of mode conversion when the incident wave is reflected. Lee and Karl [5] obtained a series of analytical solutions to the scattering of P and SV waves induced by an underground circular cavity using a large arc assumption. In addition, many other scholars have analytically studied the influence of tunnel shape [6,7,8]. However, numerous studies have been conducted on the effects excited by plane harmonic waves [3,4,5,6,7,8,9,10,11,12,13,14], while the incidence of near-source waves is still at a research stage. Most of the previous achievements of near-source effects consider incident waves to be line source cylindrical waves. In their pioneering work, Pao and Mow [3] investigated the dynamic stress concentration of a circular cavity in the entire space for incident cylindrical P waves. Smerzini et al. [15] studied the effect of underground cavities on earthquake ground motions under plane and cylindrical SH waves. Gao et al. [8] provided a rigorous solution for scattering plane and cylindrical SH waves using a horseshoe-shaped cavity. This assumption was then extended to studies of site effects on seismic waves. Gao and Zhang [16] provided a solution of wave functions for the cylindrical SH wave scattering induced by a symmetrical V-shaped canyon. Zhang et al. [17] investigated near-source site effects based on a partially filled semicircular alluvial valley. But most earthquakes occur on the faults, i.e., the Chi-Chi earthquake (1999) resulted from the reactivation of the Chelungpu Fault [1], and major shock of Wenchuan earthquake (2008) occurred on the Beichuan–Yingxiu Fault [18]. Although a line source assumption is effective in simulating a near-field earthquake, there is a notable scarcity of literature dealing with the effect of fault. Only Kara and Trifunac [19,20] investigated the scattering of semi-circular sedimentary valleys considering excitation as a circular arc fault.

The current work is motivated by a lack of studies regarding the fault-induced dynamic response of a lined tunnel. The method proposed by Kara and Trifunac [19,20] is extended herein to consider the configuration in which the fault has an arbitrary orientation. The main contributions of this paper are twofold. On the one hand, the solution to the scattering problem of a lined tunnel induced by a fault is first presented in this paper. Since the excitation by a fault is more real compared to the plane wave and the line source of the cylindrical wave, the results presented herein are very instructive for practical use. On the other hand, through the analysis of numerical results, one can gain a better understanding of the relationship between fault-induced nonplanar waves and plane waves.

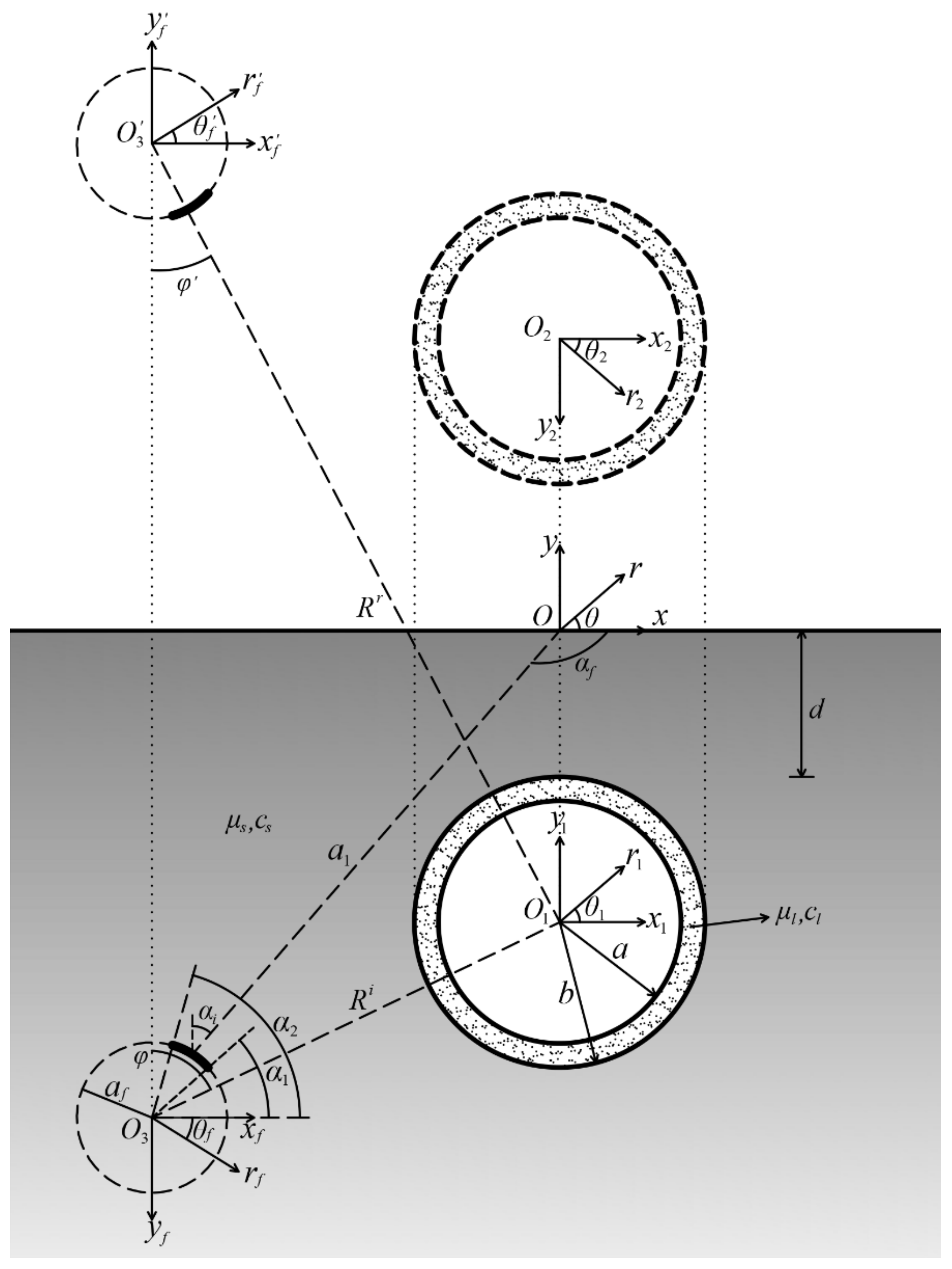
2. Materials and Methods

The 2D model is depicted in Figure 1. It represents an infinitely long, circular-lined tunnel embedded in a homogeneous, isotropic, linearly elastic, semi-infinite medium. The lining is characterized by inner radius a, outer radius b, shear modulus μ_l and shear wave velocity c_l, while the half-space is characterized by shear modulus μ_s and shear wave velocity c_s. The center of the tunnel is located at point O₁ with a distance d + b below the ground surface. The fault is considered an arch of circular O₃ with radius a₁. In coordinate system O, the fault is located at r = r_f, θ = −α_f. In coordinate system O₃, the fault is located at r₃ = a₁, between the angles 2π − α₂ and 2π − α₁. To facilitate the solution to the problem, an imaginary tunnel and an imaginary fault with respect to the ground surface are introduced herein. The definitions of the five Cartesian and five polar coordinate systems are shown in Figure 1.

The out-of-plane wave fields of all regions in the half-space must satisfy the governing equation of motion, i.e., Helmholtz equation [21].

$$\frac{{\partial }^{2}u}{\partial r^2}+\frac{1}{r}\frac{\partial u}{\partial r}+\frac{1}{r^2}\frac{{\partial }^{2}u}{\partial {\theta }^2}+k^{2}u=0$$

(1)

where k = ω/c is the shear wave number.

Using the method of separating variables [22,23], the general solution of Equation (1) can be written as:

$$u\left(r,\theta \right)={\displaystyle \sum }_{n=-\infty }^{\infty }{I}_n{C}_n\left(kr\right)e^{in\theta }$$

(2)

where I_n is the complex coefficient to be determined, C_n is the Bessel function with nth order, which can be either J_n, Y_n, H_n⁽¹⁾, H_n⁽²⁾ depending on the physical conditions of the problem.

Considering the image method and the Sommerfeld radiation condition, the wave field for each region in the sub-space can be written as follows. The wave field in the lining, satisfying the Sommerfeld radiation condition, is the standing wave in the finite domain and is formed by the Bessel function of the first and second kinds, written as

$$u_l={\displaystyle \sum }_{n=-\infty }^{\infty }{A}_n{J}_n\left(k_l{r}_1\right)e^{in{\theta }_1}+{\displaystyle \sum }_{n=-\infty }^{\infty }{B}_n{Y}_n\left(k_l{r}_1\right)e^{in{\theta }_1}$$

(3)

The scattering wave field generated by the tunnel and its image, characterizing the radial oscillation from the site to the infinite boundary, is formed by the Hankel function of the first and second kinds, written as:

$$u_s={\displaystyle \sum }_{n=-\infty }^{\infty }{D}_n{H}_n^{\left(1\right)}\left(k_s{r}_1\right)e^{in{\theta }_1}+{\displaystyle \sum }_{n=-\infty }^{\infty }{D}_n{H}_n^{\left(1\right)}\left(k_s{r}_2\right)e^{in{\theta }_2}$$

(4)

Since the displacement is finite within O₃, the wave field inside the circle O₃ can be written as:

$$u_i={\displaystyle \sum }_{n=-\infty }^{\infty }{E}_n{J}_n\left(k_s{r}_3\right)e^{in{\theta }_3}$$

(5)

Similar to the scattering wave field expressed in Equation (4), the wave field outside circle O₃ can be written as:

$$u_o={\displaystyle \sum }_{n=-\infty }^{\infty }{F}_n{H}_n^{\left(1\right)}\left(k_s{r}_f\right)e^{in{\theta }_f}+{\displaystyle \sum }_{n=-\infty }^{\infty }{F}_n{H}_n^{\left(1\right)}\left(k_s{r}_f^{\prime }\right)e^{in{\theta }_f^{\prime }}$$

(6)

In addition, all the waves in the sub-region should satisfy the following boundary conditions.

(1)

Stress-free boundary conditions on the flat surface and the inner surface of the lining

$$\frac{{\mu }_s}{r}\frac{\partial \left(u_s+u_o\right)}{\partial \theta }=0,\theta =\pm \frac{\pi }{2}$$

(7)

$${\mu }_l\frac{\partial u_l}{\partial r_1}=0,r_1=a$$

(8)

(2)

The continuity of both displacement and stress fields on the outer surfaces of the lining

$$u_l\left(r_1,{\theta }_1\right)=u_s\left(r_1,{\theta }_1\right)+u_o\left(r_1,{\theta }_1\right),r_1=b$$

(9)

$${\mu }_l\frac{\partial u_l}{\partial r_1}={\mu }_s\frac{\partial \left(u_s+u_o\right)}{\partial r_1},r_1=b$$

(10)

(3)

The continuity of stress field on the circle O₃

$$u_i\left(r_f,{\theta }_f\right)=u_s\left(r_f,{\theta }_f\right)+u_o\left(r_f,{\theta }_f\right),r_f=a_1$$

(11)

$${\mu }_s\frac{\partial u_i}{\partial r_f}={\mu }_s\frac{\partial \left(u_s+u_o\right)}{\partial r_f},r_f=b$$

(12)

(4)

Assuming there is a unit-amplitude dislocation with out of plane motion, the boundary condition on the fault can be written as:

$$u_i\left(r_f,{\theta }_f\right)-\left[u_s\left(r_f,{\theta }_f\right)+u_o\left(r_f,{\theta }_f\right)\right]=f\left({\theta }_f\right),r_f=a_1$$

(13)

where f(θ_f) is a function written as:

$$f\left({\theta }_f\right)=H\left[\theta -\left(2\pi -{\alpha }_1\right)\left]+H\right[\theta -\left(2\pi -{\alpha }_2\right)\right]$$

(14)

where H(θ) is the Heaviside function, such that

$$H\left(\theta \right)=\left\{\begin{array}{cc}0,& \theta <0\\ 1,& \theta \ge 0\end{array}\right.$$

(15)

The Fourier series expansion of f(θ_f) can be written as:

$$f\left({\theta }_f\right)={\displaystyle \sum }_{n=-\infty }^{\infty }{f}_n{e}^{in{\theta }_f}$$

(16)

where f_n is the Fourier transform of f(θ_f), which can be written as:

$$f_n=\frac{1}{2\pi }{{\displaystyle \int }}_0^{2\pi }f\left({\theta }_f\right)e^{-in{\theta }_f}d{\theta }_f=\left\{\begin{array}{cc}\frac{i}{2\pi n}\left(e^{in{\alpha }_1}-e^{in{\alpha }_2}\right)& ,n\ne 0\\ \frac{1}{2\pi }\left({\alpha }_1-{\alpha }_2\right)& ,n=0\end{array}\right.$$

(17)

To solve the problem, Graf’s addition formula is used to transform the Bessel function from one coordinate to another.

Because of the introduction of the imaginary tunnel, the tress-free boundary condition on the flat surface is satisfied automatically. Substituting the general solution into other boundary conditions by considering the orthogonal properties of the complex exponential function, the following five equations can be obtained:

$$A_q{J}_q^{\prime }\left(k_{l}a\right)+B_q{Y}_q^{\prime }\left(k_{l}a\right)=0$$

(18)

$$\begin{array}{l}{\mu }_l{k}_l[A_q{J}_q^{\prime }\left(k_{l}b\right)+B_q{Y}_q^{\prime }\left(k_{l}b\right)]\\ ={\mu }_s{k}_s[D_q{H}_q^{\left(1\right)}{}^{\prime }\left(k_{s}b\right)+{\displaystyle {\displaystyle \sum }_{n=-\infty }^{\infty }}{D}_n{H}_{n+q}^{\left(1\right)}\left(k_{s}2d\right)J_q^{\prime }\left(k_{s}b\right)e^{i\left(n-q\right)\frac{\pi }{2}}\\ +{\displaystyle {\displaystyle \sum }_{n=-\infty }^{\infty }}{F}_n{H}_{n+q}^{\left(1\right)}\left(k_s{R}^i\right)J_q^{\prime }\left(k_{s}b\right)e^{i\left(q+n\right)\phi +i\frac{3}{2}\left(n-q\right)\pi }\\ +{\displaystyle {\displaystyle \sum }_{n=-\infty }^{\infty }}{F}_n{H}_{n-q}^{\left(1\right)}\left(k_s{R}^r\right)J_{-q}^{\prime }\left(k_{s}b\right)e^{-iq\left({\phi }^{\prime }+\frac{\pi }{2}\right)+in\left({\phi }^{\prime }+\frac{3\pi }{2}\right)}]\end{array}$$

(19)

$$\begin{array}{l}{A}_q{J}_q\left(k_{l}b\right)+B_q{Y}_q\left(k_{l}b\right)\\ =D_q{H}_q^{\left(1\right)}\left(k_{s}b\right)+{\displaystyle {\displaystyle \sum }_{n=-\infty }^{\infty }}{D}_n{H}_{n+q}^{\left(1\right)}\left(k_{s}2d\right)J_q\left(k_{s}b\right)e^{i\left(n-q\right)\frac{\pi }{2}}\\ +{\displaystyle {\displaystyle \sum }_{n=-\infty }^{\infty }}{F}_n{H}_{n+q}^{\left(1\right)}\left(k_s{R}^i\right)J_q\left(k_{s}b\right)e^{i\left(q+n\right)\phi +i\frac{3}{2}\left(n-q\right)\pi }\\ +{\displaystyle {\displaystyle \sum }_{n=-\infty }^{\infty }}{F}_n{H}_{n-q}^{\left(1\right)}\left(k_s{R}^r\right)J_{-q}\left(k_{s}b\right)e^{-iq\left({\phi }^{\prime }+\frac{\pi }{2}\right)+in\left({\phi }^{\prime }+\frac{3\pi }{2}\right)}\end{array}$$

(20)

$$\begin{array}{l}{E}_q{J}_q\left(k_s{a}_3\right)=F_q{H}_q^{\left(1\right)}\left(k_s{a}_3\right)+{\displaystyle {\displaystyle \sum }_{n=-\infty }^{\infty }}{F}_n{H}_{n+q}^{\left(1\right)}\left(k_{s}2y_0\right)J_q\left(k_s{a}_3\right)e^{i\frac{3}{2}\left(n-q\right)\pi }\\ +{\displaystyle {\displaystyle \sum }_{n=-\infty }^{\infty }}{D}_n{H}_{n+q}^{\left(1\right)}\left(k_s{R}^i\right)J_q\left(k_s{a}_3\right)e^{-i\left(n+q\right)\phi +i\frac{3}{2}\left(n-q\right)\pi }\\ +{\displaystyle {\displaystyle \sum }_{n=-\infty }^{\infty }}{D}_n{H}_{n-q}^{\left(1\right)}\left(k_s{R}^r\right)J_{-q}\left(k_s{a}_3\right)e^{-iq\left({\phi }^{\prime }+\frac{3\pi }{2}\right)+in\left({\phi }^{\prime }+\frac{\pi }{2}\right)}\end{array}$$

(21)

$$\begin{array}{l}{E}_q{J}_q\left(k_s{a}_3\right)+f_q=F_q{H}_q^{\left(1\right)}\left(k_s{a}_3\right)+{\displaystyle {\displaystyle \sum }_{n=-\infty }^{\infty }}{F}_n{H}_{n+q}^{\left(1\right)}\left(k_{s}2y_0\right)J_q\left(k_s{a}_3\right)e^{i\frac{3}{2}\left(n-q\right)\pi }\\ +{\displaystyle {\displaystyle \sum }_{n=-\infty }^{\infty }}{D}_n{H}_{n+q}^{\left(1\right)}\left(k_s{R}^i\right)J_q\left(k_s{a}_3\right)e^{-i\left(n+q\right)\phi +i\frac{3}{2}\left(n-q\right)\pi }\\ +{\displaystyle {\displaystyle \sum }_{n=-\infty }^{\infty }}{D}_n{H}_{n-q}^{\left(1\right)}\left(k_s{R}^r\right)J_{-q}\left(k_s{a}_3\right)e^{-iq\left({\phi }^{\prime }+\frac{3\pi }{2}\right)+in\left({\phi }^{\prime }+\frac{\pi }{2}\right)}\end{array}$$

(22)

The unknown coefficients A_n, B_n, D_n, E_n and F_n can be obtained by combining Equations (18)–(22) and truncating the infinite series in these equations to a finite number. Once the coefficients are known, the wave fields in the half-space are ready for numerical computation. A detailed flowchart for the summarization of the present method is shown in Figure 2.

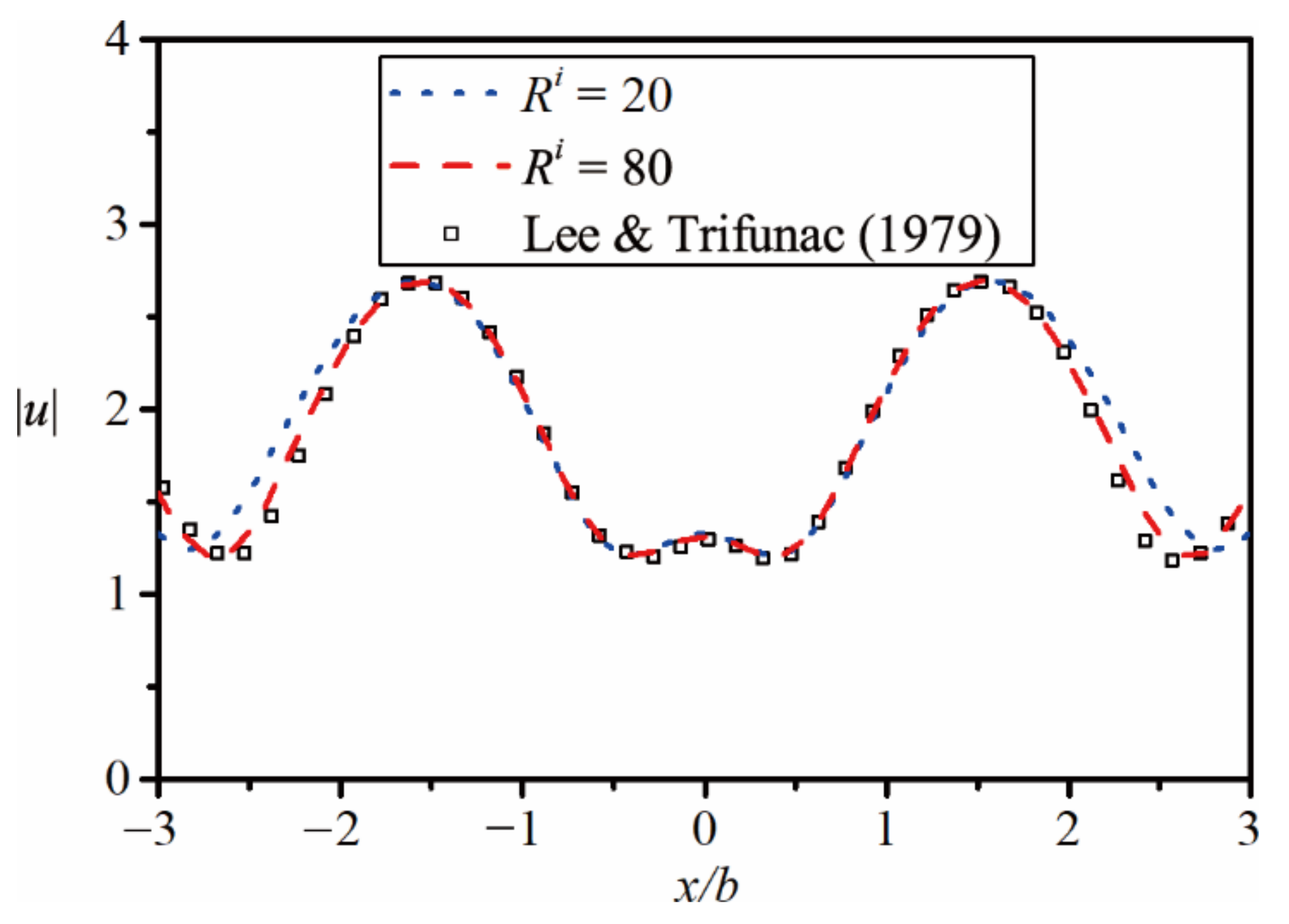
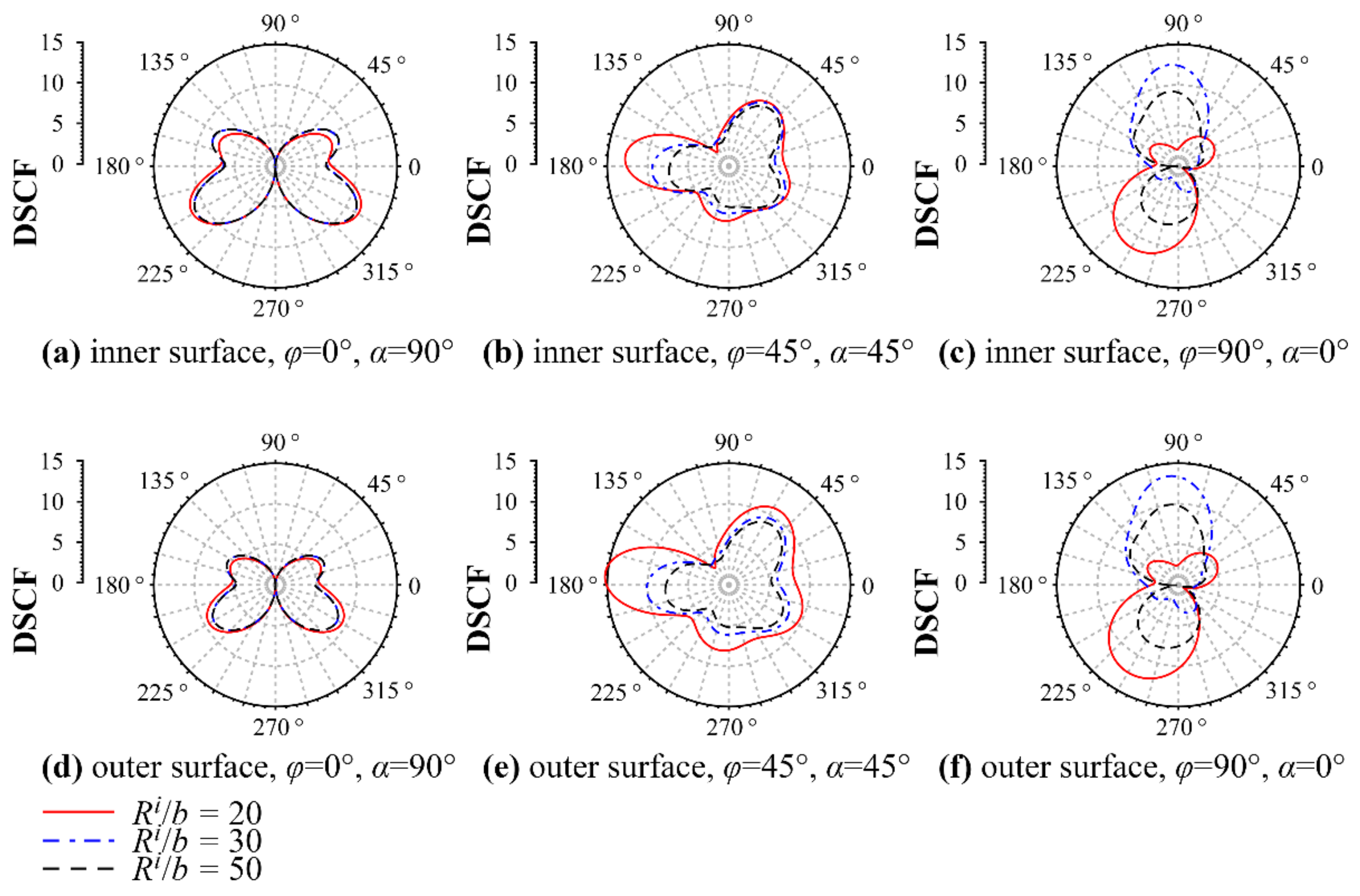
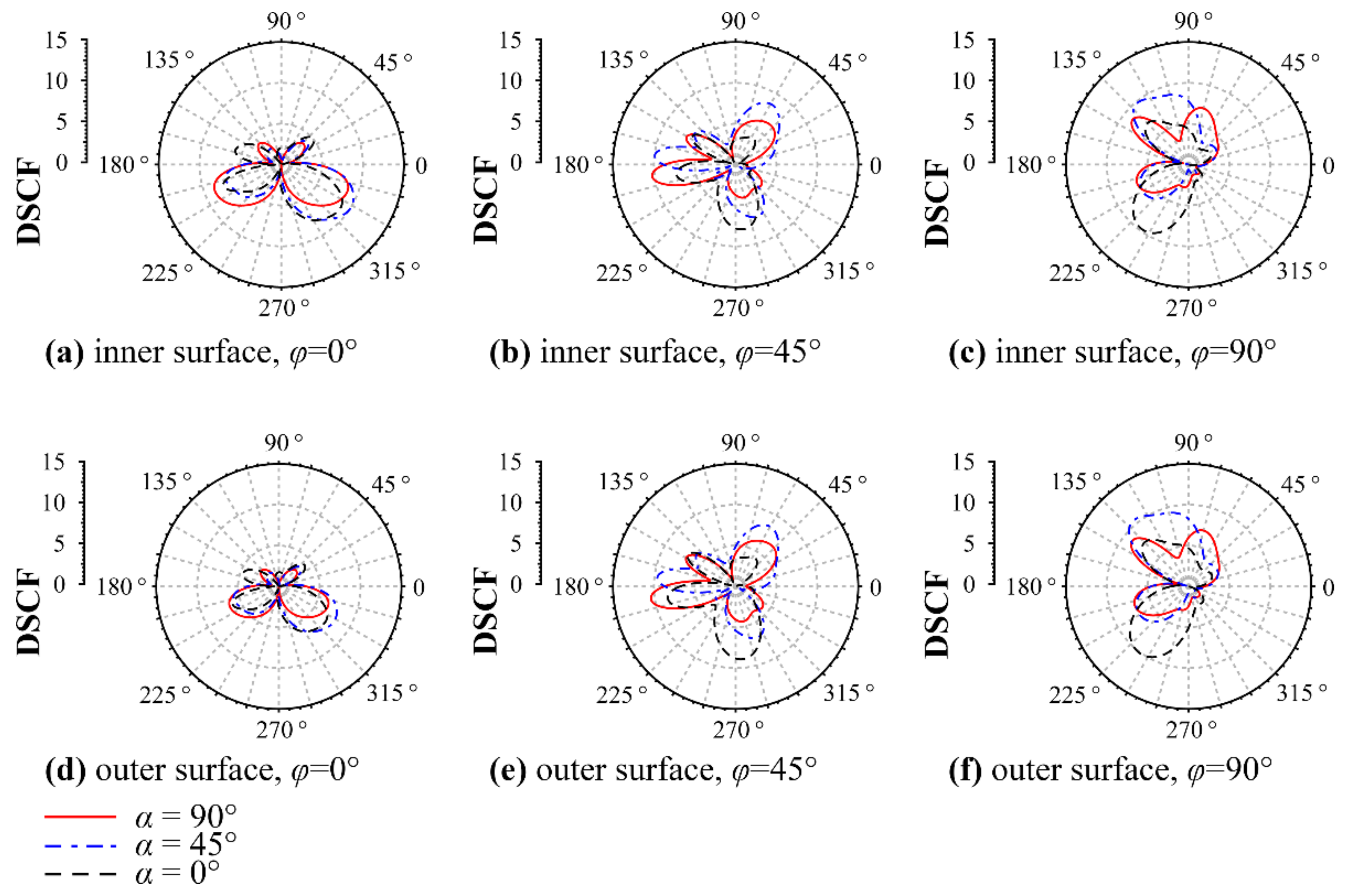
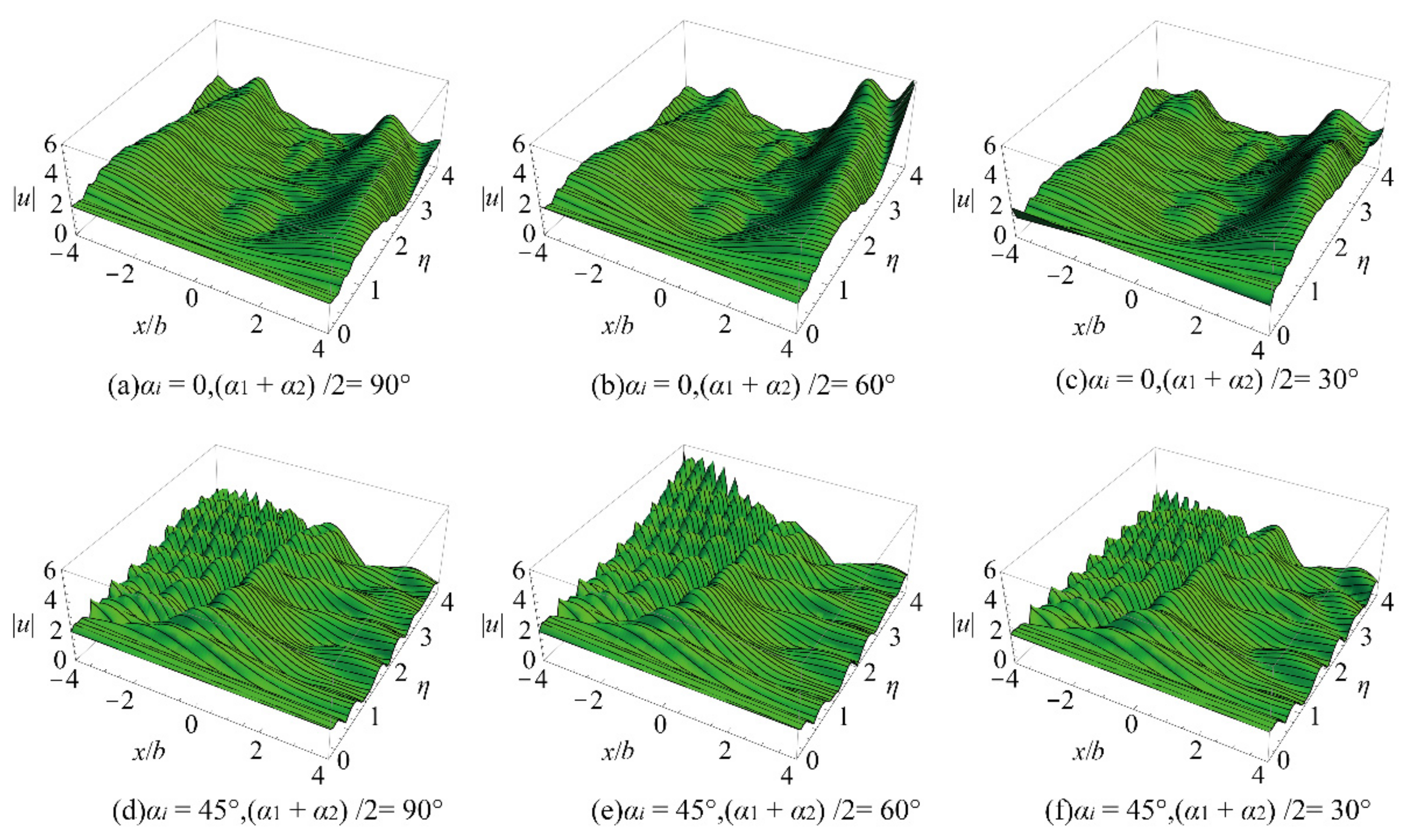
3. Numerical Results and Discussion

As for earthquake engineering, researchers are more interested in the displacement amplitude |u|. It is defined as:

$$\left|u\right|=\sqrt{\left[\mathit{Re}(u\right){]}^2+\left[Im(u\right){]}^2}$$

(23)

where Re(·) and Im(·) are the real and imaginary parts of a complex expression, respectively.

Furthermore, it is convenient to define the dimensionless frequency η as:

$$\eta =\frac{\omega b}{\pi c_s}=\frac{2b}{{\lambda }_s}=\frac{k_{s}b}{\pi }$$

(24)

where λ_s is the wavelength of the incident SH waves.

The parameters of the cavity studied below are chosen as a/b = 0.9, d/b = 3, and the material properties c_s/c_l = 2/5, μ_s/μ_l = 8/75 [15].

There has been strict mathematical proof that the line source cylindrical waves can be reduced to plane waves for a sufficiently large source–receiver distance [16,17]. If the excitation is changed as a finite fault, however, does the same conclusion stand? To facilitate the comparison, all transfer functions for excitation by the fault are normalized by letting the free-field displacement amplitude at point O equal to 2. The effects of fault distance on the displacement amplitudes at three representative points on the ground surface are shown in Figure 3. To illustrate the asymptotic relationship, the corresponding results for plane waves (gray dashed lines) are given as well. Figure 3a,b shows the displacement amplitudes for the vertical incidence and oblique incidence for η = 1. Figure 3c,d correspond to the results for η = 4. As expected, the displacements at three points induced by the fault approach the corresponding values of plane waves as the fault moves away. That is to say, similar to the line source cylindrical waves, fault-induced nonplanar waves are reduced to plane waves for a sufficiently large source-receiver distance as well.

To facilitate this further, the normalized displacement on the ground surface is compared with the previous solution induced by plane waves. Figure 4 shows the comparison of ground motion between the present assumption and that of plane waves presented by Lee & Trifunac (1979) [4]. The parameters are set as a/b = 0.9, d/b = 1.5, c_s/c_l = 1, μ_s/μ_l = 1/3, α = 0°, φ = 90°. One can see that the present results are in excellent agreement with those by Lee & Trifunac (1979) [4] for large source-receiver distance.

To investigate the effect of distance between fault and tunnel on the dynamic response of tunnel, Figure 5 and Figure 6 exhibit the dynamic stress concentration factor (DSCF) along the inner surface and outer surfaces of the lining for different distances between fault and tunnel. To keep the fault curvature and orientation consistent with each other, α = 90° is set for φ = 0°, α = 45° for φ = 45°, α = 0° for φ = 90°, and a₁/b = 8 for each case. Figure 5 represents the case for η = 1, and Figure 6 represents the case for η = 2.

The definition of the DSCF in this study is written as [3]:

$$\mathrm{DSCF}=\frac{{\sigma }_{\theta z}}{{\mu }_l{k}_l^2}$$

(25)

where σ_θz represents the shear stress in the lining.

One can observe bilateral symmetry in the distribution curves of the DSCF for vertical incident waves (α = 90° and φ = 0°). Most of the distribution curves are approximately in the shape of a clover with four local maxima. The distribution of the DSCF along the inner and outer surface of the lining is similar. However, their values are different. The DSCF along the lower part of the tunnel is larger than that along the upper part of the tunnel. The reason is that the existence of the tunnel obstructs the transmission of seismic waves. Similar trends can be seen in the case of horizontal incident waves (α = 0° and φ = 90°). The DSCF is larger along the left part of the tunnel than that along the right part of the tunnel. Similar to the pattern of incident plane waves, when the dimensionless frequency η increases, the ability of short waves to penetrate the tunnel becomes weaker and weaker. Hence, the shielding effect is more significant for η = 2. Comparing the DSCF of different source-receiver distances, one can find that the DSCF is larger for smaller source-receiver distances than for larger source-receiver distances overall. This means that the damage to the near-fault earthquake is larger for the far-field earthquake.

To investigate the effect of fault orientation α on the dynamic response of tunnels, Figure 7 and Figure 8 exhibit the DSCF along the inner surface and outer surfaces of the lining for different fault orientations. The parameters are set as a₁/b = 8 and Rⁱ/b = 30. Figure 7 represents the case for η = 1, and Figure 8 represents the case for η = 2. Fault orientation plays an important role in DSCF. Comparing Figure 7a to Figure 7d, one can find that the location of the maximum DSCF changed from the lower part of the tunnel to the upper part of the tunnel as α changed from 90° to 0°. Similar trends can be seen by comparing Figure 7c to Figure 7f. However, the location of the maximum DSCF is almost unchanged compared to Figure 7b to Figure 7e. That means, different from the plane wave assumption, the fault orientation should be considered for the seismic design of tunnels.

Figure 9 illustrates the ground surface displacement amplitudes as a function of the dimensionless distance x/b and dimensionless frequency η for the same location but different fault orientations. For the case of vertical incidence (α_i = 0) in Figure 9a, the shaded area, where the displacement amplitudes reduce, appears on the ground surface right over the tunnel. What’s more, with the increase of dimensionless frequency η, the reduction of displacement amplitudes becomes more and more obvious. For cases of non-vertical incidence (α_i ≠ 0, Figure 9d–f), one can also see the illuminated area on the left ground and the shaded area on the right ground. The motions on the ground surface decrease quickly from the illuminated area to the shaded area. Comparing the ground motion for different fault orientations, one can find that there is almost no difference in the ground motion for horizontal fault orientation ((α₁ + α₂)/2 = 90°) and vertical fault ((α₁ + α₂)/2 = 0°). However, the ground motion for the oblique fault ((α₁ + α₂)/2 = 60°) is obviously different from the vertical and horizontal cases. Moreover, the ground motion over the illuminated area for oblique faults is larger than that for vertical and horizontal faults. This means that the damage to the oblique fault is greater than the vertical and horizontal faults.

4. Conclusions

The scattering of nonplanar SH waves emanating from a finite source by a lined tunnel is studied in this paper. A simplified circular arc fault model is adopted. The influence of fault distance, fault curvature, and fault orientation are considered in the study. Similar to the line source cylindrical waves, the results of fault-induced nonplanar waves tend to be equivalent to those of plane waves for a sufficiently large source–receiver distance. Through the investigation of DSCF along the inner and outer surfaces of the lining, one can find that the distribution of the DSCF along the inner and outer surface of lining is similar. However, the values are slightly different. Fault orientation and source-receiver distance play an important role in the DSCF of lining. It was found that the tunnel can obstruct the transmission of seismic waves and make the DSCF smaller at the shaded side of the tunnel. The damage to the near-fault earthquake is larger for the far-field earthquake. Through the investigation of ground motion, one can find that fault orientation can significantly change ground motion for certain fault orientations. The damage to the oblique fault is greater than the vertical and horizontal faults.