Abstract
Greece is divided into three earthquake hazard zones: Zone I, Zone II and Zone III. In the present research work, the same building in the three seismic zones in Greece was modeled, analyzed and dimensioned. Then, the construction cost of its structural body was estimated. The building modeling was performed in SAP2000 using frame elements. The analysis of the building was performed by dynamic spectral analysis methods using the design spectrum EC8. A five-story building with a standard rectangular floor plan per floor was used. The purpose of this research paper is to demonstrate whether the cost of construction of a load-bearing body of a reinforced concrete (R/C) building is influenced by the area of an earthquake hazard through a comparative analytical estimation of construction costs. It was determined if this impact is important and to what extent. Helpful conclusions were drawn in relation to the influence of seismicity on the construction cost of the load-bearing structure of R/C buildings. Furthermore, the probable environmental impact was examined.
1. Introduction
One matter that has troubled consultant engineers worldwide is the correct design and detailing of reinforced concrete (R/C) buildings [1,2,3,4,5,6,7,8,9]. However, another matter that has troubled engineers is the economical design of R/C buildings as far as the construction cost of the load-bearing structure is concerned. Several studies worldwide have considered this matter to find the most economical way of designing and detailing the load-bearing body in structures, whether these structures are buildings [10,11,12], bridges [13,14,15,16,17], etc. It is accepted worldwide that a R/C building should be able to adequately resist all kinds of different loads [18,19]. A significant factor that is considered is the seismicity of the area where the building is located. Relevant seismic codes, like Eurocode 8 [20] or the Greek Seismic Code 2000 [21], include seismic hazard maps that show in which seismic zone each area belongs. Each building is designed against earthquake action according to the seismic zone in which it belongs. However, it must be noted that a higher earthquake zone can be chosen by the engineer, in order for the construction to be on the safe side. Naturally, along with the safety of a structure, its cost of construction is affected [10,11,12,22,23,24]. In this case, other occurrences have to be considered, e.g., the transverse instability of R/C shear walls, and cracking [25,26,27,28,29,30,31,32,33].
In Greece, for the majority of buildings, R/C is used as a construction material. Greece is a seismically active country, and as earthquake action is a dangerous and destructive natural phenomenon, the buildings, whether they are new or old, must deal with it effectively [14,26,27,34,35,36,37,38,39,40,41]. Currently, high-rise buildings are being constructed. One of the main problems of these buildings is that during an earthquake, some of their floors move in one direction, while at the same time, other floors move in the opposite direction [42,43]. Therefore, engineers should take the seismic zone in which each building is constructed very seriously. Engineers have the ability to dimension a building in a higher seismic zone than the one to which the building belongs if they deem it necessary. However, the engineer should not forget that their choice might increase the final construction cost. Furthermore, an increase to the final construction cost because of bigger material quantities used can lead to an increment to the emissions produced during the fabrication process of these materials.
Some researchers worldwide have studied the energy aspect concerning modern building and urban design [44,45,46,47,48,49,50,51,52,53]. Specifically, Birol and Siir [44] have studied a “hydrogen city” model with two cycles at the district and building levels for the energy base of urban settlements to have greater integration of renewable energy sources. The main cycle comprises hydrogen gas production, hydrogen storage, and a hydrogen distribution network. Hydrogen was then used in central fuel cells to meet the power demands of urban infrastructure. The hydrogen city model was applied to a new settlement area with an expected 200,000 inhabitants, to find that the proposed model can enable a nearly net-zero exergy district status. The results had implications for settlements using hydrogen energy towards meeting net-zero targets.
Urban water-energy (WE) nexus is regarded as highly important in managing resource shortage crises in cities. Fan et al. [45] presented a comprehensive review on urban WE nexus from the perspective of urban metabolism. Ferrara et al. [46] presented the conception of a replicable methodology, including the integrated tools and metrics, for supporting the integrated design of the building envelope, aiming at minimizing the building’s total energy demand (resulting from the sum of heating, cooling and lighting energy needs) in a thermal and visual comfort context. The methodology relied on a simulation-based optimization process. Seyfettin [47] examined the effects of technological innovation on the carbon emissions caused by the building sector by using panel data methods for the BRICS countries (Brazil, Russia, India, China, and South Africa) during the period of 1992–2018. It has been observed that there is a long-term relationship between the series.
Xu et al. [48] addressed the nexus of intense urbanization, building energy and air pollution, a topic minimally explored in the literature. The models used for their investigation were combined with observations from two meteorological towers, one located in downtown and the other on the outskirts. Model validation was conducted for environmental variables and for building energy demands against surface weather observations and actual electricity data, showing good agreement in all cases. Sun et al. [49] proposed the problems encountered in the transformation of the gray infrastructure of the sponge city to the green infrastructure, and the necessary measures to be taken. The integrated indicator system was used to comprehensively evaluate the integration of the gray-green facilities. Sun et al. [50] developed a methodology of modeling and analysis to provide insights into the nexus of thermal resilience and the energy efficiency of buildings. Results showed that passive measures of opening windows and doors for natural ventilation, as well as miscellaneous load reduction, are very effective in eliminating extremely dangerous occasions. However, to maintain safe conditions, active measures such as on-site power generators and thermal storage are also needed.
Purwanto et al. [51] developed a qualitative causal model of a water, energy, and food (WEF) security nexus system to be used in analyzing the interlinkages among those and other sectors that influence and are influenced by each other in a local context. Mehrjerdi et al. [52] studied the efficiency-resilience nexus in building energy management. The building was supplied by solar, diesel, battery, and grid. The purpose was to improve both the efficiency and resilience of the system. The model found a minimum level for non-restored loads, an optimal operating pattern for energy resources, minimum investment costs, and minimum operating costs, while keeping the acceptable level of service under events. Buildings are the end-users of water and energy systems, and they have been identified as a major sector of water and energy consumption in an urban framework. Thus, the water-energy nexus (WEN) approach to analyze the use of two essential resources in buildings can lead to a more sustainable design and the operation of water and energy systems. Heidari and Khovalyg [53] have stated that despite advancing the research, implementation of the WEN approach to design and operate building services should account for existing challenges, such as lack of cooperation between different agencies and inadequate regional pricing of water and energy.
From the aforementioned, it can be derived that research dealing worldwide with the issue of the economy when designing the same building for different seismic zones is not adequate in number. Especially, when relating the matter of economy with the problem of the emissions produced, then this inadequacy in the number of studies performed becomes even bigger. Thus, there is space for more research on this matter, since the results could be very useful both for researchers and practicing engineers. Moreover, it is important to note that the current analytical study will also be beneficial because it will be proven to be very useful in the establishment of an analytical database, where the results from buildings with different number of storeys, supports, floor plans, loadings, etc., will be stored for future use and study. Thus, another use of the present research is the help that it provides for an analytical database to be built and enriched. This database will be proven extremely helpful in the future for an even better analytical investigation from future researchers. This work examines the impact of the construction cost of a five-story building when it passes from one earthquake zone to a higher one, and also the impact to the emissions produced. Engineers worldwide could find the conclusions of this study useful for their work. The regulations used are Eurocode 2 [54] for concrete design and Eurocode 8 [20] for seismic design.
2. Analytical Research
2.1. Construction Details
The present work includes a five-story building without the presence of a basement. This building is rectangular and has dimensions equal to 25 m × 25 m. Thus, the total surface of the rectangular plan was E = 625 m2 (Figure 1). Two structural walls existed in the Y direction at the building perimeter, whereas at the center of the building, an elevator and a staircase existed closed off on all sides by eight walls that formed two symmetrical cores. It is noteworthy that the shear walls and central core have been placed having in mind that they are the structural elements that mainly resist the horizontal actions, such as seismic actions. Figure 1 displays the floor plan of the building. The ground floor height was 4.5 m, whereas the rest of the floors had a height of 3.0 m. Therefore, the total height of the building was htot = 16.5 m. Rigid supports were used, and the effect of the soil was neglected [55,56]. The column sections reduced throughout the height of the building and their section reduction was equal to 5 cm for both section sides per each floor. The wall thickness remained the same for all five floors and was 25 cm. The geometrical specifications for the load-bearing elements are given in Table 1 for all five floors.
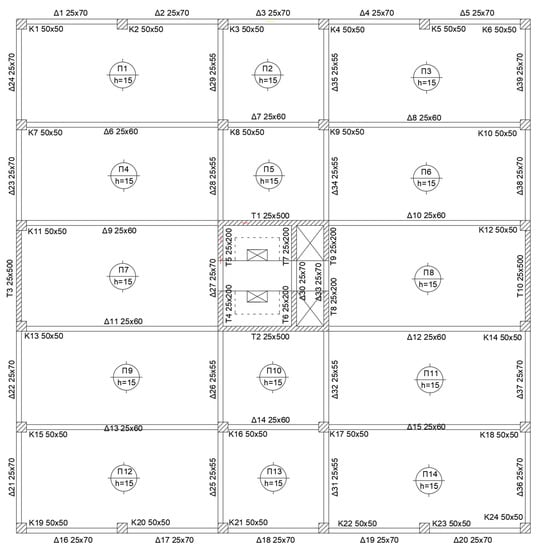
Figure 1.
Floor plan for the building.

Table 1.
Geometrical specifications of the load-bearing elements.
The main element of the load-bearing structure can be characterized as the main core, which was located in the center of the building and included the elevators and stairwells. Regarding the dimensions of the structural elements, there were small differences from floor to floor. There were also structural walls in the building. These were structural walls, T3 and T10, at the two sides of the plan for the building (Figure 1). It can be seen from Figure 1 that all slabs have a thickness of 15 cm. It is noted that all these slabs are bi-directional, and eventually they will be detailed as bi-directional slabs accordingly. Finally, as far as beams are concerned, they were located along the perimeter and internally. The dimensions of the perimetric beams and the beams in the core were 25 × 70 cm, and the internal ones had dimensions of 25 × 60 cm. The cross sections of the load-bearing elements are shown in Table 1. It is noted that the dimensions of all structural elements have been selected in order to match the typical dimensions used in construction practice in Greece for buildings with similar geometrical and loading characteristics. In some cases, the minimum dimensions were chosen, e.g., for the beam width.
2.2. Materials
For all the load-bearing structural elements in the building considered herein, the concrete quality was C30/37 and the steel quality was B500C for the reinforcement bars. Eurocode 2 [54] specifies that for concrete quality C30/37, the modulus of elasticity is Ecm = 32 GPa. The Poisson ratio was considered to be zero (ν = 0) for cracked sections. The B500C steel has a characteristic strength of fyk = 500 Mpa.
2.3. Analysis Method
The building was analyzed for the vertical loads applied under the combination of 1.35G + 1.50Q, as well as for seismic actions under the combination of G + ψ2Q ± Ε. The dynamic spectral method was used for the dynamic analysis of the building. The building was analyzed and examined in three different seismic hazard zones. In zone I, with a maximum seismic horizontal ground acceleration ag = 0.16 g, in zone II, with ag = 0.24 g, and in zone III, with ag = 0.36 g (where g is the acceleration of gravity and is 9.81 m/sec2). Additionally, the design spectrum of Eurocode 8 was used [20] for soil category B and spectrum type 1. Spectrum data used according to EC8 are displayed in Table 2.

Table 2.
Spectrum data used for the dynamic analysis.
As far as the response spectrum method is concerned, there are computational advantages in using this method of seismic analysis for the prediction of displacements and member forces in structural systems. The method involves the calculation of only the maximum values of the displacements and member forces in each mode, using smooth design spectra that are the average of several earthquake motions [57].
Response spectra are curves plotted between the maximum response of the single-degree-of-freedom (SDOF) system, subjected to specified earthquake ground motion and its time period (or frequency). Response spectrum can be interpreted as the locus of maximum response of a SDOF system for the given damping ratio. Response spectra thus helps in obtaining the peak structural responses under a linear range, which can be used for obtaining lateral forces developed in structures due to earthquakes thus facilitating in the earthquake-resistant design of structures. Usually, the response of a SDOF system is determined by the time domain or frequency domain analysis, and for a given time period, the maximum response is picked. This process is continued for a range of possible time periods for the SDOF system [57].
A final plot with the system time period on the x-axis and the response quantity on the y-axis is the required response spectra pertaining to a specified damping ratio and input ground motion. The same process is carried out with different damping ratios to obtain the overall response spectra [57]. After the analyses finish, then the design and detailing of all structural elements takes place according to the provisions of Eurocode 2 [54] for concrete design and Eurocode 8 [20] for seismic design. After the design and detailing, the measurement of the concrete material in terms of volume, and the steel reinforcement material in terms of mass, will take place to evaluate the influence of seismicity on the construction cost and eventually the environmental impact.
2.4. Energy Aspect
It has to be noted the fact that three seismic hazard zones corresponding to three different maximum horizontal ground accelerations are used. These three different seismic zones are the typical seismic zones defined by Eurocode 8 and the Greek National Annex for the Greek region [20]. The reason for choosing the analyses, the dimensioning, and the detailing to occur for all three seismic zones is for comparison purposes. The comparison of results of the quantities of materials used (meaning concrete and reinforcement steel) will display the variation of the quantity of the materials used when moving from one seismic zone to another; meaning from Zone I to Zone II, from Zone II to Zone III, and from Zone I to Zone III. This material quantity variation translates to a construction cost variation. In addition, this construction cost variation translates, eventually, to carbon emissions variation. Thus, if there is, for example a 10% increase in the quantities of concrete and steel moving from Zone I to Zone II, this translates to a 10% increase in the construction cost, and eventually to an increase in carbon emissions. The typical values for carbon emissions and carbon footprint are given in the international literature [58,59]. There are cases where the consulting engineers choose to design a building for a higher seismic zone than the one prescribed in the Eurocode 8 seismic map for Greece [20]. Thus, the consulting engineer should bear in mind not only the possible increase in the construction cost of the load-bearing structure of the building, but also the possible increment in the carbon emissions affecting the environment. That means, that the consulting engineer should consider also green building construction characteristics, too, and not only safety criteria—a fact that the modern design logic advises and prescribes. This is an important energy aspect that should be taken into account, and the research in question tries to investigate using a typical five-story building for Greek construction practice, as well as for other countries’ construction practice.
2.5. Gravity Loads
The load of the partition masonry was considered to be distributed evenly over the whole surface of the floor plan, influencing the design of the slabs, and the load of the perimeter masonry was applied only directly on the perimeter beams, influencing the design of the external beams. In addition, on the roof, a parapet all around the perimeter was considered with a height of 0.90 m, eventually influencing the design of the external beams positioned at the perimeter of the building’s roof. The flooring was considered to have a load of 1.40 kN/m2. The permanent load for the masonry structures was 1.00 kN/m2 for the internal brick structures used as partitions, and 8.00 kN/m for the masonry structures at the perimeter of the slab of the building. The roofing was considered to have a load of 3.50 kN/m2, and the load for the parapet at the perimeter of the roof was assumed to be 3.60 kN/m2. Live loads, representing the loads from humans, furniture, etc., were considered to be 2.00 kN/m2 at every floor slab (i.e., the ground floor, the other typical floors and the roof). The permanent and live loads are shown in Table 3. Eventually, permanent and live loads affect the design of the building both for vertical load combination (1.35G + 1.50Q) and seismic combination (G + 0.3Q ± Ε). For the vertical load combination, loads distributed on slabs (e.g., flooring) affect the design of slabs and of all structural elements underneath the slabs, e.g., beams, columns, etc., whereas loads distributed on perimeter beams (e.g., parapet, perimeter brick structure, etc.) do not affect the design of the slabs, but rather affect the design of the perimeter beams and all structural elements underneath the perimeter beams, e.g., columns, etc.

Table 3.
The permanent and live loads.
2.6. Modelling
Frame elements were used for the modelling of the various structural elements. The frame element is used to model the beam, column, truss, and brace behavior in planar and three-dimensional structures. The frame element uses a general, three-dimensional, beam-column formulation which includes the effects of biaxial bending, torsion, axial deformation, and bi-axial shear deformations [60].
A frame element is modeled as a straight line connecting two points. Each element has its own local coordinate system for defining section properties and loads, and for interpreting the output. Each frame element may be loaded by self-weight, multiple concentrated loads, and multiple distributed loads. End releases are also available to model different fixity conditions at the ends of the element. Element internal forces are produced at the ends of each element and at a user-specified number of equally-spaced output stations along the length of the element, if it is needed [60].
Certain assumptions were used for the design of the five-story building. The stiffness for cracked sections was considered to be 50% of the stiffness of the uncracked sections. The torsional stiffness of the cracked sections was considered to be equal to 10% of the torsional stiffness of the uncracked sections. Thus, the ratio of the cracked stiffness over the uncracked stiffness was equal to 0.50, whereas the ratio of the cracked torsional stiffness over the uncracked torsional stiffness was equal to 0.10. For the calculation of the masses of each floor, half the masses of the vertical load-bearing structural components of the underneath floor, and half the masses of the vertical load-bearing structural components of the upper floor were used. In the framework of this study, the dimensioning of the individual structural elements was carried out exclusively for the first floor (ground floor) of the five-story building for all three seismic zones. The three-dimensional model for the entire building is displayed in Figure 2. SAP2000 software was used for the building modelling.
Figure 2.
3D model for the entire structure: (a) Frame element model; (b) extruded view.
2.7. Model Inputs and Sources
Table 4 displays all the inputs used for modelling the five-story reinforced concrete building and cites, also, the sources of these inputs.

Table 4.
Model inputs and their sources.
3. Results
3.1. Measurements of the Materials
The quantities of concrete and steel used for the detailing of the structural elements of the building were measured for the ground floor and the whole building, respectively. The concrete was measured in terms of volume, and the reinforcement steel was measured in terms of weight. Table 5 displays the amount of concrete occupied by the structural elements of the load-bearing structure for all three seismic zones. The measurements of the steel calculated for the ground floor were used for the estimation of the quantities of steel needed for the load-bearing body of the whole building. Table 6 shows the quantities of steel considered herein.

Table 5.
Concrete measurements for the entire building.

Table 6.
Rebar steel measurements for the ground floor for all three earthquake zones.
3.2. Analysis of Material Measurements
The concrete percentage per floor and the concrete percentage per element are given in Figure 3. Moreover, the reinforcement steel weight increment when changing the seismic zone was calculated. This calculation occurred when changing from seismic zone I to seismic zone II, then from seismic zone II to seismic zone III and, lastly, from seismic zone II to seismic zone III (Figure 4 and Figure 5).
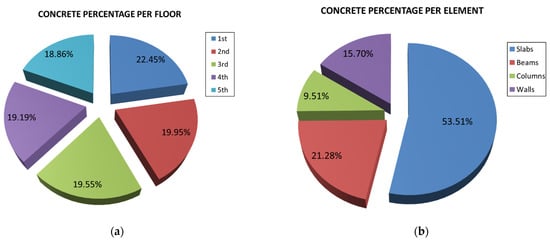
Figure 3.
Percentage of concrete material measured: (a) per story; (b) per type of structural element.
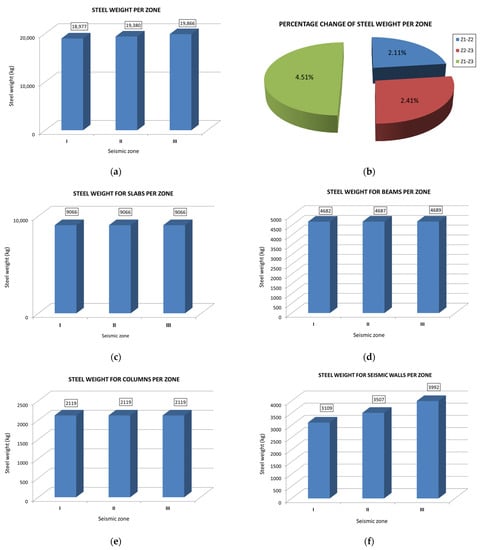
Figure 4.
Percentage change of rebar material measured for each earthquake zone and for each type of structural element.
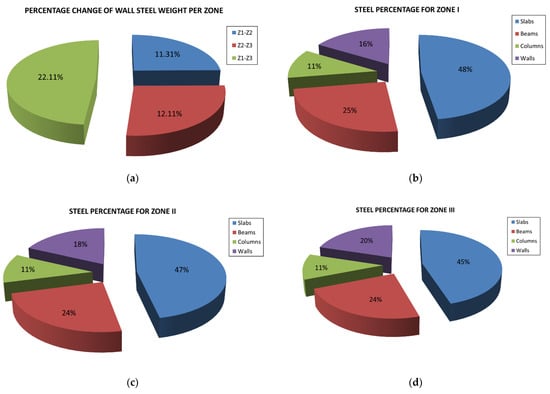
Figure 5.
Percentage change of wall rebar steel measured for each earthquake zone and steel percentages per type of element.
3.3. Analysis of CO2 Emissions
The production of every material has, eventually, a carbon footprint. This carbon footprint has been estimated in the international bibliography [58]. Thus, it is given that, for an average reinforcing steel, the CO2 emissions are approximately 35.2 kg CO2 per 100 kg of reinforcing steel production [59]. In other words, 352 kg CO2 are produced for every ton of reinforcing steel produced. Figure 6 shows the CO2 emissions for each seismic zone and their percentage change when designing for a zone with a higher seismicity compared to zone I.
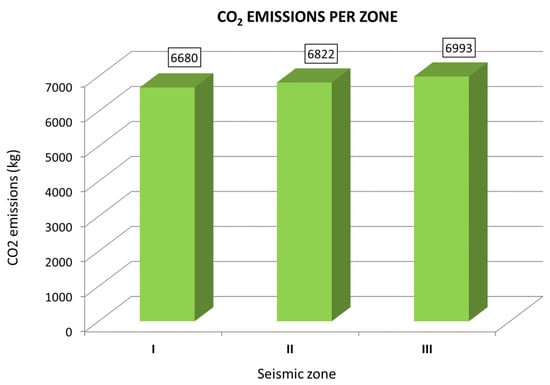
Figure 6.
CO2 emissions and their percentage change measured for each seismic zone.
3.4. Discussion
The measured rebar weight was 18,977 kg for seismic zone I, 19,380 kg for seismic zone II and 19,866 kg for seismic zone III (Table 6, Figure 4). The rebar steel weight needed for the beams and structural walls increased when passing from one earthquake hazard zone to a higher one, whereas for the structural elements of the slabs and columns, the steel requirement remained unstable when increasing the seismic zone (Table 6). This is because the structural load-bearing system of a building can be predominantly characterized as a wall system. Moreover, the following findings were observed:
The percentages of rebar steel weight required by the structural walls were: (a) Zone I = 16%, (b) Zone II = 18%, and (c) Zone III = 20% (Figure 5).
The percentages of rebar steel weight required by the beams were: (a) Zone I = 25%, (b) Zone II = 24%, and (c) Zone III = 24% (Figure 5).
The percentages of rebar steel weight required by the columns were: (a) Zone I = 11%, (b) Zone II = 11%, and (c) Zone III = 11% (Figure 5).
The percentages of rebar steel weight required by the slabs were: (a) Zone I = 48%, (b) Zone II = 47%, and (c) Zone III = 45% (Figure 5).
As far as the floor slabs are concerned, both the volume of the concrete and the weight of the steel did not change in the three seismic hazard zones.
Figure 4f and Table 6 display the increase in the steel reinforcement for the seismic walls moving from zone I to zone II and zone III. It is noticed that for zone I, the wall steel reinforcement is equal to 3109 kg, for zone II, equal to 3507 kg and for zone III, equal to 3992 kg. In addition, it can be seen from Table 6 and Figure 4 that the only significant increase that exists for the steel weight moving from zone I to zone II and III, that is for the steel weight of seismic walls and not for the other structural elements, is that either the steel weight remains the same (slabs, columns) or it increases slightly (beams). This was expected, since the building’s structural system is wall-dominant. Thus, the increase in steel weight was expected to take place, basically, in the structural elements of the seismic walls and not in the other types of structural elements, as it eventually happens. What was not expected was the small increase in steel weight generally, compared to the size of increase in seismicity moving from zone I to zone II and III. Moreover, this is one of the basic matters regarding the present research.
Collectively, in terms of reinforced steel weight, there was an increase of 2.11% from seismic zone I to II, 2.41% from seismic zone II to III and 4.51% from seismic zone I to III (Figure 4).
It is more than obvious from the findings of Figure 4 that there is an increment in the material quantities used when moving from a lower seismic zone to a higher one, meaning from Zone I to Zone II, from Zone II to Zone III and from Zone I to Zone III. This increase in material quantities eventually leads to an increase in the construction cost of the load-bearing structure of the building. In turn, this increment in the construction cost when moving from a lower seismic hazard zone to a higher one translates inevitably to an increase in the carbon emissions produced for the fabrication of these materials. Higher material quantities used for the building construction means higher material quantities fabricated, which in turn means higher carbon emissions, and emissions generally, produced. Thus, the choice of a higher seismic hazard zone taken from the consulting engineer is not only a techno-economical choice (meaning a choice associated with safety and construction cost criteria), but also a choice with clear energy aspects concerning and connecting to the emissions produced for the fabrication of the required material quantities for the building’s construction. Thus, the results of the diagrams of Figure 4 and Figure 5 can be interpreted not only as material quantities and construction cost variations, but also as emission variations regarding the energy aspect and nexus matters. Furthermore, this is also shown in the diagrams of Figure 6, where it is obvious that there is an increase in CO2 emissions and, moreover, the percentage increase in steel quantities follows the percentage increase in CO2 emissions.
4. Conclusions
A five-story building with a rectangular plan was analyzed using a spectral dynamic analysis, and it was designed utilizing Eurocode 2 for the concrete design and Eurocode 8 for the seismic design. The measurement of the concrete volume and rebar steel weight provided the following conclusions:
From seismic zone I to zone II, there was an increase in seismic acceleration by 50%, from I to III the increase was 125% and from II to III the increase was 50%. These percentages should be compared mainly with the percentages of the increase in weight of steel to prove if the construction cost of the building is within reasonable limits.
As far as seismic acceleration is concerned, the following were noticed:
- Moving from Zone I to Zone II, the earthquake acceleration increased by about 50%, whereas the steel demand for the entire building increment was much smaller and equal to 2.11%;
- Moving from Zone II to Zone III, the earthquake acceleration increased by about 50%, whereas the steel demand for the entire building increment was much smaller and equal to 2.41%;
- Moving from Zone I to Zone III, the earthquake acceleration increased by about 125%, whereas the steel demand for the entire building increment was much smaller and equal to 4.51%.
The sizing of the slabs, whether it concerns the reinforcement (steel weight) or the cross sections (volume of concrete), remained constant across all three seismic zones. Therefore, the ratio of steel to concrete in the slabs also remained constant for all floors and finally throughout the construction.
In conclusion, observing the results obtained for all the structural elements in the three seismic zones, it can be said that the rate of increase in construction costs from one zone to another was quite small in relation to the rate of increase in the seismic acceleration in the respective seismic hazard zones. Thus, if an engineer wishes to dimension a construction using the immediately larger seismic zone than the one in which the construction is located for increased safety, they can do so without significantly increasing the cost of materials.
Obviously, if construction cost could be lowered by using a decreased amount of materials (resulting in lesser rebars and concrete volume being used), this could lead to lower costs for structures and decreased emissions during the process of manufacturing these materials. The amount of materials utilized is related to the emissions released to the environment. If great material quantities are utilized to construct a building, then the emissions are also large. However, if a decreased amount of material quantities is utilized, then the emissions decrease. Generally, it can be stated that the percentage increase in CO2 emissions follows the percentage increase in the reinforcing steel when designing for higher seismic zones to zone I. Future studies should emphasize that the minimization of construction material quantities (concrete and steel rebars) minimizes the construction cost and decreases emissions. Thus, the environment is positively affected.
Future research should consider more parameters, such as different floor plans and the number of floors. Furthermore, the effect of the soil and the foundation should be considered, too, in contrast to the utilization of fixed supports for all columns and structural walls at the ground floor.
Author Contributions
Conceptualization, T.C.; methodology, T.C.; formal analysis, D.M. and E.T.; data curation, N.A. and D.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Elwood, K.J.; Eberhard, M.O. Effective Stiffness of Reinforced Concrete Columns. ACI Struct. J. 2009, 106, 476–484. [Google Scholar]
- Watson, S.; Zahn, F.A.; Park, R. Confining Reinforcement for Concrete Columns. J. Struct. Eng. 2006, 120, 1798–1824. [Google Scholar] [CrossRef]
- Devi, G.N.; Subramanian, K.; Santhakumar, A.R. Experimental Investigations on Reinforced Concrete Lateral Load Resisting Systems under Lateral Loads. Exp. Tech. 2011, 35, 59–73. [Google Scholar] [CrossRef]
- Bechtoula, H.; Sakashita, M.; Kono, S.; Watanabe, F.; Eberhard, M.O. Cyclic Performance of Lower Stories of Mid-Rise Reinforced Concrete Frame Buildings. ACI Struct. J. 2006, 103, 513–521. [Google Scholar]
- Francisco, S. Response Analysis of Reinforced Concrete C-Bent Columns. Spring 2006, 23, 33–48. [Google Scholar]
- Barron, J.M.; Hueste, M.B.D. Diaphragm Effects in Rectangular Reinforced Concrete Buildings. ACI Struct. J. 2004, 101, 615–624. [Google Scholar]
- Tavio; Teng, S. Effective Torsional Rigidity of Reinforced Concrete Members. ACI Struct. J. 2004, 101, 252–260. [Google Scholar]
- Mansour, M.; Hsu, T.T.C. Behavior of Reinforced Concrete Elements under Cyclic Shear. II: Theoretical Model. J. Struct. Eng. 2004, 131, 54–65. [Google Scholar] [CrossRef]
- Harasimowicz, A.P.; Goel, R.K. Seismic Code Analysis of Multi-Storey Asymmetric Buildings. Earthq. Eng. Struct. Dyn. 1998, 27, 173–185. [Google Scholar] [CrossRef]
- Chrysanidis, T.; Panoskaltsis, V.; Tegos, I. Preliminary Design and Analysis of Cost Parameters of a High-Rise Building: Braced Shear Wall Core System. Int. J. Civ. Eng. Technol. 2016, 7, 137–152. [Google Scholar]
- Chrysanidis, T.; Panoskaltsis, V.; Tegos, I. Parametrical Cost Analysis of an Ultra High-Rise Building: Detailed Design. Int. J. Appl. Eng. Res. 2016, 11, 9644–9650. [Google Scholar]
- Chrysanidis, T.; Tegos, I. Cost Comparison and Parametrical Investigation of the R/C Shear Wall Core of a Tall Building. Int. J. Eng. Res. Technol. 2016, 5, 592–595. [Google Scholar]
- Tegos, I.; Giannakas, N.; Chrysanidis, T. Serviceability Cracking Check of Circular Section Piers. Bridg. Struct. 2011, 7, 43–52. [Google Scholar] [CrossRef]
- Tegos, I.; Giannakas, N.; Chrysanidis, T. Cross-Correlation of Stresses in the Transverse Reinforcement under Shear Load and Confinement. In Proceedings of the 2013 International Van Earthquake Symposium, Van, Turkey, 23–27 October 2013. [Google Scholar]
- Parapanisiou, A.; Argyropoulou, D.; Andreadou, E.; Demertzi, X.; Chrysanidis, T.; Tegos, I. A Suggestion of a Quick and Economic Method of Strengthening Bridge Piers. In Proceedings of the International Conference: Innovations on Bridges and Soil-Bridge Interaction (IBSBI 2011), Athens, Greece, 13–15 October 2011; pp. 419–426. [Google Scholar]
- Tegos, I.; Giannakas, N.; Chrysanidis, T. Seismic Design of Circular Section Piers under Axial Load and Biaxial Bending Belonging to Low Ductility Bridges: Analytical and Experimental Investigation of Bending Resistance. In Proceedings of the International Conference: Innovations on Bridges and Soil-Bridge Interaction (IBSBI 2011), Athens, Greece, 13–15 October 2011; pp. 141–148. [Google Scholar]
- Tegos, I.; Kifokeris, D.; Chrysanidis, T. Seismic Design of R/C Piers of Hollow Circular Cross Sections. In Proceedings of the 2013 International Van Earthquake Symposium, Van, Turkey, 23–27 October 2013. [Google Scholar]
- Penelis, G.; Stylianidis, K.; Kappos, A.; Ignatakis, C. Reinforced Concrete Structures; A.U.Th. Press: Thessaloniki, Greece, 1995. [Google Scholar]
- Penelis, G.G.; Kappos, A.J. Earthquake-Resistant Concrete Structures; E & F N SPON (Chapman & Hall): London, UK, 1996. [Google Scholar]
- European Committee for Standardization BS EN 1998-1:2004; Eurocode 8: Design of Structures for Earthquake Resistance—Part 1: General Rules, Seismic Actions and Rules for Buildings. BSI Standards: London, UK, 2013.
- Ministry of Environment Planning and Public Works Greek Earthquake Resistant Design Code; O.A.S.P.: Athens, Greece, 2003. (In Greek)
- Papageorgiou, G.; Papadimitriou, E.; Alamanis, N.; Xafoulis, N.; Chouliaras, I.; Lazogiannis, K. Construction Cost Comparative Analysis of Highways in Greece. PRIME Int. J. Pract. Res. Innov. Manag. Entrep. 2019, 12, 68–85. [Google Scholar]
- Srivastava, M.; Kumar, V. The Methods of Using Low Cost Housing Techniques in India. J. Build. Eng. 2018, 15, 102–108. [Google Scholar] [CrossRef]
- Jasvi, A.; Bera, D. Sustainable Use of Low Cost Building Materials in the Rural India. Int. J. Res. Eng. Technol. 2015, 4, 534–547. [Google Scholar] [CrossRef]
- Chrysanidis, T. The Effect of Longitudinal Reinforcement Ratio on the Lateral Buckling Behavior of R/C Walls Modelled Using Prism Elements. J. Build. Eng. 2021, 42, 102456. [Google Scholar] [CrossRef]
- Chrysanidis, T. Evaluation of Out-of-Plane Response of R/C Structural Wall Boundary Edges Detailed with Maximum Code-Prescribed Longitudinal Reinforcement Ratio. Int. J. Concr. Struct. Mater. 2020, 14, 3. [Google Scholar] [CrossRef]
- Chrysanidis, T. Influence of Elongation Degree on Transverse Buckling of Confined Boundary Regions of R/C Seismic Walls. Constr. Build. Mater. 2019, 211, 703–720. [Google Scholar] [CrossRef]
- Haro, A.; Kowalsky, M.; Chai, Y.; Lucier, G. Boundary Elements of Special Reinforced Concrete Walls Tested under Different Loading Paths. Earthq. Spectra 2018, 34, 1267–1288. [Google Scholar] [CrossRef]
- Welt, T.; Massone, L.; LaFave, J.; Lehman, D.; McCabe, S.; Polanco, P. Confinement Behavior of Rectangular RC Prisms Simulating Wall Boundary Elements. J. Struct. Eng. 2017, 143, 1–12. [Google Scholar] [CrossRef]
- Terzioglu, T.; Orakcal, K.; Massone, L.M. Cyclic Lateral Load Behavior of Squat Reinforced Concrete Walls. Eng. Struct. 2018, 160, 147–160. [Google Scholar] [CrossRef]
- Ho, N.M.; Doh, J.H.; Fragomeni, S. Instability Analysis of Reinforced Concrete Walls with Various Support Conditions. Struct. Des. Tall Spec. Build. 2017, 26, e1353. [Google Scholar] [CrossRef]
- Lim, J.-J.; Park, H.-G.; Eom, T.-S. Cyclic Load Tests of Reinforced Concrete Columns with High-Strength Bundled Bars. ACI Struct. J. 2017, 114, 197–207. [Google Scholar] [CrossRef]
- Chrysanidis, T.; Panoskaltsis, V. Experimental Investigation on Cracking Behavior of Reinforced Concrete Tension Ties. Case Stud. Constr. Mater. 2022, 16, e00810. [Google Scholar] [CrossRef]
- Raza, S.; Khan, M.; Menegon, S.; Tsang, H.-H.; Wilson, J. Strengthening and Repair of Reinforced Concrete Columns by Jacketing: State-of-the-Art Review. Sustainability 2019, 11, 3208. [Google Scholar] [CrossRef]
- Chrysanidis, T.; Tegos, I. Axial and Transverse Strengthening of R/C Circular Columns: Conventional and New Type of Steel and Hybrid Jackets Using High-Strength Mortar. J. Build. Eng. 2020, 30, 101236. [Google Scholar] [CrossRef]
- Tegos, I.; Chrysanidis, T.; Tsitotas, M. Seismic Behaviour of R/C Columns and Beams with Interlocking Spirals. Int. J. Sci. Eng. Res. 2014, 5, 310–319. [Google Scholar]
- Tegos, I.; Chrysanidis, T. Spare Additional Confinement in Spiral Arrangements. Int. J. Sci. Res. 2014, 3, 110–113. [Google Scholar]
- Tegos, I.; Chrysanidis, T. Columns With Spiral Reinforcement Under Concentric Compression. Int. J. Res. Eng. Technol. 2014, 3, 125–132. [Google Scholar] [CrossRef]
- Minafò, G.; Papia, M. Concrete Softening Effects on the Axial Capacity of RC Jacketed Circular Columns. Eng. Struct. 2016, 128, 215–224. [Google Scholar] [CrossRef]
- Minafò, G. A Practical Approach for the Strength Evaluation of RC Columns Reinforced with RC Jackets. Eng. Struct. 2015, 85, 162–169. [Google Scholar] [CrossRef]
- Takeuti, A.; de Hanai, J.; Mirmiran, A. Preloaded RC Columns Strengthened with High-Strength Concrete Jackets under Uniaxial Compression. Mater. Struct. 2008, 41, 1251–1262. [Google Scholar] [CrossRef]
- Taghavi, S.; Miranda, E. Approximate Floor Acceleration Demands in Multistory Buildings. II: Applications. J. Struct. Eng. 2005, 131, 212–220. [Google Scholar] [CrossRef]
- Otani, S.; Kabeyasawa, T.; Shlohara, H.; Aoyama, H. Analysis of the Full Scale Seven Story Reinforced Concrete Test Structure. Symp. Pap. 1984, 84, 203–239. [Google Scholar]
- Kilkiş, B.; Kilkiş, Ş. Hydrogen Economy Model for Nearly Net-Zero Cities with Exergy Rationale and Energy-Water Nexus. Energies 2018, 11, 1226. [Google Scholar] [CrossRef]
- Fan, J.L.; Kong, L.S.; Wang, H.; Zhang, X. A Water-Energy Nexus Review from the Perspective of Urban Metabolism. Ecol. Modell. 2019, 392, 128–136. [Google Scholar] [CrossRef]
- Ferrara, M.; Sirombo, E.; Fabrizio, E. Automated Optimization for the Integrated Design Process: The Energy, Thermal and Visual Comfort Nexus. Energy Build. 2018, 168, 413–427. [Google Scholar] [CrossRef]
- Erdogan, S. Dynamic Nexus between Technological Innovation and Buildings Sector’s Carbon Emission in BRICS Countries. J. Environ. Manag. 2021, 293, 112780. [Google Scholar] [CrossRef]
- Xu, X.; González, J.E.; Shen, S.; Miao, S.; Dou, J. Impacts of Urbanization and Air Pollution on Building Energy Demands—Beijing Case Study. Appl. Energy 2018, 225, 98–109. [Google Scholar] [CrossRef]
- Sun, Y.; Deng, L.; Pan, S.-Y.; Chiang, P.-C.; Sable, S.S.; Shah, K.J. Integration of Green and Gray Infrastructures for Sponge City: Water and Energy Nexus. Water Energy Nexus 2020, 3, 29–40. [Google Scholar] [CrossRef]
- Sun, K.; Specian, M.; Hong, T. Nexus of Thermal Resilience and Energy Efficiency in Buildings: A Case Study of a Nursing Home. Build. Environ. 2020, 177, 106842. [Google Scholar] [CrossRef]
- Purwanto, A.; Sušnik, J.; Suryadi, F.X.; de Fraiture, C. Using Group Model Building to Develop a Causal Loop Mapping of the Water-Energy-Food Security Nexus in Karawang Regency, Indonesia. J. Clean. Prod. 2019, 240, 118170. [Google Scholar] [CrossRef]
- Mehrjerdi, H.; Saad, M.; Lefebvre, S. Efficiency-Resilience Nexus in Building Energy Management Under Disruptions and Events. IEEE Syst. J. 2022, 16, 299–308. [Google Scholar] [CrossRef]
- Heidari, A.; Khovalyg, D. Exploring Water-Energy Nexus at the Building Level. ASHRAE Trans. 2020, 126, 308–314. [Google Scholar]
- European Committee for Standardization BS EN 1992-1-1:2004; Eurocode 2: Design of Concrete Structures—Part 1-1: General Rules and Rules for Buildings. BSI Standards: London, UK, 2008.
- Alamanis, N.; Dakoulas, P. Investigation on the Effect of Spatial Variability of Soil Properties on Permanent Seismic Displacements of Slopes in Load. In Proceedings of the 14th Baltic Sea Geotechnical Conference 2020, Helsinki, Finland, 25–27 May 2020. [Google Scholar]
- Alamanis, N.; Dakoulas, P. Vulnerability of Soil Slopes against Seismic Damage Based on the Effect of Spatial Variability of Soil Properties on the Development of Permanent Seismic Displacements. In Proceedings of the International Conference on Research in Engineering, Technology and Science, Lisbon, Portugal, 3–7 February 2019. [Google Scholar]
- Teja, P.; Shahab, S.J. Dynamic Analysis Using Response Spectrum Seismic Loading. Int. J. Magazone Eng. Technol. Manag. Res. 2017, 4, 802–808. [Google Scholar]
- Alcorn, A. Embodied Energy and CO2 Coefficients for NZ Building Materials; Centre for Building Supporting Research: Wellington, New Zealand, 2003. [Google Scholar]
- Yeo, D.; Gabbai, R.D. Sustainable Design of Reinforced Concrete Structures through Embodied Energy Optimization. Energy Build. 2011, 43, 2028–2033. [Google Scholar] [CrossRef]
- Computers and Structures Inc. SAP2000 Basic Analysis Reference Manual, Version 19; Berkley, CA, USA; 2006. Available online: https://docs.csiamerica.com/manuals/sap2000/CSiRefer.pdf (accessed on 21 February 2022).
- Standardization, E.C. for BS EN 1991-1-1:2002; Eurocode 1: Actions on Structures—Part 1-1: General Actions—Densities, Self-Weight, Imposed Loads for Buildings. BSI Standards: London, UK, 2004.
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).