Two-Step Pricing Decision Models for Manufacturer-Led Dual-Channel Supply Chains
Abstract
:1. Introduction
2. Modeling Methodology
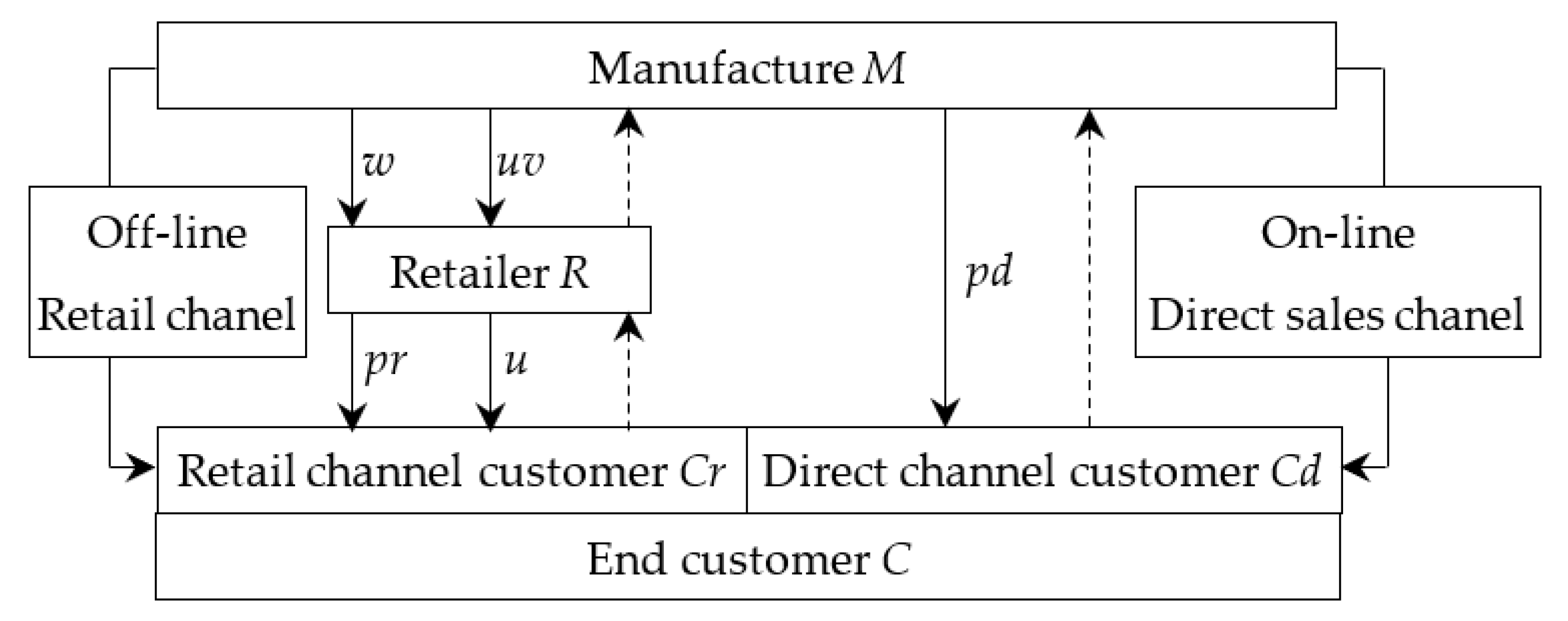
2.1. Model Description
2.2. Symbol Description
2.3. Establishment of Decision-Making Model
3. Basic Decision Model of Dual-Channel Supply Chain
3.1. Centralized Decision Model of Dual-Channel Supply Chain
3.2. Decentralized Decision Model of Dual-Channel Supply Chain
4. Two-Step Pricing Decision Models under the Coordinated Decisions of a Dual-Channel Supply Chain
5. Changes in Supply Chain Profit
6. Numerical Results and Analysis
7. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, J.; Zhang, W.; Liu, Z. Joint pricing, services and quality decisions in a dual-channel supply chain. RAIRO-Oper. Res. 2020, 54, 1041–1056. [Google Scholar] [CrossRef]
- Esmaeili, M.; Aryanezhad, M.B.; Zeephongsekul, P. A game theory approach in seller–buyer supply chain. Eur. J. Oper. Res. 2009, 195, 442–448. [Google Scholar] [CrossRef]
- Shin, J. How does free riding on customer service affect competition. Mark. Sci. 2007, 26, 488–503. [Google Scholar] [CrossRef]
- Wu, D.; Ray, G.; Geng, X.; Whinston, A. Implications of reduced search cost and free riding in E-commerce. Mark. Sci. 2004, 23, 255–262. [Google Scholar] [CrossRef]
- Park, S.Y.; Keh, H.T. Modelling hybrid distribution channels: A game-theoretic analysis. J. Retail. Consum. Serv. 2003, 10, 155–167. [Google Scholar] [CrossRef]
- Cachon, G.P.; Kök, A.G. Competing manufacturers in a retail supply chain: On contractual form and coordination. Manag. Sci. 2010, 56, 571–589. [Google Scholar] [CrossRef]
- Giannoccaro, I.; Pontrandolfo, P. Supply chain coordination by revenue sharing contracts. Int. J. Prod. Econ. 2004, 89, 131–139. [Google Scholar] [CrossRef]
- Boyaci, T. Competitive stocking and coordination in a multiple-channel distribution system. IIE Trans. 2005, 37, 407–427. [Google Scholar] [CrossRef]
- Cui, T.H.; Raju, J.S.; Zhang, Z.J. Fairness and channel coordination. Manag. Sci. 2007, 53, 1303–1314. [Google Scholar]
- Chiang, W. Product availability in competitive and cooperative dual-channel distribution with stock-out based substitution. Eur. J. Oper. Res. 2010, 200, 111–126. [Google Scholar] [CrossRef]
- John, R.B. Handbooks in Operations Research and Management Science; Linetsky, V., Ed.; Elsevier Science: Amsterdam, The Netherlands, 2007; pp. 104–126. [Google Scholar]
- Cai, G. Channel Selection and coordination in dual-channel supply chains. J. Retail. 2010, 86, 22–36. [Google Scholar] [CrossRef]
- Wang, X.; Zhu, Q.; Cheng, T. Subcontracting price schemes for order acceptance and scheduling. Omega 2015, 54, 1–10. [Google Scholar] [CrossRef]
- Tsay, A.A.; Agrawal, N. Channel dynamics under price and service competition. Manuf. Serv. Oper. Manag. 2000, 2, 372–391. [Google Scholar] [CrossRef]
- Lau, A.; Lau, H.S.; Wang, J.C. How a dominant retailer might design a purchase contract for a newsvendor-type product with price-sensitive demand. Eur. J. Oper. Res. 2008, 190, 443–458. [Google Scholar] [CrossRef]
- Shugan, J. Managing Channel Profits. Mark. Sci. 1983, 2, 239–272. [Google Scholar]
- Oliveira, F.S.; Ruiz, C.; Conejo, A.J. Contract design and supply chain coordination in the electricity industry. Eur. J. Oper. Res. 2013, 227, 527–537. [Google Scholar] [CrossRef]
- Cai, H.; Song, Q. Pricing strategies in a two-echelon supply chain with sales efforts and channel conflicts. IEEE Access 2020, 99, 83238–83247. [Google Scholar] [CrossRef]
- Zhang, C.; Liu, Y.; Han, G. Two-stage pricing strategies of a dual-channel supply chain considering public green preference. Comput. Ind. Eng. 2020, 151, 106988. [Google Scholar] [CrossRef]
- Lei, Q.; He, J.; Ma, C.; Jin, Z. The impact of consumer behavior on preannounced pricing for a dual-channel supply chain. Int. Trans. Oper. Res. 2020, 27, 2949–2975. [Google Scholar] [CrossRef]
- Pu, X.; Sun, S.; Han, G. Differentiated-product distribution in a dual-channel supply chain. Manag. Decis. Econ. 2019, 4, 363–373. [Google Scholar] [CrossRef]


| Symbols and Variables | Definitions |
|---|---|
| s | The ratio of demand for products by offline retail customers |
| 1-s | The ratio of demand for products by online direct customers |
| a | The total basic demand of the market |
| Pr | The product transaction price for offline retail channel retailers |
| Pd | The product transaction price for online direct channel manufacturers with customers |
| α | The sensitivity of product interaction between online and offline dual channels |
| β | The sensitivity to market demand in online and offline dual channels |
| Dr | Demand for the product by offline retail channel customers |
| Dd | Demand for online direct channel customers |
| πr | The profit of the retailer |
| πd | The profit of the manufacturer |
| πz | The overall profit of the supply chain |
| w | The wholesale price of the wholesale product of the retailer from the manufacturer |
| c | The cost of the manufacturer to produce the product (per unit) |
| u | Promotion level of the retailer’s offline retail product promotion |
| βu | The change in demand when the promotion level is |
| uv | The compensation given by the manufacturer to the retailer after the retailer’s promotion |
| u2 | The cost of the retailer’s online promotion |
| v2 | The cost of the manufacturer’s compensation for retailer promotions |
| Superscript L | Two-step pricing decisions |
| Superscript j | Centralized decision model |
| Superscript f | Decentralized decision model |
| 0.1 | 4 | 9.38 | 0.01 | 9.36 | 9.35 | 0.01 | 9.37 | 9.38 |
| 0.2 | 4 | 6.82 | 0.03 | 6.76 | 6.73 | 0.08 | 6.74 | 6.82 |
| 0.3 | 4 | 4.71 | 0.06 | 4.58 | 4.51 | 0.22 | 4.49 | 4.71 |
| 0.4 | 4 | 3.03 | 0.11 | 2.81 | 2.70 | 0.40 | 2.63 | 3.03 |
| 0.5 | 4 | 1.79 | 0.17 | 1.45 | 1.28 | 0.64 | 1.15 | 1.79 |
| 0.6 | 4 | 0.98 | 0.24 | 0.50 | 0.26 | 0.92 | 0.06 | 0.98 |
| 0.7 | 4 | 0.62 | 0.32 | −0.03 | −0.35 | 1.26 | −0.64 | 0.62 |
| 0.8 | 4 | 0.69 | 0.42 | −0.15 | −0.57 | 1.64 | −0.95 | 0.69 |
| 0.5 | 4 | 1.79 | 0.17 | 1.45 | 1.28 | 0.66 | 0.64 | 1.79 |
| 0.5 | 4.1 | 1.79 | 0.17 | 1.45 | 1.28 | 0.65 | 1.14 | 1.79 |
| 0.5 | 4.2 | 1.79 | 0.17 | 1.45 | 1.28 | 0.65 | 1.14 | 1.79 |
| 0.5 | 4.3 | 1.79 | 0.17 | 1.45 | 1.28 | 0.64 | 1.15 | 1.79 |
| 0.5 | 4.4 | 1.79 | 0.17 | 1.45 | 1.28 | 0.64 | 1.15 | 1.79 |
| 0.5 | 4.5 | 1.79 | 0.17 | 1.45 | 1.28 | 0.64 | 1.15 | 1.79 |
| 0.5 | 4.6 | 1.79 | 0.17 | 1.45 | 1.28 | 0.63 | 1.16 | 1.79 |
| 0.5 | 4.7 | 1.79 | 0.17 | 1.45 | 1.28 | 0.63 | 1.16 | 1.79 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Wu, D.; Zhao, X. Two-Step Pricing Decision Models for Manufacturer-Led Dual-Channel Supply Chains. Sustainability 2022, 14, 10005. https://doi.org/10.3390/su141610005
Zhang X, Wu D, Zhao X. Two-Step Pricing Decision Models for Manufacturer-Led Dual-Channel Supply Chains. Sustainability. 2022; 14(16):10005. https://doi.org/10.3390/su141610005
Chicago/Turabian StyleZhang, Xuelong, Doudou Wu, and Xiangzhong Zhao. 2022. "Two-Step Pricing Decision Models for Manufacturer-Led Dual-Channel Supply Chains" Sustainability 14, no. 16: 10005. https://doi.org/10.3390/su141610005
APA StyleZhang, X., Wu, D., & Zhao, X. (2022). Two-Step Pricing Decision Models for Manufacturer-Led Dual-Channel Supply Chains. Sustainability, 14(16), 10005. https://doi.org/10.3390/su141610005






