Forecasting Fine Particulate Matter Concentrations by In-Depth Learning Model According to Random Forest and Bilateral Long- and Short-Term Memory Neural Networks

Abstract

Accurate prediction of fine particulate matter concentration in the future is important for human health due to the necessity of an early warning system. Generally, deep learning methods, when widely used, perform better in forecasting the concentration of PM_2.5. However, the source information is limited, and the dynamic process is uncertain. The method of predicting short-term (3 h) and long-term trends has not been achieved. In order to deal with the issue, the research employed a novel mixed forecasting model by coupling the random forest (RF) variable selection and bidirectional long- and short-term memory (BiLSTM) neural net in order to forecast concentrations of PM_2.5/0~12 h. Consequently, the average absolute percentage error of 1, 6, and 12 h shows that the PM_2.5 concentration prediction is 3.73, 9.33, and 12.68 μg/m³ for Beijing, 1.33, 3.38, and 4.60 μg/m³ for Guangzhou, 1.37, 4.19, and 6.35 μg/m³ for Xi’an, and 2.20, 7.75, and 10.07 μg/m³ for Shenyang, respectively. Moreover, the results show that the suggested mixed model is an advanced method that can offer high accuracy of PM_2.5 concentrations from 1 to 12 h post.

1. Introduction

Air contamination can be one of the most severe worldwide issues causing ecological and environmental damage [1,2,3] as well as damage to human fitness [4,5,6], especially under long-term high-PM_2.5 (diameter less than or equal 2.5 μg/m³) concentration conditions, which would pose serious threats to public health and respiratory filtration systems. PM_2.5 is known as “pulmonary particulate matter” and is a key index for assessing fitness harm [7,8]. Therefore, an accurate understanding of PM_2.5 concentration is of great significance for early warning of atmospheric quality, which helps to reduce health damage and economic loss.

It is indeed challenging to use a single linear model to consider the complex, multi-parameter, nonlinear PM_2.5 concentration prediction process [3,9,10]. For example, Lu et al. [11] showed that the coupled model of back-propagation artificial neural network (BPANN) as well as support vector regression (SVR) have a significant advantage in solving the nonlinear relationship between the input parameters and dependent variable than those of partial least squares regression (PLSR) under the same input parameters. Thus, more and more research has employed the machine learning methods to manage the nonlinear problems. By using the artificial neural network (ANN), support vector machine (SVM), and other machine study algorithms, Zhu and Lu [12] obtained a higher correlation with R² value at 0.8 than the linear methods performed during the PM_2.5 and PM₁₀ (diameter less than or equal 10 μg/m³) concentration forecasts. Moreover, in order to catch the hourly variation of the PM_2.5 concentration, Shang et al. [13] employed the extreme learning machine (ELM) and classification regression tree (CART) mixed models.

Gradually, with the deepening of research, a series of deep networks, such as deep belief network (DBN) and long- and short-memory neural network (LSTM), were introduced to verify its performance. Each model showed better results than traditional machine learning ways [2,14,15,16,17]. Therefore, the in-depth neural nets were treated as advanced methods with systematic and scientific neuron and network structures and performed well in capturing input–output parameter characteristics. In addition to the abovementioned, BiLSTM has much more strength for forecasting PM_2.5 concentration. Without considering the input parameters of forward and backward information, the normal time series features are extracted from the forward LSTM layer, and the future change information is obtained from the reverse LSTM layer to further improve the prediction results.

However, with a single deep neural net, it is hard to achieve a precise forecast of the PM_2.5 concentration. For example, Dai et al. [18] showed that the RNN (recurrent neural network) model could calculate obvious deviation with gradient explosion and gradient disappearance, which is the same as the LSTM model [19], and could hardly reflect spatial information. Therefore, more and more studies introduced mixed models for prediction, which are beneficial to a singular model [9,20,21]. Using this method, each step would perform better with the advantage utilized, such as maximizing input parameter information [22], spatiotemporal data [23], deviation correction data [24], etc., to calculate more precise estimate consequences. As Zhang et al. [25] demonstrated, the PM_2.5 concentration prediction could be treated as a statistical method by capturing the historical trend and assessing the future periods. Additionally, the univariate and multivariate parameters constitute forecasting input elements. Taking the autoregressive integrated moving average (ARIMA) mode as an example [26], we could acquire accuracy results just by using the PM_2.5 series data information in the short term. A much better prediction could be obtained if studies apply plenty of variables as input parameters to acquire the variation of influencing factors and forecast targets [27,28]. An adaptive method for decomposing was widely used based on the RF algorithm, and the prediction of PM_2.5 concentration can serve as a statistical method by capturing historical trends and assessing future periods. Univariate and multivariate parameters constitute the predictive inputs. Taking ARIMA as an example [26], accurate results can be obtained in a short period using only PM_2.5 series data information.

However, the accuracy of prediction results is greatly reduced due to the increasing uncertainty of disturbance factors when dealing with a long-term forecast. Chen [29] and Sawlani et al. [30] reported that meteorological conditions and other air pollution are the main influencing factors (such as PM₁₀, SO₂, VOCs, and NOx, etc.) for changes in PM_2.5 concentrations. If many variables are used as input parameters to obtain the change in influencing factors and forecast targets, better prediction results can be obtained [27,28]. An adaptive decomposition method based on the RF (random forest) algorithm was widely used, and it had advantages in managing complicated nonlinear relations between variables. Bai et al. [4] used a radio-frequency model that incorporated different spatial–temporal variable sources for PM_2.5 predictions in New York state and achieved good consequences. Based on this function, the RF model has the advantage of using time series data and reflecting changing features, while the Fourier transforms method and other methods could not achieve those functions as well as the wavelet decomposition method.

In fact, the PM_2.5 concentration prediction methods are in depth but still present challenges. Most of the existing time series prediction focuses on the increasing forecast performance of the original sequence without making full use of the effective information implicit in the predictive error sequence. For instance, both precision of peak forecast [31] and the long-term forecast error reduction [29] need improvement. Considering the aforementioned issues, a novel mixed model was proposed with the (RF-BiLSTM) bonding RF approach as well as BiLSTM model to forecast the concentration of PM_2.5 in the short term (T + 1, T + 3 moments) as well as the long term (T + 12 moments).

Herein, we present the following innovations: (1) A novel PM_2.5 concentration forecast mixed model was recommended to significantly ameliorate forecast precision for the short term as well as the long term. (2) The results showed that the RF model is introduced to decompose the test set independently while the BiLSTM model is coupled. (3) The model was compared with LSTM, SVM, RF, and Tree algorithms. (4) The model was compared with other algorithms, such as LSTM, SVM, RF, and tree. The parameters of different models were adjusted according to the model performance, and the data of different lead times were selected to observe the experimental results. (5) The new mixed-mixing model performs well in spatiotemporal generalization and in reflecting the context relationship of the time point.

2. Methods and Materials

2.1. Study Area and Materials

Beijing, Guangzhou, Xi’an, and Shenyang are the typical representatives of China’s capital, south, central, and northeast regions with high population density and economic prosperity. Beijing is bordered by Tianjin in the east and Hebei in the west, with high terrain in the northwest. Guangzhou presents the characteristics of high terrain in the northeast, high terrain in the southwest, and mountains next to the sea. Xi’an is the highest of all the Chinese cities, and its meteorological characteristics vary greatly from season to season. Shenyang has obvious location advantages and dense transportation networks. It is a famous industrial city that focuses on equipment manufacturing. Under such circumstances, more scientific and precise prediction consequences of PM_2.5 concentration is needed to reduce risk exposure.

In the research, the surface meteorological and air quality data from January 2013 to December 2015 were applied as input parameters for the model. Therein, meteorological data including dew point temperature (DT), hourly temperature (T), wind direction at 2 m (U), and wind speed at 2 m (V) were downloaded from the national oceanic and atmospheric administration (https://www.ncdc.noaa.gov/, accessed on 6 July 2022). Hourly data of six pollutants (e.g., PM_2.5, PM₁₀ (particulate matter 10), SO₂ (sulfur dioxide), NO₂ (nitrogen dioxide), O₃ (ozone), and CO₂ (carbon dioxide)) were acquired from the Chinese ministry of environment (http://www.cnemc.cn/, accessed on 6 June 2022). The position of the research area is illustrated in Figure 1. Since there are transmission errors and sensor failures at the observation points [32], abnormal issues and irregular disappearance in the monitor information need verification as well as testing. Meanwhile, an unmodified, objective, and relatively complete basic data set of time series is the cornerstone of prediction. From previous studies, we chose the mean completion to recension pollutants concentration data, while the missing rate between 0% and 3%, and missing rate between 3.01% and 10% was applied using linear interpolation.

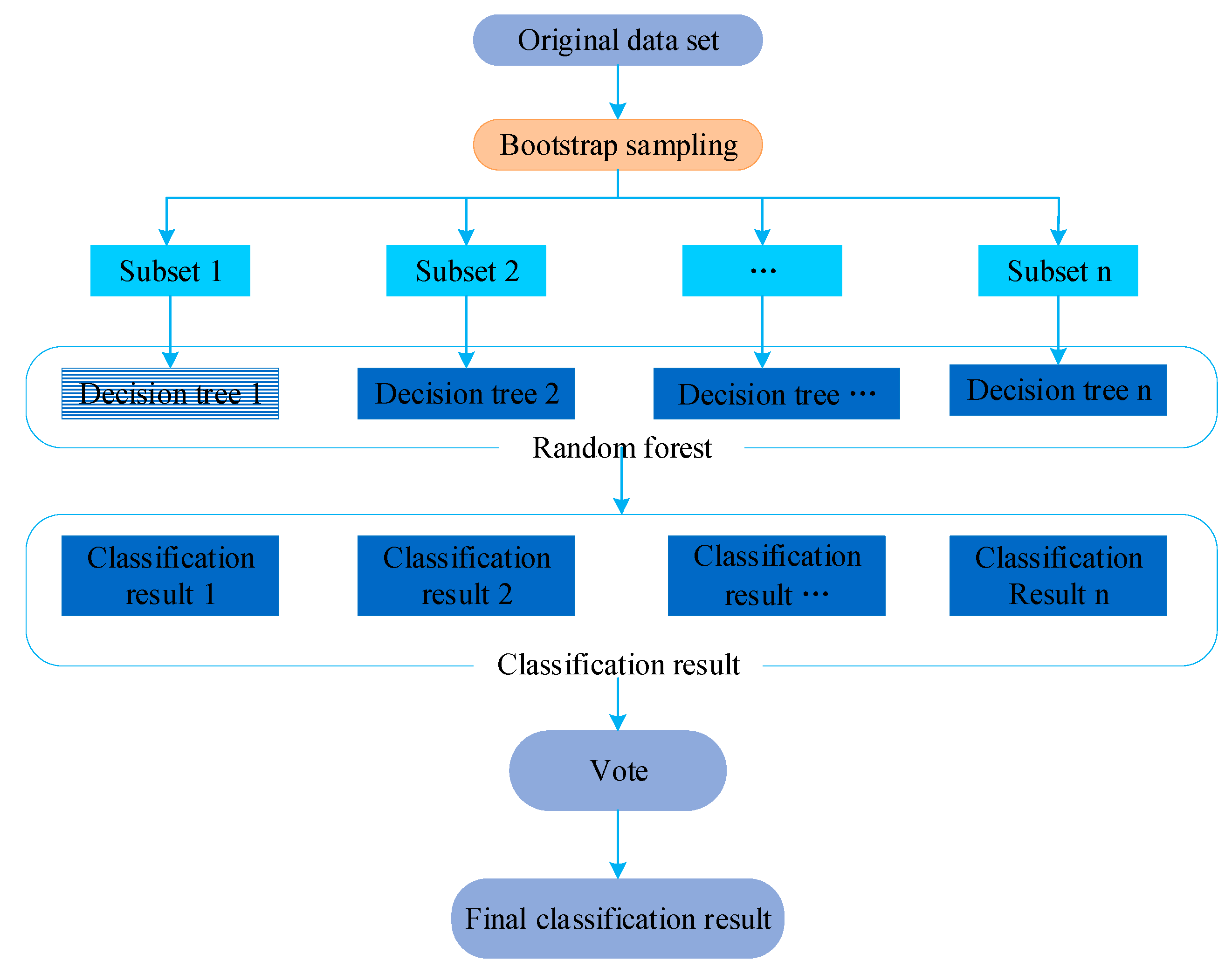
2.2. Random Forest

Random forest is a supervisory machine study algorithm. It extracts multiple subsets from the original data, trains each subset, and summarizes the classification results of different subsets to get the final result (Figure 2). In addition, random forest has an important feature which can calculate the importance of individual feature variables. Therefore, this study calculated the importance of each feature’s influence on PM_2.5 concentration, sorted these features, and screened out the most important feature.

2.3. Bi-Directional Long Short-Term Memory

Before introducing BiLSTM, we need to know about the LSTM. Hochreiter and Schmidhuber [33] were the first researchers to propose the model of LSTM, which has achieved great success in solving many problems and has been used in many subjects [34,35]. Compared to other models, the scale of data required for LSTM studies is not as long.

LSTM consists of the import word $X_t$, cell status $C_t$, temporary cell status ${\tilde{C}}_t$, concealed layer status $h_t$, forgetting gate $f_t$, memory gate $i_t$, as well as output gate $o_t$ at time t. The calculation procedure is below:

(1) Count the forgetting gate and choose the data to be forgotten.

Import: concealed layer status $h_{t-1}$ of former time, import word $X_t$ of present time.

Export: forgetting gate score $f_t$.

(2) Calculate the memory gate and select the information to be memorized.

Input: hidden layer state $h_{t-1}$ of the previous time, input word $X_t$ of the current time.

Output: memory gate value $i_t$, temporary cell state ${\tilde{C}}_t$.

(3) Calculate the cell state at the current time.

Input: memory gate value $i_t$, forgetting gate value $f_t$, temporary cell state ${\tilde{C}}_t$, last moment cell status $C_{t-1}$.

Output: cell state C at the current time.

(4) Calculate the output gate and current hidden layer state.

Import: hidden layer state $h_{t-1}$ of the previous time, the input word $X_t$ of the current time, cell status $C_t$ of the present time.

Export: output gate value o, hidden layer state $h_t$.

In a word, the calculation process of LSTM is to take the operation of forgetting data and remembering novel data to the cell status, move the helpful data for succeeding time, and output concealed layer status at every time point. BiLSTM is the integration of forwarding LSTM as well as backward LSTM. The hidden layer needs to store two values, one for forwarding calculation and the other for reverse calculation. The final output value depends on these two values.

2.4. Modeling Process

Figure 3 describes the research framework of this paper. It consists of three parts:

(1) Selection of variables.

Wind direction, humidity, air pressure, air temperature, and other features were selected as the more important features of the input variables [36]. Additionally, to ensure the complete integrity of the PM_2.5 sample in the time series, linear interpolation was employed to fill the missing value.

(2) Model parameter adjustment and training.

Then, the time series of training, test, and validation sets were different, and the data set ratio was shown in the following in detail. Additionally, the number of components was also different. After a comparison of different components, the fitter component could be chosen as fixed input variables. Next, the input parameters of LSTM, SVM, RF, and Tree models were adjusted to predict PM_2.5 concentration.

(3) Effect evaluation.

Mean absolute error (MAE) and root mean square error (RMSE) are applied to assess the prediction results of the model and contrast them with other models to discuss the effect of the model in different regions and different lead times.

Each city’s time series data is separated into three data sets in the ratio of 7:1:2, which are the training set, the validation set, and the test set. The training set data is hourly data from April 1, 2013, to March 5, 2015, and the subsequent hourly data is the verification set from June 13. The validation set serves as a reference for fine-tuning model parameters, whereas the training set is utilized for initial model training. The split-out test set is primarily utilized to validate the model’s validity since the trained model has never encountered it before. The hourly environmental data from 14 June 2015 to 31 December 2015 was used as the test set. By comparing with the LSTM, SVM, RF, and tree models, the advantages of the RF-BiLSTM model are shown in Section 3.2.

2.5. Evaluation Indicators

To evaluate the performance, we adopted 3 statistical indexes: coefficient of determination (R²), MAE, and RMSE, which have been widely used in the assessment of precise indictors in former research scholar’s work [32,37]. The definitions of those indicators are as follows:

$$R^2=1-\frac{{\displaystyle {\sum }_{i=1}^T{\left(y_i-{\widehat{y}}_i\right)}^2}}{{\displaystyle {\sum }_{i=1}^T{\left(y_i-{\overline{y}}_i\right)}^2}}$$

(1)

$$MAE=\frac{{\displaystyle {\sum }_{t=1}^T\left|y_i-{\overline{y}}_i\right|}}{T}$$

(2)

$$RMSE=\sqrt{\frac{1}{T}{\displaystyle {\sum }_{t=1}^T{\left(y_i-{\overline{y}}_i\right)}^2}}$$

(3)

where i represents the time a serial number of prediction and observation specimens, T represents the amount time serial number of prediction and observation samples, $y_i$ denotes the PM_2.5 concentration in time I, ${\widehat{y}}_i$ represents concentration of PM_2.5 forecasting consequence of sample in time i, and ${\overline{y}}_i$ represents the mean value the observation concentration of sample in time i. R² denotes the degree of fitting value among the prediction concentration as well as actual concentration at the corresponding time, which when closer to the value of 1, the precise result performed much better. Additionally, the rest of the indictors of RMSE and MAPE are error assessment indicators that analyze deviation among prediction as well as actual value simultaneously.

3. Results and Discussion

3.1. Prediction Result of RF-BiLSTM

3.1.1. Prediction Results of RF Model

The time sequences of PM_2.5 are usually non-stationary. This is mainly caused by the impact of air PM_2.5 on meteorology and pollution emissions. RF could decompose non-stative PM_2.5 time sequences in major factors and non-major factors. In order to avoid data disclosure, the meteorological parameters were decomposed using the radio frequency method, and the contribution efficiency of meteorological parameters to forecast results was evaluated by OOB value. The model was trained by randomly selecting data, and then the meteorological data were classified, and the classified data was learned, thereby increasing the precision of this model.

It is indicated in Figure 4 that five meteorology parameters were employed with the RF method to classify the importance of each element. Different meteorology parameters have different OOB values among different cities. In Beijing, the OOB value of air temperature is the highest at t-1 and has the greatest influence on PM_2.5 concentration, followed by DEWP, while the OOB value of Iws is the lowest at T-4 and has little influence on PM_2.5 concentration.

The OOB value of DEWP is the highest, followed by TEMP, and Iws is the lowest in different periods. Guangzhou and Xi’an have significant importance in DEWP and PRES, but HUMI has the highest importance only in Guangzhou. These phenomena show that the dew point and temperature vary greatly from day to night, and the increase rate of high PM_2.5 concentration (such as BJ, SY, and XA) in winter is relatively small. It is easy to cause fine particles to adhere and condense into nucleation, and the increase in temperature and light in summer will promote atmospheric oxidation and conversion of secondary pollutants.

The results show that DEWP, TEMP, and PRES have a great influence on PM_2.5 concentration. However, Guangzhou is close to the ocean, and its humidity is relatively high, which has a great relationship with PM_2.5 concentration. In addition, whether it is dew point, temperature, or other factors, the RF model will conduct a preliminary screening of invalid information as input parameters of the BiLSTM model, which can significantly improve the accuracy of prediction [1,26].

3.1.2. The Comparison of Prediction Results between LSTM and RF-BiLSTM for Short-Term

Through the established model testing, it is found that the RF model classification results will have a great positive effect on the final prediction results. The R² has increased significantly from 0.99 (LSTM model) to 0.995 (RF-BiLSTM) at the T + 1 moment. Without RF model classification, forecasting at the T + 1 moment will evaluate PM_2.5 concentration at a high level. After conducting the RF model classification based on the useless information filter of previous data with similar input parameters of the BiLSTM model, the high evaluation of predicting consequences could be noticeably modified. RMSE was decreased significantly by ~26.4% (from 9.87 μg/m³ to 7.26 μg/m³), and MAE was decreased from 5.15 μg/m³ to 3.73 μg/m³, with a decrease of 27.6%. The consequences validated fully illustrate that RF classification is a very necessary step which could significantly improve the forecast precision of the mixed model.

From Figure 5a1,b1,c1, the improvement of the prediction accuracy can also be indicated at other times. The results with the RF classified results at the T + 2 and T + 3 moments are similar to those at the T + 1 moment. Additionally, forecast precision is significantly modified, especially in the capacity to forecast peak score. The degree of RF-BiLSTM strength of forecast accuracy consequences alters with time, and the R² value ranged from 0.989 (T + 3) to 0.995 (T + 1). The reason may be that the prediction error of components increases rapidly with predicting time growth. Additionally, the same pattern applied in SY, XA, and GD cities is shown in Supplementary Materials Table S1, Figures S1–S3.

3.2. Contrast of Forecast Consequence of Different Models

3.2.1. Contrast Short-Term Forecast Consequences with SVM, TREE, and RF Models

The different forecast consequences of in-depth learning at short-term moments (T + 1 to T + 3) are indicated in

Table 1. Forecast consequences of the distinct models at short-term moments in BJ.

Model	BJ(T + 1)			BJ(T + 2)			BJ(T + 3)
	R2	MAE	RMSE	R2	MAE	RMSE	R2	MAE	RMSE
LSTM	0.99	5.15	9.86	0.99	6.45	12.21	0.98	6.96	13.41
RF-BiLSTM	1.00	3.73	7.26	0.99	5.23	10.2	0.99	5.36	10.47
SVM	0.97	9.87	18.6	0.91	16.82	31.15	0.84	22.28	40.39
RF	0.94	11.48	23.96	0.87	19.09	36.69	0.76	25.37	49.49
Tree	0.95	11.29	21.82	0.88	18.66	34.57	0.80	24.47	45.23

as well as Figure 6.

Table 1 shows the relationship between the concentration of PM_2.5 prediction results and the actual PM_2.5 concentration among the different lead times. In general, RF-BILSTM has the best performance, and MAE and RMSE have small evaluation errors. The main reason was that, based on the feature selection of the RF model, the rF-BILSTM coupling model has a lower interference factor and a higher relationship influence factor than the traditional model.

Therefore, the advantages of the RF model in reducing data noise are quite different from those of BiLSTM. MAE is 0.04–2.4 μg/m³ higher than other models, and RMSE is 0.98~5.49 μg/m³ higher than other models. The MAE and RMSE were 1.52–3.71 μg/m³ and 3.19–6.95 μg/m³ higher than those of other models. The RF-BiLSTM model was the best choice for BJ to forecast the concentration of PM_2.5 3 hours ahead. The accuracy of MAE is 0.28–2.73 μg/m³ higher than other models, and RMSE is 0.31–7.53 μg/m³ higher than other models.

Through a comprehensive analysis of the three tables, the MAE and RMSE values will increase significantly with the increase in lead time, no matter which model is used in the Shenyang area. This is understandable because the longer the lead time, the lower the accuracy. In the other three locations, the trend is not obvious, and the prediction error of each model is the largest in the two-hours-ahead model, which means that the RF-BiLSTM model with one-hour-ahead is the most suitable for predicting PM_2.5 concentration.

During the experiment, the parameters of different models were optimized and iterated in different ways. The specific optimization settings were as follows:

(1) The Adaptive Moment Estimation (Adam) algorithm can be used in the paper to update weight parameters of neural net. Adam is an adaptive learning rate method, of which the first and second moments of gradient are used to estimate the learning rate of dynamically adjusted parameters. The initial learning rate can be set as 0.005, the maximal epochs (number of iterations) are 100, and the number of concealed layer neurons is set to 200. To adjust model parameters more delicately during training, the learning rate will be scaled in a certain multiple after every 30 iterations, and 0.2 times will be used in modeling. The advantage of Adam is primarily that after deviation amendment, the study ratio of every iteration has some scope, making parameters relatively steady.

In this experiment, we set the threshold value of the gradient to 1 and clipped the gradient information exceeding this value to ensure the stability of the model. We standardized the model input to avoid information loss caused by different data weights.

(2) Since both decision trees and random forests are tree regression models, the optimization settings of the two models are similar, which are optimized on the number of decision trees, the minimum number of cotyledon nodes, as well as the maximal number of branch nodes. Due to the relatively wide range of parameters and their values to be optimized, in order to decrease the search time, the random search method could be adopted to adjust the parameters during the optimization process. This approach may reduce the accuracy of the model to some extent but can save up to 90% in running time.

(3) The SVM model needs to normalize the model input and adopt the Gaussian regression kernel for modeling. The values of C and Gamma are optimized using Bayes, where C represents the tolerance of the model to errors. If C is too large or too small, the phenomenon of over-fitting and under-fitting will occur, respectively. Gamma is an argument that comes with the RBF function when you select it as the kernel. The number of support vectors effects the velocity of training as well as the forecast.

3.2.2. Contrasting the Long-Term Forecast Consequences of Models Applied in Some Existing Researches

Some researches employed mixed models to forecast the PM_2.5 concentration; however, none of them make long-term predictions, such as the GRU, SVM, and LSTM models suggested by [4,9,38], as well as RF and Tree referred to in the previous section. Long-term prediction consequences of the RF-BiLSTM method are shown in Figure 7 and

Table 2. Forecast consequences of distinct moments in BJ.

Moment	T + 1	T + 2	T + 3	T + 4	T + 5	T + 6	T + 7	T + 8	T + 9	T + 10	T + 11	T + 12
R2	1.00	0.99	0.99	0.98	0.98	0.97	0.96	0.97	0.97	0.96	0.94	0.95
MAE	3.73	5.23	5.36	7.29	7.35	9.33	11.89	10.42	9.85	10.84	12.89	12.68
RMSE	7.26	10.20	10.47	13.69	12.81	16.93	19.03	17.61	17.11	19.01	24.14	23.33

.

Along with time increase, the forecast precision of the model reduced little by little. Although the R² remained at more than 0.9, the MAE and RESM had a huge error compared to the moment at T + 1. It is obvious that the long-term PM_2.5 concentration forecast remains challenging as well as situated further discovered. Meanwhile, the mixed model suggested in the research keeps optimal consequences at T + 1 to T + 6 moments (with R² 0.97–1.00, RMSE 7.26–16.93 μg/m³, MAE 3.73–9.33μg/m³). Consequently, in traditional machine study models, the R² value is usually lower than 0.8 at T + 6. All those results indicated that the RF-BiSLTM model is more suited to the integration of RF than other deep learning machine models, and mixed models could offer an efficient reference for policy execution.

3.3. The Evaluation of the Model Robustness and Spatiotemporal Generalization

3.3.1. Validation of Spatial Generalization of Mixed Model

To test the spatial generalization of the mixed model, we randomly chose Guangzhou, Xi’an, and Shenyang, three cities distributed in northeast, northwest, and south China and with large geographical differences from Beijing and serious changes to forecast future variation of PM_2.5 concentration. The RF-BiLSTM mixed model prediction results in the next six moments and further span in the twelve moments are shown in

Table 3. Forecast consequences of distinct models at short-term moments in GZ.

Model	GZ(T + 1)			GZ(T + 2)			GZ(T + 3)
	R2	MAE	RMSE	R2	MAE	RMSE	R2	MAE	RMSE
LSTM	0.98	1.98	2.68	0.98	2.39	3.3	0.96	2.85	4.03
RF-BiLSTM	0.99	1.33	1.77	0.98	2.06	2.82	0.98	2.26	3.13
SVM	0.89	4.64	6.93	0.79	6.58	9.77	0.70	7.91	11.66
RF	0.89	4.89	7.12	0.78	6.91	10.09	0.70	8.31	11.78
Tree	0.89	4.96	4.96	0.78	6.86	10.01	0.69	8.4	11.93

,

Table 4. Forecast consequences of distinct models at short-term moments in XA.

Model	XA(T + 1)			XA(T + 2)			XA(T + 3)
	R2	MAE	RMSE	R2	MAE	RMSE	R2	MAE	RMSE
LSTM	1.00	1.65	3.07	0.99	2.09	3.92	0.99	2.08	4.43
RF-BiLSTM	1.00	1.37	2.75	0.99	1.65	3.52	0.99	1.78	4.16
SVM	0.99	3.03	4.72	0.96	5.75	8.85	0.92	8.07	12.19
RF	0.99	3.37	5.3	0.96	6.04	9.25	0.91	8.51	12.91
Tree	0.99	3.58	5.44	0.95	6.36	9.61	0.91	8.83	13.2

and

Table 5. Forecast consequences of distinct models at short-term moments in SY.

Model	SY(T + 1)			SY(T + 2)			SY(T + 3)
	R2	MAE	RMSE	R2	MAE	RMSE	R2	MAE	RMSE
LSTM	0.99	3.85	9.22	0.98	5.11	11.24	0.97	6.11	15.07
RF-BiLSTM	1.00	2.2	4.51	0.99	3.17	6.71	0.99	4.79	10.35
SVM	0.97	8.31	15.3	0.91	14.07	25.58	0.84	18.36	33.17
RF	0.93	9.85	21.58	0.84	16.68	33.59	0.72	22.17	44.08
Tree	0.94	10.58	20.67	0.83	16.82	34.66	0.76	21.54	41.05

and Supplementary Materials Figures S7–S9, and the kinds of input parameters were all classified using RF model.

Consequences indicated that the mixed model and change variation of forecast results in this study are also suitable for Guangzhou, Xi’an, and Shenyang (the R² value at the T + 1 moment could be 0.99, 1.00, and 1.00, separately), proving that the mixed model has great spatial generalization. GZ and XA have the best results in the three cities. On the other hand, the suspension of training group, continuous training group, and experimental group have significant influence on the prediction results. Compared with the LSTM, SVM, RF, and Tree model, the same regulars can be found in these three cities. Although R² can sometimes keep the same value, the MAE and RMSE can have bigger errors than RF-BiLSTM. Taking XA for example, the MAE and RMSE of the Tree model have more than 4~5 times the errors than the former model results. The results demonstrated that the mixed model has great generalization and firmness in the short term.

3.3.2. Validation of Temporal Generalization of Mixed Model

To test the mixed model long-term robustness and generalization, this study compared long-term prediction results. The forecast consequences of the RF-BiLSTM model at further time are indicated in

Table 6. Forecast consequences of distinct moments in GZ.

Moment	T + 1	T + 2	T + 3	T + 4	T + 5	T + 6	T + 7	T + 8	T + 9	T + 10	T + 11	T + 12
R2	0.99	0.98	0.98	0.96	0.95	0.95	0.94	0.93	0.94	0.93	0.92	0.91
MAE	1.33	2.06	2.26	2.91	3.19	3.38	3.57	3.84	3.75	3.97	4.13	4.6
RMSE	1.77	2.82	3.13	4.20	4.60	4.87	5.14	5.48	5.36	5.67	5.91	6.52

,

Table 7. Forecast consequences of distinct moments in XA.

Moment	T + 1	T + 2	T + 3	T + 4	T + 5	T + 6	T + 7	T + 8	T + 9	T + 10	T + 11	T + 12
R2	1.00	0.99	0.99	0.99	0.98	0.97	0.97	0.97	0.98	0.97	0.95	0.94
MAE	1.37	1.65	1.78	2.16	2.69	4.19	3.98	4.09	3.61	4.67	5.93	6.35
RMSE	2.75	3.52	4.16	4.82	5.82	7.12	7.26	7.32	7.01	8.19	9.57	10.38

and

Table 8. Forecast consequences of distinct moments in SY.

Moment	T + 1	T + 2	T + 3	T + 4	T + 5	T + 6	T + 7	T + 8	T + 9	T + 10	T + 11	T + 12
R2	1.00	0.99	0.99	0.97	0.71	0.94	0.94	0.93	0.94	0.90	0.87	0.91
MAE	2.2	3.17	4.79	5.9	6.2	7.75	7.88	8.89	8.45	10.6	10.65	10.07
RMSE	4.51	6.71	10.35	14.14	14.17	20.27	19.90	22.20	20.73	26.52	29.59	25.37

, and the types of import parameters are identical as those in the short term. For GZ and XA, the R² have better performance with the value at 0.9, which demonstrated that the mixed model can reproduce PM_2.5 concentration variation trend characteristics.

However, MAE and RMSE values would be closely related to local conditions for simulating contaminant concentrations in the area. For example, when the background concentration of XA and GZ is relatively low, the deviation of prediction results of the model is small (GZ MAE: 1.33–4.60 μg/m³, 1.77–6.52 μg/m³, MAE: 1.37–6.35 μg/m³, RMSE: The deviation of the model prediction results was large (MAE: 2.20–6.35 μg/m³, GZ: 4.51–25.37 μg/m³). This result indicated that the mixed model could better predict the concentration change trend with time going on, regardless of BJ or other regions, but the accuracy decreases gradually at the T + 6 moment.

4. Conclusions

The environmental damage caused by frantic industrial development will eventually have an impact on human health, and PM_2.5 is not the only product, but it is a crucial one. Accurately predicting PM_2.5 concentrations can help to issue air quality alerts, allow people to avoid long-term exposure to high pollution levels, and ease the pain of respiratory diseases. The PM_2.5 concentration curves of four typical cities with regional characteristics, Shenyang, Beijing, Xi’an, and Guangzhou, were illustrated by using the random forest model. The conclusion is as follows:

(1) The variation of the concentration of PM_2.5 in China is related to lifestyle and meteorological factors. Xi’an is located in the mainland, so the accumulation of pollutants is mainly due to the more stationary wind. Meanwhile, Guangzhou is located in the south, adjacent to the Pearl River, and the air humidity is higher than in other areas, so the pollutant accumulation level is low. By comparing weekend and weekday PM_2.5 concentrations, it was found that human activities also have an impact on pollutant levels in the area.

(2) Feature selection can effectively reduce the model complexity by compressing the input variable dimensions. In this paper, the DEWP, TEMP, HUMI, PRES, and Iws of different lead times are selected as input variables according to the correlations assessed using RF. The selected variables contain most of the previous environmental attributes to ensure the accuracy of the model. Since the input dimension was reduced by 80%, the memory required for model operation was doubled, making it possible to deploy edge computing on low-performance computers.

(3) The proposed RF-BiLSTM mixed model shows superior performance on different statistical indicators compared to others. The model can identify and fit the variation rule of concentration, and it can also identify the key variables to some extent. At the same time, it is highly portable and can be used to predict pollutants in different geographical areas at a low cost. In future work, the model will be improved in the following aspects: for regions with the same geographical characteristics, input variables are selected to verify the universality of the model, and the random forest feature selection method is selected. Other feature selection methods will also be tested for better performance.

(4) In recent years, the majority of cities in China have witnessed the high frequency of haze pollution. With the help of the forecasting model, especially in short- and long-term prediction, PM_2.5 concentration variation characteristics have been significantly captured based on the RF-BiLSTM model. Under this circumstance, joint prevention and control and targeted policies to reduce emissions could be established and implemented, and human health can be significantly improved.