Simulation of Triaxial Tests for Unsaturated Soils under a Tension–Shear State by the Discrete Element Method
Abstract
:1. Introduction
2. Selection of the Grain-Scale Contact Model
3. Back Analysis of Grain-Scale Parameters
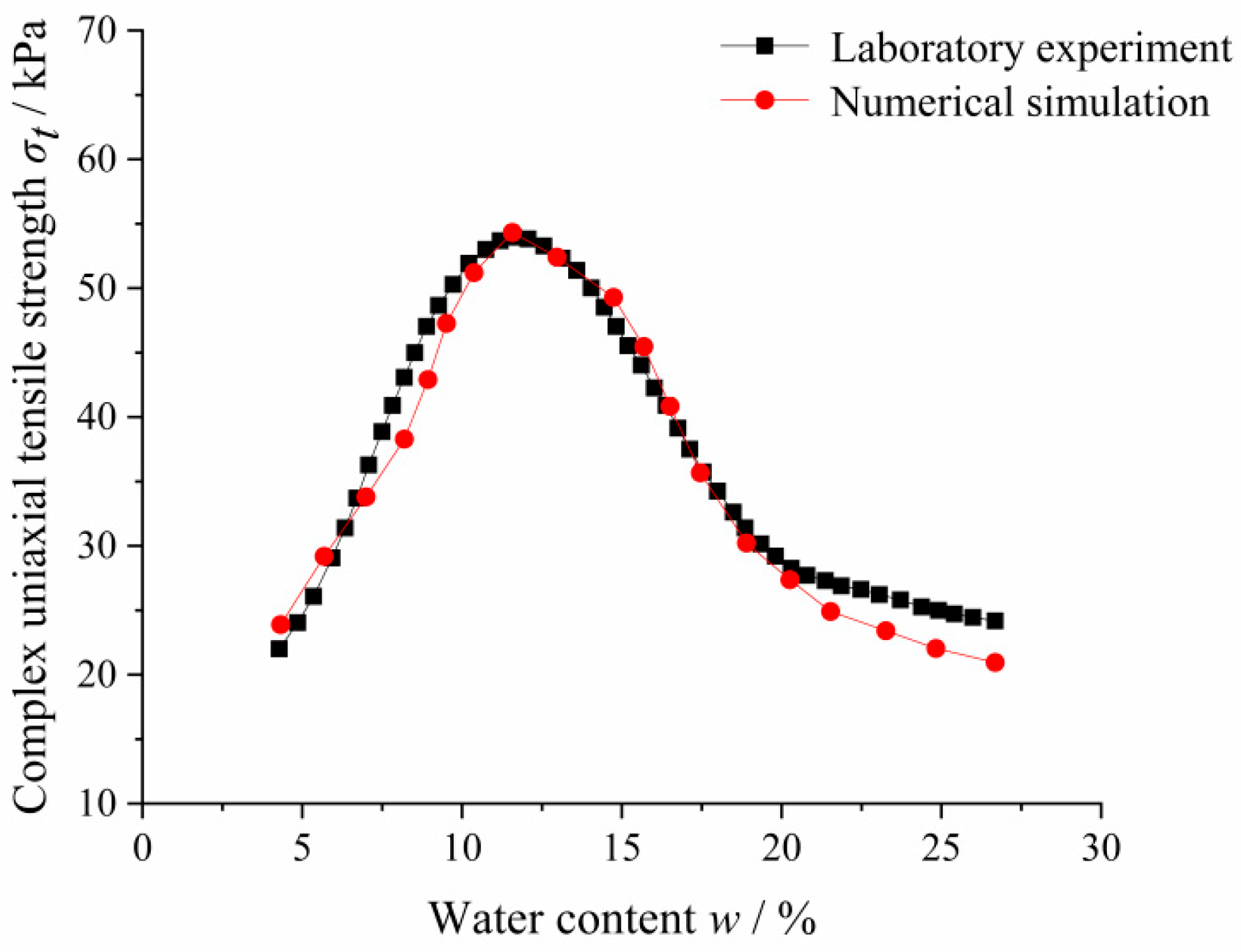
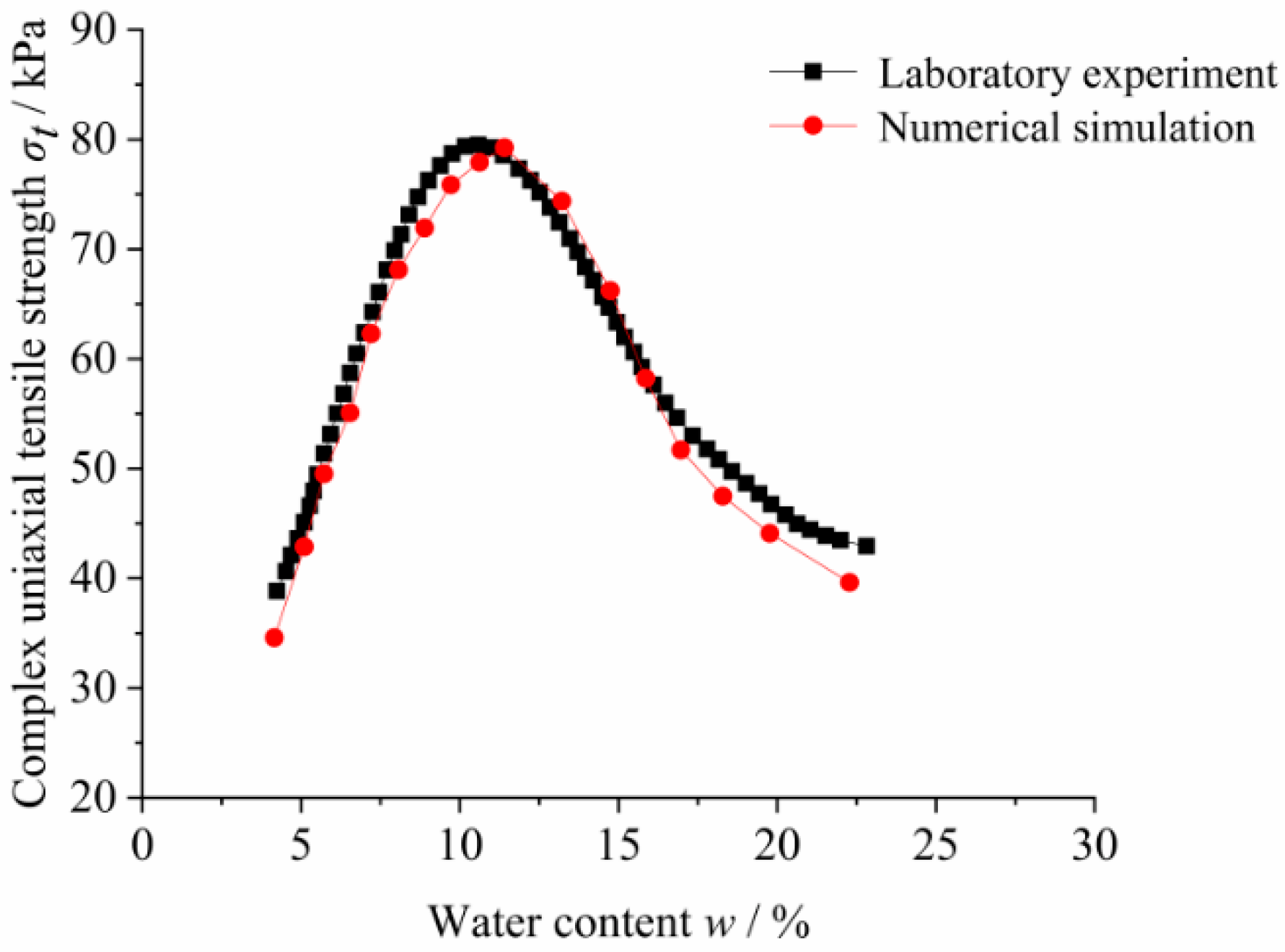
3.1. Determining Grain-Scale Parameters by Complex Uniaxial Tensile Test Simulation
3.2. Impact Analysis of Material Parameters on the Discrete Element Simulation
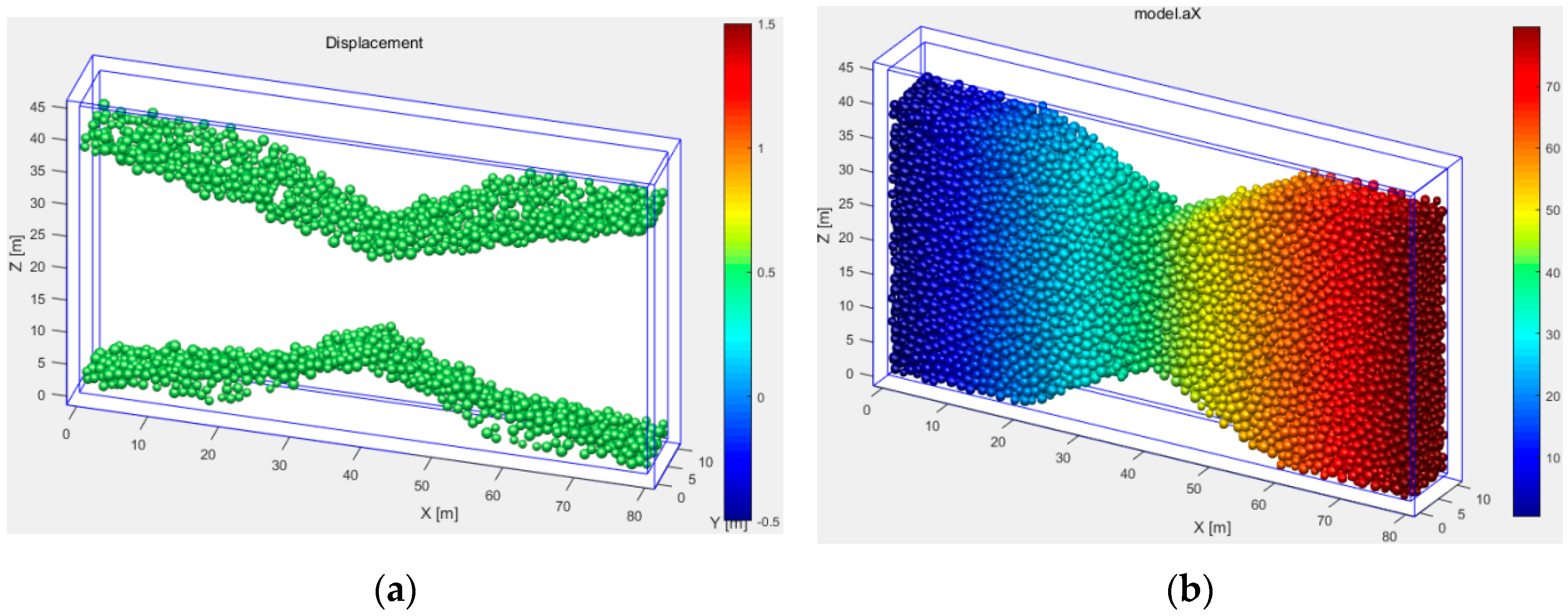
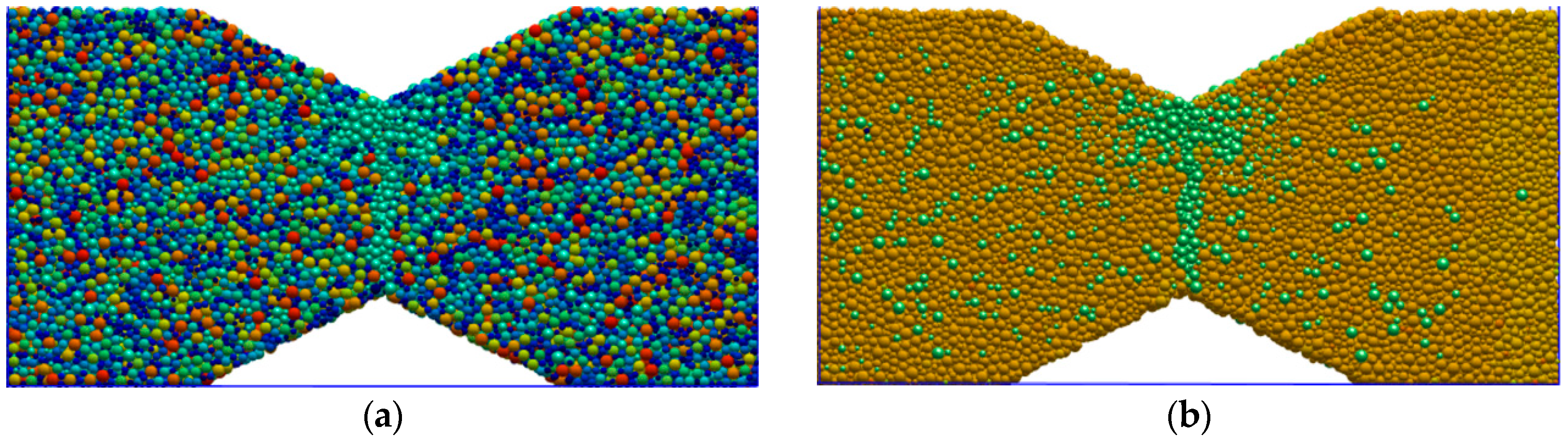
3.2.1. Creating a MatDEM Model for the Complex Uniaxial Tensile Test
3.2.2. Loading Mode of the Numerical Model and the Calculation Rule of Tensile Strength
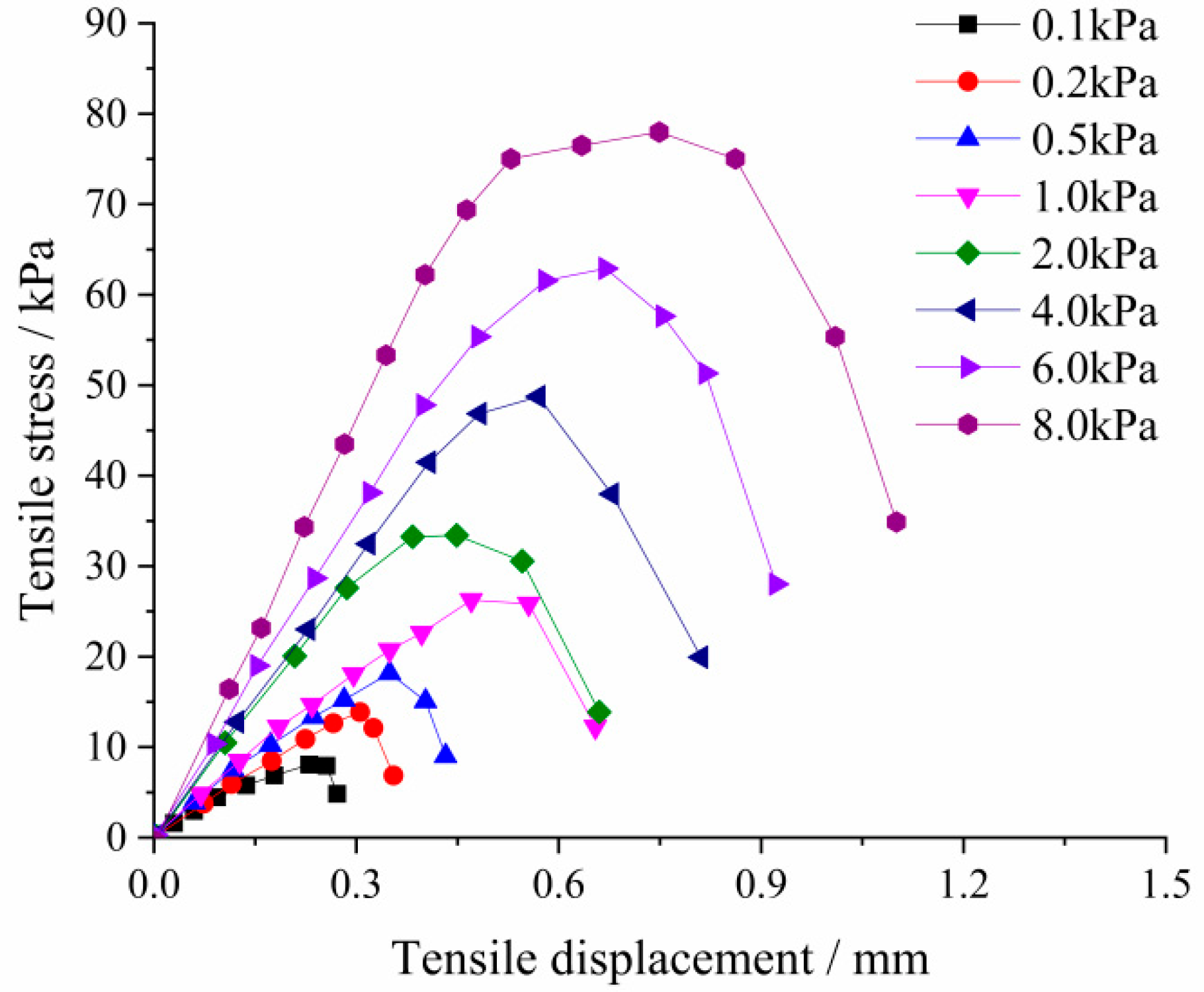
3.2.3. Influences of Material Parameters on the Complex Uniaxial Tensile Strength
- Impact analysis of the tensile strength on the complex uniaxial tensile strength
- Impact analysis of Young’s modulus on the complex uniaxial tensile strength
- Impact analysis of Poisson’s ratio on the complex uniaxial tensile strength
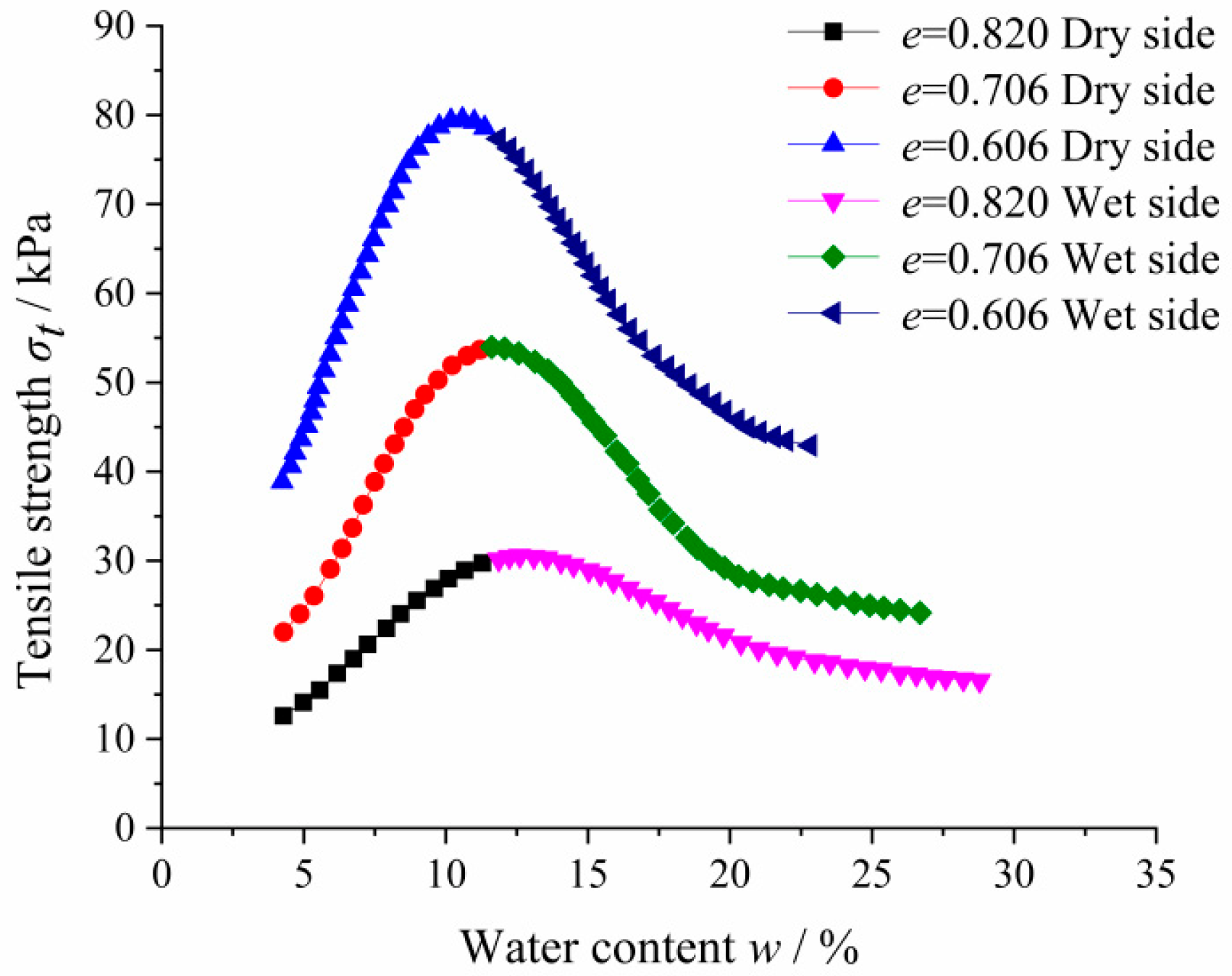
3.3. Relationship between Water Content and the Complex Uniaxial Tensile Strength of Unsaturated Clay
- (1)
- Dry side (0 < w < 11.5%)where is the uniaxial tensile strength, w is the water content, and Ad, Bd, and Cd are coefficients related to the initial void ratio under dry side. The values of Ad, Bd, and Cd for specimens with different initial void ratios are shown in Table 4.
- (2)
- Wet side (11.5% < w < 35%)where Aw, Bw, and Cw are coefficients under wet side. The values of Aw, Bw, and Cw for specimens with different initial void ratios are shown in Table 5.
3.4. Relation between the Tensile Strength Tu and Complex Uniaxial Tensile Strength σt
3.5. Relationship between MatDEM Material Parameters and the Water Content w of Unsaturated Clay
- (1)
- For the dry side (0 < w < 11.5%),Substituting Equation (15) into Equation (14) obtains
- (2)
- For the wet side (11.5% < w < 35%),Substituting Equation (17) into Equation (14) obtains
4. Simulation of Triaxial Tests for Unsaturated Soils under a Tension–Shear State
4.1. Simulation Steps
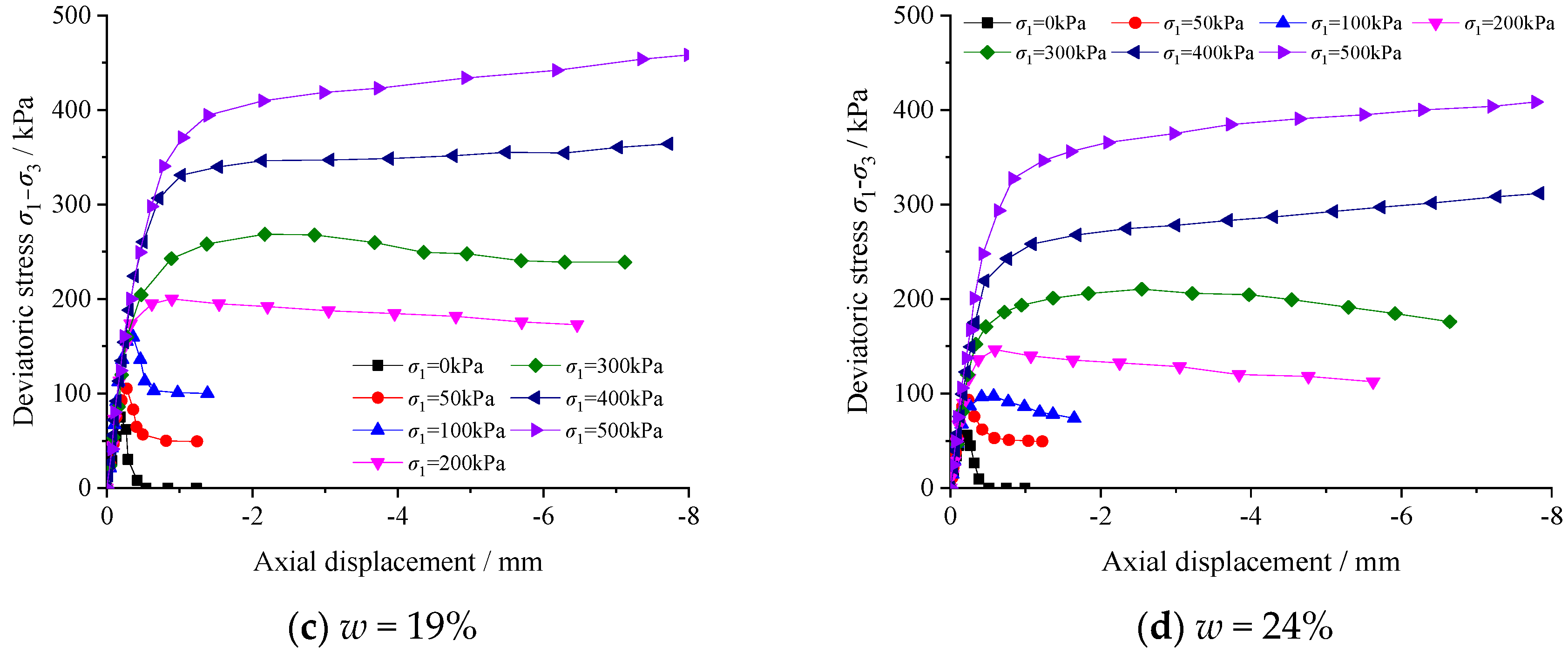
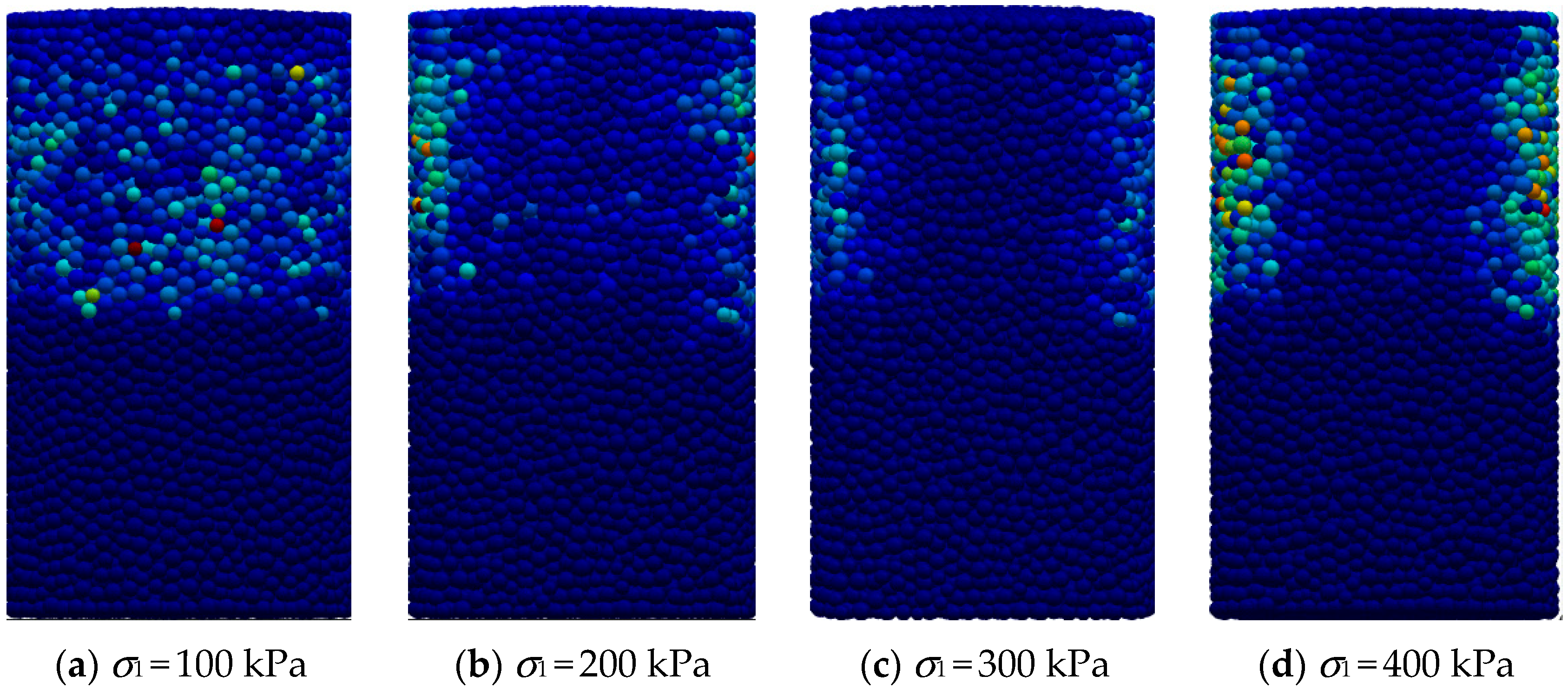
4.2. Simulation Results
4.2.1. The Relationship between Deviatoric Stress and Axial Displacement
4.2.2. Displacement Field
4.2.3. Heat and Energy Field
5. Conclusions
- The water content affects the peak deviatoric stress, dilatancy behavior, and failure mode.
- The strength increases with the decreasing of water content and the increasing of confining pressure.
- The dilatancy phenomena is obvious for the specimens with a low confining pressure range and water content.
- The specimens undergo pure tensile failure under a small confining pressure condition, shear elongation and tensile failure under a middle confining pressure condition, and shear failure under a large confining pressure condition.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Haefeli, R. Investigation and measurements of shear strength of saturated cohesive soil. Géotechnique 1951, 2, 186–208. [Google Scholar] [CrossRef]
- Parry, R.H.G. Triaxial compression and extension tests on remolded saturated clay. Géotechnique 1960, 10, 166–180. [Google Scholar] [CrossRef]
- Zhou, H.K. The mechanism of fracture of soil samples in triaxial tensile test. Chin. J. Geotech. Eng. 1984, 6, 12–23. (In Chinese) [Google Scholar]
- Yu, X.J.; Jiang, P. Experimental study on shocking crack of impervious soil in earth-rock dams. J. Hohai Univ. 1996, 24, 68–75. (In Chinese) [Google Scholar]
- Zhang, S.H.; Guo, M.X.; Xing, Y.C. Test technology on triaxial extension. J. Water Resour. Water Eng. 2001, 12, 24–27. (In Chinese) [Google Scholar] [CrossRef]
- Ibarra, S.Y.; McKyes, E.; Broughton, R.S. Measurement of tensile strength of unsaturated sandy loam soil. Soil Till. Res. 2005, 81, 15–23. [Google Scholar] [CrossRef]
- Lu, N.; Wu, B.; Tan, C.P. Tensile strength characteristics of unsaturated sands. J. Geotech. Geoenviron. 2007, 133, 144–154. [Google Scholar] [CrossRef]
- Zhu, C.H.; Liu, J.M.; Yan, B.W.; Ju, J.L. Experimental study on relationship between tensile and shear strength of unsaturation clay earth material. Chin. J. Rock Mech. Eng. 2008, 27, 3453–3458. (In Chinese) [Google Scholar] [CrossRef]
- Ran, L.Z.; Song, X.D.; Tang, C.S. Laboratorial investigation on tensile strength of expansive soil during drying. J. Eng. Geol. 2011, 19, 620–625. (In Chinese) [Google Scholar] [CrossRef]
- Tang, C.S.; Pei, X.J.; Wang, D.Y.; Shi, B.; Li, J. Tensile strength of compacted clayey soil. J. Geotech. Geoenviron. 2015, 141, 04014122. [Google Scholar] [CrossRef]
- Ji, E.; Chen, S.; Zhu, J.; Fu, Z. Experimental study on the tensile strength of gravelly soil with different gravel content. Geomech. Eng. 2019, 17, 271–278. [Google Scholar] [CrossRef]
- Li, H.D.; Tang, C.S.; Cheng, Q.; Li, S.J.; Gong, X.P.; Shi, B. Tensile strength of clayey soil and the strain analysis based on image processing techniques. Eng. Geol. 2019, 253, 137–148. [Google Scholar] [CrossRef]
- Alonso, E.E.; Gens, A.; Josa, A. A constitutive model for partially saturated soils. Géotechnique 1990, 40, 405–430. [Google Scholar] [CrossRef] [Green Version]
- Wheeler, S.J.; Sharma, R.S.; Buisson, M.S.R. Coupling of hydraulic hysteresis and stress-strain behaviour in unsaturated soils. Géotechnique 2003, 53, 41–54. [Google Scholar] [CrossRef]
- Gallipoli, D.; Gens, A.; Sharma, R.; Vaunat, J. An elasto-plastic model for unsaturated soil incorporating the effects of suction and degree of saturation on mechanical behaviour. Géotechnique 2003, 53, 123–135. [Google Scholar] [CrossRef]
- Li, X.S. Thermodynamics-based constitutive framework for unsaturated soils 2: A basic triaxial model. Géotechnique 2007, 57, 423–435. [Google Scholar] [CrossRef]
- Sun, D.A.; Sheng, D.C.; Xiang, L.; Sloan, S.W. Elastoplastic prediction of hydro-mechanical behaviour of unsaturated soils under undrained conditions. Comput. Geotech. 2008, 35, 845–852. [Google Scholar] [CrossRef]
- Charlier, R. Approche Unifiée de Quelques Problèmes non Linéaires de Mécanique des Milieux Continus par la Méthode des Éléments Finis. Ph.D. Thesis, Université de Liège, Liège, Belgium, 1987. [Google Scholar]
- Olivella, S.; Carrera, J.; Gens, A.; Alonso, E.E. Nonisothermal multiphase flow of brine and gas through saline media. Transp. Porous Med. 1994, 15, 271–293. [Google Scholar] [CrossRef]
- Chen, Y.; Zhou, C.; Jing, L. Modeling coupled THM processes of geological porous media with multiphase flow: Theory and validation against laboratory and field scale experiments. Comput. Geotech. 2009, 36, 1308–1329. [Google Scholar] [CrossRef]
- Wei, C.F. Static and Dynamic Behavior of Multiphase Porous Media: Governing Equations and Finite Element Implementation. Ph.D. Thesis, University of Oklahoma, Norman, OK, USA, 2001. [Google Scholar]
- Cundall, P.A. The Measurement and Analysis of Acceleration in Rock Slopes. Ph.D. Thesis, University of London, London, UK, 1971. [Google Scholar]
- Cundall, P.A.; Strack, O.D.L. A discrete numerical model for granular assemblies. Géotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Fakhimi, A.; Carvalho, F.; Ishida, T.; Labuz, J.F. Simulation of failure around a circular opening in rock. Int. J. Rock Mech. Min. 2002, 39, 507–515. [Google Scholar] [CrossRef]
- Potyondy, D.O. A bonded-disk model for rock: Relating microproperties and macroproperties. In Proceedings of the Third International Conference on Discrete Element Methods, Santa Fe, NM, USA, 23–25 September 2002; pp. 340–345. [Google Scholar] [CrossRef]
- Potyondy, D.O.; Cundall, P.A. A bonded-particle model for rock. Int. J. Rock Mech. Min. 2004, 41, 1329–1364. [Google Scholar] [CrossRef]
- Backstrom, A.; Antikainen, J.; Backers, T.; Feng, X.T.; Jing, L.R.; Kobayashi, A.; Koyama, T.; Pan, P.Z.; Rinne, M.; Shen, B.T.; et al. Numerical modelling of uniaxial compressive failure of granite with and without saline porewater. Int. J. Rock Mech. Min. 2008, 45, 1126–1142. [Google Scholar] [CrossRef]
- Hsieh, Y.M.; Li, H.H.; Huang, T.H.; Jeng, F.S. Interpretations on how the macroscopic mechanical behavior of sandstone affected by microscopic properties—Revealed by bonded-particle model. Eng. Geol. 2008, 99, 1–10. [Google Scholar] [CrossRef]
- Sitharam, T.G.; Vinod, J.S.; Ravishankar, B.V. Post-liquefaction undrained monotonic behavior of sands: Experiments and DEM simulations. Géotechnique 2009, 59, 739–749. [Google Scholar] [CrossRef]
- Sadek, M.A.; Chen, Y. Simulating shear behavior of a sandy soil under different soil conditions. J. Terramechanics 2011, 48, 451–458. [Google Scholar] [CrossRef]
- Obermayr, M.; Dressler, K.; Vrettos, C.; Eberhard, P. A bonded-particle model for cemented sand. Comput. Geotech. 2013, 49, 299–313. [Google Scholar] [CrossRef]
- Xu, W.J.; Li, C.Q.; Zhang, H.Y. DEM analyses of the mechanical behavior of soil and soil-rock mixture via the 3D direct shear test. Geomech. Eng. 2015, 9, 815–827. [Google Scholar] [CrossRef]
- Jian, G.; Jun, L. Analysis of the thresholds of granular mixtures using the discrete element method. Geomech. Eng. 2017, 12, 639–655. [Google Scholar] [CrossRef]
- Zhu, X.; Liu, W.; Lv, Y. The investigation of rock cutting simulation based on discrete element method. Geomech. Eng. 2017, 13, 977–995. [Google Scholar] [CrossRef]
- Li, T.; Xiao, J. Discrete element simulation analysis of biaxial mechanical properties of concrete with large-size recycled aggregate. Sustainability 2021, 13, 7498. [Google Scholar] [CrossRef]
- Qi, Y.; Indraratna, B.; Ngo, T.; Ferreira, F.B. Advancements in geo-inclusions for ballasted track: Constitutive modelling and numerical analysis. Sustainability 2021, 13, 9048. [Google Scholar] [CrossRef]
- An, H.; Wu, S.; Liu, H.; Wang, X. Hybrid finite-discrete element modelling of various rock fracture modes during three conventional bending tests. Sustainability 2022, 14, 592. [Google Scholar] [CrossRef]
- Wang, Y.; Li, X.; Li, J.; Xu, J. Numerical simulation of impact rockburst of elliptical caverns with different axial ratios. Sustainability 2022, 14, 241. [Google Scholar] [CrossRef]
- Jiang, M.J.; Leroueil, S.; Konrad, J.M. Insight into shear strength functions of unsaturated granulates by DEM analyses. Comput. Geotech. 2004, 31, 473–489. [Google Scholar] [CrossRef]
- Trabelsi, H.; Jamei, M.; Zenzri, H.; Olivella, S. Crack patterns in clayey soils: Experiments and modeling. Int. J. Numer. Anal. Met. 2012, 36, 1410–1433. [Google Scholar] [CrossRef]
- Konrad, J.M.; Ayad, R. An idealized framework for the analysis of cohesive soils undergoing desiccation. Can. Geotech. J. 1997, 34, 477–488. [Google Scholar] [CrossRef]
- El Youssoufi, M.S.; Delenne, J.Y.; Radjai, F. Self-stresses and crack formation by particle swelling in cohesive granular media. Phys. Rev. E 2005, 71, 513–519. [Google Scholar] [CrossRef] [Green Version]
- Peron, H.; Delenne, J.Y.; Lalouia, L.; El Youssoufi, M.S. Discrete element modelling of drying shrinkage and cracking of soils. Comput. Geotech. 2009, 36, 61–69. [Google Scholar] [CrossRef]
- Sima, J.; Jiang, M.J.; Zhou, C.B. Modelling desiccation cracking in thin clay layer using three-dimensional discrete element method. In Proceedings of the 7th International Conference on the Micromechanics of Granular Media (Powders and Grains 2013), Sydney, Australia, 8–12 July 2013; pp. 245–248. [Google Scholar] [CrossRef] [Green Version]
- Boutt, D.F.; Mcpherson, B.J.O.L. Simulation of sedimentary rock deformation: Lab-scale model calibration and parameterization. Geophys. Res. Lett. 2002, 29, 13-1–13-4. [Google Scholar] [CrossRef] [Green Version]
- Ergenzinger, C.; Seifried, R.; Eberhard, P. A discrete element model to describe failure of strong rock in uniaxial compression. Granul. Matter. 2011, 13, 341–364. [Google Scholar] [CrossRef]








| Average Particle Radius rave/m | Particle Diameter Dispersion Coefficient Rate | Specific Gravity Gs | Young’s Modulus E/MPa | Poisson’s Ratio ν | Compressive Strength Cu/kPa | Internal Friction Coefficient of Material μi |
|---|---|---|---|---|---|---|
| 0.002 | 0.6 | 2.73 | 20 | 0.3 | 20 | 0.4 |
| Variable | Value | |||||||
|---|---|---|---|---|---|---|---|---|
| Tensile strength Tu/kPa | 0.1 | 0.2 | 0.5 | 1 | 2 | 4 | 6 | 8 |
| Tensile failure displacement /mm | 0.230 | 0.306 | 0.349 | 0.470 | 0.449 | 0.570 | 0.669 | 0.749 |
| Complex uniaxial tensile strength /kPa | 8.081 | 13.872 | 18.182 | 26.263 | 33.401 | 48.754 | 62.896 | 77.979 |
| Soil Properties | Specific Gravity | Consistency Limit | USCS Classification | Compaction Characteristics | Particle Size Analysis | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Liquid Limit (%) | Plastic Limit (%) | Plasticity Index (%) | Optimum Water Content (%) | Maximum Dry Density (g/cm3) | Sand (%) | Silt (%) | Clay (%) | |||
| Value | 2.73 | 37 | 20 | 17 | CL | 16.5 | 1.7 | 2 | 76 | 22 |
| Initial Void Ratio e | Ad | Bd | Cd | Determination Factor |
|---|---|---|---|---|
| 0.820 | −3.14821 | 3.88897 | −0.08224 | 0.99546 |
| 0.706 | −12.37397 | 8.52281 | −0.22218 | 0.98924 |
| 0.606 | −29.40861 | 18.88517 | −0.81092 | 0.99389 |
| Initial Void Ratio e | Aw | Bw | Cw | Determination Factor |
|---|---|---|---|---|
| 0.820 | 55.8452 | −2.40208 | 0.03514 | 0.9753 |
| 0.706 | 132.56575 | −8.20754 | 0.15516 | 0.9791 |
| 0.606 | 184.43806 | −11.7487 | 0.24232 | 0.99729 |
| Initial Dry Density g/cm3 | Particle Size Analysis % | Initial Void Ratio e | Total Number of Particles | ||
|---|---|---|---|---|---|
| 1.5 | Laboratory test | Sand/Silt/Clay | 2/76/22 | 0.820 | 65,139 |
| Numerical test | Sand/Silt/Clay | 1.3/74/24.7 | 0.872 | ||
| 1.6 | Laboratory test | Sand/Silt/Clay | 2/76/22 | 0.706 | 65,338 |
| Numerical test | Sand/Silt/Clay | 1.8/78/20.2 | 0.816 | ||
| 1.7 | Laboratory test | Sand/Silt/Clay | 2/76/22 | 0.606 | 66,327 |
| Numerical test | Sand/Silt/Clay | 2.2/76/21.8 | 0.762 | ||
| Initial Void Ratio for Laboratory Test e0 | Initial Void Ratio for Numerical Test e0 | Total Number of Particles | Tensile Strength Tu/kPa | Complex Uniaxial Tensile Strength /kPa | Complex Uniaxial Tensile Failure Displacement /mm |
|---|---|---|---|---|---|
| 0.820 | 0.872 | 65,139 | 0.5 | 10.12 | 0.12 |
| 1 | 12.23 | 0.15 | |||
| 2 | 13.45 | 0.25 | |||
| 3 | 14.11 | 0.34 | |||
| 4 | 15.45 | 0.38 | |||
| 5 | 16.89 | 0.40 | |||
| 6 | 17.98 | 0.42 | |||
| 7 | 19.56 | 0.45 | |||
| 8 | 22.46 | 0.48 | |||
| 9 | 24.56 | 0.51 | |||
| 10 | 25.79 | 0.58 | |||
| 11 | 26.89 | 0.67 | |||
| 12 | 27.36 | 0.75 | |||
| 13 | 28.45 | 0.80 | |||
| 14 | 29.35 | 0.86 | |||
| 15 | 30.15 | 0.89 | |||
| 16 | 32.12 | 0.95 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, G.; Li, J.; Liu, S.; Li, J.; Han, B.; He, X.; Zhao, C. Simulation of Triaxial Tests for Unsaturated Soils under a Tension–Shear State by the Discrete Element Method. Sustainability 2022, 14, 9122. https://doi.org/10.3390/su14159122
Cai G, Li J, Liu S, Li J, Han B, He X, Zhao C. Simulation of Triaxial Tests for Unsaturated Soils under a Tension–Shear State by the Discrete Element Method. Sustainability. 2022; 14(15):9122. https://doi.org/10.3390/su14159122
Chicago/Turabian StyleCai, Guoqing, Jian Li, Shaopeng Liu, Jiguang Li, Bowen Han, Xuzhen He, and Chenggang Zhao. 2022. "Simulation of Triaxial Tests for Unsaturated Soils under a Tension–Shear State by the Discrete Element Method" Sustainability 14, no. 15: 9122. https://doi.org/10.3390/su14159122
APA StyleCai, G., Li, J., Liu, S., Li, J., Han, B., He, X., & Zhao, C. (2022). Simulation of Triaxial Tests for Unsaturated Soils under a Tension–Shear State by the Discrete Element Method. Sustainability, 14(15), 9122. https://doi.org/10.3390/su14159122





