Research on Flow Field Characteristics in Water Jet Nozzle and Surface Damage Caused by Target Impact
Abstract
:1. Introduction
2. Theoretical Model and Calculation Method
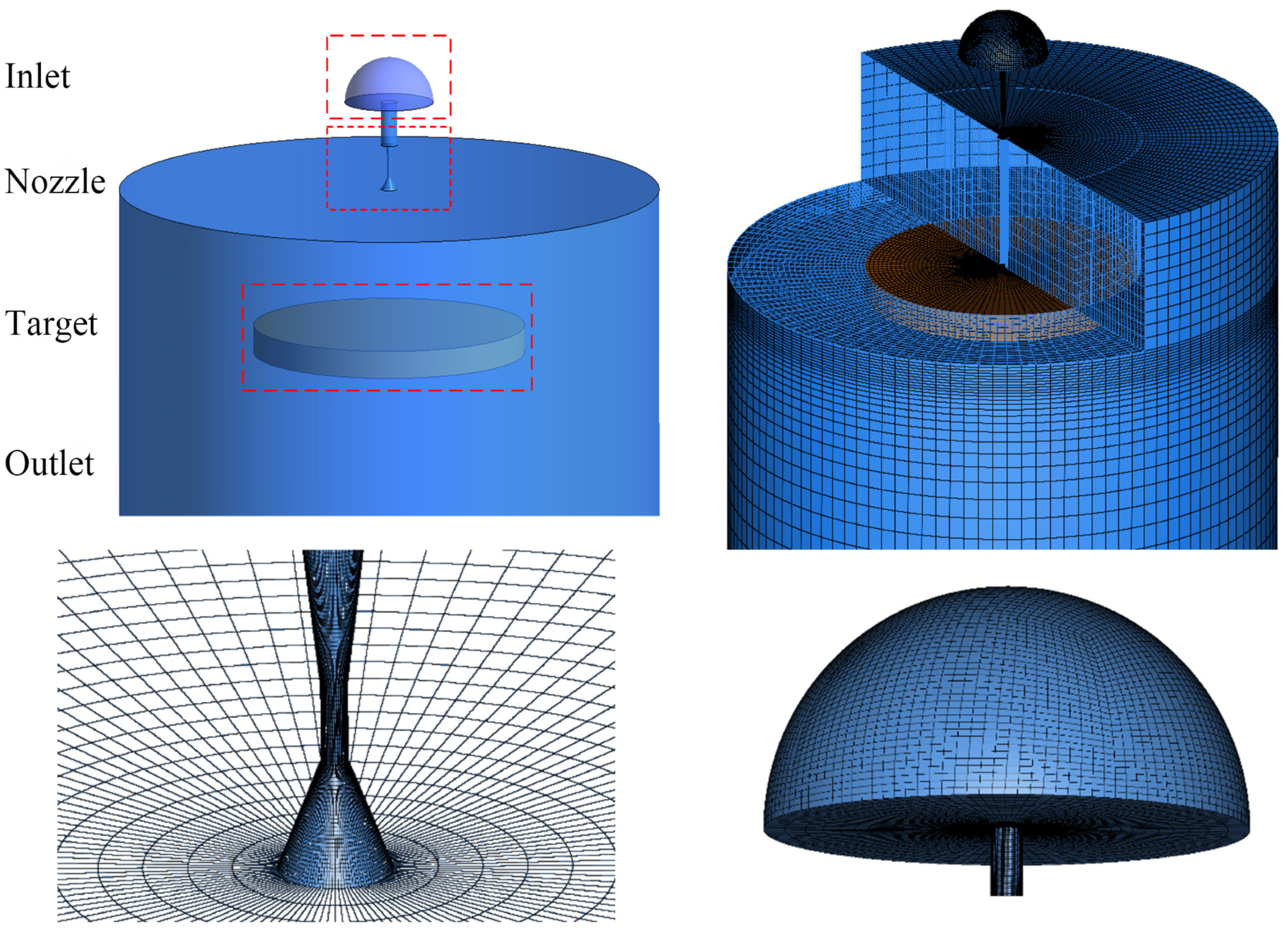
2.1. Geometry and Meshing
2.2. Boundary Conditions and Parameter Settings
3. Results and Analysis of Numerical Calculation
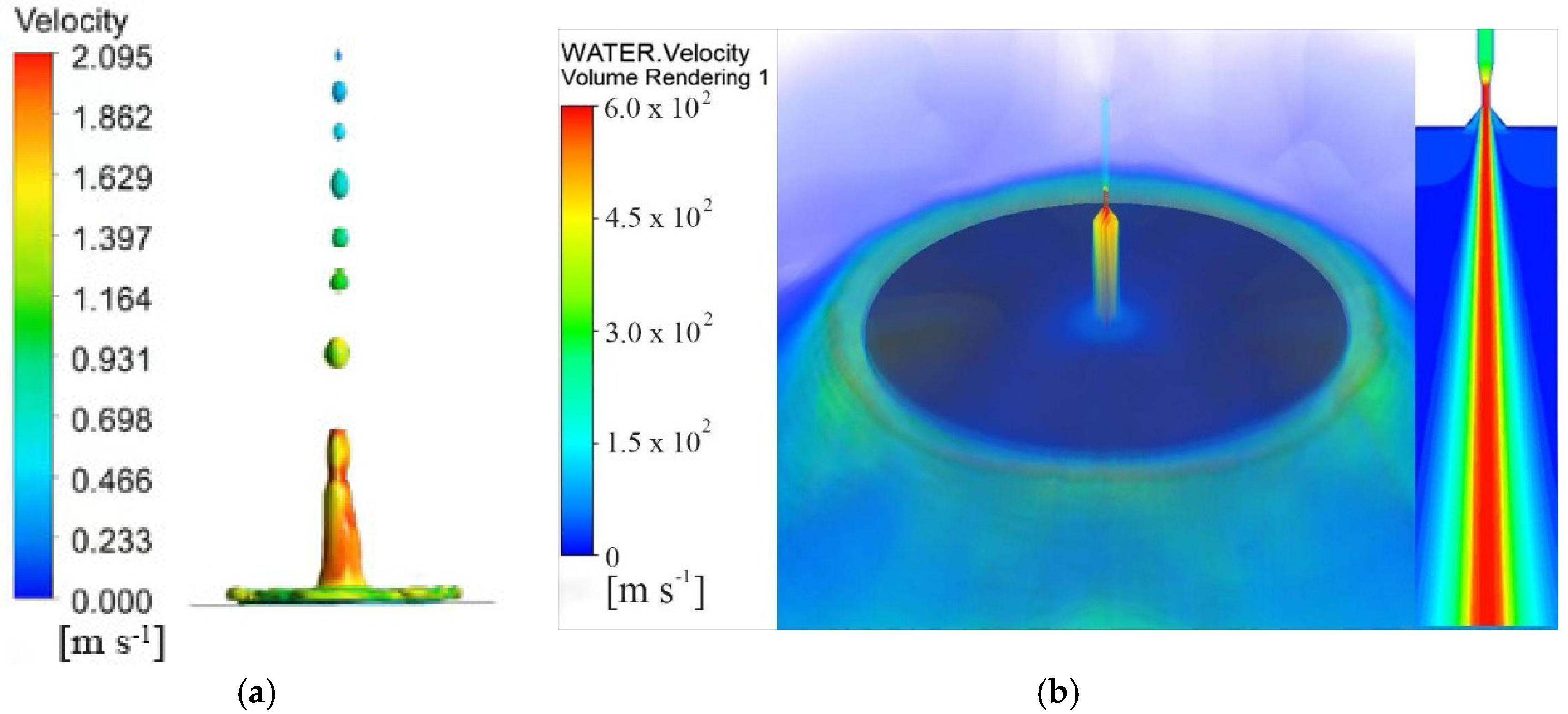
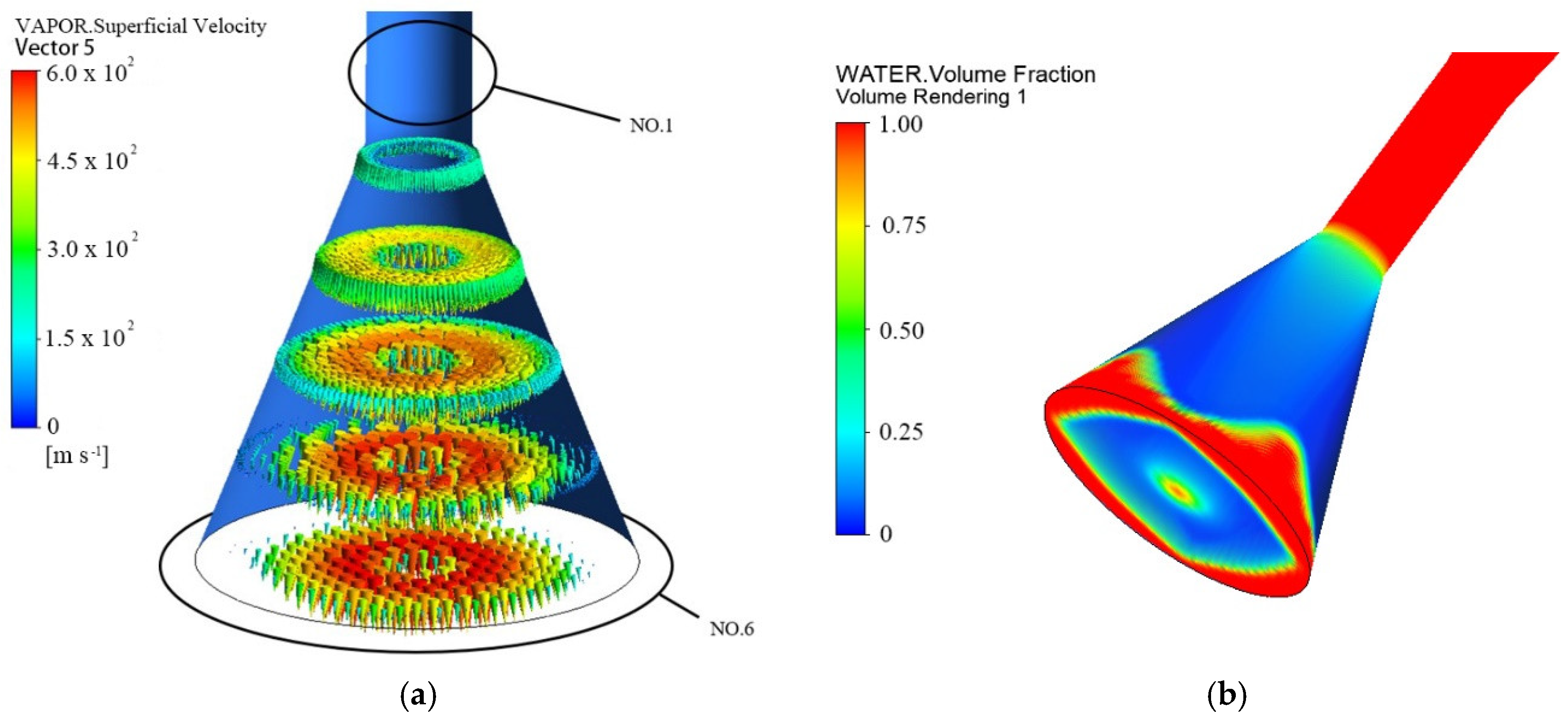
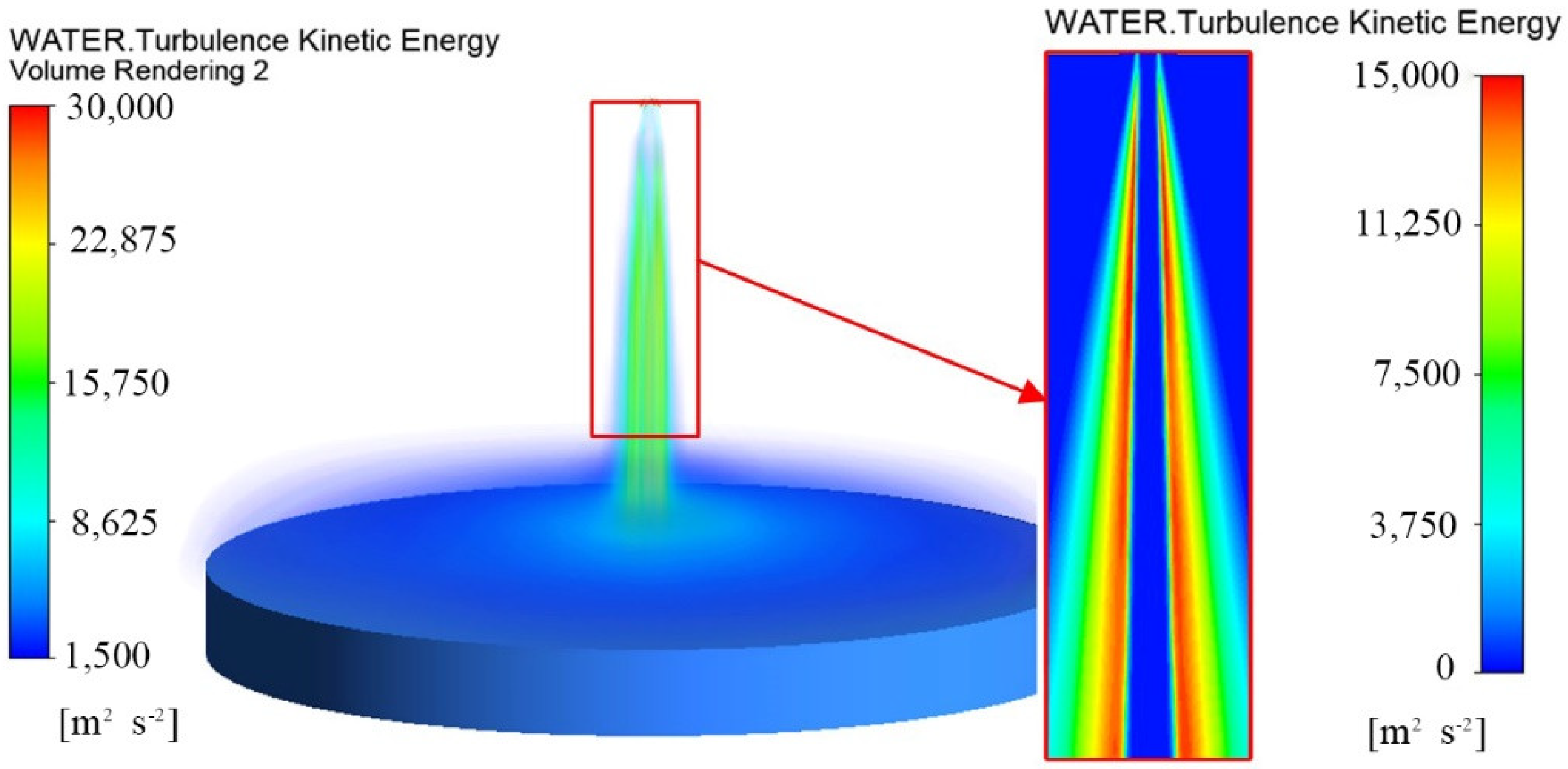
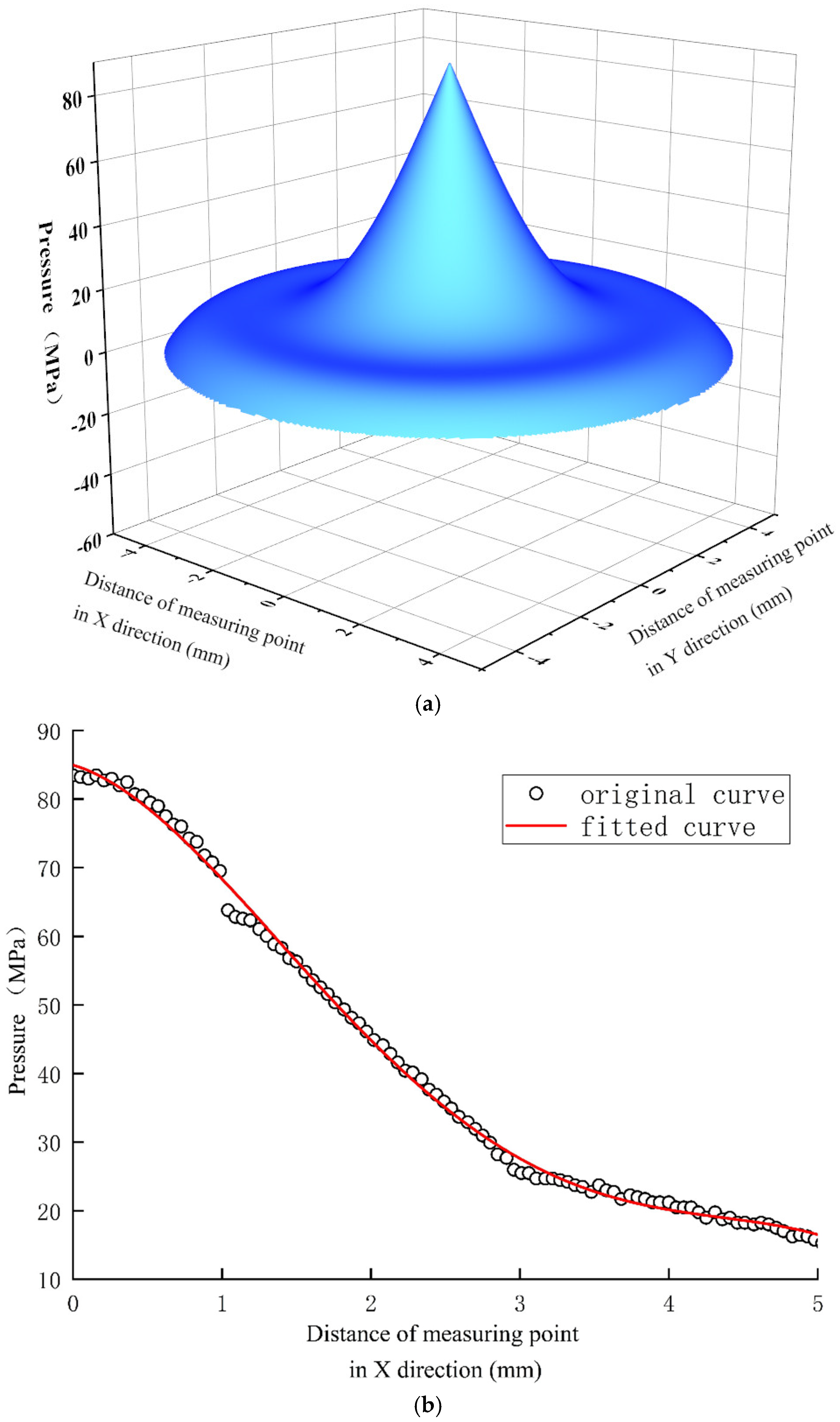
3.1. Analysis of Flow Field Calculation Results
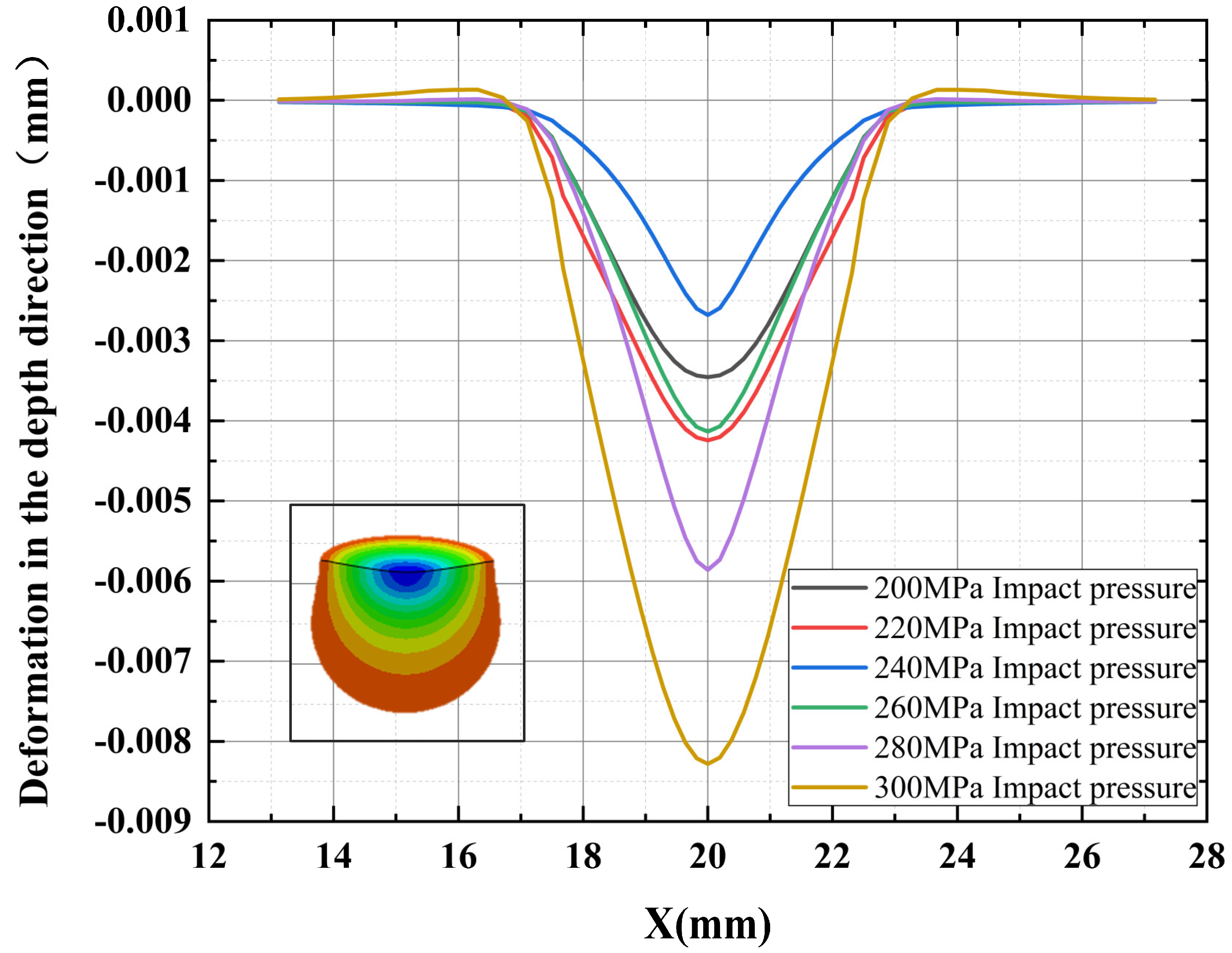
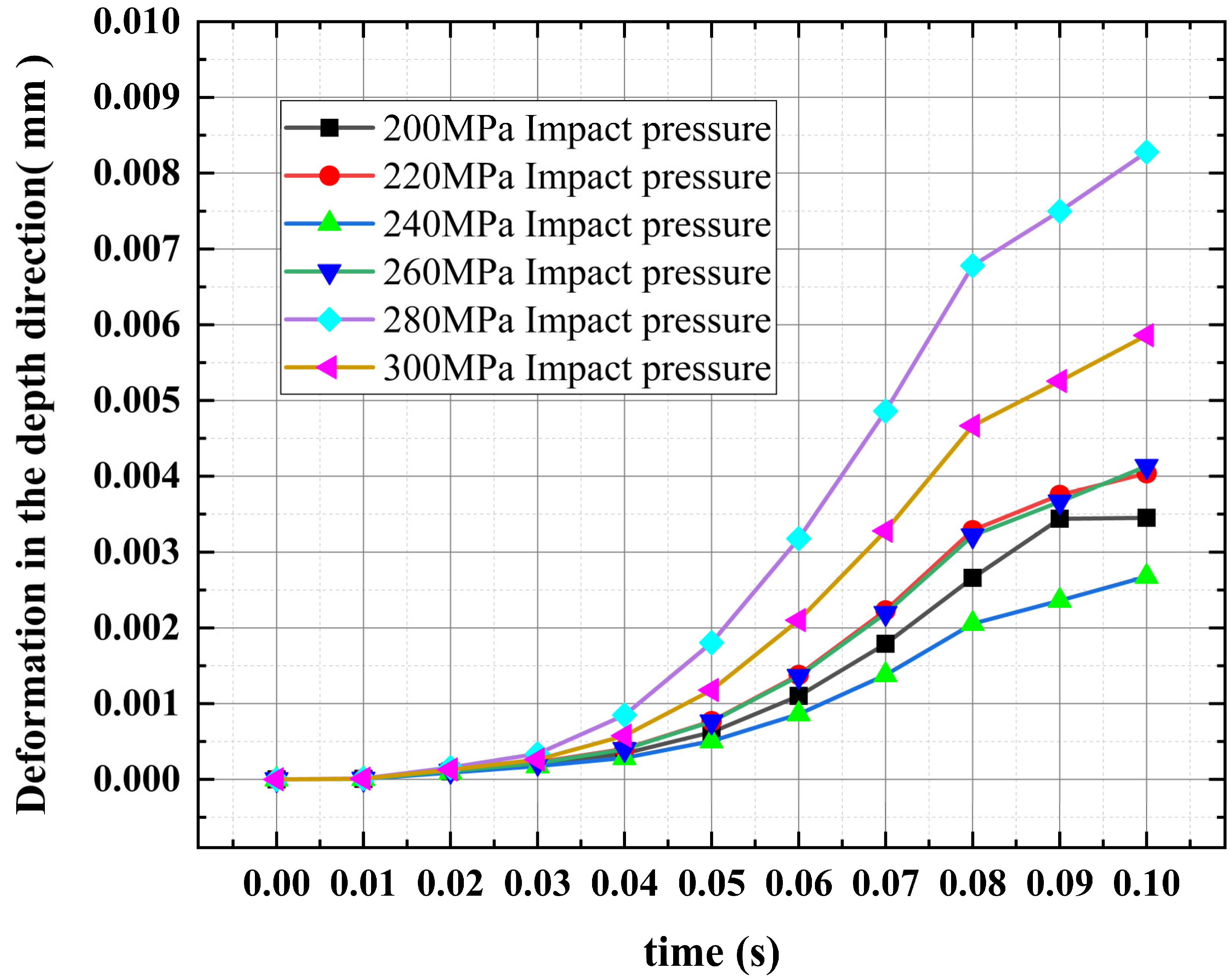
3.2. Numerical Simulation Analysis of Matrix Damage
4. Experimental Analysis
4.1. Experimental Design
4.2. Analysis of Experimental Results
5. Conclusions
- (1)
- The water jet is divided into three regions along the axial direction: the cavitation jet in the nozzle, the free jet, and the stagnation zone. It is divided into a core area and an atomization area along the radial direction. The distribution of turbulent kinetic energy in the atomization area can be used as the basis for judging the degree of jet diffusion and the rate of energy decay. The peak point of turbulent kinetic energy can be used as the boundary between the inner and outer jets.
- (2)
- After the water jet impactes the surface of the target, a crater-like crater is formed. With the increase of impact pressure, the overall deformation showes an increasing trend. And the increasing trend is obviously rising. Without considering the accumulated damage, the jet pressure is the most important factor.
- (3)
- The depression of the erosion area is caused by the destruction of the material by the stagnation pressure. Accumulated damage has a serious impact on the surface erosion damage of the target.
Author Contributions
Funding
Conflicts of Interest
References
- Duplessis, M.P.; Hashish, M. High Energy Water Jet Cutting Equations for Wood. J. Eng. Ind. 1978, 100, 452. [Google Scholar] [CrossRef]
- Leu, M.C.; Meng, P.; Geskin, S.; Tismeneskiy, L. Mathematical Modeling and Experimental Verification of Stationary Waterjet Cleaning Process. J. Manuf. Sci. Eng. 1998, 120, 571–579. [Google Scholar] [CrossRef]
- Meng, P.; Geskin, E.S.; Leu, M.C.; Li, F.; Tismeneskiy, L. An Analytical and Experimental Study of Cleaning with Moving Waterjets. J. Manuf. Sci. Eng. 1998, 120, 580–589. [Google Scholar] [CrossRef]
- Guha, A.; Barron, R.M.; Balachandar, R. Numerical simulation of high-speed turbulent water jets in air. J. Hydraul. Res. 2010, 48, 119–124. [Google Scholar] [CrossRef]
- Mabrouki, T.; Raissi, K.; Cornier, A. Numerical simulation and experimental study of the interaction between a pure high-velocity waterjet and targets: Contribution to investigate the decoating process. Wear 2000, 239, 260–273. [Google Scholar] [CrossRef]
- Mabrouki, T.; Raissi, K. Stripping process modelling: Interaction between a moving waterjet and coated target. Int. J. Mach. Tools Manuf. 2002, 42, 1247–1258. [Google Scholar] [CrossRef] [Green Version]
- Ramulu, M.; Hashish, M.; Cantrell, A. High Pressure Waterjets—An Innovative Means of Alpha Case Removal for Superplastically Formed Titanium Alloys. Key Eng. Mater. 2010, 433, 103–111. [Google Scholar]
- Guha, A.; Barron, R.M.; Balachandar, R. An experimental and numerical study of water jet cleaning process. J. Mater. Process. Technol. 2011, 211, 610–618. [Google Scholar] [CrossRef] [Green Version]
- Kunaporn, S.; Ramulu, M.; Hashish, M. Mathematical Modeling of Ultra-High-Pressure Waterjet Peening. J. Eng. Mater. Technol. 2005, 127, 186–191. [Google Scholar] [CrossRef]
- Glover, H.; Brass, T.; Bhagat, R.; Davidson, J.; Pratt, L.; Wilson, D. Cleaning of complex soil layers on vertical walls by fixed and moving impinging liquid jets. J. Food Eng. 2016, 178, 95–109. [Google Scholar] [CrossRef] [Green Version]
- Azhari, A.; Schindler, C.; Hilbert, K.; Godard, C.; Kerscher, E. Influence of waterjet peening and smoothing on the material surface and properties of stainless steel 304. Surf. Coat. Technol. 2014, 258, 1176–1182. [Google Scholar] [CrossRef] [Green Version]
- Nayak, B.B.; Abhishek, K.; Mahapatra, S.S.; Das, D. Application of WPCA based taguchi method for multi-response optimization of abrasive jet machining process. Mater. Today Proc. 2018, 5, 5138–5144. [Google Scholar] [CrossRef]
- Amri, R.; Laamouri, A.; Manchoul, S.; Fathallah, R. Transient dynamic finite element simulation for prediction of surface integrity induced by waterjet peening. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2019, 234, 105–119. [Google Scholar] [CrossRef]
- Barsukov, G.V.; Zhuravleva, T.A.; Kozhus, O.G. The Research and Simulation (Modelling) of the Destruction of a Single Abrasive Particle during Waterjet Cutting. Mater. Sci. Forum 2020, 989, 235–241. [Google Scholar] [CrossRef]
- Hamid, A.; Atan, R. Spray characteristics of jet–swirl nozzles for thrust chamber injector. Aerosp. Sci. Technol. 2009, 13, 192–196. [Google Scholar] [CrossRef]
- Aganin, A.; Guseva, T. The Influence of the End Shape of the Liquid Jet on Its Impact onto a Dry Wall. Uchenye Zap. Kazan. Univ. Ser. Fiz.-Mat. Nauki 2019, 161, 39–52. [Google Scholar] [CrossRef]
- Mieszala, M.; Torrubia, P.L.; Axinte, D.; Schwiedrzik, J.; Guo, Y.; Mischler, S.; Michler, J.; Philippe, L. Erosion mechanisms during abrasive waterjet machining: Model microstructures and single particle experiments. J. Mater. Process. Technol. 2017, 247, 92–102. [Google Scholar] [CrossRef] [Green Version]
- Thakur, R.K.; Singh, K.K.; Ramkumar, J. Impact of nanoclay filler reinforcement on CFRP composite performance during abrasive water jet machining. Mater. Manuf. Process. 2021, 36, 1264–1273. [Google Scholar] [CrossRef]
- Lohar, S.R.; Kubade, P.R. Investigation of Effect of Abrasive Water Jet Machining (AWJM) Process Parameters on Performance Characteristics of High Carbon High Chromium Steel (AISI D3). IARJSET 2017, 4, 152–158. [Google Scholar] [CrossRef]
- Liu, J.; Chen, Y.; Zhu, Y. Breaking Mechanism and Damage Evolution Rule of Ultra-High-Pressure Water Jet Impacting Steel Fiber Reinforced Concrete. Adv. Civ. Eng. 2021, 2021, 6697409. [Google Scholar] [CrossRef]
- Zhang, Y.; Zang, W.; Zheng, J.; Cappietti, L.; Zhang, J.; Zheng, Y.; Fernandez-Rodriguez, E. The influence of waves propagating with the current on the wake of a tidal stream turbine. Appl. Energy 2021, 290, 116729. [Google Scholar] [CrossRef]
- Sembrat, J.; Miller, P.; Skavdahl, J.; Frenzel, L. Conservation of Historic Metals by Waterjetting Techniques. J. Archit. Conserv. 2005, 11, 121–146. [Google Scholar] [CrossRef]
- Han, Y.; Zhou, L.; Bai, L.; Shi, W.; Agarwal, R. Comparison and validation of various turbulence models for U-bend flow with a magnetic resonance velocimetry experiment. Phys. Fluids 2021, 33, 125117. [Google Scholar] [CrossRef]
- Chillman, A.; Ramulu, M.; Hashish, M. Waterjet and Water-Air Jet Surface Processing of a Titanium Alloy: A Parametric Evaluation. J. Manuf. Sci. Eng. 2010, 132, 011012. [Google Scholar] [CrossRef]
- Ayed, Y.; Robert, C.; Germain, G.; Ammar, A. Development of a numerical model for the understanding of the chip formation in high-pressure water-jet assisted machining. Finite Elem. Anal. Des. 2016, 108, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Yildizeli, A.; Cadirci, S. Multi-objective optimization of multiple impinging jet system through genetic algorithm. Int. J. Heat Mass Transf. 2020, 158, 119978. [Google Scholar] [CrossRef]
- Znamenskaya, I.A.; Nersesyan, D.A.; Sysoev, N.N.; Koroteeva, E.Y.; Shirshov, Y.N. An optical study of high-pressure water-jet dynamics. Mosc. Univ. Phys. Bull. 2016, 71, 405–412. [Google Scholar] [CrossRef]
- Henning, A.; Liu, H.T.; Olsen, C. Economic and Technical Efficiency of High Performance Abrasive Waterjet Cutting. J. Press. Vessel Technol. 2012, 134, 21405. [Google Scholar] [CrossRef]
- Chillman, A.; Hashish, M.; Ramulu, M. Energy Based Modeling of Ultra High-Pressure Waterjet Surface Preparation Processes. J. Press. Vessel Technol. 2011, 133, 061205. [Google Scholar] [CrossRef]




| Test Group | Number of Grid Cells | Maximum Pressure of the Impacted Surface of the Target (MPa) |
|---|---|---|
| A1 | 324,651 | 59.439 |
| A2 | 632,218 | 71.965 |
| A3 | 975,376 | 79.731 |
| A4 | 1,262,945 | 82.686 |
| A5 | 1,794,662 | 83.127 |
| A6 | 2,036,387 | 83.238 |
| A7 | 2,560,398 | 83.367 |
| Broken Mode | Jet Characteristics |
|---|---|
| Rayleigh broken | liquid Weber number and the air Weber number |
| Atomization and crushing | Air Weber number |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Q.; Shi, Z.; Shi, W.; Xie, Z.; Tan, L.; Yang, Y. Research on Flow Field Characteristics in Water Jet Nozzle and Surface Damage Caused by Target Impact. Sustainability 2022, 14, 9074. https://doi.org/10.3390/su14159074
Zhang Q, Shi Z, Shi W, Xie Z, Tan L, Yang Y. Research on Flow Field Characteristics in Water Jet Nozzle and Surface Damage Caused by Target Impact. Sustainability. 2022; 14(15):9074. https://doi.org/10.3390/su14159074
Chicago/Turabian StyleZhang, Qinghong, Zhouhao Shi, Weidong Shi, Zhanshan Xie, Linwei Tan, and Yongfei Yang. 2022. "Research on Flow Field Characteristics in Water Jet Nozzle and Surface Damage Caused by Target Impact" Sustainability 14, no. 15: 9074. https://doi.org/10.3390/su14159074
APA StyleZhang, Q., Shi, Z., Shi, W., Xie, Z., Tan, L., & Yang, Y. (2022). Research on Flow Field Characteristics in Water Jet Nozzle and Surface Damage Caused by Target Impact. Sustainability, 14(15), 9074. https://doi.org/10.3390/su14159074





