A Comprehensive Evaluation Model on Optimal Operational Schedules for Battery Energy Storage System by Maximizing Self-Consumption Strategy and Genetic Algorithm
Abstract
:1. Introduction
2. Materials and Methods
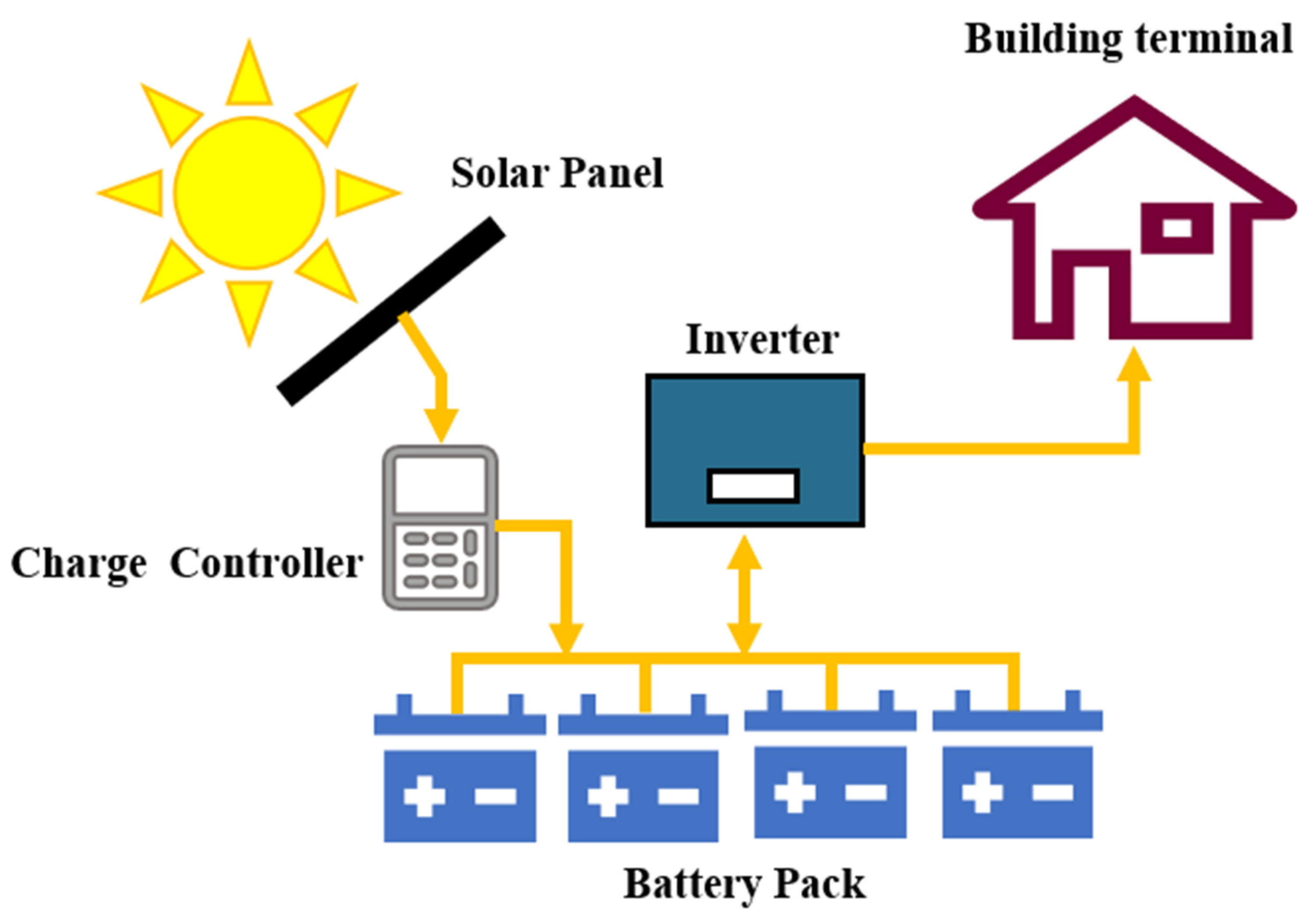
2.1. Configuration of the Battery Energy System
2.2. Mathematical Modeling on the Energy Storage Component
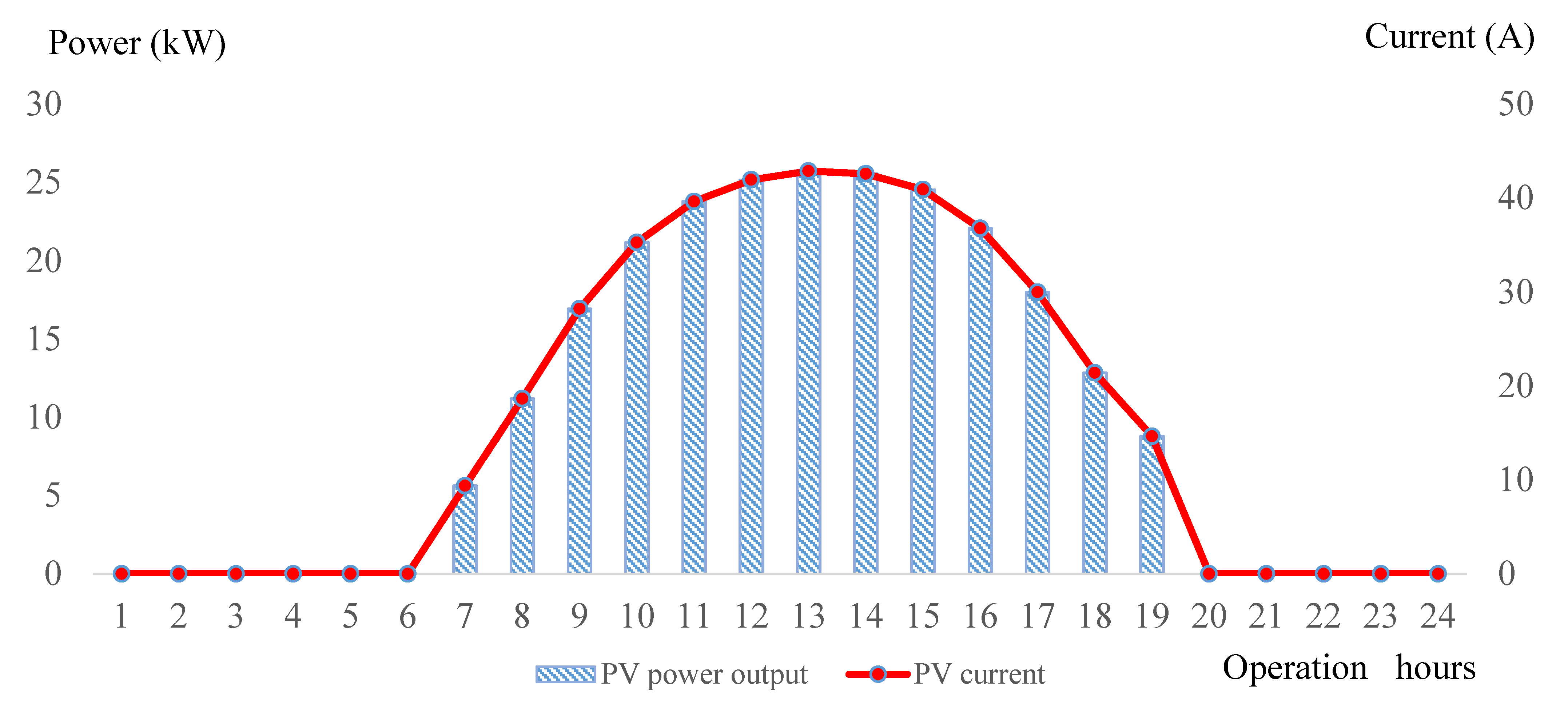
2.2.1. PV Array
2.2.2. Battery Bank
2.3. Performance Indicators for System Evaluation
2.3.1. Technical Indicators
2.3.2. Economic Indicators
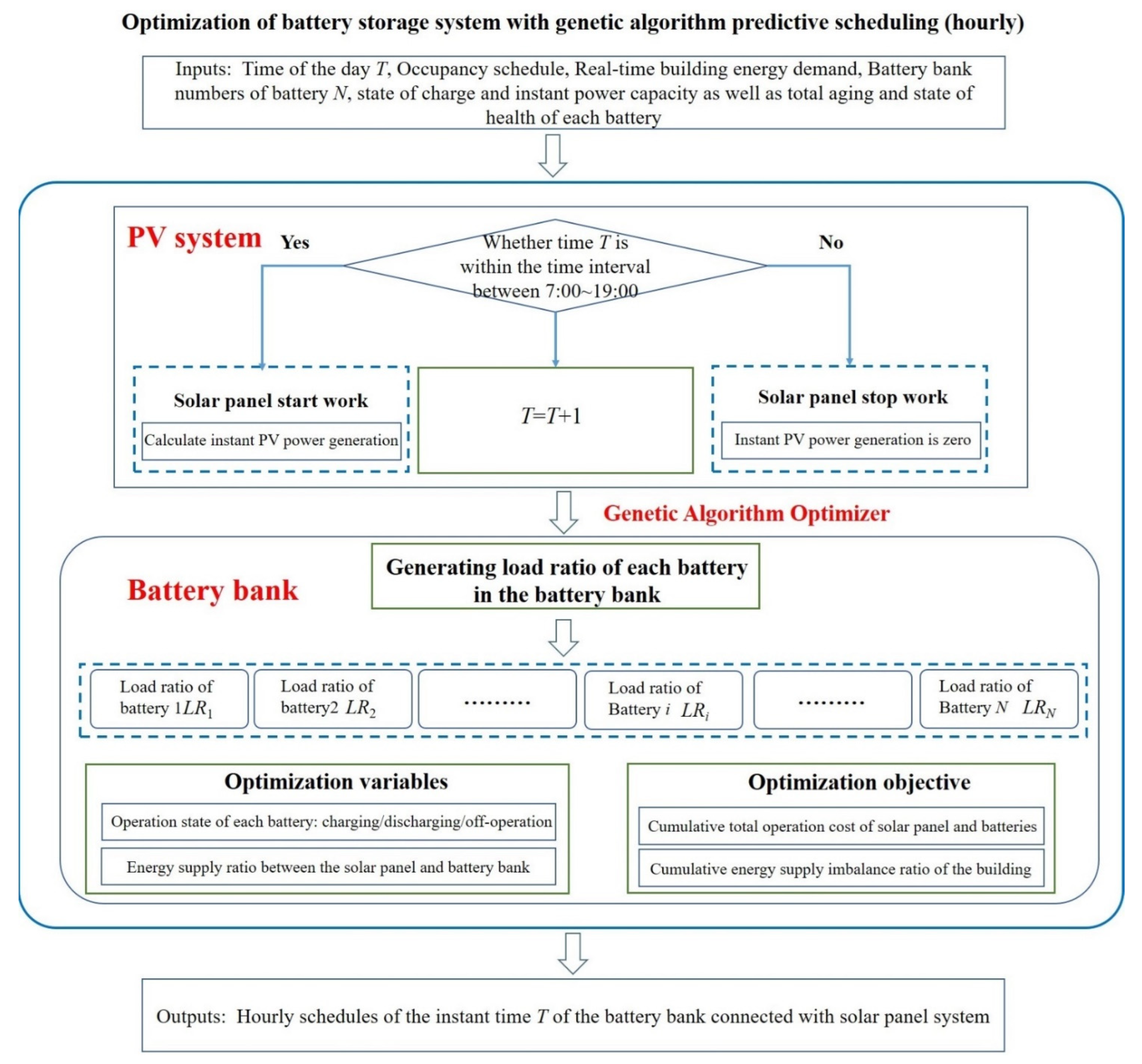
2.4. Rule-Based MSC Strategy
- (1)
- Battery charge/discharge rate limit:
- (2)
- The state of charge (SOC) limit:
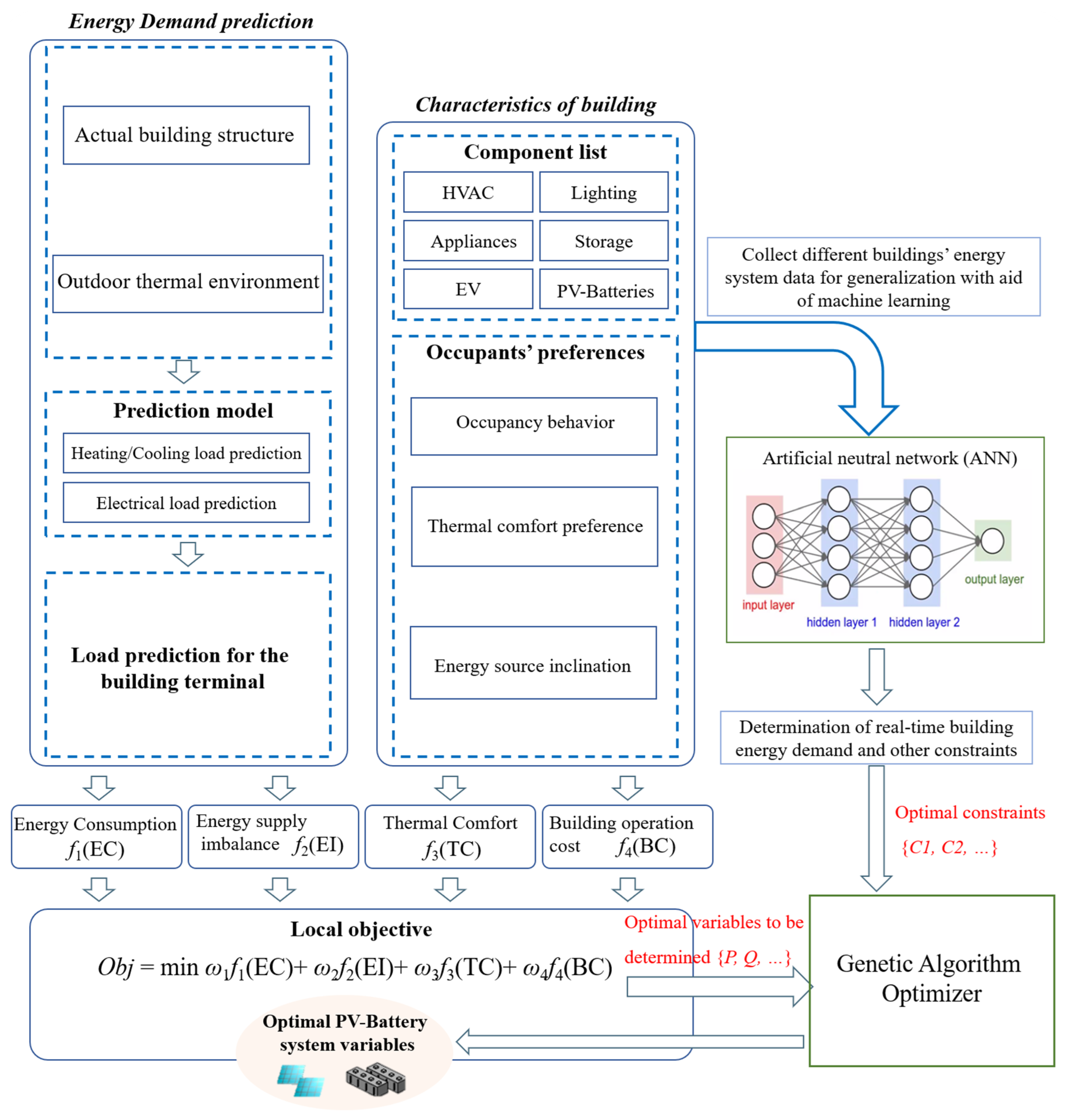
2.5. Building Energy Demand Prediction
2.5.1. Individual Needs and Preferences
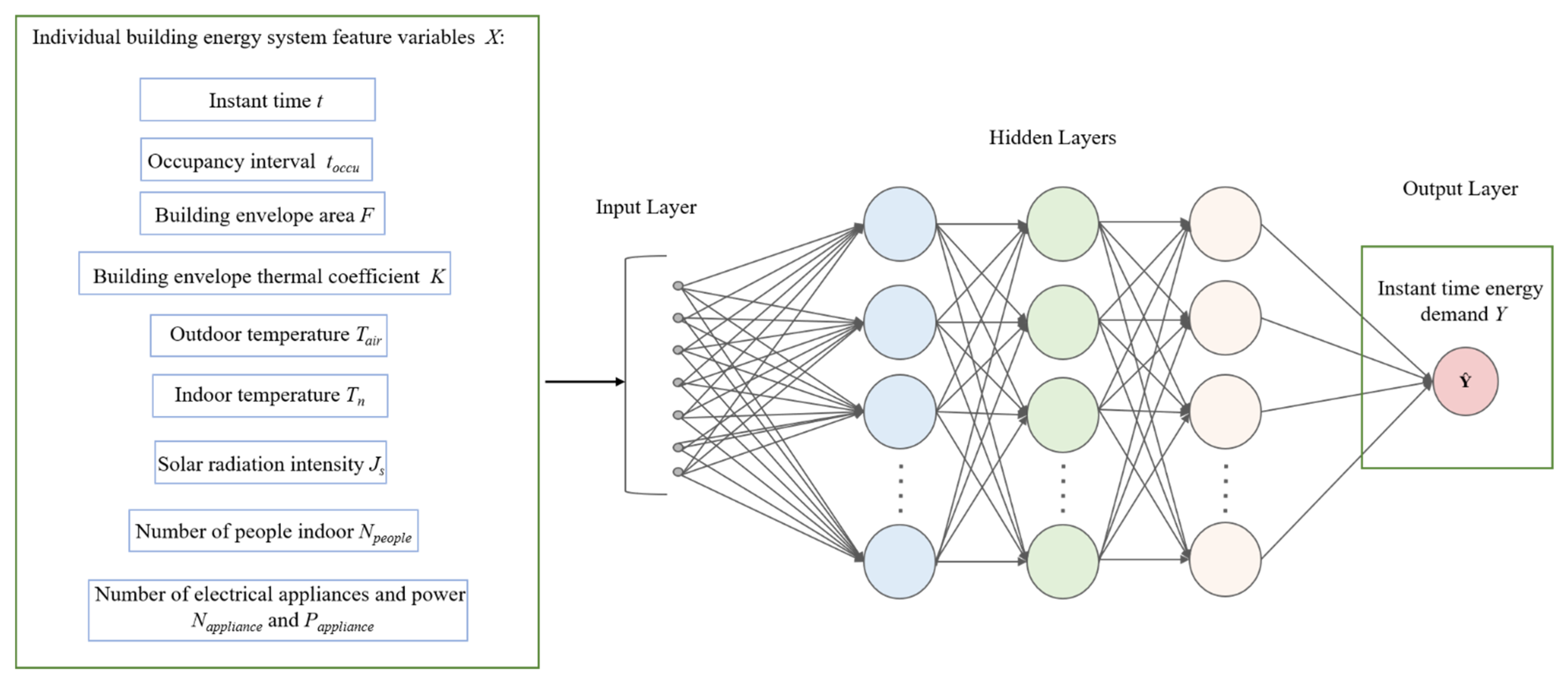
2.5.2. Establishment of Building Energy Demand Model
- (1)
- External envelope
- (2)
- Load from people indoor
- (3)
- Lighting and household electric appliances load
2.5.3. Machine Learning Approach for Building Energy Demand
3. Results
3.1. Data Collection and Analysis for Battery Storage System
3.1.1. Number of People Using Energy
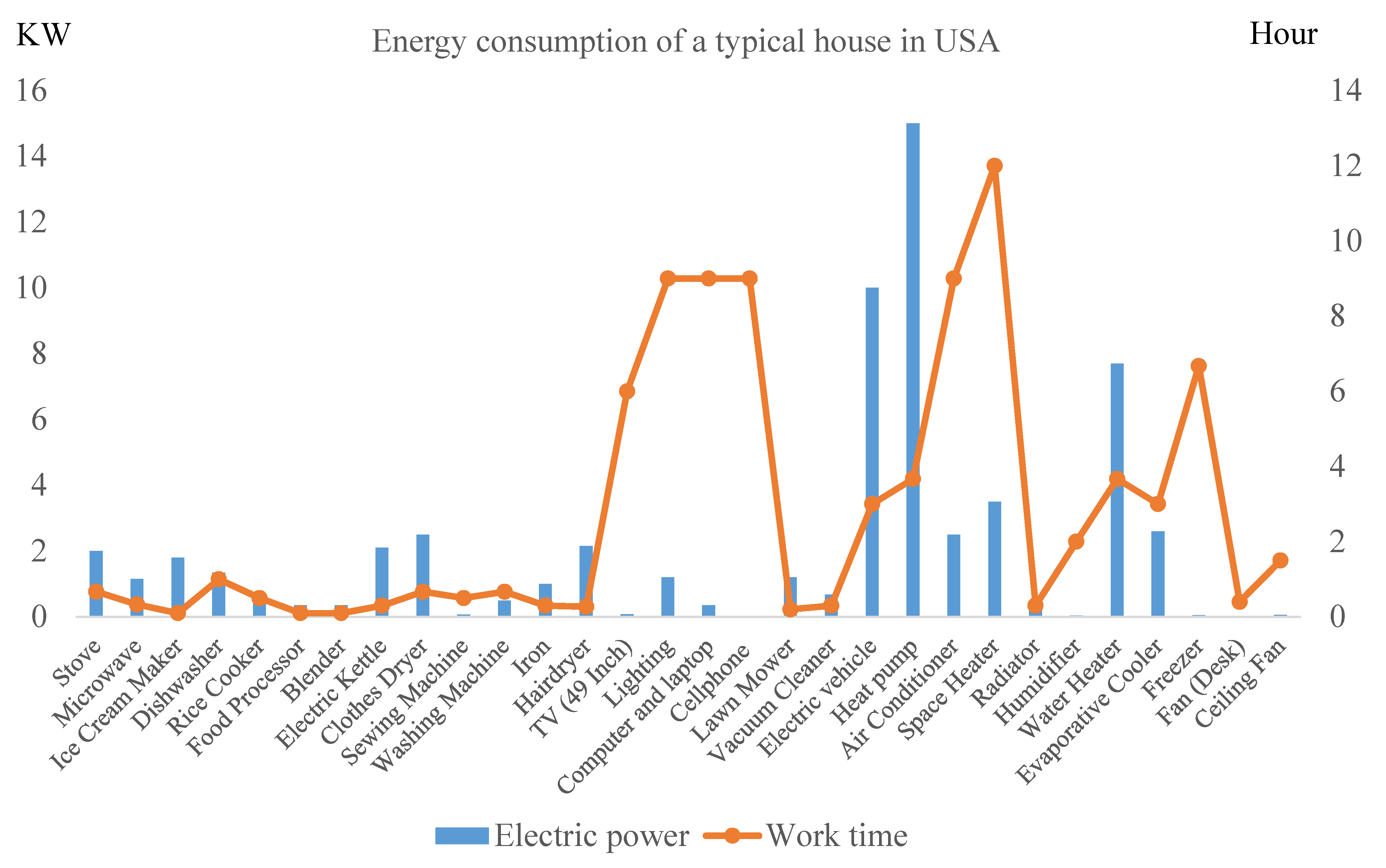
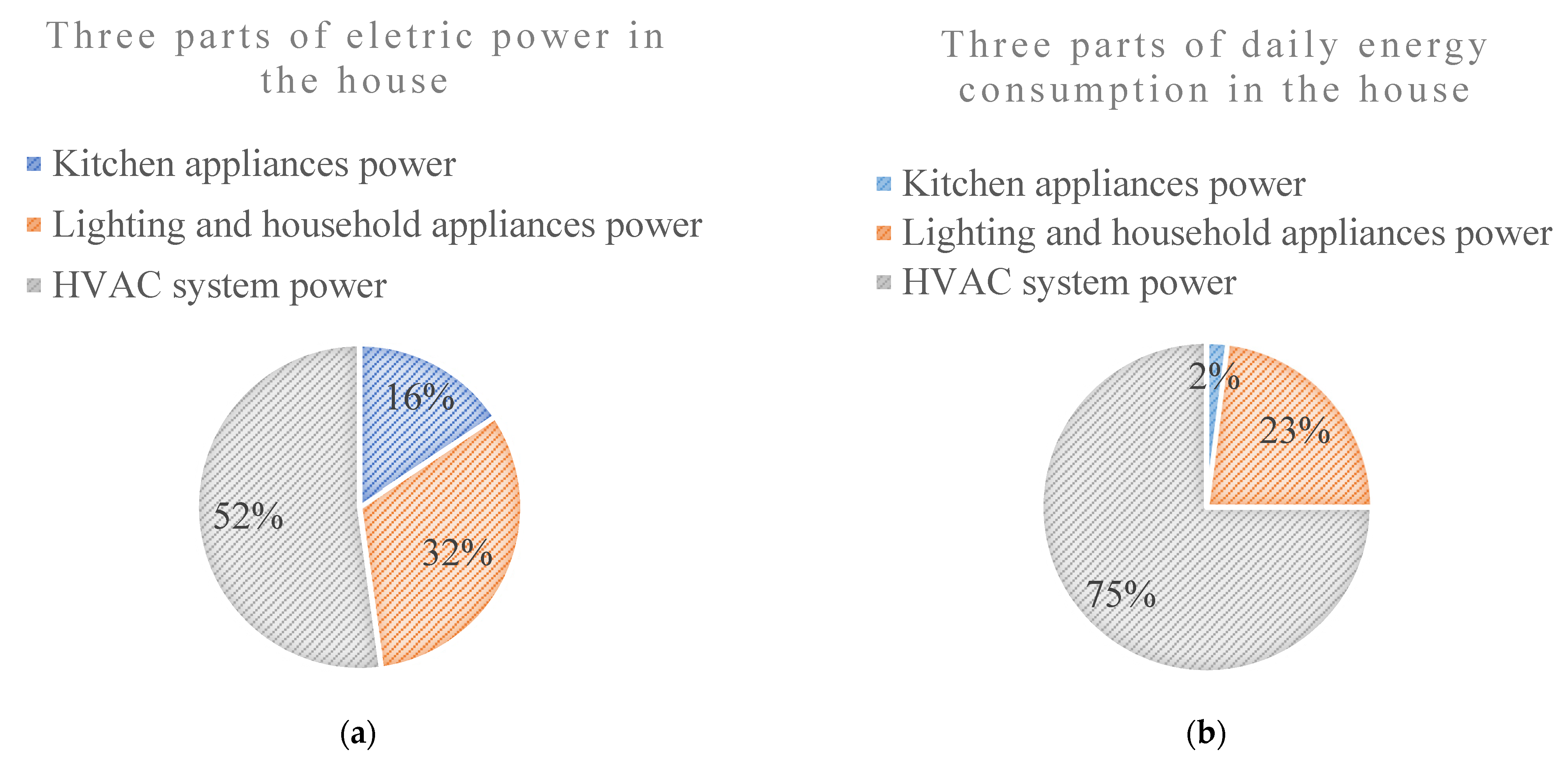
3.1.2. Appliances That Need Energy
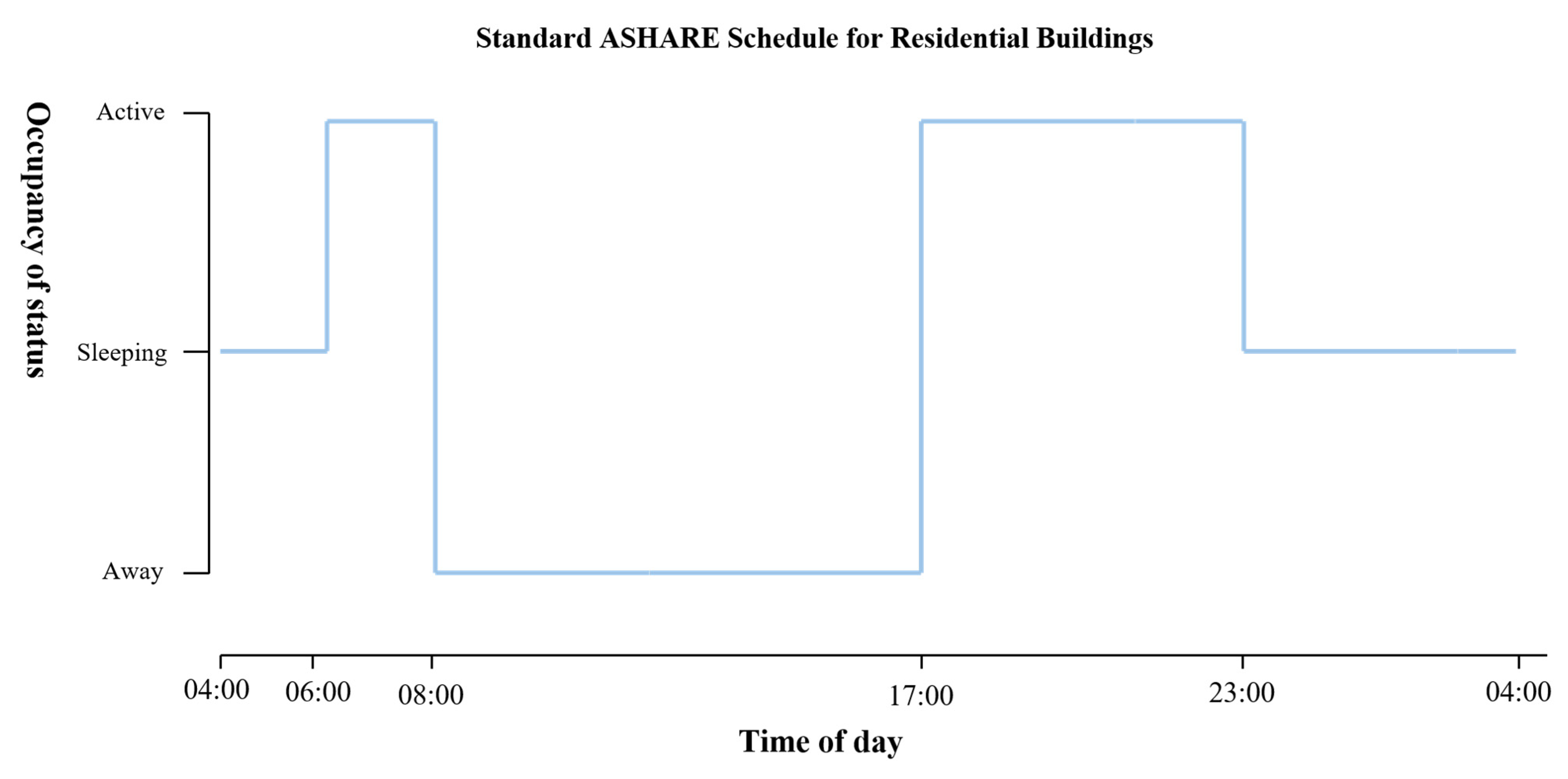
3.1.3. Time Intervals When People at Home Use Energy
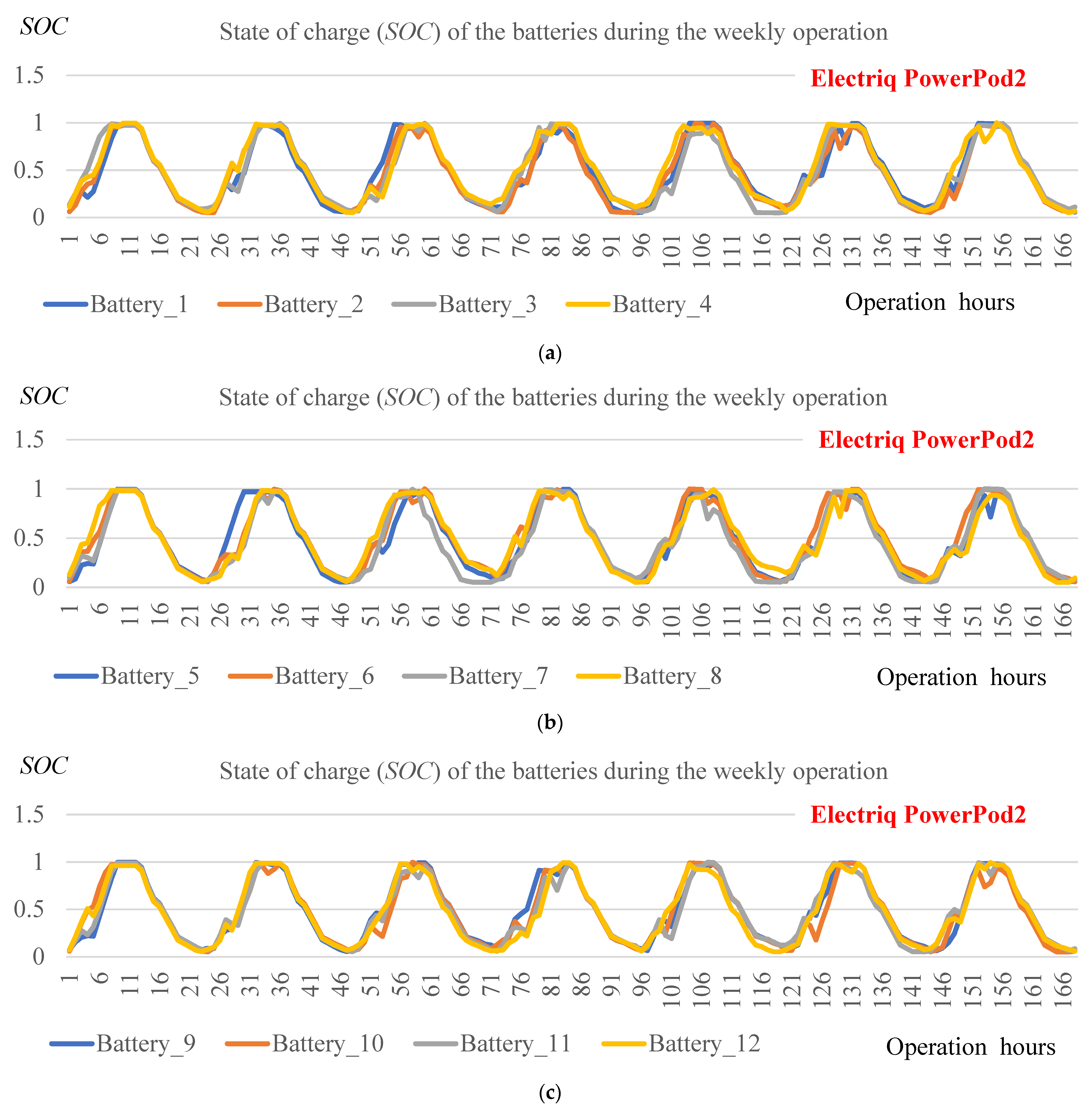
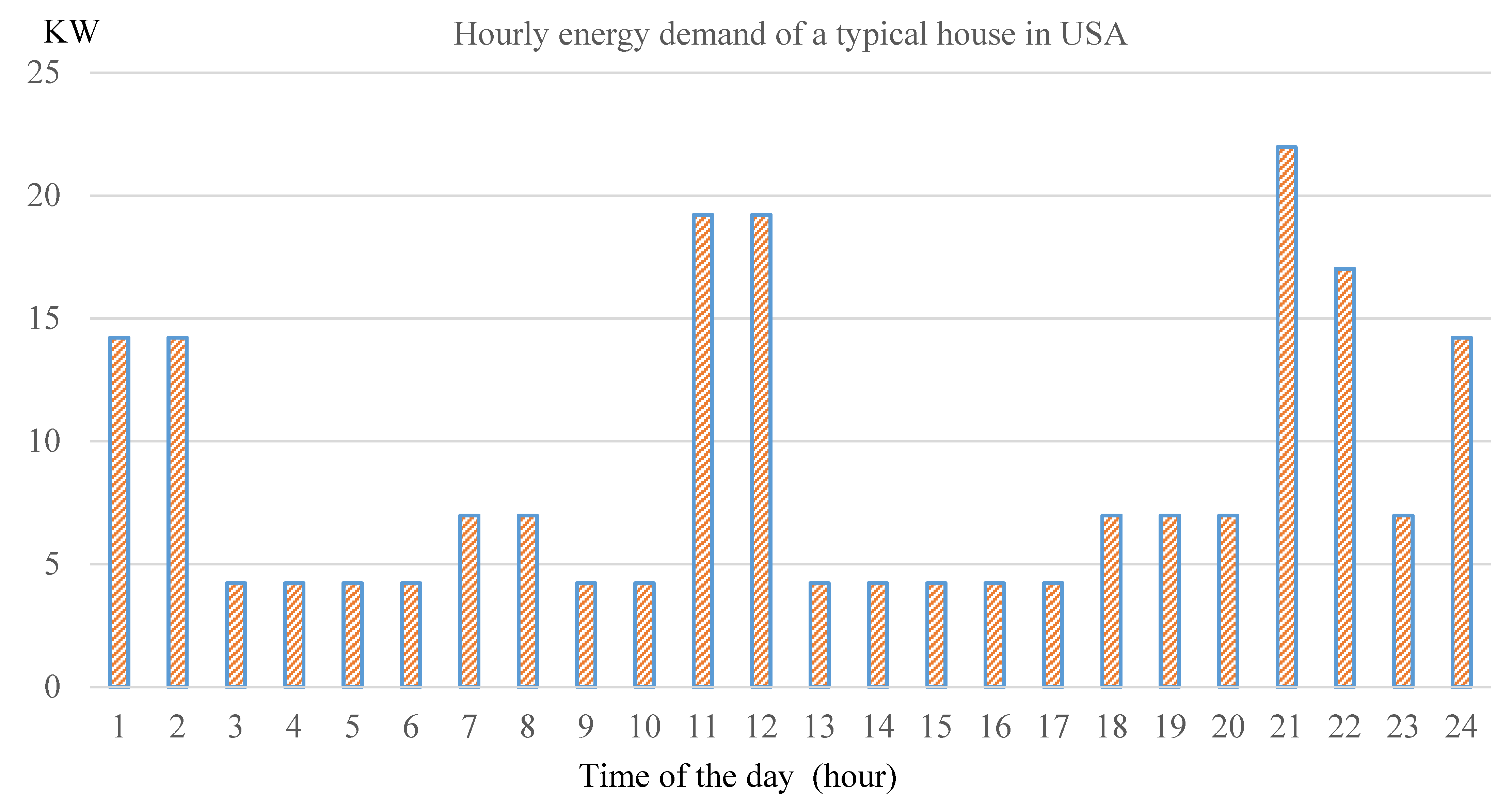
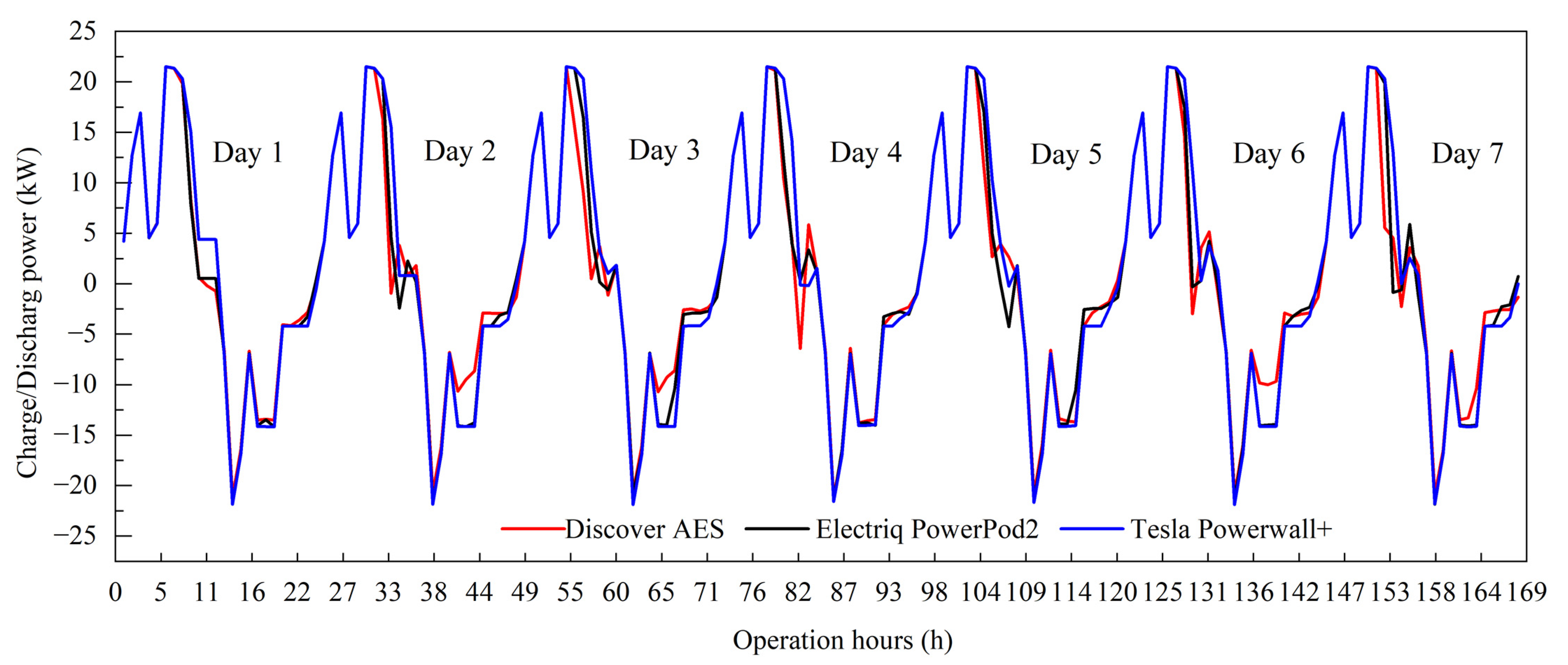
3.2. Operation Schedules of the Battery Storage System for a Typical House
3.3. Operation Schedules of the Battery Storage System with Energy Demand Prediction
4. Discussion
- (1)
- Generic applicability: Building energy demand acts as the optimization objective for the energy storage strategy but it has many techno-economic indicators. This model was enhanced from previous studies, which typically focused on only one or two evaluation indicators. It could comprehensively evaluate the integrated objective, and is thus more applicable to complex scenarios.
- (2)
- Convenient implementation: As shown in the flow chart for simulation in Figure 3, this model could easily be applied in a real project. It performs simplified modeling on the core components of the battery system and commonly used techno-economic indicators. Moreover, it is based on the GA approach for global optimization, and makes a clear distinction between the charging and discharging phase considering the classical MSC strategy. Therefore, the optimization could be conveniently implemented for a real control strategy
- (3)
- Good scalability: The model shows great potential in terms of its scalability. This paper investigated a simple battery energy system configuration, and more energy storage components could be easily incorporated and integrated with the original system. Moreover, this model also provides a test bed for new techno-economic indicators applicable to the optimization and evaluation of the system.
5. Conclusions
- (1)
- This comprehensive evaluation model for the operational schedule of a battery storage system could account for both technological and economic indicators, and the optimal solution based on MSC strategy genetic algorithm could be found.
- (2)
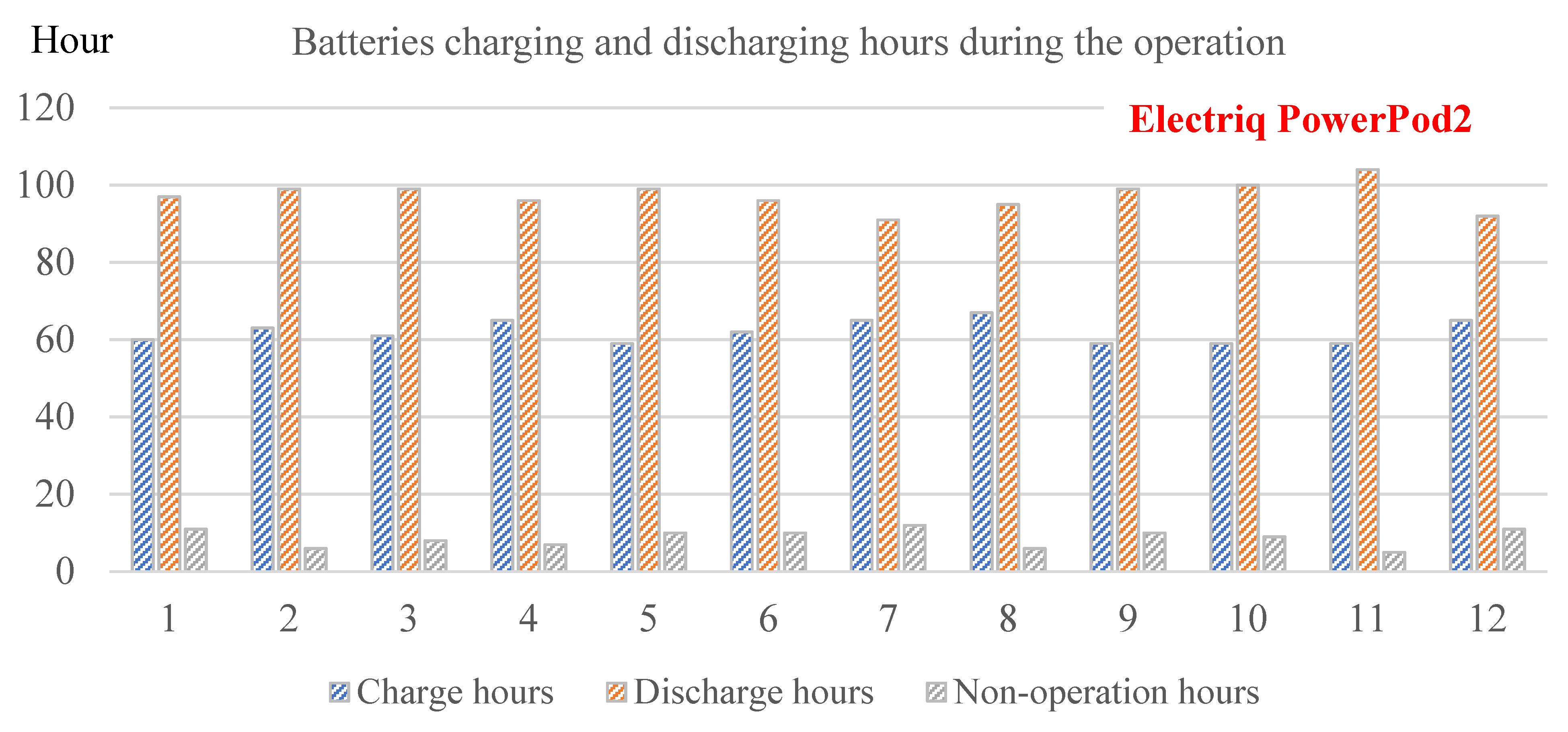
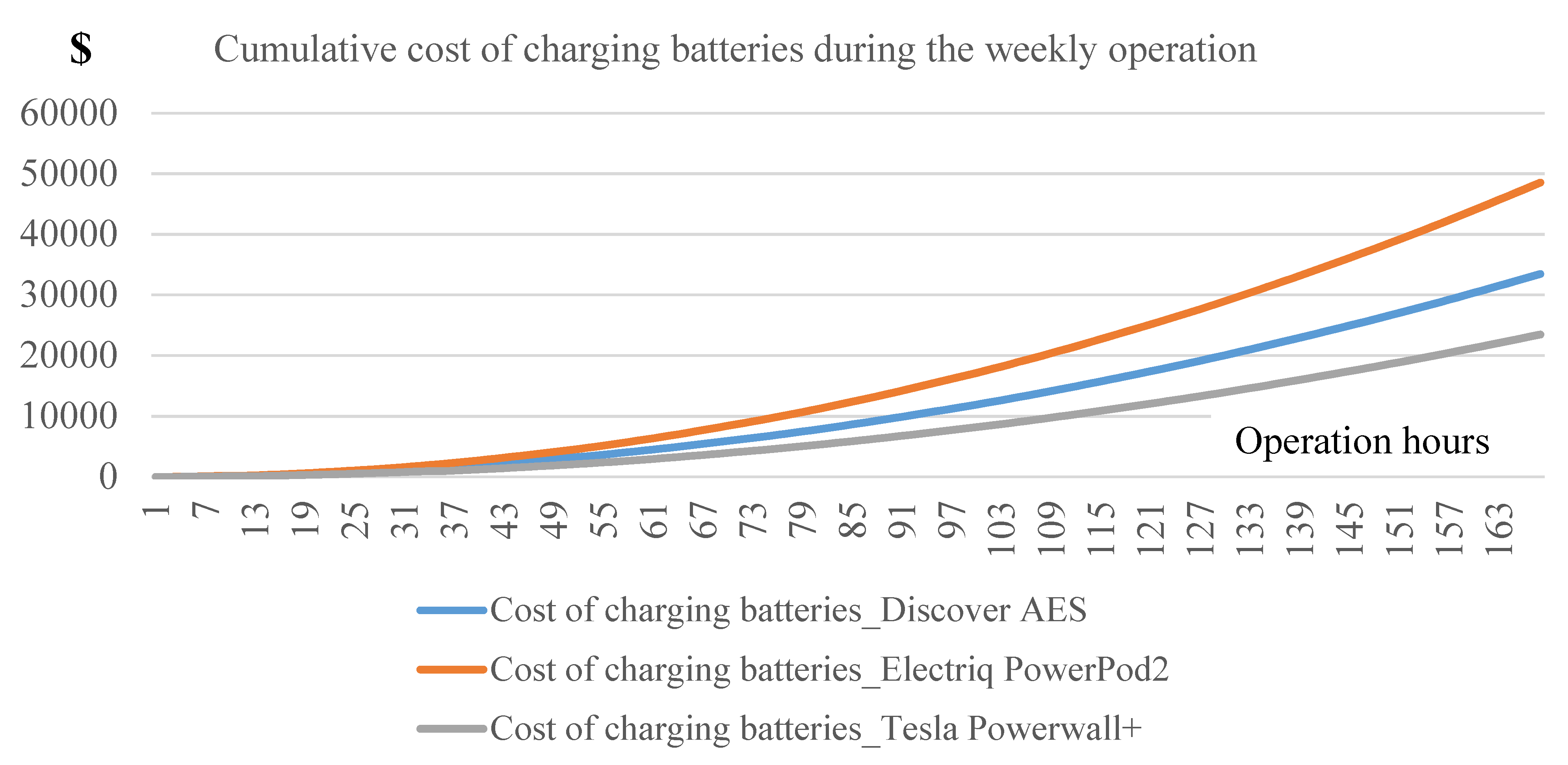
- The three types of batteries including Discover AES, Electriq PowerPod2 and Tesla Powerwall+ could be considered as options for energy storage. For short term operation, there exists subtle differences in the technical performance among them but Tesla Powerwall+ was the most cost-effective option.
- (3)
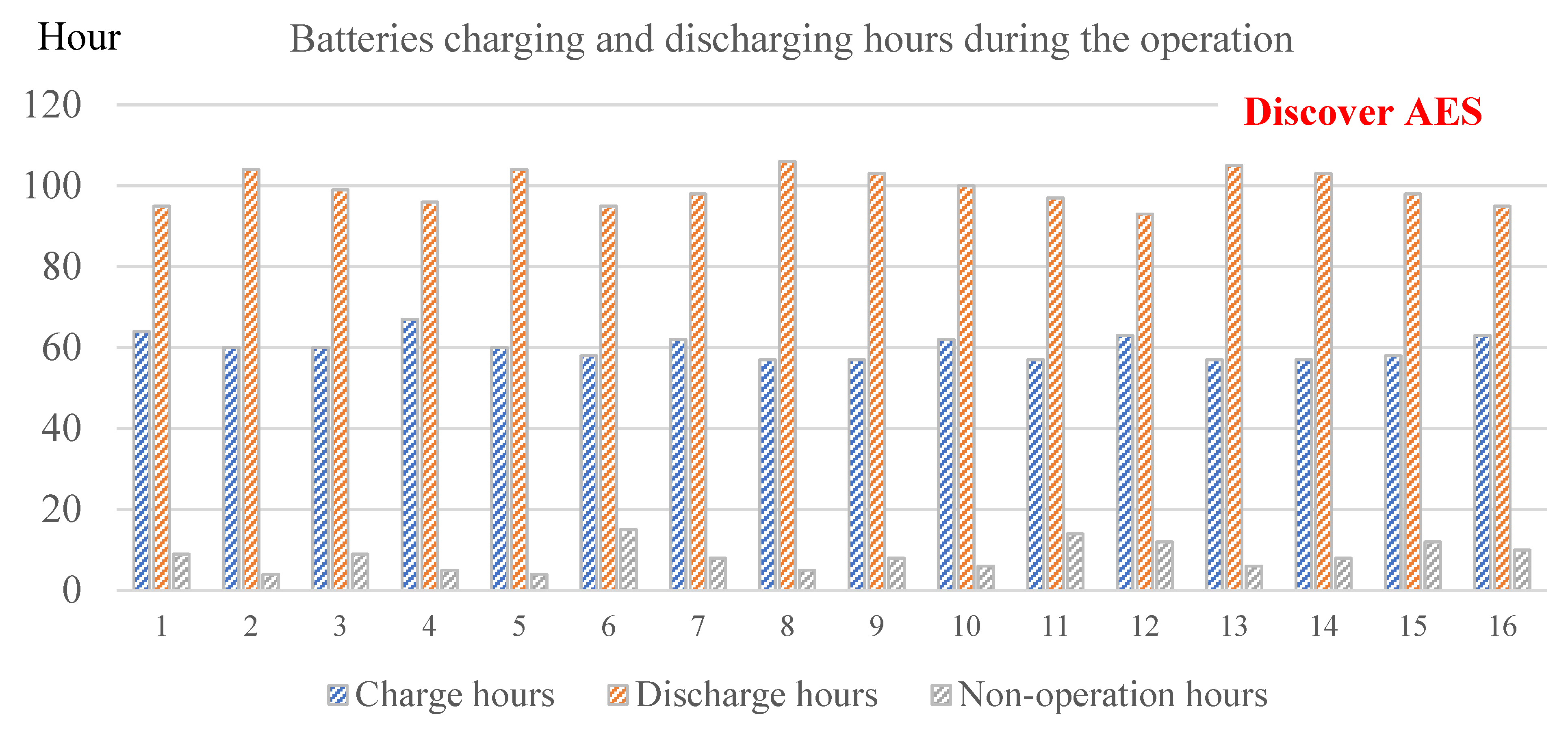
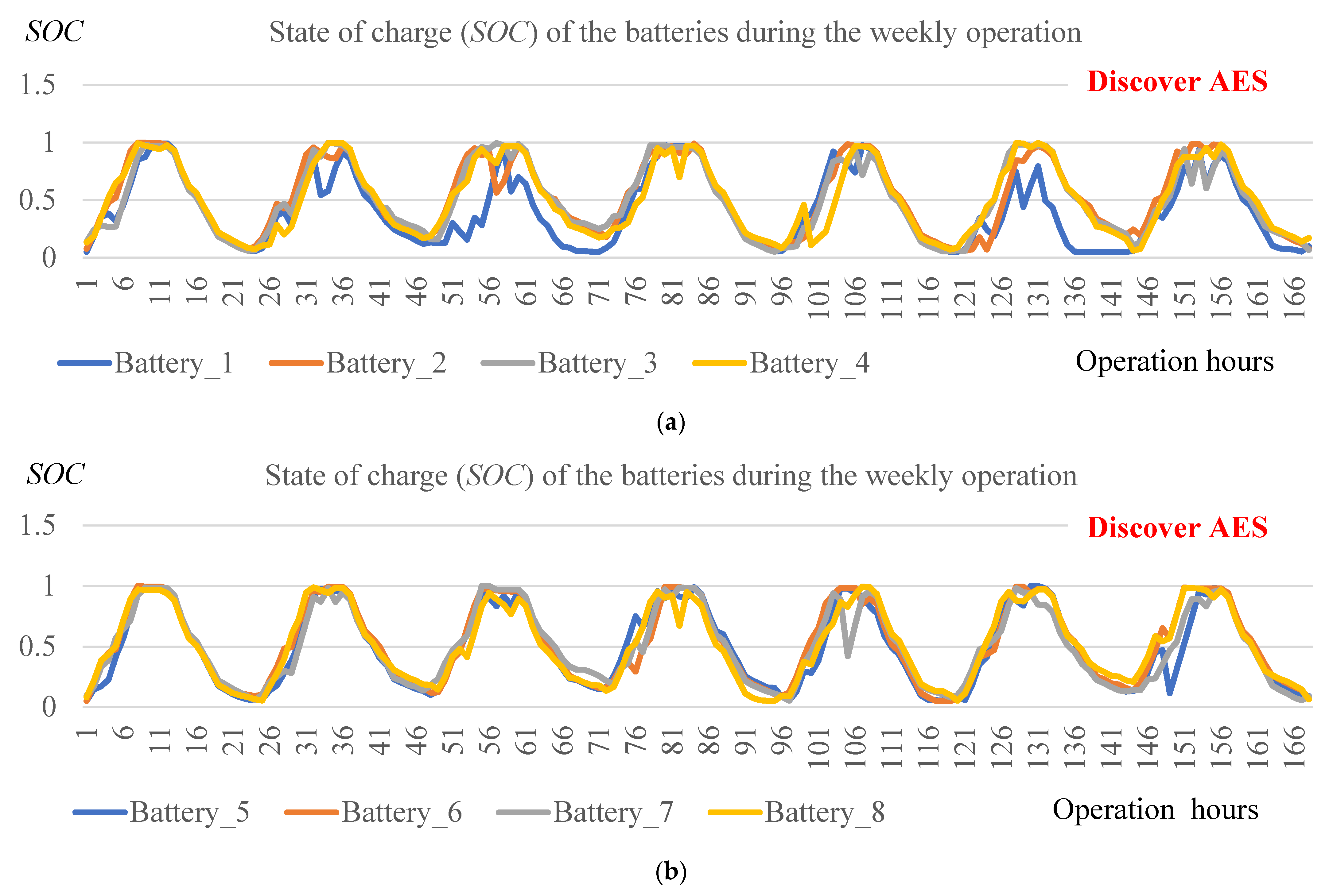
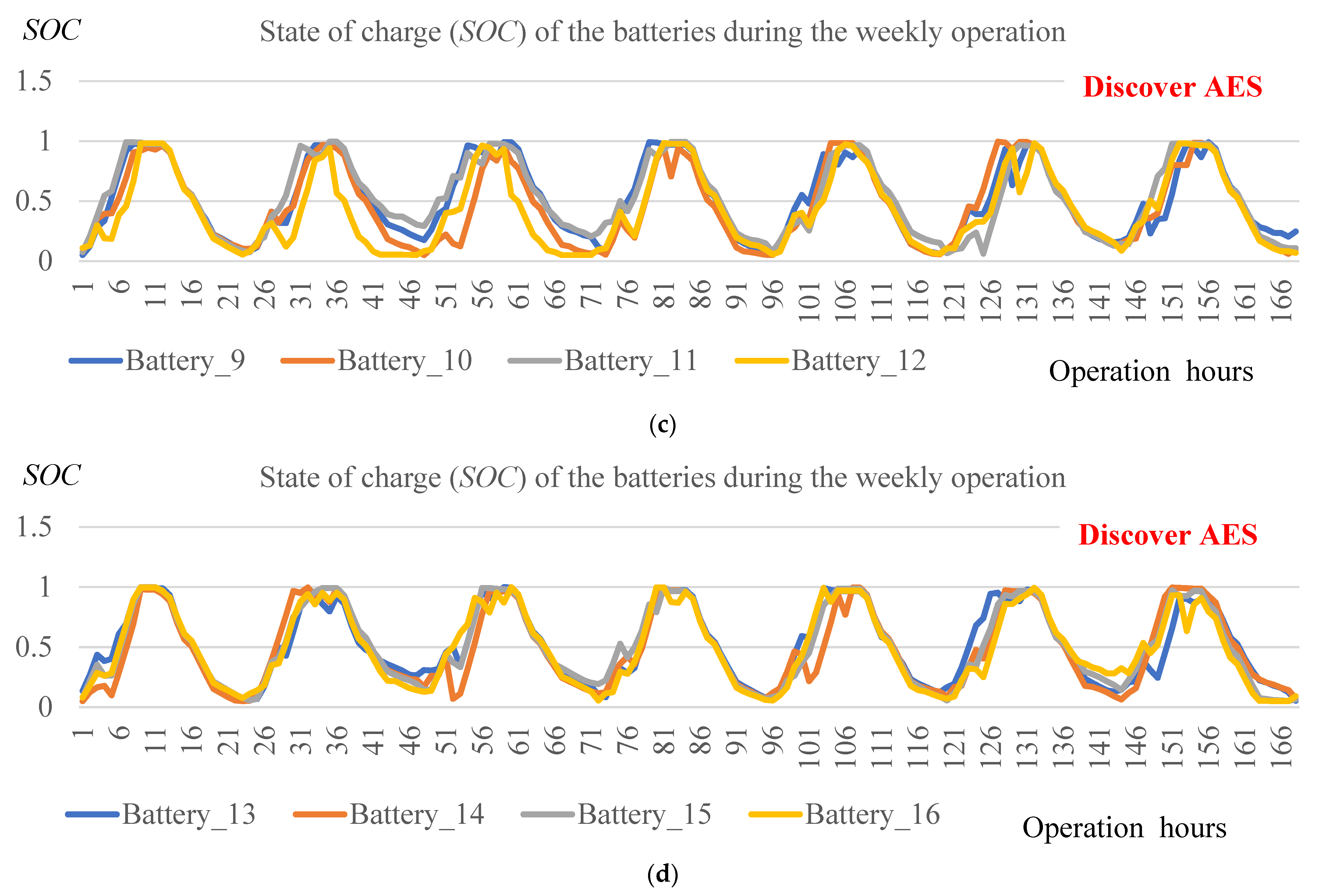
- According to long-term simulation, Discover AES had a relatively higher total operation cost, but it resulted in the lowest level of battery aging. Therefore, Discover AES has the advantage of using PV generation in a timely manner to suit the load demand.
- (4)
- The machine learning approach provides a feasible option for us to adapt our optimization model based on the MSC strategy and GA method for arbitrary battery storage scenarios with different energy demand features.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Cabeza, L.F.; Chàfer, M. Technological options and strategies towards zero energy buildings contributing to climate change mitigation: A systematic review. Energy Build. 2020, 219, 110009. [Google Scholar] [CrossRef]
- Peng, J.; Yan, J.; Zhai, Z.; Markides, C.N.; Lee, E.S.; Eicker, U.; Zhao, X.; Kuhn, T.E.; Sengupta, M.; Taylor, R.A. Solar energy integration in buildings. Appl. Energy 2020, 264, 114740. [Google Scholar] [CrossRef]
- Zhang, Y.; Lundblad, A.; Campana, P.E.; Yan, J. Employing battery storage to increase photovoltaic self-sufficiency in a residential building of Sweden. Energy Procedia 2016, 88, 455–461. [Google Scholar] [CrossRef] [Green Version]
- Schram, W.L.; Lampropoulos, I.; van Sark, W.G.J.H.M. Photovoltaic systems coupled with batteries that are optimally sized for household self-consumption: Assessment of peak shaving potential. Appl. Energy 2018, 223, 69–81. [Google Scholar] [CrossRef]
- Guichi, A.; Talha, A.; Berkouk, E.M.; Mekhilef, S. Energy management and performance evaluation of grid connected PV-battery hybrid system with inherent control scheme. Sustain. Cities Soc. 2018, 41, 490–504. [Google Scholar] [CrossRef]
- Zou, B.; Peng, J.; Li, S.; Li, Y.; Yan, J.; Yang, H. Comparative Study of the Dynamic Programming-Based and Rule-Based Operation Strategies for Grid-Connected PV-Battery Systems of Office Buildings. Appl. Energy 2022, 305, 117875. [Google Scholar] [CrossRef]
- Braun, M.; Büdenbender, K.; Magnor, D.; Jossen, A. Photovoltaic self-consumption in Germany—Using lithium-ion storage to increase self-consumed photovoltaic energy. In Proceedings of the 24th European Photovoltaic Solar Energy Conference, Hamburg, Germany, 21–25 September 2009. [Google Scholar]
- Luthander, R.; Widén, J.; Nilsson, D.; Palm, J. Photovoltaic self-consumption in buildings: A review. Appl. Energy 2015, 142, 80–94. [Google Scholar] [CrossRef] [Green Version]
- Boussetta, M.; El Bachtiri, R.; Khanfara, M.; El Hammoumi, K. Assessing the potential of hybrid PV–Wind systems to cover public facilities loads under different Moroccan climate conditions. Sustain. Energy Technol. Assess. 2017, 22, 74–82. [Google Scholar] [CrossRef]
- Azuatalam, D.; Paridari, K.; Ma, Y.; Förstl, M.; Chapman, A.C.; Verbič, G. Energy management of small-scale PV-battery systems: A systematic review considering practical implementation, computational requirements, quality of input data and battery degradation. Renew. Sustain. Energy Rev. 2019, 112, 555–570. [Google Scholar] [CrossRef] [Green Version]
- Hussein Ala, A.; Fardoun Abbas, A. Design considerations and performance evaluation of outdoor PV battery chargers. Renew. Energy 2015, 82, 85–91. [Google Scholar] [CrossRef]
- Roy, A.; Bandyopadhyay, S. Design and optimization of wind-PV-battery hybrid system. In Wind Power Based Isolated Energy Systems; Springer: Berlin/Heidelberg, Germany, 2019; pp. 167–180. [Google Scholar]
- Cai, J.; Zhang, H.; Jin, X. Aging-aware predictive control of PV-battery assets in buildings. Appl. Energy 2019, 236, 478–488. [Google Scholar] [CrossRef]
- Chakir, A.; Tabaa, M.; Moutaouakkil, F.; Medromi, H.; Julien-Salame, M.; Dandache, A.; Alami, K. Optimal energy management for a grid connected PV-battery system. Energy Rep. 2020, 6, 218–231. [Google Scholar] [CrossRef]
- Hern’andez, J.C.; Sanchez-Sutil, F.; Mu˜noz-Rodríguez, F.J. Design criteria for the optimal sizing of a hybrid energy storage system in PV household-prosumers to maximize self-consumption and self-sufficiency. Energy 2019, 186, 115827. [Google Scholar] [CrossRef]
- Sharma, V.; Haque, M.H.; Aziz, S.M. Energy cost minimization for net zero energy homes through optimal sizing of battery storage system. Renew. Energy 2019, 141, 278–286. [Google Scholar] [CrossRef]
- Khan, F.; Pal, N.; Saeed Syed, H. Review of solar photovoltaic and wind hybrid energy systems for sizing strategies optimization techniques and cost analysis methodologies. Renew. Sustain. Energy Rev. 2018, 92, 937–947. [Google Scholar] [CrossRef]
- Zhang, Y.; Ma, T.; Elia Campana, P.; Yamaguchi, Y.; Dai, Y. A techno-economic sizing method for grid-connected household photovoltaic battery systems. Appl. Energy 2020, 269, 115106. [Google Scholar] [CrossRef]
- Mokrani, Z.; Rekioua, D.; Rekioua, T. Modeling control and power management of hybrid photovoltaic fuel cells with battery bank supplying electric vehicle. Int. J. Hydrog. Energy 2014, 39, 15178–15187. [Google Scholar] [CrossRef]
- Alramlawi, M.; Gabash, A.; Mohagheghi, E.; Li, P. Optimal operation of hybrid PV-battery system considering grid scheduled blackouts and battery lifetime. Sol. Energy 2018, 161, 125–137. [Google Scholar] [CrossRef]
- Angenendt, G.; Zurmühlen, S.; Axelsen, H.; Sauer, D.U. Comparison of different operation strategies for PV battery home storage systems including forecast-based operation strategies. Appl. Energy 2018, 229, 884–899. [Google Scholar] [CrossRef]
- Talavera, D.L.; Mu˜noz-Rodriguez, F.J.; Jimenez-Castillo, G.; Rus-Casas, C. A new approach to sizing the photovoltaic generator in self-consumption systems based on cost–competitiveness, maximizing direct self-consumption. Renew. Energy 2019, 130, 1021–1035. [Google Scholar] [CrossRef]
- Nyholm, E.; Goop, J.; Odenberger, M.; Johnsson, F. Solar photovoltaic-battery systems in Swedish households—Self-consumption and self-sufficiency. Appl. Energy 2016, 183, 148–159. [Google Scholar] [CrossRef] [Green Version]
- Verma, D.; Nema, S.; Shandilya, A.M.; Dash Soubhagya, K. Maximum power point tracking (MPPT) techniques: Recapitulation in solar photovoltaic systems. Renew. Sustain. Energy Rev. 2016, 54, 1018–1034. [Google Scholar] [CrossRef]
- Barth, N.; Jovanovic, R.; Ahzi, S.; Khaleel, M.A. PV panel single and double diode models: Optimization of the parameters and temperature dependence. Sol. Energy Mater. Sol. Cells 2016, 148, 87–98. [Google Scholar] [CrossRef]
- Abdmouleh, Z.; Gastli, A.; Ben-Brahim, L.; Haouari, M.; Al-Emadi, N.A. Review of optimization techniques applied for the integration of distributed generation from renewable energy sources. Renew. Energy 2017, 113, 266–280. [Google Scholar] [CrossRef]
- 2021 ASHRAE Fundamentals Handbook, SI. Available online: https://www.ashrae.org/technical-resources/ashrae-handbook/ashrae-handbook-online (accessed on 15 May 2022).
- U.S. Energy Information Administration—EIA—Independent Statistics and Analysis. Residential Energy Consumption Survey (RECS)-Data-U.S. Energy Information Administration (EIA). 2015. Available online: https://www.eia.gov/consumption/residential/data/2015/index.php?view=consumption#undefined (accessed on 15 May 2022).
- List of the Power Consumption of Typical Household Appliances. “Power Consumption of Typical Household Appliances” . Daft Logic, Daft Logic. Available online: https://www.daftlogic.com/information-appliance-power-consumption.htm (accessed on 6 November 2021).
- Teacher, English. “Home Appliances: 30 Best Household Electrical Appliances for Your Home”. Visual Dictionary, Visual Dictionary. Available online: https://visualdictionary.org/homeappliances/ (accessed on 19 April 2021).
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Leshno, M.; Lin, V.Y.; Pinkus, A.; Schocken, S. Multilayer feedforward networks with a nonpolynomial activation function can approximate any function. Neural Netw. 1993, 6, 861–867. [Google Scholar] [CrossRef] [Green Version]
- Wu, W.; Kanamori, Y.; Zhang, R.; Zhou, Q.; Takahashi, K.; Masui, T. Implications of declining household economies of scale on electricity consumption and sustainability in China. Ecol. Econ. 2021, 184, 106981. [Google Scholar] [CrossRef]
- Ellsworth-Krebs, K. Implications of declining household sizes and expectations of home comfort for domestic energy demand. Nat. Energy 2019, 5, 1–6. [Google Scholar]
- Diao, L.; Sun, Y.; Chen, Z.; Chen, J. Modeling energy consumption in residential buildings: A bottom-up analysis based on occupant behavior pattern clustering and stochastic simulation. Energy Build. 2017, 147, 47–66. [Google Scholar] [CrossRef]
- Moy, K.; Lee, S.B.; Harris, S.J.; Onori, S. Design and Validation of Synthetic Duty Cycles for Grid Energy Storage Dispatch Using Lithium-ion Batteries. Adv. Appl. Energy 2021, 4, 100065. [Google Scholar] [CrossRef]
- Zhang, E.Q.; Tang, L. Rechargeable Concrete Battery. Buildings 2021, 11, 103. [Google Scholar] [CrossRef]
- Wen, S.; Chung, D.D.L. Pyroelectric behavior of cement-based materials. Cem. Concr. Res. 2003, 33, 1675–1679. [Google Scholar] [CrossRef]
- Malewar, A. Rechargeable Cement-Based Battery Could Let Buildings Store Energy. Inceptive Mind. Available online: https://www.inceptivemind.com/worlds-first-rechargeable-cement-based-battery-concept/19037/ (accessed on 4 August 2021).

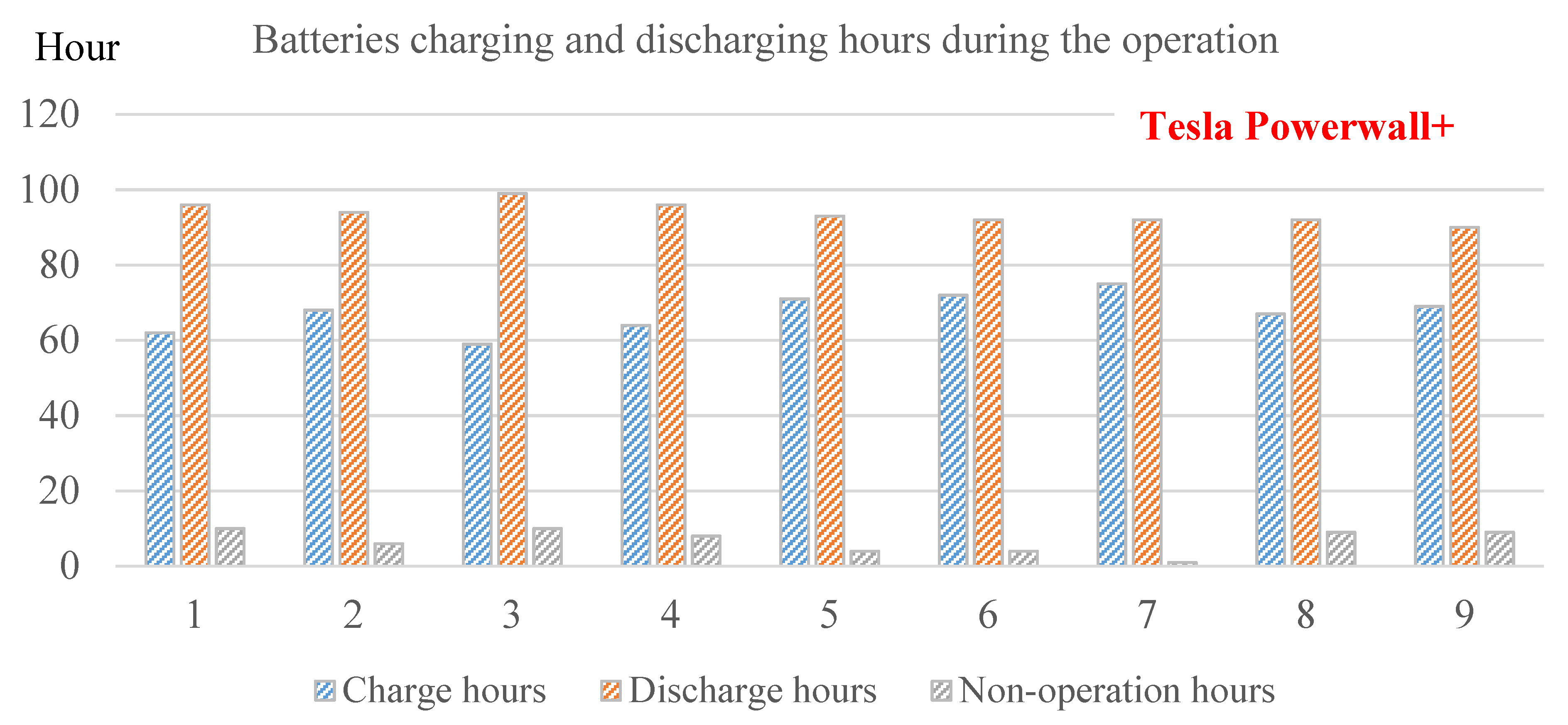

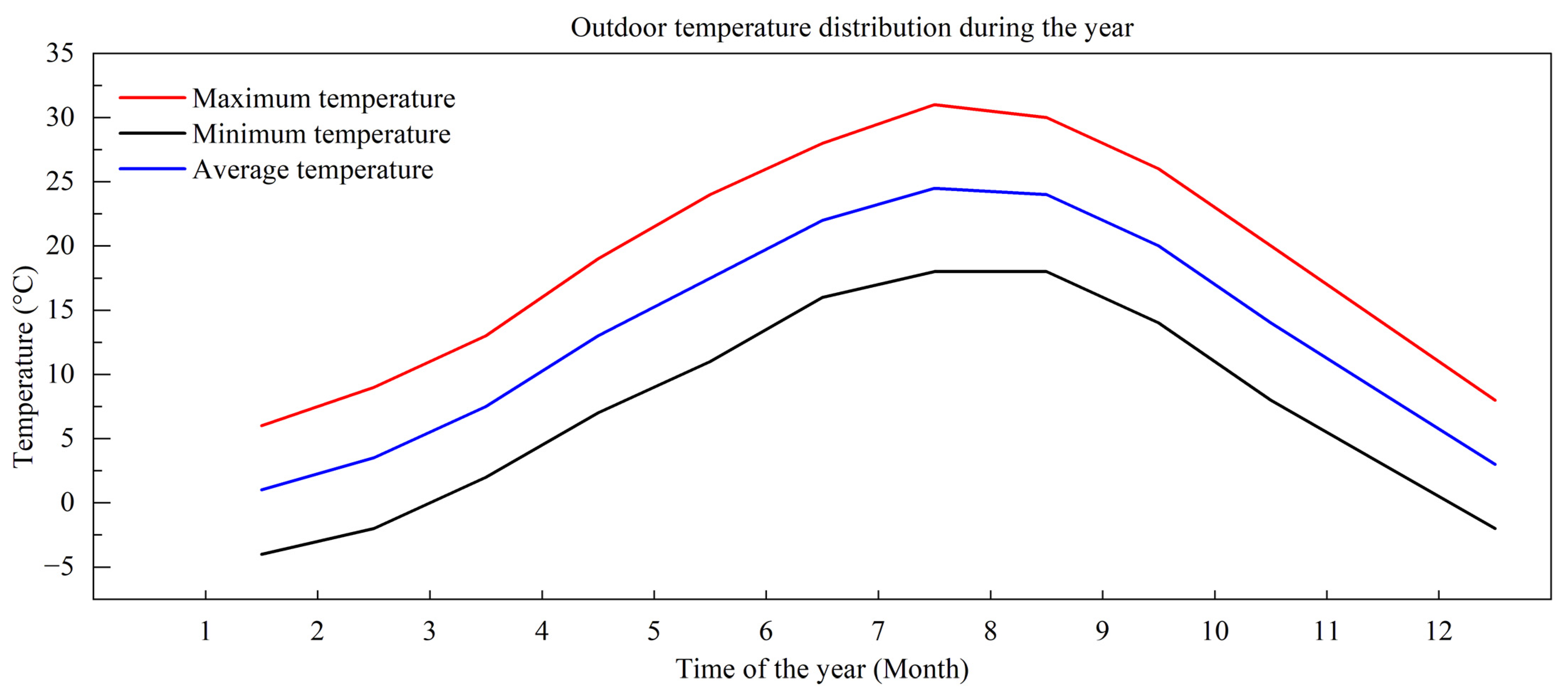
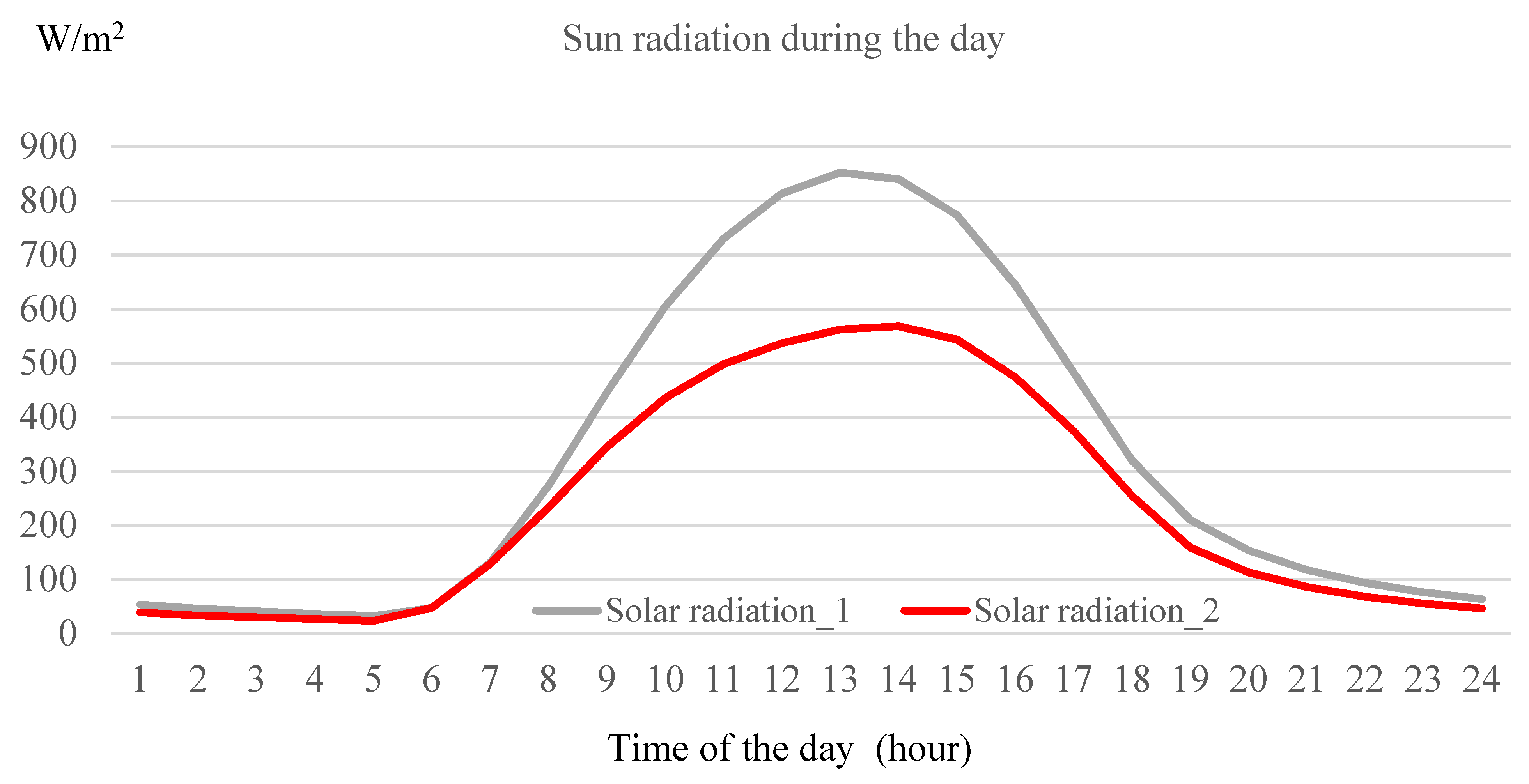


| Parameter | Range of Value |
|---|---|
| Occupancy interval (h) | 0.5~10 |
| Building floor area (ft2) | 600~2600 |
| Thermal conductivity (W/m/K) | 0.1~0.5 |
| Outdoor temperature (°C) | −4~30 |
| Indoor temperature (°C) | 24~26 |
| Solar radiation intensity (W/m2) | 50~850 |
| Number of people per house | 1~4 |
| Number of electric appliances per house | 15~45 |
| Average electric power of appliances (kW) | 0.5~5 |
| Number | Electrical Appliance | Average Power Consumption and Daily Work Hours | Number | Electrical Appliance | Average Power Consumption and Daily Work Hours |
|---|---|---|---|---|---|
| 1 | Stove | 2.00 kW/0.67 h | 16 | Computer and laptop | 0.350 kW/9.0 h |
| 2 | Microwave | 1.150 kW/0.33 h | 17 | Cellphone | 0.005 kW/9.0 h |
| 3 | Ice Cream Maker | 1.800 kW/0.1 h | 18 | Lawn Mower | 1.200 kW/0.2 h |
| 4 | Dishwasher | 1.350 kW/1.0 h | 19 | Vacuum Cleaner | 0.675 kW/0.3 h |
| 5 | Rice Cooker | 0.500 kW/0.5 h | 20 | Electric vehicle | 10.00 kW/3.0 h |
| 6 | Food Processor | 0.350 kW/0.1 h | 21 | Heat pump | 15.00 kW/3.67 h |
| 7 | Blender | 0.350 kW/0.1 h | 22 | Air Conditioner | 2.500 kW/9.0 h |
| 8 | Electric Kettle | 2.100 kW/0.3 h | 23 | Space Heater | 3.500 kW/12.0 h |
| 9 | Clothes Dryer | 2.500 kW/0.67 h | 24 | Radiator | 0.500 kW/0.3 h |
| 10 | Sewing Machine | 0.075 kW/0.5 h | 25 | Humidifier | 0.038 kW/2.0 h |
| 11 | Washing Machine | 0.500 kW/0.67 h | 26 | Water Heater | 7.700 kW/3.67 h |
| 12 | Iron | 1.000 kW/0.3 h | 27 | Evaporative Cooler | 2.600 kW/3.0 h |
| 13 | Hairdryer | 2.150 kW/0.27 h | 28 | Freezer | 0.050 kW/6.67 h |
| 14 | TV (49 Inch) | 0.085 kW/6.0 h | 29 | Fan (Desk) | 0.018 kW/0.4 h |
| 15 | Lighting | 1.200 kW/9.0 h | 30 | Ceiling Fan | 0.065 kW/1.5 h |
| Battery | Cost (USD) | Battery Type | Weight (lbs.) | Dimension (L × W × D in inches) |
| Deka solar 8GCC2 6V 198 | $368 | SGLA | 68 | 10.25 × 7.1 × 10.9 |
| Trojan L-16-SPRE 6V 415 | $492 | FLA | 118 | 11.7 × 6.9 × 17.6 |
| Discover AES 7.4 kWh | $6478 | LFP | 192 | 18.5 × 13.3 × 14.7 |
| Electriq PowerPod2 | $13,000 | LFP | 346 | 27.5 × 50 × 9 |
| Tesla Powerwall+ | $8500 | NMC | 343.9 | 62.8 × 29.7 × 6.3 |
| Continuous Power Rating (kW) | Instaneous Power Rating (kW) | Round-Trip Efficiency (%) | Usable Capacity (kWh) | |
| 0.049 kW (for 20 h)−0.017 kW (for 100 h) | Not Available | 80~85% | 1.18 kWh | |
| 0.19 kW (for 10 h)−0.023 kW (for 100 h) | Not Available | 80~85% | 2.5 kWh | |
| 6.65 kW | 14.4 kW (for 3 s) | >95% | 7.4 kWh | |
| 7.6 kW | 9 kW (for 60 s) | 96.60% | 10 kWh | |
| 7 kW | 10 kW (for 10 s) | 90.00% | 13.5 kWh | |
| Parameter | Value |
|---|---|
| Life cycle number | 4000 |
| SOCmin | 0.05 |
| SOCmax | 1 |
| Parameter | Value |
|---|---|
| PV curve-fitting parameter γ | 0.004576 °C/V |
| Module series resistance | 10 Ω |
| Regression coefficient of photocurrent | 0.075 A m2/W |
| Regression coefficient of module temperature | 0.03125 °C m2/W |
| Referrence diode reverse saturation current | 90 A |
| PV voltage adjustment range by MPPT controller | 200~600 V |
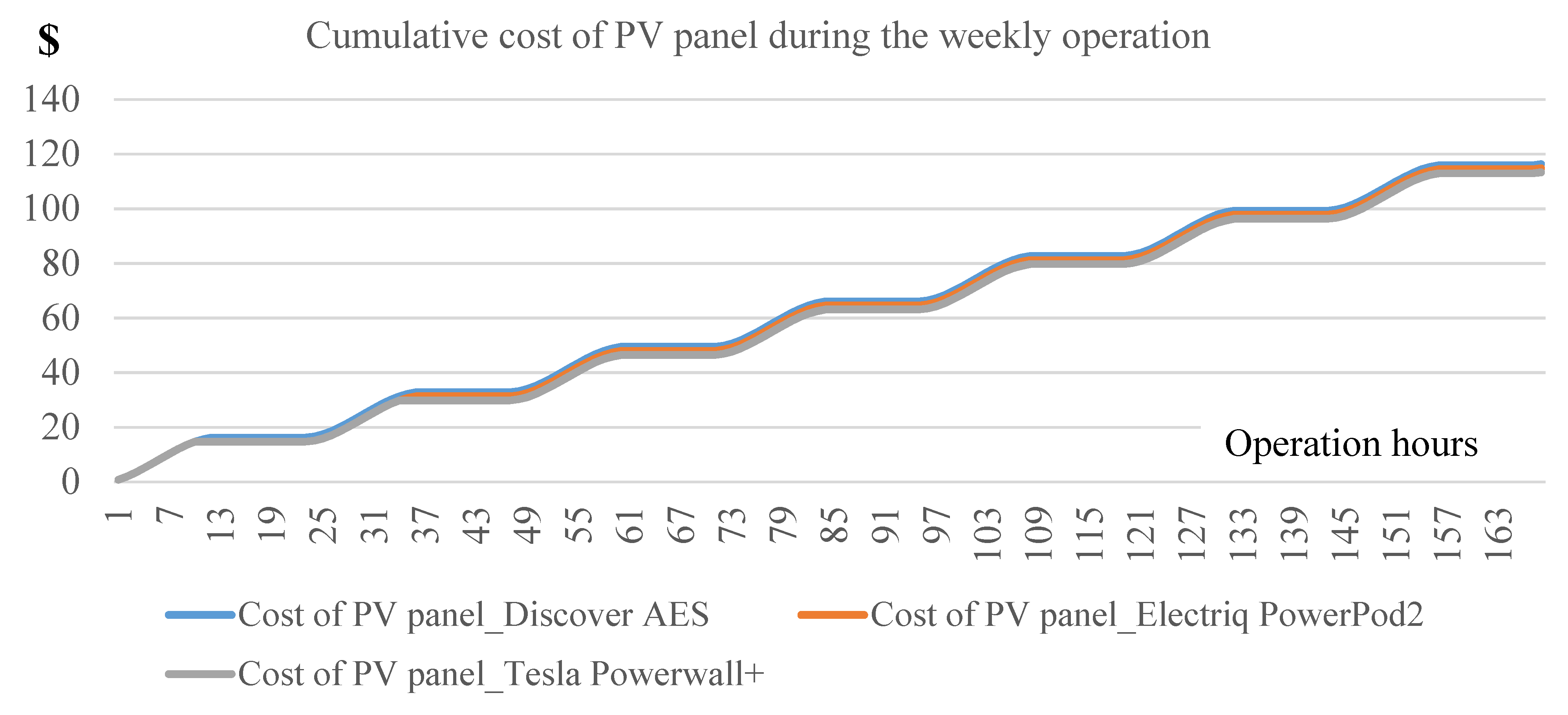
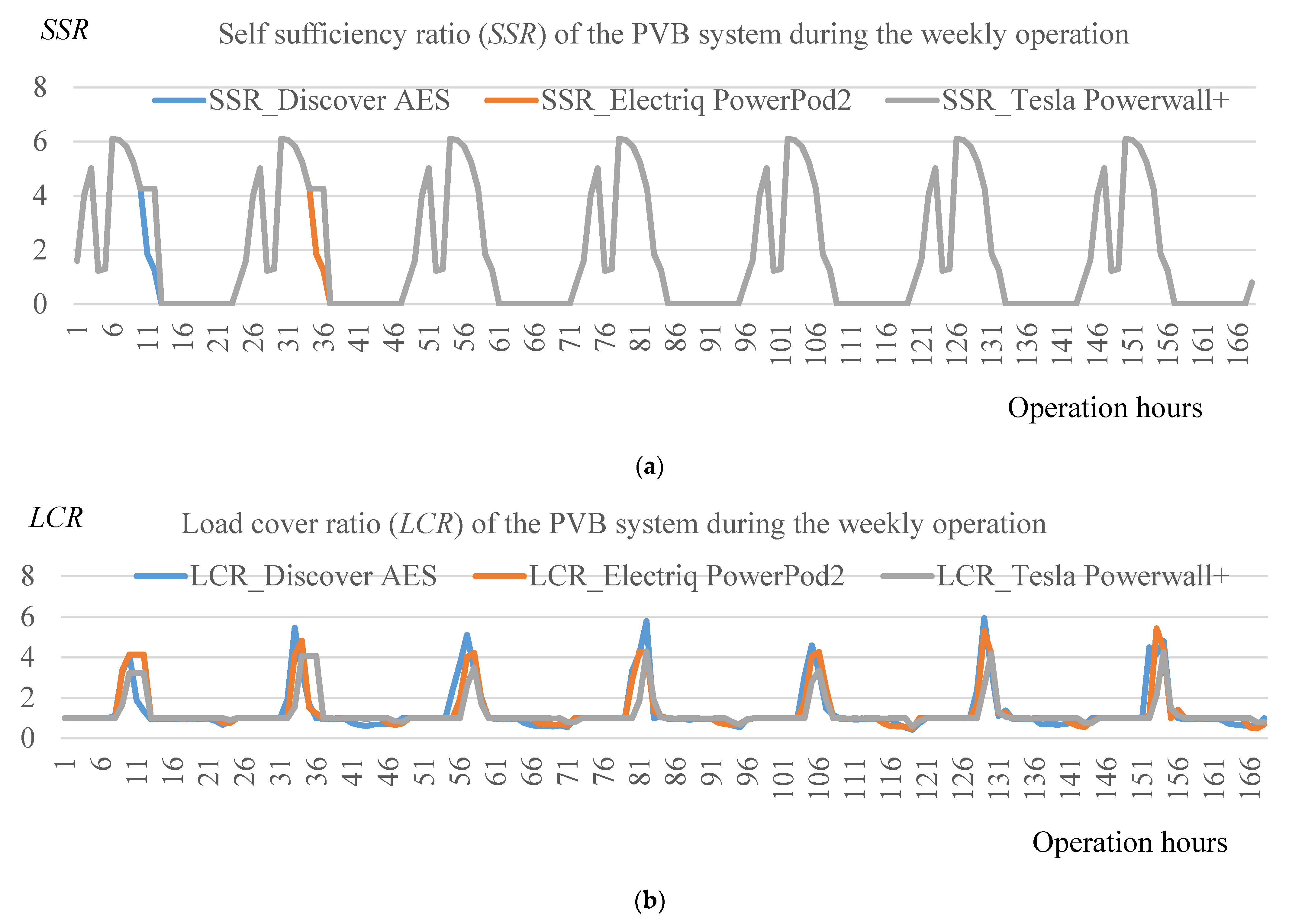
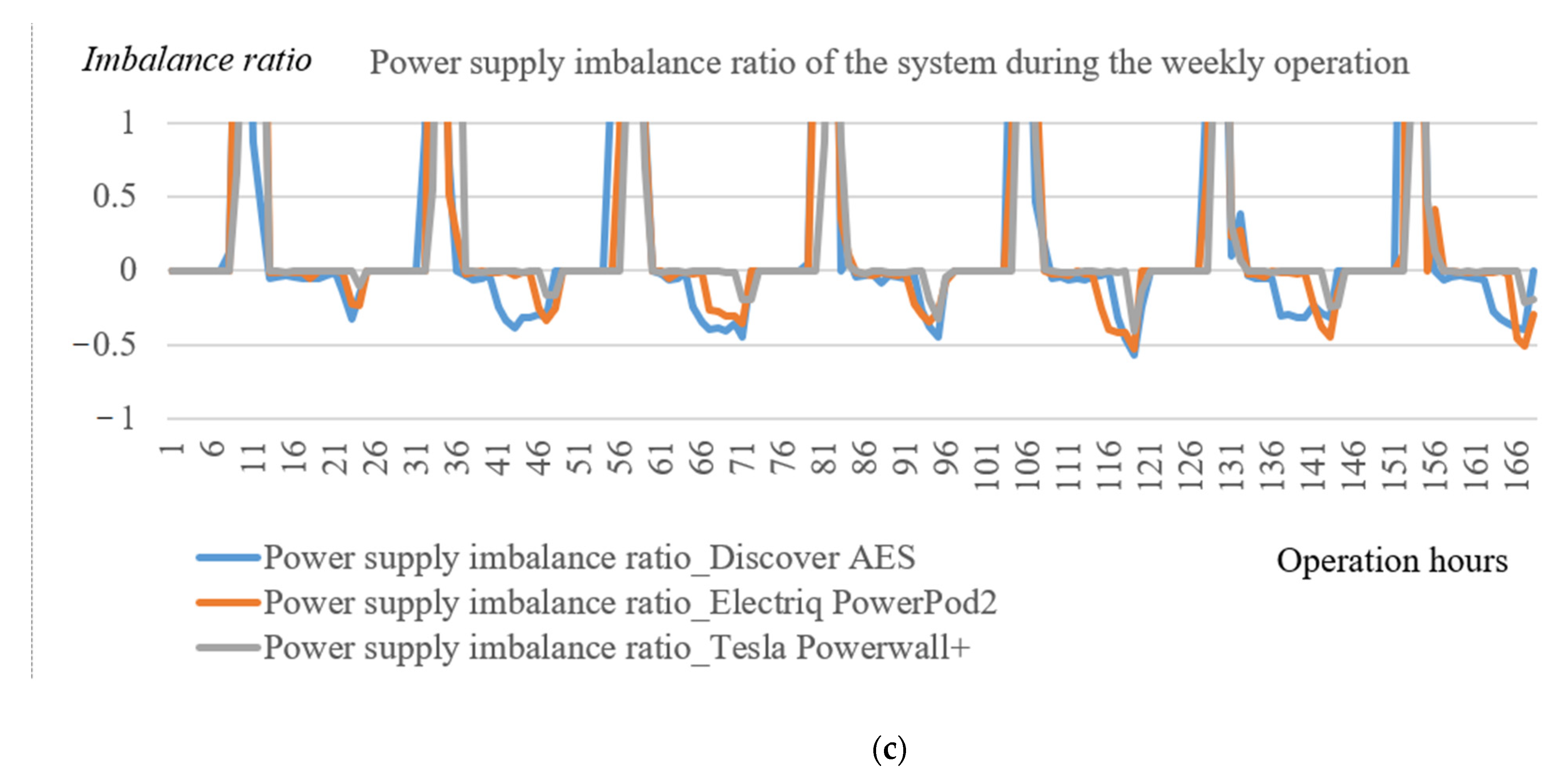
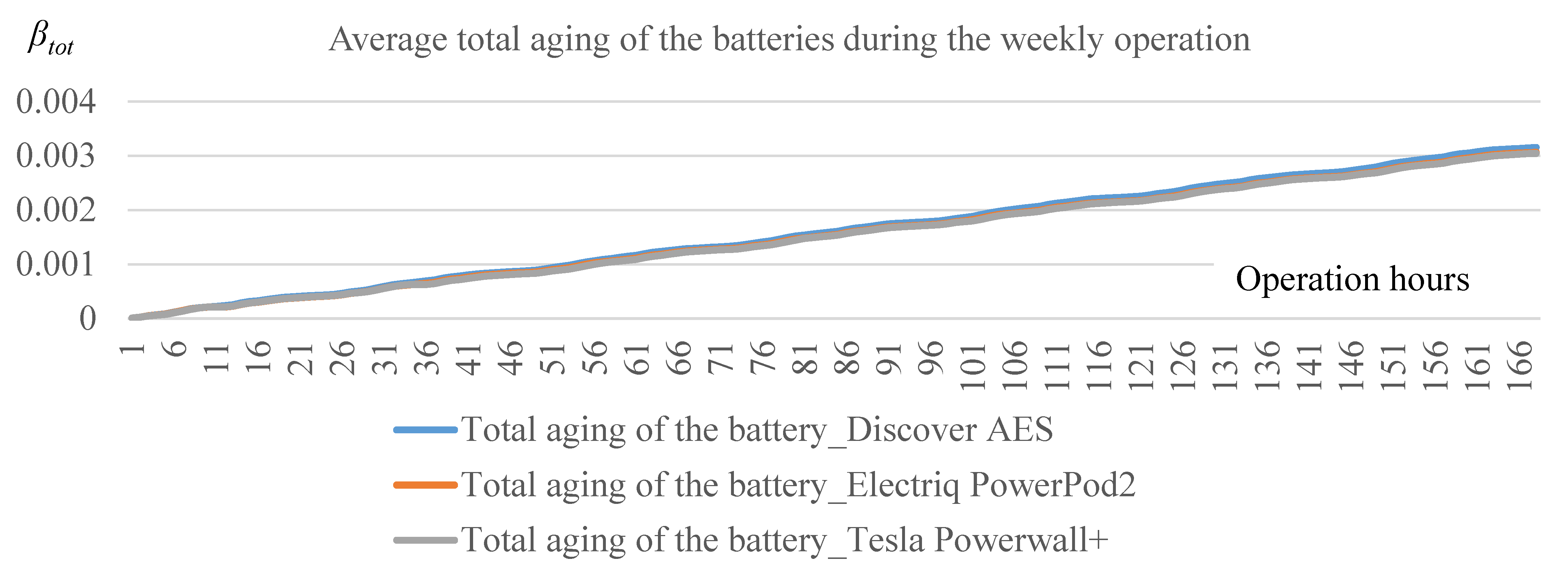
| Indicators | Discover AES | Electriq PowerPod2 | Tesla Powerwall+ |
|---|---|---|---|
| SOH | 0.999 | 0.999 | 0.999 |
| Total cost ($) | 3.36 × 104 | 4.87 × 104 | 2.36 × 104 |
| SCR during the day | 1.0 | 1.0 | 1.0 |
| SSR (max) | 6.1 | 6.1 | 6.1 |
| SSR (min) | 0.8 | 0.8 | 0.8 |
| LCR (max) | 5.9 | 5.4 | 4.3 |
| LCR (min) | 0.43 | 0.47 | 0.59 |
| Power supply imbalance ratio (max) | 4.94 | 4.44 | 3.3 |
| Power supply imbalance ratio (min) | −0.57 | −0.52 | −0.41 |
| Operation Time | Indicators | Discover AES | Electriq PowerPod2 | Tesla Powerwall+ |
|---|---|---|---|---|
| One year | SOH | 0.967 | 0.952 | 0.943 |
| Total cost ($) | 3.36 × 104 | 4.87 × 104 | 2.36 × 104 | |
| Two years | SOH | 0.934 | 0.904 | 0.886 |
| Total cost ($) | 6.72 × 104 | 9.74 × 104 | 4.72 × 104 | |
| Three years | SOH | 0.901 | 0.856 | 0.829 |
| Total cost ($) | 1.08 × 105 | 1.46 × 105 | 7.08 × 104 | |
| Four years | SOH | 0.868 | 0.808 | 0.772 |
| Total cost ($) | 1.34 × 105 | 1.95 × 105 | 9.44× 104 | |
| Five years | SOH | 0.835 | 0.76 | 0.715 |
| Total cost ($) | 1.68 × 105 | 2.44 × 105 | 1.18 × 105 |
| Parameter | Value |
|---|---|
| Building floor area (ft2) | 2000 |
| Number of people per area (/ft2) | 4 |
| Occupancy interval (h) | 7 |
| Thermel resistance (m2‧ K/W) | 1.35 |
| Thermal conductivity (W/m/K) | 0.17 |
| Specific thermal capacity (J/kg/K) | 800 |
| Thermal diffusion coefficient (m2/s) | 4.98 × 10−5 |
| Wall thickness (mm) | 230 |
| Delay of the temperature wave | 0.1963 |
| Month | Daily Temperature Distribution | Month | Daily Temperature Distribution |
|---|---|---|---|
| January | July | ||
| February | August | ||
| March | September | ||
| April | October | ||
| May | November | ||
| June | December |
| Parameter | Value |
|---|---|
| Total power generation of PV (kWh) | 193.16 |
| Total building demand during the day (kWh) | 30.48 |
| Total building demand during the night (kWh) | 23.92 |
| Energy demand gap (kWh) | 138.75 |
| Energy imbalance ratio | 71.83% |
| Number of batteries needed for Discover AES | 4 |
| Number of batteries needed for Electriq PowerPod2 | 3 |
| Number of batteries needed for Tesla Powerwall+ | 2 |
| Parameter | Value |
|---|---|
| Total power generation of PV (kWh) | 193.16 |
| Total building demand during the day (kWh) | 122.9 |
| Total building demand during the night (kWh) | 146.07 |
| Energy demand gap (kWh) | −75.8 |
| Energy imbalance ratio | 39.24% |
| Number of batteries needed for Discover AES | 17 |
| Number of batteries needed for Electriq PowerPod2 | 13 |
| Number of batteries needed for Tesla Powerwall+ | 10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Y.; Qin, X.; Shi, X. A Comprehensive Evaluation Model on Optimal Operational Schedules for Battery Energy Storage System by Maximizing Self-Consumption Strategy and Genetic Algorithm. Sustainability 2022, 14, 8821. https://doi.org/10.3390/su14148821
Zhao Y, Qin X, Shi X. A Comprehensive Evaluation Model on Optimal Operational Schedules for Battery Energy Storage System by Maximizing Self-Consumption Strategy and Genetic Algorithm. Sustainability. 2022; 14(14):8821. https://doi.org/10.3390/su14148821
Chicago/Turabian StyleZhao, Yazhou, Xiangxi Qin, and Xiangyu Shi. 2022. "A Comprehensive Evaluation Model on Optimal Operational Schedules for Battery Energy Storage System by Maximizing Self-Consumption Strategy and Genetic Algorithm" Sustainability 14, no. 14: 8821. https://doi.org/10.3390/su14148821
APA StyleZhao, Y., Qin, X., & Shi, X. (2022). A Comprehensive Evaluation Model on Optimal Operational Schedules for Battery Energy Storage System by Maximizing Self-Consumption Strategy and Genetic Algorithm. Sustainability, 14(14), 8821. https://doi.org/10.3390/su14148821







