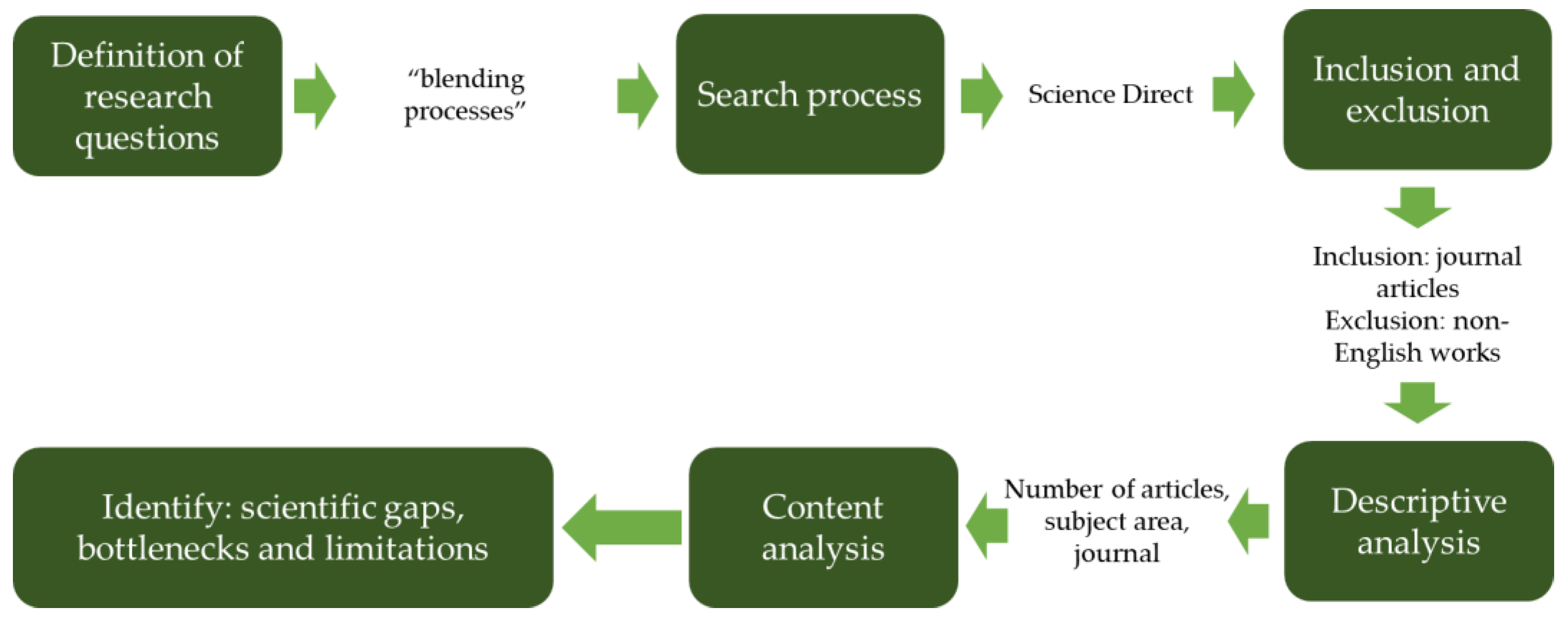
3. Materials and Methods
Blending problems represent a special field of production technologies, where different raw materials are mixed together, and the quality of the final product depends on the quality of raw materials and the final quality of the final product can be computed using the quality parameters of the required raw materials. Within the frame of the first part of this chapter, the conventional model of the blending problems is described. The second part of this chapter discusses an extended version of the blending problem. This extended model integrated the technology and quality-related parameters of the conventional blending model and the logistics-related parameters of supply chain and logistics operations.
Input parameters: in the basic model of the blending problems, the following parameters are assumed to be given:
yj customer’s demand for product j,
pik quality parameter k of raw material i,
lower bound for parameter k of finished product j,
upper bound for parameter k of finished product j,
price of raw material i.
Decision variable: the decision parameter of the blending problems is which represents the amount of raw material i assigned to product j.
Objective function (
profit maximization): in the basic model of the blending problems, the objective function is the maximization of profit, which can be written as a function of the revenue from the finished products sold and the purchase price of the raw materials needed to produce the finished product, as follows:
where
bj is the specific purchasing price of product
j (EUR/kg).
Constraint 1 (
quality of final product): in the basic model of the blending problem, two basic constraints must be taken into consideration. For the first constraint, we can define the limits of the technological specifications for the quality of the final product. For these limit values, a constraint for the lower and upper limit values can be specified as a separate constraint in the following way:
However, these inequalities are non-linear. In order to solve the problem as a linear programming problem, the above non-linear constraints must be transformed into linear constraints as follows:
Based on the above reasoning, the linearized constraint can be formulated as follows:
Based on the upper bound constraint, the lower bound constraint can be written in a similar form:
Constraint 2 (
meet customer’s demand)
: The second constraints for the basic model defines the need to obtain a quantity of raw materials that can meet customer demand:
Constraint 3 (
production capacity)
: In general, the production capacity for blending problems can be considered as given. This condition modifies the basic model in the sense that, for this constraint, customer requirements are not given per product, but can be freely modified according to the production capacity. Due to the production capacity constraint, the limitation on the quantity of raw materials to be purchased can be written in the following form:
Constraint 4 (
built-in rate of raw materials)
: for the basic model, we did not take into consideration the fact that, depending on the nature of the raw materials and the processing technology, not all of them are built into the finished product, and that the parameters affecting the quality of the finished product are not fully reflected in the finished product. Based on this condition, it is possible to modify the basic model in two directions and add a new constraint focusing on the build-in proportion. In the first case, the purchased raw material is not processed in its full quantity, and therefore its parameters influence the parameters characterizing the finished product according to the built-in rate. For example, if broccoli is used to prepare a dish, the stems and leaves of the broccoli purchased are not processed and therefore the nutrients and vitamins they contain are not built into this final dish. For this model, we can define the
percentage of the purchased raw material
i that can be used to produce the final product. If we take this constraint into consideration, the objective function is still to maximize profit, but the revenue from the finished products sold is affected by the built-in rate of the raw materials. Since the full quantity is not built in, it is necessary to purchase a larger quantity depending on the built-in rate of the raw material, which increases the cost of the raw material associated with the finished product:
When defining the limits of the technological specifications for the quality of the finished product, the following calculation should be used to take into account the parameters affecting the quality of the raw materials in the finished product:
In linear form, non-linear inequalities can be written as follows:
If we take this constraint into consideration, the constraint that the quantity of raw material to be procured must be sufficient to meet customer needs must also be met, and therefore the basic constraints must be modified to take into account the built-in rate of the raw material in the following form:
We can define a second type of built-in rate for the raw materials. In the second case, the entire quantity of the purchased raw material is processed, its parameters fully influencing the parameters describing the finished product (and hence the quality of the finished product) as formulated above, but the built-in rate of the raw materials into the finished product cannot be taken into account. For example, when strawberry jam is made, the sugar content of the processed strawberries is fully incorporated into the sugar content of the finished product (strawberry jam), but part of the strawberry mass is not included in the mass of the finished product (mainly due to evaporation during cooking). Thus, in this case, the parameter affecting the quality of the finished product can be taken into consideration in its entirety, while the mass of the raw material can be taken into account regarding the built-in rate.
As the parameter influencing the quality of the finished product during the incorporation of the raw materials fully affects the quality of the finished product, but the raw material itself is not fully present in the finished product due to the nature of the processing technology, this constraint should be formulated as follows:
In linear form, non-linear inequalities can be written as follows:
Constraint 5 (
limited raw material sources)
: This constraint specifies that the maximum or minimum quantity of available raw materials must be taken into account when placing an order. As a consequence, a lower and an upper limit constraint are also included:
where
is the upper limit of available raw material
i [pcs],
is the lower limit of available raw material
i [pcs].
Constraint 6 (marketing increases customer’s demand): In this model of the blending problem, targeted, product-specific promotion can be used to increase demand for each finished product, resulting in increased demand for the finished product and thus higher profits. Assuming that the expenditure on advertising is directly proportional to the increase in demand for the finished product generated by the advertising, there is a change in our objective functions used earlier.
In addition to the input parameters, the decision variable , which gives the number of advertisements per product, is added to the decision variable .
The following parameters must be taken into consideration of this constraint:
yj customer’s demand for finished product j without advertising,
hj is an advertising cost for product j,
gj the rate of increase in demand for product j caused by advertisements,
zj number of advertisements for product j.
This constraint defines the need to obtain a sufficient quantity of raw materials to meet the increased demand from customers due to advertising:
In the basic model of the blending problems, the objective function is profit maximization, which in this case takes into account the cost of advertising and the additional revenue from increased sales as a result of advertising, in addition to the revenue from finished goods sold and the purchase price of the raw materials needed to produce the finished product:
It is also possible to consider a marketing model for this constraint whereby a general promotion of the entire product range under consideration can be used to increase demand for the entire product range under consideration, resulting in increased demand for the finished product and thus higher profits. Additionally, in the case of this constraint, the expenditure on advertising is directly proportional to the increase in demand for the finished product generated by the advertising.
In this case, the following parameters must be taken into consideration of this constraint:
y customer’s demand without advertising,
h is the cost of an advertising,
g the rate of increase in demand caused by advertisements,
z number of advertisements.
In addition to the input parameters listed above, the decision variable
z, which represents the number of advertisements, is added to the decision variable
in the calculations. If we take into account this advertising model, the objective function can be defined in the following way:
Constraint 7 (
lot size of raw materials)
: for the basic model, we did not take into consideration the fact that the lot sizes of raw materials to be ordered can be defined. Taking this lot size- or batch size-related constraint into consideration, we can define the following constraint:
where
is the lot size of raw material
i and
.
Constraint 8 (
capacity of transportation)
: for the basic model, we did not take into consideration the capacity of transportation vehicles from raw material suppliers to the production plant. If transportation processes are taken into consideration, then the capacities can be defined in two different ways. If the required raw materials are transported with the same vehicle from the same supplier, then the constraints can be written as follows:
where
is the amount of raw material
i assigned to product
j from supplier
,
is the capacity of transportation vehicles from supplier
to the manufacturer.
If the required raw materials are transported separated, then the constraints can be written as follows:
where
is the capacity of transportation vehicles from supplier
to the manufacturer for raw material
i.
In this case, the transportation cost must be taken into consideration in the objective function. The decision variables are extended with an additional parameter, because the supplier-related costs must be taken into consideration:
where
is the specific transportation cost of raw material
i from supplier
,
price of raw material
i purchased from supplier
Constraint 9 (
capacity of warehouses)
: we can define a capacity of warehouses for raw materials and these limited capacities can be taken into consideration using the following constraint:
where
is the capacity of the warehouse for raw material
i.
It is also possible that the capacity of the warehouse cannot be defined for each type of raw materials, therefore the warehouse capacity can be defined for all raw materials as a common constraint:
where
is the capacity of the warehouse for all raw materials.
In this case, the inventory holding cost must be taken into consideration in the objective function:
where
is the specific inventory holding cost of raw material
i from supplier
.
Constraint 10 (
capacity of loading and unloading operation)
: for the basic model, we did not take into consideration the capacity of loading and unloading equipment. Loading and unloading operations must be performed at the suppliers (loading) and at the manufacturer (unloading). If loading and unloading processes are taken into consideration, then the capacities can be defined in two different ways. If the required raw materials are transported with the same vehicle from the same supplier, then the related loading and unloading operations are assigned to these supplies in the same way, therefore the loading and unloading constraint can be written as follows:
where
is the available loading capacity of supplier
.
If the required raw materials are transported separated, then the constraints can be written as follows:
where:
is the available loading capacity of supplier
for raw material
i.
In this case, the loading and unloading cost must be taken into consideration in the objective function. The decision variables are extended with an additional parameter, because the supplier-related costs must be taken into consideration:
where:
is the specific loading cost of raw material
i from supplier
.
The unloading cost can be calculated in the same way, but we use -specific unloading cost instead of -specific loading cost.
Sign restrictions: since in the course of solving the optimization problem it is possible that, based on the parameters of different types of raw materials, the optimal solution is obtained by assigning a negative quantity of certain raw materials, it is useful to formulate a sign restriction on the decision variables, which defines that no negative quantity of raw materials can be assigned to products:
5. Conclusions and Discussion
Within the frame of this research work, the authors developed a mathematical model, which makes it possible to extend the conventional mathematical model of blending problems and add logistics aspects to the model. More generally, this paper focused on the mathematical description of the supply chain framework of blending technologies taking the following logistics-related aspects into consideration: transportation, warehousing and inventory holding, packaging, loading and unloading, lot sizes, outsourcing potentials, lot sizes and batches. Why is effort being put into this research? The role of blending technologies becomes more and more important, especially in the chemical and food industry, where companies have to improve their cost-efficiency. This cost-efficiency can be achieved though optimizing technological and logistics processes. The existing research results are focusing on the technological aspects of blending processes in different fields of manufacturing (oil blending [
5], metallurgical industry [
14], asphalt mixtures [
19]) and they do not take the impact of logistics aspects on the performance of the blending process into consideration. The technological aspects are deeply analyzed in a wide range of articles (aging characteristics in blending processes [
61], experimental and discrete element models in blending processes [
62], recycling aspects in blending [
63], monitoring and sensoring of blending processes [
64,
65]). The process optimization approaches are focusing on the process monitoring [
31], adaptive algorithms of control processes [
33], and imaging techniques to determine mixture components [
35], but they are not focusing on the integrated mathematical modelling and optimization of blending processes from both the point of view of technological and logistical aspects.
The added value of the paper is the description of the supply chain framework of blending technologies, which makes it possible to take logistics-related parameters into consideration. The scientific contribution of this paper for researchers in this field is the mathematical modelling and the analysis of the impact of logistics parameters on the cost-efficiency. The results can be generalized because the model can be applied for different production technologies. The described methodology makes it possible to analyze the impact of logistics and technological parameters on costs and incomes of a wide range of manufacturing systems and processes and it can be used in the field of automotive, mechatronics assembly and other engineering fields. The described method can support managerial decisions, because the strategic decisions regarding logistics operation, purchasing and procurement can be based on the results of the optimization approach. The theoretical implication of the study is the new mathematical model, which focuses on the impact of potential constraints of logistics services and technological environment: quality of final product, customers’ demands, production capacity, built-in rate of raw materials, limited raw material sources, marketing increasing customer’s demand, lot size of raw materials, capacity of transportation, capacity of warehouses, capacity of loading and unloading operation. The described methodology and the results of the study have a great impact on the efficiency of manufacturing plants using blending technologies, because it is possible to analyze the impact of logistics and technological parameters on the performance of the whole blending process.
However, there are also limitations of the study. The parameters of the model are deterministic and the uncertainties caused by demands, quality parameters and process availability are not taken into consideration. These limitations show the directions for further research. In further studies, the model can be extended to a more complex model including Fuzzy model to describe the stochastic environment.