A Novel Travel Time Estimation Model for Modeling a Green Time-Dependent Vehicle Routing Problem in Food Supply Chain
Abstract
1. Introduction
2. Literature Review
| Algorithm 1: Travel Time Measurement |
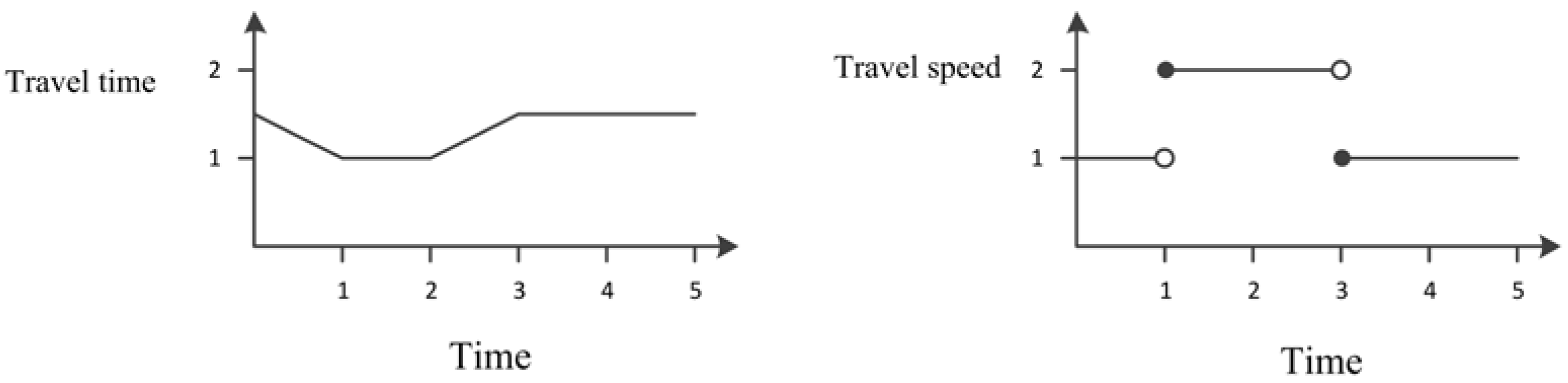
3. Methodology
| Algorithm 2: Pseudo code of calculating travel time between two consecutive nodes (i,j). |
| Input: i,j, t, , s,,,, ; Output: , 1: set , 2: for to 3: set 4: find t in which departure time of the vehicle () has occurred () 5: if () then 6: set 7: set 8: set 9: if () then 10: set 11: else 12: while () do 13: set 14: set 15: set 16: set 17: end while 18: set 19: end ifv20: else 21: set 22: set 23: set 24: set 25: if () then 26: set 27: else 28: while () do 29: set 30: set 31: set 32: set 33: end while 34: set 35: end if 36: end if 37: save 38: set 39: end for 40: set |
4. Case Study and Results
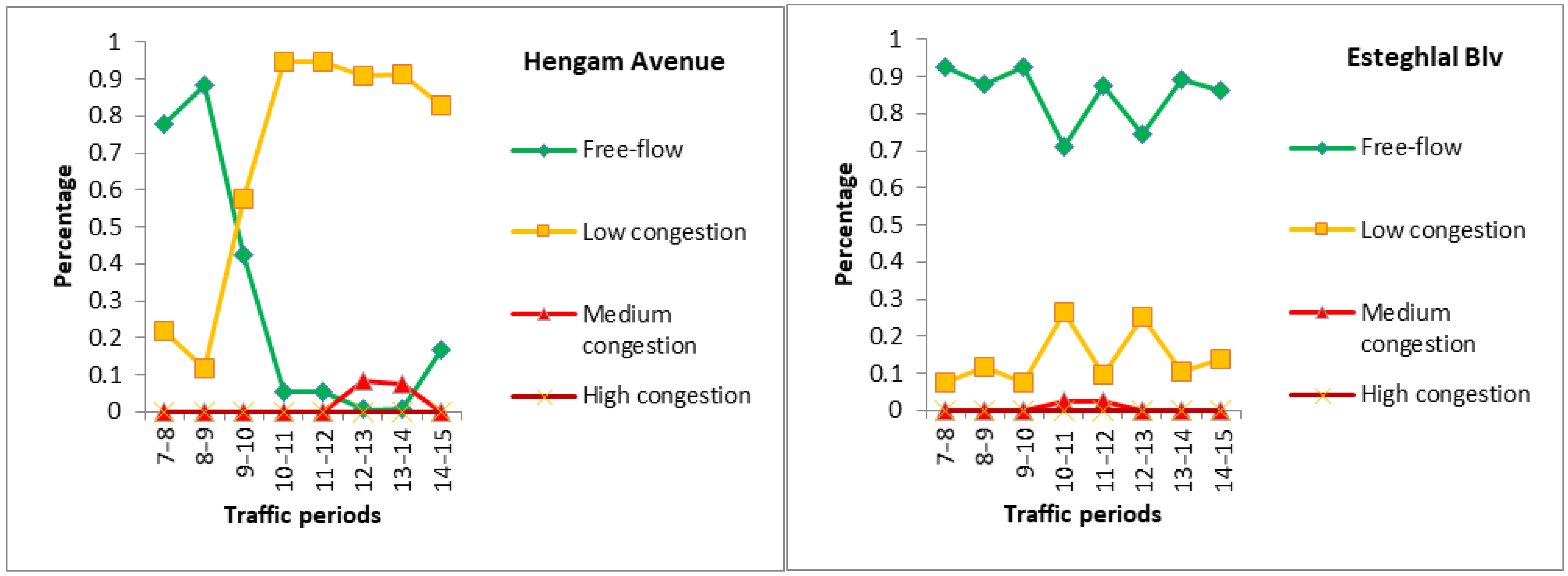
- Congestion highly depends on the road type. The congestion pattern was not similar in different road types. For instance, Figure 5 reveals that the congestion pattern of the route between customer 6 and the depot varied from one section (Esteghlal Boulevard) to another section (Hengam Avenue). On Esteghlal Boulevard, the free-flow traffic mode had the largest share in all periods; however, this amount fluctuated between 70% and 92%. High congestion in both sections was not anticipated during the given traffic period, where in the Hengam Avenue section, free-flow traffic mode had the largest share until 9:00 and then low congestion replaced it until the end of the traffic period (i.e., 15:00).
- Congestion patterns in the same road types were different. As an illustration (Figure 6), on Zeinodin Expressway, the pattern was uniform and only a free-flow traffic mode existed during the given traffic period. Nevertheless, both the free-flow mode and low congestion existed on Baqeri Expressway.
- Congestion highly depended on the time. Each section of the route in different traffic modes illustrated different behaviour during the whole period, as follows.
- ○
- Uniform behaviour (i.e., free-flow traffic mode on Zeinodin Expressway)
- ○
- Sinusoidal behaviour (i.e., free-flow traffic mode on Baqeri Expressway)
- ○
- Cosine behaviour (i.e., low congestion on Baqeri Expressway)
- ○
- Ascending behaviour (i.e., low congestion on Hengam Avenue)
- ○
- Descending behaviour (i.e., free-flow traffic mode on Hengam Avenue)
- ○
- Oscillating behaviour (i.e., free-flow traffic mode and low congestion on Esteghlal Boulevard)
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lin, C.; Choy, K.L.; Ho, G.T.S.; Chung, S.H.; Lam, H.Y. Survey of Green Vehicle Routing Problem: Past and future trends. Expert Syst. Appl. 2014, 41, 1118–1138. [Google Scholar] [CrossRef]
- Demir, E. Models and Algorithms for the Pollution-Routing Problem and Its Variations. Ph.D. Thesis, University of Southampton, Southampton, UK, 2012. [Google Scholar]
- Demir, E.; Bektaş, T.; Laporte, G. A review of recent research on green road freight transportation. Eur. J. Oper. Res. 2014, 237, 775–793. [Google Scholar] [CrossRef]
- Ichoua, S.; Gendreau, M.; Potvin, J.-Y. Vehicle dispatching with time-dependent travel times. Eur. J. Oper. Res. 2003, 144, 379–396. [Google Scholar] [CrossRef]
- Maden, W.; Eglese, R.W.; Black, D. Vehicle routing and scheduling with time-varying data: A case study. J. Oper. Res. Soc. 2010, 61, 515–522. [Google Scholar] [CrossRef]
- El-Berishy, N.M.; Scholz-Reiter, B. Development and implementation of a green logistics-oriented framework for batch process industries: Two case studies. Logist. Res. 2016, 9, 9. [Google Scholar] [CrossRef]
- Goodchild, A. Cost, Emissions, and Customer Service Trade-Off Analysis in Pickup and Delivery Systems; University of Washington: Washington, DC, USA, 2011. [Google Scholar]
- Pitera, K.; Sandoval, F.; Goodchild, A. Evaluation of Emmissions Reduction in Urban Pickup Systems. Transp. Res. Rec. J. Transp. Res. Board 2011, 2224, 8–16. [Google Scholar] [CrossRef]
- Alizadeh-Foroutan, R.; Rezaeian, J.; Mahdavi, I. Green vehicle routing and scheduling problem with heterogeneous fleet including reverse logistics in the form of collecting returned goods. Appl. Soft Comput. 2020, 94, 106462. [Google Scholar] [CrossRef]
- Heni, H.; Coelho, L.C.; Renaud, J. Determining time-dependent minimum cost paths under several objectives. Comput. Oper. Res. 2019, 105, 102–117. [Google Scholar] [CrossRef]
- Liu, C.; Kou, G.; Zhou, X.; Peng, Y.; Sheng, H.; Alsaadi, F.E. Time-dependent vehicle routing problem with time windows of city logistics with a congestion avoidance approach. Knowl.-Based Syst. 2020, 188, 104813. [Google Scholar] [CrossRef]
- Pan, B.; Zhang, Z.; Lim, A. Multi-Trip Time-Dependent Vehicle Routing Problem with Time Windows. Eur. J. Oper. Res. 2020, 291, 218–231. [Google Scholar] [CrossRef]
- Rincon-Garcia, N.; Waterson, B.; Cherrett, T.J.; Salazar-Arrieta, F. A metaheuristic for the time-dependent vehicle routing problem considering driving hours regulations—An application in city logistics. Transp. Res. Part A 2020, 137, 429–446. [Google Scholar] [CrossRef]
- Sun, P.; Veelenturf, L.P.; Dabia, S.; Woensel, T.V. The Time-Dependent Capacitated Profitable Tour Problem with Time Windows and Precedence Constraints. Eur. J. Oper. Res. 2018, 264, 1058–1073. [Google Scholar] [CrossRef]
- Tikani, H.; Setak, M. Effi cient solution algorithms for a time-critical reliable transportation problem in multigraph networks with FIFO property. Appl. Soft Comput. 2019, 74, 504–528. [Google Scholar] [CrossRef]
- Chen, P.W.; Nie, Y.M. Stochastic optimal path problem with relays. Transp. Res. Part C 2015, 59, 48–65. [Google Scholar] [CrossRef]
- Li, Q.; Nie, Y.M.; Vallamsundar, S.; Lin, J.; Homem-de-Mello, T. Finding Efficient and Environmentally Friendly Paths for Risk-Averse Freight Carriers. Netw. Spat. Econ. 2016, 16, 255–275. [Google Scholar] [CrossRef]
- Nasri, M.I.; Bekta¸s, T.; Laporte, G. Route and Speed Optimization for Autonomous Trucks. Comput. Oper. Res. 2018, 100, 89–101. [Google Scholar] [CrossRef]
- Tajik, N.; Tavakkoli-Moghaddam, R.; Vahdani, B.; Mousavi, S.M. A robust optimization approach for pollution routing problem with pickup and delivery under uncertainty. J. Manuf. Syst. 2014, 33, 277–286. [Google Scholar] [CrossRef]
- Figliozzi, M. The impacts of congestion on time-definitive urban freight distribution networks CO2 emission levels: Results from a case study in Portland, Oregon. Transp. Res. Part C Emerg. Technol. 2011, 19, 766–778. [Google Scholar] [CrossRef]
- Androutsopoulos, K.N.; Zografos, K.G. An integrated modelling approach for the bicriterion vehicle routing and scheduling problem with environmental considerations. Transp. Res. Part C 2017, 82, 180–209. [Google Scholar] [CrossRef]
- Naderipour, M.; Alinaghian, M. Measurement, evaluation and minimization of CO2, NOx, and CO emissions in the open time dependent vehicle routing problem. Measurement 2016, 90, 443–452. [Google Scholar] [CrossRef]
- Alinaghian, M.; Naderipour, M. A novel comprehensive macroscopic model for time-dependent vehicle routing problem with multi-alternative graph to reduce fuel consumption: A case study. Comput. Ind. Eng. 2016, 99, 210–222. [Google Scholar] [CrossRef]
- Raeesi, R.; Zografos, K.G. The multi-objective Steiner pollution-routing problem on congested urban road networks. Transp. Res. Part B 2019, 22, 457–485. [Google Scholar] [CrossRef]
- Franceschetti, A.; Honhon, D.; Woensel, T.V.; Bektas, T.; Laporte, G. The time-dependent pollution routing problem. Transp. Res. Part B Methodol. 2013, 56, 265–293. [Google Scholar] [CrossRef]
- Jabali, O.; Woensel, T.V.; Kok, A.d. Analysis of travel times and CO2 emissions in time-dependent vehicle routing. Prod. Oper. Manag. 2012, 21, 1060–1074. [Google Scholar] [CrossRef]
- Lu, J.; Chen, Y.; Hao, J.-K.; He, R. The Time-Dependent Electric Vehicle Routing Problem: Model and Solution. Expert Syst. Appl. 2020, 161, 1113593. [Google Scholar] [CrossRef]
- Çimen, M.; Soysal, M. Time-dependent green vehicle routing problem with stochastic vehicle speeds: An approximate dynamic programming algorithm. Transp. Res. Part D 2017, 54, 82–98. [Google Scholar] [CrossRef]
- Soysal, M.; Bloemhof-Ruwaard, J.M.; Bektaş, T. The time-dependent two-echelon capacitated vehicle routing problem with environmental considerations. Int. J. Prod. Econ. 2015, 164, 366–378. [Google Scholar] [CrossRef]
- Soysal, M.; Çimen, M.C. A Simulation Based Restricted Dynamic Programming Approach for the Green Time Dependent Vehicle Routing Problem. Comput. Oper. Res. 2017, 88, 297–305. [Google Scholar] [CrossRef]
- Fleischmann, B.; Gietz, M.; Gnutzmann, S. Time-Varying Travel Times in Vehicle Routing. Transp. Sci. 2004, 38, 160–173. [Google Scholar] [CrossRef]
- Mancini, S. A combined multistart random constructive heuristic and set partitioning based formulation for the vehicle routing problem with time dependent travel times. Comput. Oper. Res. 2017, 88, 290–296. [Google Scholar] [CrossRef]
- Horn, M.E.T. Effcient Modeling of Travel in Networks with Time-Varying Link Speeds. NETWORKS 2000, 36, 80–90. [Google Scholar] [CrossRef]
- Androutsopoulos, K.N.; Zografos, K.G. A bi-objective time-dependent vehicle routing and scheduling problem for hazardous materials distribution. EURO J. Transp. Logist. 2012, 1, 157–183. [Google Scholar] [CrossRef]
- Kuo, Y. Using simulated annealing to minimize fuel consumption for the time-dependent vehicle routing problem. Comput. Ind. Eng. 2010, 59, 157–165. [Google Scholar] [CrossRef]
- Figliozzi, M. Vehicle routing problem for emissions minimization. Transp. Res. Rec. J. Transp. Res. Board 2010, 2197, 1–7. [Google Scholar] [CrossRef]
- Saberi, M.; Verbas, I.O. Continuous approximation model for the vehicle routing problem for emissions minimization at the strategic level. J. Transp. Eng. 2012, 138, 1368–1376. [Google Scholar] [CrossRef][Green Version]
- Xiao, Y.; Konak, A. A simulating annealing algorithm to solve the green vehicle routing & scheduling problem with hierarchical objectives and weighted tardiness. Appl. Soft Comput. 2015, 34, 372–388. [Google Scholar]
- Zhang, J.; Zhao, Y.; Xue, W.; Li, J. Vehicle routing problem with fuel consumption and carbon emission. Int. J. Prod. Econ. 2015, 170, 234–242. [Google Scholar] [CrossRef]
- Xiao, Y.; Konak, A. The heterogeneous green vehicle routing and scheduling problem with time-varying traffic congestion. Transp. Res. Part E 2016, 88, 146–166. [Google Scholar] [CrossRef]
- Huang, Y.; Zhao, L.; Woensel, T.V.; Gross, J.-P. Time-dependent vehicle routing problem with path flexibility. Transp. Res. Part B 2017, 95, 169–195. [Google Scholar] [CrossRef]
- Saint-Guillain, M.; Paquay, C.; Limbourg, S. Time-Dependent Stochastic Vehicle Routing Problem with Random Requests: Application to online police patrol management in Brussels. Eur. J. Oper. Res. 2020, 292, 869–885. [Google Scholar] [CrossRef]
- Fan, H.; Zhang, Y.; Tian, P.; Lv, Y.; Fan, H. Time-dependent multi-depot green vehicle routing problem with time windows considering temporal-spatial distance. Comput. Oper. Res. 2021, 129, 105211. [Google Scholar] [CrossRef]




| References | Approach | Congestion Period | Case Study | Speed Profile | Intermediate Node | Multiple Traffic Modes | Route Dependency | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| JM | M and A | M | JA | S | I | D | V | R | C | |||||||
| [5] | Stochastic | * | ||||||||||||||
| [35] | continuous | * | * | * | ||||||||||||
| [36] | continuous | * | * | * | ||||||||||||
| [20] | continuous | * | * | * | * | |||||||||||
| [8] | Discrete | * | * | |||||||||||||
| [26] | continuous | * | * | * | * | |||||||||||
| [37] | continuous | * | * | * | ||||||||||||
| [25] | continuous | * | * | |||||||||||||
| [38] | continuous | * | * | |||||||||||||
| [16] | Stochastic | * | * | |||||||||||||
| [29] | continuous | * | * | * | * | |||||||||||
| [39] | continuous | * | * | * | ||||||||||||
| [40] | continuous | * | * | |||||||||||||
| [17] | Stochastic | * | * | |||||||||||||
| [22] | continuous | * | * | * | ||||||||||||
| [6] | Stochastic | * | * | |||||||||||||
| [23] | continuous | * | * | * | * | |||||||||||
| [41] | continuous | * | * | * | ||||||||||||
| [10] | continuous | * | * | |||||||||||||
| [13] | continuous | * | * | * | * | * | ||||||||||
| [11] | continuous | * | * | |||||||||||||
| [27] | continuous | * | * | |||||||||||||
| [42] | continuous | * | * | * | ||||||||||||
| [43] | continuous | * | * | |||||||||||||
| This paper | continuous | * | * | * | * | * | * | * | * | * | * | * | ||||
| Notation | Definition |
|---|---|
| N | Nodes related to warehouse and customers (a warehouse is indicated by o) |
| i, j | Nodes |
| f | Four traffic modes include (1) free-flow mode (green colour), (2) low congestion (orange colour), (3) medium congestion (red colour), and (4) high congestion (crimson colour) based on Google Maps. |
| s | Route segment |
| t | Traffic period. Here, each day is divided into different time intervals. Each time interval represents one traffic period. For example, third time interval is the third traffic period. |
| The departure time of vehicle k from ith node | |
| Speed (km/h) at segment s of the route from node i to j in traffic mode f | |
| The average speed at segment s of the route from node i to j in traffic mode f | |
| Travel time of segment s of the route from node i to j | |
| S | The set of all urban roads (alley, auxiliary street, main street, boulevard, and expressway) |
| Distance of segment s of the route from node i to j (meter) | |
| Transition time from segment s to s+1 on the route from node i to j (equal to intermediate nodes on the route from node i to j) (seconds) | |
| Number of traffic periods | |
| ) | |
| Percentage of the traversed distance in segment s of the route from node i to j in traffic mode f and traffic period t |
| No. | Road Type (S) | Average Speed (km/h) in Congestion Modes | |||
|---|---|---|---|---|---|
| Congestion | |||||
| Green (Free-Flow) | Orange (Low) | Red (Medium) | Crimson (High) | ||
| 1 | Expressway | 50–60 | 20 | 10 | 5 |
| 2 | Boulevard | 40–50 | 20 | 10 | 5 |
| 3 | Main Street | 30–40 | 20 | 10 | 5 |
| 4 | Auxiliary Street | 20–30 | 20 | 10 | 5 |
| 5 | Alley | 15 | …… | …… | …… |
| No. | Route | Departure Time | Proposed Model Estimation (min) | Without Intermediate Node, Multiple Traffic Modes, and Route Dependency | Google Estimation (min) | |||
|---|---|---|---|---|---|---|---|---|
| Hour | Minute | |||||||
| Alinaghian & Naderipour [23] | Naderipour & Alinaghian [22] | |||||||
| 1 | 1-2 | 7 | 33 | 3.4706 | 1.95 | 1.733333 | 4 | |
| 2 | 0-2 | 13 | 6 | 10.1396 | 7.2 | 4.430769 | 10 | |
| 3 | 5-1 | 13 | 47 | 5.2694 | 4.95 | 3.046154 | 5 | |
| 4 | 1-12 | 13 | 51 | 9.1104 | 8.4 | 5.169231 | 9 | |
| 5 | 9-2 | 11 | 44 | 6.4734 | 2.4 | 2.181818 | 7 | |
| 6 | 3-4 | 7 | 43 | 8.1017 | 7.05 | 6.266667 | 7 | |
| 7 | 3-15 | 9 | 5 | 7.8736 | 6 | 5.454545 | 8 | |
| 8 | 7-4 | 11 | 6 | 3.1863 | 1.92 | 1.745455 | 4 | |
| 9 | 4-9 | 14 | 10 | 10.1989 | 7.05 | 4.338462 | 10 | |
| 10 | 10-5 | 14 | 14 | 13.3933 | 10.35 | 6.369231 | 13 | |
| 11 | 9-6 | 13 | 6 | 11.211 | 8.85 | 5.446154 | 11 | |
| 12 | 6-11 | 13 | 47 | 8.1976 | 4.95 | 3.046154 | 7 | |
| 13 | 8-7 | 7 | 57 | 8.0336 | 7.8 | 6.933333 | 7 | |
| 14 | 11-7 | 13 | 6 | 6.277 | 6.6 | 4.061538 | 6 | |
| 15 | 12-8 | 13 | 47 | 2.8682 | 1.8 | 1.107692 | 4 | |
| 16 | 15-8 | 13 | 51 | 3.7801 | 2.55 | 1.569231 | 4 | |
| 17 | 12-9 | 11 | 44 | 10.0803 | 4.2 | 3.818182 | 12 | |
| 18 | 11-10 | 7 | 43 | 5.1244 | 3.3 | 2.933333 | 6 | |
| 19 | 16-10 | 9 | 5 | 1.454 | 1.08 | 0.981818 | 2 | |
| 20 | 14-11 | 11 | 6 | 2.9711 | 1.56 | 1.418182 | 3 | |
| 21 | 16-11 | 14 | 10 | 2.7063 | 1.8 | 1.107692 | 3 | |
| 22 | 11-16 | 14 | 14 | 3.1024 | 1.95 | 1.2 | 5 | |
| 23 | 13-12 | 8 | 10 | 11.2049 | 9.9 | 8.8 | 12 | |
| 24 | 16-12 | 14 | 16 | 9.8184 | 8.7 | 5.353846 | 10 | |
| 25 | 14-13 | 14 | 10 | 3.2247 | 2.1 | 1.292308 | 5 | |
| 26 | 13-14 | 10 | 38 | 2.6125 | 1.14 | 1.036364 | 3 | |
| 27 | 13-16 | 13 | 0 | 2.2063 | 1.2 | 0.738462 | 3 | |
| 28 | 15-14 | 8 | 3 | 4.4721 | 3.15 | 2.8 | 6 | |
| 29 | 16-14 | 10 | 9 | 0.5761 | 0.264 | 0.24 | 1 | |
| 30 | 16-15 | 13 | 52 | 9.7121 | 8.55 | 5.261538 | 8 | |
| Paired Differences | T | Df | Sig. (2-Tailed) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Mean | Std. Deviation | Std. Error Mean | 95% Confidence Interval of the Difference | ||||||
| Lower | Upper | ||||||||
| Pair 1 | Google—Proposed | 0.271657 | 0.889936 | 0.162479 | −0.060651 | 0.603964 | 1.672 | 29 | 0.105 |
| Paired Differences | T | Df | Sig. (2-Tailed) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Mean | Std. Deviation | Std. Error Mean | 95% Confidence Interval of the Difference | ||||||
| Lower | Upper | ||||||||
| Pair 1 | Google—Alinaghian | 1.876200 | 1.668691 | 0.304660 | 1.253100 | 2.499300 | 6.158 | 29 | 0.000 |
| Paired Differences | t | df | Sig. (2-Tailed) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Mean | Std. Deviation | Std. Error Mean | 95% Confidence Interval of the Difference | ||||||
| Lower | Upper | ||||||||
| Pair 1 | Google—Naderipour | 3.170617 | 1.853967 | 0.338486 | 2.478334 | 3.862900 | 9.367 | 29 | 0.000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Asgharizadeh, E.; Jooybar, S.; Mahdiraji, H.A.; Garza-Reyes, J.A. A Novel Travel Time Estimation Model for Modeling a Green Time-Dependent Vehicle Routing Problem in Food Supply Chain. Sustainability 2022, 14, 8633. https://doi.org/10.3390/su14148633
Asgharizadeh E, Jooybar S, Mahdiraji HA, Garza-Reyes JA. A Novel Travel Time Estimation Model for Modeling a Green Time-Dependent Vehicle Routing Problem in Food Supply Chain. Sustainability. 2022; 14(14):8633. https://doi.org/10.3390/su14148633
Chicago/Turabian StyleAsgharizadeh, Ezzatollah, Sobhan Jooybar, Hannan Amoozad Mahdiraji, and Jose Arturo Garza-Reyes. 2022. "A Novel Travel Time Estimation Model for Modeling a Green Time-Dependent Vehicle Routing Problem in Food Supply Chain" Sustainability 14, no. 14: 8633. https://doi.org/10.3390/su14148633
APA StyleAsgharizadeh, E., Jooybar, S., Mahdiraji, H. A., & Garza-Reyes, J. A. (2022). A Novel Travel Time Estimation Model for Modeling a Green Time-Dependent Vehicle Routing Problem in Food Supply Chain. Sustainability, 14(14), 8633. https://doi.org/10.3390/su14148633







