Random Forest Estimation and Trend Analysis of PM2.5 Concentration over the Huaihai Economic Zone, China (2000–2020)
Abstract
:1. Introduction
2. Data and Methods
2.1. Study Area
2.2. Data
2.2.1. Ground-Observed PM2.5 Data
2.2.2. AOD Data
2.2.3. Meteorological Data
2.2.4. Topographic Data
2.2.5. Date and Location Data
2.3. Methods
2.3.1. Pearson Correlation Analysis
2.3.2. Random Forest Modeling
2.3.3. Yearly PM2.5 Concentration Dataset
2.3.4. Trend Analysis
3. Results
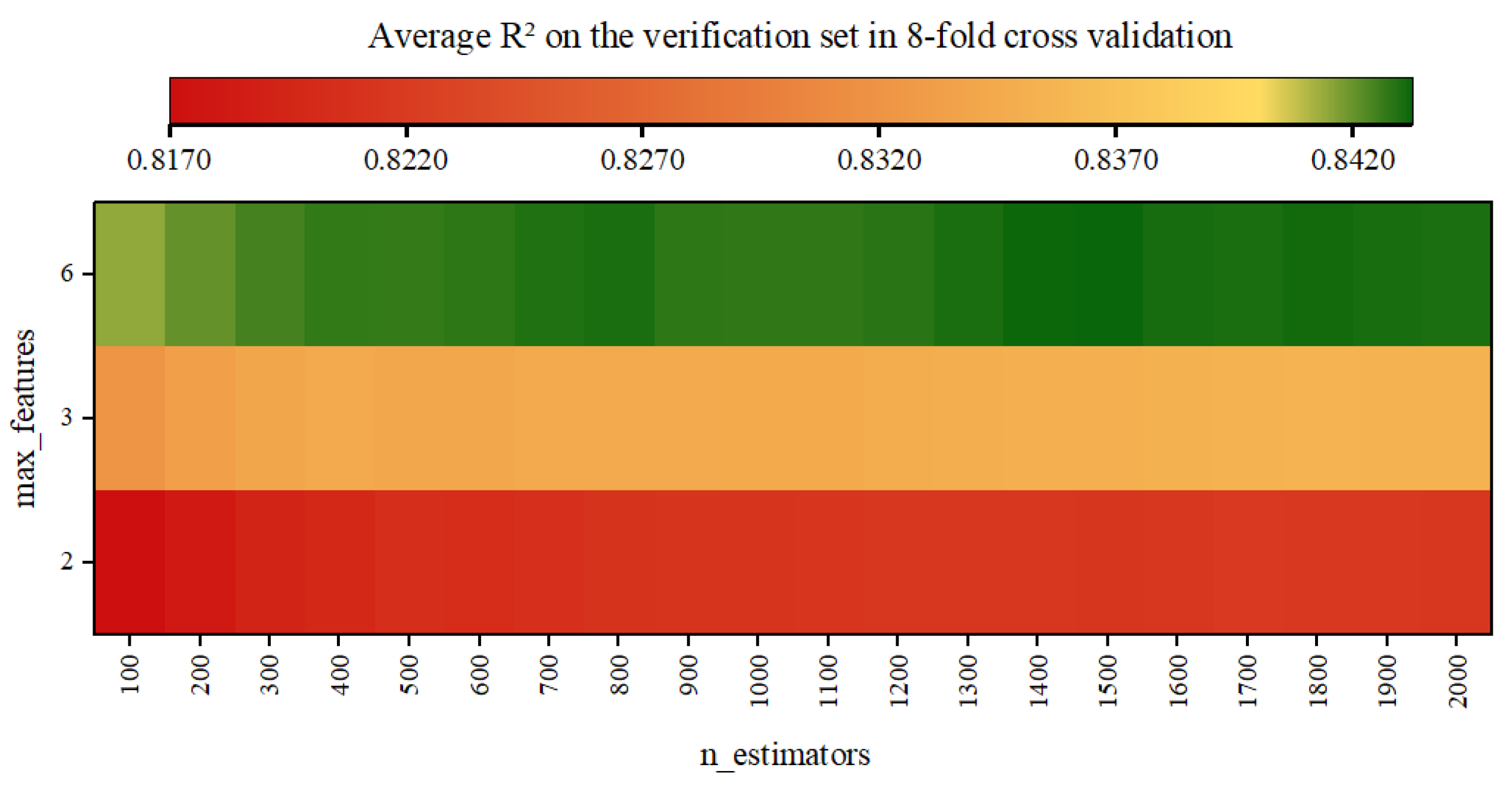
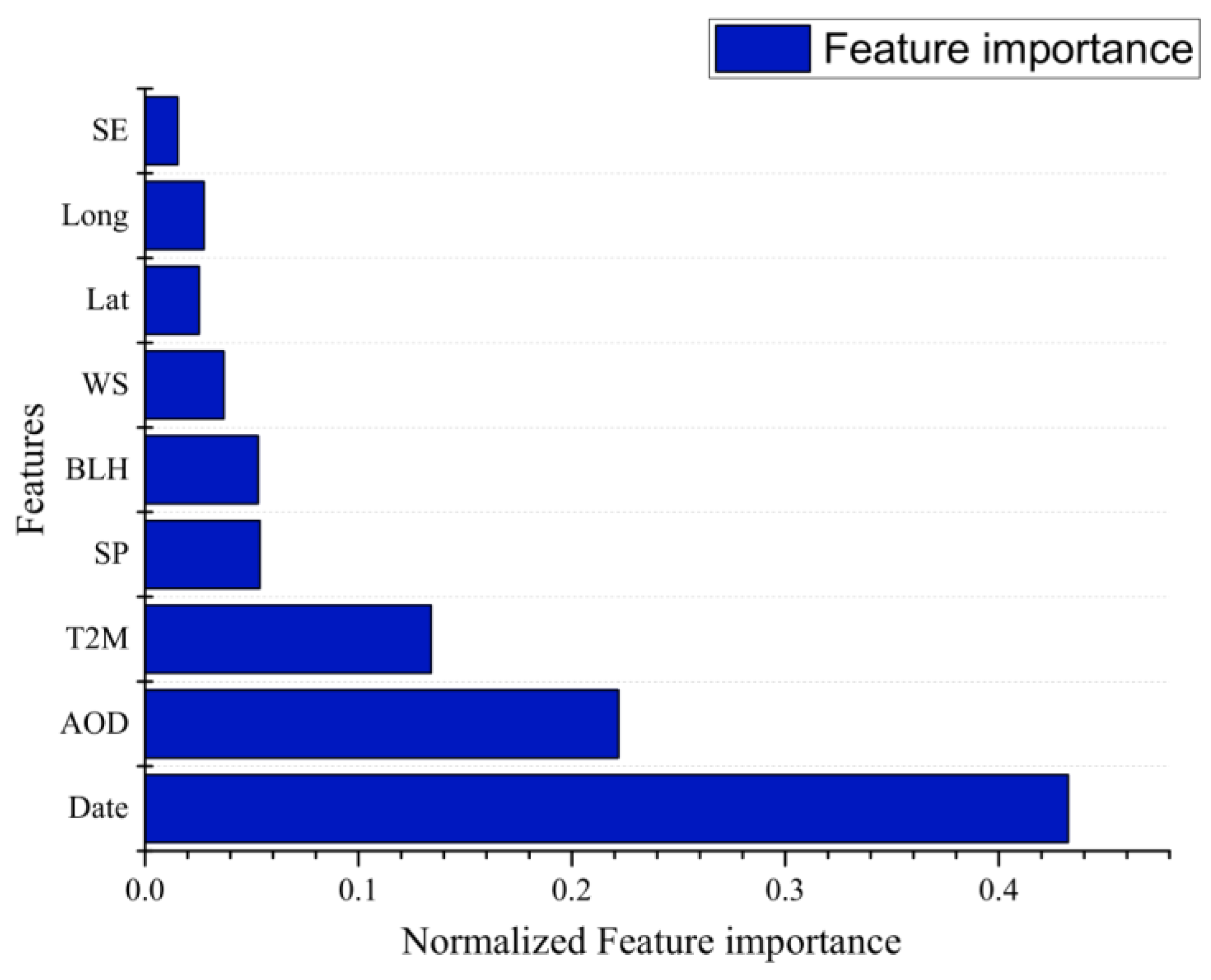
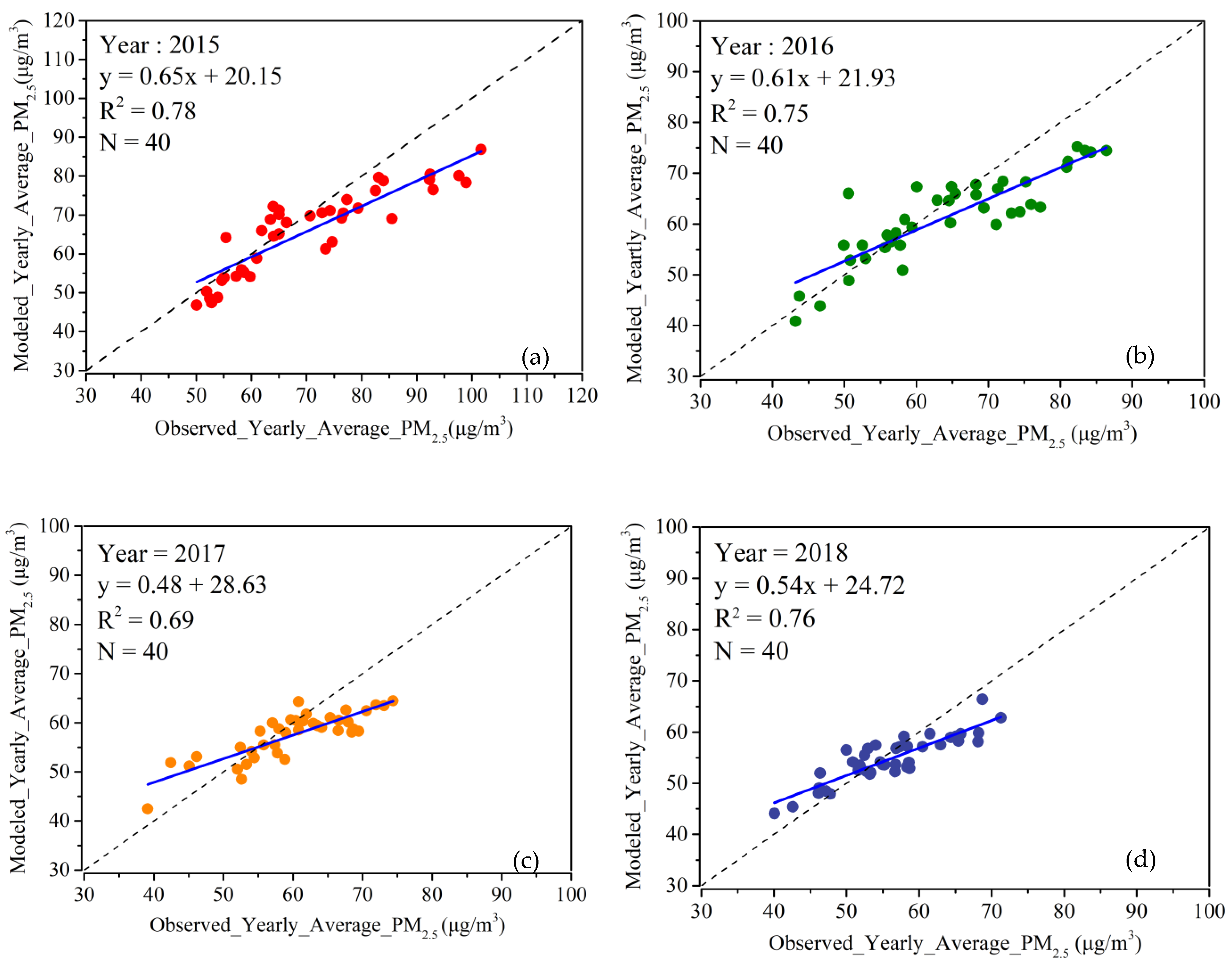
3.1. Random Forest Modeling
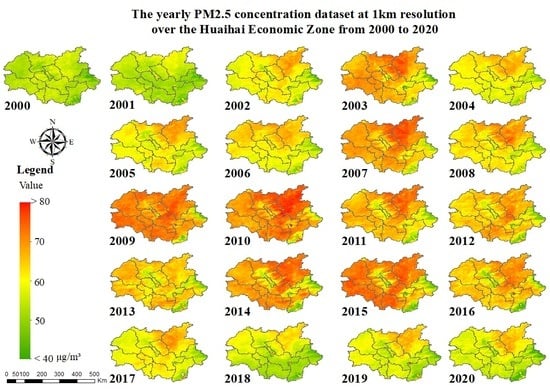
3.2. Yearly PM2.5 Concentration Dataset
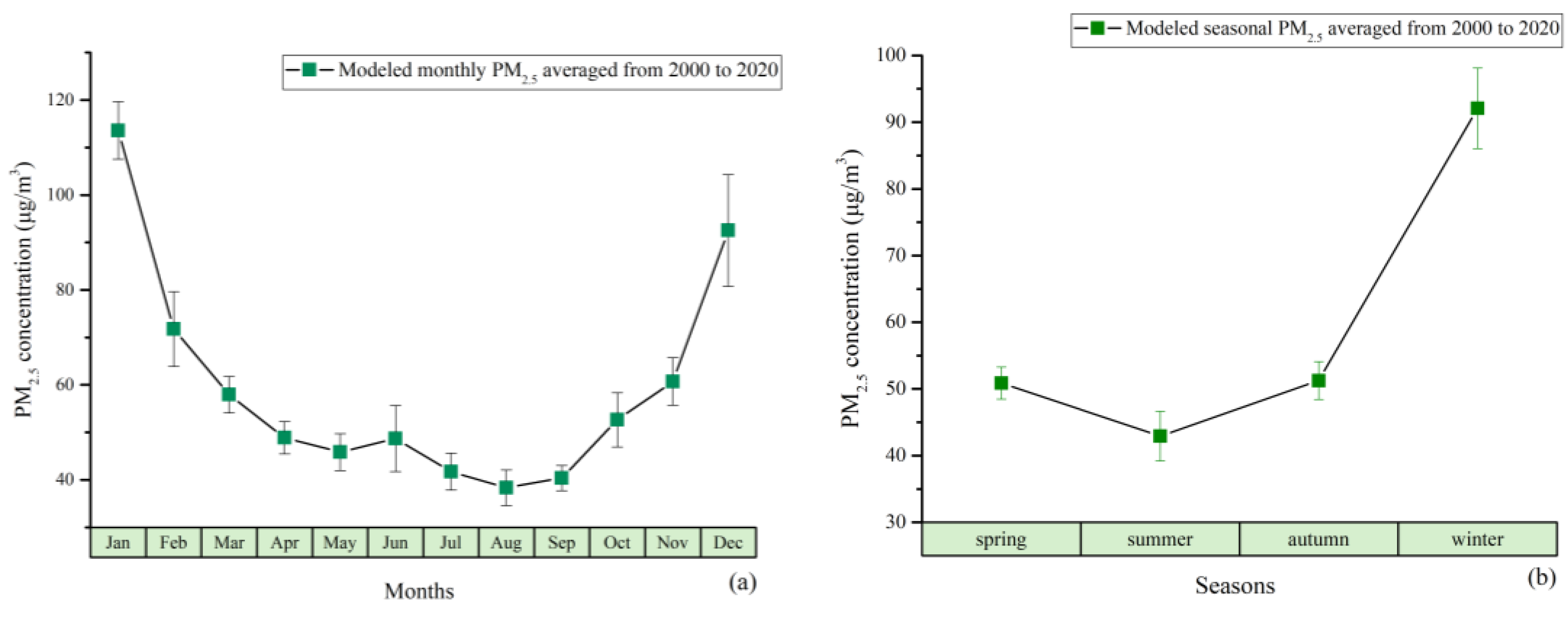
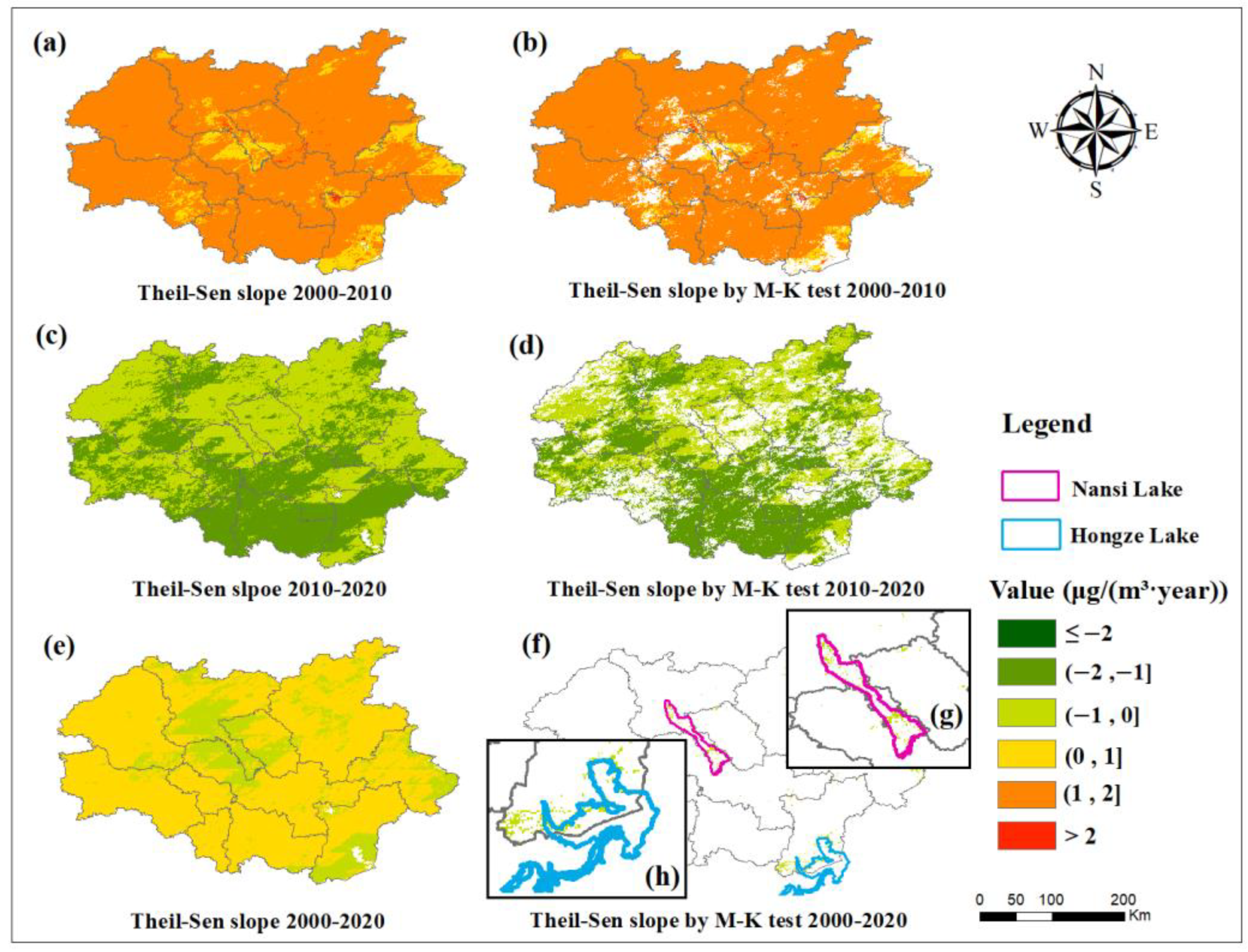
3.3. Trend Analysis
4. Discussion
4.1. Random Forest Modeling
4.2. Yearly PM2.5 Concentration Dataset
4.3. Trend Analysis
4.4. Innovations and Limitations
5. Conclusions
- Random forest is capable of modeling daily PM2.5 concentration over a large geographic area with an accuracy of = 0.85. In addition to AOD, date is an important feature that should be considered.
- A yearly PM2.5 concentration dataset at a 1 km resolution can be synthesized by averaging modeled daily PM2.5 concentration data. It has a data quality of = 0.77 and can be considered a ready-for-use dataset for various purposes.
- Although increasing from 2000–2010 and decreasing from 2010–2020, the trend of PM2.5 concentration was significantly decreasing overall over the last two decades. The area of the significantly increasing trend was small and mainly distributed in the lake areas in the zone.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A


References
- Dominski, F.H.; Branco, J.H.L.; Buonanno, G.; Stabile, L.; da Silva, M.G.; Andrade, A. Effects of air pollution on health: A mapping review of systematic reviews and meta-analyses. Environ. Res. 2021, 201, 111487. [Google Scholar] [CrossRef] [PubMed]
- World Health Organization. WHO Issues Latest Global Air Quality Report: Some Progress, but More Attention Needed to Avoid Dangerously High Levels of Air Pollution. Available online: https://www.who.int/china/news/detail/02-05-2018-who-issues-latest-global-air-quality-report-some-progress-but-more-attention-needed-to-avoid-dangerously-high-levels-of-air-pollution (accessed on 22 April 2022).
- World Health Organization. Billions of People Still Breathe Unhealthy Air: New WHO Data. Available online: https://www.who.int/news/item/04-04-2022-billions-of-people-still-breathe-unhealthy-air-new-who-data (accessed on 22 April 2022).
- State of Globe Air. Global Health Impacts of Air Pollution. Available online: https://www.stateofglobalair.org/health/global#Millions-deaths (accessed on 20 April 2022).
- Ministry of Ecology of Environment of the People’s Republic of China. China Ecological and Environmental Status Bulletin 2020. Available online: https://www.mee.gov.cn/hjzl/sthjzk/zghjzkgb/202105/P020210526572756184785.pdf (accessed on 20 April 2022).
- Li, J.; Chen, L.; Xiang, Y.; Xu, M. Research on Influential Factors of PM2.5 within the Beijing-Tianjin-Hebei Region in China. Discret. Dyn. Nat. Soc. 2018, 2018, 6375391. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Shi, M.; Li, Y.; Pang, R.; Xiang, N. Correlating PM2.5 concentrations with air pollutant emissions: A longitudinal study of the Beijing-Tianjin-Hebei region. J. Clean. Prod. 2018, 179, 103–113. [Google Scholar] [CrossRef]
- Su, Z.; Lin, L.; Chen, Y.; Hu, H. Understanding the distribution and drivers of PM2.5 concentrations in the Yangtze River Delta from 2015 to 2020 using Random Forest Regression. Environ. Monit. Assess. 2022, 194, 284. [Google Scholar] [CrossRef]
- Wang, M.; Wang, H. Spatial Distribution Patterns and Influencing Factors of PM2.5 Pollution in the Yangtze River Delta: Empirical Analysis Based on a GWR Model. Asia-Pac. J. Atmos. Sci. 2021, 57, 63–75. [Google Scholar] [CrossRef]
- Greennet Environment Protection. National air Quality Ranking and Analysis in 2020. Available online: https://mp.weixin.qq.com/s/MQp6cKdCqcSaH3em0tnmaA (accessed on 20 April 2022).
- Zhang, Y.-L.; Cao, F. Fine particulate matter (PM2.5) in China at a city level. Sci. Rep. 2015, 5, 14884. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Paciorek, C.J.; Koutrakis, P. Estimating regional spatial and temporal variability of PM2.5 concentrations using satellite data, meteorology, and land use information. Environ. Health Perspect. 2009, 117, 886–892. [Google Scholar] [CrossRef] [Green Version]
- Yang, Q.; Yuan, Q.; Yue, L.; Li, T.; Shen, H.; Zhang, L. The relationships between PM2.5 and aerosol optical depth (AOD) in mainland China: About and behind the spatio-temporal variations. Environ. Pollut. 2019, 248, 526–535. [Google Scholar] [CrossRef]
- Lin, C.Q.; Li, Y.; Yuan, Z.B.; Lau, A.K.H.; Li, C.C.; Fung, J.C.H. Using satellite remote sensing data to estimate the high-resolution distribution of ground-level PM2.5. Remote Sens. Environ. 2015, 156, 117–128. [Google Scholar] [CrossRef]
- He, Q.Q.; Gu, Y.F.; Zhang, M. Spatiotemporal trends of PM2.5 concentrations in central China from 2003 to 2018 based on MAIAC-derived high-resolution data. Environ. Int. 2020, 137, 105536. [Google Scholar] [CrossRef]
- Xu, X.; Zhang, C.; Liang, Y. Review of satellite-driven statistical models PM2.5 concentration estimation with comprehensive information. Atmos. Environ. 2021, 256, 118302. [Google Scholar] [CrossRef]
- Lu, J.; Zhang, Y.H.; Chen, M.X.; Wang, L.; Zhao, S.H.; Pu, X.; Chen, X.G. Estimation of monthly 1 km resolution PM2.5 concentrations using a random forest model over “2 + 26” cities, China. Urban Clim. 2021, 35, 100734. [Google Scholar] [CrossRef]
- Masini, R.P.; Medeiros, M.C.; Mendes, E.F. Machine Learning Advances for Time Series Forecasting. J. Econ. Surv. 2021, 36. in press. [Google Scholar] [CrossRef]
- Wu, D.J.; Zewdie, G.K.; Liu, X.; Kneen, M.A.; Lary, D.J. Insights into the Morphology of the East Asia PM2.5 Annual Cycle Provided by Machine Learning. Environ. Health Insights 2017, 11, 7. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mhawish, A.; Banerjee, T.; Sorek-Hamer, M.; Bilal, M.; Lyapustin, A.I.; Chatfield, R.; Broday, D.M. Estimation of High-Resolution PM2.5 over the Indo-Gangetic Plain by Fusion of Satellite Data, Meteorology, and Land Use Variables. Environ. Sci. Technol. 2020, 54, 7891–7900. [Google Scholar] [CrossRef]
- Choubin, B.; Abdolshahnejad, M.; Moradi, E.; Querol, X.; Mosavi, A.; Shamshirband, S.; Ghamisi, P. Spatial hazard assessment of the PM10 using machine learning models in Barcelona, Spain. Sci. Total Environ. 2020, 701, 134474. [Google Scholar] [CrossRef]
- Han, S.; Yang, X.; Zhou, Q.; Zhuang, J.; Wu, W. Predicting biomarkers from classifier for liver metastasis of colorectal adenocarcinomas using machine learning models. Cancer Med. 2020, 9, 6667–6678. [Google Scholar] [CrossRef]
- Jamthikar, A.; Gupta, D.; Khanna, N.N.; Saba, L.; Araki, T.; Viskovic, K.; Suri, H.S.; Gupta, A.; Mavrogeni, S.; Turk, M.; et al. A low-cost machine learning-based cardiovascular/stroke risk assessment system: Integration of conventional factors with image phenotypes. Cardiovasc. Diagn. Ther. 2019, 9, 420–430. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.L.; Lai, C.G.; Chen, X.H.; Yang, B.; Zhao, S.W.; Bai, X.Y. Flood hazard risk assessment model based on random forest. J. Hydrol. 2015, 527, 1130–1141. [Google Scholar] [CrossRef]
- Wei, J.; Huang, W.; Li, Z.Q.; Xue, W.H.; Peng, Y.R.; Sun, L.; Cribb, M. Estimating 1-km-resolution PM2.5 concentrations across China using the space-time random forest approach. Remote Sens. Environ. 2019, 231, 111221. [Google Scholar] [CrossRef]
- Guo, B.; Zhang, D.; Pei, L.; Su, Y.; Wang, X.; Bian, Y.; Zhang, D.; Yao, W.; Zhou, Z.; Guo, L. Estimating PM2.5 concentrations via random forest method using satellite, auxiliary, and ground-level station dataset at multiple temporal scales across China in 2017. Sci. Total Environ. 2021, 778, 146288. [Google Scholar] [CrossRef] [PubMed]
- Shogrkhodaei, S.Z.; Razavi-Termeh, S.V.; Fathnia, A. Spatio-temporal modeling of PM2.5 risk mapping using three machine learning algorithms. Environ. Pollut. 2021, 289, 117859. [Google Scholar] [CrossRef] [PubMed]
- Stafoggia, M.; Bellander, T.; Bucci, S.; Davoli, M.; de Hoogh, K.; de’Donato, F.; Gariazzo, C.; Lyapustin, A.; Michelozzi, P.; Renzi, M.; et al. Estimation of daily PM10 and PM2.5 concentrations in Italy, 2013-2015, using a spatiotemporal land-use random-forest model. Environ. Int. 2019, 124, 170–179. [Google Scholar] [CrossRef]
- Hu, X.F.; Belle, J.H.; Meng, X.; Wildani, A.; Waller, L.A.; Strickland, M.J.; Liu, Y. Estimating PM2.5 Concentrations in the Conterminous United States Using the Random Forest Approach. Environ. Sci. Technol. 2017, 51, 6936–6944. [Google Scholar] [CrossRef] [PubMed]
- Yazdi, M.D.; Kuang, Z.; Dimakopoulou, K.; Barratt, B.; Suel, E.; Amini, H.; Lyapustin, A.; Katsouyanni, K.; Schwartz, J. Predicting Fine Particulate Matter (PM2.5) in the Greater London Area: An Ensemble Approach using Machine Learning Methods. Remote Sens. 2020, 12, 914. [Google Scholar] [CrossRef] [Green Version]
- Ghahremanloo, M.; Choi, Y.; Sayeed, A.; Salman, A.K.; Pan, S.; Amani, M. Estimating daily high-resolution PM2.5 concentrations over Texas: Machine Learning approach. Atmos. Environ. 2021, 247, 118209. [Google Scholar] [CrossRef]
- Tian, H.; Zhao, Y.; Luo, M.; He, Q.; Han, Y.; Zeng, Z. Estimating PM2.5 from multisource data: A comparison of different machine learning models in the Pearl River Delta of China. Urban Clim. 2021, 35, 100740. [Google Scholar] [CrossRef]
- Ma, Z.W.; Hu, X.F.; Sayer, A.M.; Levy, R.; Zhang, Q.; Xue, Y.G.; Tong, S.L.; Bi, J.; Huang, L.; Liu, Y. Satellite-based spatiotemporal trends in PM2.5 Concentrations: China, 2004–2013. Environ. Health Perspect. 2016, 124, 184–192. [Google Scholar] [CrossRef] [Green Version]
- Yang, W.T.; Deng, M.; Xu, F.; Wang, H. Prediction of hourly PM2.5 using a space-time support vector regression model. Atmos. Environ. 2018, 181, 12–19. [Google Scholar] [CrossRef]
- Connell, D.P.; Withum, J.A.; Winter, S.E.; Statnick, R.M.; Bilonick, R.A. The Steubenville Comprehensive Air Monitoring Program (SCAMP): Overview and statistical considerations. J. Air Waste Manag. Assoc. 2005, 55, 467–480. [Google Scholar] [CrossRef] [Green Version]
- State Council of the People’s Republic of China. The Approval of the State Council on the Overall Urban Planning of Xuzhou. Available online: http://www.gov.cn/zhengce/content/2017-06/23/content_5204776.htm (accessed on 19 April 2022).
- National Development and Reform Commission. Notice of the National Development and Reform Commission concerning Printing and Distributing the Huaihe Ecological Ecomnmic Belt Development Plan. Available online: https://www.ndrc.gov.cn/xxgk/zcfb/ghwb/201811/t20181107_962252.html?code=&state=123 (accessed on 20 April 2022).
- Lyapustin, A. Description of MCD19A2 v006. Available online: https://lpdaac.usgs.gov/products/mcd19a2v006/ (accessed on 26 April 2022).
- Cheng, L.; Li, L.; Chen, L.; Hu, S.; Yuan, L.; Liu, Y.; Cui, Y.; Zhang, T. Spatiotemporal Variability and Influencing Factors of Aerosol Optical Depth over the Pan Yangtze River Delta during the 2014–2017 Period. Int. J. Environ. Res. Public Health 2019, 16, 3522. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bai, Y.; Wu, L.; Qin, K.; Zhang, Y.; Shen, Y.; Zhou, Y. A Geographically and Temporally Weighted Regression Model for Ground-Level PM2.5 Estimation from Satellite-Derived 500 m Resolution AOD. Remote Sens. 2016, 8, 262. [Google Scholar] [CrossRef] [Green Version]
- Ni, X.; Cao, C.; Zhou, Y.; Cui, X.; Singh, R.P. Spatio-Temporal Pattern Estimation of PM2.5 in Beijing-Tianjin-Hebei Region Based on MODIS AOD and Meteorological Data Using the Back Propagation Neural Network. Atmosphere 2018, 9, 105. [Google Scholar] [CrossRef] [Green Version]
- Cheng, L. Research on Remote Sensing Estimation of PM 2.5 Concentration and Its Interaction with Urbanization in the Yangtze River Delta; China University of Mining and Technology: Xuzhou, China, 2021. [Google Scholar] [CrossRef]
- European Centre for Medium-Range Weather Forecasts. ECMWF Reanalysis v5—Land (ERA5-LAND). Available online: https://www.ecmwf.int/en/forecasts/dataset/ecmwf-reanalysis-v5-land (accessed on 22 April 2022).
- European Centre for Medium-Range Weather Forecasts. CDS Dataset Documentation of ERA5. Available online: https://confluence.ecmwf.int/display/CKB/ERA5 (accessed on 23 April 2022).
- Jing, Z.; Liu, P.; Wang, T.; Song, H.; Lee, J.; Xu, T.; Xing, Y. Effects of Meteorological Factors and Anthropogenic Precursors on PM2.5 Concentrations in Cities in China. Sustainability 2020, 12, 3550. [Google Scholar] [CrossRef]
- Zang, Z.; Wang, W.; Cheng, X.; Yang, B.; Pan, X.; You, W. Effects of Boundary Layer Height on the Model of Ground-Level PM2.5 Concentrations from AOD: Comparison of Stable and Convective Boundary Layer Heights from Different Methods. Atmosphere 2017, 8, 104. [Google Scholar] [CrossRef] [Green Version]
- Lou, M.Y.; Guo, J.P.; Wang, L.L.; Xu, H.; Chen, D.D.; Miao, Y.C.; Lv, Y.M.; Li, Y.; Guo, X.R.; Ma, S.L.; et al. On the Relationship Between Aerosol and Boundary Layer Height in Summer in China Under Different Thermodynamic Conditions. Earth Space Sci. 2019, 6, 887–901. [Google Scholar] [CrossRef] [Green Version]
- Jin, X.; Cai, X.; Yu, M.; Song, Y.; Wang, X.; Kang, L.; Zhang, H. Diagnostic analysis of wintertime PM2.5 pollution in the North China Plain: The impacts of regional transport and atmospheric boundary layer variation. Atmos. Environ. 2020, 224, 117346. [Google Scholar] [CrossRef]
- Zhang, L.; Guo, X.; Zhao, T.; Gong, S.; Xu, X.; Li, Y.; Luo, L.; Gui, K.; Wang, H.; Zheng, Y.; et al. A modelling study of the terrain effects on haze pollution in the Sichuan Basin. Atmos. Environ. 2019, 196, 77–85. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Li, L.; Solana, C.; Canters, F.; Kervyn, M. Testing random forest classification for identifying lava flows and mapping age groups on a single Landsat 8 image. J. Volcanol. Geotherm. Res. 2017, 345, 109–124. [Google Scholar] [CrossRef] [Green Version]
- Rodriguez-Galiano, V.; Sanchez-Castillo, M.; Chica-Olmo, M.; Chica-Rivas, M. Machine learning predictive models for mineral prospectivity: An evaluation of neural networks, random forest, regression trees and support vector machines. Ore Geol. Rev. 2015, 71, 804–818. [Google Scholar] [CrossRef]
- Goetz, J.N.; Brenning, A.; Petschko, H.; Leopold, P. Evaluating machine learning and statistical prediction techniques for landslide susceptibility modeling. Comput. Geosci. 2015, 81, 1–11. [Google Scholar] [CrossRef]
- Boulesteix, A.L.; Janitza, S.; Kruppa, J.; Konig, I.R. Overview of random forest methodology and practical guidance with emphasis on computational biology and bioinformatics. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2012, 2, 493–507. [Google Scholar] [CrossRef] [Green Version]
- Liaw, A.; Wiener, M. Classification and regression by randomforest. Forest 2001, 2, 18–22. [Google Scholar]
- Scikit Learn. Random Forest Regressor. Available online: https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.RandomForestRegressor.html (accessed on 22 April 2022).
- Arlot, S.; Celisse, A. A survey of cross-validation procedures for model selection. Statist. Surv. 2010, 4, 40–79. [Google Scholar] [CrossRef]
- Liu, H.; Cocea, M. Semi-random partitioning of data into training and test sets in granular computing context. Granul. Comput. 2017, 2, 357–386. [Google Scholar] [CrossRef] [Green Version]
- Bui, D.T.; Pradhan, B.; Lofman, O.; Revhaug, I. Landslide Susceptibility Assessment in Vietnam Using Support Vector Machines, Decision Tree, and Naive Bayes Models. Math. Probl. Eng. 2012, 2012, 974638. [Google Scholar] [CrossRef] [Green Version]
- Vrigazova, B. The Proportion for Splitting Data into Training and Test Set for the Bootstrap in Classification Problems. Bus. Syst. Res. J. 2021, 12, 228–242. [Google Scholar] [CrossRef]
- Jung, Y. Multiple predicting K-fold cross-validation for model selection. J. Nonparametr. Stat. 2018, 30, 197–215. [Google Scholar] [CrossRef]
- Radhakrishna, R.C.; Shalabh; Helge, T.; Christian, H. Linear Models and Generalizations, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Li, L.; Bakelants, L.; Solana, C.; Canters, F.; Kervyn, M. Dating lava flows of tropical volcanoes by means of spatial modeling of vegetation recovery. Earth Surf. Process. Landf. 2018, 43, 840–856. [Google Scholar] [CrossRef]
- Li, L.; Zhou, X.S.; Chen, L.Q.; Chen, L.G.; Zhang, Y.; Liu, Y.Q. Estimating Urban Vegetation Biomass from Sentinel-2A Image Data. Forests 2020, 11, 24. [Google Scholar] [CrossRef] [Green Version]
- Gocic, M.; Trajkovic, S. Analysis of changes in meteorological variables using Mann-Kendall and Sen’s slope estimator statistical tests in Serbia. Glob. Planet. Change 2013, 100, 172–182. [Google Scholar] [CrossRef]
- Sen, P.K. Estimates of the Regression Coefficient Based on Kendall’s Tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Wang, X.; Li, T.; Ikhumhen, H.O.; Sá, R.M. Spatio-temporal variability and persistence of PM2.5 concentrations in China using trend analysis methods and Hurst exponent. Atmos. Pollut. Res. 2022, 13, 101274. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric Tests Against Trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods; Griffin: London, UK, 1975. [Google Scholar]
- Wang, F.; Shao, W.; Yu, H.; Kan, G.; He, X.; Zhang, D.; Ren, M.; Wang, G. Re-evaluation of the Power of the Mann-Kendall Test for Detecting Monotonic Trends in Hydrometeorological Time Series. Front. Earth Sci. 2020, 8, 14. [Google Scholar] [CrossRef]
- Ma, Z.; Hu, X.; Huang, L.; Bi, J.; Liu, Y. Estimating Ground-Level PM2.5 in China Using Satellite Remote Sensing. Environ. Sci. Technol. 2014, 48, 7436–7444. [Google Scholar] [CrossRef]
- Di, Q.; Amini, H.; Shi, L.; Kloog, I.; Silvern, R.; Kelly, J.; Sabath, M.B.; Choirat, C.; Koutrakis, P.; Lyapustin, A.; et al. An ensemble-based model of PM2.5 concentration across the contiguous United States with high spatiotemporal resolution. Environ. Int. 2019, 130, 104909. [Google Scholar] [CrossRef]
- Sun, J.; Gong, J.; Zhou, J. Estimating hourly PM2.5 concentrations in Beijing with satellite aerosol optical depth and a random forest approach. Sci. Total Environ. 2021, 762, 144502. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Huang, X. The 30 m annual land cover dataset and its dynamics in China from 1990 to 2019. Earth Syst. Sci. Data 2021, 13, 3907–3925. [Google Scholar] [CrossRef]
- Wu, X.G.; Ding, Y.Y.; Zhou, S.B.; Tan, Y. Temporal characteristic and source analysis of PM2.5 in the most polluted city agglomeration of China. Atmos. Pollut. Res. 2018, 9, 1221–1230. [Google Scholar] [CrossRef]
- Gao, S.L.; Yang, L.; Dong, S.Z.; Sun, W.; Zha, K.C.; Zhao, J.D. A Study on Spatial-temporal Distribution Characteristics of PM2.5 Concentrations in Nanjing during 2012–2016. In Proceedings of the 2nd International Conference on Materials Science, Energy Technology and Environmental Engineering (MSETEE), Zhuhai, China, 28–30 April 2017. [Google Scholar] [CrossRef]
- Wang, Z.-B.; Fang, C.-L. Spatial-temporal characteristics and determinants of PM2.5 in the Bohai Rim Urban Agglomeration. Chemosphere 2016, 148, 148–162. [Google Scholar] [CrossRef] [PubMed]
- Aldrich, C.; Auret, L. Fault detection and diagnosis with random forest feature extraction and variable importance methods. IFAC Proc. Vol. 2010, 43, 79–86. [Google Scholar] [CrossRef]
- Leonardi, G.S.; Houthuijs, D.; Steerenberg, P.A.; Fletcher, T.; Armstrong, B.; Antova, T.; Lochman, I.; Lochmanova, A.; Rudnai, P.; Erdei, E.; et al. Immune biomarkers in relation to exposure to particulate matter: A cross-sectional survey in 17 cities of central Europe. Inhal. Toxicol. 2000, 12, 1–14. [Google Scholar] [CrossRef]
- Badyda, A.J.; Grellier, J.; Dabrowiecki, P. Ambient PM2.5 Exposure and Mortality Due to Lung Cancer and Cardiopulmonary Diseases in Polish Cities. In Respiratory Treatment and Prevention; Pokorski, M., Ed.; Springer: Berlin/Heidelberg, Germany, 2017; Volume 944, pp. 9–17. [Google Scholar] [CrossRef]
- Lang, J.; Cheng, S.; Li, J.; Chen, D.; Zhou, Y.; Wei, X.; Han, L.; Wang, H. A Monitoring and Modeling Study to Investigate Regional Transport and Characteristics of PM2.5 Pollution. Aerosol Air Qual. Res. 2013, 13, 943–956. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Liu, Y.; Hao, L. Contributions of open crop straw burning emissions to PM2.5 concentrations in China. Environ. Res. Lett. 2016, 11, 14014. [Google Scholar] [CrossRef]
- Xiong, T.Q.; Jiang, W.; Gao, W.D. Current status and prediction of major atmospheric emissions from coal-fired power plants in Shandong Province, China. Atmos. Environ. 2016, 124, 46–52. [Google Scholar] [CrossRef]
- Yang, Y.; Christakos, G. Spatiotemporal Characterization of Ambient PM2.5 Concentrations in Shandong Province (China). Environ. Sci. Technol. 2015, 49, 13431–13438. [Google Scholar] [CrossRef]
- Chen, L.G.; Li, L.; Yang, X.Y.; Zhang, Y.; Chen, L.Q.; Ma, X.D. Assessing the Impact of Land-Use Planning on the Atmospheric Environment through Predicting the Spatial Variability of Airborne Pollutants. Int. J. Environ. Res. Public Health 2019, 16, 172. [Google Scholar] [CrossRef] [Green Version]
- Shi, C.; Yuan, R.; Wu, B.; Meng, Y.; Zhang, H.; Zhang, H.; Gong, Z. Meteorological conditions conducive to PM2.5 pollution in winter 2016/2017 in the Western Yangtze River Delta, China. Sci. Total Environ. 2018, 642, 1221–1232. [Google Scholar] [CrossRef]
- Ministry of Ecology and Environment of the People’s Republic of China. Ambient Air Quality Standards. Available online: https://www.mee.gov.cn/ywgz/fgbz/bz/bzwb/dqhjbh/dqhjzlbz/201203/W020120410330232398521.pdf (accessed on 3 May 2022).
- Ouyang, Y. China wakes up to the crisis of air pollution. Lancet Resp. Med. 2013, 1, 12. [Google Scholar] [CrossRef]
- The Central People’s Government of the People’s Republic of China. Notice of the State Council Concerning Printing and Distribution the Air Pollution Prevention and Control Action Plan. Available online: http://www.gov.cn/zwgk/2013-09/12/content_2486773.htm (accessed on 3 May 2022).
- Statistics Bureau of Anhui Province. Anhui Statistical Yearbook. Available online: http://tjj.ah.gov.cn/ssah/qwfbjd/tjnj/index.html (accessed on 1 May 2022).
- Statistics Bureau of Jiangsu Province. Jiangsu Statistical Yearbook. Available online: http://www.jiangsu.gov.cn/col/col76741/index.html (accessed on 1 May 2022).
- Statistics Bureau of Shandong Province. Shandong Statistical Yearbook. Available online: http://tjj.shandong.gov.cn/jsearchfront/search.do?websiteid=370000000000009&searchid=4966&pg=&p=1&tpl=105&cateid=15216&total=&q=%E7%BB%9F%E8%AE%A1%E5%B9%B4%E9%89%B4&pq=&oq=&eq=&pos=&begin=&end= (accessed on 1 May 2022).
- Statistics Bureau of Henan Province. Henan Statistical Yearbook. Available online: https://tjj.henan.gov.cn/tjfw/tjcbw/tjnj/ (accessed on 1 May 2022).





| Type | Name (Abbreviation) | Data Source | Description | Time Period |
|---|---|---|---|---|
| Ground Observed PM2.5 Data | PM2.5 | http://www.cnemc.cn/zzjj/ (accessed on 5 April 2022) | Hourly PM2.5 from 10:00 am to 2:00 pm was averaged as Daily PM2.5 | 1 January 2015– 31 December 2020 |
| AOD Data | AOD | MODIS/Terra Land Aerosol Optical Thickness Daily L2G Global 1 km SIN Grid V006 https://search.earthdata.nasa.gov (accessed on 10 April 2022) | 1 km resolution | 1 January 2000– 31 December 2020 |
| Meteorological Data | Wind speed (WS) | ERA5-Land hourly data from 1950 to present https://cds.climate.copernicus.eu (accessed on 7 April 2022) | Originally 0.1° and resampled to 1 km | 1 January 2000– 31 December 2020 |
| boundary layer height (BLH) | ||||
| 2m temperature (T2M) | ||||
| near-surface pressure (SP) | ||||
| Total precipitation (TP) | ||||
| Topographic Data | Surface elevation (SE) | STRMDEM dataset http://www.gscloud.cn/search (accessed on 10 April 2022) | Originally 90 m and resampled to 1 km | -- |
| Date and Location Data | The order of the day when PM2.5 was observed in a year (Date) | -- | -- | 1 January 2000– 31 December 2020 |
| Longitude (Long) | -- | |||
| Latitude (Lat) | -- |
| Variable | Date | Long | Lat | AOD | WS | T2M | BLH | SP | TP | SE | PM2.5 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Date | 1 | 0.009 | −0.010 | −0.007 | −0.358 ** | −0.163 ** | −0.190 ** | 0.263 ** | −0.023 | −0.015 | 0.185 ** |
| Long | 1 | −0.287 ** | −0.093 ** | 0.014 | 0.027 | 0.074 ** | −0.001 | 0.063 ** | −0.207 ** | −0.140 ** | |
| Lat | 1 | 0.092 ** | −0.045 ** | −0.236 ** | −0.042 ** | 0.005 | 0.015 | 0.493 ** | 0.176 ** | ||
| AOD | 1 | −0.004 | −0.087 ** | 0.006 | 0.070 ** | 0.020 | 0.064 ** | 0.477 ** | |||
| WS | 1 | 0.292 ** | 0.807 ** | −0.308 ** | 0.109 ** | −0.062 ** | −0.123 ** | ||||
| T2M | 1 | 0.274 ** | −0.825 ** | 0.050 ** | −0.158 ** | −0.413 ** | |||||
| BLH | 1 | −0.236 ** | 0.092 ** | −0.076 ** | −0.183 ** | ||||||
| SP | 1 | −0.110 ** | −0.180 ** | 0.226 ** | |||||||
| TP | 1 | 0.015 | −0.015 | ||||||||
| SE | 1 | 0.135 ** | |||||||||
| PM2.5 | 1 |
| Year | Number of Available Sites | Time Range | Number of Available Data Items | Proportion of Available Data |
|---|---|---|---|---|
| 2015 | 40 | 1 January–31 December 2015 | 65,714 | 90.02% |
| 2016 | 40 | 1 January–31 December 2016 | 68,109 | 93.05% |
| 2017 | 40 | 1 January–31 December 2017 | 68,626 | 94.01% |
| 2018 | 40 | 1 January–31 December 2018 | 67,282 | 92.17% |
| 2019 | 79 | 1 January–31 December 2019 | 130,729 | 90.43% |
| 2020 | 79 | 1 January–31 December 2020 | 90,251 | 62.43% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Li, L.; Chen, L.; Zhang, T.; Xiao, J.; Chen, L. Random Forest Estimation and Trend Analysis of PM2.5 Concentration over the Huaihai Economic Zone, China (2000–2020). Sustainability 2022, 14, 8520. https://doi.org/10.3390/su14148520
Li X, Li L, Chen L, Zhang T, Xiao J, Chen L. Random Forest Estimation and Trend Analysis of PM2.5 Concentration over the Huaihai Economic Zone, China (2000–2020). Sustainability. 2022; 14(14):8520. https://doi.org/10.3390/su14148520
Chicago/Turabian StyleLi, Xingyu, Long Li, Longgao Chen, Ting Zhang, Jianying Xiao, and Longqian Chen. 2022. "Random Forest Estimation and Trend Analysis of PM2.5 Concentration over the Huaihai Economic Zone, China (2000–2020)" Sustainability 14, no. 14: 8520. https://doi.org/10.3390/su14148520
APA StyleLi, X., Li, L., Chen, L., Zhang, T., Xiao, J., & Chen, L. (2022). Random Forest Estimation and Trend Analysis of PM2.5 Concentration over the Huaihai Economic Zone, China (2000–2020). Sustainability, 14(14), 8520. https://doi.org/10.3390/su14148520