Total Variation-Based Metrics for Assessing Complementarity in Energy Resources Time Series
Abstract
:1. Introduction
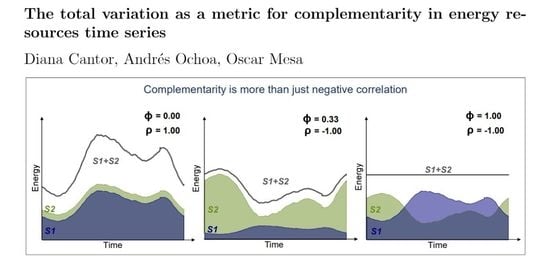
- Negative correlation is not complementarity. Although complementarity entails negative correlation, negative correlation does not entail complementarity. For example, the correlation between speed and height in a pendulum is negative, but they are not complementary.
- Dimensions matter. In the above example, speed and height have different units. Obviously, for two or more variables to complement, they must have the same dimension. If they have different dimensions, one cannot sum them, and their complementarity has no sense. In the pendulum example above, the complementary variables are kinetic energy and potential energy.
- The scale of the variables does matter. For example, streamflows from a large river and a small creek could exhibit a sizable negative correlation, but the large one dominates their sum. Hence, the complementarity value could be small.
- Linearity of the relation is also an issue. Even if correlation coefficients were suitable for assessing complementarity, selecting Pearson’s, Kendall’s, Spearman’s, or any other coefficient needs a physical or mathematical justification.
- It is natural to consider the complementarity of more than two resources, but a satisfactory correlation analysis is limited to two series.
2. Materials and Methods
2.1. Total Variation
- The total variation of a constant function is zero, and conversely, if then f is constant on .
- The total variation of a monotonic function f on is .
- for any constant .
- If and are functions of bounded variation, then so is , and
- If then
2.2. Total Variation Complementarity Index
- If is the vertical reflection of , then is a constant, therefore, and .
- . For the extreme cases, means that there is perfect complementarity, and for there is no complementarity.
- is symmetric, this is, . Similarly, the symmetry holds for any permutation of the arguments in the case of more than two functions.
- The index presents the same result when evaluated on anomaly series compared with its corresponding pure series (see Equation (6)).
- The index could be applied to two or more series.
2.3. Variance Complementarity Index
- If is the vertical reflection of , , then , and .
- . For the extreme cases, means that there is perfect complementarity, and for there is no complementarity.
- is symmetric.
- The index presents the same result when evaluated on anomaly series compared with its corresponding pure series.
- The index could be applied just to two series.
2.4. Standard Deviation Complementarity Index
3. Results
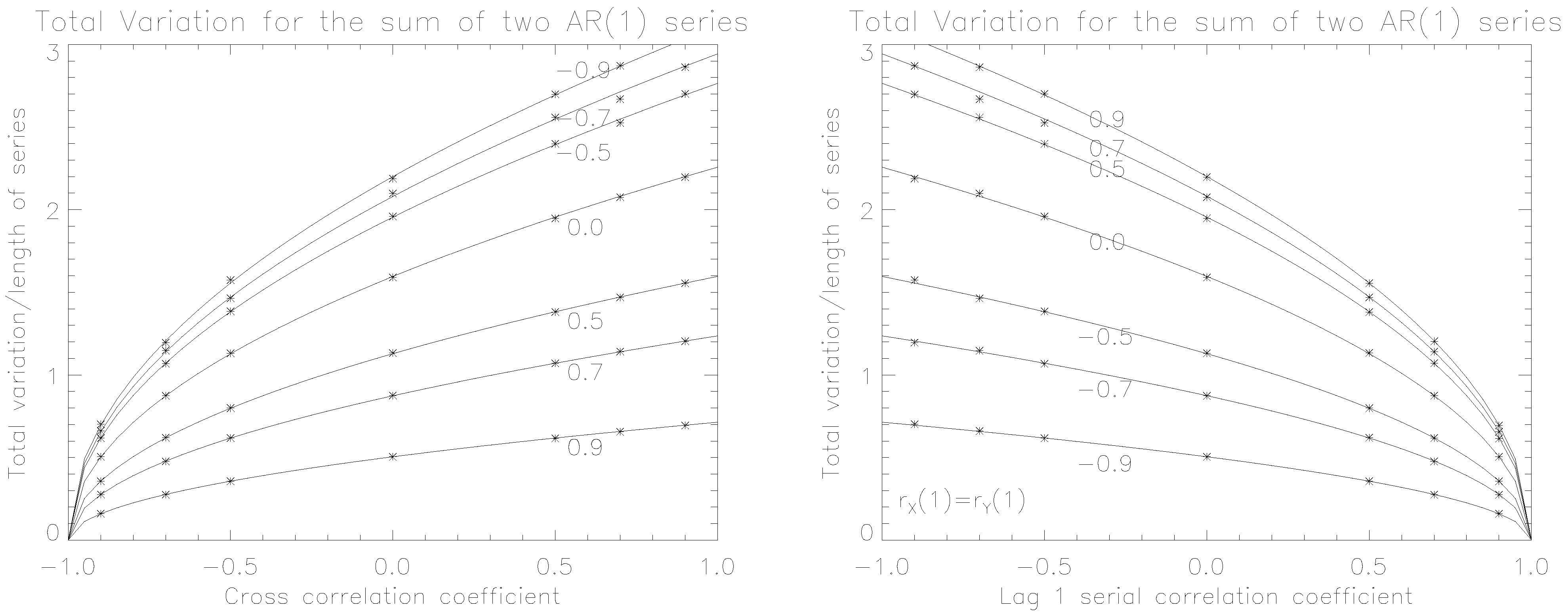
3.1. Case Study 1: Two First-Order Autoregressive Processes
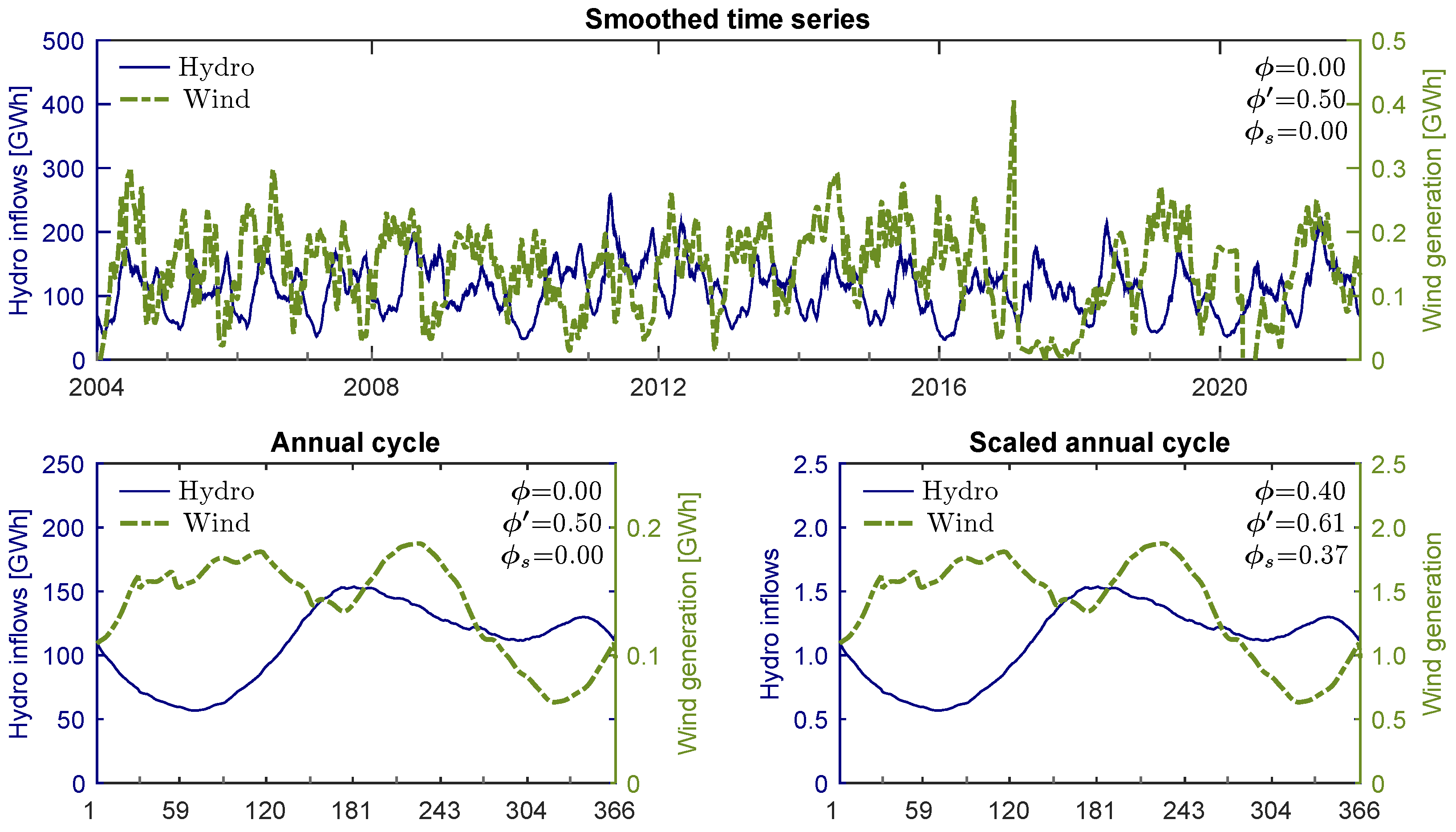
3.2. Case Study 2: Wind vs. Hydro in the Colombian Electricity Market
3.3. Case Study 3: Two Hydropower Sources in the Colombian Electricity Market
3.4. Case Study 4: Hydropower-Integrated Sources in the Colombian Electricity Market
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jurasz, J. Modeling and forecasting energy flow between national power grid and a solar–wind–pumped-hydroelectricity (PV–WT–PSH) energy source. Energy Convers. Manag. 2017, 136, 382–394. [Google Scholar] [CrossRef]
- Moura, P.S.; de Almeida, A.T. Multi-objective optimization of a mixed renewable system with demand-side management. Renew. Sustain. Energy Rev. 2010, 14, 1461–1468. [Google Scholar] [CrossRef]
- Castro, R.; Crispim, J. Variability and correlation of renewable energy sources in the Portuguese electrical system. Energy Sustain. Dev. 2018, 42, 64–76. [Google Scholar] [CrossRef]
- Ren, G.; Wan, J.; Liu, J.; Yu, D. Spatial and temporal assessments of complementarity for renewable energy resources in China. Energy 2019, 177, 262–275. [Google Scholar] [CrossRef]
- Monforti, F.; Huld, T.; Bódis, K.; Vitali, L.; D’Isidoro, M.; Lacal-Arántegui, R. Assessing complementarity of wind and solar resources for energy production in Italy. A Monte Carlo approach. Renew. Energy 2014, 63, 576–586. [Google Scholar] [CrossRef]
- François, B.; Borga, M.; Anquetin, S.; Creutin, J.; Engeland, K.; Favre, A.C.; Hingray, B.; Ramos, M.; Raynaud, D.; Renard, B.; et al. Integrating hydropower and intermittent climate-related renewable energies: A call for hydrology. Hydrol. Process. 2014, 28, 5465–5468. [Google Scholar] [CrossRef]
- Slusarewicz, J.H.; Cohan, D.S. Assessing solar and wind complementarity in Texas. Renew. Wind. Water Sol. 2018, 5, 7. [Google Scholar] [CrossRef] [Green Version]
- Schindler, D.; Behr, H.D.; Jung, C. On the spatiotemporal variability and potential of complementarity of wind and solar resources. Energy Convers. Manag. 2020, 218, 113016. [Google Scholar] [CrossRef]
- Kay, M. Forecasting and Characterising Grid Connected Solar Energy and Developing Synergies with Wind Project Results and Lessons Learnt; Australian Renewable Energy Agency: Canberra, Australia, 2015; p. 24.
- Silva, A.R.; Pimenta, F.M.; Assireu, A.T.; Spyrides, M.H.C. Complementarity of Brazil’s hydro and offshore wind power. Renew. Sustain. Energy Rev. 2016, 56, 413–427. [Google Scholar] [CrossRef]
- de Oliveira Costa Souza Rosa, C.; Costa, K.; da Silva Christo, E.; Braga Bertahone, P. Complementarity of Hydro, Photovoltaic, and Wind Power in Rio de Janeiro State. Sustainability 2017, 9, 1130. [Google Scholar] [CrossRef] [Green Version]
- dos Anjos, P.S.; da Silva, A.S.A.; Stošić, B.; Stošić, T. Long-term correlations and cross-correlations in wind speed and solar radiation temporal series from Fernando de Noronha Island, Brazil. Phys. A Stat. Mech. Its Appl. 2015, 424, 90–96. [Google Scholar] [CrossRef] [Green Version]
- Cantão, M.P.; Bessa, M.R.; Bettega, R.; Detzel, D.H.; Lima, J.M. Evaluation of hydro-wind complementarity in the Brazilian territory by means of correlation maps. Renew. Energy 2017, 101, 1215–1225. [Google Scholar] [CrossRef]
- Xu, L.; Wang, Z.; Liu, Y. The spatial and temporal variation features of wind-sun complementarity in China. Energy Convers. Manag. 2017, 154, 138–148. [Google Scholar] [CrossRef]
- Li, H.; Liu, P.; Guo, S.; Ming, B.; Cheng, L.; Yang, Z. Long-term complementary operation of a large-scale hydro-photovoltaic hybrid power plant using explicit stochastic optimization. Appl. Energy 2019, 238, 863–875. [Google Scholar] [CrossRef]
- Cao, Y.; Zhang, Y.; Zhang, H.; Zhang, P. Complementarity assessment of wind-solar energy sources in Shandong province based on NASA. J. Eng. 2019, 2019, 4996–5000. [Google Scholar] [CrossRef]
- Widen, J. Correlations Between Large-Scale Solar and Wind Power in a Future Scenario for Sweden. IEEE Trans. Sustain. Energy 2011, 2, 177–184. [Google Scholar] [CrossRef]
- Peña Gallardo, R.; Medina Ríos, A.; Segundo Ramírez, J. Analysis of the solar and wind energetic complementarity in Mexico. J. Clean. Prod. 2020, 268, 122323. [Google Scholar] [CrossRef]
- Denault, M.; Dupuis, D.; Couture-Cardinal, S. Complementarity of hydro and wind power: Improving the risk profile of energy inflows. Energy Policy 2009, 37, 5376–5384. [Google Scholar] [CrossRef]
- D’Isidoro, M.; Briganti, G.; Vitali, L.; Righini, G.; Adani, M.; Guarnieri, G.; Moretti, L.; Raliselo, M.; Mahahabisa, M.; Ciancarella, L.; et al. Estimation of solar and wind energy resources over Lesotho and their complementarity by means of WRF yearly simulation at high resolution. Renew. Energy 2020, 158, 114–129. [Google Scholar] [CrossRef]
- Solomon, A.; Child, M.; Caldera, U.; Breyer, C. Exploiting wind-solar resource complementarity to reduce energy storage need. AIMS Energy 2020, 8, 749–770. [Google Scholar] [CrossRef]
- Genchi, S.A.; Vitale, A.J.; Piccolo, M.C.; Perillo, G.M. Assessing wind, solar, and wave energy sources in the southwest of Buenos Aires province (Argentina). Investig. Geogr. 2018, 97. [Google Scholar] [CrossRef]
- Bett, P.E.; Thornton, H.E. The climatological relationships between wind and solar energy supply in Britain. Renew. Energy 2016, 87, 96–110. [Google Scholar] [CrossRef] [Green Version]
- Sahin, A.Z. Applicability of Wind-Solar Thermal Hybrid Power Systems in the Northeastern Part of the Arabian Peninsula. Energy Sources 2000, 22, 845–850. [Google Scholar] [CrossRef]
- Odeh, R.P.; Watts, D. Impacts of wind and solar spatial diversification on its market value: A case study of the Chilean electricity market. Renew. Sustain. Energy Rev. 2019, 111, 442–461. [Google Scholar] [CrossRef]
- Viviescas, C.; Lima, L.; Diuana, F.A.; Vasquez, E.; Ludovique, C.; Silva, G.N.; Huback, V.; Magalar, L.; Szklo, A.; Lucena, A.F.; et al. Contribution of Variable Renewable Energy to increase energy security in Latin America: Complementarity and climate change impacts on wind and solar resources. Renew. Sustain. Energy Rev. 2019, 113, 109232. [Google Scholar] [CrossRef]
- Gutiérrez, C.; Gaertner, M.Á.; Perpiñán, O.; Gallardo, C.; Sánchez, E. A multi-step scheme for spatial analysis of solar and photovoltaic production variability and complementarity. Sol. Energy 2017, 158, 100–116. [Google Scholar] [CrossRef]
- Kougias, I.; Szabó, S.; Monforti-Ferrario, F.; Huld, T.; Bódis, K. A methodology for optimization of the complementarity between small-hydropower plants and solar PV systems. Renew. Energy 2016, 87, 1023–1030. [Google Scholar] [CrossRef]
- Canales, F.A.; Jurasz, J.; Kies, A.; Beluco, A.; Arrieta-Castro, M.; Peralta-Cayón, A. Spatial representation of temporal complementarity between three variable energy sources using correlation coefficients and compromise programming. MethodsX 2020, 7, 100871. [Google Scholar] [CrossRef]
- Paredes, J.R.; Ramírez, J.J. Variable Renewable Energies and Their Contribution to Energy Security: Complementarity in Colombia. Technical Report; Inter-American Development Bank: Washington, DC, USA, 2017. [Google Scholar]
- Canales, F.A.; Jurasz, J.; Kies, A.; Beluco, A.; Arrieta-castro, M.; Peralta-cayón, A. Temporal complementarity between three variable renewable energy resources: A spatial representation. In Proceedings of the 11th International Conference on Applied Energy (ICAE), Västerås, Sweden, 12–15 August 2019; pp. 1–6. [Google Scholar]
- Peña Gallardo, R.; Ospino Castro, A.; Medina Ríos, A. An Image Processing-Based Method to Assess the Monthly Energetic Complementarity of Solar and Wind Energy in Colombia. Energies 2020, 13, 1033. [Google Scholar] [CrossRef] [Green Version]
- Parra, L.; Gómez, S.; Montoya, C.; Henao, F. Assessing the Complementarities of Colombia’s Renewable Power Plants. Front. Energy Res. 2020, 8. [Google Scholar] [CrossRef]
- Henao, F.; Viteri, J.P.; Rodríguez, Y.; Gómez, J.; Dyner, I. Annual and interannual complementarities of renewable energy sources in Colombia. Renew. Sustain. Energy Rev. 2020, 134, 110318. [Google Scholar] [CrossRef]
- Cantor, D.; Ochoa, A.; Mesa, O. Complementariedad hidrológica en Colombia. In Proceedings of the Día de la Energía 2019; Universidad EIA: Envigado, Colombia, 2019. [Google Scholar] [CrossRef]
- Cantor, D.; Mesa, O.; Ochoa, A. Complementarity beyond correlation. In Complementarity of Variable Renewable Energy Sources; Jurasz, J., Beluco, A., Eds.; Academic Press: London, UK, 2022. [Google Scholar] [CrossRef]
- Beluco, A.; de Souza, P.K.; Krenzinger, A. A dimensionless index evaluating the time complementarity between solar and hydraulic energies. Renew. Energy 2008, 33, 2157–2165. [Google Scholar] [CrossRef]
- Borba, E.M.; Brito, R.M. An Index Assessing the Energetic Complementarity in Time between More than Two Energy Resources. Energy Power Eng. 2017, 9, 505–514. [Google Scholar] [CrossRef] [Green Version]
- Han, S.; Zhang, L.n.; Liu, Y.q.; Zhang, H.; Yan, J.; Li, L.; Lei, X.h.; Wang, X. Quantitative evaluation method for the complementarity of wind–solar–hydro power and optimization of wind–solar ratio. Appl. Energy 2019, 236, 973–984. [Google Scholar] [CrossRef]
- Neto, P.B.L.; Saavedra, O.R.; Oliveira, D.Q. The effect of complementarity between solar, wind and tidal energy in isolated hybrid microgrids. Renew. Energy 2020, 147, 339–355. [Google Scholar] [CrossRef]
- Canales, F.A.; Jurasz, J.; Beluco, A.; Kies, A. Assessing temporal complementarity between three variable energy sources through correlation and compromise programming. Energy 2020, 192, 116637. [Google Scholar] [CrossRef] [Green Version]
- Jurasz, J.; Canales, F.; Kies, A.; Guezgouz, M.; Beluco, A. A review on the complementarity of renewable energy sources: Concept, metrics, application and future research directions. Sol. Energy 2020, 195, 703–724. [Google Scholar] [CrossRef]
- Kolmogorov, A.; Fomin, S. Introduction Real Analysis; Rev. English, Ed.; Dover: Mineola, NY, USA, 1970. [Google Scholar]
- Lasota, A.; Mackey, M.C. Chaos, Fractals, and Noise: Stochastic Aspects of Dynamics, 2nd ed.; Springer: New York, NY, USA, 1994. [Google Scholar] [CrossRef]
- Box, G.E.; Jenkins, G.M.; Reinsel, G.C. Time Series Analysis: Forecasting and Control; John Wiley & Sons: Hoboken, NJ, USA, 2011; Volume 734. [Google Scholar]
- Matalas, N.C. Mathematical assessment of synthetic hydrology. Water Resour. Res. 1967, 3, 937–945. [Google Scholar] [CrossRef]
- Urrea, V.; Ochoa, A.; Mesa, O. Seasonality of Rainfall in Colombia. Water Resour. Res. 2019, 55, 4149–4162. [Google Scholar] [CrossRef]
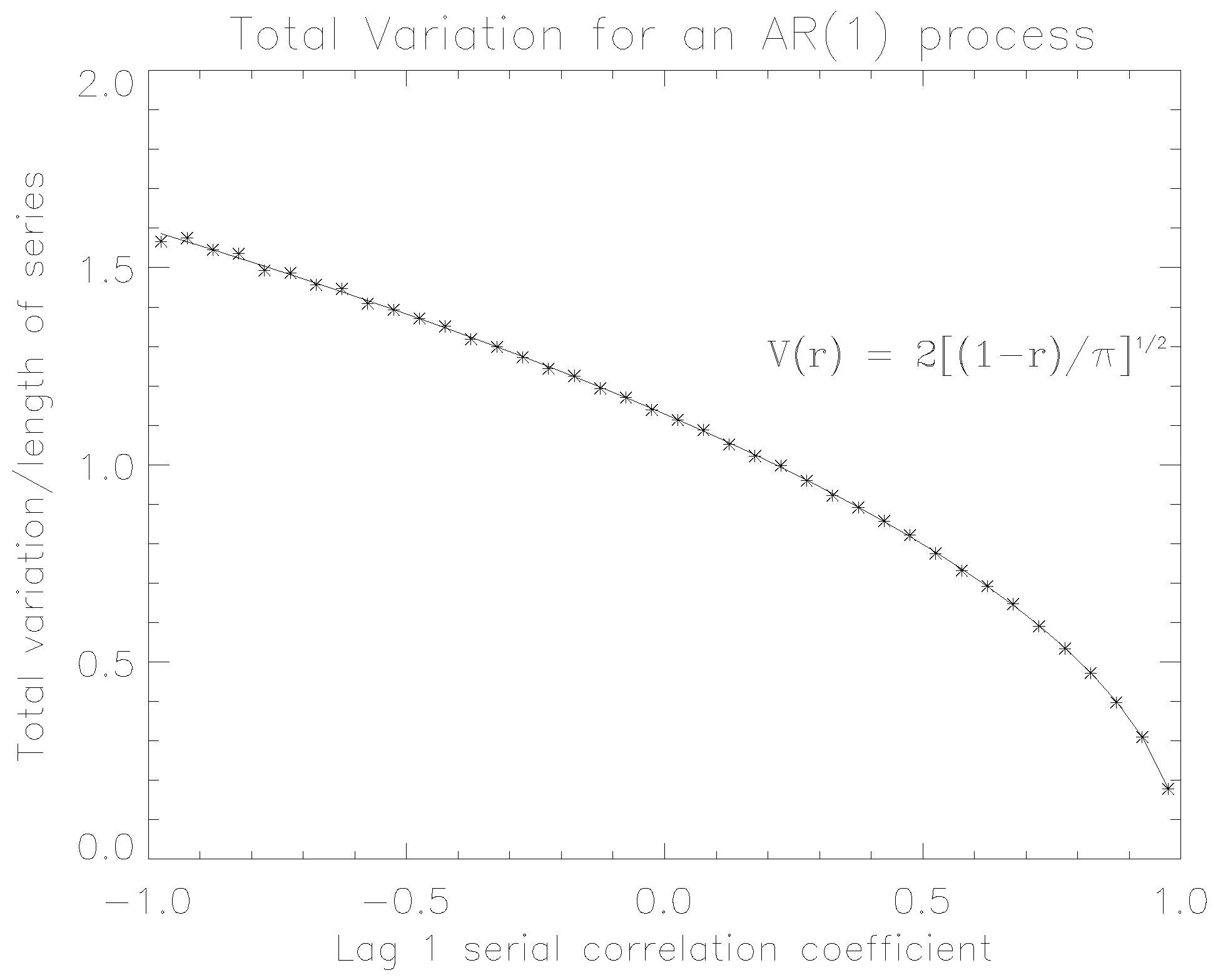

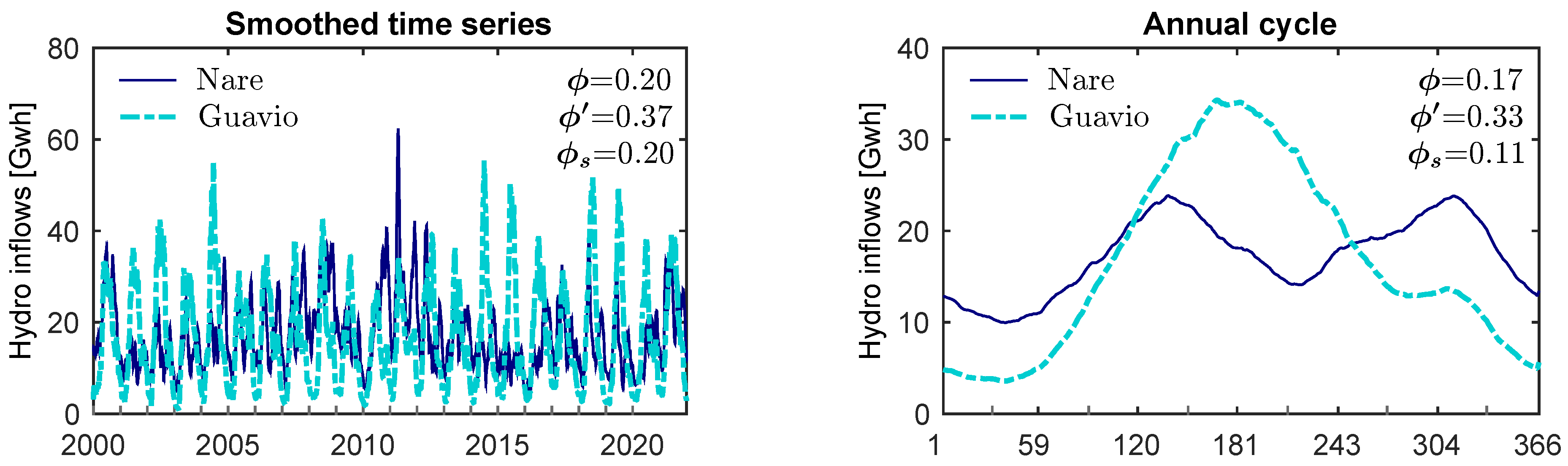
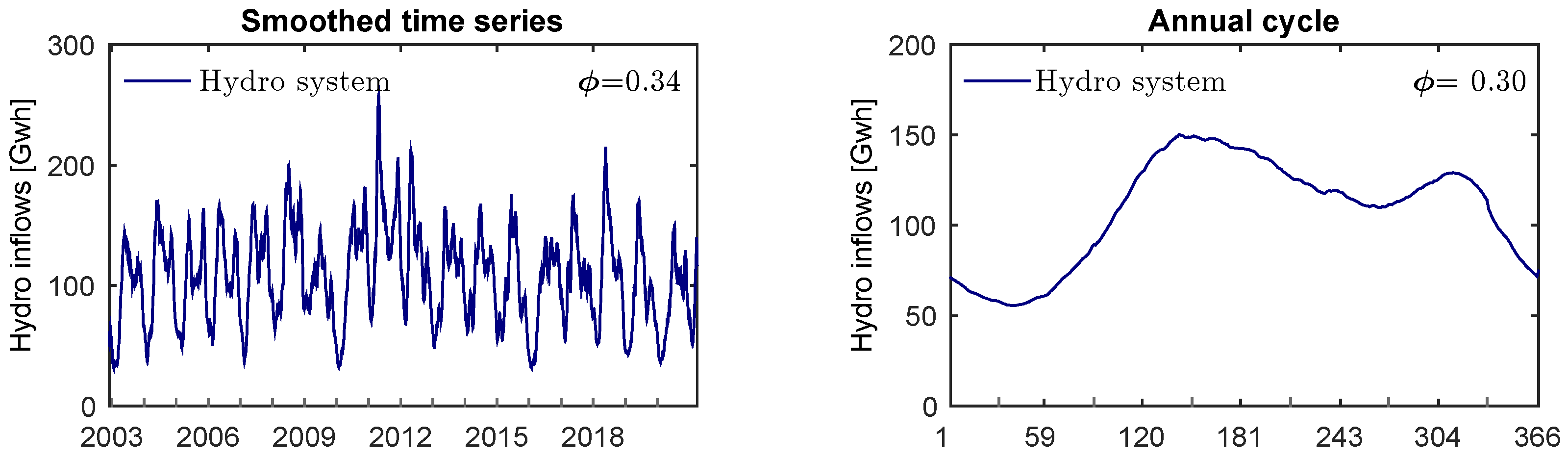
| Group | [] | [-] | [] | [-] | [-] | [-] | [-] | [-] |
|---|---|---|---|---|---|---|---|---|
| Smoothed time series | 1508 | 0.98 | 0.01 | 0.98 | −0.14 | 0.00 | 0.50 | 0.00 |
| Annual cycle | 878 | - | 0.00 | - | −0.22 | 0.00 | 0.50 | 0.00 |
| Scaled series | 0.09 | - | 0.13 | - | −0.22 | 0.40 | 0.61 | 0.37 |
| Group | [] | [-] | [] | [-] | [-] | [-] | [-] | |
|---|---|---|---|---|---|---|---|---|
| Smoothed time series | 62 | 0.98 | 129 | 0.98 | 0.27 | 0.20 | 0.37 | 0.20 |
| Annual cycle | 17 | - | 101 | - | 0.50 | 0.17 | 0.33 | 0.11 |
| Scaled series | 0.46 | - | 1.45 | - | 0.50 | 0.18 | 0.29 | 0.12 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cantor, D.; Ochoa, A.; Mesa, O. Total Variation-Based Metrics for Assessing Complementarity in Energy Resources Time Series. Sustainability 2022, 14, 8514. https://doi.org/10.3390/su14148514
Cantor D, Ochoa A, Mesa O. Total Variation-Based Metrics for Assessing Complementarity in Energy Resources Time Series. Sustainability. 2022; 14(14):8514. https://doi.org/10.3390/su14148514
Chicago/Turabian StyleCantor, Diana, Andrés Ochoa, and Oscar Mesa. 2022. "Total Variation-Based Metrics for Assessing Complementarity in Energy Resources Time Series" Sustainability 14, no. 14: 8514. https://doi.org/10.3390/su14148514
APA StyleCantor, D., Ochoa, A., & Mesa, O. (2022). Total Variation-Based Metrics for Assessing Complementarity in Energy Resources Time Series. Sustainability, 14(14), 8514. https://doi.org/10.3390/su14148514