Experimental Investigation of Wind Loads on Roof-Mounted Solar Arrays
Abstract
:1. Introduction
2. Wind Tunnel Tests Experimental Setup and Measurements
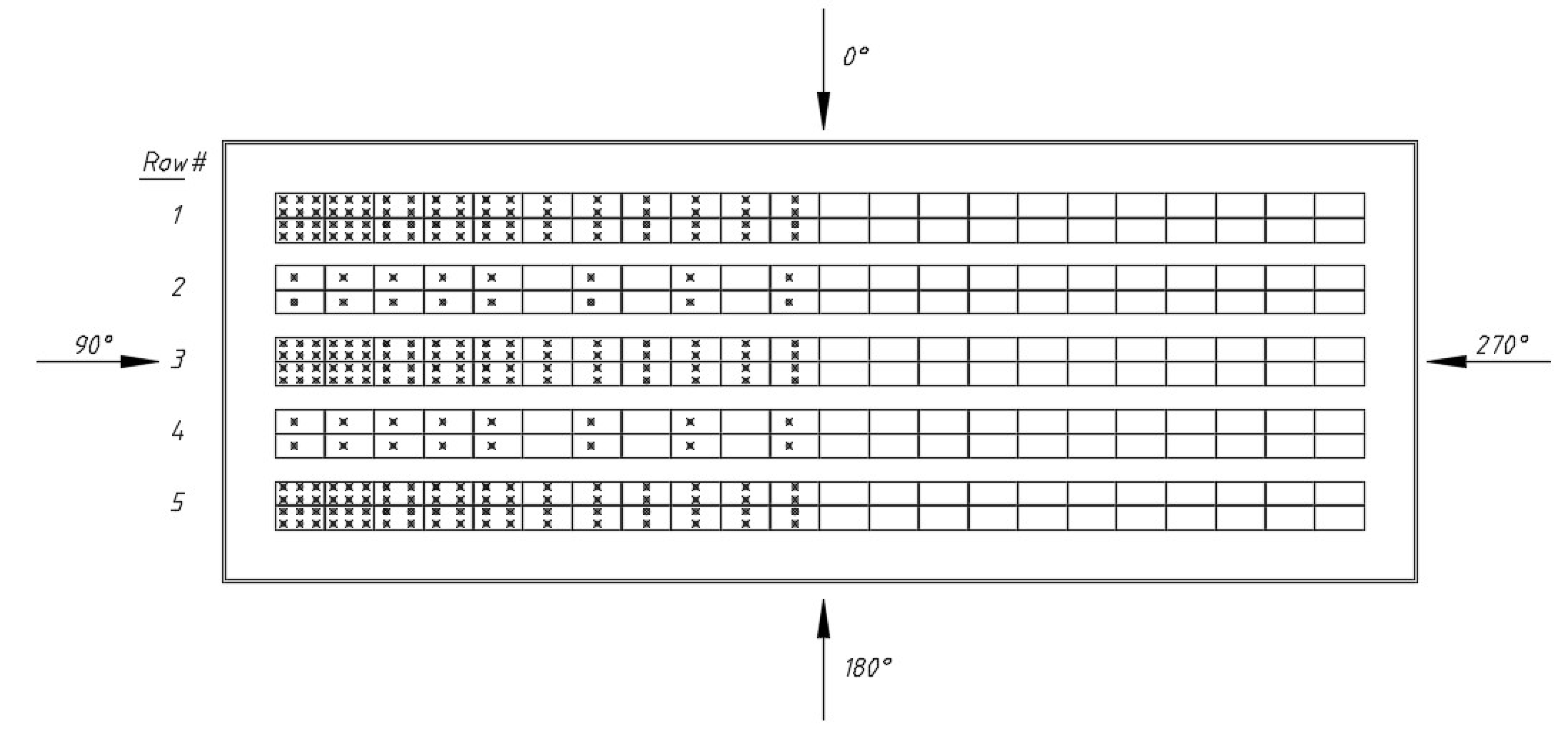
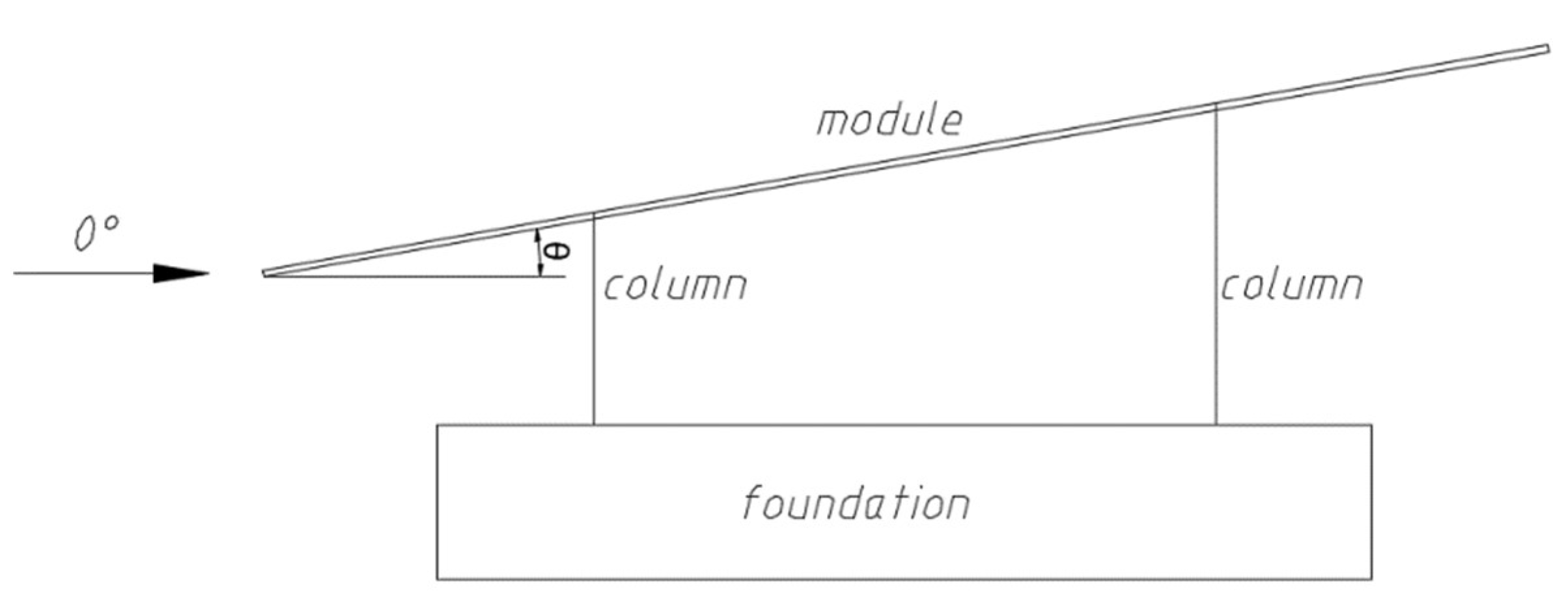
2.1. Model and Instrumentations
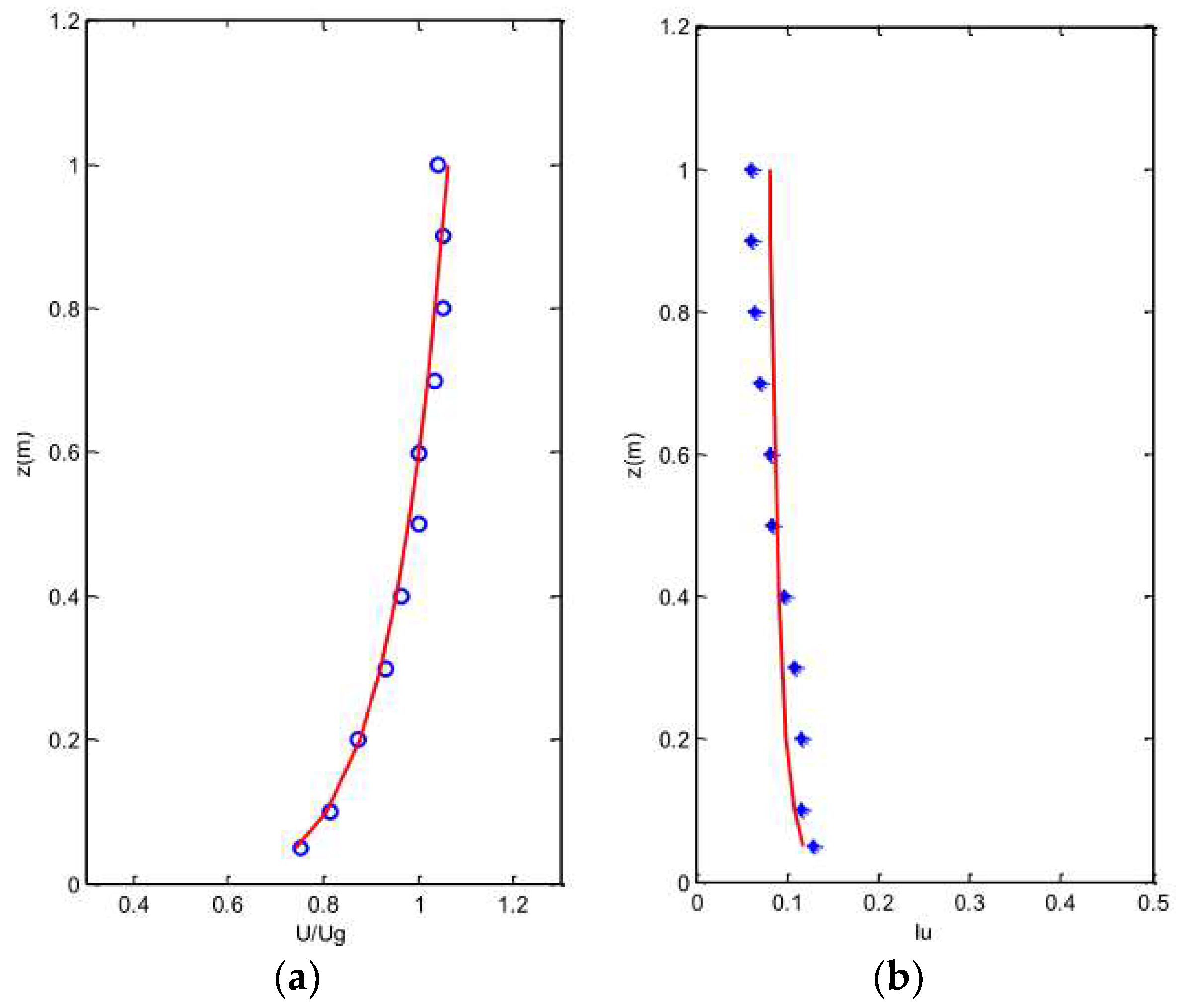
2.2. Terrain Simulation
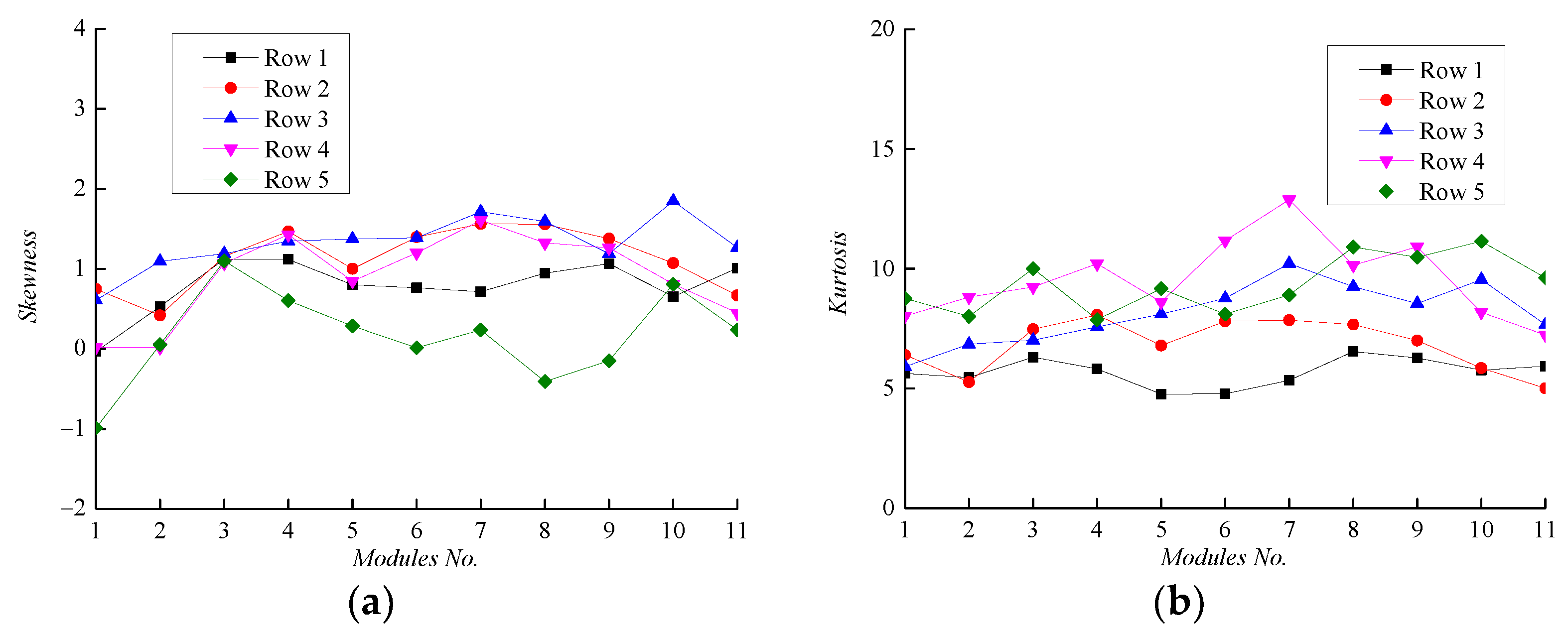
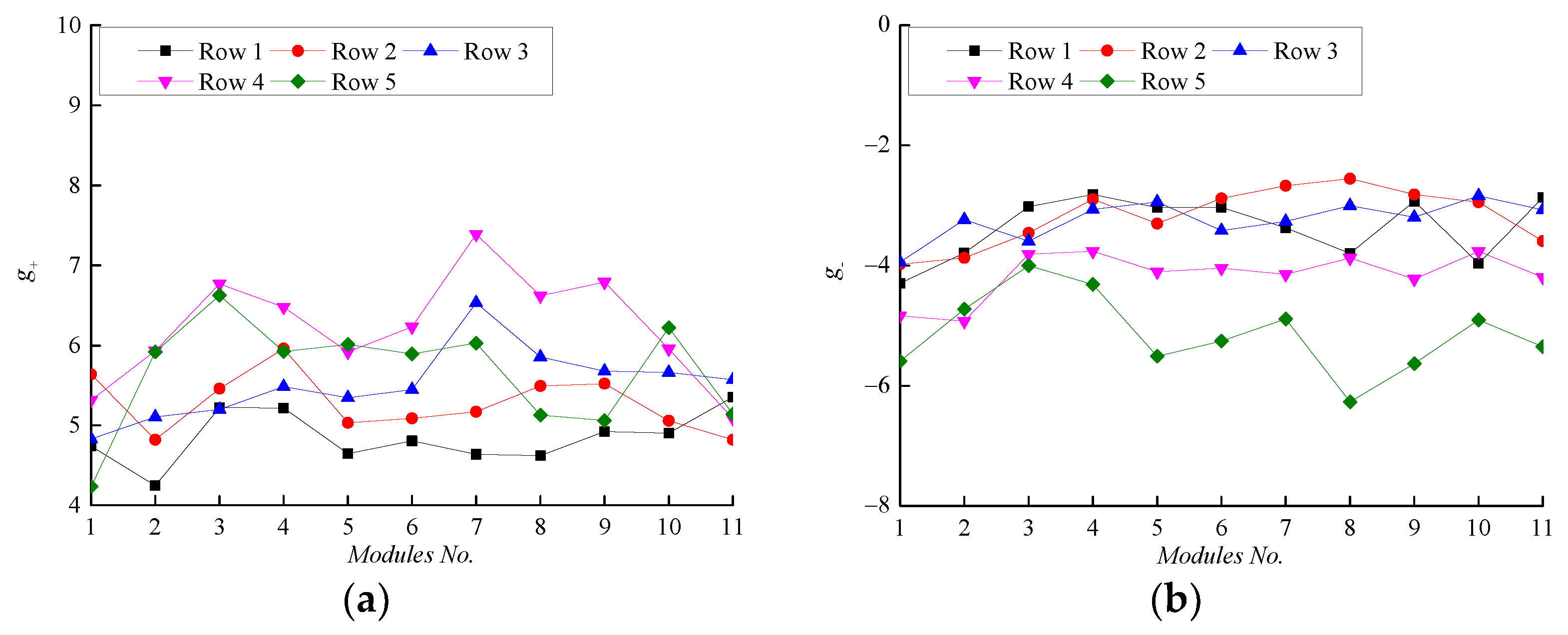
3. Data Processing
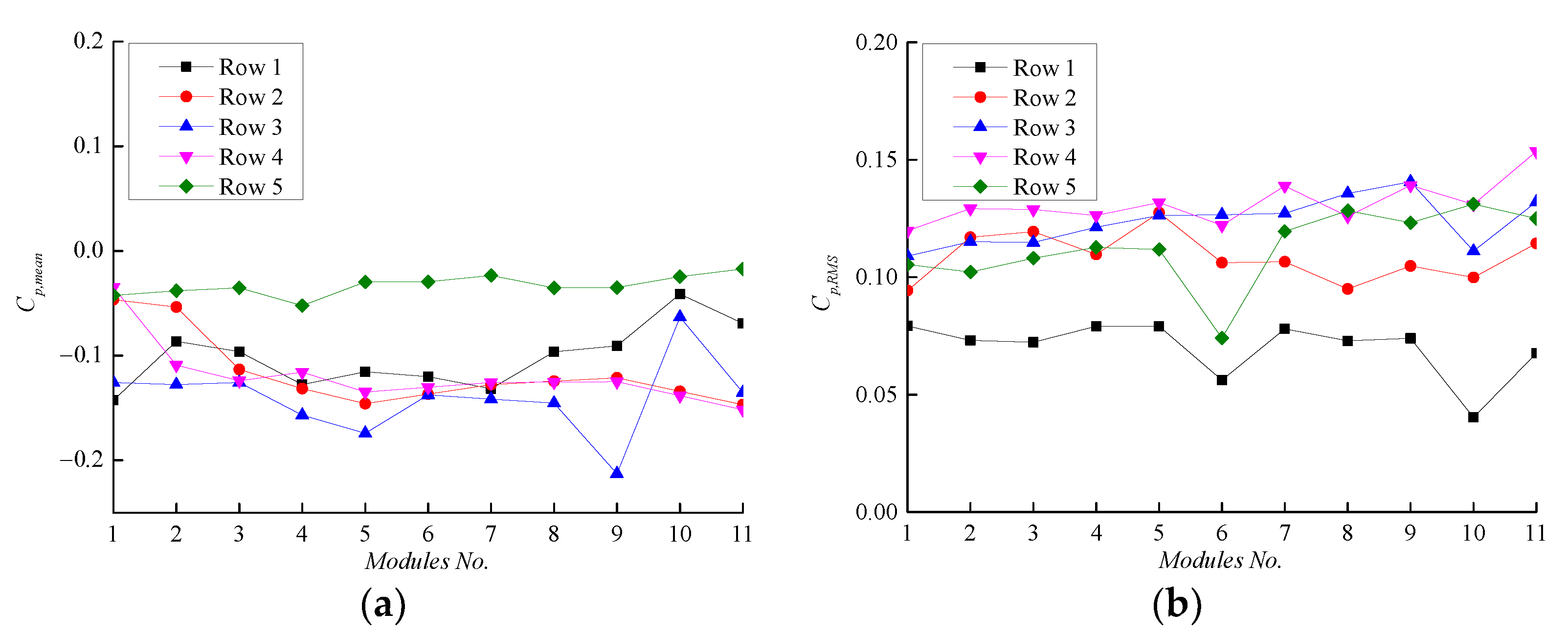
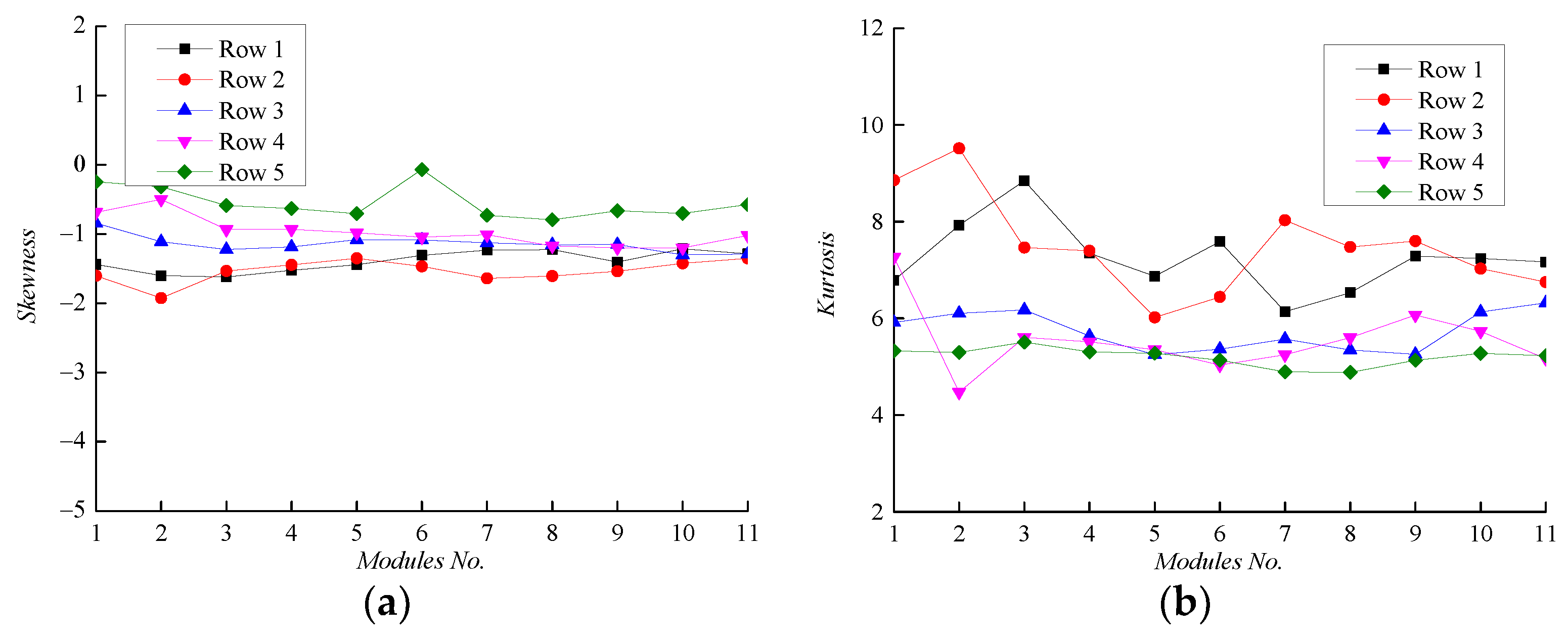
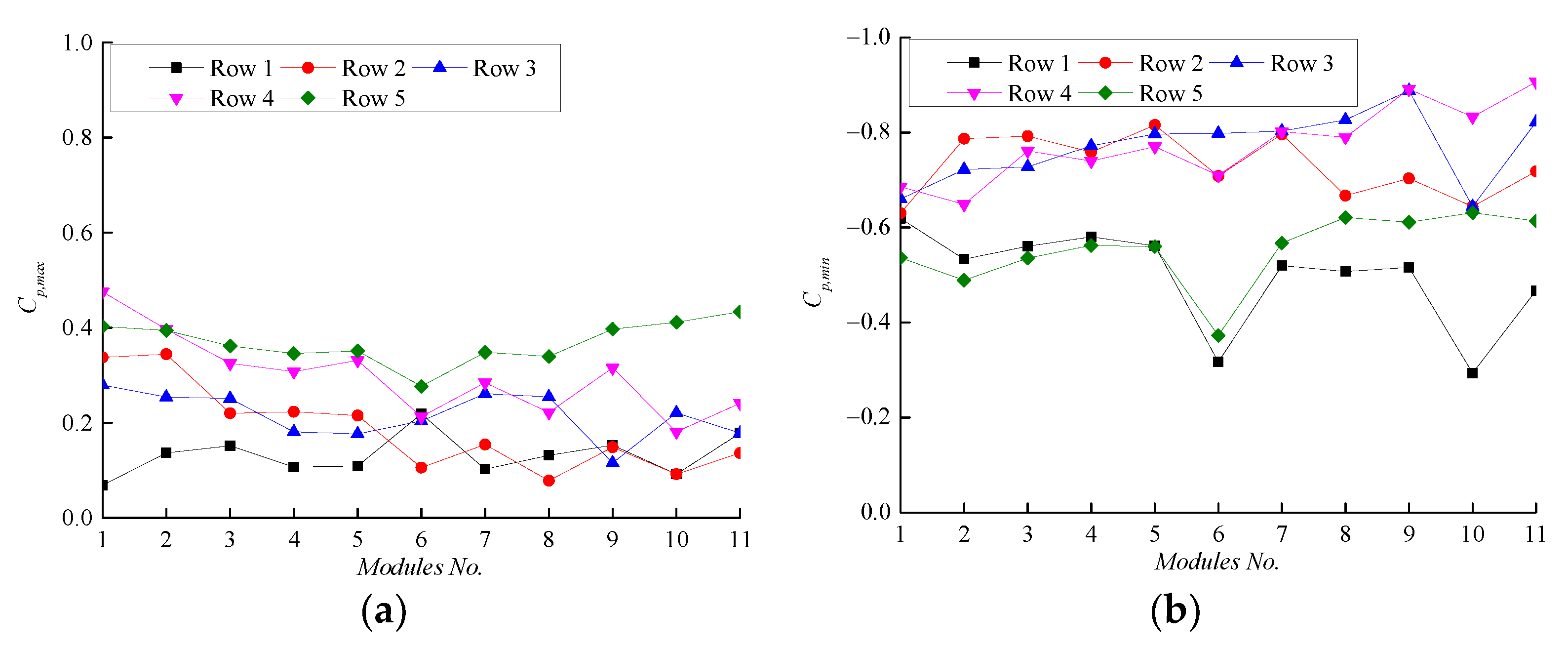
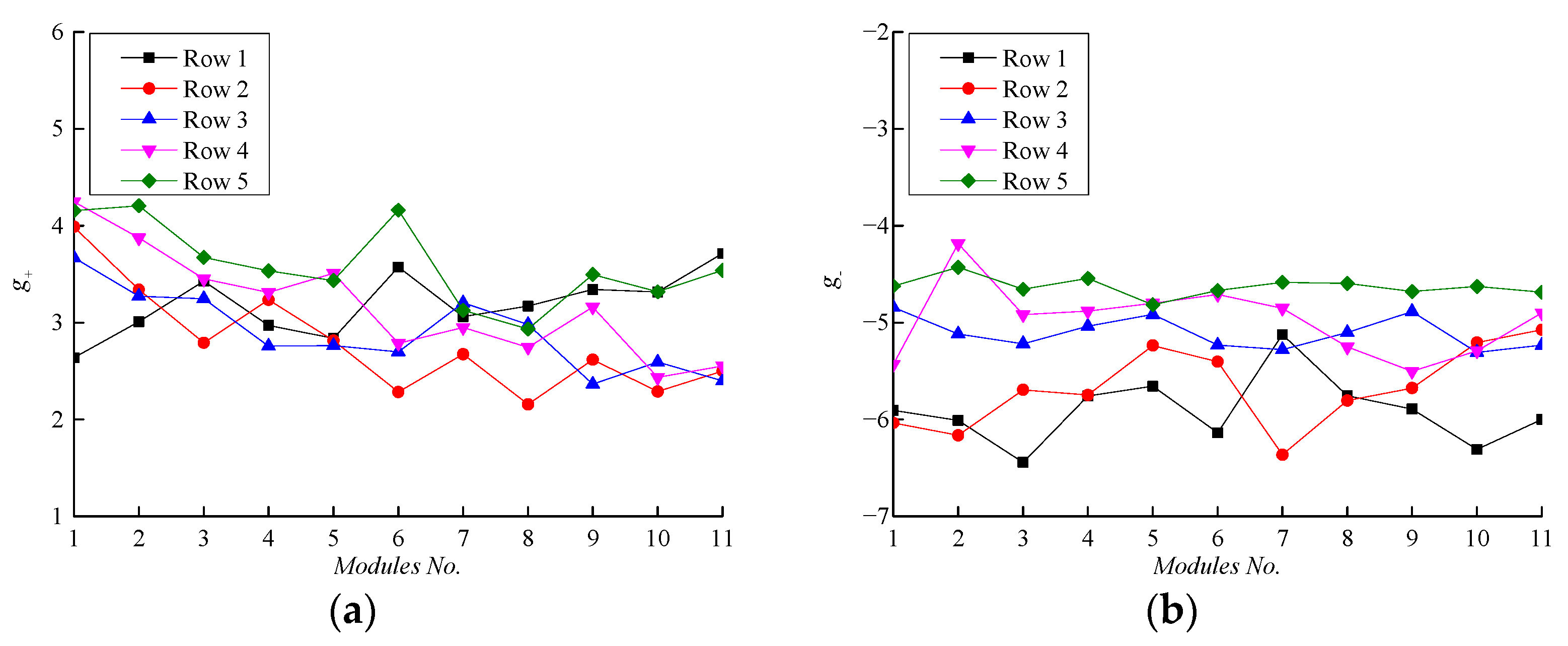
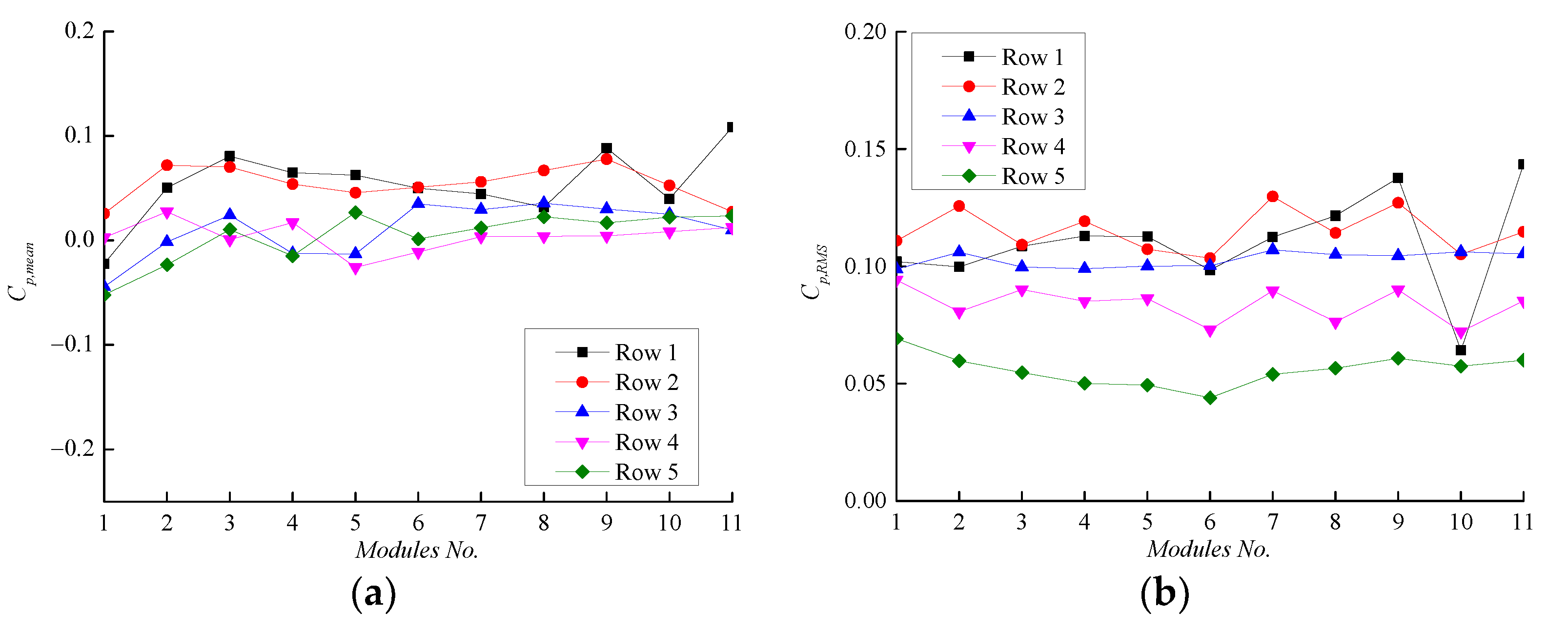
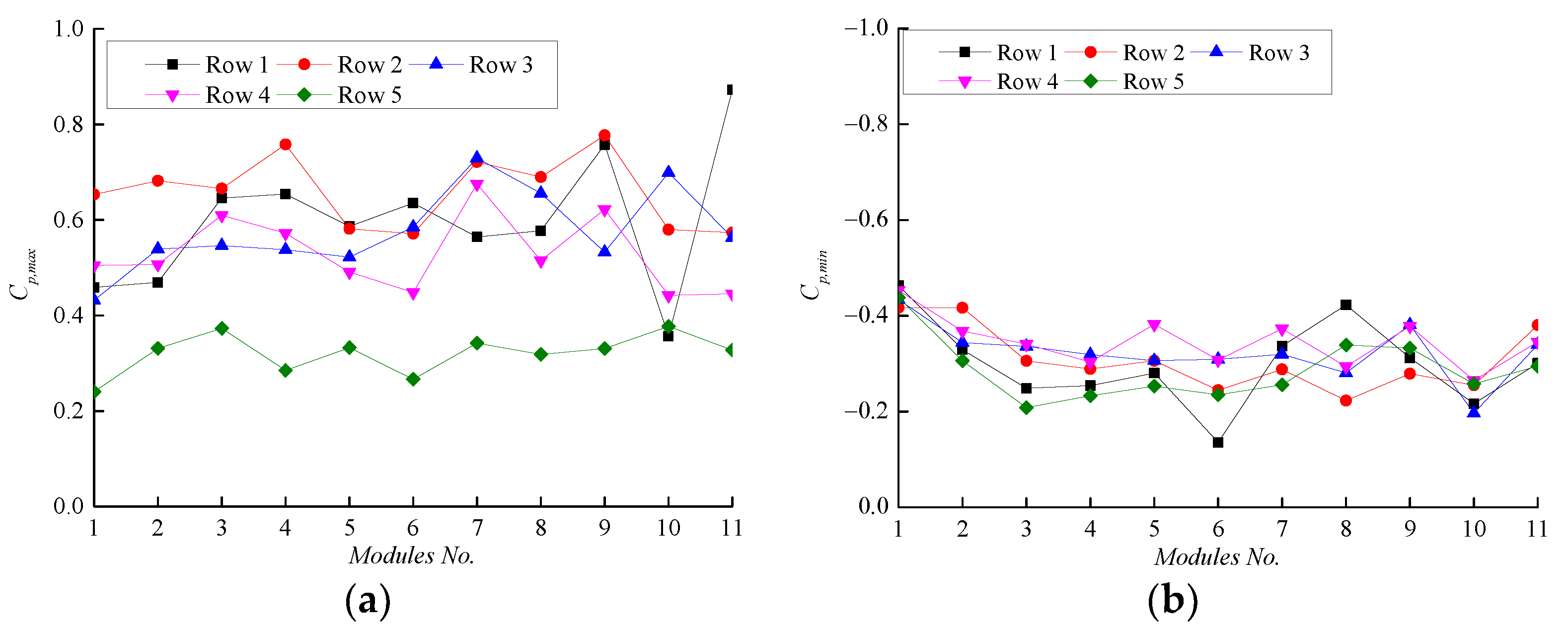
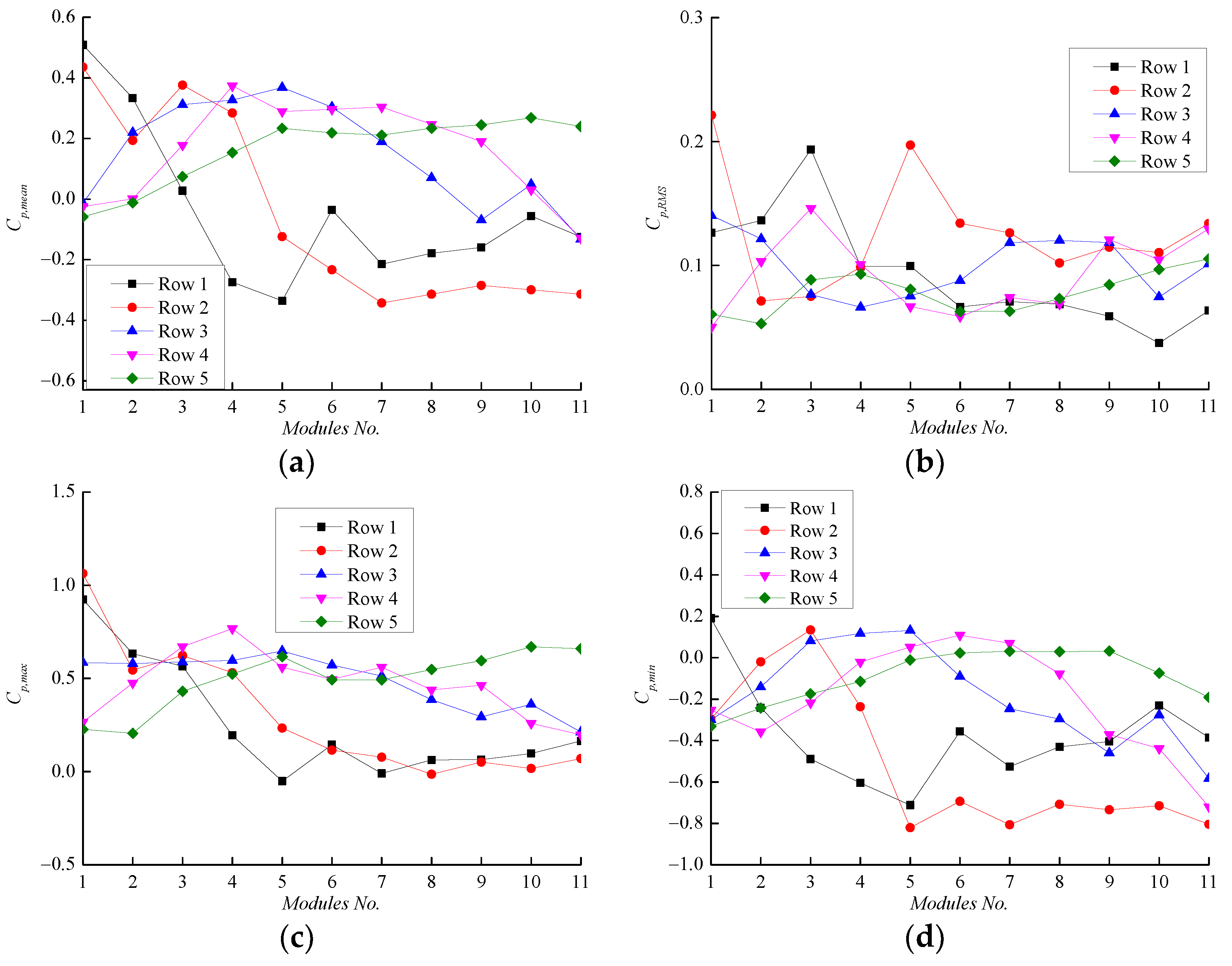
4. Results and Discussion
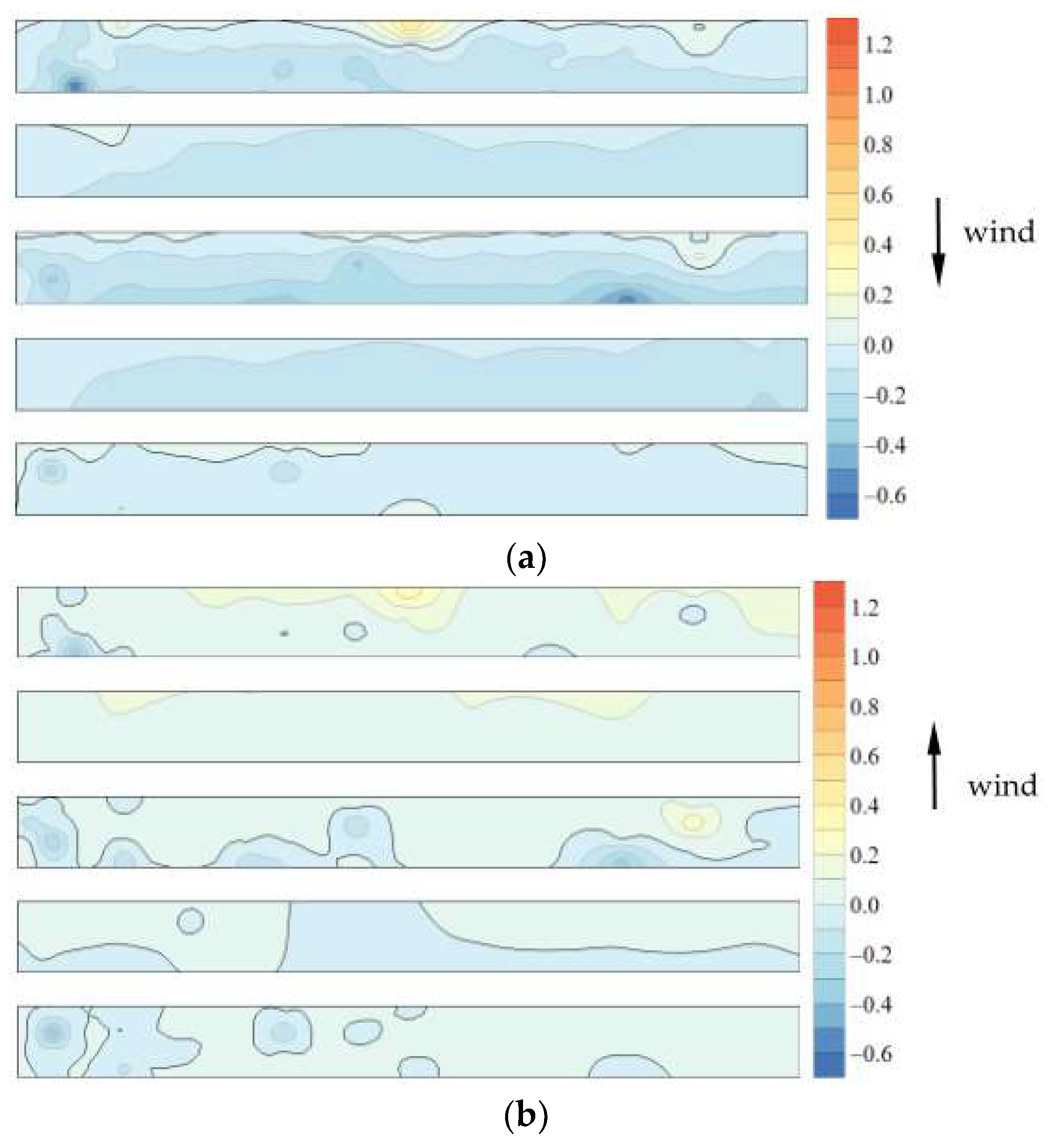
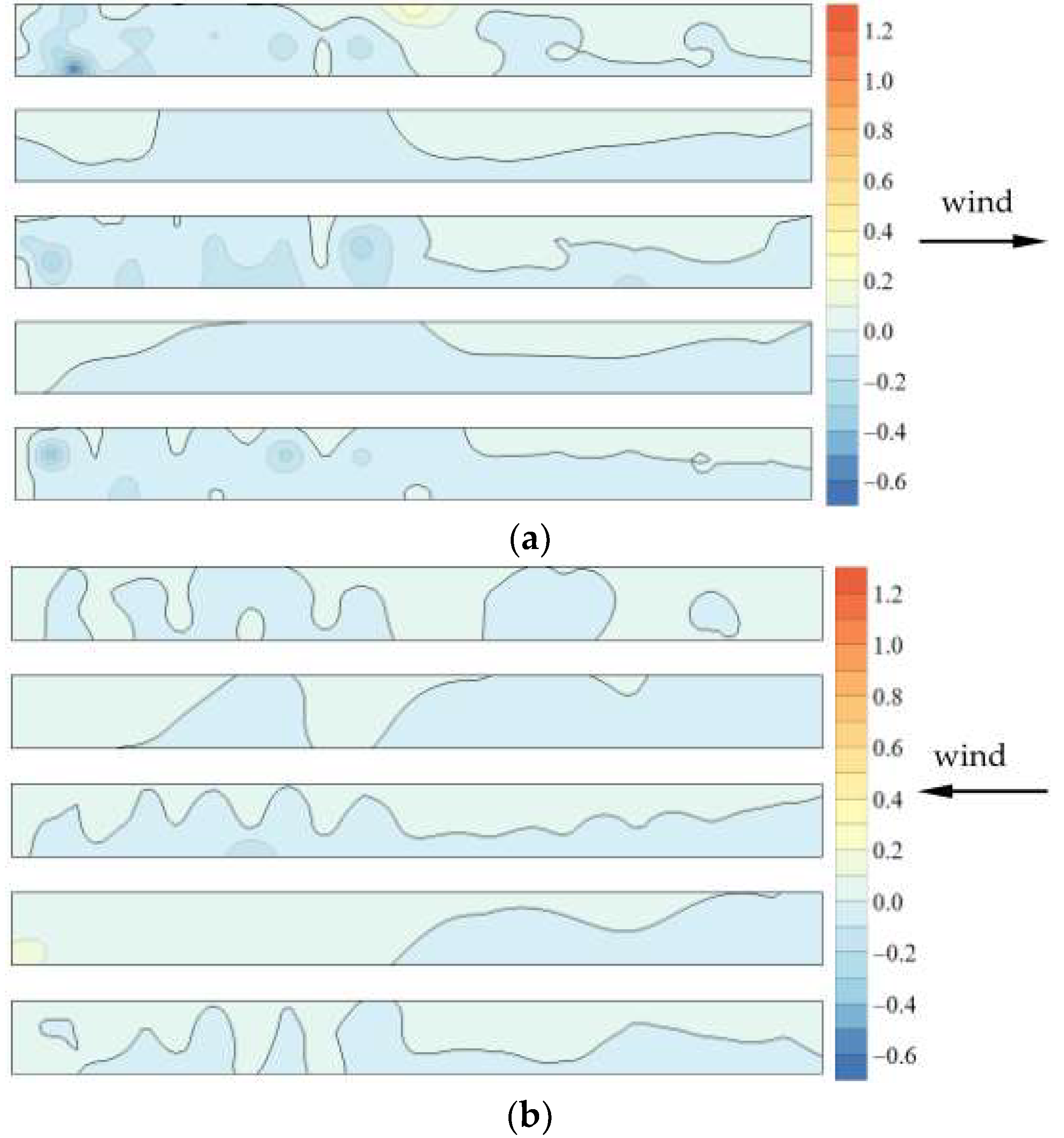
4.1. 0° and 180° Wind Directions
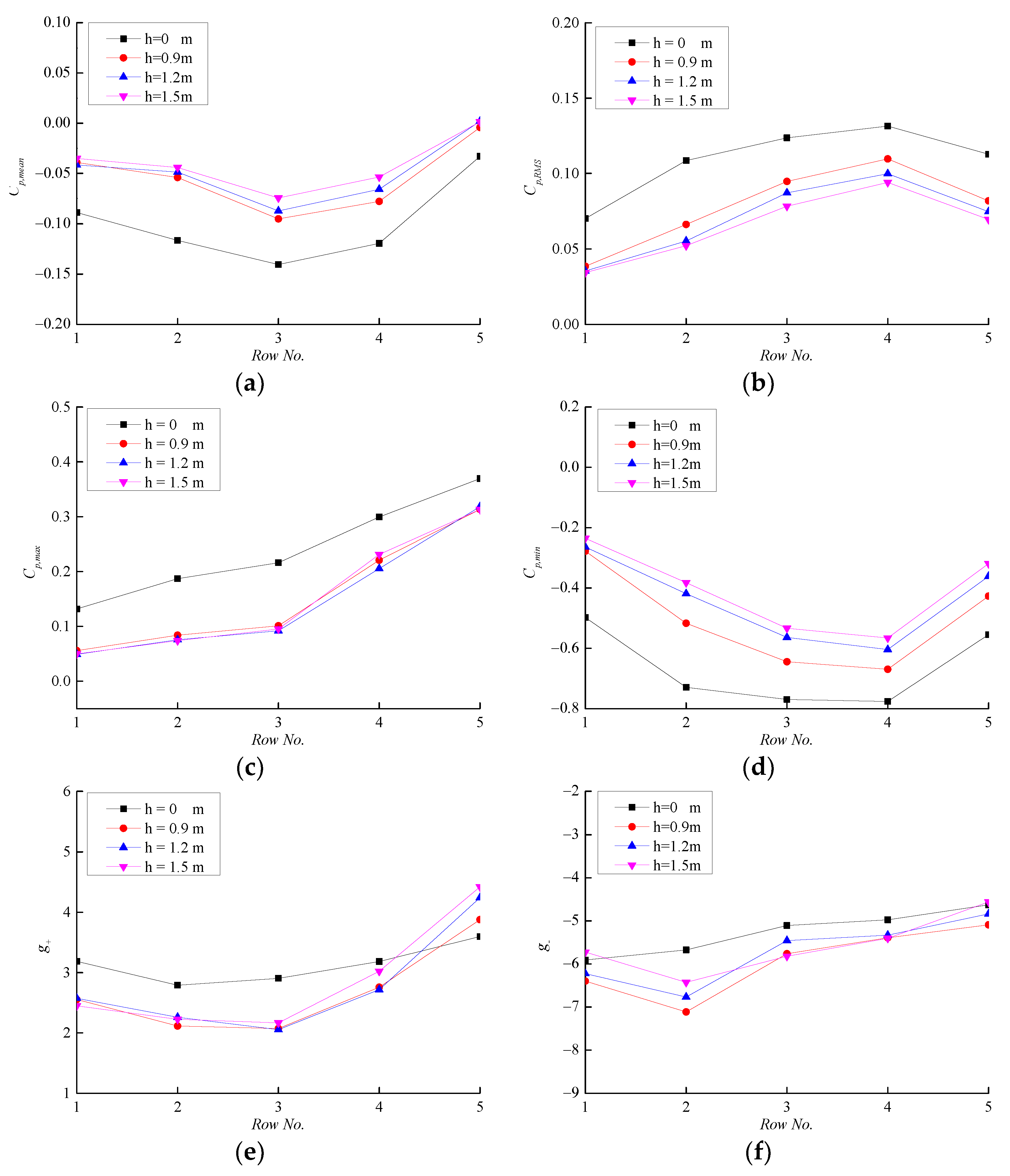
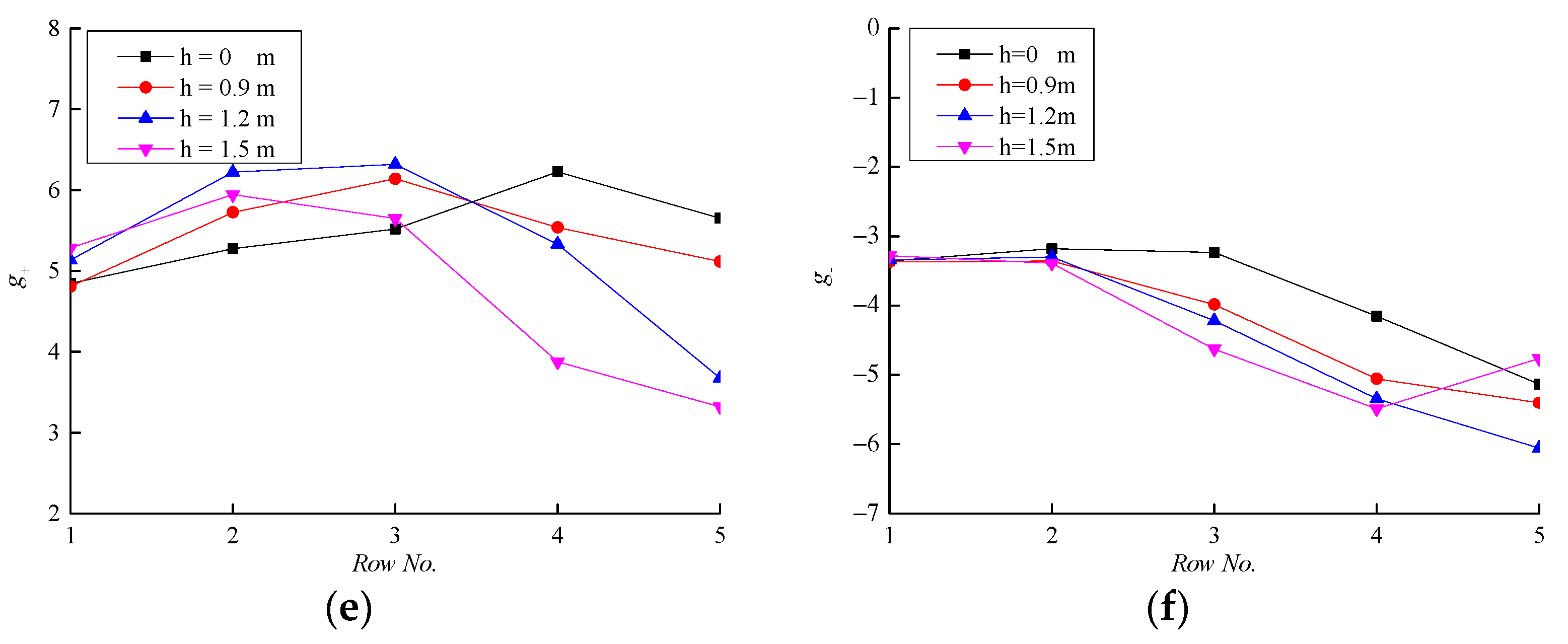
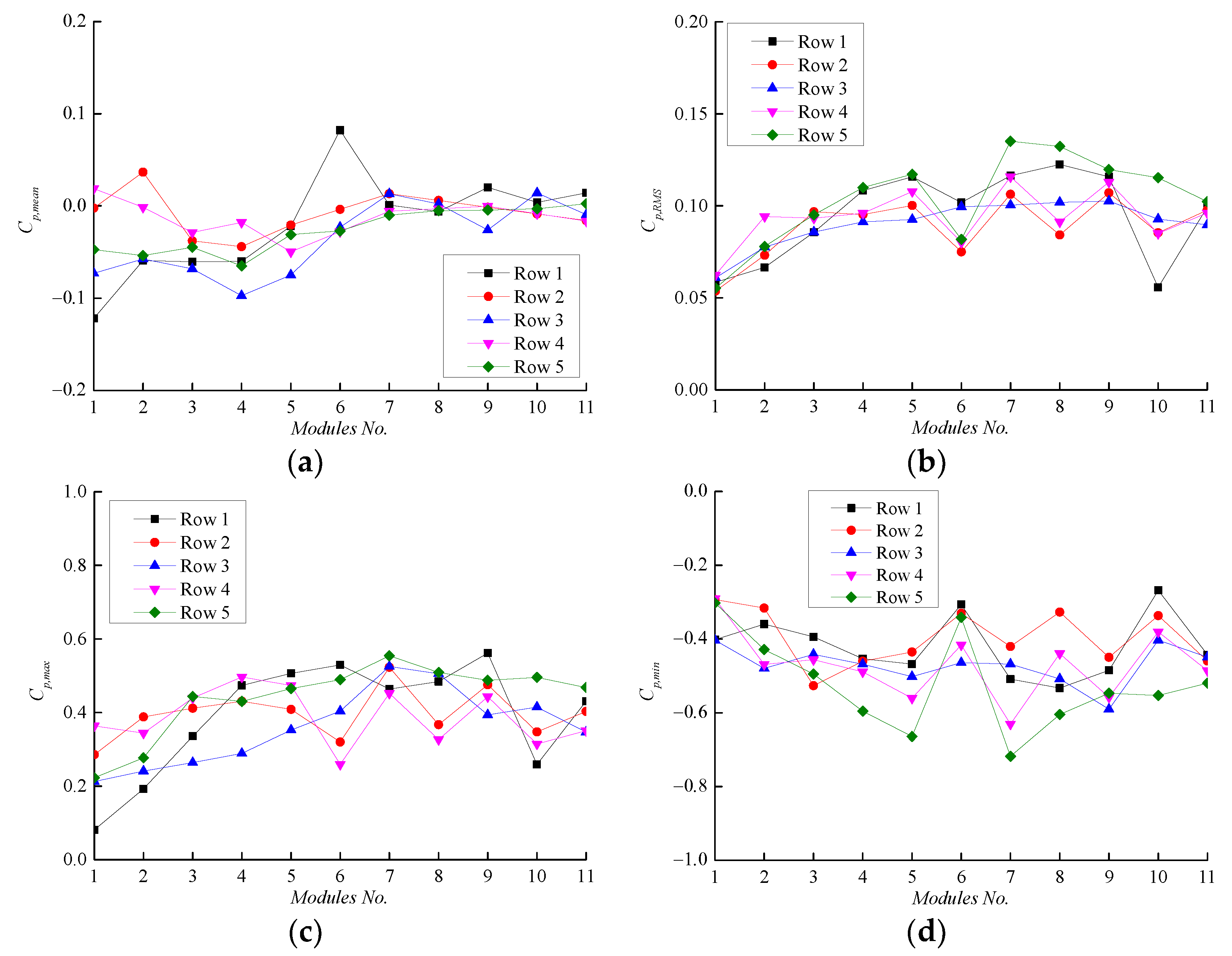
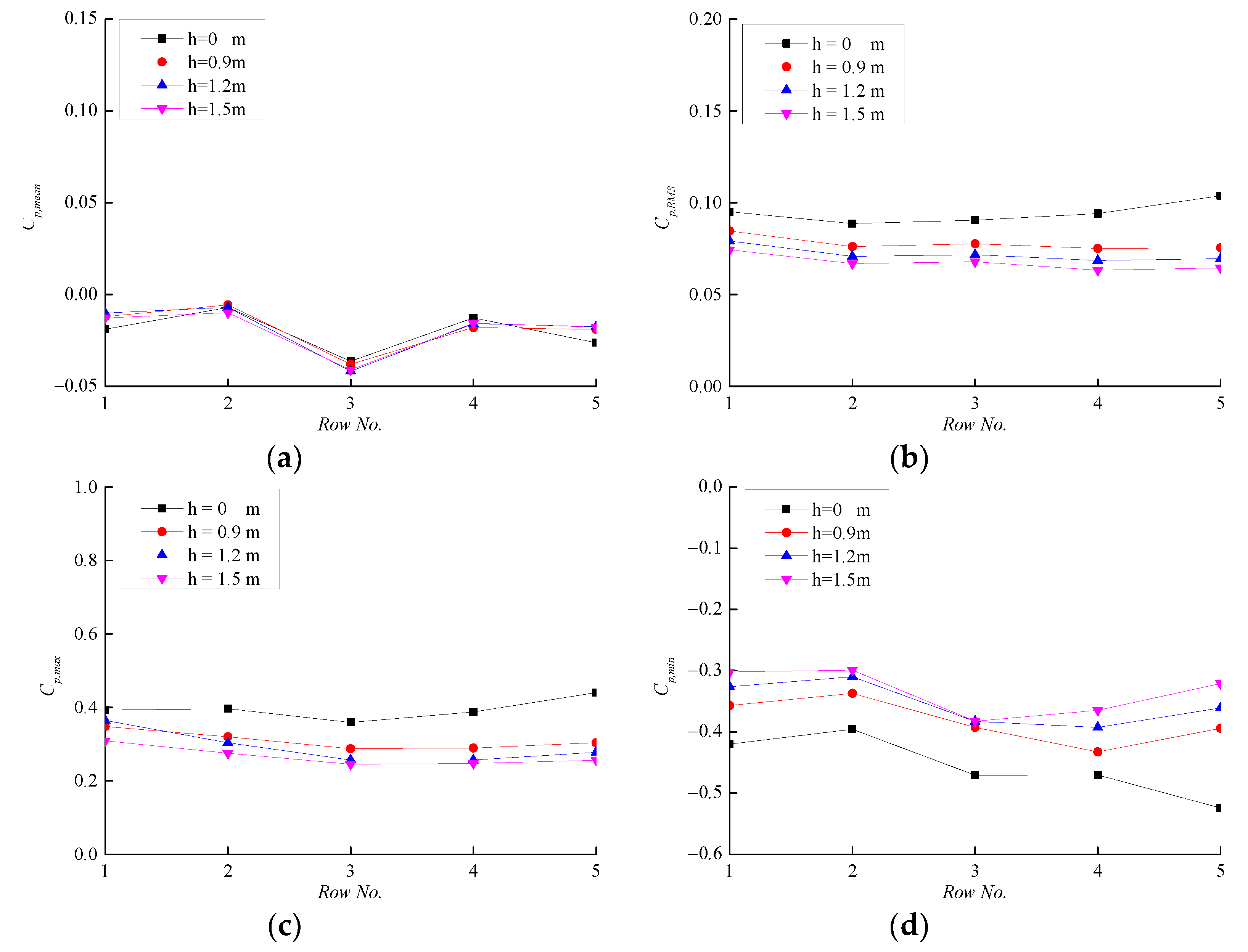
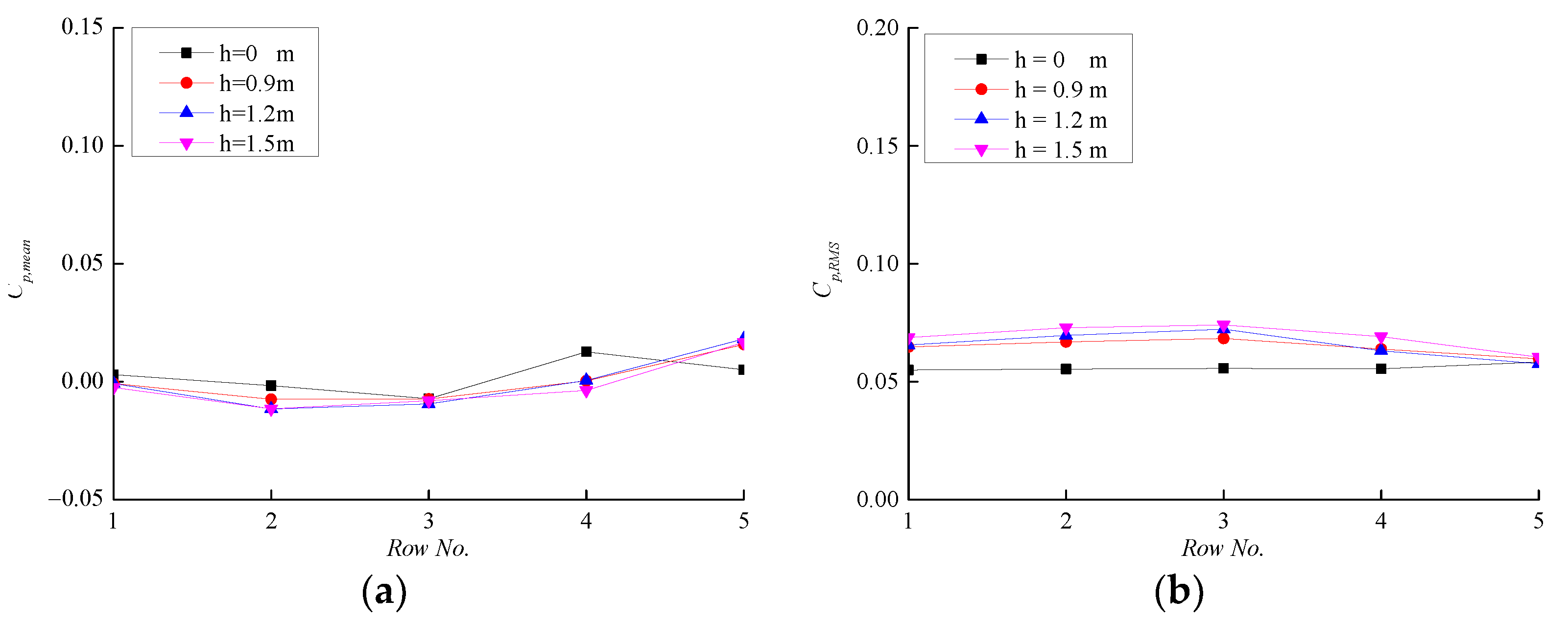
4.1.1. Effect of Parapet Height
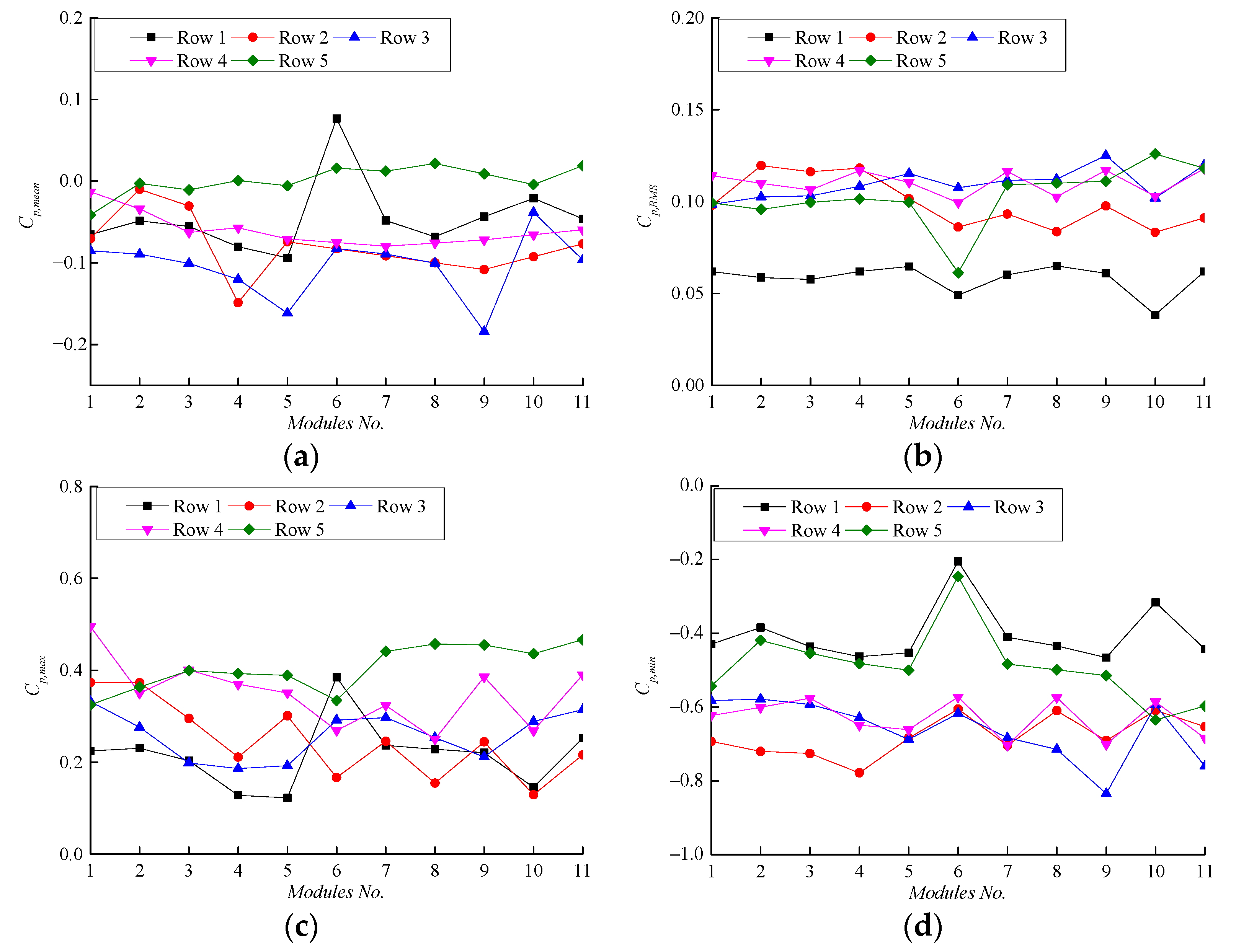
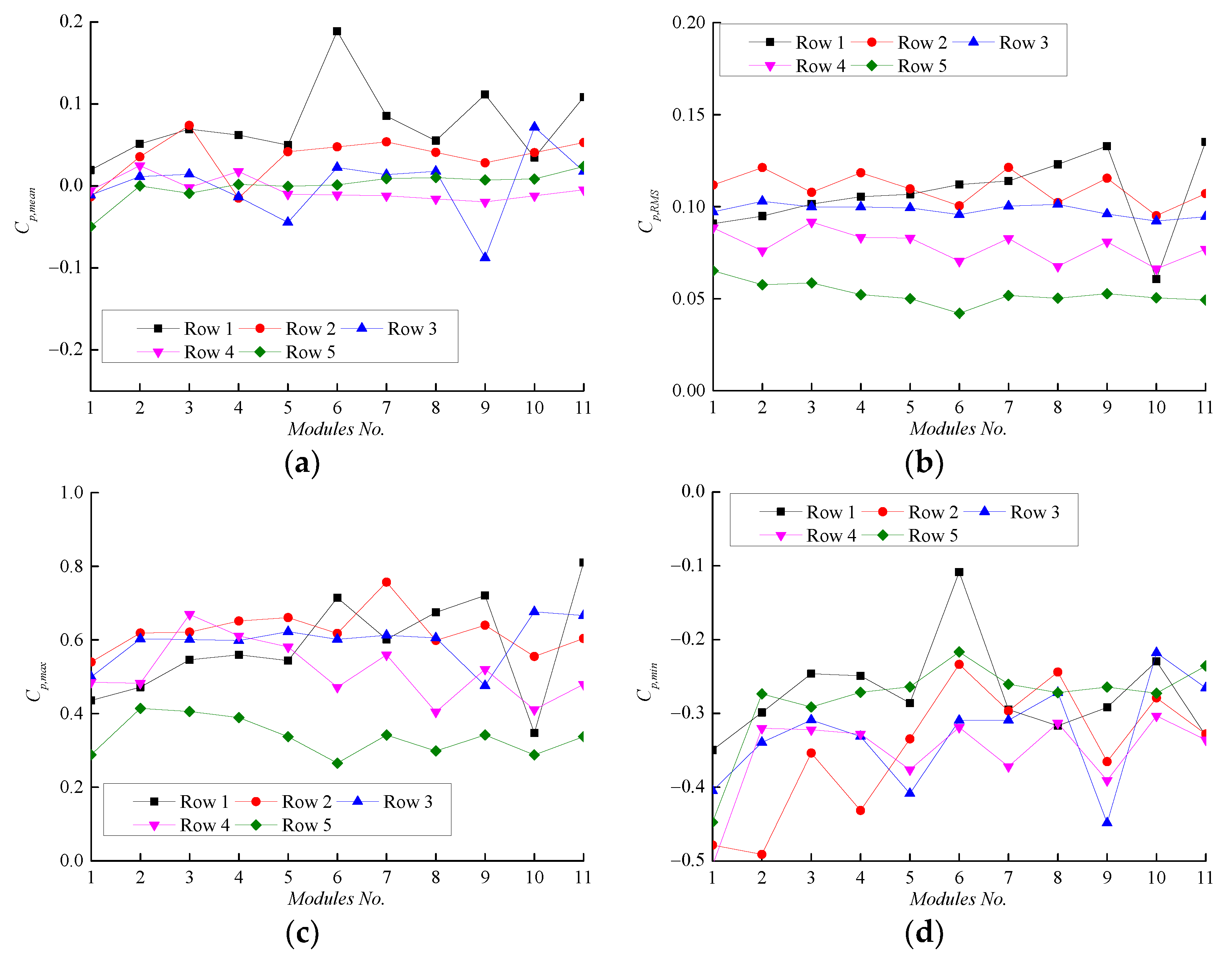
4.1.2. Effect of Tilt Angle
4.2. 90° and 270° Wind Directions
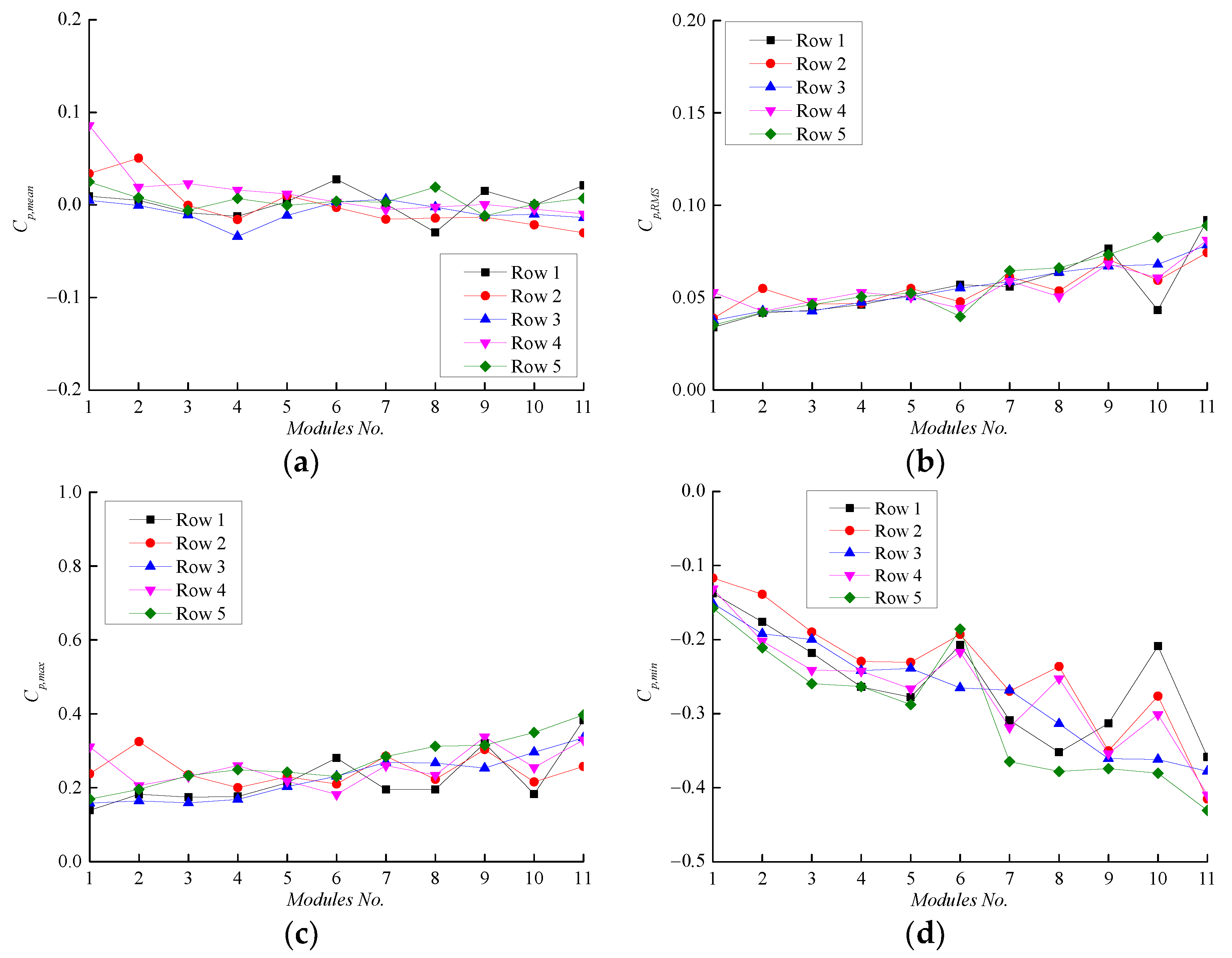
4.2.1. Effect of Parapet Height
4.2.2. Effect of Tilt Angle
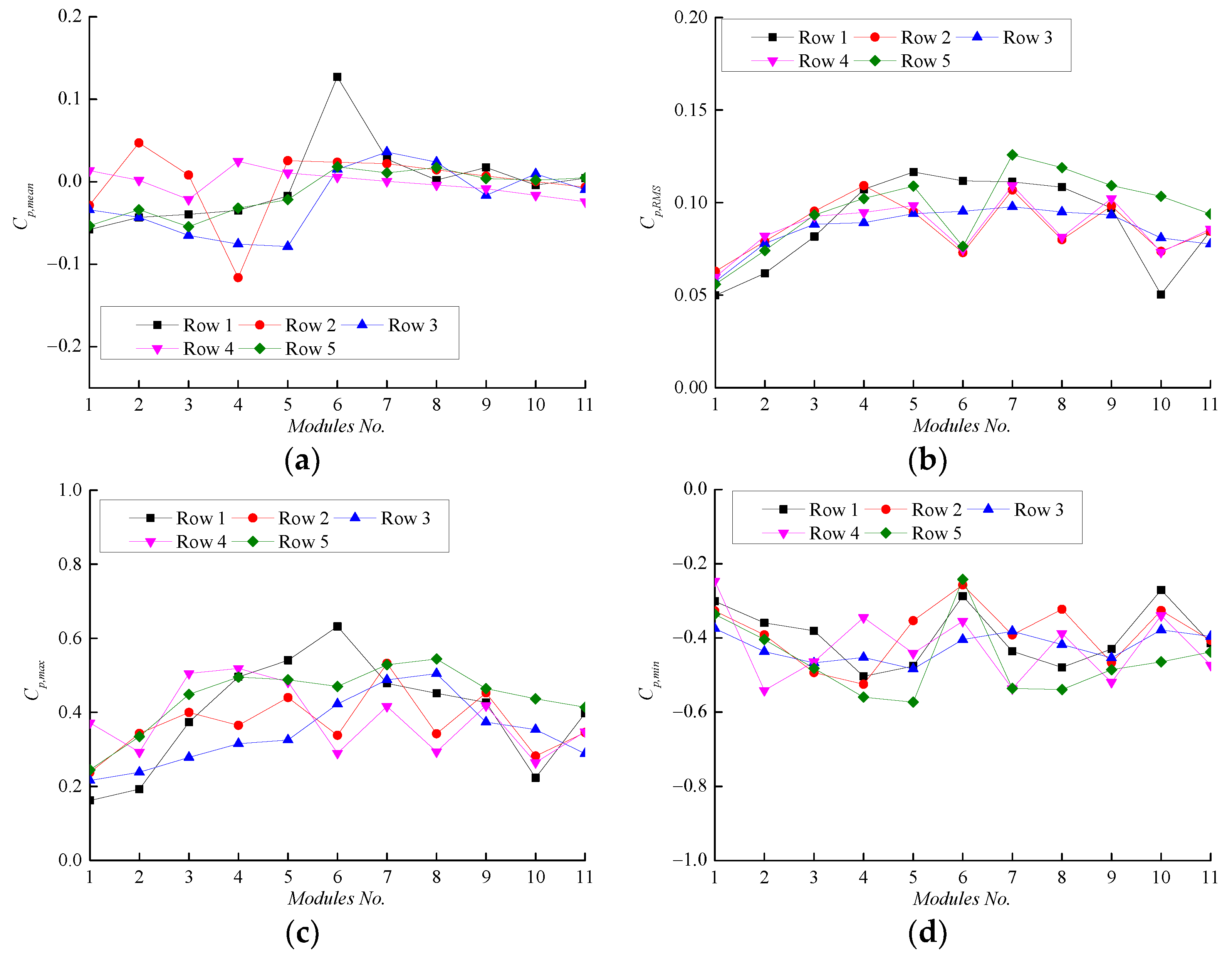
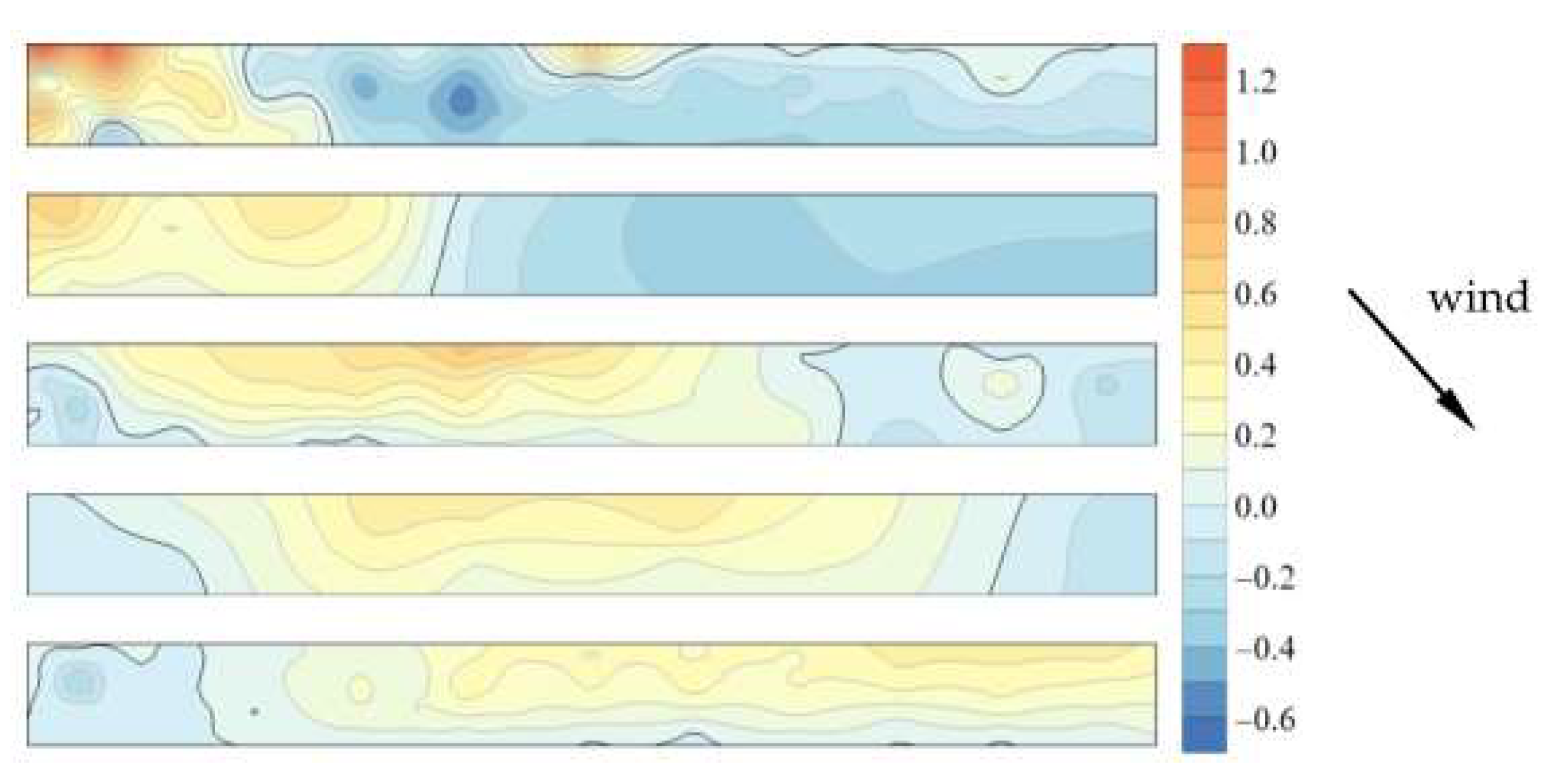
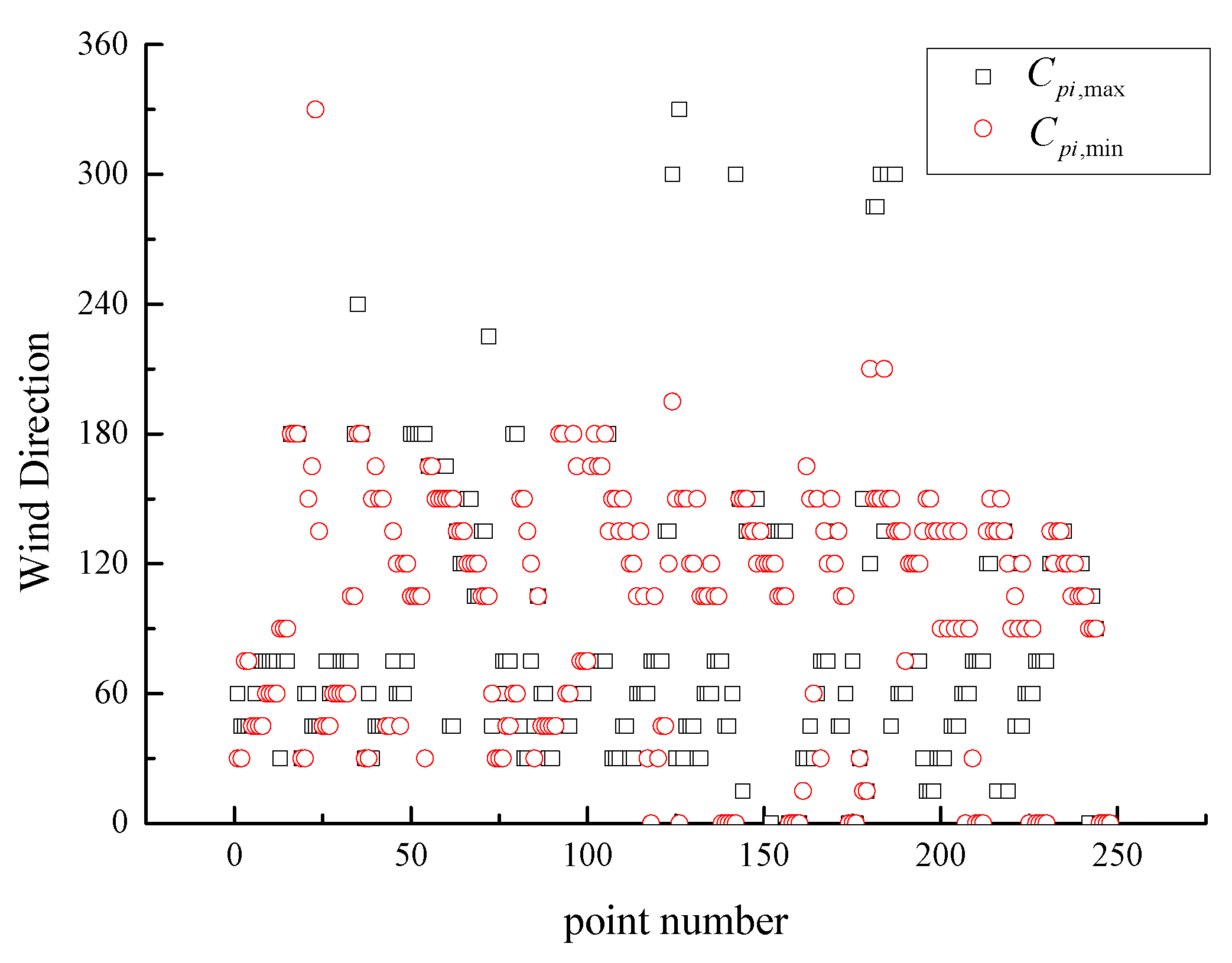
4.3. Oblique Wind Direction
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhao, X.; Xie, Y. The economic performance of industrial and commercial rooftop photovoltaic in China. Energy 2019, 187, 115961. [Google Scholar]
- Doddipatla, L.S.; Kopp, G.A. Wind loads on roof-mounted equipment on low-rise buildings with low-slope roofs. J. Wind. Eng. Ind. Aerodyn. 2021, 211, 104552. [Google Scholar] [CrossRef]
- Kopp, G.A.; Banks, D. Use of the Wind Tunnel Test Method for Obtaining Design Wind Loads on Roof-Mounted Solar Arrays. J. Struct. Eng. 2013, 139, 284–287. [Google Scholar] [CrossRef]
- Kopp, G.A.; Farquhar, S.; Morrison, M.J. Aerodynamic mechanisms for wind loads on tilted, roof-mounted, solar arrays. J. Wind Eng. Ind. Aerodyn. 2012, 111, 40–52. [Google Scholar] [CrossRef]
- Pratt, R.N.; Kopp, G.A. Velocity measurements around low-profile, tilted, solar arrays mounted on large flat-roofs, for wall normal wind directions. J. Wind Eng. Ind. Aerodyn. 2013, 123, 226–238. [Google Scholar] [CrossRef]
- Warsido, W.P.; Bitsuamlak, G.T.; Barata, J.; Chowdhury, A.G. Influence of spacing parameters on the wind loading of solar array. J. Fluids Struct. 2014, 48, 295–315. [Google Scholar] [CrossRef]
- Wang, J.; Van Phuc, P.; Yang, Q.; Tamura, Y. LES study of wind pressure and flow characteristics of flat-roof-mounted solar arrays. J. Wind Eng. Ind. Aerodyn. 2020, 198, 104096. [Google Scholar] [CrossRef]
- Dai, S.; Liu, H.; Yang, J.; Peng, H. Wind loads on roof-mounted isolated solar panels of tall buildings through wind tunnel testing. Sol. Energy 2022, 231, 607–622. [Google Scholar] [CrossRef]
- Scaletchi, I.; Visa, I.; Velicu, R. Modeling wind action on solar tracking PV platforms. Bull. Transilv. Univ. Bras. 2010, 3, 115–122. [Google Scholar]
- Pfahl, A.; Buselmeier, M.; Zaschke, M. Wind loads on heliostats and photovoltaic trackers of various aspect ratios. Sol. Energy 2011, 85, 2185–2201. [Google Scholar] [CrossRef] [Green Version]
- Abiola-Ogedengbe, A.; Hangan, H.; Siddiqui, K. Experimental investigation of wind effects on a standalone photovoltaic (PV) module. Renew. Energy 2015, 78, 657–665. [Google Scholar] [CrossRef]
- Jubayer, C.M.; Hangan, H. A numerical approach to the investigation of wind loading on an array of ground mounted solar photovoltaic (PV) panels. J. Wind Eng. Ind. Aerodyn. 2016, 153, 60–70. [Google Scholar] [CrossRef]
- Reina, G.P.; De Stefano, G. Computational evaluation of wind loads on sun-tracking ground-mounted photovoltaic panel arrays. J. Wind Eng. Ind. Aerodyn. 2017, 170, 283–293. [Google Scholar] [CrossRef]
- Taylor, Z.J.; Browne, M.T.L. Hybrid pressure integration and buffeting analysis for multi-row wind loading in an array of single-axis trackers—ScienceDirect. J. Wind Eng. Ind. Aerodyn. 2020, 197, 104056. [Google Scholar] [CrossRef]
- NB/T 10115-2018; Code for Design of Photovoltaic Modules Support Structures. China Jihua Press: Beijing, China, 2018.
- ASCE7–05; Minimum Design Loads for Buildings and Other Structures. ASCE: Reston, VA, USA, 2006.
- ASCE7-10; Minimum Design Loads for Buildings and Other Structures. ASCE: Reston, VA, USA, 2010.
- GB 50009-2012; Load Code for the Design of Building Structures. China Architecture and Building Press: Beijing, China, 2012.
- Huang, M.F.; Lou, W.; Pan, X.; Chan, C.M.; Li, Q.S. Hermite extreme value estimation of non-Gaussian wind load process on a long-span roof structure. J. Struct. Eng. 2014, 140, 04014061. [Google Scholar] [CrossRef]
- JGJ/T 481-2019; Standard for Wind Loads on Roof Structures. China Architecture and Building Press: Beijing, China, 2019.
- Wint´erstein, S.R. Nonlinear Vibration Models for Extremes and Fatigue. J. Eng. Mech. 1988, 114, 1772–1790. [Google Scholar] [CrossRef]
- Kwon, D.; Kareem, A. Peak factors for non-Gaussian load effects revisited. J. Struct. Eng. 2011, 10, 1611–1619. [Google Scholar] [CrossRef]
- Shademan, M.; Barron, R.; Balachandar, R.; Hangan, H. Numerical simulation of wind loading on ground-mounted solar panels at different flow configurations. Can. J. Civ. Eng. 2014, 41, 728–738. [Google Scholar] [CrossRef]


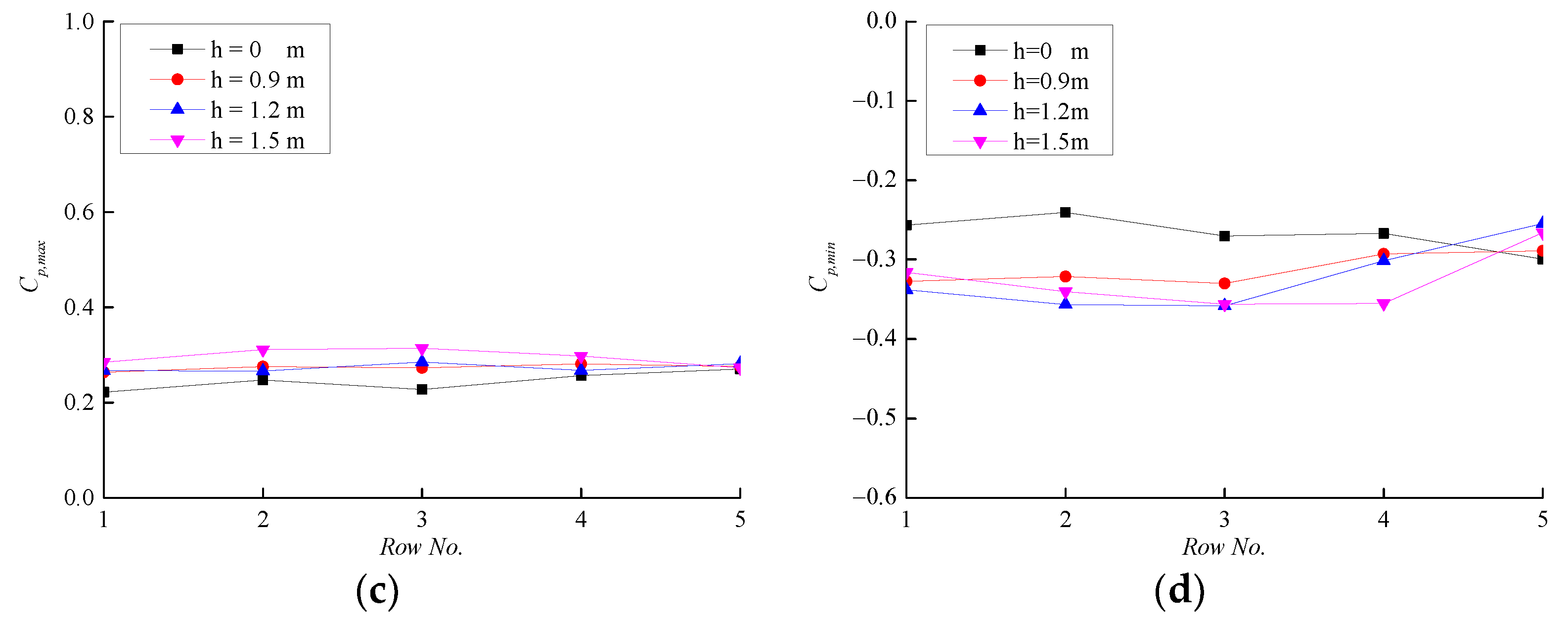
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, J.; Tu, Z.; Wang, D.; Shen, G.; Lou, W. Experimental Investigation of Wind Loads on Roof-Mounted Solar Arrays. Sustainability 2022, 14, 8477. https://doi.org/10.3390/su14148477
Yao J, Tu Z, Wang D, Shen G, Lou W. Experimental Investigation of Wind Loads on Roof-Mounted Solar Arrays. Sustainability. 2022; 14(14):8477. https://doi.org/10.3390/su14148477
Chicago/Turabian StyleYao, Jianfeng, Zhibin Tu, Dong Wang, Guohui Shen, and Wenjuan Lou. 2022. "Experimental Investigation of Wind Loads on Roof-Mounted Solar Arrays" Sustainability 14, no. 14: 8477. https://doi.org/10.3390/su14148477
APA StyleYao, J., Tu, Z., Wang, D., Shen, G., & Lou, W. (2022). Experimental Investigation of Wind Loads on Roof-Mounted Solar Arrays. Sustainability, 14(14), 8477. https://doi.org/10.3390/su14148477







