Prediction of Runoff in Watersheds Located within Data-Scarce Regions
Abstract
1. Introduction
2. Materials and Methods
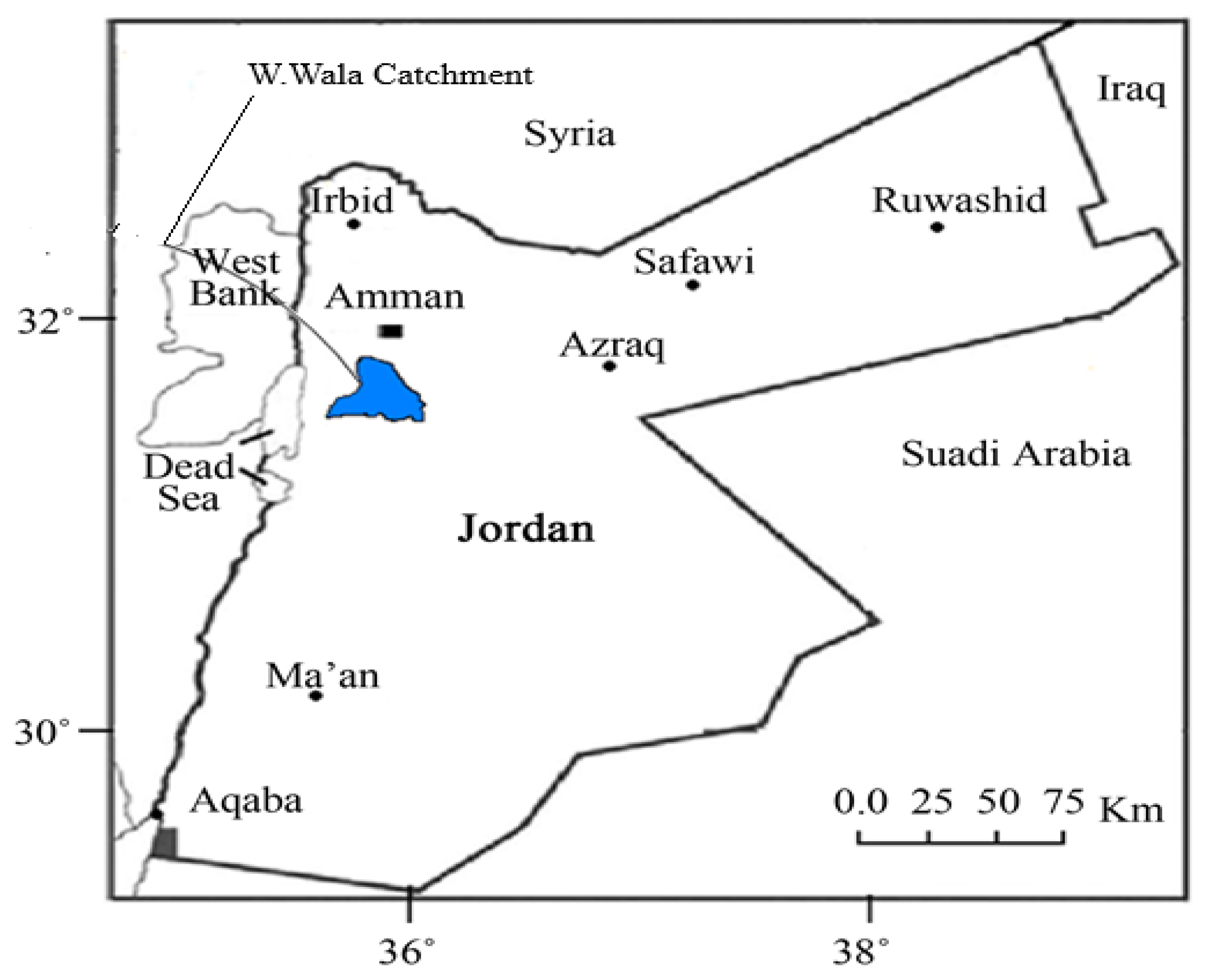
2.1. Hydrologic Data
2.1.1. Soil Condition
2.1.2. Evaluation and Analysis of Available Data
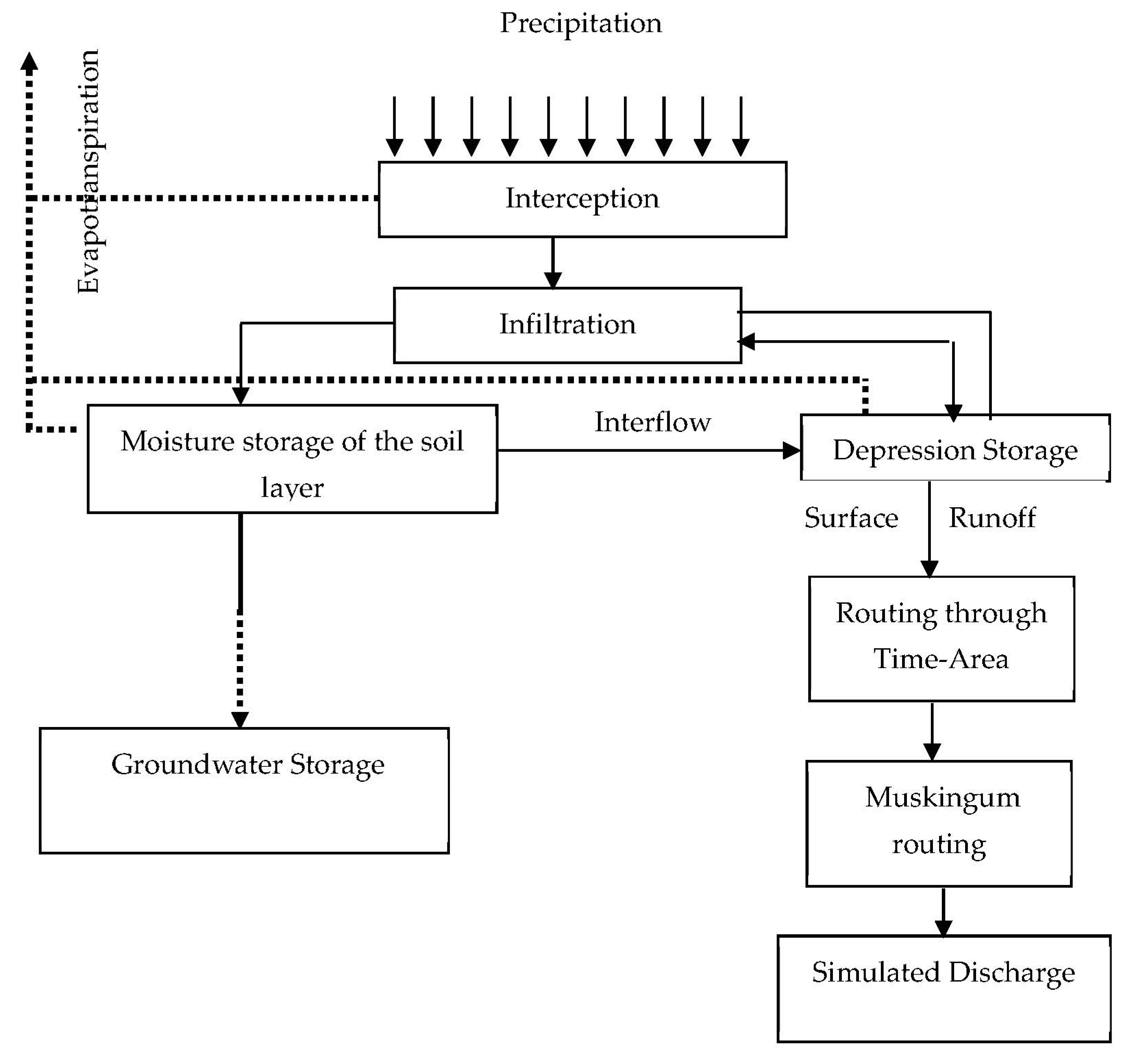
2.2. Model Structure
- Ra = the total surface runoff depth (mm);
- Pa = the total precipitation depth (mm);
- Fa = the total infiltration depth (mm);
- Sin = the interception storage depth (mm);
- PET = the potential evapotranspiration depth (mm);
- Ds = the surface depression storage depth (mm).
2.2.1. Model Components and Conceptualization
- f = the infiltration capacity rate (mm/h);
- Sa = the available storage capacity depth from the surface (mm).
- DRO = the direct surface runoff (mm);
- Sci = the capacity depth of inflow into interception storage (mm) for each time increment;
- Dc = the capacity depth of inflow into surface depression storage for each time increment.
- PET = the potential evapotranspiration rate (mm/h);
- PER = the percolation (mm);
- SSF = the subsurface flow (mm);
- Δt = the time increment (h);
- t = the time index.
2.2.2. Streamflow Recession
- Q0 = the flow at any time in cumecs;
- Qt = the flow one time unit later in cumecs;
- Kr = the recession constant (Kr, the seventh model parameter).
2.2.3. Catchment Routing
- Tc = time of concentration in hours;
- Lc = channel reach length (m);
- So = mean slope of channel reach.
- A = the catchment area (km2), starting point from the Wadi outlet to the most remote point of surface runoff movement):
- c & d = regression coefficients.
- Re = the rainfall excess array (mm/h);
- Aw = the watershed wetted subarea column vector (km2);
- q = the wetted area outflow discharge column vector;
- Nr = the number of ordinates of rainfall excess;
- M = the number of wetted subarea;
- J = the number of wetted area outflow discharge.
- k = the travel time of the flood wave through the channel reach in an hour (k is the eighth model parameter);
- x = the weighing factor ranging from 0 to 0.5 (x is the ninth model parameter. The model performs channel routing using the Muskingum routing equations (Equations (16)–(19)):
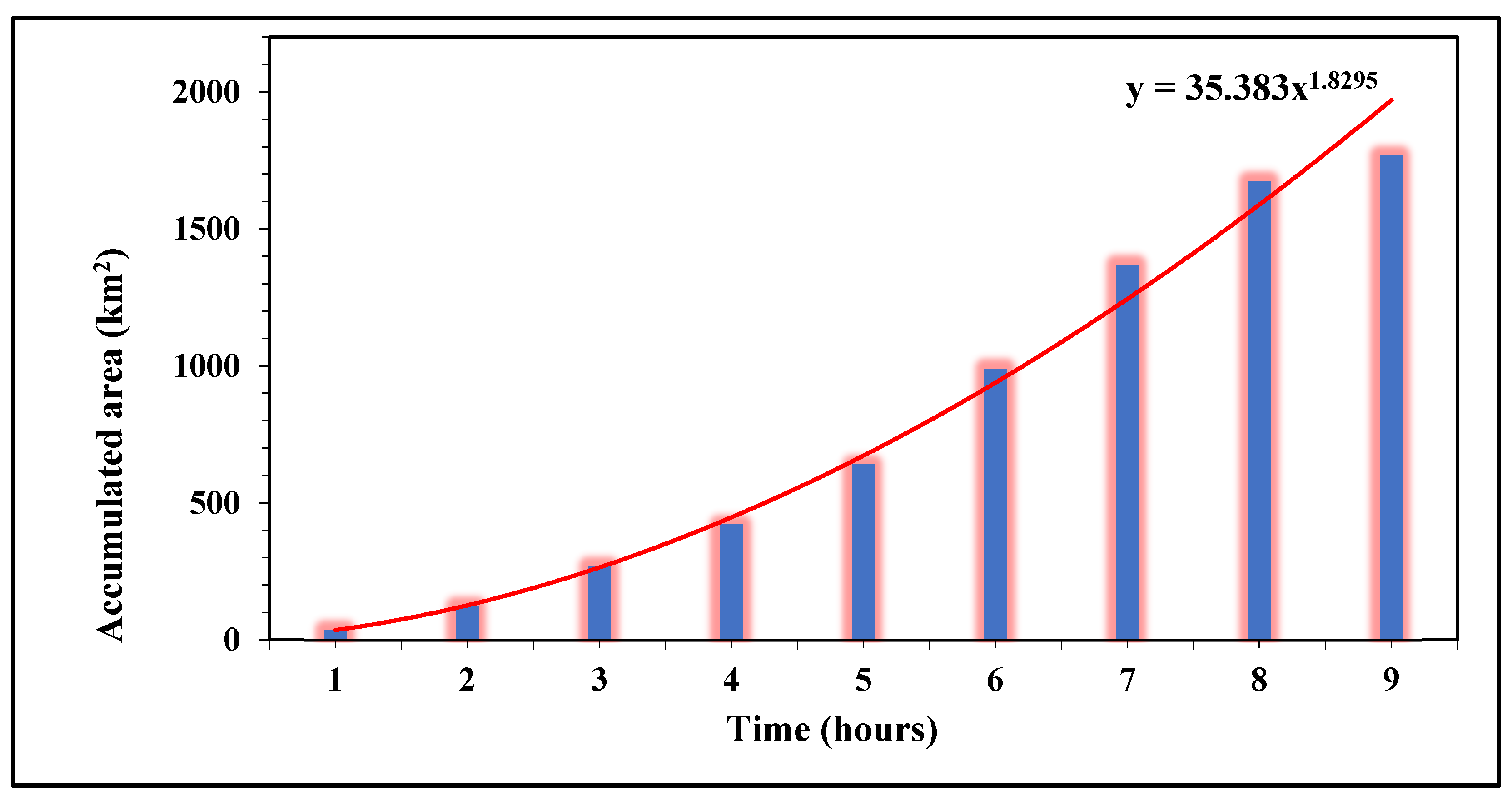
2.2.4. Lag Time and Wetted Area Approach
2.2.5. Catchment Area Parceling Condition
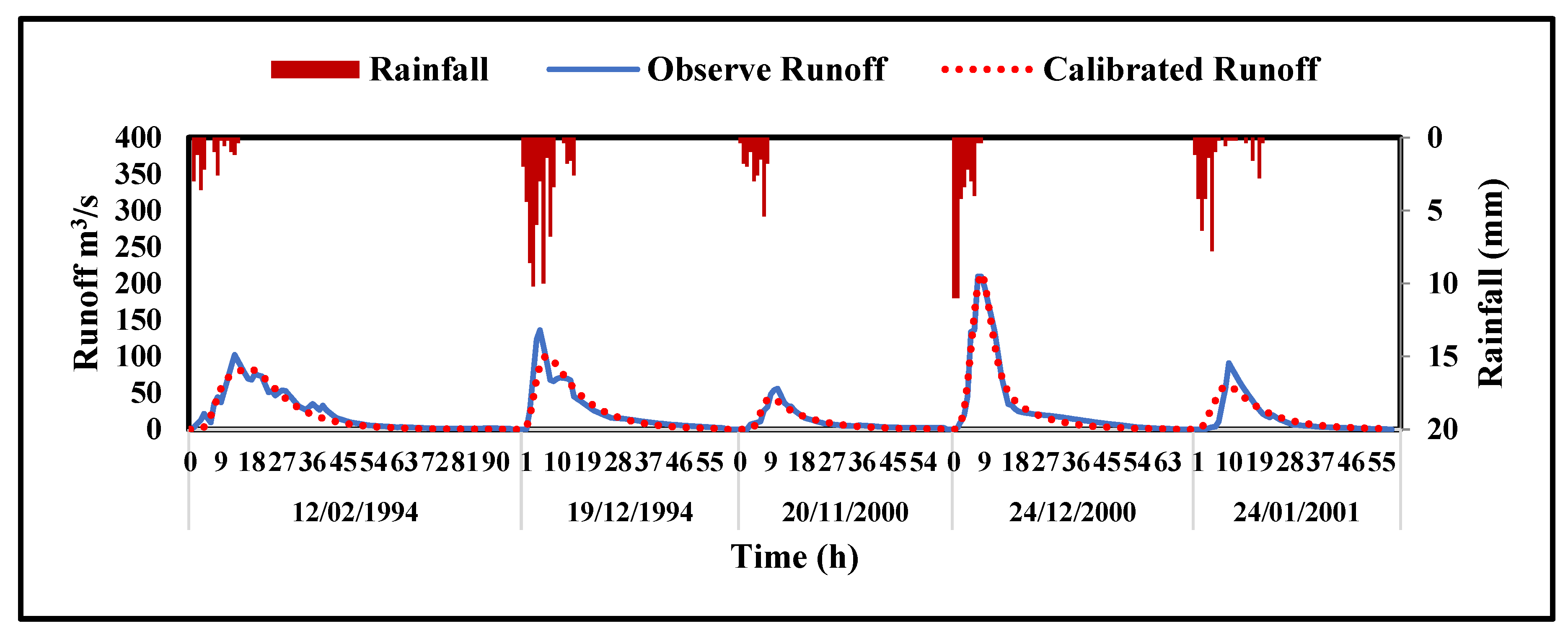
2.3. Model Calibration
- OF (LS) = a least-square objective function;
- Qobsi = the observed flow on any hour i;
- Qsimi = the simulated flow on any hour i;
- N = the number of record observations.
2.4. Model Validation
Performance Evaluation of the Proposed Model
- f (Qobsi) = the observed streamflow;
- f (Qsimi) = the simulated streamflow over the calibration period;
- N = the number of record observations.
- (Qp)obs = the observed peak;
- (Qp)sim = the estimated peak.
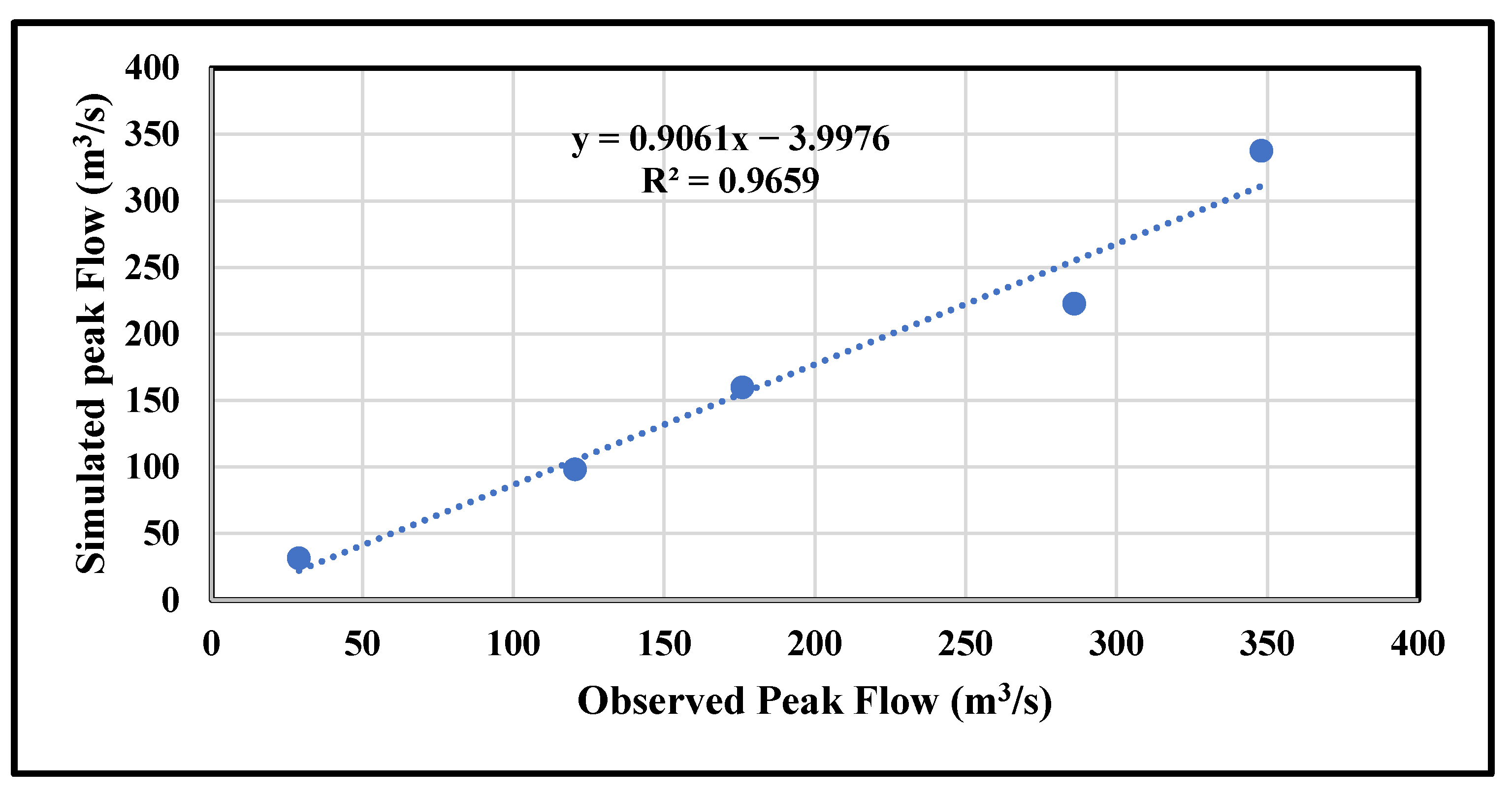
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kan, G.; He, X.; Ding, L.; Li, J.; Liang, K.; Hong, Y. Study on Applicability of Conceptual Hydrological Models for Flood Forecasting in Humid, Semi-Humid Semi-Arid and Arid Basins in China. Water 2017, 9, 719. [Google Scholar] [CrossRef]
- Lei, T.; Pang, Z.; Wang, X.; Li, L.; Fu, J.; Kan, G.; Zhang, X.; Ding, L.; Li, J.; Huang, S.; et al. Drought and Carbon Cycling of Grassland Ecosystems under Global Change: A Review. Water 2016, 8, 460. [Google Scholar] [CrossRef]
- Nash, J.E. The Form of the Instantaneous Unit Hydrograph. Available online: https://iahs.info/uploads/dms/045011.pdf (accessed on 9 May 2022).
- Mroczkowski, M.; Raper, G.P.; Kuczera, G. The quest for more powerful validation of conceptual catchment models. Water Resour. Res. 1997, 33, 2325–2335. [Google Scholar] [CrossRef]
- Crawford, N.H.; Linsley, R.K. Digital Simulation in Hydrology’ Stanford Watershed Model 4. Available online: https://trid.trb.org/view/99040 (accessed on 9 May 2022).
- Bergstrom, S.; Forsman, A. Development of a Conceptual Deterministic Rainfall-Runoff Model. Hydrol. Res. 1973, 4, 147–170. [Google Scholar] [CrossRef]
- Franchini, M.; Pacciani, M. Comparative analysis of several conceptual rainfall-runoff models. J. Hydrol. 1991, 122, 161–219. [Google Scholar] [CrossRef]
- Chiew, F.; McMahon, T. Application of the daily rainfall-runoff model MODHYDROLOG to 28 Australian catchments. J. Hydrol. 1994, 153, 383–416. [Google Scholar] [CrossRef]
- Zhao, R.J.; Zhang, Y.L.; Fang, L.R.; Liu, X.R.; Zhang, Q.S. The Xinanjiang model. In Proceedings of the Hydrological Forecasting Symposium, Wallingford, UK, 15–18 April 1980; IAHS: Wallingford, UK, 1980; pp. 351–356. [Google Scholar]
- Todini, E. The ARNO rainfall—runoff model. J. Hydrol. 1996, 175, 339–382. [Google Scholar] [CrossRef]
- Linsley, R.K. Flood estimates: How good are they? Water Resour. Res. 1986, 22, 159S–164S. [Google Scholar] [CrossRef]
- Klemeš, V. Dilettantism in hydrology: Transition or destiny? Water Resour. Res. 1986, 22, 177S–188S. [Google Scholar] [CrossRef]
- Sun, S.; Bertrand-Krajewski, J.L. Parsimonious conceptual hydrological model selection with different modeling objectives. In Proceedings of the Novatech 2013—8th International Conference on Planning and Technologies for Sustainable Management of Water in the City, Lyon, France, 24–26 June 2013; HAL Open Science: Lyon, France, 2013. [Google Scholar]
- Karabová, B.; Sikorska, A.E.; Banasik, K.; Kohnová, S. Parameters determination of a conceptual rainfall-runoff model for a small catchment in Carpathians. Ann. Wars. Univ. Life Sci. 2012, 44, 155–162. [Google Scholar] [CrossRef]
- Carbone, M.; Garofalo, G.; Nigro, G.; Piro, P. A Conceptual Model for Predicting Hydraulic Behaviour of a Green Roof. Procedia Eng. 2014, 70, 266–274. [Google Scholar] [CrossRef]
- Loliyana, V.D.; Patel, P.L. Lumped conceptual hydrological model for Purna river basin, India. Sadhana-Acad. Proc. Eng. Sci. 2015, 40, 2411–2428. [Google Scholar] [CrossRef][Green Version]
- Hublart, P.; Ruelland, D.; Garcĺa De Cortázar Atauri, I.; Ibacache, A. Reliability of a conceptual hydrological model in a semi-arid Andean catchment facing water-use changes. IAHS-AISH Proc. Rep. 2015, 371, 203–209. [Google Scholar] [CrossRef]
- Hatmoko, W.; Levina; Diaz, B. Comparison of rainfall-runoff models for climate change projection—Case study of Citarum River Basin, Indonesia. IOP Conf. Ser. Earth Environ. Sci. 2020, 423, 012045. [Google Scholar] [CrossRef]
- Buzacott, A.J.V.; Tran, B.; van Ogtrop, F.F.; Vervoort, R.W. Conceptual Models and Calibration Performance—Investigating Catchment Bias. Water 2019, 11, 2424. [Google Scholar] [CrossRef]
- Cirilo, J.A.; Verçosa, L.F.D.M.; Gomes, M.M.D.A.; Feitoza, M.A.B.; Ferraz, G.D.F.; Silva, B.D.M. Development and application of a rainfall-runoff model for semi-arid regions. RBRH 2020, 25, 1–19. [Google Scholar] [CrossRef]
- Abandah, A. Long Range Forecasting Seasonal Rainfall in Jordan; National Water Authority: Amman, Jordan, 1978.
- Japan International Cooperation Agency Hydrological and Water Use Study of Mujib Watershed. Available online: https://openjicareport.jica.go.jp/pdf/10406973_01.pdf (accessed on 9 May 2022).
- Rawls, W.J.; Brakensiek, C.L.; Saxton, K.E. Estimation of Soil Water Properties. Trans. ASAE 1982, 25, 1316–1320. [Google Scholar] [CrossRef]
- Fleming, G. Deterministic models in hydrology. FAO Irrig. Drain. Pap. 1979, 32, 1–86. [Google Scholar]
- Holtan, H.N. A Concept for Infiltration Estimates in Watershed Engineering. Available online: https://ia600702.us.archive.org/11/items/conceptforinfilt51holt/conceptforinfilt51holt.pdf (accessed on 9 May 2022).
- Adeyi, G.O.; Adigun, A.I.; Onyeocha, N.C.; Okeke, O. Unit Hydrograph: Concepts, Estimation Methods and Applications in Hydrological Sciences. Int. J. Eng. Sci. Comput. 2020, 10, 26211–26217. [Google Scholar]
- Duan, Q.; Sorooshian, S.; Gupta, V. Effective and efficient global optimization for conceptual rainfall-runoff models. Water Resour. Res. 1992, 28, 1015–1031. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Beran, M. Hydrograph prediction-how much skill? Hydrol. Earth Syst. Sci. 1999, 3, 305–307. [Google Scholar] [CrossRef]
- Legates, D.R.; McCabe, G.J. Evaluating the use of “goodness-of-fit” Measures in hydrologic and hydroclimatic model validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]

| Parameter | Lower Bound | Upper Bound | Optimum Value |
|---|---|---|---|
| a | 0.08 | 0.9 | 0.658 |
| n | 0.1 | 1.5 | 0.336 |
| fc (mm/h) | 1.27 | 3.8 | 1.27 |
| Sc | 0.0 | 0.9 | 0.272 |
| Dmax (mm) | 0.0 | 50.0 | 11.924 |
| Kr | 0.1 | 0.99 | 0.91 |
| K (h) | 0.0 | TL | 1.255 |
| X | 0.0 | 0.5 | 0.002 |
| Sai (mm) | 0.0 | 141.6 | 26.8 (average) |
| NA (h) | 1.0 | 9 | 2.8 (average) |
| Storm Event | Observed | Simulated | IVF | RE | ||||
|---|---|---|---|---|---|---|---|---|
| Time to Peak (h) | Peak Flow (m3/s) | Runoff Volume (m3 × 106) | Time to Peak (Hours) | Peak Flow (m3/s) | Runoff Volume (m3 × 106) | |||
| 31 December 1991 | 11 | 28.97 | 3.73 | 11 | 31.3 | 3.33 | 0.893 | 0.080 |
| 7 February 1992 | 13 | 348 | 38.27 | 14 | 337.51 | 37.23 | 0.973 | 0.030 |
| 25 February 1992 | 24 | 120.5 | 19.88 | 24 | 98. 13 | 19.33 | 0.972 | 0.186 |
| 4 January 1994 | 11 | 176 | 11.99 | 10 | 159.7 | 11.36 | 0.947 | 0.093 |
| 24 November 1994 | 3 | 286 | 22.00 | 5 | 222.4 | 20.90 | 0.950 | 0.222 |
| Storm Event | Peak Flow (m3/s) | Rainfall Depth (mm) | Runoff Depth (mm) | Sai (mm) | NA | Runoff Coefficient C |
|---|---|---|---|---|---|---|
| 31 December 1991 | 31.3 | 13 | 1.43 | 7.7 | 2 | 0.11 |
| 7 February 1992 | 337.51 | 14.2 | 6.39 | 0.02 | 6 | 0.45 |
| 25 February 1992 | 98.13 | 33 | 13.2 | 1.4 | 5 | 0.4 |
| 4 January 1994 | 159.7 | 33 | 6.6 | 27.9 | 3 | 0.2 |
| 24 November 1994 | 222.4 | 32.6 | 11.41 | 11.9 | 2 | 0.35 |
| Parameter | Optimum Value | O.F. (m3/s) | Increase of 10% in Parameter Value | O.F. (m3/s) | SEN * |
|---|---|---|---|---|---|
| a | 0.658 | 9053 | 0.724 | 42,381 | 36.8 |
| n | 0.336 | 9053 | 0.369 | 61,417 | 57.8 |
| fc | 1.27 | 9053 | 1.397 | 5.9 | |
| Sc | 0.272 | 9053 | 0.299 | 9053 | 0 |
| Dmax | 11. 924 | 9053 | 13.116 | 26,909 | 20 |
| Kr | 0.91 | 9053 | - | - | - |
| K | 1.255 | 9053 | 1.381 | 12,361 | 3.7 |
| x | 0.002 | 9053 | 0.0022 | 9053 | 0 |
| Sai | 141.29 | 9053 | - | - | - |
| NA | 1.187 | 9053 | 2 | 21,867 | 14 |
| Parameter | Optimum Value | O.F. (m3/s) | Decrease of 10% in Parameter Value | O.F. (m3/s) | SEN * |
|---|---|---|---|---|---|
| a | 0.658 | 9053 | 0.592 | 43,790 | 38.4 |
| n | 0.336 | 9053 | 0.302 | 59,572 | 55.8 |
| fc | 1.27 | 9053 | - | - | - |
| Sc | 0.272 | 9053 | 0.245 | 9053 | 0 |
| Dmax | 11.924 | 9053 | 10.732 | 91,775 | 91 |
| Kr | 0.91 | 9053 | 0.819 | 22,220 | 14.5 |
| K | 1.255 | 9053 | 1.129 | 10,913 | 2.1 |
| x | 0.002 | 9053 | 0.0018 | 9053 | 0 |
| Sai | 141.29 | 9053 | 127.16 | 94,166 | 94 |
| NA | 1.187 | 9053 | - | - | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghanim, A.A.J.; Beddu, S.; Abd Manan, T.S.B.; Al Yami, S.H.; Irfan, M.; Mursal, S.N.F.; Mohd Kamal, N.L.; Mohamad, D.; Machmudah, A.; Yavari, S.; et al. Prediction of Runoff in Watersheds Located within Data-Scarce Regions. Sustainability 2022, 14, 7986. https://doi.org/10.3390/su14137986
Ghanim AAJ, Beddu S, Abd Manan TSB, Al Yami SH, Irfan M, Mursal SNF, Mohd Kamal NL, Mohamad D, Machmudah A, Yavari S, et al. Prediction of Runoff in Watersheds Located within Data-Scarce Regions. Sustainability. 2022; 14(13):7986. https://doi.org/10.3390/su14137986
Chicago/Turabian StyleGhanim, Abdulnoor A. J., Salmia Beddu, Teh Sabariah Binti Abd Manan, Saleh H. Al Yami, Muhammad Irfan, Salim Nasar Faraj Mursal, Nur Liyana Mohd Kamal, Daud Mohamad, Affiani Machmudah, Saba Yavari, and et al. 2022. "Prediction of Runoff in Watersheds Located within Data-Scarce Regions" Sustainability 14, no. 13: 7986. https://doi.org/10.3390/su14137986
APA StyleGhanim, A. A. J., Beddu, S., Abd Manan, T. S. B., Al Yami, S. H., Irfan, M., Mursal, S. N. F., Mohd Kamal, N. L., Mohamad, D., Machmudah, A., Yavari, S., Mohtar, W. H. M. W., Ahmad, A., Wan Rasdi, N., & Khan, T. (2022). Prediction of Runoff in Watersheds Located within Data-Scarce Regions. Sustainability, 14(13), 7986. https://doi.org/10.3390/su14137986






