ILS Validity Analysis for Secondary Grade through Factor Analysis and Internal Consistency Reliability

Abstract

In differentiated learning, the teacher needs to be aware of the learning styles of students in the classroom to accommodate specific learning preferences, e.g., the Felder–Silverman learning style model. The corresponding instrument, i.e., the Felder–Silverman Index of Learning Style (ILS), was designed to assess learning styles, specifically for engineering students. The ILS has been tested at the middle school level to identify the learning styles; however, validity/reliability had not been established in earlier studies with large samples. The focus of this study was to identify the validity and reliability of an ILS instrument for middle school students ($N=450$) by investigating the factor structure through factor analysis. This includes internal consistency reliability and constructing validity report of the ILS. An exploratory and confirmatory factor analysis was undertaken to investigate the factor structure to establish validity. As a result of the study, the reliability of the instrument was established. Five-factors emerged through exploratory factor analysis (EFA), which were subjected to confirmatory factor analysis (CFA). The outcome provided five-factors (i.e., Comparative Fit Index (CFI), Tucker–Lewis Index (TLI), Root Mean Square Error of Approximation (RMSEA), Standardized Root Mean Residual (SRMR), and Goodness of Fit (GFI)), out of which four factors were related to the four dimensions of the Felder–Silverman model, and the fifth factor was related to the association of sensing/intuitive and sequential/global dimensions of the model, which is in agreement with the theoretical construct of ILS. As a result of CFA, ILS entailing 24 items indicates a good fit with five-factor structure. $CFI=0.922;TLI=0.927$; $RMSEA=0.026$; $SRMR=0.585;GFI=0.911;X2=277;df=42;p=0.60$. This study suggests that the ILS for the secondary-grade students needs to be revised with fewer items to improve the reliability, as supported by empirical evidence through the EFA and CFA.

1. Introduction

Differentiated instruction/learning is a process where the instructor adapts several strategies according to the learning needs and preferences of individual students, in a heterogeneous classroom. Hence, with such strategies, the instructors/learners strive to achieve various characteristics with the aim of developing social, moral, and intellectual abilities that allow students to be more integrated in modern communities [1,2]. The student’s individual preferences have been interpreted in several ways, e.g., adapting instruction and monitoring each student’s progress [3] and student’s ability preferences [4], in which case the teaching method is varied while monitoring their progress and making decisions based on historical data. Similarly, there is a reactive response differentiation approach where individual students are recognized based on their background knowledge, language, and interests and are responded to accordingly [5]. In addition, the authors of [6] created a five-dimensional differentiation framework, i.e., teaching arrangements, learning environment, teaching methods, support materials, and assessment. Students’ other capabilities include their verbal abilities, family environment, social skills, and extra co-curricular activities [7].

The Felder–Silverman Learning Style (FSLSM) model is centered around the students’ preferences, i.e., presenting students with their distinctive learning styles. On the other hand, the teachers must deliver materials that address the various learning preferences of the students. There are various dimensions of learning preferences: An active learner can learn best by actively working and trying/applying the material, an intuitive learner can learn via abstract learning material, and some learners can best learn with visual effects, e.g., diagrammatic illustrations. Similarly, there are categories of learners that sequentially learn with linear learning progress; in contrast, other learners can consume learning material in abundance and use a holistic process. According to [8], personalization and differentiation should be used to meet the preferences and goals of individual students while at the same time authorizing them to actively participate in the design of their learning. A comprehensive article showed how personalized learning [9] and differentiated learning [10] could be applied in the classroom. It is evident that students with a strongly specific learning style may face learning complications if the teaching style is incompatible with their preferred learning style [11,12]. The authors of [13] carried out a study with students who attended an online course. Those with adaptive learning styles achieved significantly better results compared to those students whose preferred learning style was not catered for.

The Felder–Silverman Index of Learning Style (ILS) is a 44-item questionnaire [12] developed by Solomon and Felder for identifying learner’s learning styles. It is a renowned and mostly used among researchers and educationists. There are static and automatic approaches to analyzing the resultant questionnaire responses to detect various learning styles [14]. A static approach for learning style detection is carried out by filling out the questionnaires [15,16,17]. It is possible that some of the questionnaires will not be filled in properly, which may lead to inaccurately detecting the learning styles [18,19,20]. The other approaches are based on data-driven methods to build classification models that use the sample data and ILS. Henceforth, various classification techniques have widely been used to detect learning styles, e.g., using neural networks [21,22,23], decision trees [24,25,26], and Bayesian networks [27,28,29,30]. The authors of [31] provided a detailed overview of how to analyze the response data of the ILS questionnaire for identifying a group of learners’ preferences for various dimensions, in addition to verifying the validity and reliability of the used instrument, while these studies support the reliability and validity of ILS, there still exist some open issues related to dependencies between learning styles and a learner’s undeveloped dimension(s) that further needs investigations [32].

We carried out a comprehensive study on the ILS’s validity and reliability using the data collected from three different secondary schools who voluntarily participated. The students were 11–16 years old, from grades 6 to 10 inclusive. This study was carried out with 450 students (among them, 29 did not complete the questionnaire; hence, only 421 surveys were considered in our study). We obtained signed consent from their parents and verbal consent form the participants. We first randomly split the data into two halves and then applied the EFA (on 201 data samples) and CFA (on 200 data samples) to two samples. Note that the authors of [33] suggest that arguably, up to 150 samples are considered acceptable; hence, our sample size was adequate. Next, we examined the suitability of sampled data for factor analysis through the Kaiser–Meyer–Olkin test and the Bartlett test of sphericity [34]; however, we used small eigenvalues for this method (e.g., <1.0). Henceforth, we explored a five-factor solution on the basis of Catell’s scree plot [34] for a range of eigenvalues. In addition, we note that using this method, the cumulative variance may decrease with a range of eigenvalues; hence, we used oblique rotation instead of Varimax rotation [35] and compared their results for reliability. Furthermore, to best fit our model, we used chi-square (X2), Root Mean Square Error of Approximation (RMSEA), Goodness of Fit (GFI) and Standardized Root Mean Residual (SRMR) for absolute fit indices; and Comparative Fit Index (CFI) and Tucker–Lewis Index (TLI) for incremental fit indices.

Our exploratory analysis shows an increased number of factors when we used the Kaiser’s criterion method. Hence, we used the Catell’s scree test that extracted the five-component solution with a total of 31.55% variance contributing to the five factors, respectively, of 9.128%, 7.841%, 6.377%, 4.773% and 3.795% variance. During our analysis, we examined that the five factors analysis presented better results compared to 16 factors solutions where all the four dimensions were successfully loaded, i.e., Active/Reflective (AR), Sequential/Global (SG), Visual/Verbal (VV), and Sensing/Intuitive (SI) (detailed discussions over these Felder–Silverman Learning Style Model dimensions can be found in Section 2.1). Furthermore, for absolute fit indices, we assess the X2, RMSEA, GFI, and SRMR models, whereases for incremental fit indices, we tested the CFI and TLI models. For CFA, our analysis resulted in good fit indices of $CFI=0.759$; $TLI=0.745$; $RMSEA=0.015$; $SPRMR=0.067$; $GFI=0.815$; $p\left(0.05\right)=0.000$; $X2/df=2.185$ for diverse settings of various fitting models. Our investigations suggest that, if ILS is used for identification of learning styles of secondary-grade students, it needs to be revised with reduced items as supported by empirical evidence provided by EFA, where several items have cross loadings, do not load well (i.e., $>0.3$) and through CFA in the present study. Moreover, construct validity through factorial validity also needs to be verified using CFA along with EFA.

Our main contributions in this paper are:

• To carry out a comprehensive study on the ILS validity and reliability using the data collected from different secondary schools.
• A comprehensive evaluation of psychometric analysis of ILS to investigate the learning styles of secondary-grade students.
• To explore the internal consistency reliability and construct validity using exploratory and confirmatory factor analysis of the Felder–Silverman’s ILS for the secondary grade students.
• The use of various fitting models to designate the best fit for the collected data.
• To inspect the average item correlation and exploratory and confirmatory factor analysis for the statistical evidence of validity and reliability of ILS for secondary-grade students.

We organize the paper in the following sections. Section 2 presents the background on Felder–Silverman Learning Style Model and ILS. Section 3 presents literature work. We present our methodology in Section 4. Results are dicussed in Section 5 and finally we conclude in Section 6.

2. Background

For many years, it has been claimed that understanding of learning styles has an effective role in the learning practices of the educators and students. Learning styles advocate Differentiated Instruction (DI) where each student to process information in the way they process information. Several learning style models have been introduced, among which, model proposed by Felder and Silverman is most commonly used by teachers, students and researchers.

2.1. Felder–Silverman Learning Style Model

The Felder–Silverman experiential, phenomenological and sensory model was initially presented in 1988, designed to explore the learning preferences of higher education students, specifically the engineering major. According to this model, each student has specific learning styles over multiple bipolar axes. Educators need to understand these specific learning preferences of the students to accommodate their learning needs [36]. The model categorizes learner’s preferences in bipolar dimensions, which are Active (learning by doing and working with other) vs. Reflective (learning by thinking or reflecting and working alone), Sensing (practical, concerned with procedure and facts) vs. Intuitive (creative, concerned with theory and concepts), sequential (prefer stepwise information) vs. Global (learn holistically, understand the whole theme), Visual (prefer visual representation of information) vs. Verbal (prefer spoken or written information), and Deductive (general to specific presentation) vs. Inductive (specific to general presentation).

The designed model is not entirely original, but derived from other experiential, phenomenological and sensory models. For example, Active/Reflective (AR) dimension was derived from Kolb’s experiential model [37], Sensing/Intuitive (SI) was derived from Jung’s theory [38], and Visual/Verbal (VV) dimension was taken form Dunn and Dunn model [11]. The Sequential/Global (SG) dimension proposed by Felder–Silverman model was original. The psychometric assessment instrument associated with the model is called index of learning style (ILS).

2.2. Index of Learning Styles (ILS)

Index of learning style is the diagnostic tool, comprising 44 items, to explore the Felder–Silverman model along four bipolar dimensions, i.e., AR, VV, SI and SG. It was designed by Richer. M. Felder and Barbara A. Solomon in 1991 [39]. The bipolar dimensions AR, VV, SI and SG are related to the process, input, perception and understanding of information, respectively. Deductive/Inductive (DIn) dimension was not included in the assessment tool because it was claimed that the educators need to design instruction in for both DIn for DI (i.e., Differentiated Instruction). Each characteristics of the ILS is allocated in opposing learning preference.

The ease of access due to free availability of the online version of ILS is one of the main reasons that it is widely utilized to assess leaning styles of students for various disciplines in higher education. Although, the model and the instrument was designed to identify the learning preferences of engineering students, however, it is also used for secondary-grade students [40,41]. The scoring of the instrument is automatic for online version, even the paper pencil test scoring is also very easy and takes less than two minutes. Each of the four bipolar dimensions has 11 questions, thus a total of 44 questions. The answer to a question of one of the two poles of applicable bipolar modality is according to the set pattern. This means that questions are designed in a way that students have to choose one option out of two (either ‘a’ or ‘b’). The pattern for scoring is that if answer is ‘a’, then it will be scored for Pole A and if the answer is ‘b’, then the score will be for Pole B. For example, if bipolar dimension is Active Reflective (AR) and response ‘a’, the score will be for active and if response is ‘b’, the score will be for Reflective. The scores are complementary so they sum of scores is 11. The difference in the cumulative scores of ‘a’ and ‘b’ aids to distinguish the preference in the given modality. Each pole scores can range from 0 to 11. The students can be categorized in neutral, moderate or strong preferences of the dimensions based on the scoring. 1 and 3 reflects a neutral along the bipolar continuum, 5 and 7 reflects a moderate inclination whereas 9 and 11 show a strong inclination.

Rahadian and Budiningsih [40] recommended the Felder–Silverman [36] model to recognize the preferences of secondary-grade students, so that the teaching and medium of instruction can be designed for personalized leaning (2018). However, the instrument was designed to identify learning preferences of students of higher education, specifically engineering students [36]. To identify learning style of middle school students, ILS tool need to be tested for it’s reliably and validity for middle school students. The measurement of validity and reliability is essential before the use of instrument for research study. These measurements are required beforehand for the interpretation of study findings [42]. Although there are several studies, which report the validity and reliability of ILS for higher education [17,31,35,43,44,45,46,47], however, we could not find reliability and validity report on middle school students. Thus, the present study has been conducted purposely to explore the most essential prospective of the instrument for secondary-grade students.

2.3. Assessment Tools

Internal Consistency Reliability: Internal consistency is an essential assessment tool to examine the uniformity of construct, whereas, reliability information illustrates the correlation among the items of the tool and is reported using the Cronbach’s alpha value [48]. It also measures the stability, consistency, and accuracy of the instrument [49]. If the scale has a high correlation between the items, the alpha ($\alpha$) value increases accordingly. Reliability is a necessary component for the instrument to be standardized, but it is not sufficient for the validity of that instrument.

Construct Validity: Validity measures the degree to which the instrument provides consistent results and the amount to which the test predicts other observed variables of interest [50]. According to [50] “construct validity is involved whenever a test is to be interpreted as a measure of some attribute or quality which is not operationally defined” and factor analysis is used to assess whether the test measures hypothesized learning ability. The factor analysis is the set of statistical approaches used to assess the relationships between a group of observed variables that are assessed through a number of items or questions.

Exploratory Factor Analysis: Exploratory Factor Analysis (EFA) is used to recognize the association between the variables to comprehend the underlying constructs [51]. The steps include examining the measure of the association and suggestion of factorability of the variables [52], extracting a set of factors from the correlation matrix, determining the number of factors using the Kaiser Criterion method and the scree plot method, rotation of factors to increase interpretability, and lastly, comprehension of results and identification of nature of factors [53].

Confirmatory Factor Analysis: The EFA specifies the essential quantity of factors, then the confirmatory factor analysis (CFA) confirms how well the analyzed variables characterize a smaller number of construct [49]. To cross-validate the factor structure, CFA is used to analyze the adequacy of the model. The adequacy of the model is calculated initially with Chi-square test statistics and then fit indices [53].

3. Literature Review

According to Felder, students have different characteristics and strengths: some are more inclined reflection and work alone, and others like to work in a group and prefer discussion and brainstorming. Some learners wish to learn through facts; others are more comfortable with the theoretical explanations. Few in the classroom prefer to learn through visual representation of information and others learn tends to learn through verbal or written explanation [36]. M. Felder and Barbara A. Solomon develop psychometric assessment tools called Index of Learning style in 1991 to assess the learning preferences of engineering students based on Felder–Silverman’s model. The model explores the learner styles of the 44-item survey. Index of the learning style is a concise and comprehensive tool, freely available online to assess learning style. Thus, it is widely used to explore learning styles of engineering students [17,35,43,47] and higher education students from other fields of studies [17,43,45,47,54,55]. Every year several educators and students use free of cost web-based version of ILS [43].

When the psychometric tool is used for a research study with a new population, the assessment of validity is fundamental requirement [42]. Felder and Spurlin [31] states that several studies used ILS for assessing psychological, affective, and cognitive behavior in terms of their learning preferences. The authors in [35] examined the relationship between learning styles and performance in hypermedia-assisted learning environment and provided the statistical evidence of ILS reliability through test–retest reliability, internal consistency reliability, and validity through exploratory factor analysis for engineering students. The study recommended that ILS identify separate qualities as predicted theoretically and established the reliability through alpha coefficient, however, the resultant five factors of EFA had cross-loadings among SI and SG domain [35]. The association among the dimensions of Felder–Silverman model is claimed to be expected as it is suggested by Felder and Spurlin [31]. The relationship between SI and SG is consistent with basic theory of ILS [31].

Relatively, ref. [43], identified reliability and validity of ILS and assessed the learning styles regarding the field of studies (i.e., engineering, liberal arts, and education students) and gender. The collective samples from all three fields of studies were subjected to analyze internal consistency reliability and factorial analysis through EFA, ref. [43]. The alpha coefficient provided the evidence of the reliability of ILS and eight-factor solution estimated through EFA combined with reliability assessment was said claimed as evidence of construct validity [43]. However, a few items did not load well and items deletions were suggested to improve reliability with the concern of issues in ILS-scoring [43]. Then, ILS was modified by [44] in 2007, using five option response scale, assessed for reliability and validity. The construct validity was analyzed through direct student feedback about their learning preferences [44]. It was established that alteration in scale does not transform the factor structure but has a positive impact on scale reliability [44] as recommended in [43]. ILS was also used to identify learning the styles of medical students [42]. When they tested the temporal stability, factorial structure, and reliability, it was established that ILS is an appropriate tool to examine the learning styles of medical students. Though the reliability was found moderate to high, the construct validity was established through EFA and few items (i.e., 17, 32, and 40) did not load well on any factor [42]. The translated version of ILS has also been used to assess learner preferences of students [17,45].

Wang and Medori [17] contributed to validating the Mandarin translation of ILS] by presenting the evidence of internal consistency reliability, inter-scale correlation. They used the Felder–Silverman’s model to recognize the learning styles of language students ($N=138$) and ($N=60$) engineering students. The evidence of internal consistency for the mandarin version of ILS satisfies the acceptability criteria; however, to determine to construct validity, learning style trends were associated with gender and field of study [17]. This does not provide the evidence of construct validity using the scientific method suggest by [48]. The authors in [48] state that construct validation is a scientific method and can be carried out by analyzing the reliability and factorial structure. Kaliská [45] provided the evidence of test–retest stability, through Pearson’s correlation coefficient for ILS translated version in Slovakia but did not provide the evidence of construct validity as recommended by [48]. The non-significant correlation was reported for two (AR, SG) out of four dimensions. These findings may be caused because of insignificant sample size (37), poor translation of ILS, and weak motivation of participants [45]. Linear discriminant analyses were used to assess the representative features of identified learning styles through ILS [47]. The authors in [47] state that the identified description of learning style dimensions was found more significant for incorporation in technology-based education. They used a hybrid approach to analyze the dimensions of the model for technological education and online environment in 2007.

Rinehart, Sharkey, and Kahl [54] examined the association of learning styles and responsibilities and professional positions of librarians. Their result showed the statistical significance in terms of the relationship between the learning styles of librarians and their responsibilities [54], but the instrument was not developed to assess the learning styles of librarians but explicitly for engineers [36] and it is vital to assess the validity of tool before interpreting the findings of the study when the study is contextually sensitive [48]. Similarly, another study carried out on higher education students of mathematics, interpret their findings without reporting the validity of the tool for the said sample [55]. They assessed learning styles using ILS, to examine the association of attitude and learning style concerning mathematics. When a tool is used in a new context or population its reliability and validity report is required. The authors in [54] mentioned that respondents (librarians) do not find the ILS appropriate in their context as it has various items designed for understanding the learning preferences of students in a classroom. In these studies, ref. [40,55], ILS has been used to assess the learning preferences of higher education students, but [41] used ILS to estimate difference in learning style of monolingual and bilingual secondary-grade students after providing the reliability evidence through test retest reliability. Although [41] found strong test-rest reliability as shown in the

Table 1. Comparison of the Cronbach’s alpha value for the present study and the prior work for 11 items.

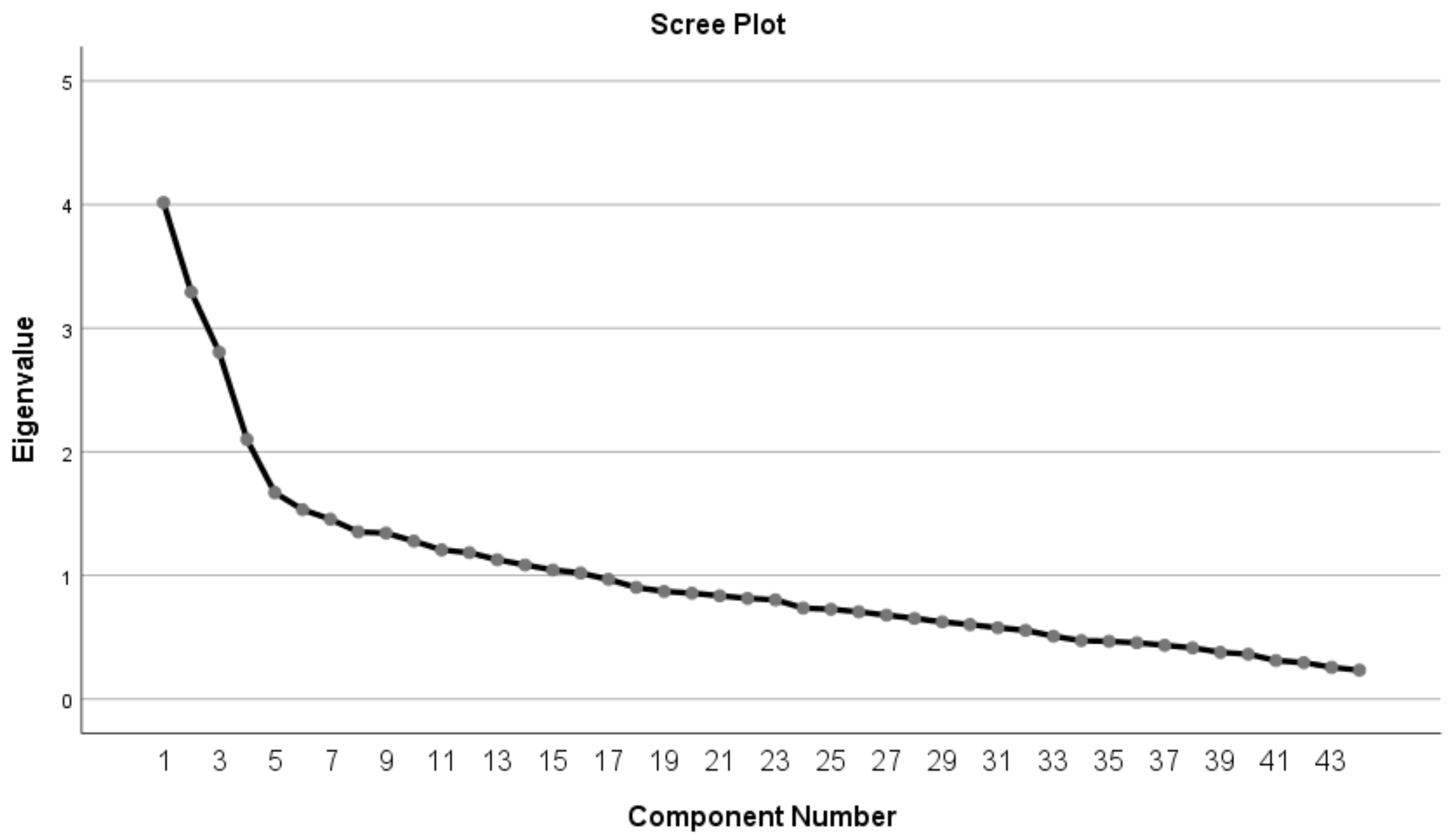
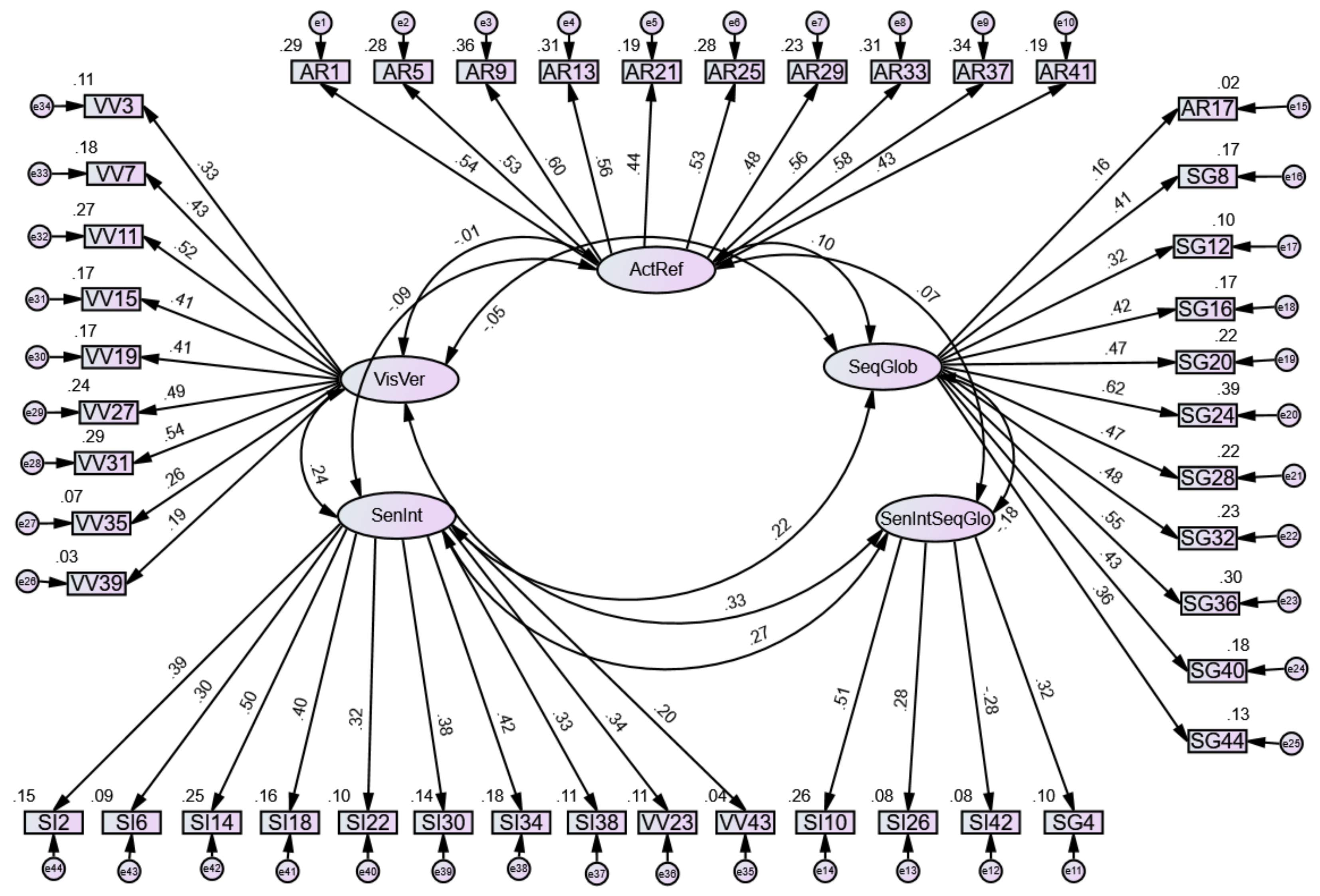
Study	N	AR	SI	VV	SG
[35]	56	0.59	0.70	0.63	0.53
[17]	198	0.51	0.63	0.64	0.51
[56]	572	0.51	0.65	0.56	0.41
[31]	584	0.70	0.76	0.69	0.55
[57]	242	0.56	0.72	0.62	0.54
[21]	500	0.87	0.77	0.77	0.61
[42]	358	0.63	0.76	0.64	0.62
Present	421	0.61	0.52	0.55	0.62

, but [48] review of the use of psychometric measures revealed that construct validity needs to be a fundamental prerequisite for interpreting the result of study for a new population or context and solely reporting alpha coefficient is not sufficient.

Comparably, ref. [40] suggested that ILS have helped when applying instructions with various adaptations to assess the finest strategy by referring to the studies carried out on tertiary level [58,59]. The authors in [40,41] used ILS to examine the relationship of learning styles with instructional strategy and media on secondary-grade students without providing any evidence of reliability alpha coefficient or construct validity. This practiced is frowned upon. According to [48,49], provision of evidence of structural validity of the instrument is prerequisite, for replication study or if the study is carried out on new population. ILS was used to determine learning styles of secondary-grade students in a recent study by [40,41] without providing empirical evidence of reliability and validity on said population. The present study, therefore, inspected the average item correlation and exploratory and confirmatory factor analysis to provide the statistical evidence of reliability and validity of ILS for secondary-grade students.

4. Methodology

The index of learning styles (ILS) is widely used to identify the learning preferences of the students. Although the instrument is designed primarily for the engineering students, in a few recent studies, it has also been used to determine the learning styles of the secondary-grade students [40,41]. The evidence of the validity of existing tools, specifically, construct validity, needs to be examined when existing tool is used in a new context [48]. Since ILS has not been validated to investigate the learning styles of the secondary-grade students, this study examines the psychometric analysis of the ILS as suggested by [48]. This study explores the internal consistency reliability and the construct validity using exploratory and confirmatory factor analysis of the Felder–Silverman’s ILS for the secondary-grade students.

4.1. Participants

The study for the validity and reliability of ILS was carried out on the data collected from three secondary schools ($N=450$). The age of the students was between 11 and 16 years, and the grades of the students were between 6 and 10. Signed consent forms were obtained from the parents before the study, and verbal consent was taken from the students. Thus, participation from all the students in this study was voluntary. It was made clear to the students that if they did not wish to participate, they would not be exposed to any academic deficiency. Some of the students ($N=29$) did not complete the survey; therefore, all such data were excluded from the study. Only the valid dataset ($N=421$) was used for the analysis.

4.2. Research Design

To validate the index of learning style (ILS) instrument for the secondary-grade students, internal consistency reliability and construct validity were examined through a step-wise approach. Average items correlation was identified by Cronbach’s alpha coefficient to find the internal consistency reliability of an instrument. The construct validity of the tool was identified using Structural or factorial validity (exploratory and confirmatory factor analysis). The researcher should provide the evidence of construct validity; even the reliability of the instrument has been established [48]. ILS has been only validated by various researchers using EFA [17,31,35,43,44,45]; however, researchers have argued that factorial validity also needs to be verified using CFA [49]. Exploratory Factor Analysis (EFA) provides the necessary amount of factors to represent the data. It is a measure to examine the dimension of a group of items [49]. Confirmatory factor analysis confirms how well the estimated variables represent the small number of constructs and approves the structural model of the tool [49].

The instrument was administered in the mid of the session of the academic year 2018. The paper–pencil form of instruments was used for the study. This made it easy for the students and teachers (who helped in conducting the survey) as they were able to obtain the data in their classes and did not require going to the computer lab. Initially, the scale scoring was carried out manually on the form, and later the data was digitized to be used in Statistical Package for Social Sciences (SPSS) version 20. For construct validity and internal consistency reliability, 421 valid ILS surveys were utilized. The sample was split randomly in half to analyze factorial structure to minimize the chance of overanalyzing the data. The EFA and CFA were carried out on separated sub-samples. When sample was randomly split, it reduces the sample size for EFA ($N=201$) and CFA ($N=220$), but ref. [60] suggests small sample size for factor analysis. According to [33], the sample size up to 150 is considered acceptable; hence the sample size was adequate for the present study.

The suitability of data was first, examined for factor analysis through Kaiser–Meyer–Olkin and Bartlett’s test of Sphericity [34]. The data analysis for EFA was conducted on SPSS 25.0 software. Kaiser’s criterion method with Varimax rotational was used first to retain a number of factors. Kaiser’s criterion method with Eigen values less than 1.0 sometimes extracts too many factors [34]. Thus, five factors solution was investigated based on Catell’s scree plot test, which often extracts very few factors. The scree plot test implicates plotting each of the eigenvalues of the factor and examining the plot to look for a point where the shape of the curve alters the direction and becomes horizontal [34]. Both Kaiser’s criterion method and scree plot were used to extract factors and the results were assessed for consistency. When factors are extracted using scree plot tests, the cumulative variance may decrease. Then Oblique rotation instead of Varimax rotation was used since different factors were expected to correlate as suggested by [35] and oblique rotation helps provide a clear pattern than Varimax rotation. The solution attained through both methods was compared for consistency.

CFA was conducted on the second sub-sample ($N=220$) to cross-validate the factor structure identified by EFA using AMOS version 26.0. This technique helps to confirm the structural model of the tool. In CFA, a model that consists of a number of items and the number of factors as retained from EFA was assessed. KMO and Bartlett’s Test of Sphericity was examined to test the suitability of data and then the goodness-of-fit-indices were examined.

For absolute fit indices that establish how well a priori model fits sample data initially, a model chi-square statistics investigation is required to calculate that the model fits exactly in the population (i.e., $p>0.05$). However, Chi-Square statistic is sensitive to the sample size (i.e., it rejects the large sample size and lacks power if a small sample size is used) [61] and assessing CFA for the instrument with several items (i.e., $N=44$), Chi-square statistics must not be seen as standard and only goodness of fit index [53,62]. For, absolute fit indices, model chi-square (X2), RMSEA Root Mean Square Error of Approximation), GFI (Goodness of Fit), and SRMR (Standardized Root Mean Residual) were assessed, to determine the indication of the amount at which the proposed theory fits the data [61]. For incremental fit indices, CFI (Comparative Fit Index) and TLI (Tucker–Lewis Index) were examined. The study strives for a value of CFI (Comparative Fit Index) GFI (Goodness of Fit) and TLI (Tucker–Lewis Index) around 0.90 and RMSEA (Root Mean Square Error of Approximation) less than 0.05, and SRMR (Standardized Root Mean Residual) value less than 0.08 [33,61]. RMSEA determines how well the proposed model works; it tests whether unfamiliar but optimally selected factor estimates would fit the population covariance matrix. SRMR provides the square root of the difference between residuals of the sample covariance matrix and hypothesized covariance model [61]. CFI compares the dataset covariance matrix with the null model and it is not sensitive to sample size [62]. GFI estimates the proportion of variance that is accounted for by calculated population covariance [61].

5. Findings

Internal Consistency Reliability

The study analyzed the internal consistency reliability of ILS on secondary-grade students with 421 valid instruments. The analysis was not conducted on the missing data hence, cases ($N=29$) with missing responses of participants were eliminated from the data analysis.

Table 2. Cronbach’s alpha values for index of learning style of the secondary-grade students for internal consistency reliability.

Learning Style	Valid Cases	Items	Mean	Variance	Cronbach Alpha ($\mathit{\alpha }$)
AR	421	11	7.34	6.45	0.61
SI	421	11	5.50	4.92	0.52
VV	421	11	6.95	4.84	0.55
SG	421	11	6.90	5.70	0.62

provides the Cronbrach value of each bipolar dimension of Felder’s learning style model for secondary-grade students. It was found that Cronbach’s alpha value was between 0.518 and 0.618. Table 1 provides the comparison of Cronbach’s alpha value of the present study with other studies, which shows that the reliability report is quite similar. However, the rest of the studies were carried out on higher education students and the present study finds the reliability of ILS for secondary-grade students.

The internal consistency reliability of the index of learning style was identified through Cronbach’s alpha then construct validity must be explicitly reported as suggested by [48]. To establish the construct validity, Structural or factorial validity (exploratory and confirmatory factor analysis) was carried out. The dataset was randomly split to minimize the chance of the over-analyzing of the data and EFA was analyzed on the first subset of data. The exploratory factor analysis was carried out to extract the factors using principal component analysis (PCA). ILS is a psychometric test developed to identify the learning preferences of higher education students specifically engineering students. Its construct validity has been established for only higher-grade students by exploratory factor analysis (EFA) in various studies. The present study analyzed the EFA of ILS for secondary-grade students for the first time because the tool has been used in secondary-grade by [40,41]. The data analysis for EFA, Kaiser–Meyer–Olkin (KMO), and Bartlett’s Test of sphericity, was performed on SPSS 25.0.

The splitting of data reduced the sample size for EFA that is ($N=201$). According to Pallant, a sample size of up to $N=150$ cases can be sufficient if the solution has high loading markers variable [34], however, Kyriazos [60] recommends a small sample size for factor analysis. Kaiser–Meyer–Olkin and Bartlett’s Test of Sphericity was performed on the first half of the random split dataset to assess the suitability of data for EFA [34]. The KMO measures the sample adequacy, its index ranges from 0 to 1 with 0.6 suggested as good for factor analysis [63]. The estimated Kaiser–Meyer–Olkin (KMO) value was 0.630 and Bartlett’s Test of Sphericity was significant ($p=0.000$), where $p<0.05$ is considered significant [53]. Hence, the given dataset was suitable for EFA.

Two techniques (i.e., Kaiser’s criterion and Catell’s scree test) were used to retain the number of factors and then were examined for consistency. First, Kaiser’s criterion method was used to extract factors, that help in deciding the number of factors that can be retained using the eigenvalue of a factor [34]. The factors were extracted by identifying items that loaded greater than 0.3 as suggested by Tabachnick and Fidell [53], that in order to inspect the factorability, a correlation coefficient over 0.3 should be considered. Loading less than $\pm 0.3$ is considered minimal value as a rule of thumb [34]. This sixteen-factor solution was estimated with a total variance of 62.515% and the distribution of loading above 0.3 is shown in

Table 3. The amount of factor loading (>0.3) in rotated component matrix of the 16-factor solution. The rotation method used is oblivion with Kaiser Normalization.

Learning Styles	Factors
	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
AR	10					1			1	1
SG		10		1	1		1		1	1			1	1	1	1
VV			10	4	2	2	1	1		1	1		1	2
SI			3	5	3	3	2	1	2			1			1

. However, in a study carried out by [35], a total variance was 54.1% when 14 factors were extracted using the Kaiser criterion method [63]. In the present study, a 16-factor solution, ten items—1, 5, 9, 13, 21, 25, 29, 33, 37 and 41—have high loading, i.e., greater than 0.4 in factor 1 and; one item, 17, does not load well (i.e., less than 0.3) on any factor. However, cross-loadings were observed on factors 6, 9, and 10 for items 5, 25, and 29, respectively. All of these items were related to the active-reflective (AR) dimension. Ten Items (i.e., 8, 12, 16, 20, 24, 28, 32, 36, 40 and 44) related to sequential-global (SG) dimension loaded on factor 2 but item 32 also cross-loaded on factors 14 and 15. One item, 4, loaded on factor 5 with cross-loading on factors 9 and 13. More cross-loading was observed in SG on factors 7, 10, and 16 for items 12, 20, 8, respectively.

For the visual-verbal (VV) dimension, ten items (i.e., 3, 8, 11, 15, 19, 23, 27, 31, 35, 39 and 43) loaded on factor 3. One item, 43, loaded on factor 7. Several cross-loadings were observed (i.e., item 3 also loaded on factors 4 and 11, item 8 on factors 6, item 11 on factors 5, item 15 on factors 14, Item 19 on factors 4 and 14, item 23 on factors 4, 8, 10, item 27 on factors 4, item 35 on factors 6 and 13, item 39 on factor 5, item 43 on factor 7. Five items (i.e., 2, 18, 30, 34, and 42) in the sensing-intuitive (SI) dimension loaded on factor 4, though cross-loadings for item 2 are on factors 7 and item 42 on factor 5 and 9. Items 14, 22, and 38 loaded on factor 3 with cross loadings of item 14 on factor 8, 22 on factor 12, item 38 on factors 6, 9, and 15. Item 6 loaded on 6, item 10 loaded on factors 5 and 6, and item 26 loaded on factors 5 and 7. The resulting table implicates that three of the four scales (i.e., active-reflective, sequential-global and visual-verbal) were relatively orthogonal with AR largely loading on factor 1, SG on factor 2, and VV on factor 3. However, SI loaded on several factors. However, there were a lot of cross-loadings observed in the 16-factor solution, as shown in Table 3.

Additionally, the Kaiser’s criterion method sometimes extracts too many factors; thus, it was vital to look at the scree plot to retain an appropriate number of factors as suggested in [34,35]. Therefore, the 5 factors were extracted using Catell’s Scree test. All factors above the elbow were retained because these factors deliver the most to the validation of variance in the data set. Then, five factors were examined, and the associated Scree plot is shown in Figure 1. These five-component solution explained a total of 31.55% variance with components 1, 2, 3, 4 and 5 contributing 9.128%, 7.841%, 6.377%, 4.773% and 3.795%, respectively. However, in [35], the total variance was 28.9% when five factors were reduced form a 14-factor solution. Next, the factors were rotated to have a pattern of loading with better and easier interpretation. Oblique rotation was used instead of Varimax rotation to avoid the overlap as suggested by [35]. Moreover, Oblimin rotation provides information about the degree of correlation between the factors [34]. The five-factor solution is provided in

Table 4. The rotated component matrix of the 5-factor solution. The Rotation method used is Oblimin with Kaiser Normalization, Rotation converged in 11 iterations.

	Components					Components
	1	2	3	4	5		1	2	3	4	5
AR1	0.636	0.137	−0.009	0.076	0.054	SG8	0.117	0.503	0.109	−0.119	0.129
AR5	0.595	−0.019	0.115	−0.016	0.163	SG12	−0.014	0.407	−0.167	0.027	0.186
AR9	0.684	0.104	−0.117	−0.127	−0.079	SG16	0.101	0.560	0.064	−0.018	−0.124
AR13	0.633	0.111	0.096	−0.026	0.072	SG20	0.155	0.562	−0.046	0.049	0.006
AR21	0.479	−0.066	−0.061	0.061	−0.298	SG24	0.022	0.726	0.039	0.029	0.007
AR25	0.551	0.151	−0.084	−0.069	0.109	SG28	−0.084	0.512	−0.193	0.223	0.115
AR29	0.534	−0.004	−0.068	−0.076	−0.099	SG32	−0.080	0.557	−0.001	0.029	−0.112
AR33	0.610	−0.080	−0.022	−0.057	0.069	SG36	0.100	0.600	−0.063	0.182	−0.170
AR37	0.666	−0.003	0.169	−0.038	−0.195	SG40	−0.112	0.513	0.024	−0.018	−0.155
AR41	0.474	−0.004	0.142	0.039	−0.108	SG44	0.148	0.411	−0.036	0.128	−0.279
AR17	0.09	0.218	−0.079	0.197	0.155	SG4	0.104	−0.129	0.170	0.052	0.357
VV3	−0.055	0.061	0.407	−0.057	0.274	SI2	−0.151	−0.043	−0.002	0.442	0.094
VV7	0.069	−0.110	0.480	0.240	0.077	SI6	0.039	0.179	0.157	0.310	−0.213
VV11	−0.142	−0.133	0.560	0.058	−0.200	SI14	−0.150	0.054	0.218	0.450	0.178
VV15	−0.177	−0.047	0.477	0.142	0.040	SI18	0.145	−0.030	0.025	0.480	−0.173
VV19	0.085	0.120	0.483	−0.014	0.084	SI22	−0.071	0.208	0.171	0.337	0.003
VV27	0.052	0.017	0.600	−0.088	0.130	SI30	−0.180	0.046	−0.024	0.462	0.269
VV31	0.082	−0.130	0.629	0.079	−0.157	SI34	−0.070	0.098	−0.144	0.550	−0.084
VV35	0.053	0.070	0.319	0.125	0.126	SI38	−0.064	−0.038	0.141	0.364	0.120
VV39	0.240	−0.023	0.321	0.262	−0.257	SI10	0.054	−0.115	0.145	0.141	0.559
VV23	0.113	0.062	0.126	0.504	0.128	SI26	−0.122	−0.031	0.021	0.297	0.425
VV43	0.153	0.073	0.044	0.367	−0.248	SI42	−0.112	0.072	−0.299	0.245	−0.345

.

The solution greater than 0.4 is considered as high loading, because the correlation coefficient $\pm 0.40$ is considered important and $\pm 0.50$ is considered significant [34].The clear pattern can be observed with high loadings ($>\pm 0.40$) through Table 4 for each dimension. The loading ($>0.3$) of five-factor solution of ILS for Secondary grade students is identified in ‘bold’ in Table 4 and the distribution of loading ($>0.3$) is also provided in

Table 5. The distribution of loading ($>0.3$) of the 5-factor solution. The rotation method used is Oblimin with Catell’s scree test. Rotation converged in 11 iterations.

Learning Styles	Factors
	1	2	3	4	5
AR	10
SG		10			1
VV			9	2
SI				8	3

to have easier comparison with 16 factor solution provided in Table 3. Item 17 does not load well on any factor and highlighted by underlining in Table 4 and

Table 6. Factors in the five factor solution.

Factors	Items	Label	Factors Explained
1	1, 5, 9, 13, 21, 25, 29, 33, 37, 41, 17	AR	Action first or reflection first
2	17, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44	SG	Linear VS sequential or random VS holistic thinking
3	3, 8, 11, 15, 19, 27, 31, 35, 39	VV	Information format preferred as input or memory
4	23, 43, 2, 6, 14, 18, 22, 30, 34, 37	SI	Information format preferred and preference of concrete or abstract information
5	4, 10, 26, 42	SI-SG	Conceptual VS factual and detail VS theme

.

In Table 5, well-defined pattern can be seen in 5 factor solution as compared to 16 factor solution. All four dimensions load predominantly (i.e., AR on factor 1, SG on factor 2 VV on factor 3, and SI on factor 4). However, three items of SI and one item of SG loaded on factor 5 and VV (i.e., two items) somewhat overlap with SI. Subsequently, items were reviewed concerning factor loadings to determine the nature of factors, and are summarized in Table 6.

The item: 17 did not load well is given below:

When I start a homework problem, I am more likely to: (a) Start working on solution immediately; (b) Try to fully understand the problem first.

Item 17 of the AR scale requires students to choose one of the two options in the given context. The students were asked to generalize their approach to doing their homework however the approach to doing homework is subjective with respect to discipline. This item may need revision if ILS needs to be administered to identify the leaning preferences of secondary-grade students. A slight revision of the item with minor word changes would compensate for the weakness, which is also supported by [35]. For construct validity, factor analysis using EFA joined with the evaluation of reliability is provided, and according to [35], this provides the evidence of construct validity. The finding shows strong evidence for AG and SG with ten items loaded on a single factor in both 16-factor solution and 5-factor solution with appropriate Cronbach’s alpha value. Evidence of construct value is also good for VV and SI as most of the items load on single factor. However, few items of VV were shared with SI and one item of SG is shared with SI, which implies that dimensions are not orthogonal and these dimensions have somewhat association with each other and these findings are similar to [31,35,43,44,56,57]. However, they provided evidence of construct validity for tertiary grade students. The association between these scales is consistent with the underlying theory of ILS and it does not impact the validity of tool [31].

Next, The five factors and corresponding 44 items were subjected to CFA. The second part of the randomly split sample ($N=220$) was analyzed through CFA to cross-validate the factorial validity identified by EFA. The suitability of the data was checked before analysis through Kaiser–Mayer–Oklin (KMO) (i.e., 0.628) and significance was assessed through Bartlett’s test of sphericity. The KMO was 0.628 and Bartlett’s Test of sphericity reached significance ($X2=0.628$, $df=946$, $p=0.000$). This indicates that existing commonalities are appropriate in the manifest variables in order to conduct factor analysis [34].

The path diagram (Figure 2) displays the standardized regression weight for the common factors and each of the indicators. For absolute fit indices that establish how well a priori model fits sample data initially, a model chi-square statistics examination is required to assess the model fit exactly in the population (i.e., $p>0.05$). However, Chi-Square statistic is sensitive to the sample size (i.e., it rejects the large sample size and lacks power if a small sample size is used) [61] and with the complex model as in the case of ILS Model 1 (Figure 2) and assessing CFA for the instrument with several items (i.e., $N=44$), Chi-square statistics must not be seen as valid and only goodness-of-fit index [53]. Hence, for, absolute fit indices, model chi-square (X2), RMSEA, GFI, and SRMR were assessed, to determine the indication of the amount at which the proposed theory fits the data. For well-fitting model, RMSEA value less than 0.05, GFI greater than 0.90, and SRMR below 0.08 are needed. For incremental fit indices, CFI and TLI were examined and strived for values less than 0.90 [61].

The result of CFA points to moderate but still insufficiently high fit indices ($CFI=0.759$; $TLI=0.745$; $RMSEA=0.015$; $SPRMR=0.067$; $GFI=0.815$; $p\left(0.05\right)=0.000$; $X2/df=2.185$). The fit indices are contradicting each other. Although the RMSEA, SPRMR, and X2/df provide a good fit for model 1 but, CFI, TLI, and X2 significantly suggest that model- 1 does not fit well. In order to achieve a good fit, changes were made to model 1 and re-tested. Items (i.e., SG44, AR25, SG28, SG8, AR37, VV31, AR9, SI2, VV23, VV43, SI42) were removed as the modification indices indicated that the error covariance must be included among these test scores and test scores of the other scale [33]. Standardized residual covariance matrix was also examined for re-specification of the model. The items (i.e., AR17, SI26, VV35, VV39, SG16, AR33, SI28) with a value above one was deleted. The nested model is provided in Figure 3.

This leads to new five factor structure with 28 items and with well model fit ($CFI=0.922$; $TLI=0.927$; $RMSEA=0.026$; $SRMR=0.585$; GFI= $0.911$; $X2=277$; $df=242$; $p=0.60$; $X2/df=2.62$). The several item reduced impact the scoring of ILS but it does not impact the underlying theory of Felder’s Learning style model.

6. Conclusions

This study examined the internal consistency reliability and construct validity of the ILS for the secondary-school students. The internal consistency of the ILS was found appropriate since the Cronbach’s alpha value of all the items was greater than or equal to 0.5, which is the acceptable threshold to ensure the reliability of the instrument; this aligned with the previous studies for assessing learning styles for higher education students. A 16-factor solution was achieved through the Varimax rotational method but then Scree test was used to extract five factors using the oblique rotational method, except for item (AR17) which loaded poorly ($<0.03$). The five-factor model and corresponding 44 items achieved as a result of EFA were analyzed through CFA with randomly split data. The CFA of ILS has not been identified to validate the instrument by any of the research studies. We found that ILS model-1and nested ILS model-2 (Figure 3) also has similar constructs. Since the ILS model was not a sufficient fit ($CFI=0.759$; $TLI=0.74$5; $RMSEA=0.015$; $SPRMR=0.067$; $GFI=0.815$; $p\left(0.05\right)=0.000$; $X2/df=2.185$), the re-specification of model was carried out by removal of items to improve the fit. By various combination various items, a good-fit model was achieved with indices ($CFI=0.922$; $TLI=0.927$; $RMSEA=0.026$; $SRMR=0.585$; $GFI=0.911$; $X2=277$; $df=242$; $p=0.60$; $X2/df=2.62$). The present study suggests that, if ILS is further used for the identification of learning styles of secondary-grade students, it needs to be revised with reduced items as supported by empirical evidence provided by EFA, where several items have cross loadings, do not load well (i.e., $>0.3$) and through CFA. We are planning to further extend this study over a larger sample size; in addition, the revised instrument with a reduced number of items needs to be tested for reliability and construct validity CFA along with EFA. Furthermore, future studies on external validity and the test–retest reliability of ILS for secondary grade are desirable, since the validity and reliability assessed in this study were limited to construct validity and internal consistency reliability.