An Efficient Approach to Investigate the Tradeoff between Double Handling and Needed Capacity in Automated Distribution Centers
Abstract
:1. Introduction
2. Literature Review
2.1. Material Flow and Warehouse Design
2.2. Two Warehouses Design Problem
2.3. Double Handling and Study Contribution
3. Methodology
3.1. Study Scenarios and Assumptions
- Daily demand is less than a layer size (assumed to be C items in this study);
- Daily demand is equal to or greater than a layer size, but less than or equal to a pallet size (assumed to be B items in this study);
- Daily demand is greater than pallet size (assumed to be A items in this study).
- Scenario 1 (daily demand): Only the daily demand is depalletized and moved to the mini-load system.
- Scenario 2 (full layers): Lot size is an integer number of pallet layer. For example, if the current demand is 7 cases, and each layer is 5 cases, then 10 cases (two layers) must be depalletized and moved to the mini-load system.
- Scenario 3 (full pallets): Whole pallets are depalletized. For example, if the demand is 60 cases, and the pallet size is 50 cases, then two pallets must be depalletized and sent to the mini-load system.
- The capacity of the mini-load system;
- The capacity of the unit-load AS/RS (the first warehouse);
- The level of double handling in the first warehouse, which defines the warehouse throughput (the daily demand also affects the throughput);
- Try not to use the first scenario for C items.
- If scenario 1 is to be used for C items, it is better to wait until the order comes, and then cases are shipped directly without going to the second warehouse.
- If a new order for a C item comes after the first shipment in the same day, then there should be some safety stock in the second warehouse, and the extra demand is satisfied from this safety stock.
- The depalletized cases must cover at least the daily demand. In other words, the daily demand is not very large to the level it needs to be divided into several lot sizes every day.
- Before commencing the retrieval order from the first warehouse, the total daily demand for an item by all customers can be known with reasonable accuracy. Pooling the demand by all the customers can reduce the fluctuations of the demand for that item.
- Pallets come in only one size (measured in number of cases).
- Average service time for stacker cranes in each warehouse was assumed to be known.
- The variability in the total number of daily active items is not very high. Active items today are the items needed today.
- The new batch of cases of a certain item will come to the mini-load system just in time, when the old cases are consumed.
- Cross docking, in which full pallets are transshipped directly to the customer from the first warehouse, is not considered in this study.
- In reality, when an order comes for an item that is currently in the depalletizer, cases of that item can be shipped without being stored in the second warehouse. Therefore, there is no need for the capacity of the cases of that item on the second warehouse. This fact was ignored in this paper because of the dynamic nature of demand and in order to provide more buffer of capacity in the second warehouse. In other words, this capacity may be required for safety stock in order to hedge against demand uncertainty. The best safety stock level can be investigated in future research.
- The maximum inventory level (T) in the system is given. This maximum value contains the inventory in both warehouses. It should cover the demand for a certain number of days. Different classes of items can have different coverage periods. T-value can be the order quantity (Q) plus the safety stock (SS). The Q-value depends on factors such as lead time, minimum size of shipment, and setup costs. The safety stock level is also given. The total capacity of two warehouses is not exactly as the total inventory because the capacity should cover the maximum value in the beginning and the end of the day. That might also lead to different total capacity for different scenarios.
3.2. Scenario 1
3.2.1. WH1 Throughput When Daily Demand Is Less Than One Pallet
3.2.2. Throughput When Daily Demand Is Greater Than One Pallet
3.2.3. Capacity of the Mini-Load System
3.3. Scenario 2
3.3.1. Throughput When Daily Demand Is Greater Than One Pallet
3.3.2. Throughput When Daily Demand Is Less Than One Pallet
3.3.3. Capacity of the Mini-Load System
3.4. Scenario 3
3.4.1. Throughput of WH1
3.4.2. Capacity of the Mini-Load System
3.5. Costs Model
4. Results and Analysis
4.1. Scenario 1
4.2. Scenario 2: Simulation for WH1 Throughput of A Items
4.3. Scenario 2: Simulation for WH2 Capacity of C Items
4.4. Scenario 3: Simulation for WH2 Capacity for B and C Items
4.5. Results of the Three Scenarios and the Optimal Solution
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Karmaker, C.L.; Ahmed, T.; Ahmed, S.; Ali, S.M.; Moktadir, M.A.; Kabir, G. Improving supply chain sustainability in the context of COVID-19 pandemic in an emerging economy: Exploring drivers using an integrated model. Sustain. Prod. Consum. 2021, 26, 411–427. [Google Scholar] [CrossRef] [PubMed]
- Cai, J.; Li, X.; Liang, Y.; Ouyang, S. Collaborative Optimization of Storage Location Assignment and Path Planning in Robotic Mobile Fulfillment Systems. Sustainability 2021, 13, 5644. [Google Scholar] [CrossRef]
- Rajković, M.; Zrnić, N.; Kosanić, N.; Borovinšek, M.; Lerher, T. A Multi-Objective Optimization model for minimizing cost, travel time and CO2 emission in an AS/RS. FME Trans. 2017, 45, 620–629. [Google Scholar] [CrossRef] [Green Version]
- Hao, J.; Shi, H.; Shi, V.; Yang, C. Adoption of automatic warehousing systems in logistics firms: A technology–organization–environment framework. Sustainability 2020, 12, 5185. [Google Scholar] [CrossRef]
- Nikaido, M.; Kobayashi, T.; Ito, T.; Higashi, T.; Tamura, H.; Ota, J. Conceptual warehouse design algorithm using a network flow model. Adv. Robot. 2009, 23, 705–724. [Google Scholar] [CrossRef]
- Karasawa, Y.; Nakayama, H.; Dohi, S. Trade-off analysis for optimal design of automated warehouses. Int. J. Syst. Sci. 1980, 11, 567–576. [Google Scholar] [CrossRef]
- Nikaido, M.; Kobayashi, T.; Ito, T.; Higashi, T.; Tamura, H.; Ota, J. Analytic flow design method for an automated distribution center with multiple shipping areas. Adv. Robot. 2012, 26, 1229–1252. [Google Scholar] [CrossRef]
- Atieh, A.M.; Kaylani, H.; Al-Abdallat, Y.; Qaderi, A.; Ghoul, L.; Jaradat, L.; Hdairis, I. Performance improvement of inventory management system processes by an automated warehouse management system. Procedia CIRP 2016, 41, 568–572. [Google Scholar] [CrossRef] [Green Version]
- Özer, Ö.; Wei, W. Inventory control with limited capacity and advance demand information. Oper. Res. 2004, 52, 988–1000. [Google Scholar] [CrossRef]
- Fichtinger, J.; Ries, J.M.; Grosse, E.H.; Baker, P. Assessing the environmental impact of integrated inventory and warehouse management. Int. J. Prod. Econ. 2015, 170, 717–729. [Google Scholar] [CrossRef]
- Alnahhal, M.; Noche, B. Efficient material flow in mixed model assembly lines. SpringerPlus 2013, 2, 1–12. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Salah, B.; Alnahhal, M.; Ahmad, R. Automated Stacker Cranes: A Two-Step Storage Reallocation Process for Enhanced Service Efficiency. Processes 2022, 10, 2. [Google Scholar] [CrossRef]
- Alnahhal, M.; Tabash, M.I.; Ahrens, D. Optimal selection of third-party logistics providers using integer programming: A case study of a furniture company storage and distribution. Ann. Oper. Res. 2021, 302, 1–22. [Google Scholar] [CrossRef]
- Khan, M.G.; Huda, N.U.; Zaman, U.K.U. Smart Warehouse Management System: Architecture, Real-Time Implementation and Prototype Design. Machines 2022, 10, 150. [Google Scholar] [CrossRef]
- Ashayeri, J.; Gelders, L.; Wassenhove, L.V. A microcomputer-based optimization model for the design of automated warehouses. Int. J. Prod. Res. 1985, 23, 825–839. [Google Scholar] [CrossRef]
- Rosenblatt, M.J.; Roll, Y.; Vered Zyser, D. A combined optimization and simulation approach for designing automated storage/retrieval systems. IIE Trans. 1993, 25, 40–50. [Google Scholar] [CrossRef]
- Van Oudheusden, D.L.; Boey, P. Design of an automated warehouse for air cargo: The case of The Thai air cargo terminal. J. Bus. Logist. 1994, 15, 261. [Google Scholar]
- Lee, Y.H.; Lee, M.H.; Hur, S. Optimal design of rack structure with modular cell in AS/RS. Int. J. Prod. Econ. 2005, 98, 172–178. [Google Scholar] [CrossRef]
- Lerher, T.; Potrc, I.; Sraml, M. Designing automated warehouses by minimising investment cost using genetic algorithms. In Proceedings of the 11th IMHRC, Milwaukee, WI, USA, 9 January 2010; p. 18. [Google Scholar]
- Bortolini, M.; Accorsi, R.; Gamberi, M.; Manzini, R.; Regattieri, A. Optimal design of AS/RS storage systems with three-class-based assignment strategy under single and dual command operations. Int. J. Adv. Manuf. Technol. 2015, 79, 1747–1759. [Google Scholar] [CrossRef]
- Lewczuk, K.; Kłodawski, M.; Gepner, P. Energy consumption in a distributional warehouse: A practical case study for different warehouse technologies. Energies 2021, 14, 2709. [Google Scholar] [CrossRef]
- Li, D.; Wang, L.; Geng, S.; Jiang, B. Path Planning of AS/RS Based on Cost Matrix and Improved Greedy Algorithm. Symmetry 2021, 13, 1483. [Google Scholar] [CrossRef]
- Zaerpour, N.; Volbeda, R.; Gharehgozli, A. Automated or manual storage systems: Do throughput and storage capacity matter? INFOR Inf. Syst. Oper. Res. 2019, 57, 99–120. [Google Scholar] [CrossRef] [Green Version]
- Bozer, Y.A.; White, J.A. Design and performance models for end-of-aisle order picking systems. Manag. Sci. 1990, 36, 852–866. [Google Scholar] [CrossRef]
- Bozer, Y.A.; White, J.A. A generalized design and performance analysis model for end-of-aisle or-der-picking systems. IIE Trans. 1996, 28, 271–280. [Google Scholar] [CrossRef]
- Cormier, G.; Gunn, E.A. Simple models and insights for warehouse sizing. J. Oper. Res. Soc. 1996, 47, 690–696. [Google Scholar] [CrossRef]
- Rosenblatt, M.J.; Roll, Y. Warehouse capacity in a stochastic environment. Int. J. Prod. Res. 1988, 26, 1847–1851. [Google Scholar] [CrossRef]
- Shi, Y.; Guo, X.; Yu, Y. Dynamic warehouse size planning with demand forecast and contract flexibility. Int. J. Prod. Res. 2018, 56, 1313–1325. [Google Scholar] [CrossRef]
- Dessouky, M.M.; Wilson, J.R. Minimizing production costs for a robotic assembly system. Eng. Cost. Prod. Econ. 1991, 21, 81–92. [Google Scholar] [CrossRef]
- Yasunaga, T.; Ota, J.; Kobayashi, T.; Ito, T.; Higashi, T.; Tamura, H. Development of design algorithm for logistics networks. In Proceedings of the 2004 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS) (IEEE Cat. No. 04CH37566), Sendai, Japan, 28 September 2004–2 October 2004; IEEE: Piscataway, NJ, USA, 2004; Volume 2, pp. 1251–1256. [Google Scholar]
- Ozaki, M.; Hara, T.; Higashi, T.; Ota, J. Design of warehouse including temporary storage using queuing network theory. In Proceedings of the 2013 IEEE International Conference on Systems, Man, and Cybernetics, Washington, DC, USA, 13–16 October 2013; pp. 1247–1252. [Google Scholar]
- Chen, G.; Feng, H.; Luo, K.; Tang, Y. Retrieval-oriented storage relocation optimization of an automated storage and retrieval system. Transp. Res. Part E Logist. Transp. Rev. 2021, 155, 102508. [Google Scholar]
- Alnahhal, M.; Ahrens, D.; Salah, B. Modeling Freight Consolidation in a Make-to-Order Supply Chain: A Simulation Approach. Processes 2021, 9, 1554. [Google Scholar] [CrossRef]
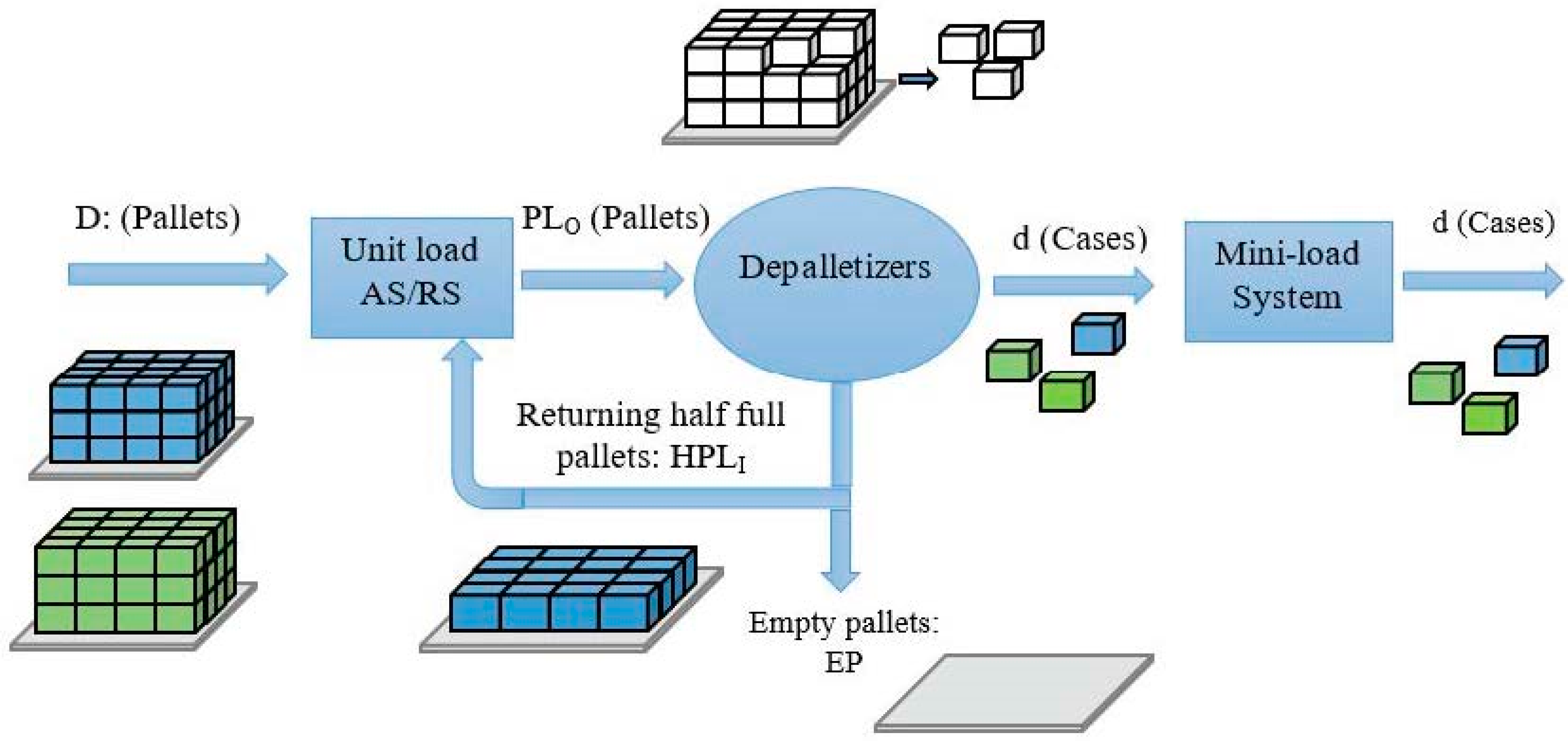



| Symbol | Meaning | Value | Unit | Formula (If Any) |
|---|---|---|---|---|
| A. Basic known parameters | ||||
| PLc | Pallet size | 50 | cases | |
| Id | Different number of active items in one day | 1000 | item types | |
| d | Average daily demand of all items | 10,000 | cases/day | |
| IA | Percent of number of different A items | 10 | % | |
| IB | Percent of number of different B items | 20 | % | |
| IC | Percent of number of different C items | 70 | % | |
| VA | Percent of demand volume for A items | 70 | % | |
| VB | Percent of demand volume for B items | 20 | % | |
| VC | Percent of demand volume for C items | 10 | % | |
| NL | Number of layers per pallet | 10 | layers | |
| Ac | Percent of daily active C items | 33.33 | % | |
| B. Input parameters for the cost model | ||||
| Mt1 | WH 1 maximum throughput per aisle | 50 | PL/hour | |
| Mt2 | WH 2 maximum throughput per aisle | 200 | case/hour | |
| Sc1 | WH 1 stacker crane cost | 350,000 | dollar | |
| Sc2 | WH 2 stacker crane cost | 250,000 | dollar | |
| Lc1 | WH 1 storage location cost | 150 | dollar | |
| Lc2 | WH 2 storage location cost | 30 | dollar | |
| Mc | Maintenance cost % | 5 | % | |
| Wp | Working period | 20 | years | |
| df | Discount factor | 0.2 | ||
| C. Calculated parameters | ||||
| D | Daily demand in pallets | 200 | pallets | d/PLc |
| DA | Daily demand in pallets of class A items | 140 | pallets | VA D |
| DB | Daily demand in pallets of class B items | 40 | pallets | VB D |
| DC | Daily demand in pallets of class C items | 20 | pallets | VC D |
| NA | Number of different A items | 100 | item types | Id IA |
| NB | Number of different B items | 200 | item types | Id IB |
| NC | Number of different C items in one day | 700 | item types | Id IC |
| dA | Daily demand (in cases) of class A | 7000 | cases | d VA |
| dB | Daily demand (in cases) of class B | 2000 | cases | d VB |
| dC | Daily demand (in cases) of class C | 1000 | cases | d VC |
| PPIA | Daily demand per item of class A | 1.4 | pallets per item | NA/DA |
| PPIB | Daily demand per item of class B | 0.2 | pallets per item | NB/DB |
| PPIC | Daily demand per item of class C | 0.03 | pallets per item | NC/DC |
| Ls | Layer size | 5 | cases per layer | PLc/NL |
| TNC | Total number of different C items | 2100 | cases | NC/Ac |
| D. Model decision variables | ||||
| Y1 and Y2 | Number of stacker cranes in WH1 and WH2 | Equations (15) and (16) | ||
| Cap1 | WH1 capacity | storage locations (Pallets) | Equation (22) | |
| Cap2 | WH2 capacity | storage locations (cases) | Equation (28) | |
| Cap2xi | Needed capacity of WH2 for x items based on scenario i | cases | Equations (26) and (27) | |
| Th1 | WH1 throughput | PL/day | Equation (24) | |
| Th1i | Total WH1 throughput if scenario i is used | PL/day | Equations (8), (13) and (14) | |
| Th1xi | WH1 throughput for x items if scenario i is used | PL/day | Part of Th1i or Simulation | |
| SCC | Storage capacity cost | dollar | Equation (18) | |
| TMC | Total maintenance costs | dollar | Equation (17) | |
| TC | Total costs | dollar | Equation (19) | |
| Day | Random “d” | Accumulated “d” | Round Up | Lot Size | Total Handling (PL) | Throughput | Empty Pallets | |||
|---|---|---|---|---|---|---|---|---|---|---|
| Full Pallet (1) | First Half Pallet (2) | Second Half Pallet (3) | Reverse Pallet Size (4) | |||||||
| 1 | 9 | 9 | 10 | 10 | 0.2 | 0 | 0.2 | 0 | 0.8 | 0 |
| 2 | 10 | 19 | 20 | 10 | 0.4 | 0 | 0.2 | 0 | 0.6 | 0 |
| 3 | 14 | 33 | 35 | 15 | 0.7 | 0 | 0.3 | 0 | 0.3 | 0 |
| 4 | 7 | 40 | 40 | 5 | 0.8 | 0 | 0.1 | 0 | 0.2 | 0 |
| 5 | 5 | 45 | 45 | 5 | 0.9 | 0 | 0.1 | 0 | 0.1 | 0 |
| 6 | 11 | 56 | 60 | 15 | 1.2 | 0 | 0.1 | 0.2 | 0.8 | 1 |
| 7 | 7 | 63 | 65 | 5 | 1.3 | 0 | 0.1 | 0 | 0.7 | 0 |
| 8 | 15 | 78 | 80 | 15 | 1.6 | 0 | 0.3 | 0 | 0.4 | 0 |
| 9 | 13 | 91 | 95 | 15 | 1.9 | 0 | 0.3 | 0 | 0.1 | 0 |
| 10 | 11 | 102 | 105 | 10 | 2.1 | 0 | 0.1 | 0.1 | 0.9 | 1 |
| Scenario 1 | Scenario 2 | Scenario 3 | ||||
|---|---|---|---|---|---|---|
| Item | WH 1 Throughput | WH 2 Capacity | WH 1 Throughput | WH 2 Capacity | WH 1 Throughput | WH 2 Capacity |
| A | Formula | Formula | Simulation | Formula | Formula | Formula |
| B | Formula | Formula | Formula | Formula | Formula | Simulation |
| C | Formula | Formula | Formula | Simulation | Formula | Simulation |
| Item Class | Scenario 1 | Scenario 2 | Scenario 3 |
|---|---|---|---|
| A (Q = 5 PL, SS =2 PL) | 6.4 | 6.4 | 5.54 |
| B (Q = 2 PL, SS =1 PL) | 2.5 | 2.5 | 1.6 |
| C (Q = 1 PL, SS =1 PL) | 2 | 1.94 | 1 |
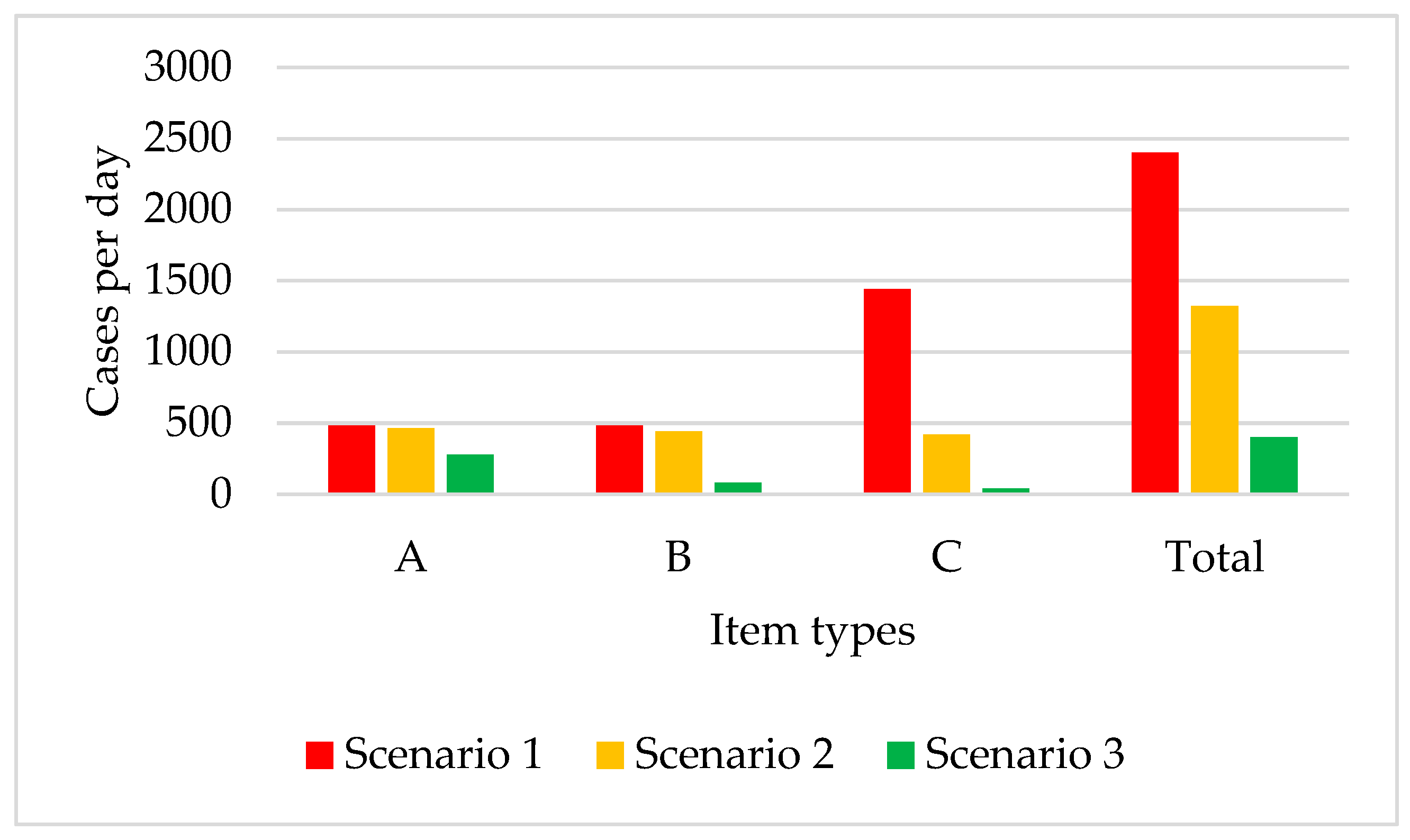
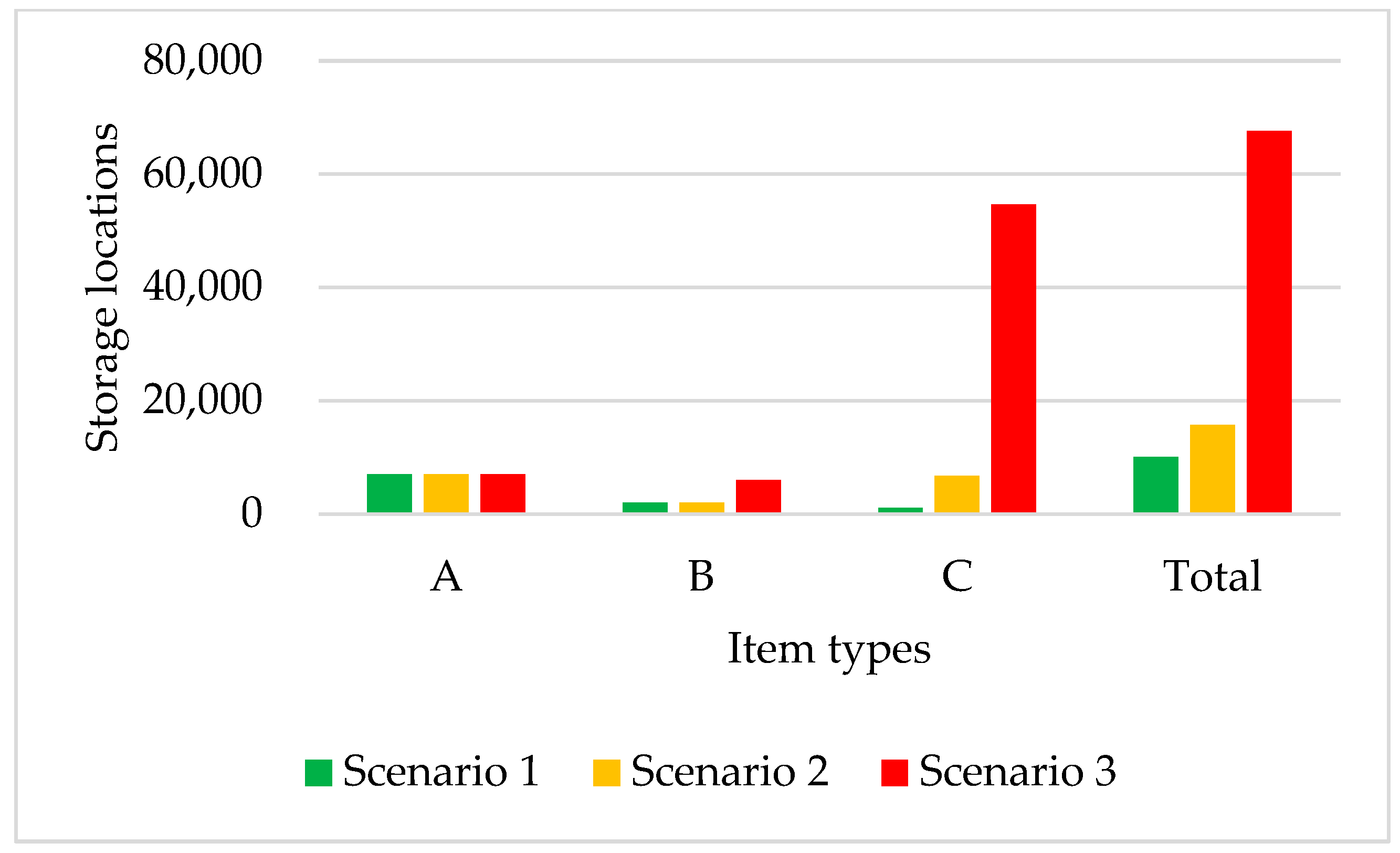
| Item | PLO | HPLI | Th1 (PLO + HPLI + D) | Cap2 |
|---|---|---|---|---|
| A. Scenario 1 | ||||
| A | 240 | 100 | 480 | 7000 |
| B | 240 | 200 | 480 | 2000 |
| C | 720 | 700 | 1440 | 1000 |
| Total | 2447 | 10,000 | ||
| B. Scenario 2 | ||||
| A | 323 * | 463 | 7000 | |
| B | 220 | 180 | 440 | 2000 |
| C | 210 | 190 | 420 | 6720 * |
| Total | 1323 | 15,720 | ||
| C. Scenario 3 | ||||
| A | 140 | 0 | 280 | 7000 |
| B | 40 | 0 | 80 | 6000 * |
| C | 20 | 0 | 40 | 54,600 * |
| Total | 400 | 67,600 | ||
| Day | Number of Cases at the Beginning of Day (1) | Batch Size (2) | Needed Capacity (Max (1, 2)) | Number of Cases at the End of Day |
|---|---|---|---|---|
| 1 | 50 | 0 | 50 | 30 |
| 2 | 30 | 0 | 30 | 10 |
| 3 | 10 | 50 | 50 | 40 |
| 4 | 40 | 0 | 40 | 20 |
| 5 | 20 | 0 | 20 | 0 |
| Average | 38 | 20 | ||
| Average Daily Demand Per Item | Average Needed Capacity in WH2 |
|---|---|
| 5 | 27.5 |
| 10 | 30 |
| 15 | 36 |
| 20 | 38 |
| 25 | 37.5 |
| 30 | 44 |
| 35 | 47 |
| 40 | 48 |
| 45 | 49.5 |
| 50 | 50 |
| # | Scenarios for | WH1 Throughput (Pallets/hour) | WH1 Number of Stacker Cranes | WH 1 Capacity (Pallets) | WH 2 Capacity (Cases) | Total Cost (USD MM) | % Stacker Cranes Costs | ||
|---|---|---|---|---|---|---|---|---|---|
| A Items | B Items | C Items | |||||||
| 1 | 3 | 3 | 2 | 97.5 | 2 | 4938 | 19,720 | 6.24 | 78.7 |
| 2 | 3 | 1 | 2 | 147.5 | 3 | 5118 | 15,720 | 6.59 | 81.2 |
| 3 | 3 | 2 | 2 | 142.5 | 3 | 5118 | 15,720 | 6.59 | 81.2 |
| 4 | 2 | 3 | 2 | 120.4 | 3 | 5024 | 19,720 | 6.69 | 79.9 |
| 5 | 1 | 3 | 2 | 122.5 | 3 | 5024 | 19,720 | 6.69 | 79.9 |
| 6 | 3 | 3 | 3 | 50.0 | 1 | 2974 | 67,600 | 6.95 | 64.4 |
| 7 | 2 | 2 | 2 | 165.4 | 4 | 5204 | 15,720 | 7.03 | 82.2 |
| 8 | 2 | 1 | 2 | 170.4 | 4 | 5204 | 15,720 | 7.03 | 82.2 |
| 9 | 1 | 2 | 2 | 167.5 | 4 | 5204 | 15,720 | 7.03 | 82.2 |
| 10 | 1 | 1 | 2 | 172.5 | 4 | 5204 | 15,720 | 7.03 | 82.2 |
| 11 | 3 | 2 | 3 | 95.0 | 2 | 3154 | 63,600 | 7.29 | 67.4 |
| 12 | 3 | 1 | 3 | 100.0 | 2 | 3154 | 63,600 | 7.29 | 67.4 |
| 13 | 3 | 3 | 1 | 225.0 | 5 | 5074 | 14,000 | 7.40 | 84.0 |
| 14 | 2 | 3 | 3 | 72.9 | 2 | 3060 | 67,600 | 7.40 | 66.4 |
| 15 | 1 | 3 | 3 | 75.0 | 2 | 3060 | 67,600 | 7.40 | 66.4 |
| 16 | 2 | 3 | 1 | 247.9 | 5 | 5160 | 14,000 | 7.41 | 83.9 |
| 17 | 1 | 3 | 1 | 250.0 | 5 | 5160 | 14,000 | 7.41 | 83.9 |
| 18 | 3 | 2 | 1 | 270.0 | 6 | 5254 | 10,000 | 7.74 | 85.9 |
| 19 | 3 | 1 | 1 | 275.0 | 6 | 5254 | 10,000 | 7.74 | 85.9 |
| 20 | 2 | 2 | 3 | 117.9 | 3 | 3240 | 63,600 | 7.74 | 69.1 |
| 21 | 2 | 1 | 3 | 122.9 | 3 | 3240 | 63,600 | 7.74 | 69.1 |
| 22 | 1 | 2 | 3 | 120.0 | 3 | 3240 | 63,600 | 7.74 | 69.1 |
| 23 | 1 | 1 | 3 | 125.0 | 3 | 3240 | 63,600 | 7.74 | 69.1 |
| 24 | 2 | 2 | 1 | 292.9 | 6 | 5340 | 10,000 | 7.75 | 85.8 |
| 25 | 2 | 1 | 1 | 297.9 | 6 | 5340 | 10,000 | 7.75 | 85.8 |
| 26 | 1 | 2 | 1 | 295.0 | 6 | 5340 | 10,000 | 7.75 | 85.8 |
| 27 | 1 | 1 | 1 | 300.0 | 6 | 5340 | 10,000 | 7.75 | 85.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alnahhal, M.; Salah, B.; Ruzayqat, M. An Efficient Approach to Investigate the Tradeoff between Double Handling and Needed Capacity in Automated Distribution Centers. Sustainability 2022, 14, 7678. https://doi.org/10.3390/su14137678
Alnahhal M, Salah B, Ruzayqat M. An Efficient Approach to Investigate the Tradeoff between Double Handling and Needed Capacity in Automated Distribution Centers. Sustainability. 2022; 14(13):7678. https://doi.org/10.3390/su14137678
Chicago/Turabian StyleAlnahhal, Mohammed, Bashir Salah, and Mohammed Ruzayqat. 2022. "An Efficient Approach to Investigate the Tradeoff between Double Handling and Needed Capacity in Automated Distribution Centers" Sustainability 14, no. 13: 7678. https://doi.org/10.3390/su14137678
APA StyleAlnahhal, M., Salah, B., & Ruzayqat, M. (2022). An Efficient Approach to Investigate the Tradeoff between Double Handling and Needed Capacity in Automated Distribution Centers. Sustainability, 14(13), 7678. https://doi.org/10.3390/su14137678






