A Comparative Study on Different Online State of Charge Estimation Algorithms for Lithium-Ion Batteries
Abstract
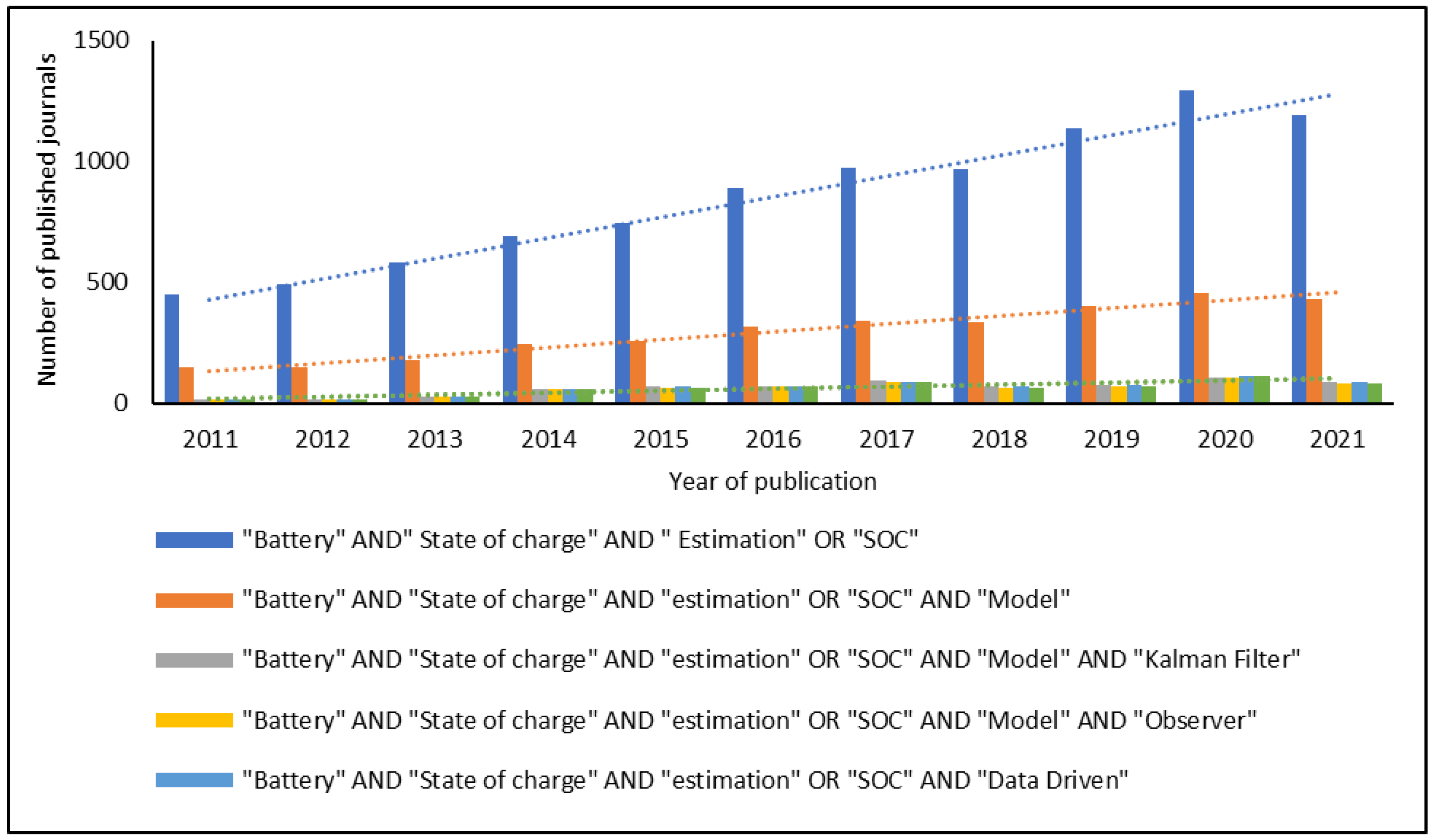
:1. Introduction
Key Contributions
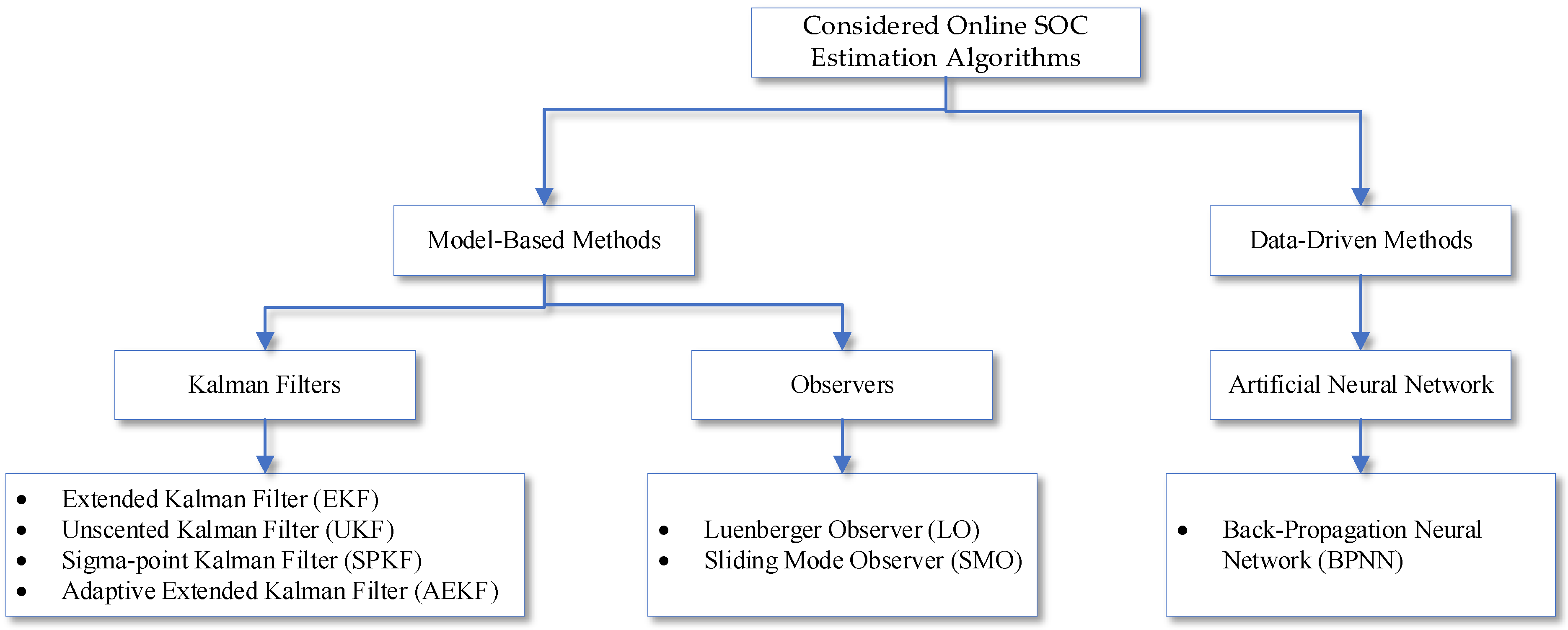
- Seven different widely used SOC estimation algorithms, EKF, AEKF, SPKF, UKF, LO, SMO, and BPNN, were considered to develop a comparative study.
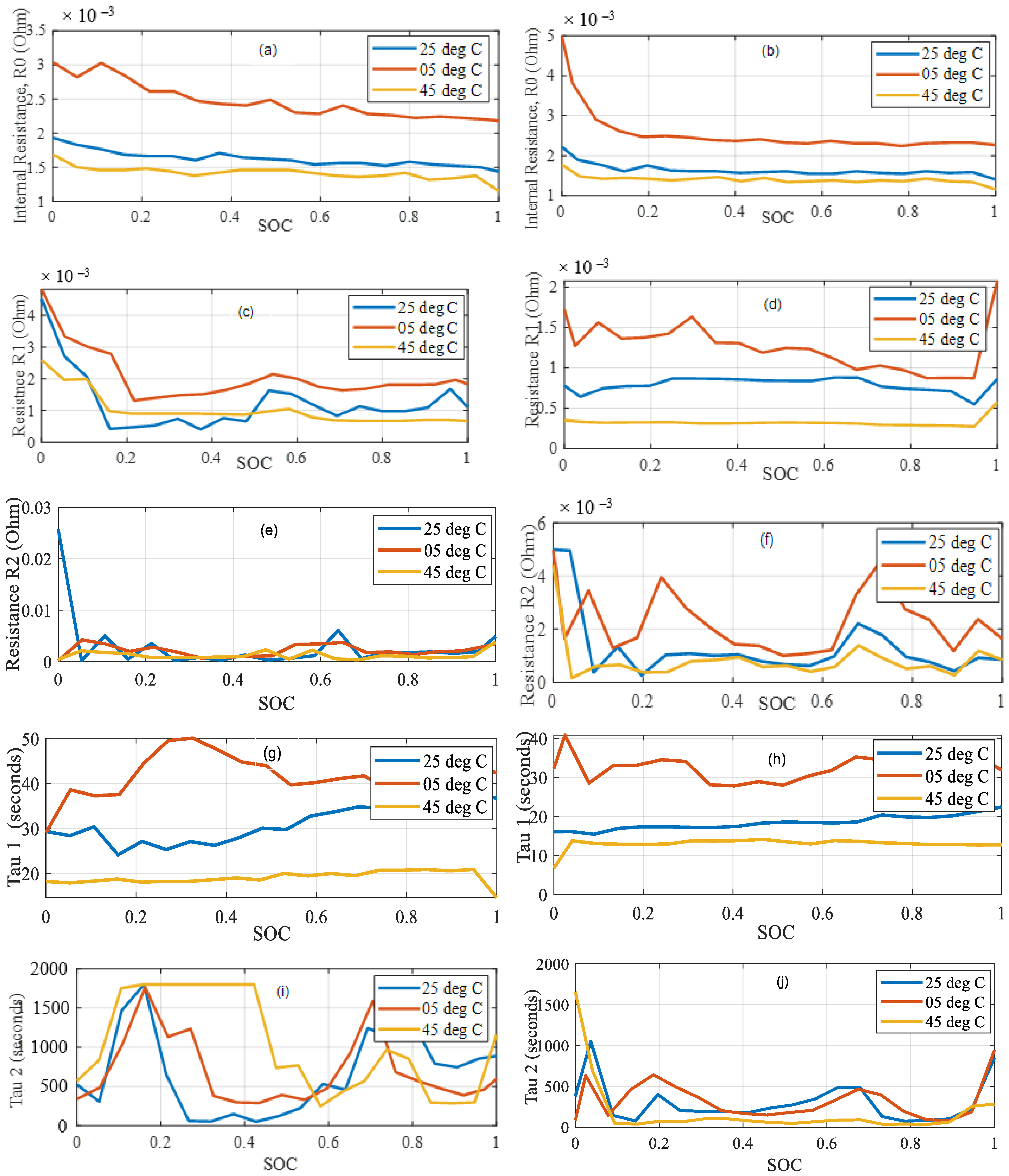
- The effect of temperature on two RC battery model parameters was analyzed, and the obtained parameters were utilized for model-based SOC estimation.
- An experimental dataset collected under a dynamic load profile test on commercial 25 Ah lithium-nickel-manganese-cobalt-oxide (LiNiMnCoO2) prismatic cells was considered for SOC estimation using different algorithms. Further, the estimated SOC accuracy and computational burden were compared.
- Based on the obtained results, future recommendations are explained to assist engineers and researchers in their work.
2. Description of Considered Online SOC Estimation Algorithms
2.1. Model-Based Method
2.1.1. Extended Kalman Filter (EKF)
2.1.2. Adaptive Extended Kalman Filter (AEKF)
2.1.3. Sigma-Point Kalman Filter (SPKF)
2.1.4. Unscented KF (UKF)
2.1.5. Luenberger Observer (LO)
2.1.6. Sliding Mode Observer (SMO)
2.2. Data-Driven Method
Backpropagation Neural Network (BPNN)
3. Experimental Setup and Test Conduct
3.1. Experimental Setup
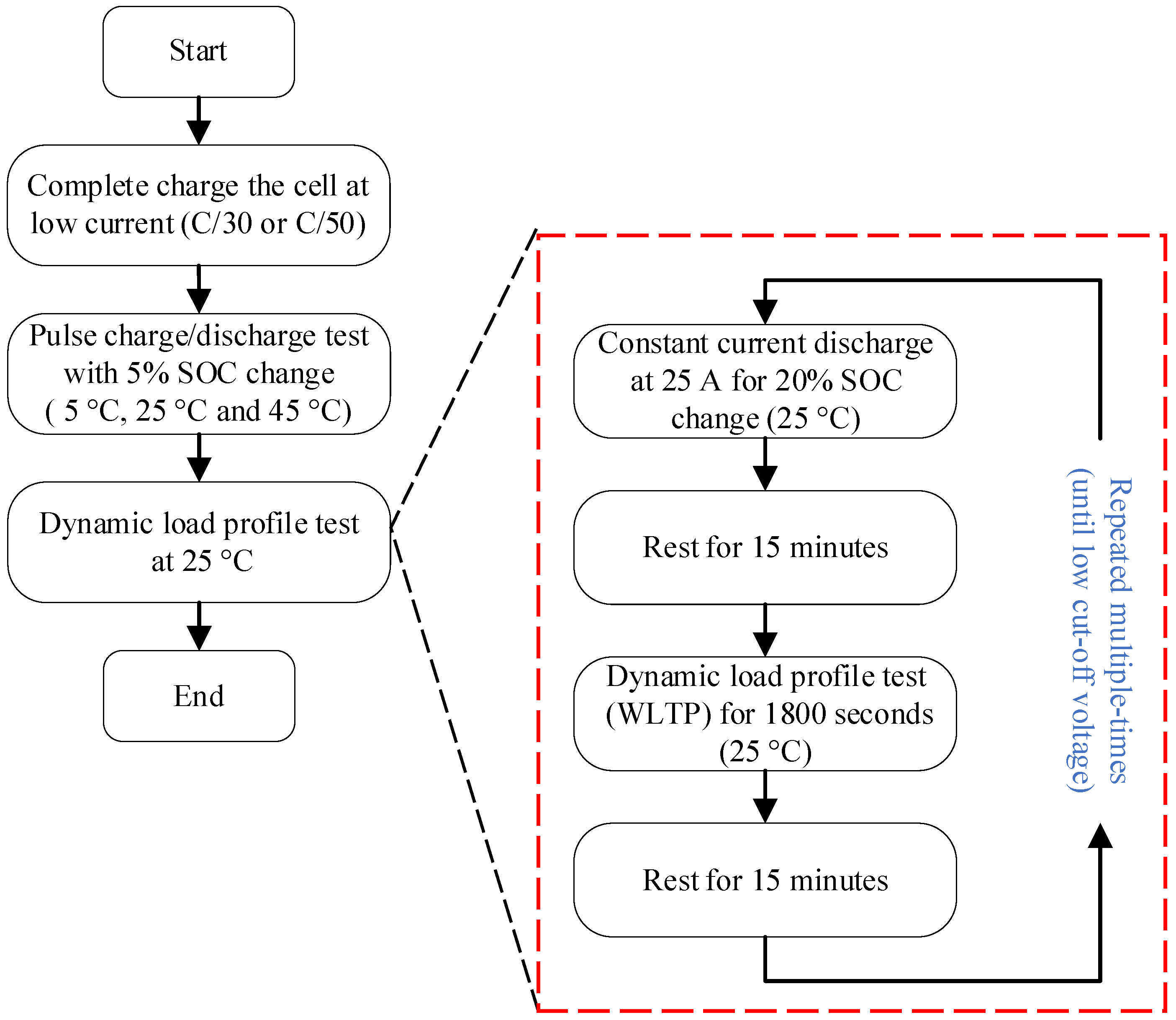
3.2. Stepwise Test Description
3.3. Pulse Charge/Discharge Test
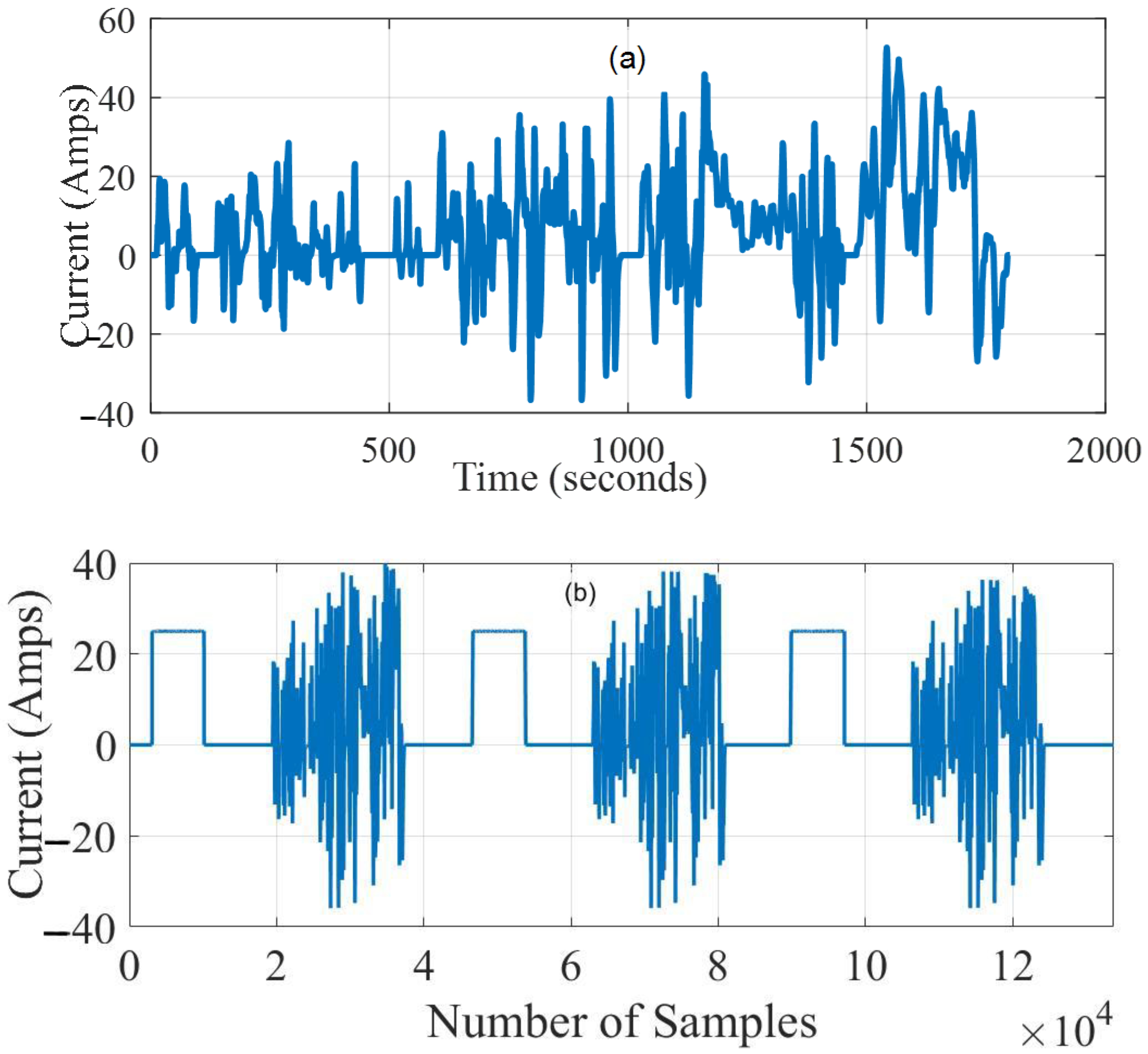
3.4. Dynamic Load Profile Test
- The cell voltage was measured before the start of the test. The voltage across the terminals was checked to be 4.10 V as specified by the manufacturer for the cell to be completely charged. If the voltage was 4.10 V, the test was started at 25 °C. If not, the cell was charged with a very low C-rate (C/30 or C/50) to bring the voltage to 4.10 V and then allowed to rest for at least 2 h to reach equilibrium.
- A discharging pulse of 25 A (1 C-rate) for 12 min was applied to discharge the cell by 20%, as shown in Figure 6b.
- A resting phase of 15 min was applied during which there was no current flow and the cell could relax.
- Figure 6b shows that a programmed WLTP class 3 drive cycle was applied to the cell under test. The drive cycle lasted for 1800 s, and during this test, the full cycle was applied.
- A resting phase of 15 min was applied again to allow the cell to relax. The above four steps were repeated multiple times until the voltage reached 3.0 V, which was the lower limit specified by the cell manufacturer.
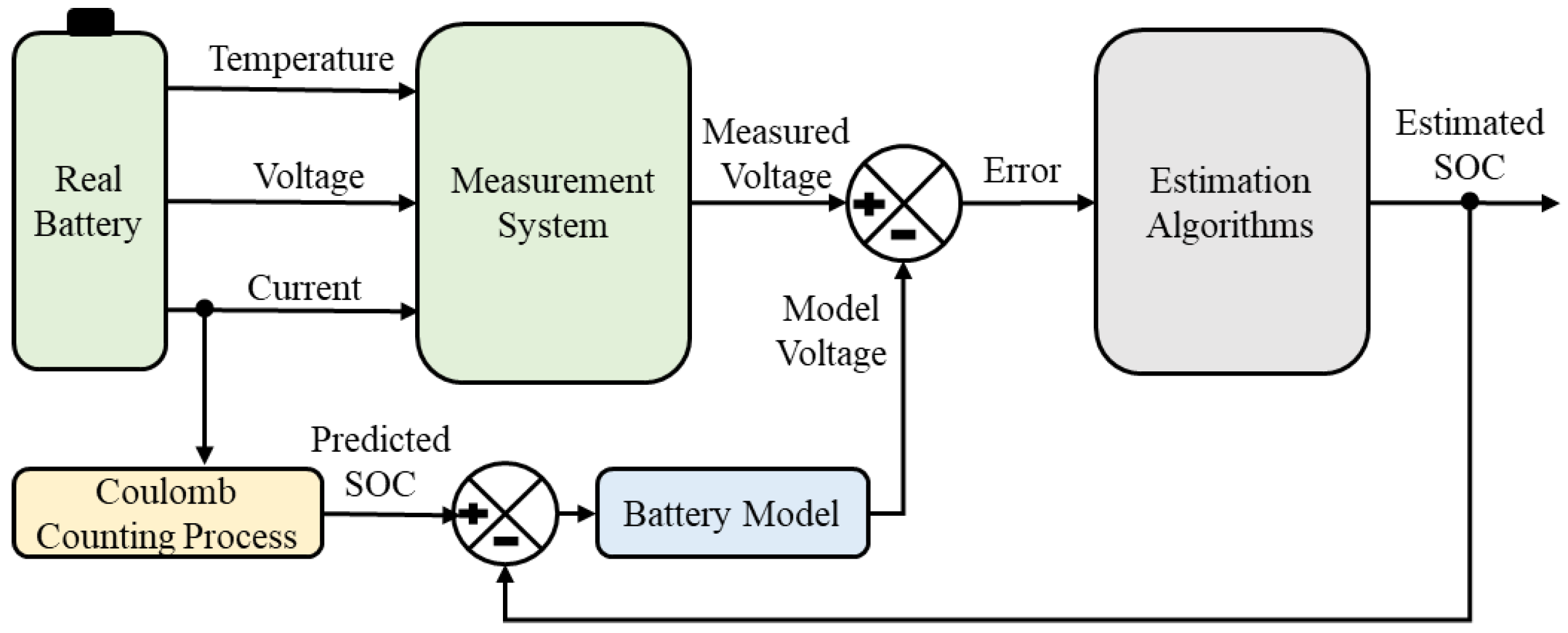
4. Evaluation Method and Battery Modeling
4.1. Evaluation Matrices
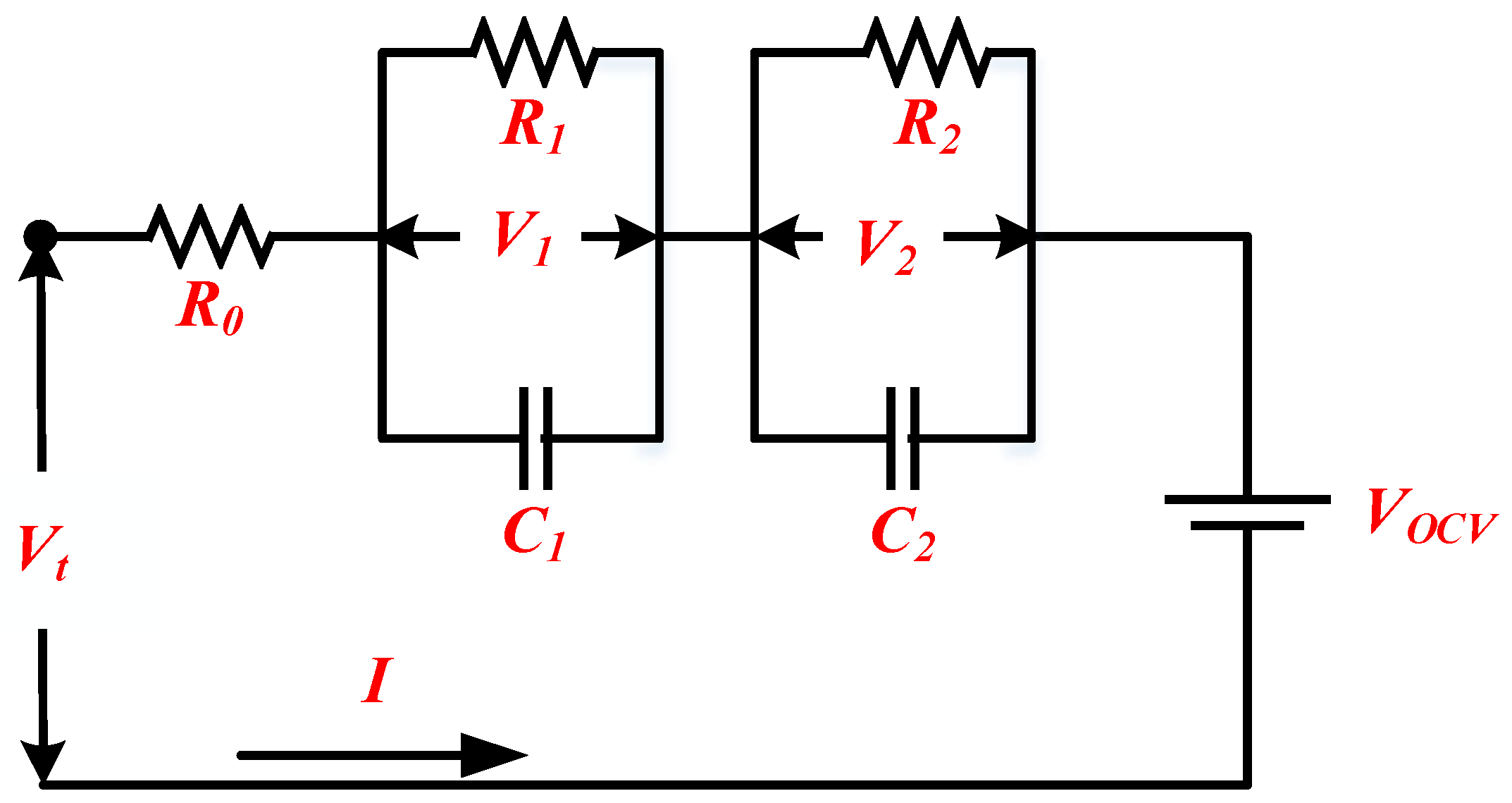
4.2. Battery Modeling
4.3. OCV vs. SOC Relationship
5. Results and Discussion
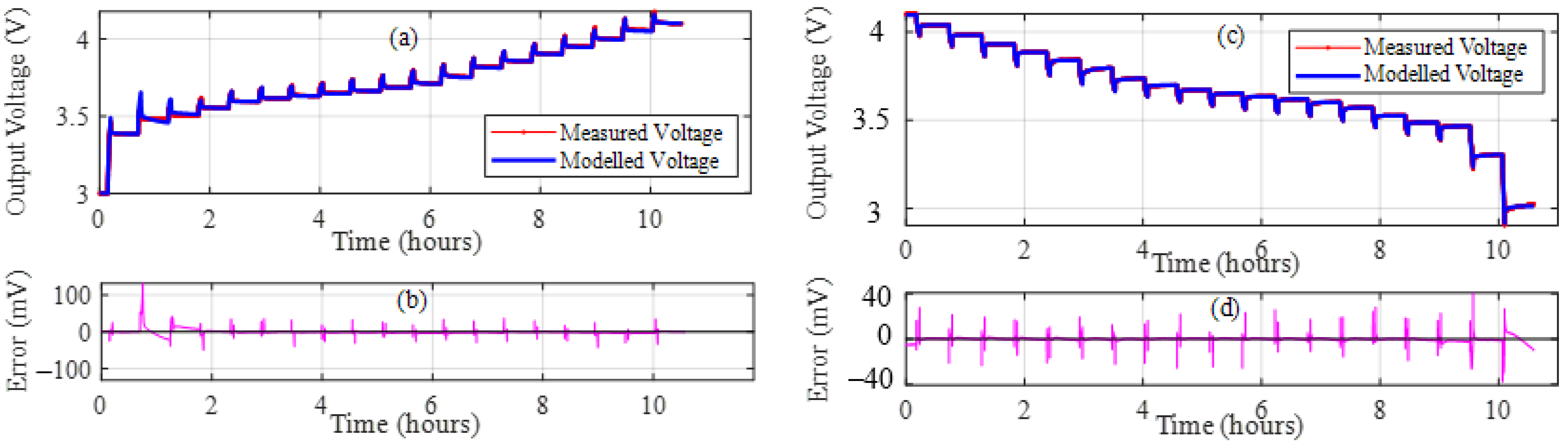
5.1. Battery Model Parameter Validation
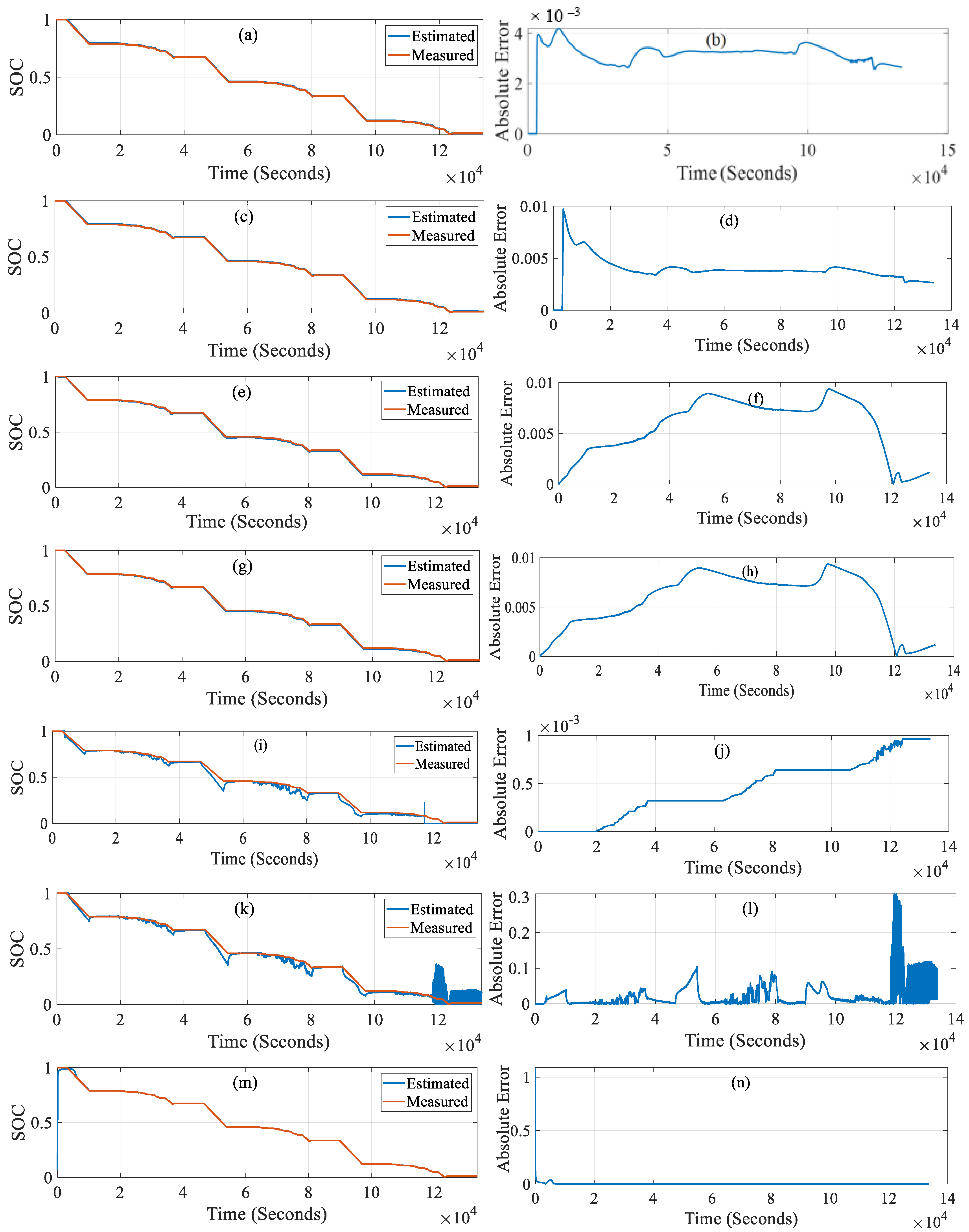
5.2. SOC Estimation Results and Their Comparison
6. Future Recommendations
- As the battery model parameters change with the battery aging, it is recommended to simultaneously estimate the battery model parameters to improve the SOC estimation accuracy using the model-based method further.
- By considering the adaptive value of sampling time, it would be possible to improve the SOC estimation accuracy and reduce the computational burden.
- Based on the obtained results, it is recommended to develop a hybrid algorithm by combining the algorithms to achieve higher SOC estimation accuracy and lower computational time.
- To achieve high accuracy of online SOC estimation in a real-time application, combining the model-based and data-driven methods in future studies is recommended.
- Because of the advancement of machine learning algorithms, the concept of a digital twin would be a good choice for online battery SOC estimation.
- To improve the efficiency of the BMS, it would be useful to develop a combined state estimation method using a data-driven as well as model-based approach.
- With the advancement of ML algorithms, it is recommended to develop a cloud-based BMS to reduce the overall cost of xEVs.
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Khan, W.; Ahmad, F.; Alam, M.S. Fast EV charging station integration with grid ensuring optimal and quality power exchange. Eng. Sci. Technol. Int. J. 2019, 22, 143–152. [Google Scholar] [CrossRef]
- Xavier, M.A.; Trimboli, M. Lithium-ion battery cell-level control using constrained model predictive control and equivalent circuit models. J. Power Sources 2015, 285, 374–384. [Google Scholar] [CrossRef] [Green Version]
- Motaqi, A.; Mosavi, M. Blind and task-ware multi-cell battery management system. Eng. Sci. Technol. Int. J. 2020, 23, 544–554. [Google Scholar] [CrossRef]
- Andre, D.; Nuhic, A.; Soczka-Guth, T.; Sauer, D.U. Comparative study of a structured neural network and an extended Kalman filter for state of health determination of lithium-ion batteries in hybrid electricvehicles. Eng. Appl. Artif. Intell. 2013, 26, 951–961. [Google Scholar] [CrossRef]
- Yang, W.; Wen, Y.; Pandžić, H.; Zhang, W. A multi-state control strategy for battery energy storage based on the state-of-charge and frequency disturbance conditions. Int. J. Electr. Power Energy Syst. 2022, 135, 107600. [Google Scholar] [CrossRef]
- Lu, L.; Han, X.; Li, J.; Hua, J.; Ouyang, M. A review on the key issues for lithium-ion battery management in electric vehicles. J. Power Sources 2013, 226, 272–288. [Google Scholar] [CrossRef]
- Li, Z.; Huang, J.; Liaw, B.Y.; Zhang, J. On state-of-charge determination for lithium-ion batteries. J. Power Sources 2017, 348, 281–301. [Google Scholar] [CrossRef] [Green Version]
- Singh, R.; Amrr, S.M.; Asghar, M.J. Supervisory control strategy for the effective solar energy utilization in a residential microgrid system using a cost-effective controller. Int. J. Electr. Power Energy Syst. 2021, 132, 107170. [Google Scholar] [CrossRef]
- Zhang, R.; Xia, B.; Li, B.; Cao, L.; Lai, Y.; Zheng, W.; Wang, H.; Wang, W. State of the Art of Lithium-Ion Battery SOC Estimation for Electrical Vehicles. Energies 2018, 11, 1820. [Google Scholar] [CrossRef] [Green Version]
- Meng, J.; Ricco, M.; Luo, G.; Swierczynski, M.J.; Stroe, D.-I.; Stroe, A.-I.; Teodorescu, R. An Overview and Comparison of Online Implementable SOC Estimation Methods for Lithium-Ion Battery. IEEE Trans. Ind. Appl. 2018, 54, 1583–1591. [Google Scholar] [CrossRef]
- Dang, X.; Yan, L.; Jiang, H.; Wu, X.; Sun, H. Open-circuit voltage-based state of charge estimation of lithium-ion power battery by combining controlled auto-regressive and moving average modeling with feedforward-feedback compensation method. Int. J. Electr. Power Energy Syst. 2017, 90, 27–36. [Google Scholar] [CrossRef]
- Rivera-Barrera, J.P.; Muñoz-Galeano, N.; Sarmiento-Maldonado, H.O. SoC Estimation for Lithium-ion Batteries: Review and Future Challenges. Electronics 2017, 6, 102. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Zhang, W.; Lei, G. A Review of Li-ion Battery Equivalent Circuit Models. Trans. Electr. Electron. Mater. 2016, 17, 311–316. [Google Scholar] [CrossRef] [Green Version]
- Lotfi, N.; Landers, R.G.; Li, J.; Park, J. Reduced-order electrochemical model-based SOC observer with output model uncertainty estimation. IEEE Trans. Control Syst. Technol. 2017, 25, 1217–1230. [Google Scholar] [CrossRef]
- Wu, B.; Yufit, V.; Marinescu, M.; Offer, G.; Martinez-Botas, R.F.; Brandon, N.P. Coupled thermal–electrochemical modelling of uneven heat generation in lithium-ion battery packs. J. Power Sources 2013, 243, 544–554. [Google Scholar] [CrossRef]
- Lai, X.; Zheng, Y.; Sun, T. A comparative study of different equivalent circuit models for estimating state-of-charge of lithium-ion batteries. Electrochimica Acta 2018, 259, 566–577. [Google Scholar] [CrossRef]
- Shrivastava, P.; Soon, T.K.; Bin Idris, M.Y.I.; Mekhilef, S.; Adnan, S.B.R.S. Combined State of Charge and State of Energy Estimation of Lithium-Ion Battery Using Dual Forgetting Factor-Based Adaptive Extended Kalman Filter for Electric Vehicle Applications. IEEE Trans. Veh. Technol. 2021, 70, 1200–1215. [Google Scholar] [CrossRef]
- Meng, J.; Luo, G.; Ricco, M.; Swierczynski, M.; Stroe, D.-I.; Teodorescu, R. Overview of Lithium-Ion Battery Modeling Methods for State-of-Charge Estimation in Electrical Vehicles. Appl. Sci. 2018, 8, 659. [Google Scholar] [CrossRef] [Green Version]
- Espedal, I.B.; Jinasena, A.; Burheim, O.S.; Lamb, J.J. Current Trends for State-of-Charge (SoC) Estimation in Lithium-Ion Battery Electric Vehicles. Energies 2021, 14, 3284. [Google Scholar] [CrossRef]
- Shrivastava, P.; Soon, T.K.; Bin Idris, M.Y.I.; Mekhilef, S. Overview of model-based online state-of-charge estimation using Kalman filter family for lithium-ion batteries. Renew. Sustain. Energy Rev. 2019, 113, 109233. [Google Scholar] [CrossRef]
- Xing, J.; Wu, P. State of Charge Estimation of Lithium-Ion Battery Based on Improved Adaptive Unscented Kalman Filter. Sustainability 2021, 13, 5046. [Google Scholar] [CrossRef]
- Xia, B.; Sun, Z.; Zhang, R.; Cui, D.; Lao, Z.; Wang, W.; Sun, W.; Lai, Y.; Wang, M. A Comparative Study of Three Improved Algorithms Based on Particle Filter Algorithms in SOC Estimation of Lithium Ion Batteries. Energies 2017, 10, 1149. [Google Scholar] [CrossRef]
- Yu, Q.; Xiong, R.; Lin, C.; Shen, W.; Deng, J. Lithium-Ion Battery Parameters and State-of-Charge Joint Estimation Based on H-Infinity and Unscented Kalman Filters. IEEE Trans. Veh. Technol. 2017, 66, 8693–8701. [Google Scholar] [CrossRef]
- Ouyang, Q.; Chen, J.; Zheng, J.; Hong, Y. SOC Estimation-Based Quasi-Sliding Mode Control for Cell Balancing in Lithium-Ion Battery Packs. IEEE Trans. Ind. Electron. 2017, 65, 3427–3436. [Google Scholar] [CrossRef]
- Li, J.; Barillas, J.K.; Guenther, C.; Danzer, M.A. A comparative study of state of charge estimation algorithms for LiFePO4 batteries used in electric vehicles. J. Power Sources 2013, 230, 244–250. [Google Scholar] [CrossRef]
- Shrivastava, P.; Soon, T.K.; Bin Idris, M.Y.I.; Mekhilef, S.; Adnan, S.B.R.S.A. Model-based state of X estimation of lithium-ion battery for electric vehicle applications. Int. J. Energy Res. 2022, 46, 10704–10723. [Google Scholar] [CrossRef]
- Al-Gabalawy, M.; Hosny, N.S.; Dawson, J.A.; Omar, A.I. State of charge estimation of a Li-ion battery based on extended Kalman filtering and sensor bias. Int. J. Energy Res. 2021, 45, 6708–6726. [Google Scholar] [CrossRef]
- Zhang, Z.; Jiang, L.; Zhang, L.; Huang, C. State-of-charge estimation of lithium-ion battery pack by using an adaptive extended Kalman filter for electric vehicles. J. Energy Storage 2021, 37, 102457. [Google Scholar] [CrossRef]
- Xu, W.; Wang, S.; Jiang, C.; Fernandez, C.; Yu, C.; Fan, Y.; Cao, W. A novel adaptive dual extended Kalman filtering algorithm for the Li-ion battery state of charge and state of health co-estimation. Int. J. Energy Res. 2021, 45, 14592–14602. [Google Scholar] [CrossRef]
- Wang, W.; Wang, X.; Xiang, C.; Wei, C.; Zhao, Y. Unscented Kalman Filter-Based Battery SOC Estimation and Peak Power Prediction Method for Power Distribution of Hybrid Electric Vehicles. IEEE Access 2018, 6, 35957–35965. [Google Scholar] [CrossRef]
- Tian, Y.; Xia, B.; Sun, W.; Xu, Z.; Zheng, W. A modified model based state of charge estimation of power lithium-ion batteries using unscented Kalman filter. J. Power Sources 2014, 270, 619–626. [Google Scholar] [CrossRef]
- Li, D.; Ouyang, J.; Li, H.; Wan, J. State of charge estimation for LiMn2O4 power battery based on strong tracking sigma point Kalman filter. J. Power Sources 2015, 279, 439–449. [Google Scholar] [CrossRef]
- Zeng, Z.; Tian, J.; Li, D.; Tian, Y. An online state of charge estimation algorithm for lithium-ion batteries using an improved adaptive Cubature Kalman filter. Energies 2018, 11, 59. [Google Scholar] [CrossRef] [Green Version]
- Ye, M.; Guo, H.; Cao, B. A model-based adaptive state of charge estimator for a lithium-ion battery using an improved adaptive particle filter. Appl. Energy 2017, 190, 740–748. [Google Scholar] [CrossRef]
- He, T.; Li, D.; Wu, Z.; Xue, Y.; Yang, Y. A modified Luenberger observer for SOC estimation of Lithium-ion battery. In Proceedings of the 2017 36th Chinese Control Conference (CCC), Dalian, China, 6–28 July 2017; pp. 924–928. [Google Scholar] [CrossRef]
- Chemali, E.; Kollmeyer, P.J.; Preindl, M.; Emadi, A. State-of-charge estimation of Li-ion batteries using deep neural networks: A machine learning approach. J. Power Sources 2018, 400, 242–255. [Google Scholar] [CrossRef]
- Ee, Y.-J.; Tey, K.-S.; Lim, K.-S.; Shrivastava, P.; Adnan, S.; Ahmad, H. Lithium-Ion Battery State of Charge (SoC) Estimation with Non-Electrical parameter using Uniform Fiber Bragg Grating (FBG). J. Energy Storage 2021, 40, 102704. [Google Scholar] [CrossRef]
- Dong, G.; Zhang, X.; Zhang, C.; Chen, Z. A method for state of energy estimation of lithium-ion batteries based on neural network model. Energy 2015, 90, 879–888. [Google Scholar] [CrossRef]
- Song, X.; Yang, F.; Wang, D.; Tsui, K.-L. Combined CNN-LSTM Network for State-of-Charge Estimation of Lithium-Ion Batteries. IEEE Access 2019, 7, 88894–88902. [Google Scholar] [CrossRef]
- Gao, T.; Lu, W. Machine learning toward advanced energy storage devices and systems. iScience 2020, 24, 101936. [Google Scholar] [CrossRef]
- Xiang, S.; Qin, Y.; Zhu, C.; Wang, Y.; Chen, H. Long short-term memory neural network with weight amplification and its application into gear remaining useful life prediction. Eng. Appl. Artif. Intell. 2020, 91, 103587. [Google Scholar] [CrossRef]
- Ma, L.; Hu, C.; Cheng, F. State of Charge and State of Energy Estimation for Lithium-Ion Batteries Based on a Long Short-Term Memory Neural Network. J. Energy Storage 2021, 37, 102440. [Google Scholar] [CrossRef]
- Lipu, M.S.H.; Hannan, M.A.; Hussain, A.; Saad, M.H.; Ayob, A.; Uddin, M.N. Extreme Learning Machine Model for State-of-Charge Estimation of Lithium-Ion Battery Using Gravitational Search Algorithm. IEEE Trans. Ind. Appl. 2019, 55, 4225–4234. [Google Scholar] [CrossRef]
- Di Domenico, D.; Creff, Y.; Prada, E.; Duchêne, P.; Bernard, J.C.; Sauvantmoynot, V. A review of approaches for the design of Li-ion BMS estimation functions. Oil Gas Sci. Technol. Rev. d’IFP Energies Nouv. 2013, 68, 127–135. [Google Scholar] [CrossRef] [Green Version]
- Campestrini, C.; Heil, T.; Kosch, S.; Jossen, A. A comparative study and review of different Kalman filters by applying an enhanced validation method. J. Energy Storage 2016, 8, 142–159. [Google Scholar] [CrossRef]
- Hannan, M.; Hoque, M.; Mohamed, A.; Ayob, A. Review of energy storage systems for electric vehicle applications: Issues and challenges. Renew. Sustain. Energy Rev. 2016, 69, 771–789. [Google Scholar] [CrossRef]
- Sepasi, S.; Ghorbani, R.; Liaw, B.Y. Improved extended Kalman filter for state of charge estimation of battery pack. J. Power Sources 2014, 255, 368–376. [Google Scholar] [CrossRef]
- Huang, C.; Wang, Z.; Zhao, Z.; Wang, L.; Lai, C.S.; Wang, D. Robustness Evaluation of Extended and Unscented Kalman Filter for Battery State of Charge Estimation. IEEE Access 2018, 6, 27617–27628. [Google Scholar] [CrossRef]
- Plett, G.L. Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs: Part 3. State and parameter estimation. J. Power Sources 2004, 134, 277–292. [Google Scholar] [CrossRef]
- Andre, D.; Appel, C.; Soczka-Guth, T.; Sauer, D.U. Advanced mathematical methods of SOC and SOH estimation for lithium-ion batteries. J. Power Sources 2013, 224, 20–27. [Google Scholar] [CrossRef]
- He, H.; Xiong, R.; Fan, J. Evaluation of Lithium-Ion Battery Equivalent Circuit Models for State of Charge Estimation by an Experimental Approach. Energies 2011, 4, 582–598. [Google Scholar] [CrossRef]
- Chen, Z.; Fu, Y.; Mi, C. State of Charge Estimation of Lithium-Ion Batteries in Electric Drive Vehicles Using Extended Kalman Filtering. IEEE Trans. Veh. Technol. 2013, 62, 1020–1030. [Google Scholar] [CrossRef]
- Xiong, R.; Cao, J.; Yu, Q.; He, H.; Sun, F. Critical Review on the Battery State of Charge Estimation Methods for Electric Vehicles. IEEE Access 2018, 6, 1832–1843. [Google Scholar] [CrossRef]
- Sepasi, S.; Ghorbani, R.; Liaw, B.Y. A novel on-board state-of-charge estimation method for aged Li-ion batteries based on model adaptive extended Kalman filter. J. Power Sources 2014, 245, 337–344. [Google Scholar] [CrossRef]
- Shrivastava, P.; Soon, T.K.; Bin Idris, M.Y.I.; Mekhlief, S. Combined SOC and SOE Estimation of Lithium-ion battery for Electric Vehicle Applications. In Proceedings of the 2020 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 11–15 October 2020; pp. 5614–5619. [Google Scholar] [CrossRef]
- Xiong, R.; He, H.; Sun, F.; Zhao, K. Evaluation on state of charge estimation of batteries with adaptive extended kalman filter by experiment approach. IEEE Trans. Veh. Technol. 2013, 62, 108–117. [Google Scholar] [CrossRef]
- He, H.; Xiong, R.; Zhang, X.; Sun, F.; Fan, J. State-of-Charge Estimation of the Lithium-Ion Battery Using an Adaptive Extended Kalman Filter Based on an Improved Thevenin Model. IEEE Trans. Veh. Technol. 2011, 60, 1461–1469. [Google Scholar] [CrossRef]
- Plett, G.L. Sigma-point Kalman filtering for battery management systems of LiPB-based HEV battery packs: Part 1: Introduction and state estimation. J. Power Sources 2006, 161, 1356–1368. [Google Scholar] [CrossRef]
- Wang, L.; Wang, L.; Liao, C.; Liu, J. Sigma-point Kalman filter application on estimating battery SOC. In Proceedings of the 5th IEEE Vehicle Power and Propulsion Conference, Dearborn, MI, USA, 7–10 September 2009; pp. 1592–1595. [Google Scholar] [CrossRef]
- He, W.; Williard, N.; Chen, C.; Pecht, M. State of charge estimation for Li-ion batteries using neural network modeling and unscented Kalman filter-based error cancellation. Int. J. Electr. Power Energy Syst. 2014, 62, 783–791. [Google Scholar] [CrossRef]
- Praly, L. Observers for Nonlinear Systems. In Encyclopedia of Systems and Control; Springer: Cham, Switzerland, 2021; pp. 1553–1561. [Google Scholar] [CrossRef]
- Barillas, J.K.; Li, J.; Günther, C.; Danzer, M.A. A comparative study and validation of state estimation algorithms for Li-ion batteries in battery management systems. Appl. Energy 2015, 155, 455–462. [Google Scholar] [CrossRef]
- Chen, X.; Shen, W.; Dai, M.; Cao, Z.; Jin, J.; Kapoor, A. Robust adaptive sliding-mode observer using RBF neural network for lithium-ion battery state of charge estimation in electric vehicles. IEEE Trans. Veh. Technol. 2016, 65, 1936–1947. [Google Scholar] [CrossRef]
- Chen, Q.; Jiang, J.; Ruan, H.; Zhang, C. Simply designed and universal sliding mode observer for the SOC estimation of lithium-ion batteries. IET Power Electron. 2017, 10, 697–705. [Google Scholar] [CrossRef]
- Tang, A.; Yao, L.; Gong, P.; Jiang, Y. Lithium-ion battery state-of-charge estimation of an order-reduced physics-based model in electric vehicles considering erroneous initialization. Int. J. Energy Res. 2021, 46, 3529–3538. [Google Scholar] [CrossRef]
- Xiao, F.; Li, C.; Fan, Y.; Yang, G.; Tang, X. State of charge estimation for lithium-ion battery based on Gaussian process regression with deep recurrent kernel. Int. J. Electr. Power Energy Syst. 2021, 124, 106369. [Google Scholar] [CrossRef]
- Amara, S.; Toumi, S.; Ben Salah, C.; Saidi, A.S. Improvement of techno-economic optimal sizing of a hybrid off-grid micro-grid system. Energy 2021, 233, 121166. [Google Scholar] [CrossRef]
- Sun, X.; Ji, J.; Ren, B.; Xie, C.; Yan, D. Adaptive Forgetting Factor Recursive Least Square Algorithm for Online Identification of Equivalent Circuit Model Parameters of a Lithium-Ion Battery. Energies 2019, 12, 2242. [Google Scholar] [CrossRef] [Green Version]


| Mode | Coefficients in the Gaussian Expression Fitted Curve | ||||
|---|---|---|---|---|---|
| Charging OCV | = 3.761 | = 1.543 | = 3.294 | = 1.368 | = 0.1842 |
| = 1.132 | = 0.7436 | = 0.3469 | = 0.00292 | = 0.04179 | |
| = 0.3507 | = 0.2674 | = 0.3965 | = 0.2271 | = 0.05305 | |
| Discharging OCV | = 4.282 | = 1.954 | = 1.599 | = 0.4318 | |
| = 1.4 | = 0.4647 | = 0.0852 | = 0.0373 | ||
| = 0.8515 | = 0.5143 | = 0.3252 | = 0.0965 | ||
| Method | Tunable parameters | RMSE (%) | Max AE (%) | Computational Time (sec) | Limitations |
|---|---|---|---|---|---|
| EKF | P (3 × 3), Q (3 × 3), R (1 × 1) | 0.5368 | 0.9721 | 145.134 | Linearizes the state and measurement equations using the first-order Taylor expansion; dependence on battery model parameters; prior knowledge of system noise signals is necessary; dependence on experimental conditions |
| AEKF | P (3 × 3), Q (3 × 3), R (1 × 1) | 0.3176 | 0.4184 | 199.908 | Complex tuning of the filter performance when simultaneously adapting matrices Q and R; dependence on battery model parameters; dependence on experimental conditions |
| SPKF | P (3 × 3), Q (3 × 3), R (1 × 1), h (1 × 1) | 0.5574 | 0.94 | 208.152 | High value of measurement noise causes filter divergence; estimation errors, and slow convergence when the dataset is too large; dependence on battery model parameters; dependence on experimental conditions |
| UKF | P (3 × 3), Q (3 × 3), R (1 × 1), α (1 × 1), β (1 × 1), κ (1 × 1) | 0.5585 | 0.91 | 213.308 | High value of measurement noise causes filter divergence; estimation errors, and slow convergence when the dataset is too large; dependence on battery model parameters; dependence on experimental conditions; 3 additional tunable parameters apart from P, Q, and R matrices |
| LO | Observer poles (3 × 1) | 1.2709 | 29.39 | 354.972 | Incorrect determination of observer poles can lead to estimation errors, and noise problems can arise when observer poles are placed farther to the left in the complex plane; dependence on battery model parameters; dependence on the experimental condition |
| SMO | R (1 × 1), Q (3 × 3), W (1 × 1), (3 × 3), ρ (1 × 1) | 0.0439 | 0.0963 | 330.013 | Ricatti Equation constants; Lyapunov dtability constants; observer switching; gain constant |
| BPNN | α (1 × 1), network size, lambda (1 × 1) | 0.8172 | 46.99 | 160.142 | Computationally expensive; requires advanced techniques for optimization |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, Z.A.; Shrivastava, P.; Amrr, S.M.; Mekhilef, S.; Algethami, A.A.; Seyedmahmoudian, M.; Stojcevski, A. A Comparative Study on Different Online State of Charge Estimation Algorithms for Lithium-Ion Batteries. Sustainability 2022, 14, 7412. https://doi.org/10.3390/su14127412
Khan ZA, Shrivastava P, Amrr SM, Mekhilef S, Algethami AA, Seyedmahmoudian M, Stojcevski A. A Comparative Study on Different Online State of Charge Estimation Algorithms for Lithium-Ion Batteries. Sustainability. 2022; 14(12):7412. https://doi.org/10.3390/su14127412
Chicago/Turabian StyleKhan, Zeeshan Ahmad, Prashant Shrivastava, Syed Muhammad Amrr, Saad Mekhilef, Abdullah A. Algethami, Mehdi Seyedmahmoudian, and Alex Stojcevski. 2022. "A Comparative Study on Different Online State of Charge Estimation Algorithms for Lithium-Ion Batteries" Sustainability 14, no. 12: 7412. https://doi.org/10.3390/su14127412
APA StyleKhan, Z. A., Shrivastava, P., Amrr, S. M., Mekhilef, S., Algethami, A. A., Seyedmahmoudian, M., & Stojcevski, A. (2022). A Comparative Study on Different Online State of Charge Estimation Algorithms for Lithium-Ion Batteries. Sustainability, 14(12), 7412. https://doi.org/10.3390/su14127412









