Train Routing and Track Allocation Optimization Model of Multi-Station High-Speed Railway Hub
Abstract
:1. Introduction
- (1)
- We construct a flexible scheme that improves the overall utilization of all stations. Different from the current fixed scheme, this scheme allows all trains to stop at any station of the multi-station hub, which balances the operation of stations and improves the whole efficiency of the hub.
- (2)
- Based on the proposed flexible scheme, we formulate a mixed-integer programming node-arc model to route trains at multi-station high-speed railway hubs. In the formulation, the individual train, rather the train flow, is taken as the basic unit, which benefits the determination of various train routes. Each train route is divided into the route between stations and the track allocation inside stations, which is a combination of macroscopic and microscopic TRP.
- (3)
- Considering the passenger demand, we set the passenger traffic zones and define passenger decision variables. Then, the passenger cost is introduced into the objective function to optimize the passenger routes.
- (4)
- A case study of the Zhengzhou railway hub in China is carried out. We analyze the optimized results and compare them with the results of two other scenarios. Scenario 1 is a fixed scheme, and Scenario 2 is the sequential optimization of train routes and passenger routes. The comparison results verify the effectiveness and the benefits of the optimized results produced by the proposed method.
2. Literature Review
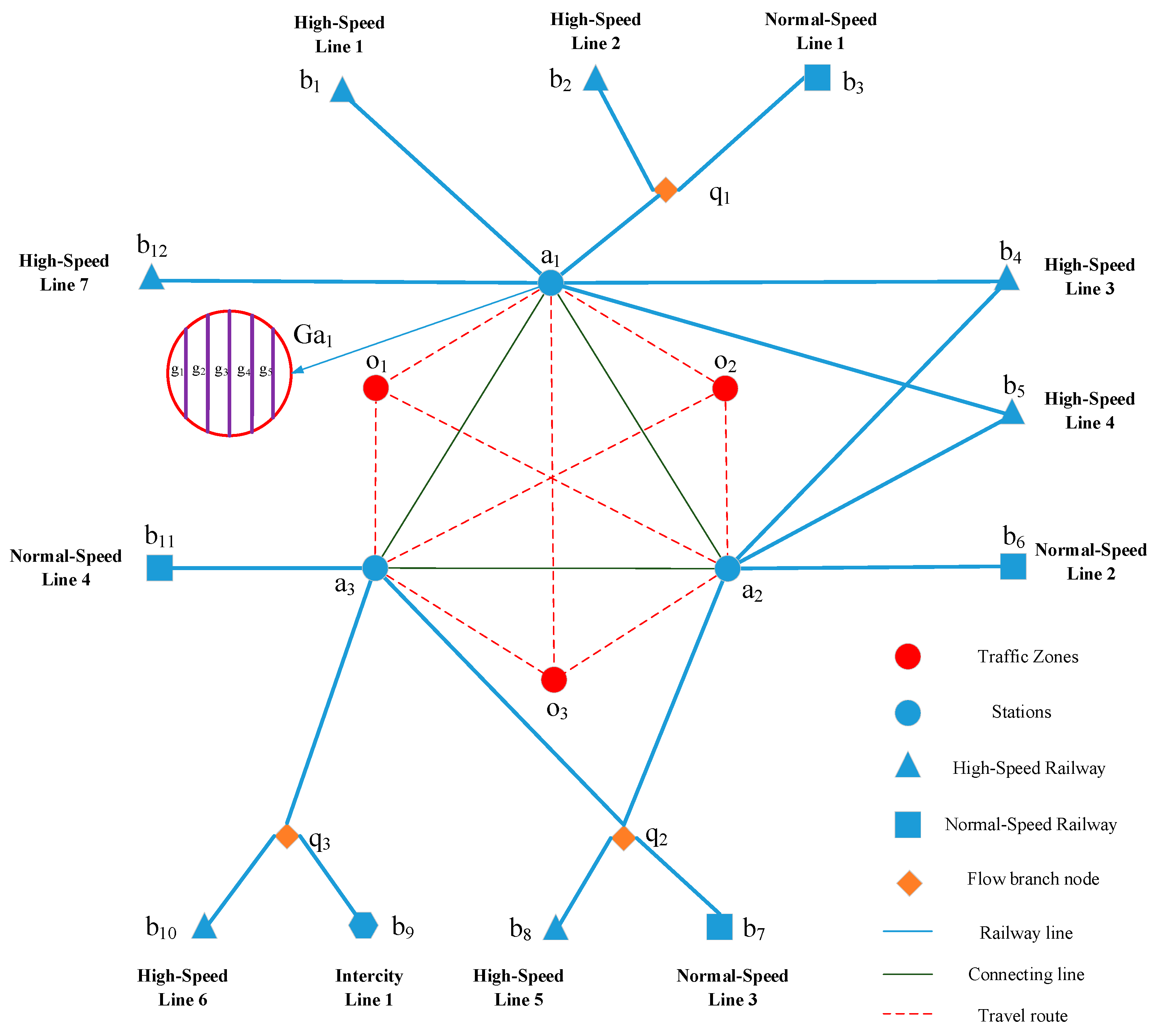
3. Problem Description
- (1)
- Set of nodes
- (2)
- Set of arcs
- (3)
- Arc capacity
- (4)
- Track capacity
4. Mathematical Model
4.1. Assumptions
- (1)
- For each connecting direction, the number of trains is predetermined, including departure, arrival, and passing trains. As the capacity occupied by the non-stopping trains is relatively small, we ignore the number of non-stopping trains.
- (2)
- Based on the flexible scheme, trains do not have preferred routes, and they can stop at any station in the hub.
- (3)
- The capacity of arcs and tracks is calculated after deducting the occupation of freight trains, and the occupation of high-speed and normal-speed trains is the same.
- (4)
- The track capacities are different, but their operational cost is the same, which ensures that the trains have no preferred tracks.
- (5)
- For traffic zones, only the passengers departing from the stations are considered. Since the arriving and transit passengers are coming from outside the cities and their amounts are less than that of departing passengers, these parts of passenger demand are ignored.
- (6)
- The scale of each station is enough to accommodate passengers boarding at this station.
- (7)
- The capacity of other hub facilities is sufficient, such as the train maintenance depot. It is because the train operation volume of these facilities is relatively small and does not affect the train routes.
4.2. Variable Definition
4.3. Formulation
5. Case Study
5.1. Data Source
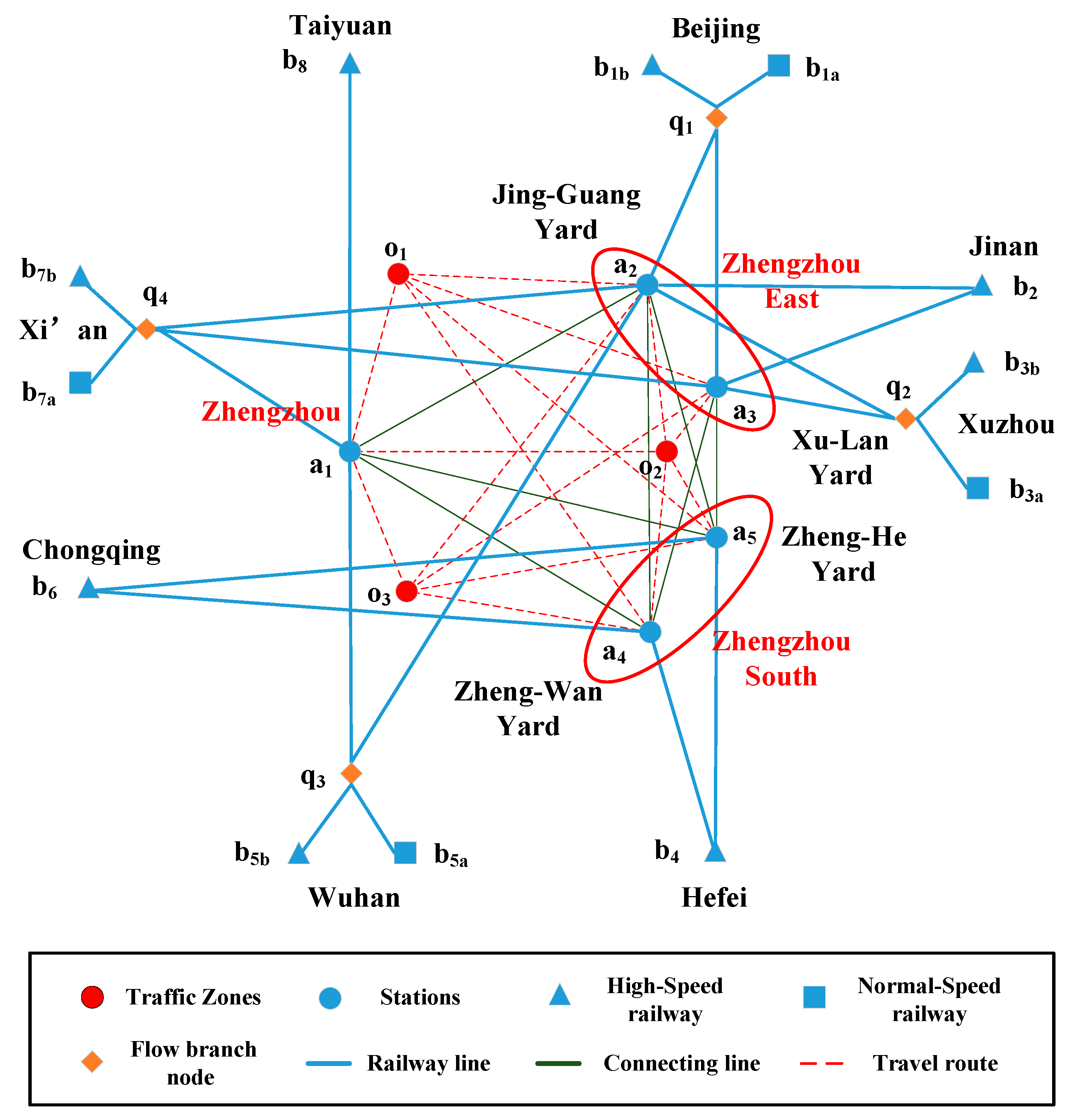
5.1.1. Description of Zhengzhou High-Speed Railway Hub
5.1.2. Related Parameters
5.2. Optimized Results
- (1)
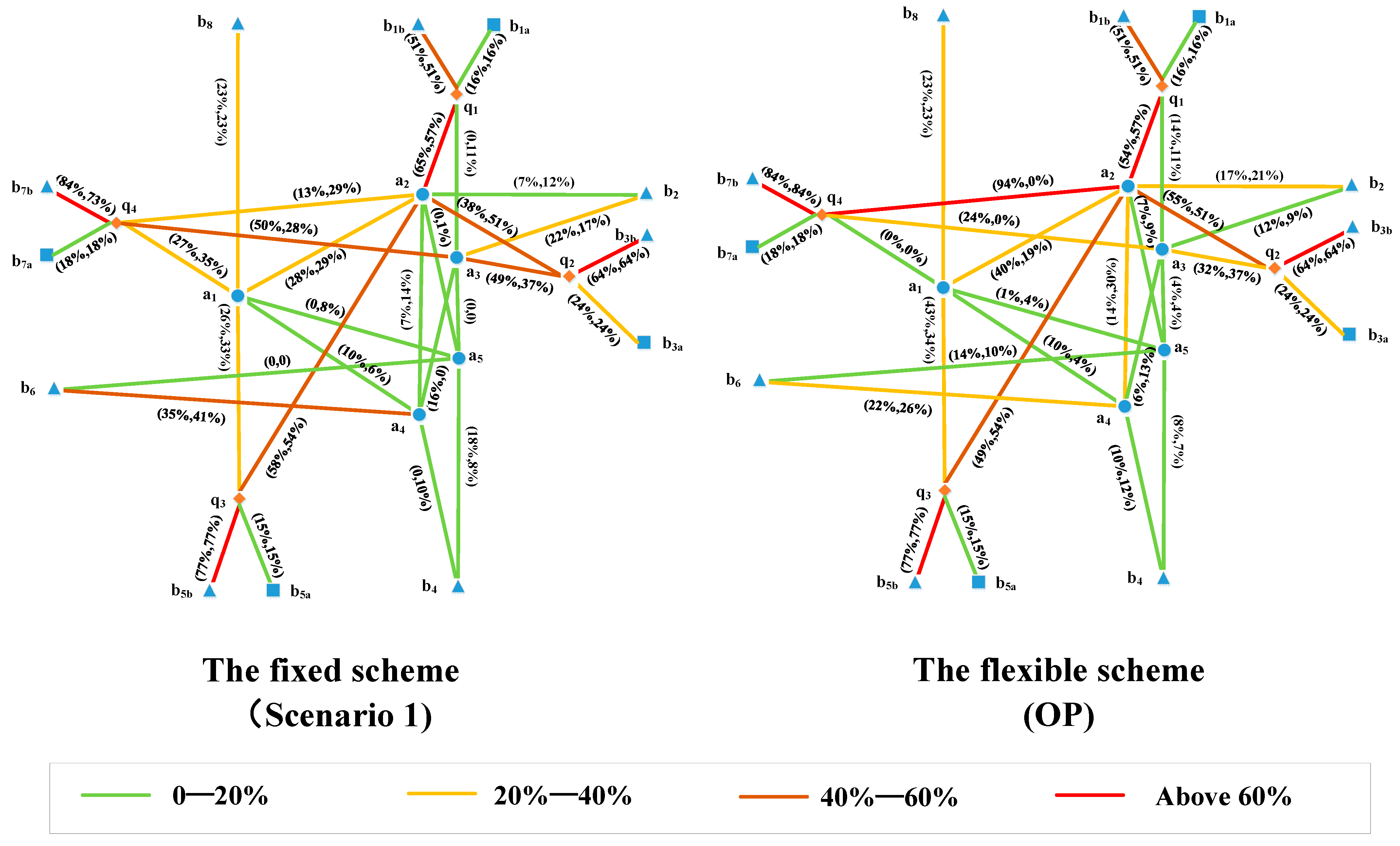
- Most trains select the shortest route of all possible routes. For example, all the departure trains in the Chongqing (b6) direction depart from the Zhengzhou South Station (a4 and a5), and most trains to Taiyuan (b8) depart from the Zhengzhou Station (a1). This result proves the effectiveness of the train cost in the objective function, which makes trains prioritize the shortest routes.
- (2)
- The trains with the same destinations take various routes, and their track allocations are also different. For instance, the arrival trains to Beijing (b1b) have five routes, and the track allocation of each train route is also different. This is because the individual train is taken as the basic unit, which diversifies the routes between the same pair of origin and destination. This result illustrates that the proposed method can avoid centralized train routes and reduce the pressure on trunk lines.
- (3)
- All of the passengers board at their nearest stations, which means the passenger cost in the objective function works and the passenger route lengths are minimized. This result illustrates that the stops of the trains are convenient for the passengers, which benefits service quality.
5.3. Discussion
5.3.1. Scenario 1: Fixed Scheme
- (1)
- The total cost of the flexible scheme is 29.35% lower than that of the fixed scheme, where the train and passenger costs are 1.13% and 50% lower, respectively. These results indicate that the optimization model identifies shorter train and passenger routes because the flexible scheme assigns most trains to the shortest routes without considering fixed directions. Additionally, it allows passengers to board at the nearest stations.
- (2)
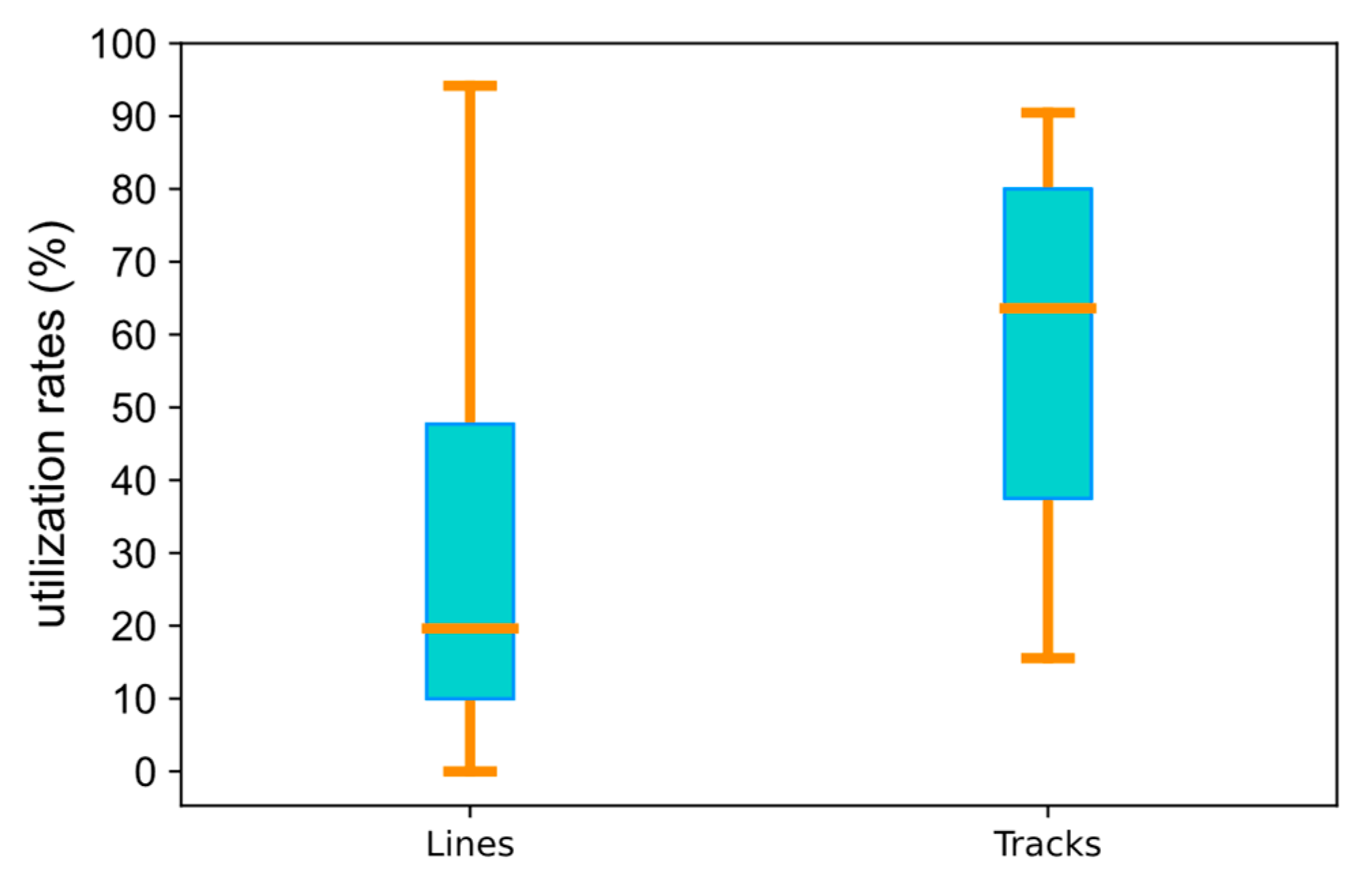
- The line capacity utilization rates of these two schemes are almost similar. Notably, the partial objective of the optimization model is to minimize the train cost, which usually concentrates trains on the shortest routes and leads to an imbalance among lines. However, for the Zhengzhou railway hub, as the difference in route lengths between routes are not too large, the imbalance in the results produced by the flexible scheme is minor.
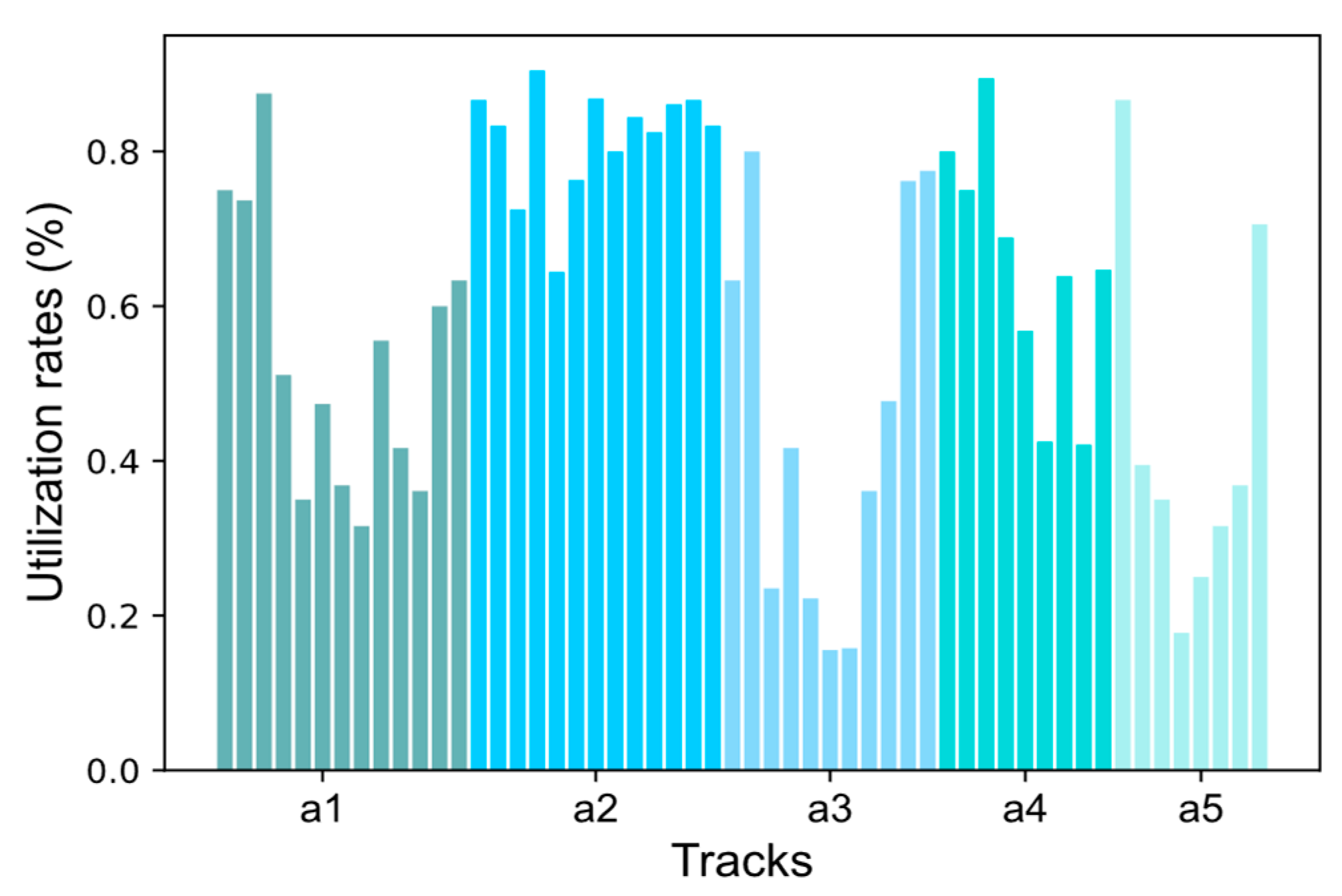
- (3)
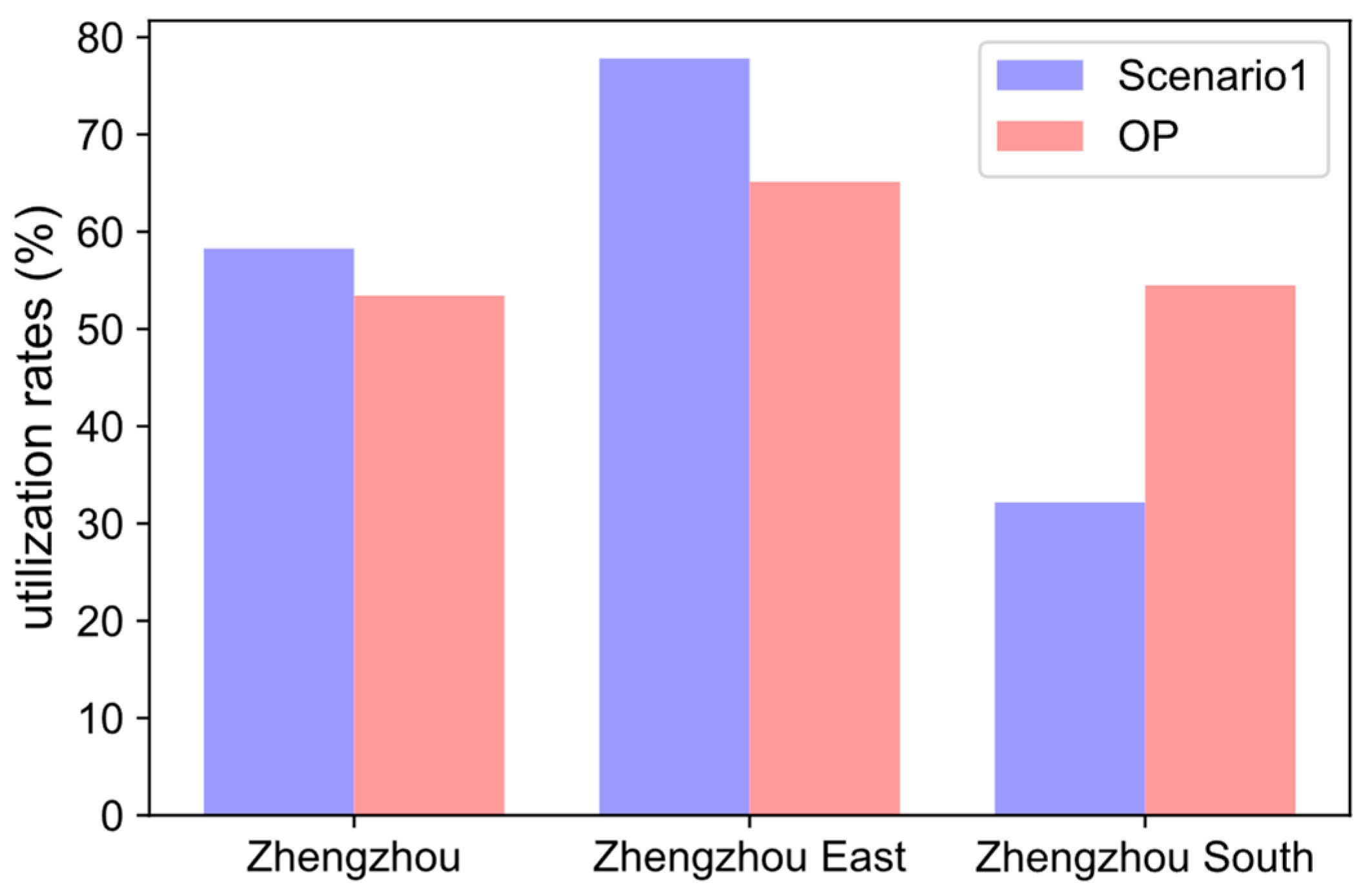
- Figure 5 shows that the average track capacity utilization rate of the Zhengzhou East Station is much larger than the Zhengzhou South Station in the fixed scheme, and the track capacity utilization between stations is imbalanced. However, this problem does not occur in the flexible scheme, where the track capacity utilization of the stations is more balanced.
5.3.2. Scenario 2: Sequentially Optimize Train and Passenger Routes
- (1)
- The total cost of Scenario 2 is 22.58% higher than that of the optimized results. Although the train cost is slightly lower in the former, the passenger cost is higher by 73.73% because the train cost is considered first in the objective and passengers are passively assigned. This sequential optimization leads to centralized train routes and to passengers in some traffic zones traveling to distant stations, resulting in an increase in passenger cost.
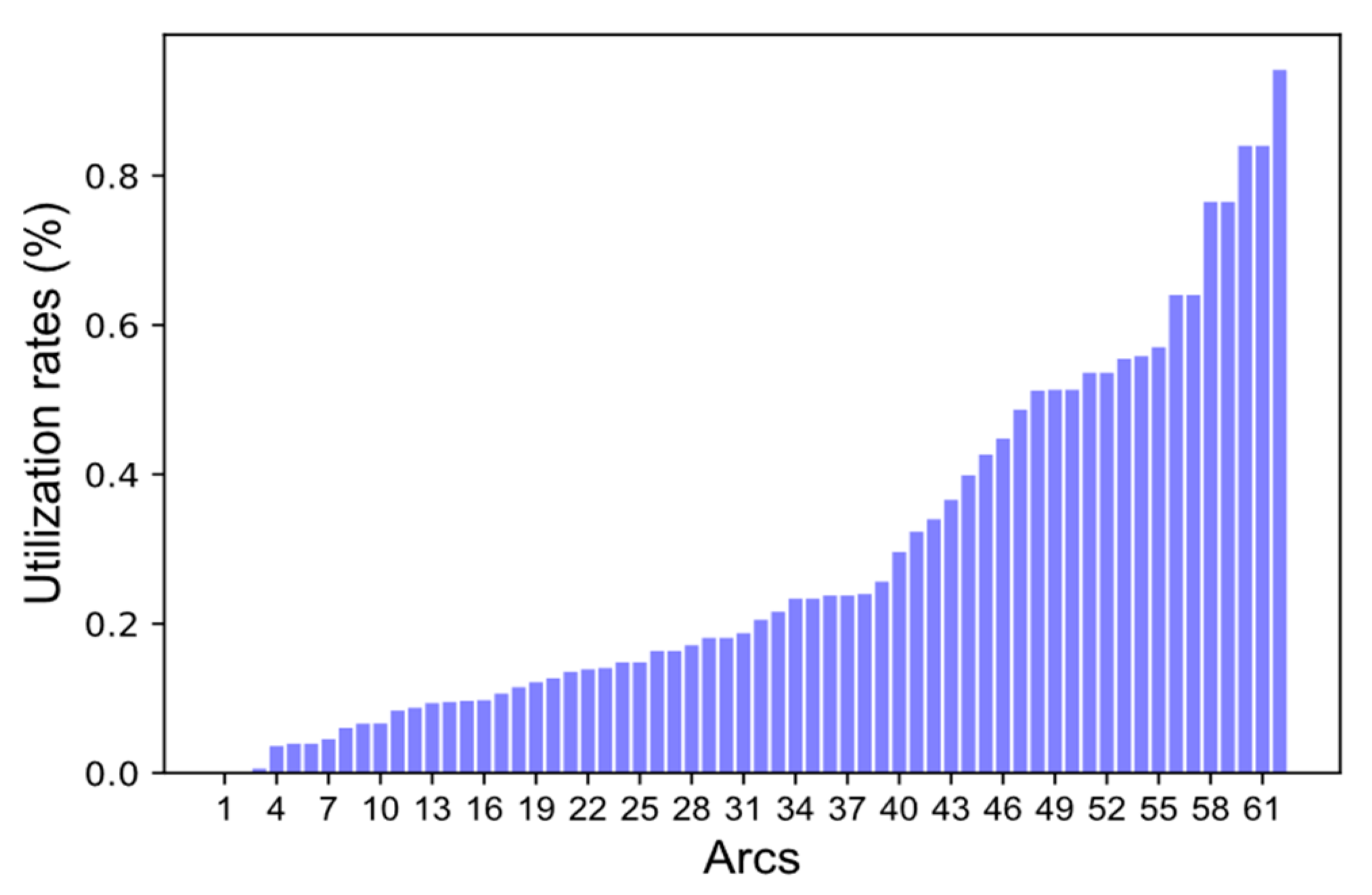
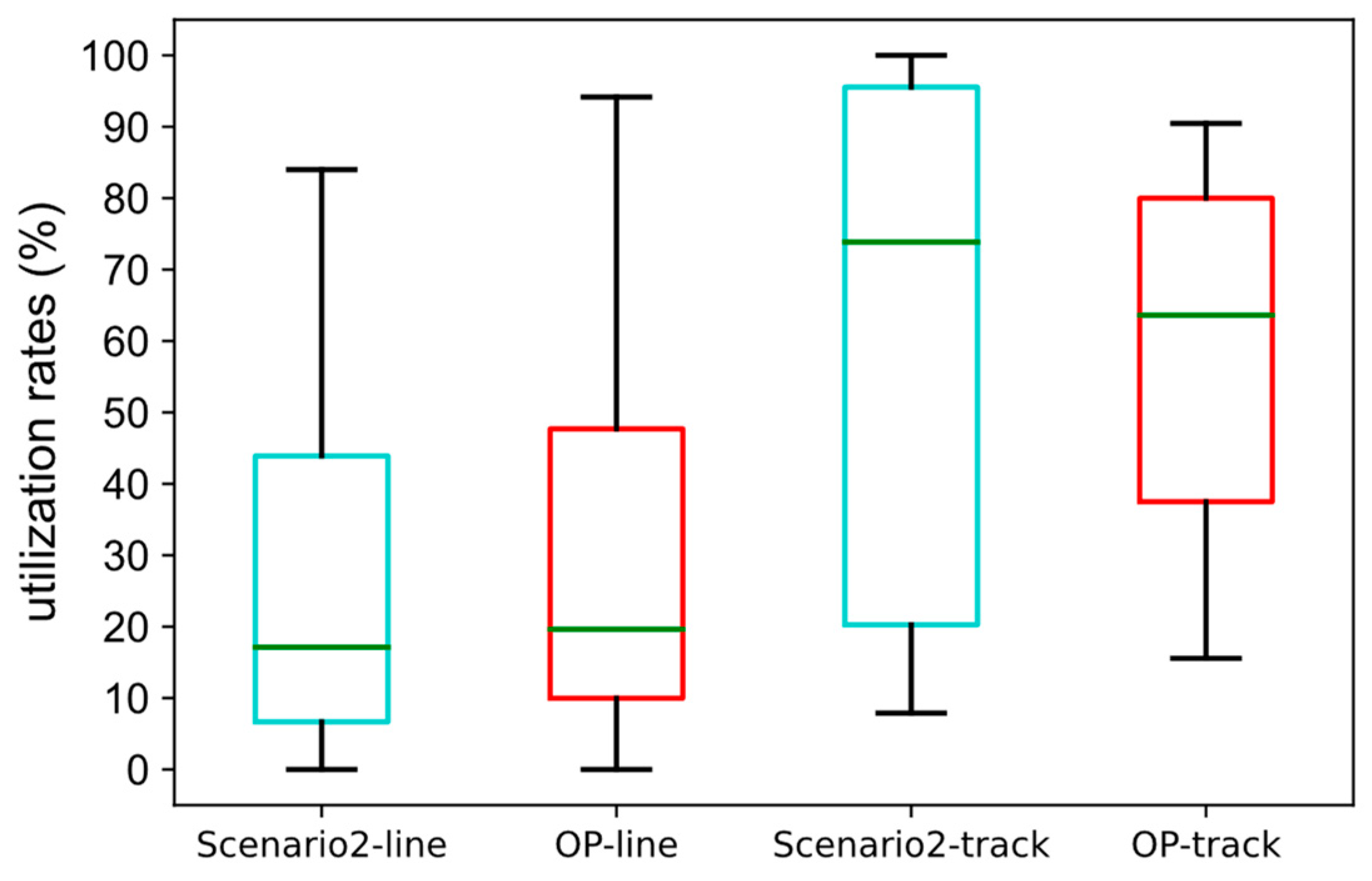
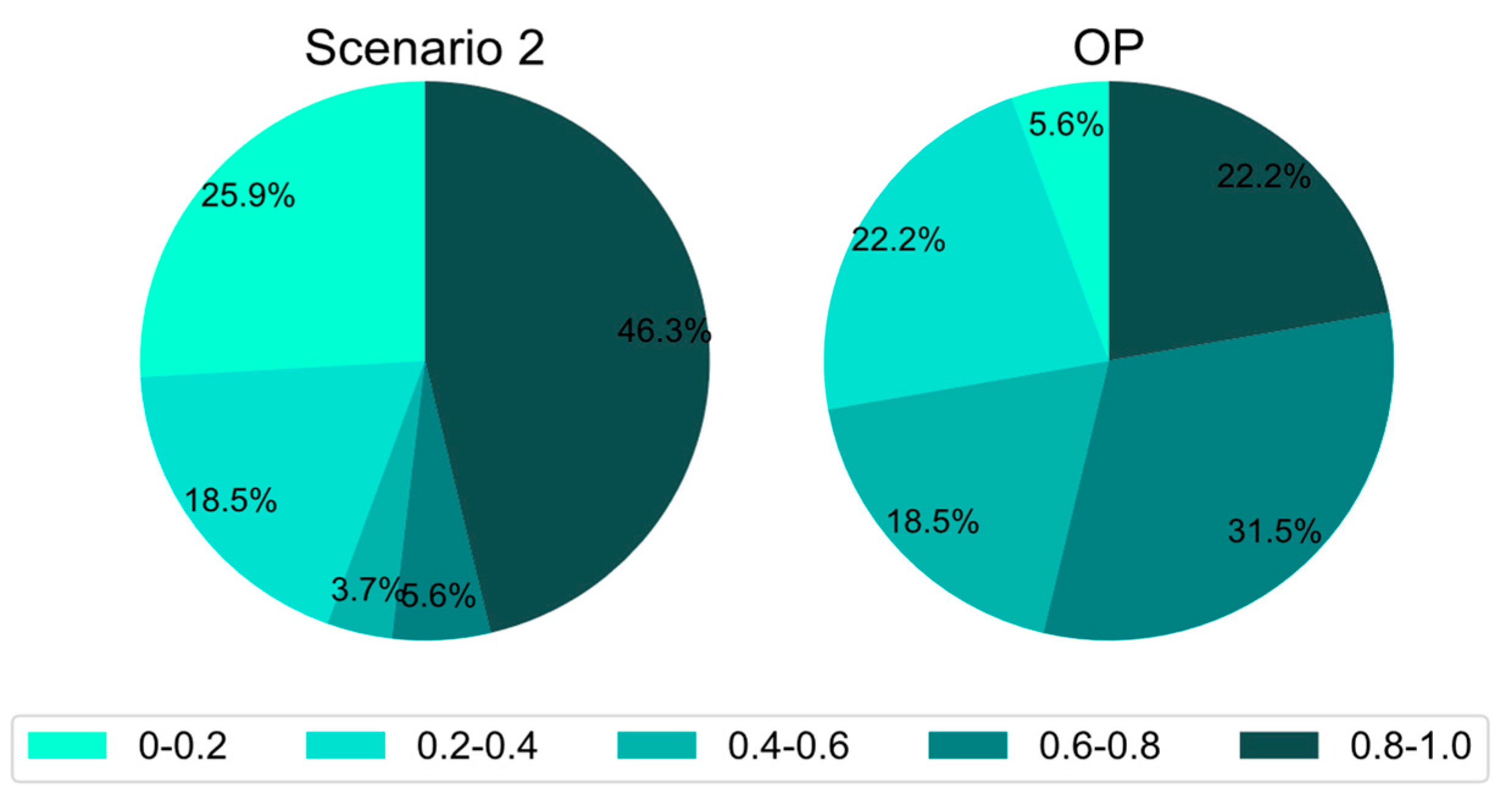
- (2)
- The line capacity utilization in Scenario 2 is more imbalanced. Moreover, Figure 7 shows that, in Scenario 2, many tracks have utilization rates of more than 80%, 18 tracks have utilization rates of more than 90%, and 8 tracks have utilization rates of 100%. Due to the centralized train routes, the operation pressure on some tracks is too high to operate new trains, so this scheme cannot be applied in practice. The above results illustrate that passenger demand should be directly introduced into the objective function rather than the sequential optimization.
6. Conclusions and Further Works
- (1)
- For railway operators, when formulating the operation scheme, all stations should be considered together and regarded as a whole. This not only takes advantage of the scale effect of multi-station hubs but also balances the operations of the different stations.
- (2)
- Multiple routes should be planned for each origin–destination pair of trains to avoid congestion on railway lines, and the routes should be detailed in terms of track allocation inside stations.
- (3)
- With the intensification of competition in the transportation market, passenger demand should be considered in the planning of train routes to improve service quality.
- (1)
- The railway hub that we study is mostly relevant to an already constructed railway hub. For hubs still in the planning stage, the location of railway passenger stations can be combined with the optimization scheme to achieve collaborative optimization.
- (2)
- We only study the departure passenger flow and do not consider the transfer passenger flow. In the next stage, we would introduce transfer passenger flow into the model to construct a transfer scheme, which could increase the suitability of the optimization scheme for the transfer passengers.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Appendix A. Input Data of the Case Study
| D | b1a | b1b | b2 | b3a | b3b | b4 | b5a | b5b | b6 | b7a | b7b | b8 | Z | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| O | ||||||||||||||
| b1a | 0 | 0 | 0 | 3 | 0 | 0 | 26 | 0 | 0 | 6 | 0 | 0 | 8 | |
| b1b | 0 | 0 | 0 | 0 | 8 | 4 | 0 | 64 | 20 | 0 | 20 | 0 | 19 | |
| b2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 19 | 12 | 0 | 17 | 0 | 29 | |
| b3a | 3 | 0 | 0 | 0 | 0 | 0 | 2 | 0 | 0 | 24 | 0 | 0 | 10 | |
| b3b | 0 | 8 | 0 | 0 | 0 | 0 | 0 | 20 | 13 | 0 | 36 | 4 | 24 | |
| b4 | 0 | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 12 | 14 | 22 | |
| b5a | 26 | 0 | 0 | 2 | 0 | 0 | 0 | 0 | 0 | 4 | 0 | 0 | 7 | |
| b5b | 0 | 64 | 19 | 0 | 20 | 0 | 0 | 0 | 0 | 0 | 15 | 10 | 25 | |
| b6 | 0 | 20 | 12 | 0 | 13 | 0 | 0 | 0 | 0 | 0 | 0 | 20 | 31 | |
| b7a | 6 | 0 | 0 | 24 | 0 | 0 | 4 | 0 | 0 | 0 | 0 | 0 | 6 | |
| b7b | 0 | 20 | 17 | 0 | 36 | 12 | 0 | 15 | 0 | 0 | 0 | 0 | 26 | |
| b8 | 0 | 0 | 0 | 0 | 4 | 14 | 0 | 10 | 20 | 0 | 0 | 0 | 19 | |
| Z | 8 | 19 | 29 | 10 | 24 | 22 | 7 | 25 | 31 | 6 | 26 | 19 | ||
| D | b1a | b1b | b2 | b3a | b3b | b4 | b5a | b5b | b6 | b7a | b7b | b8 | Total | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| O | ||||||||||||||
| o1 | 10 | 30 | 12 | 10 | 20 | 7 | 10 | 30 | 15 | 10 | 30 | 17 | 201 | |
| o2 | 10 | 30 | 12 | 10 | 20 | 7 | 10 | 30 | 15 | 10 | 30 | 17 | 201 | |
| o3 | 10 | 30 | 12 | 10 | 20 | 7 | 10 | 30 | 15 | 10 | 30 | 17 | 201 | |
| Total | 30 | 90 | 36 | 30 | 60 | 21 | 30 | 90 | 45 | 30 | 90 | 51 | ||
Appendix B. Detailed Departure and Arrival Routes of Trains
| B | Arrival Trains | Track Allocation | N | Departure Trains | Track Allocation | N |
|---|---|---|---|---|---|---|
| b4 | b4-a4 | a4 [1, 2, 3, 3, 3, 4, 4, 4, 7, 7] | 10 | a4-b4 | a4 [5, 6, 6, 7, 9, 9, 9, 9] | 8 |
| b4-a5 | a5 [1, 1, 2, 2, 3, 4, 4, 4, 5, 7, 7, 7] | 12 | a5-b4 | a5 [2, 2, 3, 4, 5, 6, 7, 8, 8, 8, 8, 8, 8, 8] | 14 | |
| b5a | b5a-q3-a2 | a2 [5, 7, 7, 11, 11, 11, 13] | 7 | a4-a2-q3-b5a | a4 [1, 2, 2, 4, 7, 7] | 6 |
| a5-a2-q3-b5a | a5 [1] | 1 | ||||
| b5b | b5b-q3-a2 | a2 [4, 4, 5, 6, 6, 6, 6, 6, 6, 7, 8, 8, 8, 8, 8, 8, 8, 8, 9, 10, 11, 11, 11, 13, 13] | 25 | a4-a2-q3-b5b | a4 [1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 4, 4, 4, 5, 5, 6, 6, 8] | 19 |
| a5-a2-q3-b5b | a5 [1, 1, 1, 1, 3, 8] | 6 | ||||
| b6 | b6-a4 | a4 [1, 1, 1, 3, 3, 3, 8] | 7 | a4-b6 | a4 [1, 1, 1, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 4, 4, 4, 7, 9, 9, 9] | 21 |
| b6-a5 | a5 [1, 1, 1, 1, 1, 1, 1, 2, 2, 3, 4, 5, 5, 6, 6, 6, 6, 6, 6, 7, 7, 7, 8, 8] | 24 | a5-b6 | a5 [1, 1, 1, 2, 3, 3, 5, 7, 7, 8] | 10 | |
| b7a | b7a-q4-a2 | a2 [5] | 1 | a1-a2-q4-b7a | a1 [1, 2, 4, 8, 12] | 5 |
| b7a-q4-a3 | a3 [2, 2, 9, 10, 10] | 5 | a4-a3-q4-b7a | a4 [1] | 1 | |
| b7b | b7b-q4-a2 | a2 [4] | 1 | a1-a2-q4-b7b | a1 [1, 2, 2, 3, 5, 6, 7, 7, 8, 9, 9, 9, 9, 9, 12, 12, 12, 13] | 18 |
| a4-a2-q4-b7b | a4 [1, 2, 5, 8, 9] | 5 | ||||
| b7b-q4-a3 | a3 [1, 2, 2, 2, 4, 4, 4, 9, 10, 10, 10, 10, 10, 10, 10, 10, 10, 11, 11, 11, 11] | 25 | a4-a3-q4-b7b | a4 [3, 8] | 2 | |
| a5-a3-q4-b7b | a5 [6] | 1 | ||||
| b8 | b8-a1 | a1 [2, 3, 3, 4, 6, 7, 8, 8, 8, 8, 9, 9, 9, 9, 11, 11, 12, 12, 13] | 19 | a1-b8 | a1 [2, 3, 3, 4, 4, 5, 6, 6, 6, 9, 10, 12, 12, 13, 13, 13, 13, 13] | 18 |
| a2-a1-b8 | a2 [10] | 1 |
References
- Garrisi, G.; Cervelló-Pastor, C. Train-scheduling optimization model for railway networks with multiplatform stations. Sustainability 2020, 12, 257. [Google Scholar] [CrossRef] [Green Version]
- Meng, X.; Wang, Y.; Lin, L.; Li, L.; Jia, L. An integrated model of train Re-scheduling and control for high-speed railway. Sustainability 2021, 13, 11933. [Google Scholar] [CrossRef]
- Zhou, W.; Oldache, M. Integrated optimization of line planning, timetabling and rolling stock allocation for urban railway lines. Sustainability 2021, 13, 13059. [Google Scholar] [CrossRef]
- Lusby, R.M. Optimization methods for routing trains through railway junctions: A new set-packing approach. Transp. Sci. 2002, 45, 228–245. [Google Scholar] [CrossRef] [Green Version]
- Yang, L.; Zhou, X. Constraint reformulation and a Lagrangian relaxation-based solution algorithm for a least expected time path problem. Transp. Res. Part B Methodol. 2014, 59, 22–44. [Google Scholar] [CrossRef]
- Lusby, R.M.; Larsen, J.; Ehrgott, M.; Ryan, D. Railway track allocation: Models and methods. OR Spectr. 2011, 33, 843–883. [Google Scholar] [CrossRef]
- Wang, L.; Jia, L.M.; Qin, Y.; Xu, J.; Mo, W.T. A two-layer optimization model for high-speed railway line planning. J. Zhejiang Univ. Sci. A 2011, 12, 902–912. [Google Scholar] [CrossRef]
- Carey, M.; Lockwood, D. A model, algorithms and strategy for train pathing. J. Oper. Res. Soc. 1995, 46, 988–1005. [Google Scholar] [CrossRef]
- Carey, M. Extending a train pathing model from one-way to two-way track. Transp. Res. Part B 1994, 28, 395–400. [Google Scholar] [CrossRef]
- Bodin, L.D.; Golden, B.L.; Schuster, A.D.; Romig, W. A model for the blocking of trains. Transp. Res. Part B 1980, 14, 115–120. [Google Scholar] [CrossRef]
- Carey, M.; Crawford, I. Scheduling trains on a network of busy complex stations. Transp. Res. Part B Methodol. 2007, 41, 159–178. [Google Scholar] [CrossRef]
- Cepeda, M.; Cominetti, R.; Florian, M. A frequency-based assignment model for congested transit networks with strict capacity constraints: Characterization and computation of equilibria. Transp. Res. Part B Methodol. 2006, 40, 437–459. [Google Scholar] [CrossRef]
- Bi, M.; He, S.; Xu, W. (Ato) Express delivery with high-speed railway: Definitely feasible or just a publicity stunt. Transp. Res. Part A Policy Pract. 2019, 120, 165–187. [Google Scholar] [CrossRef]
- Shafahi, Y.; Khani, A. A practical model for transfer optimization in a transit network: Model formulations and solutions. Transp. Res. Part A Policy Pract. 2010, 44, 377–389. [Google Scholar] [CrossRef]
- Lee, Y.; Chen, C.Y. A heuristic for the train pathing and timetabling problem. Transp. Res. Part B Methodol. 2009, 43, 837–851. [Google Scholar] [CrossRef]
- Zhang, C.; Gao, Y.; Yang, L.; Kumar, U.; Gao, Z. Integrated optimization of train scheduling and maintenance planning on high-speed railway corridors. Omega 2019, 87, 86–104. [Google Scholar] [CrossRef]
- Zhang, C.; Gao, Y.; Yang, L.; Gao, Z.; Qi, J. Joint optimization of train scheduling and maintenance planning in a railway network: A heuristic algorithm using Lagrangian relaxation. Transp. Res. Part B Methodol. 2020, 134, 64–92. [Google Scholar] [CrossRef]
- Zhou, L.; Tong, L.; Chen, J.; Tang, J.; Zhou, X. Joint optimization of high-speed train timetables and speed profiles: A unified modeling approach using space-time-speed grid networks. Transp. Res. Part B Methodol. 2017, 97, 157–181. [Google Scholar] [CrossRef] [Green Version]
- Stojadinović, N.; Bošković, B.; Trifunović, D.; Janković, S. Train path congestion management: Using hybrid auctions for decentralized railway capacity allocation. Transp. Res. Part A Policy Pract. 2019, 129, 123–139. [Google Scholar] [CrossRef]
- Valla, M.; Gašpar, J. Optimization of Timetables on the Bratislava–Žilina–Košice Route in the Period after the End of the COVID-19 Pandemic. Sustainability 2022, 14, 5031. [Google Scholar] [CrossRef]
- Zhang, Q.; Lusby, R.M.; Shang, P.; Zhu, X. Simultaneously re-optimizing timetables and platform schedules under planned track maintenance for a high-speed railway network. Transp. Res. Part C Emerg. Technol. 2020, 121, 102823. [Google Scholar] [CrossRef]
- Billionnet, A. Using Integer Programming to Solve the Train-Platforming Problem. Transp. Sci. 2003, 37, 213–222. [Google Scholar] [CrossRef]
- Cardillo, D.D.L.; Mione, N. κ L-list λ colouring of graphs. Eur. J. Oper. Res. 1998, 106, 160–164. [Google Scholar] [CrossRef]
- Zwaneveld, P.J.; Kroon, L.G.; Romeijn, H.E.; Salomon, M.; Dauzère-Pérès, S.; Van Hoesel, S.P.M.; Ambergen, H.W. Routing trains through railway stations: Model formulation and algorithms. Transp. Sci. 1996, 30, 181–194. [Google Scholar] [CrossRef] [Green Version]
- Zwaneveld, P.J.; Kroon, L.G.; Hoesel, S.P.M. Van Routing trains through a railway station based on a node packing model. Eur. J. Oper. Res. 2001, 128, 14–33. [Google Scholar] [CrossRef] [Green Version]
- Carey, M.; Carville, S. Scheduling and platforming trains at busy complex stations. Transp. Res. Part A Policy Pract. 2003, 37, 195–224. [Google Scholar] [CrossRef]
- Rodriguez, J. A constraint programming model for real-time train scheduling at junctions. Transp. Res. Part B Methodol. 2007, 41, 231–245. [Google Scholar] [CrossRef]
- Corman, F.; D’Ariano, A.; Pacciarelli, D.; Pranzo, M. A tabu search algorithm for rerouting trains during rail operations. Transp. Res. Part B Methodol. 2010, 44, 175–192. [Google Scholar] [CrossRef]
- Cacchiani, V.; Galli, L.; Toth, P. A tutorial on non-periodic train timetabling and platforming problems. EURO J. Transp. Logist. 2015, 4, 285–320. [Google Scholar] [CrossRef]
- Meng, L.; Zhou, X. Simultaneous train rerouting and rescheduling on an N-track network: A model reformulation with network-based cumulative flow variables. Transp. Res. Part B Methodol. 2014, 67, 208–234. [Google Scholar] [CrossRef]
- Samà, M.; Pellegrini, P.; D’Ariano, A.; Rodriguez, J.; Pacciarelli, D. Ant colony optimization for the real-time train routing selection problem. Transp. Res. Part B Methodol. 2016, 85, 89–108. [Google Scholar] [CrossRef]
- Xu, P.; Corman, F.; Peng, Q.; Luan, X. A train rescheduling model integrating speed management during disruptions of high-speed traffic under a quasi-moving block system. Transp. Res. Part B Methodol. 2017, 104, 638–666. [Google Scholar] [CrossRef]
- Luan, X.; Miao, J.; Meng, L.; Corman, F.; Lodewijks, G. Integrated optimization on train scheduling and preventive maintenance time slots planning. Transp. Res. Part C Emerg. Technol. 2017, 80, 329–359. [Google Scholar] [CrossRef]
- Zhang, Y.; Peng, Q.; Yao, Y.; Zhang, X.; Zhou, X. Solving cyclic train timetabling problem through model reformulation: Extended time-space network construct and Alternating Direction Method of Multipliers methods. Transp. Res. Part B Methodol. 2019, 128, 344–379. [Google Scholar] [CrossRef]
- Xu, J.; Wang, Z.; Yao, S.; Xue, J. Train Operations Organization in High-Speed Railway Station Considering Variable Configuration. Sustainability 2022, 14, 2365. [Google Scholar] [CrossRef]
- Liao, Z.; Li, H.; Miao, J.; Corman, F. Railway capacity estimation considering vehicle circulation: Integrated timetable and vehicles scheduling on hybrid time-space networks. Transp. Res. Part C Emerg. Technol. 2021, 124, 102961. [Google Scholar] [CrossRef]
- Gao, R.; Niu, H. A priority-based ADMM approach for flexible train scheduling problems. Transp. Res. Part C Emerg. Technol. 2021, 123, 102960. [Google Scholar] [CrossRef]
- Zhou, W.; Fan, W.; You, X.; Deng, L. Demand-oriented train timetabling integrated with passenger train-booking decisions. Sustainability 2019, 11, 4932. [Google Scholar] [CrossRef] [Green Version]
- Chow, A.H.F.; Pavlides, A. Cost functions and multi-objective timetabling of mixed train services. Transp. Res. Part A Policy Pract. 2018, 113, 335–356. [Google Scholar] [CrossRef]
- Meng, L.; Zhou, X. An integrated train service plan optimization model with variable demand: A team-based scheduling approach with dual cost information in a layered network. Transp. Res. Part B Methodol. 2019, 125, 1–28. [Google Scholar] [CrossRef]
- Li, X.; Li, D.; Hu, X.; Yan, Z.; Wang, Y. Optimizing train frequencies and train routing with simultaneous passenger assignment in high-speed railway network. Comput. Ind. Eng. 2020, 148, 106650. [Google Scholar] [CrossRef]
- Zhan, S.; Wong, S.C.; Shang, P.; Peng, Q.; Xie, J.; Lo, S.M. Integrated railway timetable rescheduling and dynamic passenger routing during a complete blockage. Transp. Res. Part B Methodol. 2021, 143, 86–123. [Google Scholar] [CrossRef]
- Nguyen, H.T.M.; Chow, A.H.F.; Ying, C. Pareto routing and scheduling of dynamic urban rail transit services with multi-objective cross entropy method. Transp. Res. Part E Logist. Transp. Rev. 2021, 156, 102544. [Google Scholar] [CrossRef]
- Zhao, P.; Li, Y.; Han, B.; Yang, R.; Liu, Z. Integrated Optimization of Rolling Stock Scheduling and Flexible Train Formation Based on Passenger Demand for an Intercity High-Speed Railway. Sustainability 2022, 14, 5650. [Google Scholar] [CrossRef]
- Abril, M.; Barber, F.; Ingolotti, L.; Salido, M.A.; Tormos, P.; Lova, A. An assessment of railway capacity. Transp. Res. Part E Logist. Transp. Rev. 2008, 44, 774–806. [Google Scholar] [CrossRef] [Green Version]
- Harrod, S. Capacity factors of a mixed speed railway network. Transp. Res. Part E Logist. Transp. Rev. 2009, 45, 830–841. [Google Scholar] [CrossRef]
| Parameters | Definition |
|---|---|
| Set of nodes, indexed by | |
| Set of stations in the hub, indexed by | |
| Set of connecting directions, indexed by | |
| refers to high-speed directions; refers to normal-speed directions; refers to intercity directions | |
| Set of branch nodes, indexed by | |
| Set of trains, indexed by , indicates the th train of direction | |
| is the set of departure trains in connecting direction , is the set of arrival trains in connecting direction , is the set of passing trains from direction to direction | |
| Set of tracks, indexed by | |
| is the set of tracks of station | |
| Set of traffic zones, indexed by | |
| Set of arcs, including , indexed by | |
| Set of arcs , indexed by | |
| Number of departure trains moving from the stations in the hub to direction (trains/day) | |
| Number of arrival trains moving from direction to the stations in the hub (trains/day) | |
| Number of passing trains moving from direction to direction (trains/day) | |
| Capacity of arc (trains/day) | |
| Length of arc (km) | |
| Capacity of track in station (trains/day) | |
| Number of passengers moving from traffic zone to direction (persons/day) | |
| Distance from traffic zone to station (km) | |
| Per cost of train running on lines (thousand RMB/train·km) | |
| Cost of train operation on tracks (thousand RMB/train) | |
| Per travel cost of passengers (thousand RMB/person·km) | |
| Passenger capacity of high-speed train (persons/train) | |
| Passenger capacity of normal-speed train (persons/train) | |
| Passenger capacity of intercity train (persons/train) |
| Notations | Definition |
|---|---|
| Binary {0,1}, equals 1 if the kth departure train of direction occupies arc , and 0 otherwise, | |
| Binary {0,1}, equals 1 if the th arrival train of direction occupies arc , and 0 otherwise, | |
| Binary {0,1}, equals 1 if the th passing train from direction to direction occupies arc , and 0 otherwise, , | |
| Binary {0,1}, equals 1 if the th departure train of direction stops at track , and 0 otherwise, | |
| Binary {0,1}, equals 1 if the th arrival train of direction stops at track , and 0 otherwise, | |
| Binary {0,1}, equals 1 if the th passing train from direction to direction stops at track (a, g), and 0 otherwise, , | |
| Integer representing the passenger number of traffic zone boarding at station to travel in direction , |
| Arcs | Length (km) | Capacity (Trains/Day) | Arcs | Length (km) | Capacity (Trains/Day) |
|---|---|---|---|---|---|
| Railway lines | |||||
| (q1, a2) | 179 | 263 | (q4, a1) | 331 | 150 |
| (q1, a3) | 179 | 263 | (q4, a2) | 201 | 120 |
| (b2, a2) | 237 | 263 | (q4, a3) | 201 | 221 |
| (b2, a3) | 237 | 263 | (b8, a1) | 111 | 287 |
| (q2, a2) | 250 | 164 | (b1a, q1) | 0 | 263 |
| (q2, a3) | 250 | 164 | (b1b, q1) | 0 | 263 |
| (b4, a4) | 212 | 287 | (b3a, q2) | 0 | 164 |
| (b4, a5) | 212 | 287 | (b3b, q2) | 0 | 164 |
| (q3, a1) | 102 | 150 | (b5a, q3) | 0 | 263 |
| (q3, a2) | 91 | 263 | (b5b, q3) | 0 | 150 |
| (b6, a4) | 282 | 273 | (b7a, q4) | 0 | 221 |
| (b6, a5) | 282 | 273 | (b7b, q4) | 0 | 200 |
| Connecting lines | |||||
| (a2, a4) | 36 | 331 | (a1, a4) | 43 | 331 |
| (a2, a5) | 36 | 331 | (a1, a5) | 43 | 331 |
| (a3, a4) | 36 | 331 | (a1, a2) | 15 | 331 |
| (a3, a5) | 36 | 331 | |||
| Travel routes | |||||
| (o1, a1) | 5 | - | (o2, a4) | 10 | - |
| (o1, a2) | 10 | - | (o2, a5) | 10 | - |
| (o1, a3) | 10 | - | (o3, a1) | 10 | - |
| (o1, a4) | 15 | - | (o3, a2) | 15 | - |
| (o1, a5) | 15 | - | (o3, a3) | 15 | - |
| (o2, a1) | 15 | - | (o3, a4) | 5 | - |
| (o2, a2) | 5 | - | (o3, a5) | 5 | - |
| (o2, a3) | 5 | - | |||
| Track Number | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a1 | 36 | 38 | 40 | 45 | 40 | 38 | 38 | 38 | 36 | 36 | 36 | 30 | 30 |
| a2 | 30 | 36 | 40 | 42 | 45 | 38 | 38 | 45 | 45 | 40 | 36 | 30 | 30 |
| a3 | 30 | 45 | 34 | 36 | 45 | 45 | 38 | 36 | 44 | 42 | 40 | ||
| a4 | 30 | 36 | 38 | 45 | 44 | 40 | 36 | 38 | 34 | ||||
| a5 | 30 | 38 | 40 | 45 | 36 | 38 | 38 | 34 |
| Parameters | Definition | Value |
|---|---|---|
| Per cost of train running on lines | 0.3 (thousand RMB/train·km) | |
| Cost of train operation on tracks | 50 (thousand RMB/train) | |
| Per travel cost of passengers | 0.04 (thousand RMB/person·km) | |
| Passenger capacity of the high-speed train | 1000 (persons/train) | |
| Passenger capacity of the normal-speed train | 1460 (persons/train) | |
| Passenger capacity of the passing train | 800 (persons/train) |
| B | Arrival Trains | Track Allocation | N | Departure Trains | Track Allocation | N |
|---|---|---|---|---|---|---|
| b1a | b1a-q1-a2 | a2 [5, 9, 10] | 3 | a1-a2-q1-b1a | a1 [5] | 1 |
| a4-a2-q1-b1a | a4 [1, 2] | 2 | ||||
| b1a-q1-a3 | a3 [5, 7, 7, 9,11] | 5 | a4-a3-q1-b1a | a4 [1, 2, 9] | 3 | |
| a5-a2-q1-b1a | a5 [3, 5] | 2 | ||||
| b1b | b1b-q1-a2 | a2 [4, 4, 5, 5, 8, 9, 9, 10, 11] | 9 | a1-a2-q1-b1b | a1 [1, 4, 5, 5, 5, 10, 11, 12] | 8 |
| a4-a2-q1-b1b | a4 [2, 3, 4, 5, 5, 7, 9] | 7 | ||||
| b1b-q1-a3 | a3 [6, 8, 8, 8, 9, 9, 10, 10, 10, 11] | 10 | a4-a3-q1-b1b | a4 [9] | 1 | |
| a5-a2-q1-b1b | a5 [1, 1] | 2 | ||||
| a5-a3-q1-b1b | a5 [1] | 1 | ||||
| b2 | b2-a2 | a2 [4, 6, 6, 7, 8, 8, 9] | 7 | a1-a2-b2 | a1 [3, 3, 4, 5, 6, 9, 10, 10, 10, 11, 12, 12] | 12 |
| a2-b2 | a2 [4, 5, 5, 10, 10, 13] | 6 | ||||
| b2-a3 | a3 [1, 1, 2, 3, 4, 4, 4, 5, 8, 8, 9, 9, 9, 9, 10, 10, 10, 11, 11, 11, 11,11] | 22 | a3-b2 | a3 [2, 5, 8, 9, 9, 9, 10, 11] | 8 | |
| a4-a3-b2 | a4 [4, 4] | 2 | ||||
| a5-a3-b2 | a5 [5] | 1 | ||||
| b3a | b3a-q2-a2 | a2 [5, 7, 10] | 3 | a1-a2-q2-b3a | a1 [1, 1, 2, 2, 2, 4, 4] | 6 |
| a4-a2-q2-b3a | a4 [5, 6] | 2 | ||||
| b3a-q2-a3 | a3 [3, 7, 8, 8, 10, 11] | 7 | a5-a2-q2-b3a | a5 [8] | 1 | |
| a5-a3-q2-b3a | a5 [8] | 1 | ||||
| b3b | b3b-q2-a2 | a2 [4, 4, 5, 5, 5, 6, 6, 8, 8, 8, 9, 13] | 12 | a1-a2-q2-b3b | a1 [3, 3, 3, 4, 4, 5, 6, 9, 10, 11, 11, 12, 12, 13] | 14 |
| a4-a2-q2-b3b | a4 [2, 2, 5, 5, 9, 9] | 6 | ||||
| b3b-q2-a3 | a3 [2, 6, 9, 9, 10, 10, 10, 11, 11, 11, 11, 11] | 12 | a4-a3-q2-b3b | a4 [4, 4, 5] | 3 | |
| a5-a2-q2-b3b | a5 [2] | 1 |
| O/B | b1a | b1b | b2 | b3a | b3b | b4 | b5a | b5b | b6 | b7a | b7b | b8 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| o1 | a1, 10 | a1, 30 | a1, 12 | a1, 10 | a1, 20 | a1, 7 | a1, 10 | a1, 30 | a1, 15 | a1, 10 | a1, 30 | a1, 17 |
| o2 | a2, 7.6 a3, 2.4 | a2, 21.2 a3, 8.8 | a2, 7.6 a3, 2.4 | a2, 4 a3, 8 | a3, 20 | a2, 6.2 a3, 0.8 | a2, 10 | a2, 30 | a2, 15 | a2, 7.6 a3, 2.4 | a2, 30 | a2, 17 |
| o3 | a4, 7.08 a5, 2.92 | a4, 26.2 a5, 3.8 | a4, 8.6 a5, 3.4 | a4, 5.48 a5, 4.52 | a4, 19 a5, 1 | a4, 0.2 a5, 6.8 | a4, 8.54 a5, 1.46 | a4, 19.8 a5, 10.2 | a4, 7.4 a5, 7.6 | a4, 9.2 a5, 0.8 | a4, 22.6 a5, 7.4 | a4, 8.2 a5, 8.8 |
| Station | Yard | Directions |
|---|---|---|
| Zhengzhou | a1 | b1a, b3a, b5a, b7a, b8 |
| Zhengzhou East | a2 | b1b, b5b |
| a3 | b2, b3b, b7b | |
| Zhengzhou South | a4 | b4 |
| a5 | b6 |
| Scheme | Total Cost (Thousand RMB) | Train Cost (Thousand RMB) | Passenger Cost (Thousand RMB) | Line Capacity Utilization (%) | Track Capacity Utilization (%) |
|---|---|---|---|---|---|
| Scenario 1 | 417,709 | 176,509 | 241,200 | 28.54 | 58.74 |
| OP | 295,109 | 174,509 | 120,600 | 28.73 | 58.89 |
| Scheme | Total Cost (Thousand RMB) | Train Cost (Thousand RMB) | Passenger Cost (Thousand RMB) | Line Capacity Utilization (%) | Track Capacity Utilization (%) |
|---|---|---|---|---|---|
| Scenario 2 | 381,206 | 171,686 | 209,520 | 26.01 | 58.56 |
| OP | 295,109 | 174,509 | 120,600 | 28.73 | 58.89 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Song, R.; He, S.; Song, Z. Train Routing and Track Allocation Optimization Model of Multi-Station High-Speed Railway Hub. Sustainability 2022, 14, 7292. https://doi.org/10.3390/su14127292
Wang Y, Song R, He S, Song Z. Train Routing and Track Allocation Optimization Model of Multi-Station High-Speed Railway Hub. Sustainability. 2022; 14(12):7292. https://doi.org/10.3390/su14127292
Chicago/Turabian StyleWang, Yidong, Rui Song, Shiwei He, and Zilong Song. 2022. "Train Routing and Track Allocation Optimization Model of Multi-Station High-Speed Railway Hub" Sustainability 14, no. 12: 7292. https://doi.org/10.3390/su14127292
APA StyleWang, Y., Song, R., He, S., & Song, Z. (2022). Train Routing and Track Allocation Optimization Model of Multi-Station High-Speed Railway Hub. Sustainability, 14(12), 7292. https://doi.org/10.3390/su14127292





