Research on the Destruction Resistance of Giant Urban Rail Transit Network from the Perspective of Vulnerability
Abstract
:1. Introduction
2. Literature Review
3. Methodology
3.1. GURT Network Modeling
- Assumption (1): The GURT network is regarded as an unweighted, undirected, and no self-loop network, that is, the direction and weight are not considered;
- Assumption (2): There are no duplicate edges between nodes. If adjacent station a and station b are connected by tracks, only one edge is drawn regardless of the number of track lines;
- Assumption (3): The GURT network is considered as a self-loop-free network, where nodes are not connected to themselves;
- Assumption (4): Failure repair of the GURT is not considered during the network attacks.
3.2. Network Metrics Analysis
3.2.1. Global Network Characteristic Indexes
- (1)
- Average path length and network diameter
- (2)
- Network connectivity
3.2.2. Local Characteristic Indexes
- (1)
- Degree and average degree
- (2)
- Betweenness
- (3)
- Clustering coefficient
- (4)
- Closeness centrality
3.2.3. Network Vulnerability Metrics
- (1)
- Network efficiency
- (2)
- Largest connected component ratio
3.3. Network Attack Strategies
- Random attack strategy based on node (RAS-N);
- The largest degree first attack strategy based on node (LDAS-N);
- The largest betweenness first attack strategy based on node (LBAS-N);
- Random attack strategy based on edge (RAS-E);
- The largest betweenness first attack strategy based on edge (LBAS-E).
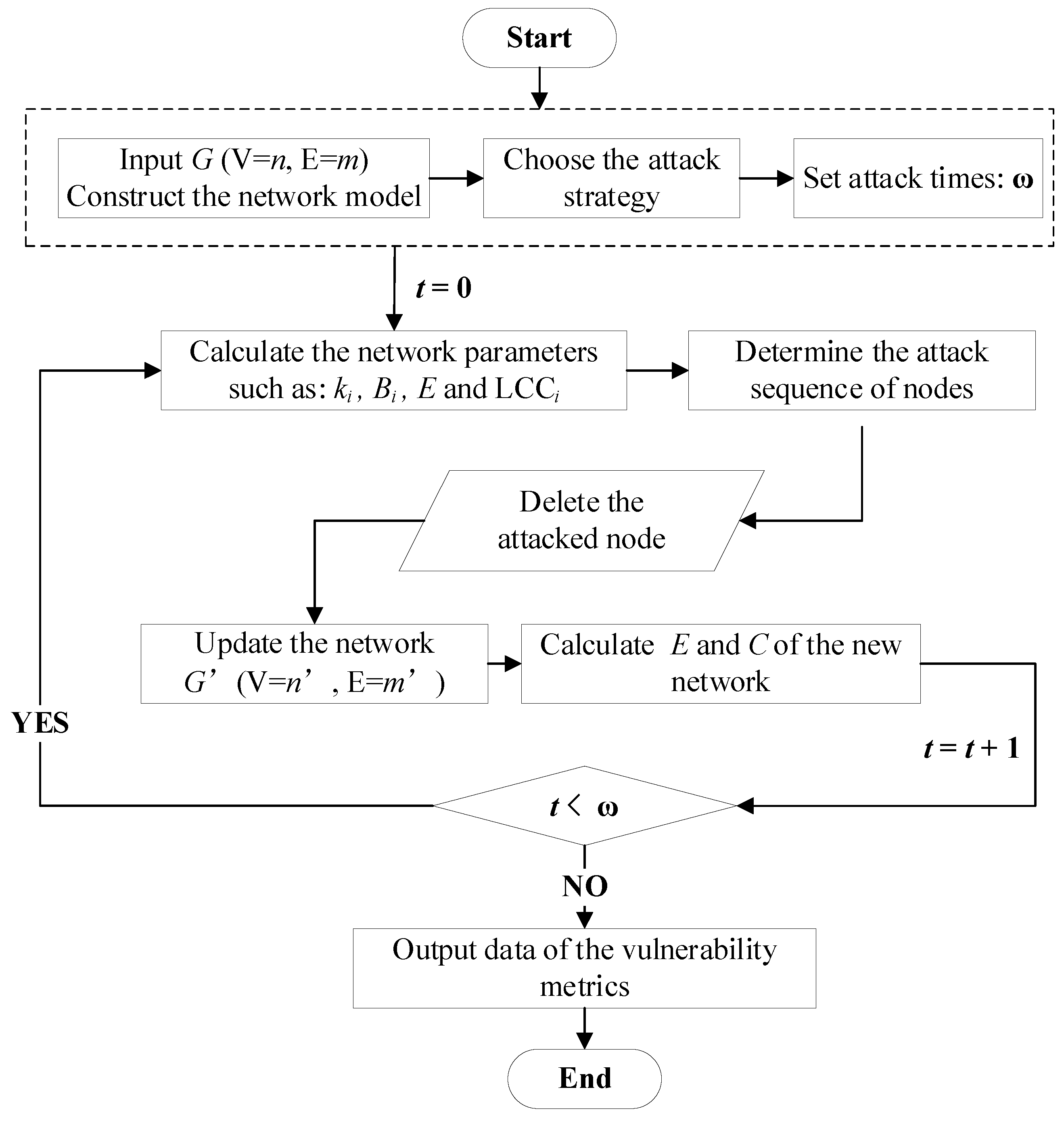
- Step (1): Construct the model of GURT network, with the stations as nodes and the rail lines as edges;
- Step (2): Calculate the network efficiency E and largest connected component ratio C in the initial state;
- Step (3): Choose an attack strategy, calculate the characteristic metrics of network nodes and edges, and determine the attack sequence;
- Step (4): Remove the attacked node or edge. When the node is removed, the edges connected to this node are removed at the same time. Then, update the network;
- Step (5): Compute the network efficiency E and the largest connected component ratio C after node or edge is deleted;
- Step (6): Go back to Step (3) and continue with the next attack until the GURT network is completely collapsed;
- Step (7): Attack ends.
4. Results
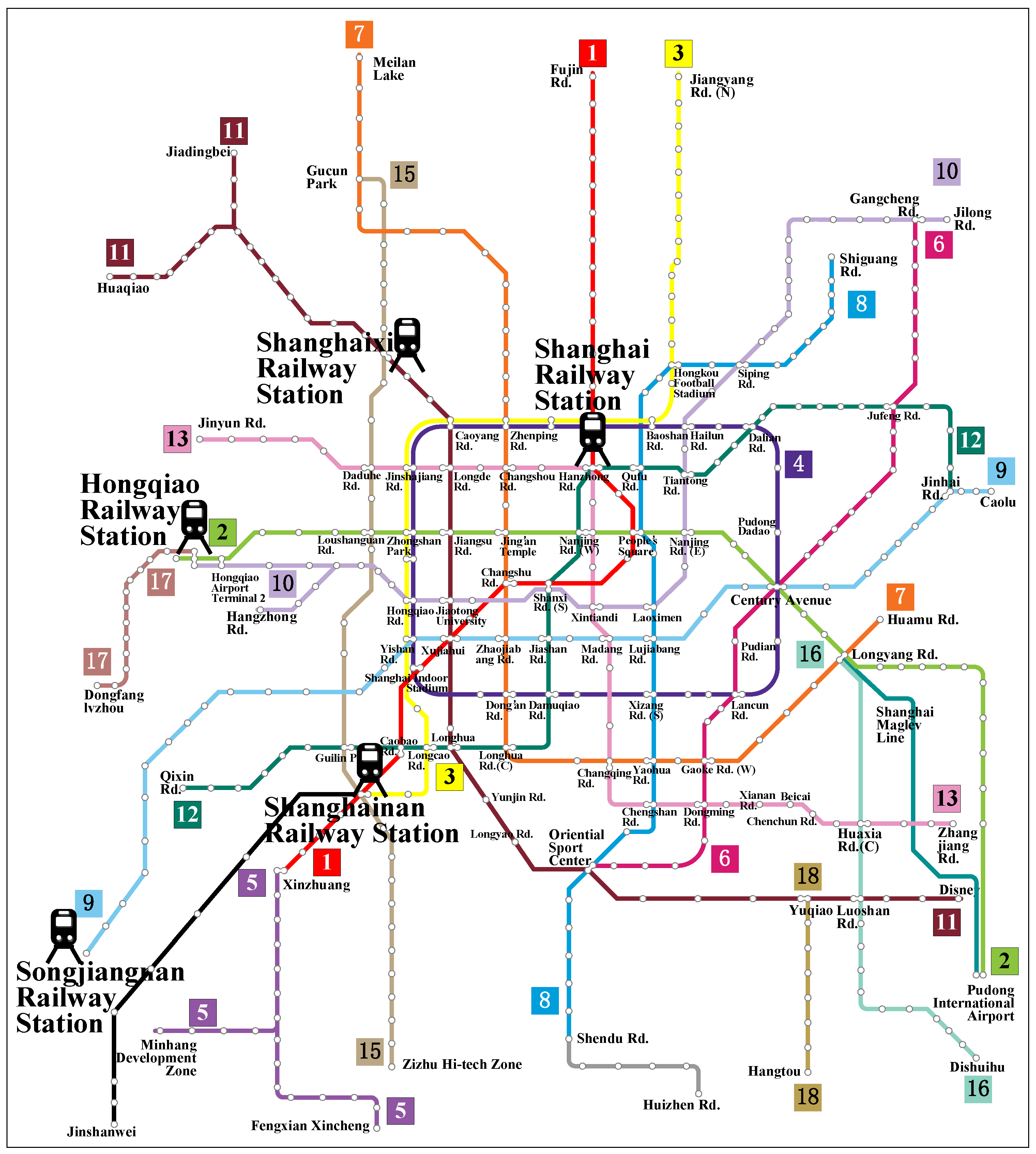
4.1. Modeling of SHRT Network
4.2. Comparison of Topology Characteristics in SHRTON and SHRTPN
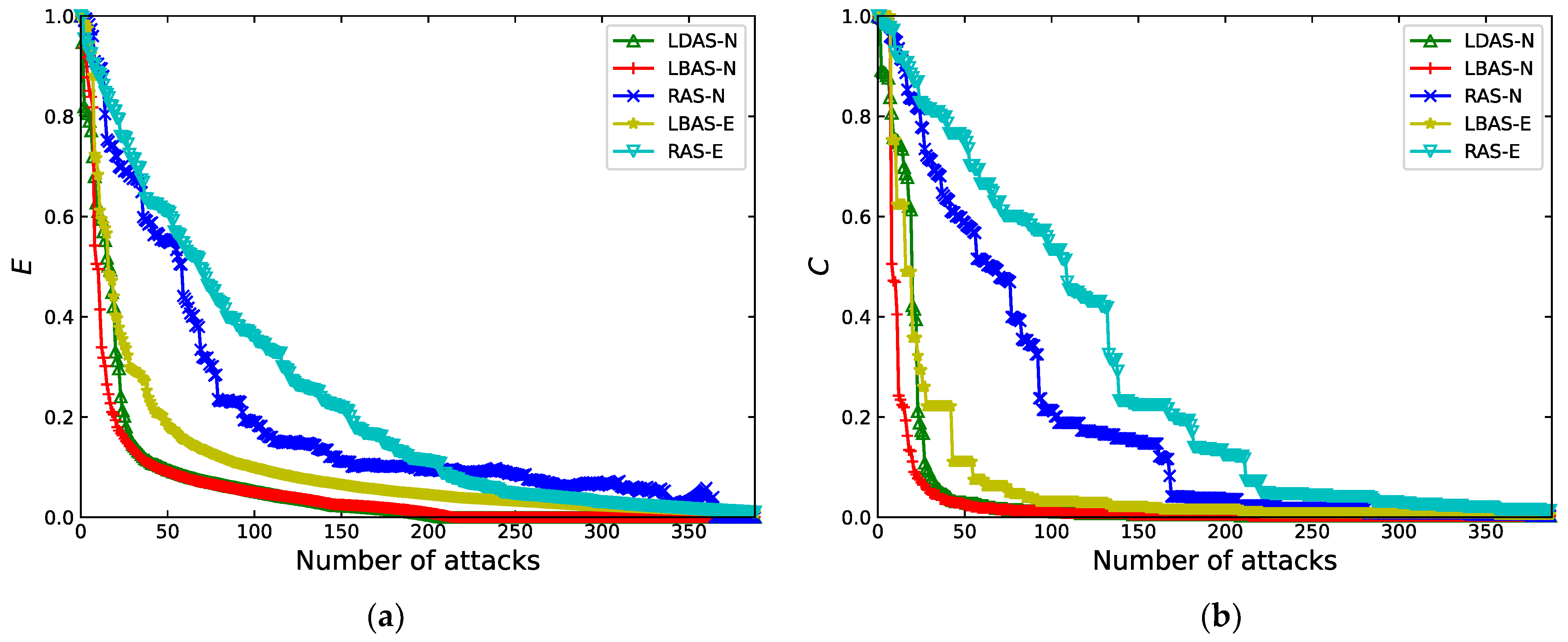
4.3. Analysis of Network Vulnerability under Different Attack Strategies
4.3.1. Vulnerability Comparison of the Theoretical Networks and SHRTON
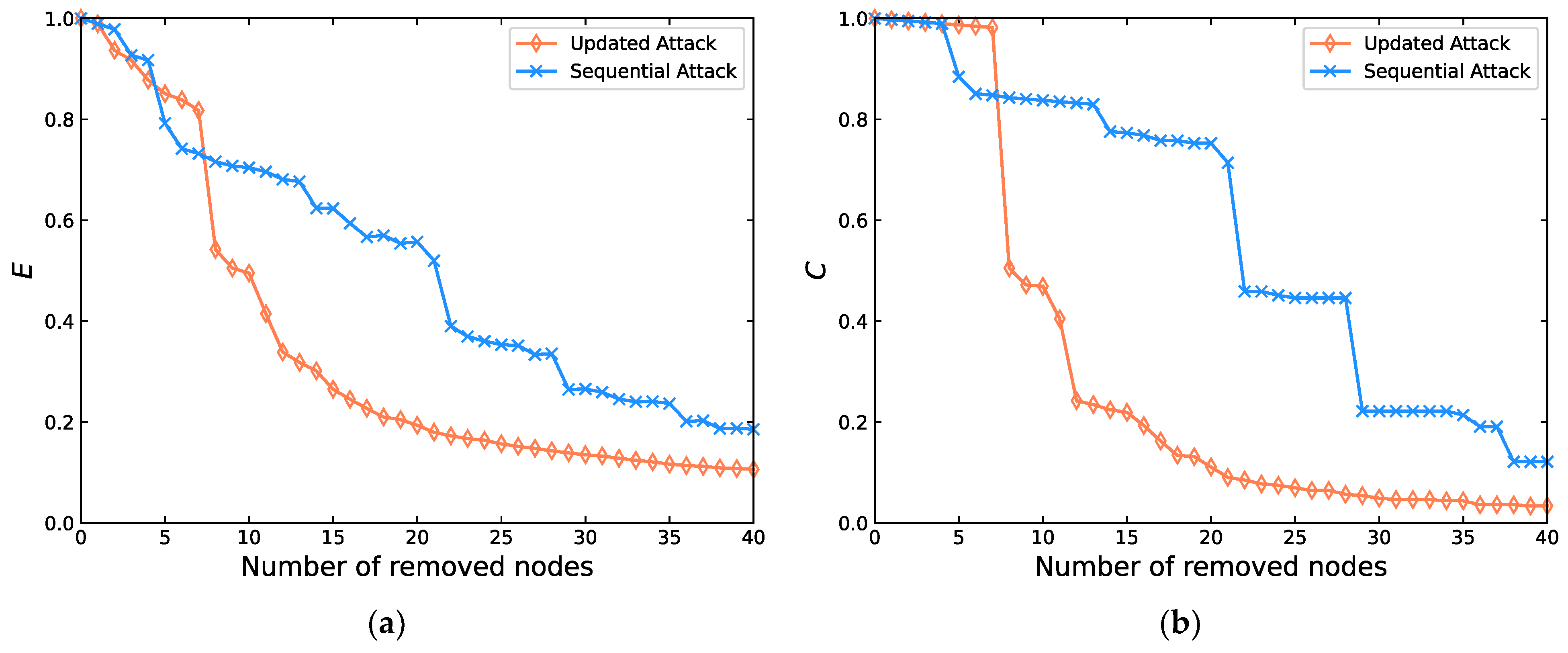
4.3.2. Vulnerability Comparison of SHRTON under Multiple Attack Strategies
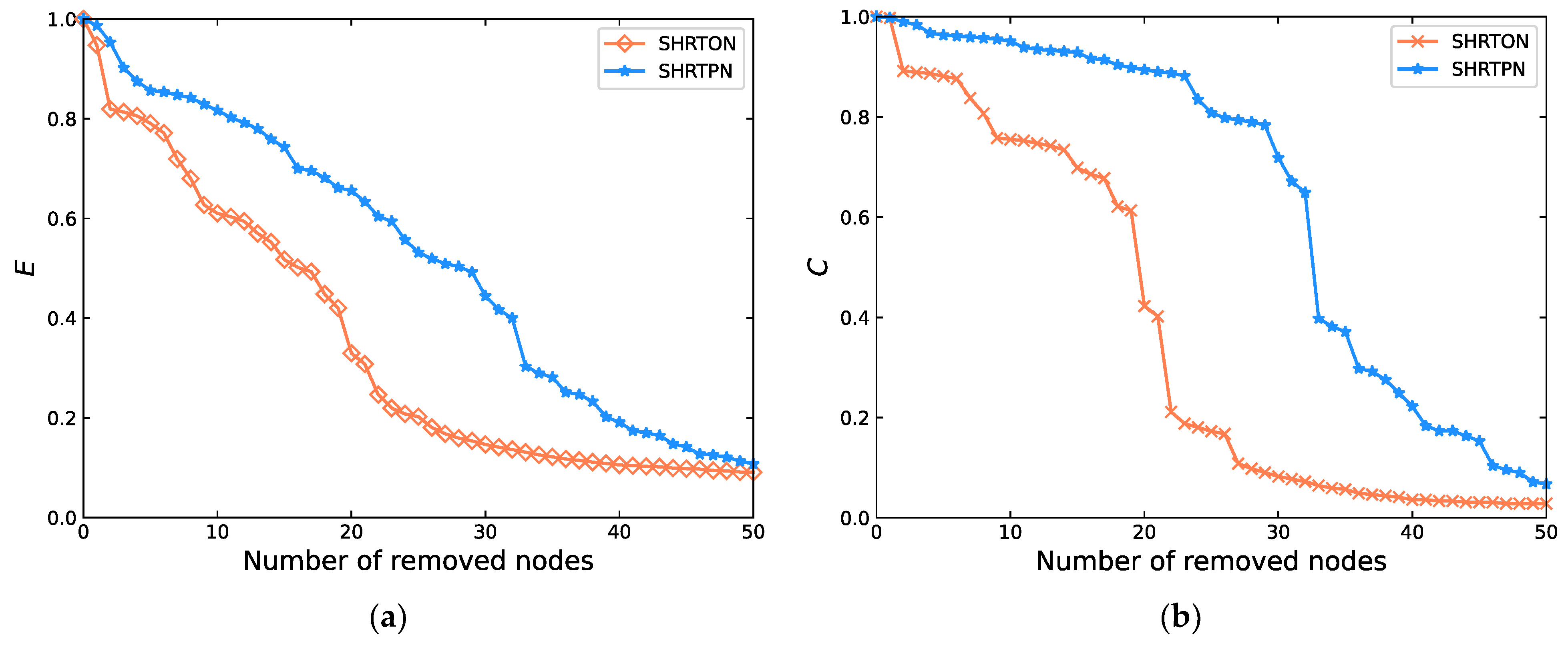
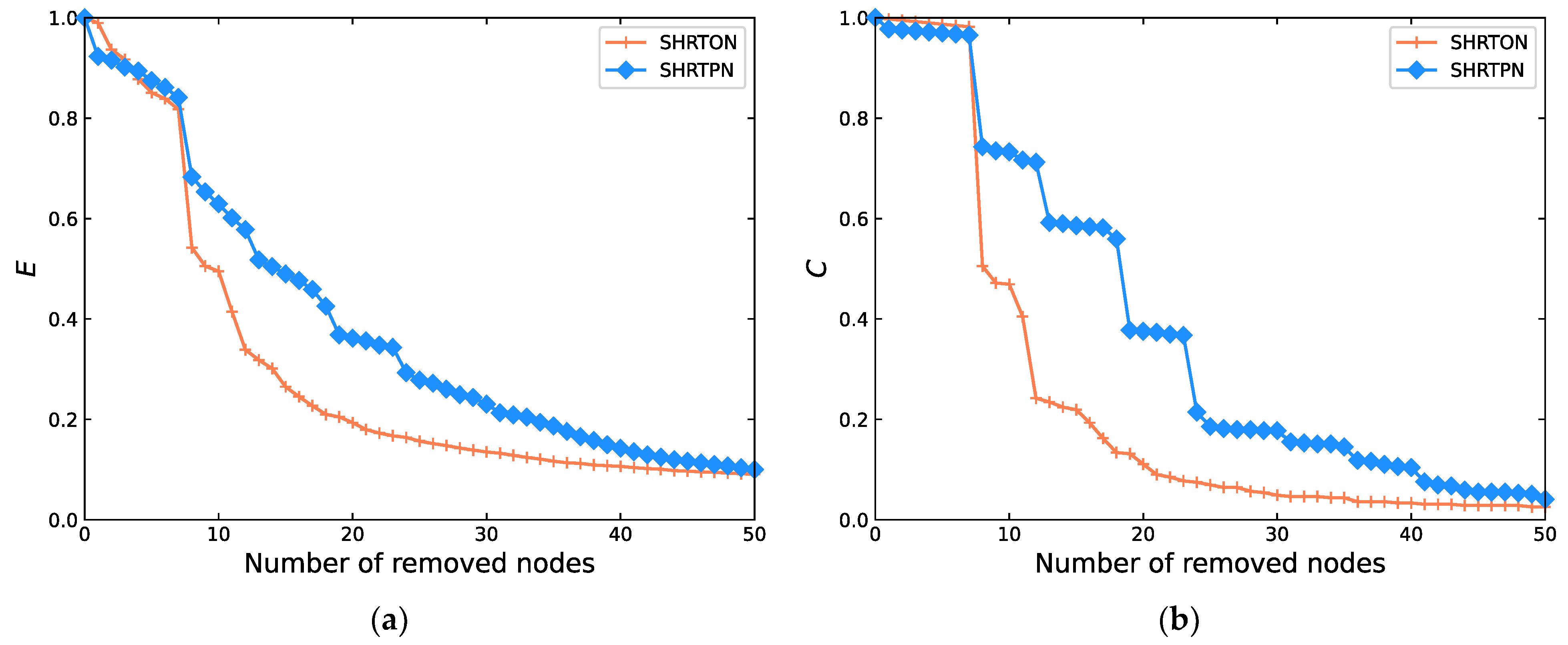
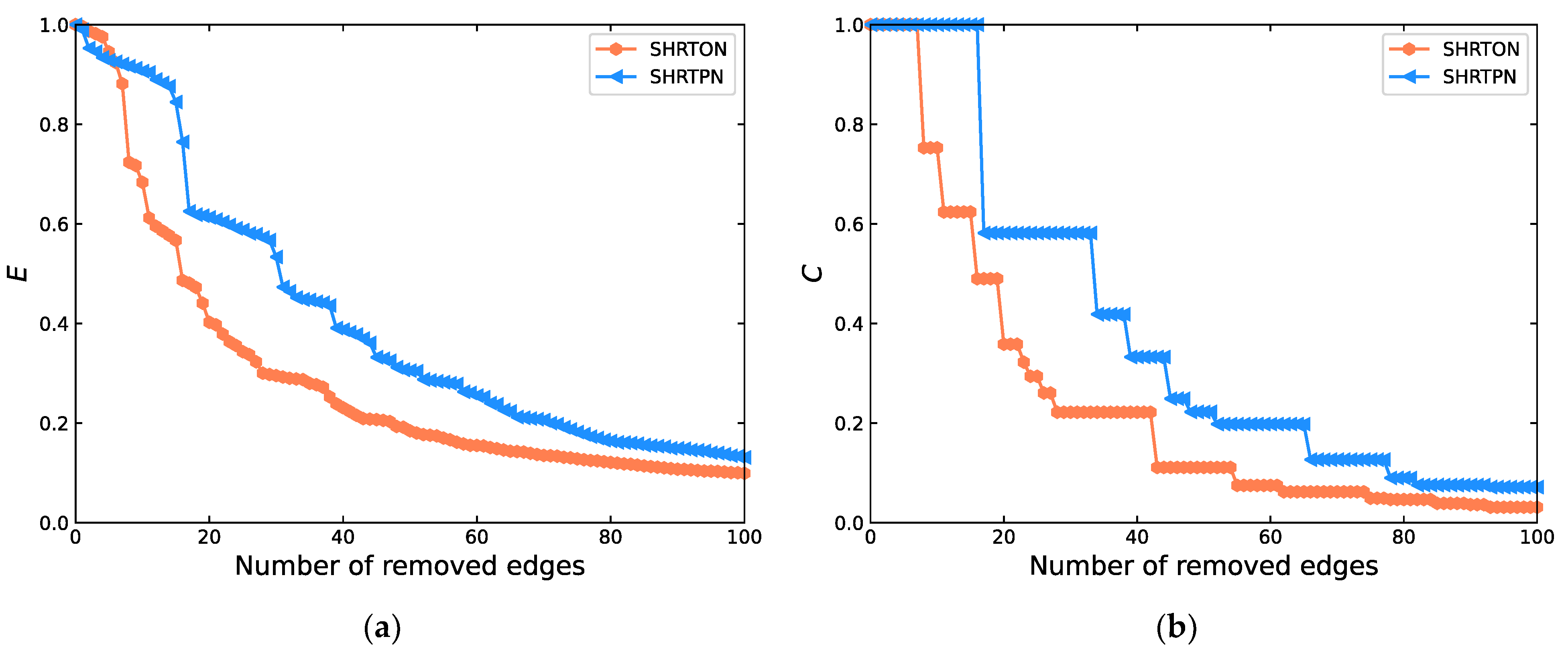
4.3.3. Vulnerability Comparison of SHRTON and SHRTPN
- (1)
- Attack network nodes
- (2)
- Attack network edges
4.4. Identification of Critical Stations and Lines of SHRT Network
4.4.1. Identification of Critical Stations
4.4.2. Identification of Critical Lines
5. Discussion
5.1. Characteristics Analysis of SHRT Network
5.2. Destruction Resistance of SHRT Network to Failures and Attacks
5.3. Strategies to Improve the Destruction Resistance of GURT Network
- (1)
- Strengthen the protection of critical stations and lines
- (2)
- Control the APL and network diameter
- (3)
- Increase the proportion of transfer station
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shi, J.G.; Wen, S.P.; Zhao, X.B.; Wu, G.D. Sustainable development of urban rail transit networks: A vulnerability perspective. Sustainability 2019, 11, 1335. [Google Scholar] [CrossRef] [Green Version]
- Cats, O.; Krishnakumari, P. Metropolitan rail network robustness. Phys. A 2020, 549, 124317. [Google Scholar] [CrossRef]
- Roth, C.; Kang, S.M.; Batty, M.; Barthelemy, M. A long-time limit for world subway networks. J. R. Soc. Interface 2012, 9, 2540–2550. [Google Scholar] [CrossRef] [PubMed]
- Zhang, D.M.; Du, F.; Huang, H.W.; Zhang, F.; Ayyub, B.M.; Beer, M. Resiliency assessment of urban rail transit networks: Shanghai metro as an example. Saf. Sci. 2018, 106, 230–243. [Google Scholar] [CrossRef]
- Saadat, Y.; Ayyub, B.M.; Zhang, Y.J.; Zhang, D.M.; Huang, H.W. Resilience-based strategies for topology enhancement and recovery of metrorail transit networks. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part A-Civ. Eng. 2020, 6, 04020017. [Google Scholar] [CrossRef]
- Sun, L.S.; Huang, Y.C.; Chen, Y.Y.; Yao, L.Y. Vulnerability assessment of urban rail transit based on multi-static weighted method in Beijing, China. Transp. Res. Part A-Policy Pract. 2018, 108, 12–24. [Google Scholar] [CrossRef]
- 2022 New York City Subway Attack. Available online: https://en.wikipedia.org/wiki/2022_New_York_City_Subway_attack (accessed on 18 May 2022).
- Shanghai Metro Official Weibo. Available online: https://weibo.com/shmetro (accessed on 16 April 2020).
- Cats, O. Topological evolution of a metropolitan rail transport network: The case of Stockholm. J. Transp. Geogr. 2017, 62, 172–183. [Google Scholar] [CrossRef] [Green Version]
- Cats, O.; Vermeulen, A.; Warnier, M.; van Lint, H. Modelling growth principles of metropolitan public transport networks. J. Transp. Geogr. 2020, 82, 102567. [Google Scholar] [CrossRef]
- Lin, J.Y.; Ban, Y.F. Complex network topology of transportation systems. Transp. Rev. 2013, 33, 658–685. [Google Scholar] [CrossRef]
- Xie, F.; Levinson, D. Modeling the growth of transportation networks: A comprehensive review. Netw Spat. Econ. 2009, 9, 291–307. [Google Scholar] [CrossRef] [Green Version]
- Latora, V.; Marchiori, M. Is the Boston subway a small-world network. Phys. A 2002, 314, 109–113. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.H.; Xu, X.M.; Hong, L.; Wang, S.L.; Fei, Q. Networked analysis of the Shanghai subway network, in China. Phys. A 2011, 390, 4562–4570. [Google Scholar] [CrossRef]
- Chopra, S.S.; Dillon, T.; Bilec, M.M.; Khanna, V. A network-based framework for assessing infrastructure resilience: A case study of the London metro system. J. R. Soc. Interface 2016, 13, 20160113. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Seaton, K.A.; Hackett, L.M. Stations, trains and small-world networks. Phys. A 2004, 339, 635–644. [Google Scholar] [CrossRef] [Green Version]
- Berdica, K. An introduction to road vulnerability: What has been done, is done and should be done. Transp. Policy 2002, 9, 117–127. [Google Scholar] [CrossRef]
- Pagani, A.; Mosquera, G.; Alturki, A.; Johnson, S.; Jarvis, S.; Wilson, A.; Guo, W.S.; Varga, L. Resilience or robustness: Identifying topological vulnerabilities in rail networks. R. Soc. Open Sci. 2019, 6, 181301. [Google Scholar] [CrossRef] [Green Version]
- Zhou, J.; Coit, D.W.; Felder, F.A.; Wang, D. Resiliency-based restoration optimization for dependent network systems against cascading failures. Reliab. Eng. Syst. Saf. 2020, 207, 107383. [Google Scholar] [CrossRef]
- Barabasi, A.L.; Albert, R. Emergence of scaling in random networks. Science 1999, 286, 509–512. [Google Scholar] [CrossRef] [Green Version]
- Opsahl, T.; Agneessens, F.; Skvoretz, J. Node centrality in weighted networks: Generalizing degree and shortest paths. Soc. Netw. 2010, 32, 245–251. [Google Scholar] [CrossRef]
- Liu, J.; Lu, H.P.; Ma, H.; Liu, W.Z. Network vulnerability analysis of rail transit plans in Beijng-Tianjin-Hebei region considering connectivity reliability. Sustainability 2017, 9, 1479. [Google Scholar] [CrossRef] [Green Version]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ‘small-world’ networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef] [PubMed]
- Erdos, P.; Rényi, A. On the evolution of random graphs. Publ. Math. Inst. Hung. Acad. Sci. 1960, 5, 17–60. [Google Scholar]
- Liu, S.; Yin, C.; Chen, D.; Lv, H.; Zhang, Q. Cascading failure in multiple critical infrastructure interdependent networks of syncretic railway system. IEEE Trans. Intell. Transp. Syst. 2021, 23, 5740–5753. [Google Scholar] [CrossRef]
- Crucitti, P.; Latora, V.; Marchiori, M. Model for cascading failures in complex networks. Phys. Rev. E 2004, 69, 045104. [Google Scholar] [CrossRef] [Green Version]
- Huang, X.; Gao, J.; Buldyrev, S.V.; Havlin, S.; Stanley, H.E. Robustness of interdependent networks under targeted attack. Phys. Rev. E 2011, 83, 065101. [Google Scholar] [CrossRef] [Green Version]
- Lopez, F.A.; Paez, A.; Carrasco, J.A.; Ruminot, N.A. Vulnerability of nodes under controlled network topology and flow autocorrelation conditions. J. Transp. Geogr. 2017, 59, 77–87. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, W.; Lee, P.T.W. Importance rankings of nodes in the China Railway Express network under the Belt and Road Initiative. Transp. Res. Part A-Policy Pract. 2020, 139, 134–147. [Google Scholar] [CrossRef]
- Meng, Y.Y.; Tian, X.L.; Li, Z.W.; Zhou, W.; Zhou, Z.J.; Zhong, M.H. Exploring node importance evolution of weighted complex networks in urban rail transit. Phys. A 2020, 558, 124925. [Google Scholar] [CrossRef]
- Yang, Y.H.; Liu, Y.X.; Zhou, M.X.; Li, F.X.; Sun, C. Robustness assessment of urban rail transit based on complex network theory: A case study of the Beijing subway. Saf. Sci. 2015, 79, 149–162. [Google Scholar] [CrossRef]
- Gauthier, P.; Furno, A.; El Faouzi, N.E. Road network resilience: How to identify critical links subject to day-to-day disruptions. Transp. Res. Rec. 2018, 2672, 54–65. [Google Scholar] [CrossRef] [Green Version]
- Dui, H.; Chen, S.; Wang, J. Failure-oriented maintenance analysis of nodes and edges in network systems. Reliab. Eng. Syst. Saf. 2021, 215, 107894. [Google Scholar] [CrossRef]
- Dunn, S.; Wilkinson, S.M. Increasing the resilience of air traffic networks using a network graph theory approach. Transp. Res. Part E-Logist. Transp. Rev. 2016, 90, 39–50. [Google Scholar] [CrossRef] [Green Version]
- Jenelius, E.; Cats, O. The value of new public transport links for network robustness and redundancy. Transp. A 2015, 11, 819–835. [Google Scholar] [CrossRef]
- Cao, X.B.; Hong, C.; Du, W.B.; Zhang, J. Improving the network robustness against cascading failures by adding links. Chaos Solitons Fractals 2013, 57, 35–40. [Google Scholar] [CrossRef]
- Ding, R.; Zhang, T.; Zhou, T.; Zhang, Y.L.; Li, T.F.; Wu, J.J. Topologic characteristics and sustainable growth of worldwide urban rail networks. Int. J. Mod. Phys. B 2021, 35, 2150151. [Google Scholar] [CrossRef]
- Derrible, S.; Kennedy, C. The complexity and robustness of metro networks. Phys. A 2010, 389, 3678–3691. [Google Scholar] [CrossRef]
- Ferber, C.; Holovatch, T.; Holovatch, Y.; Palchykov, V. Network harness: Metropolis public transport. Phys. A 2007, 380, 585–591. [Google Scholar] [CrossRef] [Green Version]
- Sienkiewicz, J.; Holyst, J.A. Statistical analysis of 22 public transport networks in Poland. Phys. Rev. E 2005, 72, 046127. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sen, P.; Dasgupta, S.; Chatterjee, A.; Sreeram, P.A.; Mukherjee, G.; Manna, S.S. Small-world properties of the Indian railway network. Phys. Rev. E 2003, 67, 036106. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- von Ferber, C.; Holovatch, T.; Holovatch, Y.; Palchykov, V. Public transport networks: Empirical analysis and modeling. Eur. Phys. J. B 2009, 68, 261–275. [Google Scholar] [CrossRef] [Green Version]
- Zhou, J.; Huang, N.; Coit, D.W.; Felder, F.A. Combined effects of load dynamics and dependence clusters on cascading failures in network systems. Reliab. Eng. Syst. Saf. 2018, 170, 116–126. [Google Scholar] [CrossRef]
- Wang, X.F.; Li, X.; Chen, G.R. Network Science: An Introduction; Higher Education Press: Beijing, China, 2012; pp. 139–161. [Google Scholar]
- Latora, V.; Marchiori, M. Efficient behavior of small-world networks. Phys. Rev. Lett. 2001, 87, 198701. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Newman, M.E. Mixing patterns in networks. Phys. Rev. E 2003, 67, 026126. [Google Scholar] [CrossRef] [Green Version]
- Shanghai. Available online: https://en.wikipedia.org/wiki/Shanghai (accessed on 30 March 2021).
- Shanghai Metro. Available online: https://en.wikipedia.org/wiki/Shanghai_Metro (accessed on 8 November 2021).
- Zeng, G.; Li, D.; Guo, S.; Gao, L.; Gao, Z.; Stanley, H.E.; Havlin, S. Switch between critical percolation modes in city traffic dynamics. Proc. Natl. Acad. Sci. USA 2019, 116, 23–28. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Du, Z.Y.; Tang, J.J.; Qi, Y.; Wang, Y.W.; Han, C.Y.; Yang, Y.F. Identifying critical nodes in metro network considering topological potential: A case study in Shenzhen city-China. Phys. A 2020, 539, 122926. [Google Scholar] [CrossRef]
- Xu, H.; Jiao, L.D.; Chen, S.L.; Deng, M.L.; Shen, N.X. An innovative approach to determining high-risk nodes in a complex urban rail transit station: A perspective of promoting urban sustainability. Sustainability 2018, 10, 2456. [Google Scholar] [CrossRef] [Green Version]
- Humphries, M.D.; Gurney, K. Network ‘Small-World-Ness’: A quantitative method for determining canonical network equivalence. PLoS ONE 2008, 3, e0002051. [Google Scholar] [CrossRef]
- Sun, D.; Zhao, Y.H.; Lu, Q.C. Vulnerability analysis of urban rail transit networks: A case study of Shanghai, China. Sustainability 2015, 7, 6919–6936. [Google Scholar] [CrossRef] [Green Version]
- Lempert, R.J.; Groves, D.G.; Popper, S.W.; Bankes, S.C. A general, analytic method for generating robust strategies and narrative scenarios. Manag. Sci. 2006, 52, 514–528. [Google Scholar] [CrossRef]






| Network Parameters | SHRTON | SHRTPN |
|---|---|---|
| Nodes | 388 | 490 |
| Edges | 448 | 614 |
| Average degree | 2.309 | 2.506 |
| Average betweenness | 2888 | 3083 |
| Average path length | 15.926 | 13.608 |
| Network diameter | 44 | 41 |
| Average clustering coefficient | 0.008 | 0.017 |
| Average closeness centrality | 0.067 | 0.077 |
| Network connectivity | 0.387 | 0.419 |
| Network efficiency | 0.0908 | 0.1004 |
| Code | Station | SHRTON | SHRTPN | ||
|---|---|---|---|---|---|
| Degree | Betweenness | Degree’ | Betweenness’ | ||
| M1 | Hongqiao Railway Station | 3 | 4874 | 6 | 22,723 |
| M2 | Shanghai Railway Station | 4 | 13,812 | 4 | 12,461 |
| M3 | Shanghainan Railway Station | 6 | 14,396 | 6 | 6817 |
| M4 | Shanghaixi Railway Station | 4 | 10,420 | 6 | 10,680 |
| M5 | People’s Square Station | 6 | 9041 | 6 | 6967 |
| M6 | Jing’an Temple Station | 4 | 10,564 | 6 | 11,392 |
| M7 | Xujiahui Station | 6 | 16,174 | 6 | 9135 |
| M8 | East Nanjing Road Station | 4 | 7877 | 4 | 4690 |
| M10 | Century Avenue Station | 8 | 15,073 | 8 | 15,820 |
| M211 | Qibao Station | 2 | 3770 | 6 | 30,578 |
| No. | Code | Station | SHRTON | SHRTPN | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| k | B | E (%) | Er (%) | k′ | B′ | E′ (%) | Er′ (%) | |||
| 1 | M3 | Shanghainan Railway Station | 6 | 14,396 | 7.906 | 12.94 | 6 | 6817 | 9.772 | 2.67 |
| 2 | M46 | Longyang Road Station | 6 | 8887 | 8.499 | 6.41 | 8 | 18,506 | 9.773 | 2.66 |
| 3 | M4 | Shanghaixi Railway Station | 4 | 10,420 | 8.531 | 6.06 | 6 | 10,680 | 9.865 | 1.74 |
| 4 | M14 | Jinjiang Park Station | 2 | 7686 | 8.541 | 5.95 | 2 | 2125 | 10.021 | 0.19 |
| 5 | M2 | Shanghai Railway Station | 4 | 13,811 | 8.576 | 5.56 | 4 | 12,461 | 9.954 | 0.86 |
| 1 | M211 | Qibao Station | 2 | 3770 | 8.815 | 2.93 | 6 | 30,578 | 9.268 | 7.68 |
| 2 | M332 | West Huajing Station | 2 | 2660 | 8.883 | 2.18 | 6 | 27,796 | 9.477 | 5.61 |
| 3 | M1 | Hongqiao Railway Station | 3 | 4874 | 8.750 | 3.64 | 6 | 22,723 | 9.519 | 5.18 |
| 4 | M264 | Chenxiang Highway Station | 2 | 4862 | 8.790 | 3.20 | 4 | 11,472 | 9.575 | 4.63 |
| 5 | M171 | Lingzhao Xincun Station | 2 | 3770 | 8.767 | 3.45 | 3 | 12,406 | 9.629 | 4.09 |
| No. | Code | Rail Lines | SHRTON | SHRTPN | ||||
|---|---|---|---|---|---|---|---|---|
| B | E (%) | Er (%) | B′ | E′ (%) | Er′ (%) | |||
| 1 | M3, M14 | Shanghainan Railway Station, Jinjiang Park Station | 8052 | 8.502 | 6.38 | 2554 | 10.006 | 0.34 |
| 2 | M13, M14 | Lianhua Road Station, Jinjiang Park Station | 7707 | 8.548 | 5.87 | 2184 | 10.036 | 0.04 |
| 3 | M12, M13 | Waihuanlu Station, Lianhua Road Station | 7360 | 8.588 | 5.43 | 2004 | 10.030 | 0.10 |
| 4 | M4, M268 | Shanghaixi Railway Station, Liziyuan Station | 6660 | 8.615 | 5.13 | 6138 | 9.824 | 2.15 |
| 5 | M11, M12 | Xinzhuang Station, Waihuanlu Station | 7011 | 8.624 | 5.03 | 2024 | 10.018 | 0.22 |
| 1 | M280, M281 | Luoshan Road Station, Xiuyan Road Station | 1155 | 8.952 | 1.42 | 1439 | 9.664 | 3.74 |
| 2 | M346, M347 | Fengxiang Road Station, Jinqiu Road Station | 2211 | 9.053 | 0.30 | 2892 | 9.717 | 3.21 |
| 3 | M279, M370 | Yuqiao Station, Kangqiao Station | 2667 | 8.842 | 2.63 | 3381 | 9.738 | 3.01 |
| 4 | M213, M214 | Jiuting Station, Sijing Station | 3040 | 8.873 | 2.29 | 3856 | 9.742 | 2.96 |
| 5 | M345, M346 | Nanda Road Station, Fengxiang Road Station | 2569 | 9.047 | 0.37 | 3356 | 9.750 | 2.88 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, X.; Xu, C.; Zhang, W. Research on the Destruction Resistance of Giant Urban Rail Transit Network from the Perspective of Vulnerability. Sustainability 2022, 14, 7210. https://doi.org/10.3390/su14127210
Xu X, Xu C, Zhang W. Research on the Destruction Resistance of Giant Urban Rail Transit Network from the Perspective of Vulnerability. Sustainability. 2022; 14(12):7210. https://doi.org/10.3390/su14127210
Chicago/Turabian StyleXu, Xueguo, Chen Xu, and Wenxin Zhang. 2022. "Research on the Destruction Resistance of Giant Urban Rail Transit Network from the Perspective of Vulnerability" Sustainability 14, no. 12: 7210. https://doi.org/10.3390/su14127210
APA StyleXu, X., Xu, C., & Zhang, W. (2022). Research on the Destruction Resistance of Giant Urban Rail Transit Network from the Perspective of Vulnerability. Sustainability, 14(12), 7210. https://doi.org/10.3390/su14127210





