An MHD Flow of Non-Newtonian Fluid Due to a Porous Stretching/Shrinking Sheet with Mass Transfer

Abstract

An examination is carried out for three-dimensional incompressible viscoelastic fluid flow over a porous stretching/shrinking sheet with hybrid nanoparticles copper-alumina $\left(Cu-A{l}_2{O}_3\right)$ in base fluid water $\left(H_{2}O\right)$. The uniform magnetic field of strength $B_0$ is applied perpendicular to the fluid flow and considered the Navier slip. The mass transfer is considered with the chemical reaction rate. The governing equation for the defined flow forms the system of partial differential equations, which are then transformed into a system of ordinary differential equations via similarity transformations. The goal is to find the exact analytical solution, and the unique solution is determined by considering the boundary layer theory. Furthermore, the obtained system is solved to get the exact analytical solution for velocity and concentration fields in exponential form and in hypergeometric form, respectively. The exact solutions are obtained for velocity and temperature profiles, Skin friction, and Nusselt number. These findings are beneficial for future research in the present area. The parameters magnetic field, Inverse Darcy number, slip parameter, chemical reaction parameter, stretching/shrinking parameter, and viscoelastic parameter, influence the flow. The effect of these parameters on fluid velocity and concentration field will be analyzed through graphs. Skin friction and Nusselt number are also analyzed. This work found many applications in machining and manufacturing, solar energy, MHD flow meters and pumps, power generators, geothermal recovery, flow via filtering devices, chemical catalytic reactors, etc.

1. Introduction

Mass transfer and momentum boundary layer flow have practical potential in the fields of polymer process and electrochemistry; the non-Newtonian fluids flow is a significant field in industry and so has become an field of interest for researchers. Several studies have been done on the flow of various non-Newtonian fluids [1,2].

Bhattacharya [3] studied the first order chemical reaction with the impact of mass transfer by using the shooting method. Akyildiz et al. [4] investigated the chemical reaction of non-Newtonian fluid through a porous medium to obtain an exact solution, which had some interesting properties that led to further study on chemically reactive species. Mahabaleshwar et al. [5,6] examined the inclined MHD flow, mass, and heat transfer with the effect of radiation and flow due to porous medium by considering different kinds of BCs. Sarpkaya [7] discussed non-Newtonian fluids over a stretching sheet. The influence of viscous dissipation and chemical reaction on the stagnation point flow of NF due to the stretching/shrinking plate was examined by Murthy et al. [8]. The viscous flow on the shrinking sheet was examined by Miklavcic and Wang [9] and showed the existence and uniqueness, or non-uniqueness, of the exact solution. Due to the importance of the porous medium in practical applications, Mahabaleshwar et al. [10] examined the impact of both heat generation/absorption and stress work on the MHD flow due to a porous stretching sheet and analyzed the Brinkman model by considering the effect of slip on a shrinking sheet. Hayat et al. [11] gave attention to the flow of non-Newtonian fluid over a stretching/shrinking sheet and investigated the effect of partial slip. Rizwan et al. [12] studied the dual nature solution of the nanofluid convective flow in porous medium due to a shrinking sheet. Pop and Merkin et al. [13,14] studied unsteady flow in a porous medium considering the thermal slips using the shooting method and studied some limited cases. They continue work on finding a more exact solution to the same problem.

Knowing that the radiation effect is important for certain isothermal processes, Siddheshwar and Mahabaleshwar et al. [15] worked on the flow and heat transfer of MHD viscoelastic fluid flow on shrinking sheet under the effects of radiation. Turkyilmazoglu [16] also examined the flow, heat, and mass transfer of viscoelastic fluid and the impact of magnetic field and slip over a stretching surface and got multiple solutions. Furthermore, [17] examined heat and mass transfer of viscoelastic fluid due to a porous stretching sheet induced with a uniform magnetic field. Sakiadis [18] and Crane [19] are pioneers in the investigation of stretching sheet problems. An analytical study of Walters’ liquid B over a stretching sheet has been discussed by Ghasemi [20]. Being motivated by these works, researchers conducted an investigation on stretching sheet problems. In the present work, there is investigation of the exact analytical solution for velocity and concentration field for 3D MHD flow viscoelastic HNF due to porous sheet which stretched/shrunk along both x and y axes with linear velocity and Navier slip. The mass transfer is analyzed with a chemical reaction rate parameter. The effects of different physical parameters on skin friction and Nusselt number are also analyzed.

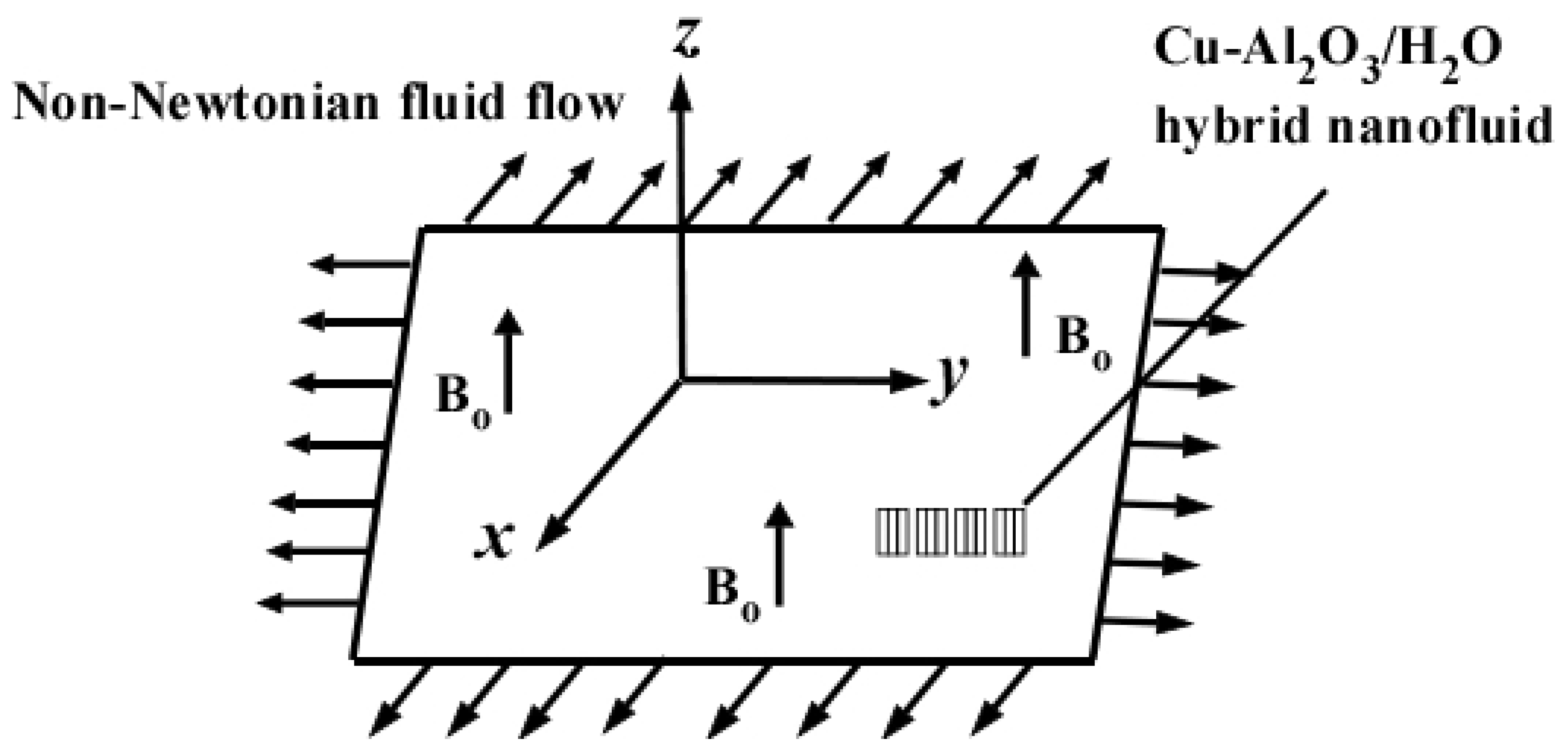
2. Physical Model

Consider the 3D incompressible viscoelastic fluid flow with HNF due to porous stretching/shrinking sheet induced by uniform magnetic field of strength $B_0$, which is applied perpendicular to the fluid flow (Figure 1). The sheet is stretched/shrunk along the x-axis and the y-axis is perpendicular to it. The mass transfer is considered with chemical reaction rate $k_C$. The governing equations for the defined flow are as follows (Turkyilmazoglu [21]).

$$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}=0,$$

(1)

$$\begin{array}{l}u\frac{\partial u}{\partial x}+\mathrm{v}\frac{\partial u}{\partial y}+w\frac{\partial u}{\partial z}=\frac{{\mu }_{eff}}{{\rho }_{hnf}}\frac{{\partial }^{2}u}{\partial z^2}+{\gamma }_{0}u-\frac{{\nu }_{hnf}}{K^1}u-\frac{{\sigma }_{hnf}{B}_0{}^2}{{\rho }_{hnf}}u\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} -k_0\left\{u\frac{{\partial }^{3}u}{\partial x\partial z^2}+w\frac{{\partial }^{3}u}{\partial z^3}-\left(\frac{\partial u}{\partial x}\frac{{\partial }^{2}u}{\partial z^2}+\frac{\partial u}{\partial z}\frac{{\partial }^{2}w}{\partial z^2}+2\frac{\partial u}{\partial z}\frac{{\partial }^{2}u}{\partial x\partial z}+2\frac{\partial w}{\partial z}\frac{{\partial }^{2}u}{\partial z^2}\right)\right\},\end{array}$$

(2)

$$\begin{array}{l}u\frac{\partial \mathrm{v}}{\partial x}+\mathrm{v}\frac{\partial \mathrm{v}}{\partial y}+w\frac{\partial \mathrm{v}}{\partial z}=\frac{{\mu }_{eff}}{{\rho }_{hnf}}\frac{{\partial }^2\mathrm{v}}{\partial z^2}+{\gamma }_0\mathrm{v}-\frac{{\nu }_{hnf}}{K^1}\mathrm{v}-\frac{{\sigma }_{nf}{B}_0{}^2}{{\rho }_{nf}}\mathrm{v}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} -k_0\left\{\mathrm{v}\frac{{\partial }^3\mathrm{v}}{\partial y\partial z^2}+w\frac{{\partial }^3\mathrm{v}}{\partial z^3}-\left(\frac{\partial \mathrm{v}}{\partial y}\frac{{\partial }^2\mathrm{v}}{\partial z^2}+\frac{\partial \mathrm{v}}{\partial z}\frac{{\partial }^{2}w}{\partial z^2}+2\frac{\partial \mathrm{v}}{\partial z}\frac{{\partial }^2\mathrm{v}}{\partial y\partial z}+2\frac{\partial w}{\partial z}\frac{{\partial }^2\mathrm{v}}{\partial z^2}\right)\right\},\end{array}$$

(3)

$$u\frac{\partial C}{\partial x}+\mathrm{v}\frac{\partial C}{\partial y}+w\frac{\partial C}{\partial z}=D_B\frac{{\partial }^{2}C}{\partial y^2}+k_C\left(C-C_{\infty }\right),$$

(4)

with traditional BCs assumption,

$$\begin{array}{l}u=ax+l\frac{\partial u}{\partial z}, \mathrm{v}=by+l\frac{\partial \mathrm{v}}{\partial z}, w=w_0, C=C_w, \mathrm{at} z=0,\\ u\to 0, \frac{\partial u}{\partial z}\to 0, \mathrm{v}\to 0, \frac{\partial \mathrm{v}}{\partial z}\to 0, C\to C_{\infty } \mathrm{as} z\to \infty \end{array}\}.$$

(5)

Here, ${\mu }_{eff}$ is the effective viscosity, ${\gamma }_0$ is porosity, $K^1$ is permeability of porous medium, $\sigma$ is electrical conductivity,$k_C$ is the chemical reaction rate parameter, a and b are stretching rates along x and y axes, l is slip parameter.

The momentum equation for the velocity component w is neglected because of boundary layer limitations (Turkyilmazoglu [22]),

• The velocity in the axial direction is much larger than that in the transverse direction, i.e.,

$$u>>v>>w.$$

• The velocity gradient in the transverse direction is much bigger than the velocity gradient in the axial direction.

Now define the similarity transformations as follows,

$$u=\left|a\right|x\frac{\partial f}{\partial \eta }, \mathrm{v}=\left|a\right|y\frac{\partial g}{\partial \eta }, w=-\sqrt{\left|a\right|\nu }\left(f\left(\eta \right)+g\left(\eta \right)\right), \varphi \left(\eta \right)=\frac{C-C_{\infty }}{C_w-C_{\infty }}$$

with

$$\eta =\sqrt{\frac{\left|a\right|}{\nu }}z,$$

(6)

Via these similarity transformations, the system PDEs in Equations (1)–(3) will transform into

$$\begin{array}{l}\frac{\Lambda }{{\epsilon }_1}{f}_{\eta \eta \eta }+f_{\eta \eta }\left(f+g\right)-f_{\eta }{}^2+\gamma f_{\eta }-\frac{1}{{\epsilon }_1}\left({\epsilon }_{2}D{a}^{-1}+{\epsilon }_{3}M\right)f_{\eta }\\ \hspace{1em}\hspace{1em}\hspace{1em} +K\left\{f_{\eta \eta \eta \eta }\left(f+g\right)+f_{\eta \eta }\left(f_{\eta \eta }-g_{\eta \eta }\right)-2f_{\eta \eta \eta }\left(f_{\eta }+g_{\eta }\right)\right\}=0\end{array}$$

(7)

$$\begin{array}{l}\frac{\Lambda }{{\epsilon }_1}{g}_{\eta \eta \eta }+g_{\eta \eta }\left(f+g\right)-g_{\eta }{}^2+\gamma g_{\eta }-\frac{1}{{\epsilon }_1}\left({\epsilon }_{2}D{a}^{-1}+{\epsilon }_{3}M\right)g_{\eta }\\ \hspace{1em}\hspace{1em}\hspace{1em} +K\left\{g_{\eta \eta \eta \eta }\left(f+g\right)+g_{\eta \eta }\left(g_{\eta \eta }-f_{\eta \eta }\right)-2g_{\eta \eta \eta }\left(f_{\eta }+g_{\eta }\right)\right\}=0\end{array}$$

(8)

$${\varphi }_{\eta \eta }+Sc\left(f+g\right){\varphi }_{\eta }+Sc\beta \varphi =0$$

(9)

and the B.Cs (5) can be reduced as follows:

$$\begin{array}{l}f\left(0\right)=V_C, f_{\eta }\left(0\right)=d+\Gamma f_{\eta \eta }\left(0\right), g_{\eta }\left(0\right)=c+\Gamma g_{\eta \eta }\left(0\right), \varphi \left(0\right)=1,\\ f_{\eta }(\infty )\to 0, f_{\eta \eta }(\infty )\to 0, g_{\eta }(\infty )\to 0, g_{\eta \eta }(\infty )\to 0, \varphi (\infty )\to 0\end{array}$$

(10)

Here, $\Lambda =\frac{{\mu }_{eff}}{{\mu }_f}$ is the Brinkman ratio, $D{a}^{-1}=\frac{{\nu }_f}{K^1\left|a\right|},$ is the inverse Darcy number, $M=\frac{{\sigma }_f{B}_0{}^2}{{\rho }_f\left|a\right|}$ is the magnetic parameter, $\gamma =\frac{{\gamma }_0}{\left|a\right|}$ is the porosity parameter, $K=\frac{k_0\left|a\right|}{\nu }$ is the viscoelastic parameter, $\Gamma =l\sqrt{\frac{\left|a\right|}{\nu }}$ is the first order velocity slip parameter,$V_C=-\frac{w_0}{\sqrt{\left|a\right|\nu }}$ indicates mass transpiration, where $V_C>0$ for suction and $V_C<0$ for injection, and $d=\frac{a}{\left|a\right|}=\pm 1$ and $c=\frac{b}{\left|a\right|}$ are the stretching/shrinking sheet parameters along the x and y axes, respectively, where $d=1$ indicates stretching rate and $d=-1$ indicates shrinking rate. $\beta =\frac{k_C}{\left|a\right|}$ is the chemical reaction rate parameter.

The quantities ${\delta }_i^{\prime }s, i=1,2,3$ in Equation (7) are defined as

$${\delta }_1=\frac{{\rho }_{hnf}}{{\rho }_f}, {\delta }_2=\frac{{\mu }_{hnf}}{{\mu }_f}, {\delta }_3=\frac{{\sigma }_{nf}}{{\sigma }_f}.$$

(11)

2.1. Analytical Solution of Momentum Problem

The solutions of Equations (7) and (8) are assumed in the following form based on the analytical solutions taken as in Turkyilmazoglu [22] and Crane [19], with BCs as in Equation (10),

$$f\left(\eta \right)=V_C+\frac{d\left(1-\exp \left(-\lambda \eta \right)\right)}{\lambda \left(1+\Gamma \lambda \right)}, g\left(\eta \right)=\frac{d\left(1-\exp \left(-\lambda \eta \right)\right)}{\lambda \left(1+\Gamma \lambda \right)}$$

(12)

Using these solutions in Equation (7) will provide the following expressions,

$$\lambda =\frac{1}{\sqrt{2K}},$$

(13)

$$-2d\left(1+K{\lambda }^2\right)+\left(1+\Gamma \lambda \right)\left\{\gamma -\frac{1}{{\delta }_1}\left({\delta }_{2}D{a}^{-1}+{\delta }_{3}M\right)-\lambda \left(V_C-\frac{\Lambda }{{\delta }_1}\lambda +K{V}_C{\lambda }^2\right)\right\}=0$$

(14)

Using Equation (13) in Equation (14) will provide the expression for mass transpiration as

$$V_C=\frac{2\left[\frac{\Lambda }{{\delta }_1}\left(\sqrt{2K}+\Gamma \right)+2K\Gamma \alpha +2K\sqrt{2K}\left(-3d+\alpha \right)\right]}{3\left(2K+\Gamma \sqrt{2K}\right)}$$

(15)

where, $\alpha =\gamma -\frac{1}{{\delta }_1}\left({\delta }_{2}D{a}^{-1}+{\delta }_{3}M\right)$ is assumed as one parameter which combines the effect of parameters, $\gamma$ and $D{a}^{-1},M>0$. The physically interested parameters and local skin friction coefficient are given by

$$f_{\eta \eta }\left(0\right)=g_{\eta \eta }\left(0\right)=-\frac{\lambda d}{\left(1+\Gamma \lambda \right)}$$

(16)

2.2. Analytical Solution of Mass Transfer Problem

To solve the Equation (9) with BCs in (10), the new variable is introduced as $\epsilon =\frac{Sc}{{\lambda }^2}{e}^{-\lambda \eta }$ which will provide

$$\epsilon \frac{{\partial }^2\varphi }{\partial {\epsilon }^2}+\left\{1-Sc{\chi }_1+\frac{2d}{1+\Gamma \lambda }\epsilon \right\}\frac{\partial \varphi }{\partial \epsilon }+\frac{Sc\beta }{{\lambda }^2}\frac{1}{\epsilon }\varphi =0$$

(17)

Here,

$${\chi }_1=\frac{V_C\lambda \left(1+\Gamma \lambda \right)+2d}{{\lambda }^2\left(1+\Gamma \lambda \right)}$$

Next, the BCs (10) are reduced to become

$$\varphi \left(\frac{Sc}{{\lambda }^2}\right)=1, \varphi \left(0\right)=0,$$

(18)

where $\epsilon =0$ is the regular singular point of $\epsilon =\frac{Sc}{{\lambda }^2}{e}^{-\lambda \eta }$. By assuming the solution of Equation (17) as power series solution $\varphi \left(\epsilon \right)={\displaystyle \sum _{r=0}^{\infty }{c}_r}{\epsilon }^{m+r}$ by adopting the Frobenius method (Hamid et al. [22]) the final solution in terms of $\epsilon$ can be obtained as

$$\varphi \left(\epsilon \right)=c_0{\epsilon }^{{\chi }_4}H\left[{\chi }_4,{\chi }_2+1,-{\chi }_3\epsilon \right]$$

(19)

The solution in terms of $\eta$ will be

$$\varphi \left(\eta \right)=c_0{\left(\frac{Sc}{{\lambda }^2}{e}^{-\lambda \eta }\right)}^{{\chi }_4}H\left[{\chi }_4,{\chi }_2+1,-{\chi }_3\frac{Sc}{{\lambda }^2}{e}^{-\lambda \eta }\right]$$

(20)

Using the BC the solution will be

$$\varphi \left(\eta \right)={\left(e^{-\lambda \eta }\right)}^{{\chi }_4}\frac{H\left[{\chi }_4,{\chi }_2+1,-{\chi }_3\frac{Sc}{{\lambda }^2}{e}^{-\lambda \eta }\right]}{H\left[{\chi }_4,{\chi }_2+1,-{\chi }_3\frac{Sc}{{\lambda }^2}\right]}$$

(21)

and the local Nusselt number is obtained as

$$-{\varphi }_{\eta }\left(0\right)=\lambda {\chi }_4-\frac{{\chi }_4}{{\chi }_2+1}\frac{{\chi }_{3}Sc}{\lambda }\frac{H\left[{\chi }_4+1,{\chi }_2+2,-{\chi }_3\frac{Sc}{{\lambda }^2}\right]}{H\left[{\chi }_4,{\chi }_2+1,-{\chi }_3\frac{Sc}{{\lambda }^2}\right]}$$

(22)

Here,

$${\chi }_2=\sqrt{S{c}^2{\chi }_1{}^2-4\frac{Sc\beta }{{\lambda }^2}}, {\chi }_3=\frac{2{\chi }_2}{1+\Gamma \lambda }, {\chi }_4=\frac{Sc{\chi }_1+{\chi }_2}{2}$$

(23)

3. Results and Discussion

The 3D incompressible viscoelastic fluid flow over porous stretching/shrinking sheet with hybrid nanoparticlesis was examined along with the mass transfer problem by considering the impact of the chemical reaction rate. The uniform magnetic field of strength $B_0$ is applied to the flow. The governing equation for the defined flow Equations (1)–(4) with B.Cs (5) forms the system of PDEs which are then transformed to a system of ODE Equations (7)–(9) by applying similarity transformations as in Equation (6). Furthermore, the system of ODEs is solved to obtain the exact analytical solution for velocity and concentration fields in exponential form and in hypergeometric form, respectively. The new defined parameter $\alpha =\gamma -\frac{1}{{\delta }_1}\left({\delta }_{2}D{a}^{-1}+{\delta }_{3}M\right)$, which includes the effect of magnetic field $\left(M\right)$, Inverse Darcy number $\left(D{a}^{-1}\right)$, porosity parameter $\left(\gamma \right)$, Brinkman ratio, $(\Lambda )$ slip parameter $(\Gamma )$, chemical reaction parameter $\left(\beta \right)$, stretching/shrinking parameter $\left(d\right)$, viscoelastic parameter $\left(K\right)$, and Schmidt number $\left(Sc\right)$, influences the flow. The effect of these parameters on fluid velocity and concentration field was analyzed through graphs. Skin friction and Nusselt number were also analyzed.The graphs are analyzed for HNF $Cu-A{l}_2{O}_3/H_{2}O$. The solid lines indicate $\Gamma =0$ and the dotted lines indicate $\Gamma =2$. The nanoparticle copper was noted to have higher rate of heat transfer and surface shear stress. To enhance the positive compatible features of each other, the appropriate composition of nanomaterials must be chosen. In previous studies, alumina has been a favorable nanoparticle due to its significant chemical motionlessness and stability.

Figure 2 and Figure 3 depict the behavior of $V_C$ with different parameters. Figure 2a,b demonstrates the solution curve of $V_C$ verses $K$ for stretching and shrinking sheet, respectively. The behavior of $V_C$ for stretching and shrinking sheet are almost same, but solution in the shrinking case will shift upward. As the parameter $\alpha$ increases, $V_C$ also increases in both the cases. It is clear that, for $\alpha <0$, $V_C$ will decrease as K increases and for $\alpha >0$, $V_C$ will increase as K increases. Furthermore, for $\alpha =0$, $V_C$ will decrease as K increases in the stretching case and $V_C$ will increase as K increases in the shrinking case. Figure 3a,b show the solution domain of $V_C$ verses $\Lambda$ and $d$, respectively. As $\alpha$ increases the mass transpiration $V_C$ also increases. Furthermore, $V_C$ increases as Casson fluid parameter $\Lambda$ increases and $V_C$ decreases as $d$ increases. $V_C$ will be greater for higher values of the slip factor.

Figure 4 depicts the transverse velocity for different values of $\alpha$ for both stretching and shrinking cases and increases with increases in $\alpha$. Transverse velocity increases with increases in slip factor in the stretching case and decreases with increases in the slip factor in the shrinking case. Figure 5 demonstrates the axial velocity for various $K,\Gamma$, and d in both stretching and shrinking cases. Axial velocity increases with increases in $K$ or d for the stretching case and decreases with increases in $K$ or d for the shrinking case. In reverse, the axial velocity is lower for higher values of $\Gamma$ in the stretching case and is higher for higher values of $\Gamma$ in the shrinking case. Axial velocity decreases up to certain values of $\eta$, then becomes constant in the stretching case and continues increasing up to certain values of $\eta$, then becomes constant in the shrinking case.

The behavior of skin friction with different parameters is analyzed in Figure 6. The effect of various values of d on skin friction versus K and versus $\Gamma$ is demonstrated in Figure 6a,b, respectively, showing that skin friction is less for higher values of d. Furthermore, the skin friction is higher in the shrinking sheet case than in the stretching sheet case. Skin friction is increases with increases in K or $\Gamma$ and becomes constant after a certain stage in the stretching case and will decrease with increases in K or $\Gamma$ for the shrinking sheet case. It can also be observed in Figure 6c, which demonstrates the skin friction verses d for different values of K, where the stretching and shrinking cases are observed in the domains $0<d\le 10$ and $-10\le d<0$, respectively. Skin friction decreases as d increases.

Figure 7, Figure 8 and Figure 9 demonstrated the concentration profile $\varphi \left(\eta \right)$ by varying different parameters. The behavior of $\varphi \left(\eta \right)$ according to the variation of $K,\beta$, and $\Gamma$ for the stretching and shrinking cases is examined, respectively in Figures a and b. $\varphi \left(\eta \right)$ will be higher for greater values of K or $\beta$. As seen earlier, $\varphi \left(\eta \right)$ will be greater for higher values of $\Gamma$ in the stretching case, and it will be less for higher values of $\Gamma$ in the shrinking case. $\varphi \left(\eta \right)$ decreases exponentially up to certain stage of $\eta$ and after that becomes constant at zero.

4. Conclusions

Consider the 3-dimensional incompressible viscoelastic fluid flow over the porous stretching/shrinking sheet with hybrid nanoparticles $Cu-A{l}_2{O}_3$ in base fluid $H_{2}O$. The uniform magnetic field of strength $B_0$ is applied perpendicular to the fluid flow and considered the Navier slip. The mass transfer is considered along with the chemical reaction rate. On converting a system of partial differential equations into system of ordinary differential equations via similarity transformations, it can be solved to get the exact analytical solution for velocity and concentration fields in exponential and hypergeometric forms, respectively. The parameters magnetic field, Inverse Darcy number, slip parameter, chemical reaction parameter, stretching/shrinking parameter, and viscoelastic parameter influence the flow. The effect of these parameters on fluid velocity and concentration field, skin friction and Nusselt number will be analyzed through graphs and the following observations can be made:

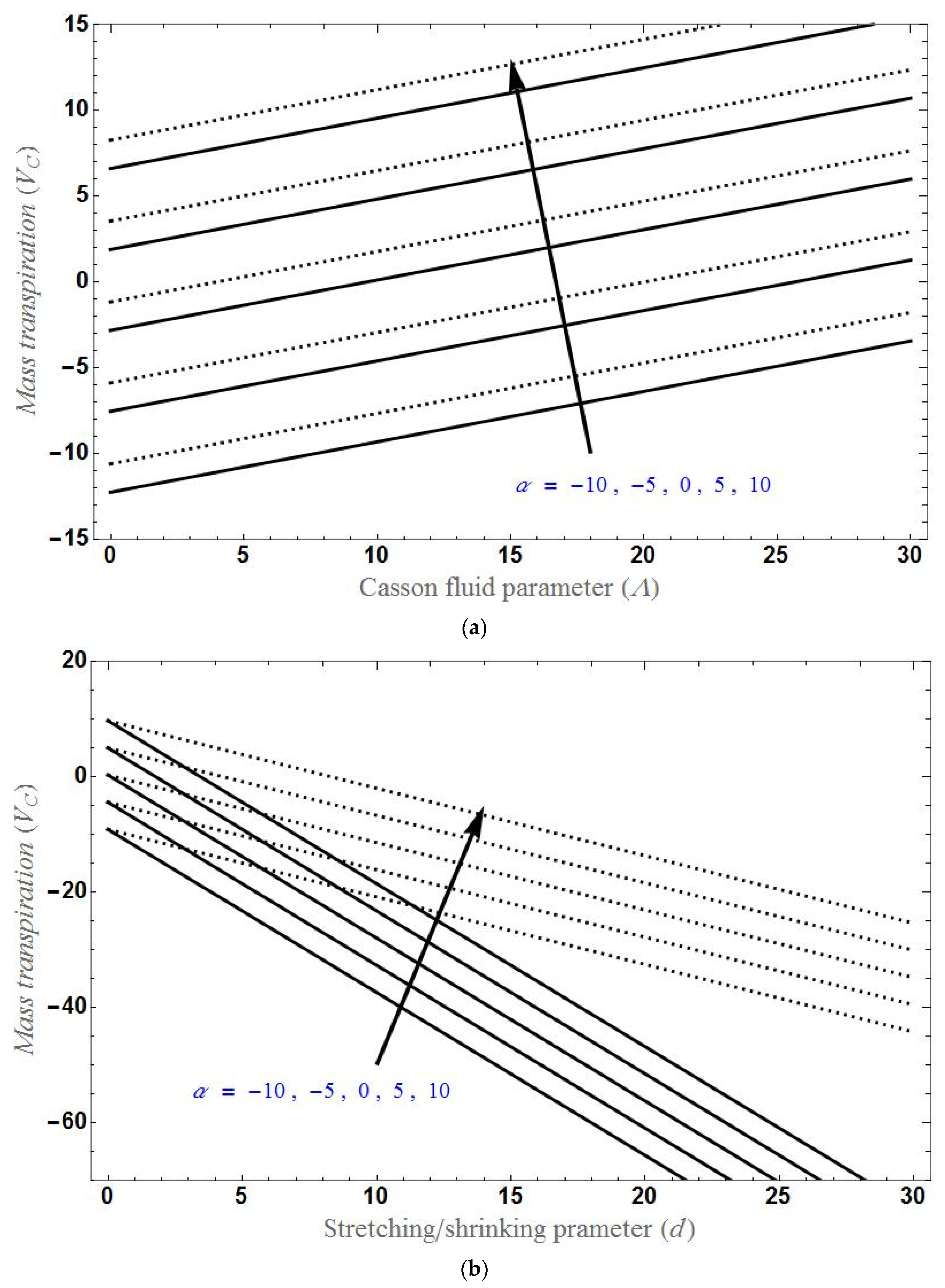
• As the parameter $\alpha$ increases, mass transpiration also increases in both the stretching and shrinking cases.
• Mass transpiration increases with increases in Casson fluid parameter $\Lambda$ and slip factor, and will decreases as $d$ increases.
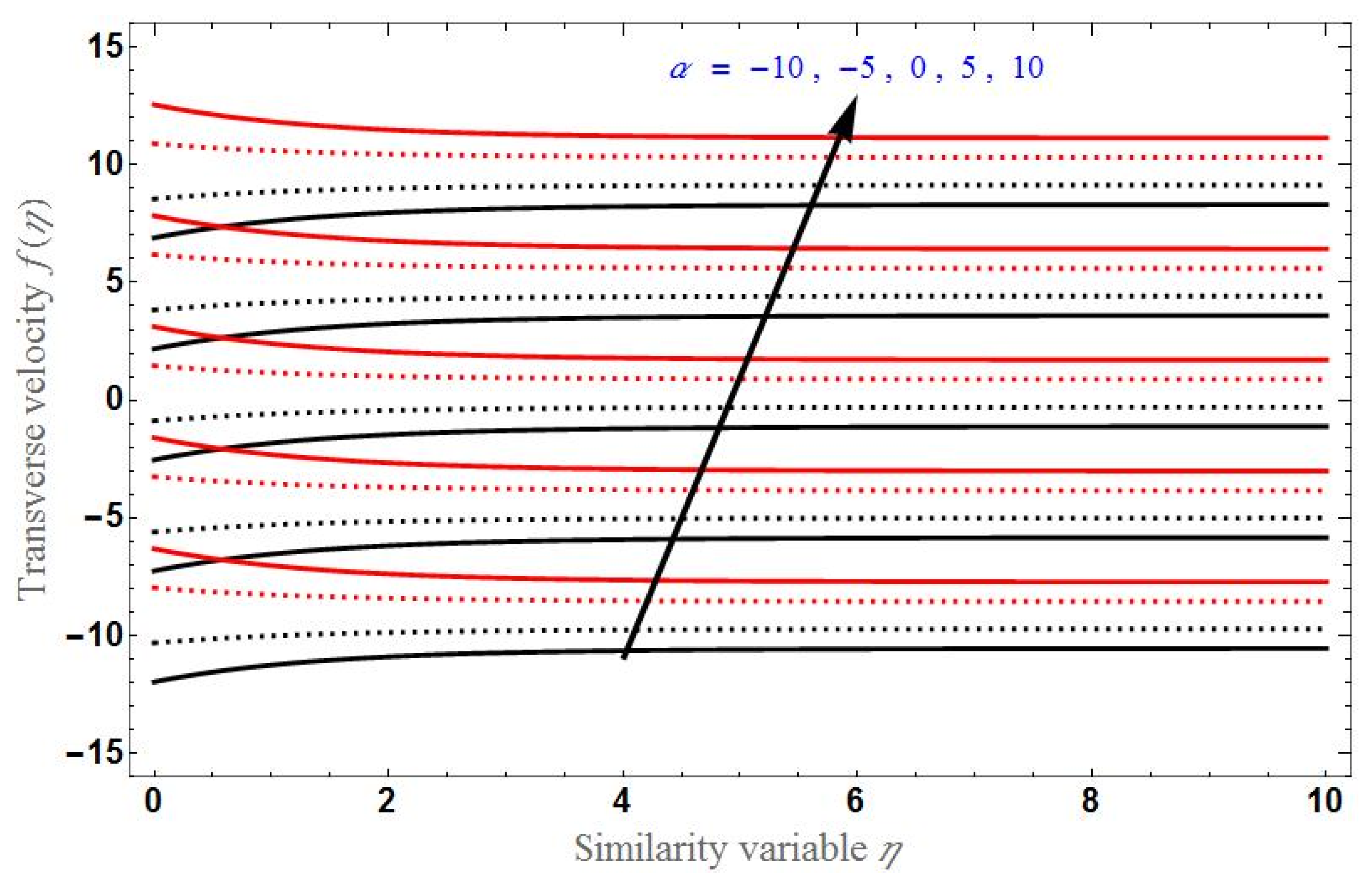
• Transverse velocity will be higher for higher values of the slip factor in the stretching case and lower for higher values of the slip factor in the shrinking case.
• Axial velocity expands with $K$ or d for the stretching case and shrinks with $K$ or d for the shrinking case. The effect is reversed while varying $\Gamma$.
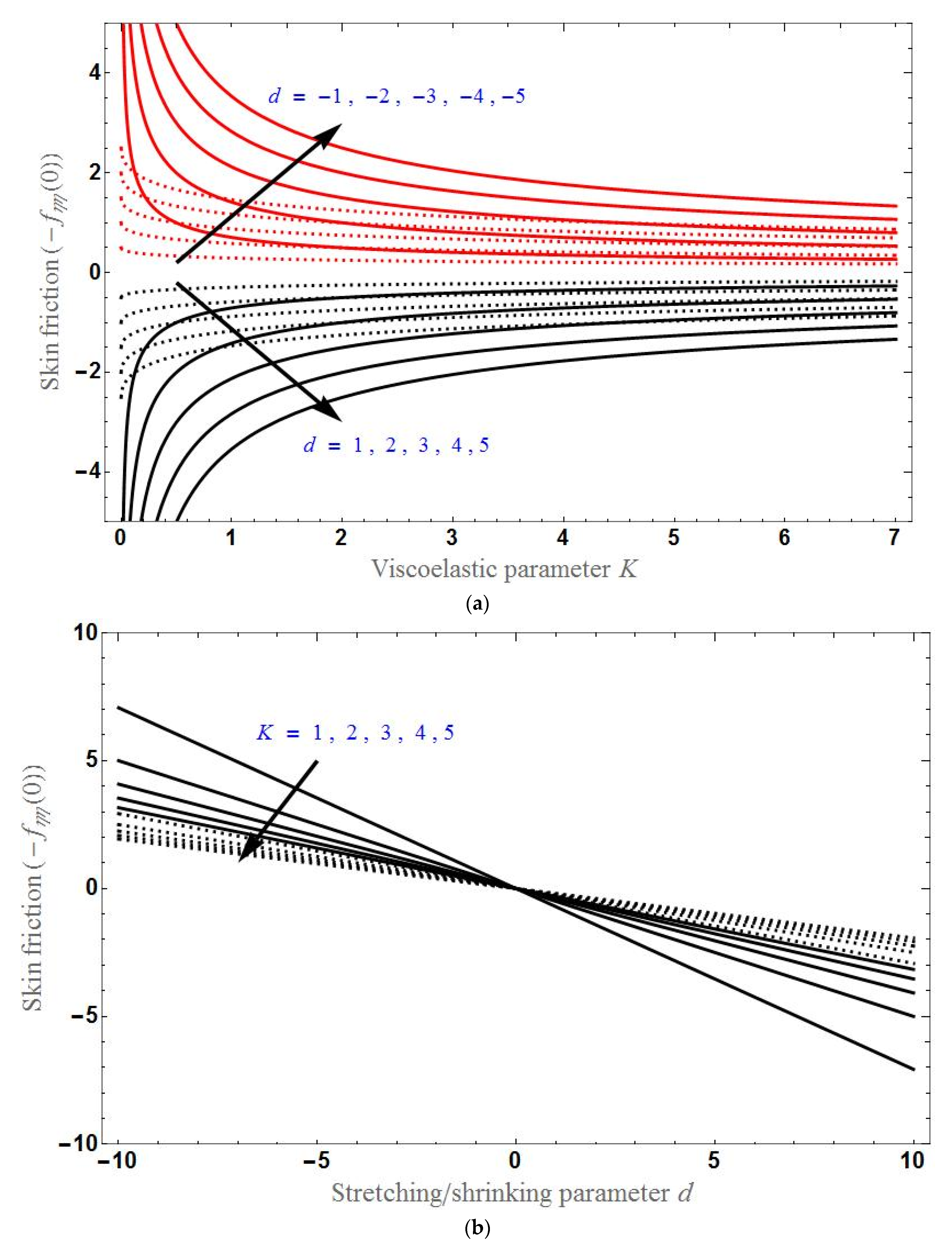
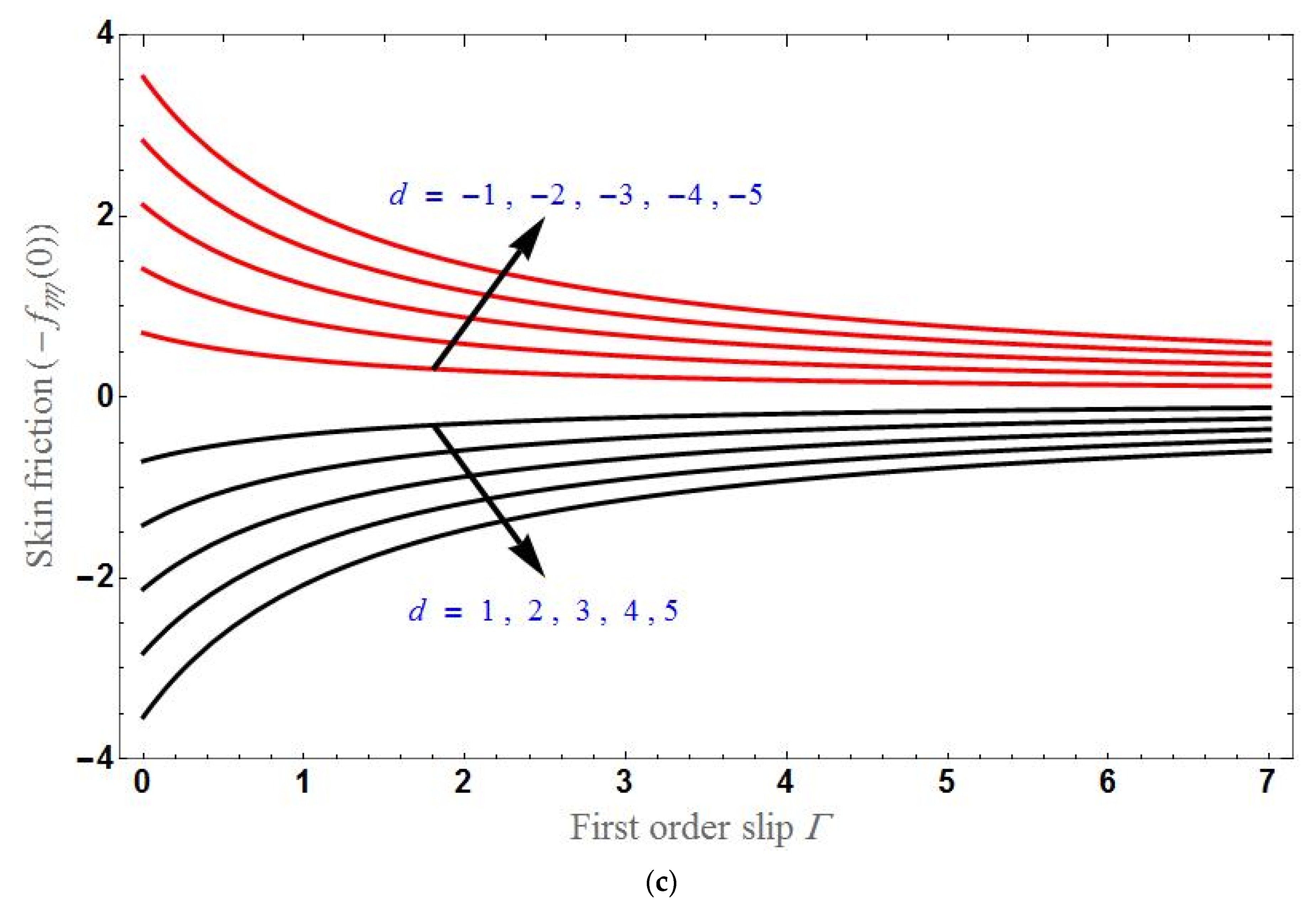
• Skin friction decreases with increases in d and it is greater in the shrinking sheet case than in the stretching sheet case.
• Skin friction increases with increases in K or $\Gamma$ in the stretching case and will decrease with increases in K or $\Gamma$ for the shrinking sheet case and become constant after a certain stage.
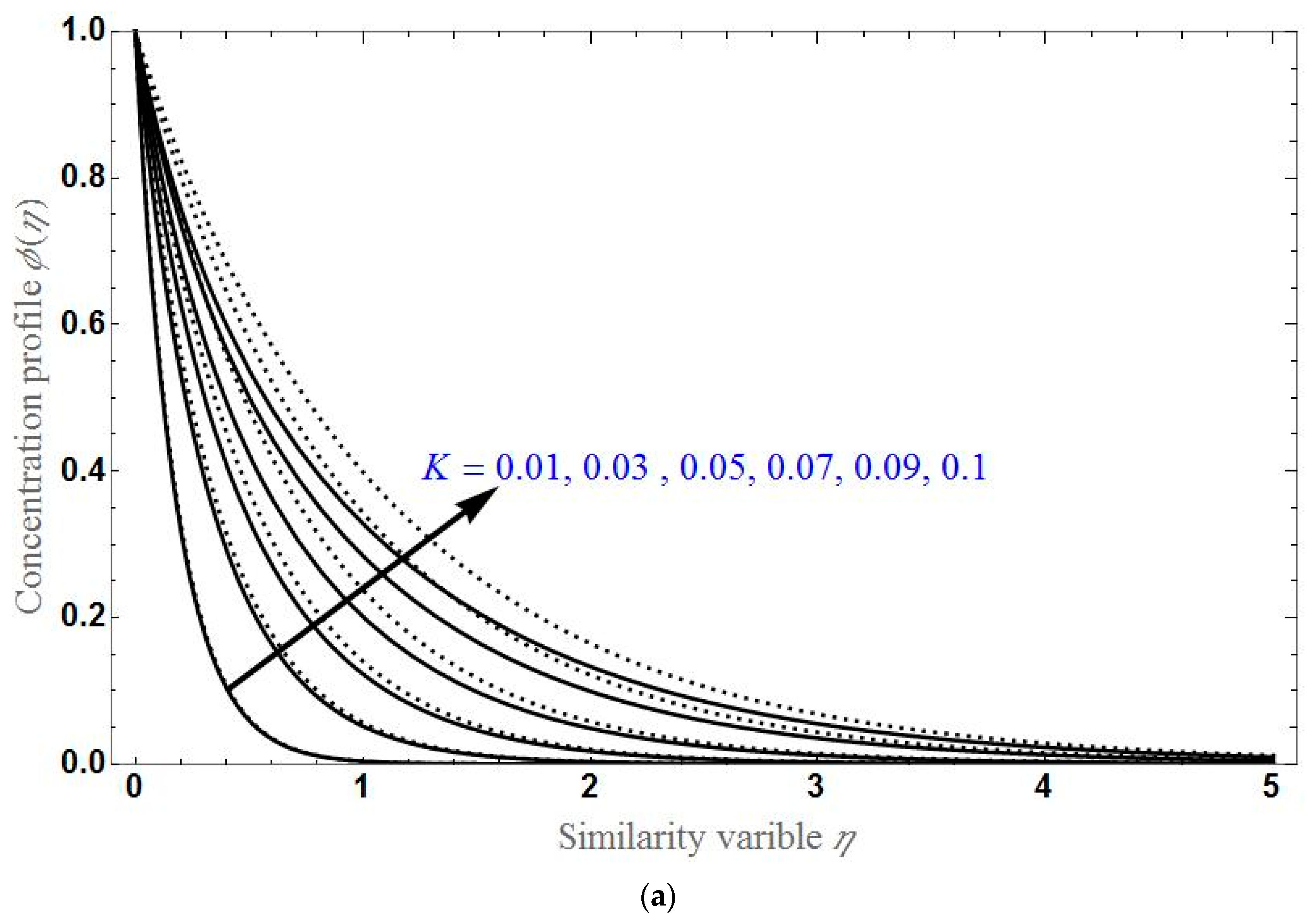
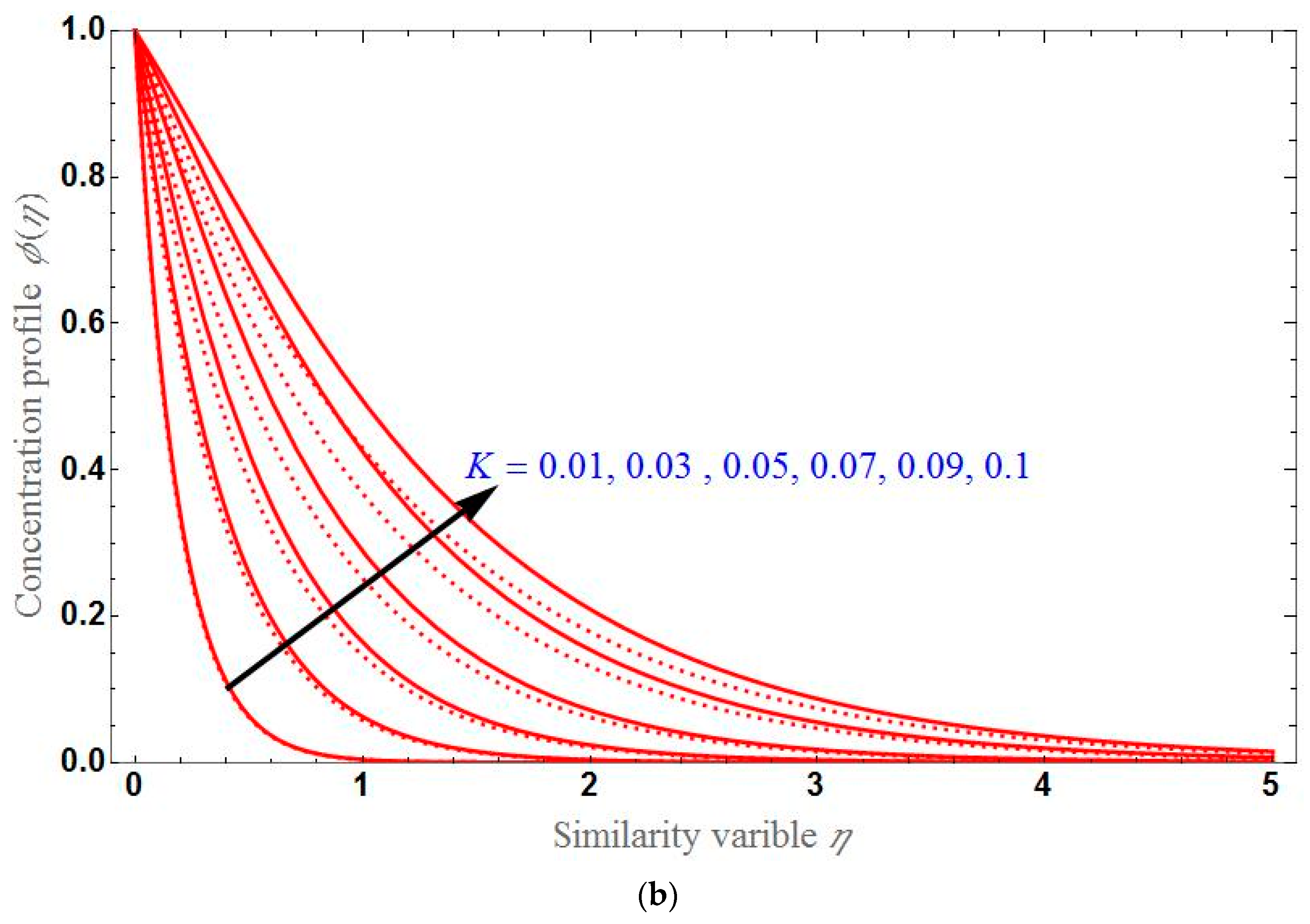
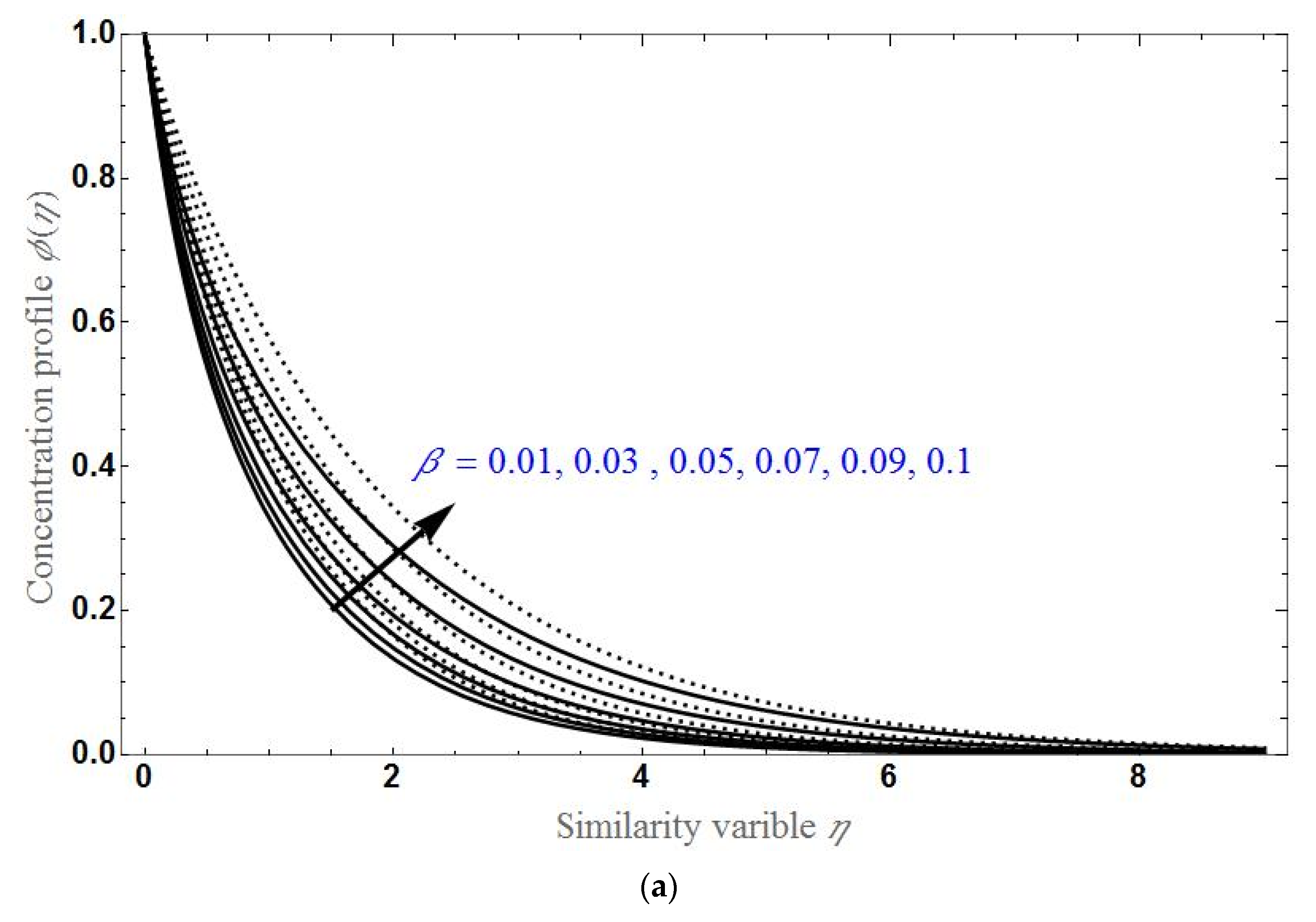
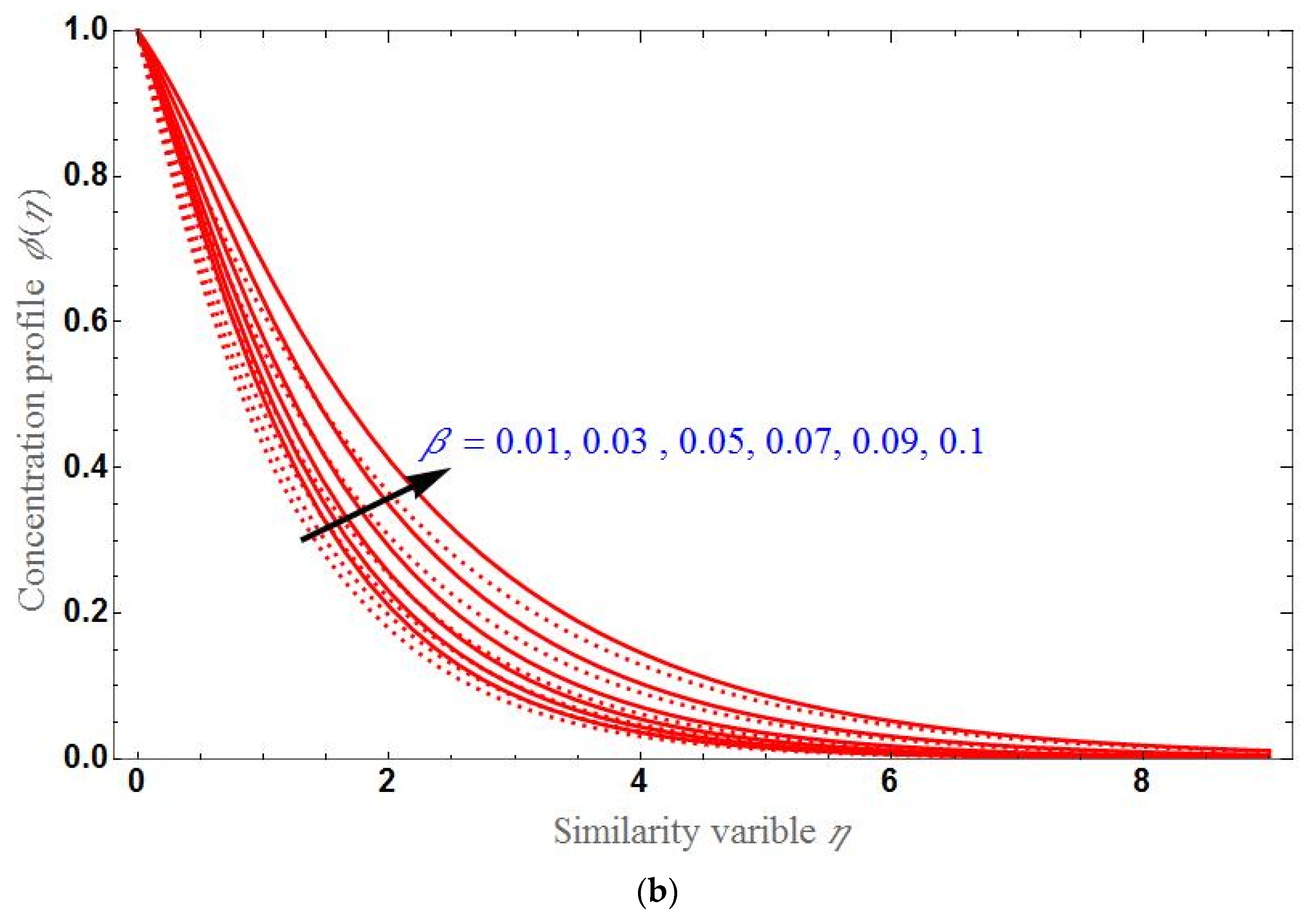
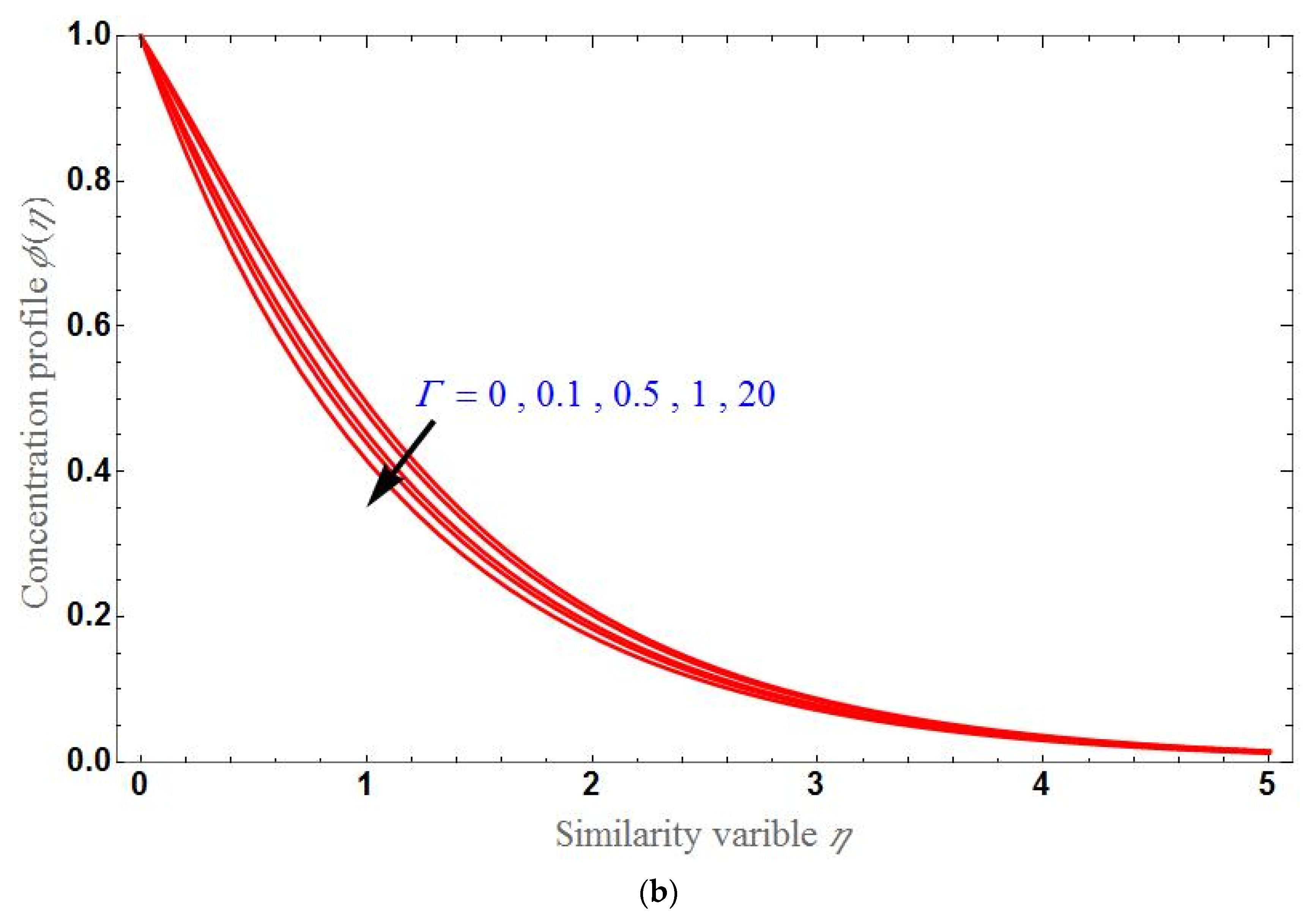
• The concentration profile will be higher for higher values of K or $\beta$; it will higher for higher values of $\Gamma$ in the stretching case and lower for higher values of $\Gamma$ in the shrinking case.