A Study of Community Group Purchasing Vehicle Routing Problems Considering Service Time Windows

Abstract

In this paper, a vehicle routing problem (VRP) model considering delivery time windows and variable service time is established for the delivery problem in community group purchasing. A solution model for an improved ant colony algorithm (ACA) is proposed by improving the initial feasible solution and the neighbourhood search mechanism of the ant colony algorithm. The algorithm of the improved ant colony and the commonly used algorithm are solved for real cases and publicly available benchmark datasets, respectively, for comparative analysis. The results show that the improved ACA has stronger optimization capability, faster convergence speed, and has advantages in solving VRPTW problems with variable service time. The computational efficiency is also improved by 41% over the genetic algorithm (GA) in the solution of the benchmark dataset, which provides a certain reference for solving the community group distribution problem.

1. Introduction

With the rapid development of mobile Internet and the widespread popularity of mobile payment technology, a new social e-commerce model-community group purchase system has emerged. Community group purchase is a kind of shopping and consumption behaviour of resident groups in real living communities. It is a regional, niche, and localized form of group purchase based on real communities. The process are as follows: the leader of the community will release various promotional activities to the community residents through a WeChat group. After the residents place orders, the platform enterprises will arrange the stock to the designated community in a timely manner. At present, the sales categories of community group purchase in operation are mainly fresh, dairy, rice, flour, oil and grain, daily chemicals, and services among which the sales volume of fresh agricultural products accounts for 60% of the total. For community group purchase dispatching, there are major differences in dispatching mode compared with a traditional distribution business, the core of which is the requirement for dispatching timeliness. The timeliness of delivery has an impact on the quality of fresh food products, and unreasonable dispatching causes fluctuations in product quality, thus affecting the reputation and demand of community group purchase. In order to ensure the quality of the food and to improve the reputation and demand of the enterprise, it is necessary to study the vehicle route planning problem in community group buying distribution, so that customers can receive better service, and thus increase the benefit of the enterprise.

Furthermore, community group purchasing has become a major purchasing lifestyle for most residents during the pandemic; however, the requirements of different regions for epidemic prevention and control, the requirement for delivery vehicles to enter the community at specified times, and the restrictions on the length of stay in the community are causing a great impact on the delivery problem of community group purchasing. It is therefore necessary to conduct further research on the distribution of community group purchasing.

The VRP has been intensively studied by many scholars including the vehicle routing problem with time windows (VRPTW) [1,2]. Researchers often use exact algorithms and metaheuristics when solving problems. In recent years, some scholars have also proposed accurate algorithms to effectively solve VRPTW, such as the branch-price algorithm and the branch-and-cut algorithm [3,4]. Exact algorithms are uniquely advantageous when solving small-scale problems (number of nodes less than 30), but when the scale becomes large, the use of these algorithms lead to excessive computational effort to effectively solve the problem and have a narrower application. Compared to the exact algorithm, the metaheuristic algorithm is more suitable for solving large-scale problems, and the search is more comprehensive, which can improve the effectiveness of the solution and is more widely applicable. Current methods for solving such problems include genetic algorithms, ant colony algorithms, simulated annealing algorithms (SAA), particle swarm algorithms [5,6,7,8,9]. Among them, ACA was proposed by Dorigo in 1996, and many scholars have used ACA for solving VRPTW problems. Because of its advantages of robustness, positive feedback, and parallelism, the ACA is widely used to solve vehicle path problems, but it can also fall into local optimum solutions, slow convergence, and unsatisfactory results. Therefore, the improvement of ACA to enhance its computational efficiency has aroused the research interest of many scholars, such as improving methods from the aspects of individuals and populations, feasible solution construction and pheromone update. However, some scholars found that when a certain algorithm is used to solve the problem, there will be premature and local optimal problems. When the algorithms are combined, they can complement each other and solve the VRP problem more effectively [10].

In contrast to current research, the contributions of this paper can be summarized in the following main points. Firstly, based on the delivery problem in community group buying, a VRP model considering the delivery time window and variable service time is developed by taking into account the hard-time window of demand information at the demand point in addition to the variable service time that exists according to the different quantity of goods demanded. Secondly, the ACA is improved by combining it with the SAA. A simulated annealing mechanism is used to quickly generate the better solution, leaving pheromones for the better path, and then the traversal is completed according to the ant colony algorithm, using simulated annealing to find another solution in the neighbourhood, and eventually, the optimal solution. Thereby an improved ACA is proposed to solve a real community group delivery problem. Finally, the superiority of the new algorithm is further verified by solving the benchmark dataset data from the Solomon benchmark with the improved algorithm and the commonly used algorithm. It is interesting to note from the comparison that commonly used algorithms for solving the VRPTW problem, such as GA, have a great advantage in solving the problem for the benchmark dataset. However, the computational performance of GA is not as significant when it is used for real-world problem solving or when we adapt the data from the benchmark dataset, for example, by making the information on the location of demand points more complex and setting variable service times depending on the amount of goods demanded.

The main components of this paper are as follows. Section 2 provides a review of the relevant literature, and Section 3 develops a model for the community group delivery problem. Section 4 presents an analysis of the principles of SAA and ACA, as well as an introduction to the improved ACA. Section 5 uses the improved ACA to solve a real community group-buying delivery problem and further explores the computational performance of the three algorithms. Finally, a summary of the whole paper is presented.

2. Literature Review

As a new business model, community group buying is popular mainly in China currently, and the corresponding research is in its infancy. In the traditional group-buying model, members are mainly relatives and friends who buy the same product in a group to recieve a discount on the price [11]. Therefore, the close social relationship is the foundation of the basic group-buying model. However, relevant scholars have noticed that the basic group-buying model is greatly influenced by geographical constraints, thus the size of the group-buying group will also be greatly affected [12,13]. To lessen the limitation of geographical factors on group purchase scale, the online group purchase model based on Internet virtual communities is more favoured by consumers [14,15,16]. Furthermore, e-commerce attracts more consumers through the Internet, and the traffic crisis has become increasingly prominent. Therefore, an increasing number of e-commerce platforms have begun to integrate the advantages of O2O omni-channel retail and online group buying. At the same time, some scholar focus on offline residential communities and start to build a new convenient community group purchase model based on residential communities [17]. The model has a positive effect on responding to market demand and satisfying the individual demand of consumers. According to the summary of the research objects, it can be found that community group buying has the characteristics of interactivity, closeness, convenience, and economy [18]. Jing et al., found that convenience and speed are the main reasons for users to choose community group buying [19]. Xu et al., studied the influence of the technical characteristics and trust of community group buying on whether consumers consume or not and found that both emotional trust and cognitive trust have a significant positive effect on consumers’ purchasing decisions [20]. Meanwhile, with the increase in income levels of Chinese residents, quality has become the most important attribute for consumers in addition to price [21]. Because of the perishable nature of fresh food, offering fresher products at a reasonable price in community group buying has become the key to attracting consumers [22]. There is not a wealth of research on the delivery problem in community group buying yet [23]. The article therefore addresses the timeliness problem in community group buying, builds a VRP model, and discusses the solution method to investigate how to efficiently complete the distribution work in community group buying at a reasonable cost.

The ACA solves the VRP by determining the parameters, constructing the solution space, updating the pheromone, and judging the termination condition. To address the drawback of being prone to local optimal solutions, Abdulkader et al., proposed a solution of combining local search and ant colony algorithms [24]. Kalayci et al., proposed a hybrid algorithm based on an ant colony algorithm and variable neighbourhood search [25]. Asghari et al., designed a reverse ant colony algorithm, where the updated pheromone has a reverse effect on the path chosen by ants [26]. Jovanovic et al., proposed a solution to the ant colony optimization algorithm for the region relocation problem, extending the basic greedy algorithm to the ant colony algorithm, giving a defined pheromone matrix and improving the performance of the algorithm [27]. Bouamama et al., improved ACA by using a variable neighbourhood search as a subroutine to address the minimal connection dominance set problem, which can also be applied to weighted and unweighted problem variables [28]. Fernandez et al., used a process similar to that of ants searching for food to search the solution space and selected feasible regions to optimize the search, thereby improving the quality of the feasible solutions [29]. Wang et al., designed an algorithm that allows ants to enter and exit multiple times until all clients are visited, simplifying the process of constructing feasible solutions [30]. Pintea et al., used sensitive ants to improve the sensitivity of the colony system when solving VRPs, where individual ants are sensitive to pheromones and potentially enhance the search ability for variable pheromones [31]. In Kao et al.’s study, not all ants were able to update their pheromones and only the elite ants were able to update their pheromones according to their own best solution, which improved the quality of understanding. Kuo et al., designed a fuzzy clustering insertion algorithm to obtain better pheromones [32]. Suggested method of improvement focuses on enhancing the computational performance of the ACA by improving the individuals and populations and pheromone updates.

When solving various types of VRPs, scholars have found that using one algorithm alone suffers from premature and local optimum problems, while combining algorithms can complement each other to solve increasingly complex VRP problems. Cruz et al., proposed a continuous ant colony system taboo search algorithm in solving a multi-product distribution VRP with a time window, first using a dual pheromone tracking strategy to accelerate the learning process of ants to generate paths, and then a memory form of taboo search to further improve the quality of understanding [33]. Li et al., generated the initial solution using a greedy heuristic algorithm [34]. The novelty of this paper is the improvement of ACA by combining SAA. The simulated annealing mechanism is used to quickly generate the better solution, leaving pheromones for the better path, and then the traversal is completed according to the ACA, using the simulated annealing method to find another solution in the neighbourhood, and finally finding the optimal solution.

Different from the studies focusing on community group purchasing models and strategies and influencing factors, this paper focuses on the vehicle path planning problem in community group purchasing delivery and establishes a vehicle path planning model considering service time and service time windows. The model is solved to overcome the problem of slow convergence of the ACA and the fact that it has fallen into a local optimum solution. By improving the initial feasible solution of the ant colony algorithm and the neighbourhood search mechanism, a simulated annealing ant colony algorithm solution model is proposed.

3. Problem Description

Within the radius of a distribution centre of a community-based e-commerce group, the distribution centre provides goods to the customer and the fleet distributes the goods from the distribution centre and organises an appropriate route back to the distribution centre. The customer’s needs are fulfilled within certain constraints with the goal of shortest distance travelled, lowest cost, and least time spent. At the same time, certain conditions are to be observed in the fulfilment of the distribution tasks:

• Each vehicle has only one delivery route to complete the delivery from and back to the distribution centre;
• Only one vehicle per head needs to be satisfied in one distribution mission;
• Vehicles must meet capacity constraints;
• Distribution centre are presumed to have prepared sufficient goods in advance.

Suppose there are $k(1,2,\dots ,k)$ heads in the service area, and the demand for goods at the ith head is set to $g_i(i=1,2,\dots ,k)$, and the distribution centre sends a vehicle with a load of q. Set $g_i<q$, and find the shortest route to meet the freight demand.

The costs of a car in distribution are equal to the sum of the stationary cost of the car and the travel expenses. The stationary cost of a vehicle mainly includes the cost of dispatching the vehicle, other factors are not taken into account, such as the acquisition cost of the vehicle or the cost of renting the vehicle. Hence, the capital cost of a vehicle is shown below:

$$Z_1=c\times s$$

(1)

where $c$ is the cost of dispatching a vehicle, which is fixed and varies with actual demand, and s represents complete vehicle count required in the route problem.

The vehicle travel cost is the cost of completing all transportation plans. Since the mileage, depreciation, and fuel costs of a vehicle are proportional to the total distance travelled in the route plan, the vehicle travel cost is the sum of these three costs. The vehicle travel cost expression is shown in the following formula, with the transport cost (i.e., distance, expense, etc.) from point i to point $j$. The number of the distribution centre is 0, and the number of each head is $i(i=1,2,\dots ,k)$. The following variables are defined: where ${\displaystyle \sum _i{\displaystyle \sum _j{\displaystyle \sum _s{x}_{ijs}}}}$ indicates the number of miles covered by the vehicle in all path models of the vehicle.

$$Z_2={\displaystyle \sum _i{\displaystyle \sum _j{\displaystyle \sum _s{c}_{ij}{x}_{ijs}}}}$$

(2)

The penalty cost is the cost of not fully satisfying the time window for each demand point in the process of finding the shortest path, which has a negative impact on the efficiency and evaluation of the contingency logistics. The penalty cost for not meeting the time window for a given demand point is expressed by the formula:

$$Z_3={\displaystyle \sum _i{\lambda }_i\times \left[\max (E{T}_i-S_i,0)+\min (S_i-L{T}_I,0)\right]}$$

(3)

where $S_i$ is the actual time of arrival of the vehicle at head $i$, $E{T}_i$ is the earliest time a vehicle is allowed to arrive at head $i$, $L{T}_i$ is the latest time a vehicle is allowed to arrive at head $i$, and ${\lambda }_i$ is the penalty cost per unit of time for not meeting the time window. When a vehicle arrives within a demand point time window, the demand point time window penalty cost is zero.

Denote by $c_{ij}$ the cost of transportation (e.g., time, distance, expense, etc.) from point $i$ to point $j$. The number of the distribution centre is 0 and the number of each head is $i(i=1,2,\dots ,k)$. The following variables are defined

$$x_{ijs}=\left\{\begin{array}{l}1\hspace{1em}vehicle \mathrm{s} \mathrm{travelling} \mathrm{from} \mathrm{point} \mathrm{i} \mathrm{to} \mathrm{point} \mathrm{j}\\ 0\hspace{1em}otherwise\end{array}\right.$$

(4)

$$y_{is}=\left\{\begin{array}{l}1\hspace{1em}customer \mathrm{i} \mathrm{is} \mathrm{delivered} \mathrm{by} \mathrm{vehicle} \mathrm{s}\\ 0\hspace{1em}otherwise\end{array}\right.$$

(5)

Objective function:

$$\min Z=Z_1+Z_2+Z_3$$

(6)

S.T.

$${\displaystyle \sum _{i=1}^k{g}_i{y}_{is}\le qs=1,2,\dots ,m}$$

(7)

$${\displaystyle \sum _{i=1}^m{y}_{is}=\left\{\begin{array}{l}1\hspace{1em}i=1,2,\dots ,k\\ 0\hspace{1em}i=0\end{array}\right.}$$

(8)

$${\displaystyle \sum _{i=0}^k{x}_{ijs}=y_{js}i,j=0,1,2,\dots ,k;s=1,2,\dots m}$$

(9)

$${\displaystyle \sum _{j=0}^k{x}_{ijs}=y_{js}i,j=0,1,2,\dots ,k;s=1,2,\dots m}$$

(10)

$$x_{ijs}=0/1\hspace{1em}\hspace{1em}i,j=0,1,\dots ,k;s=1,2,\dots m$$

(11)

$$y_{is}=0/1i=0,1,\dots ,k;s=1,2,\dots m$$

(12)

Equation (7) constrains the capacity of the vehicles; Equation (8) is designed to ensure that the transport tasks at each customer point are performed by only one vehicle, while all transport tasks are performed by m vehicles simultaneously; Equations (9)–(12) ensure that there is one and only one van arriving and departing from a given customer point.

4. Algorithm Introduction

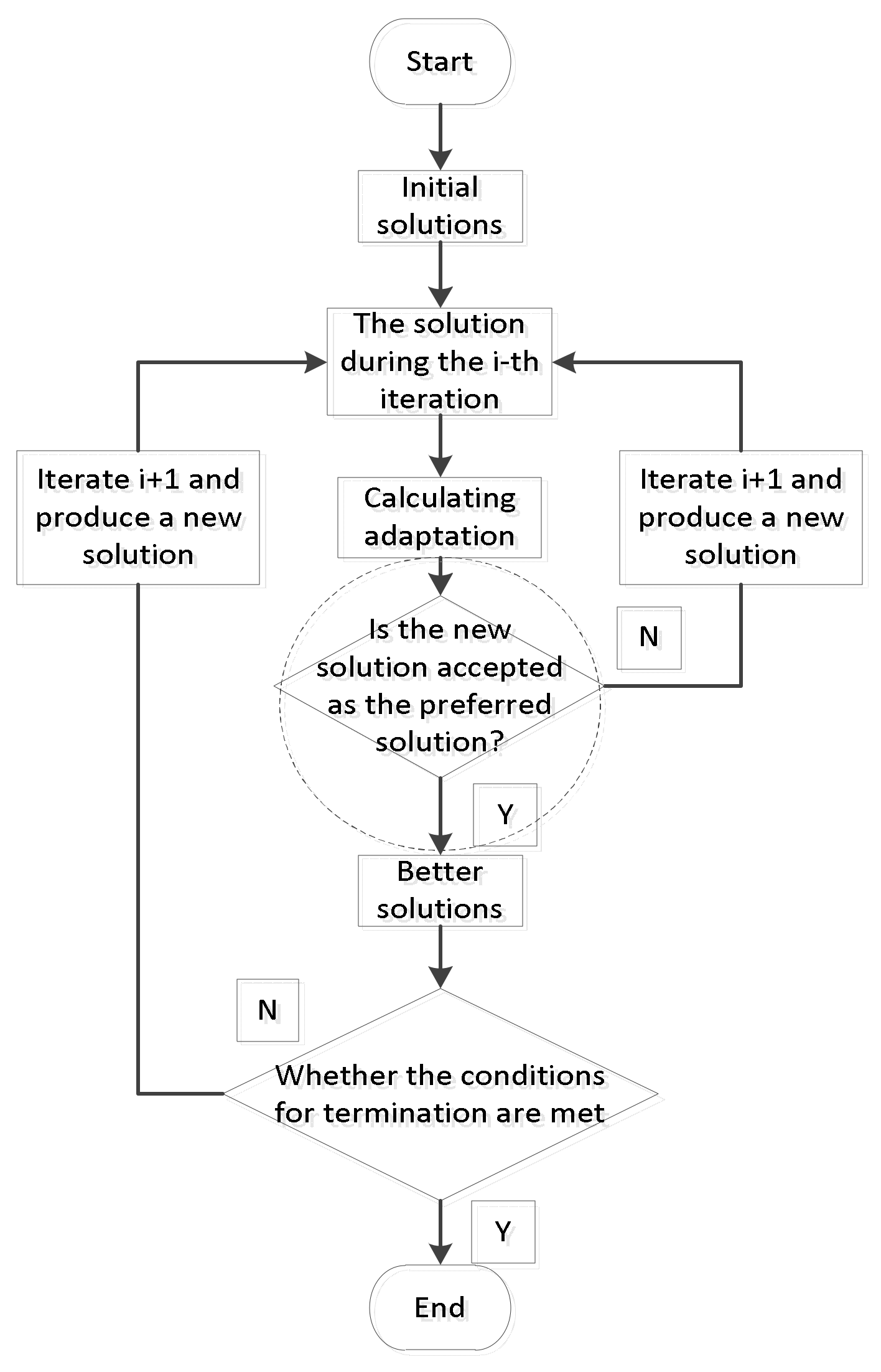
Generally, the actual problem is transformed into a sequence of combinatorial optimisation problems to be solved, and the meta-heuristic algorithm is to find a better feasible solution out of a limited computational consumption. Where this permutation is referred to as the solution, and the result computed by substituting the permutation into the actual problem is referred to as the fitness. In summary, the optimisation mechanism of the meta-heuristic algorithm, is shown in Figure 1.

4.1. Ant Colony Algorithms

The ACA simulates the path discovery behaviour of ants during their search for food. In fact, it has some similarities with the taboo search algorithm in that both can search and accept new solutions according to certain rules. The difference is that the taboo table, which is based on a positive feedback mechanism, does not simply represent a forbidden or allowed operation, but is able to tend to lead to new solutions (better solutions) by dynamically updating the probability of movement in each neighbourhood.

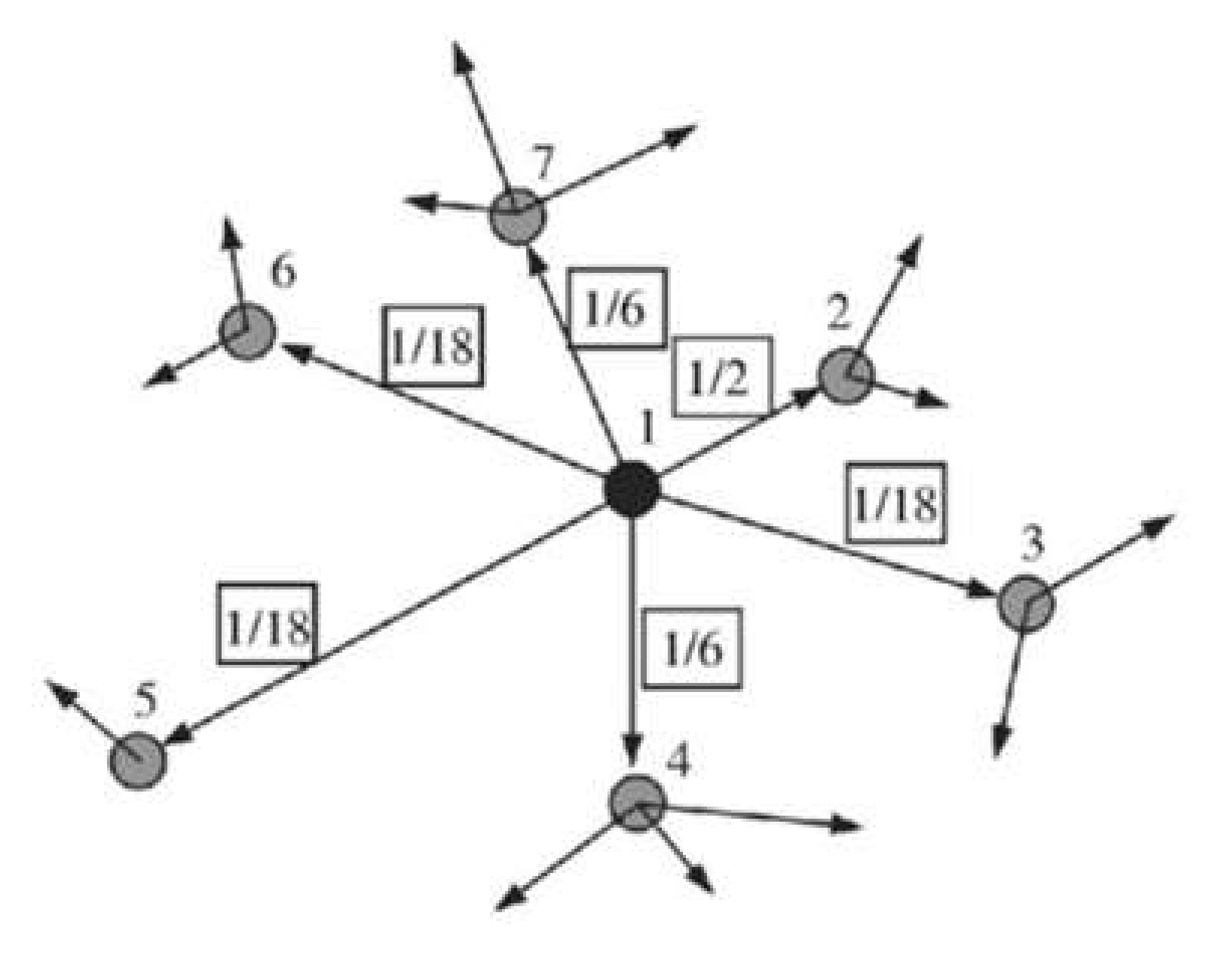
In one neighbourhood change, the probability of selection from position 1 to position 2 is 1/2, from position 1 to position 3 is 1/18 and so on, as shown in Figure 2. These selection probabilities can accumulate in each iteration, leading to the acquisition of the final better solution. Both the taboo search and ACA rely on the creation of taboo tables, and therefore their optimisation objects require a relatively stable and independent neighbourhood structure. However, the initial iterative process produces very limited pheromones, and because of the limited feedback, it requires a lengthy process and is slow to solve, making it difficult to complete solutions in a relatively short time for large-scale computational problems.

4.2. Simulated Annealing Algorithms

The SAA is derived from the principle of solid annealing: during the cooling process of a high-temperature solid, the particles contained in it are desperately converging to an equilibrium state at each moment, with their energy gradually decreasing with decreasing temperature, until the ground state is reached at room temperature. During this process, new solutions are usually generated using a random neighbourhood change method, while the acceptance of a better solution exactly mimics the annealing process of the solid, i.e., the algorithm accepts a non-better solution as a better solution with a higher probability in the early stages of execution, thus ensuring the global search capability of the algorithm, and accepts a non-better solution with a lower probability in the later stages of execution, in order to retain the currently obtained relatively better solution, where the acceptance probability becomes progressively smaller as the "annealing temperature" is changed. A comparison table of the basic concepts of the physical annealing process and SAA is shown in

Table 1. Conceptual comparison.

Physical Annealing	Optimization Issues
Physical condition	Solution
Lowest energy state of matter	Optimal solution
Annealing process	Solving process
Temperature	Control parameters
Energy	Objective function
Isothermal process	Metropolis Sampling Process

.

Simulated annealing is a heuristic stochastic method that differs from conventional stochastic approaches in that it contains not only an adequate random element but also incorporates mechanisms that are natural to the annealing process of physical systems. It can accept not only the points that make the value of the target function better during the iterative process, but also the points that make the value of the target function worse with some probability, and the acceptance probability decreases as the temperature decreases. Due to the uncertainty of the value of the solution in the entire neighbourhood, the algorithm can bypass the local optimal solution to obtain the global optimal solution, which is conducive to improving the global search ability. Although it can search globally on a large scale, the SAA does not have an effective positive feedback mechanism and tends to make some useless iterations when the solution reaches a certain level, hence the low value of solution accuracy.

4.3. Improved Ant Colony Algorithm

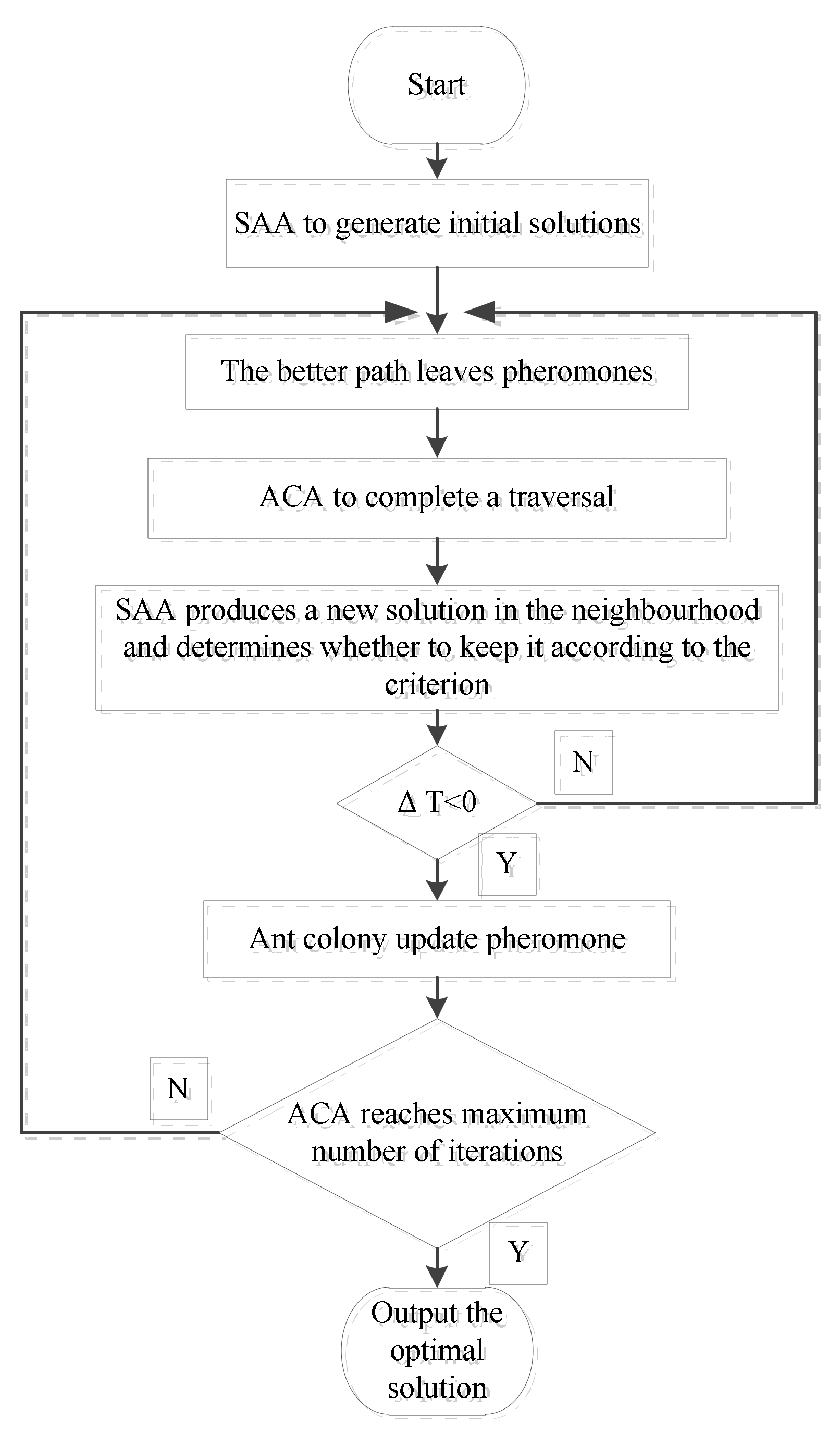
It is recommended to mix the SAA with the ACA method to solve the vehicle path planning problem. The SAA is used to quickly generate a solution, distribute the pheromones on this solution, and use the positive feedback mechanism of the ACA to find the exact solution to complement each other’s strengths and weaknesses, expecting to obtain a win-win situation in terms of optimization and quickly obtaining the solution.

The idea of the hybrid algorithm is to first generate the better solution quickly by using the SAA, the better path leaves pheromones; then let the ants follow the ACA, using the pheromones left behind to complete a traversal after using the simulated annealing method to find another solution in the neighbourhood. This new solution may not be better, since this time, the acceptance criterion uses the idea of simulated annealing, allowing the objective function to worsen in a limited range, in order to simplify the computation and not by probability trade-offs. If the path length difference $\Delta E<e$ is accepted, $e$ allows the objective function worsen in the range.

Each ant leaves pheromones behind on the path it takes, while simultaneously some of the pheromones from the original path is volatilised, so the pheromone update is divided into a local pheromone update and a global pheromone update. The local pheromone update is for the selected edge to have less influence on the later ants, thus making the ants have more influence on the unselected edge. After the ants move from position i to position $j$, the pheromone on edge $(i,j)$ is updated according to the following equation, where ${\tau }_0$ is a constant and $\eta$ is an adjustable parameter.

$${\tau }_{ij}=(1-\eta ){\tau }_{ij}+\eta {\tau }_0$$

(13)

When the global optimal solution has been searched once by all ants, it is updated with the global pheromone. At this time, only the pheromone enhancement is performed on the optimal path, so that the pheromone difference between the optimal path and the worst path becomes larger, and the ants can concentrate near the optimal path faster and accelerate the global convergence.

The flow chart is shown in Figure 3.

(1)

SAA generates initial solution;

(2)

The better path leaves the pheromone;

(3)

The ACA completes a facilitation to produce a solution;

(4)

SAA finds a new solution in the neighbourhood of the solution generated by the ACA;

(5)

Determine if it is less than 0. If so, the ant colony updates the pheromone, otherwise return to step 2;

(6)

Determine if the ACA has reached the maximum number of iterations, if so, output the optimal solution, otherwise return to step 2 and continue the cycle.

5. Case Study

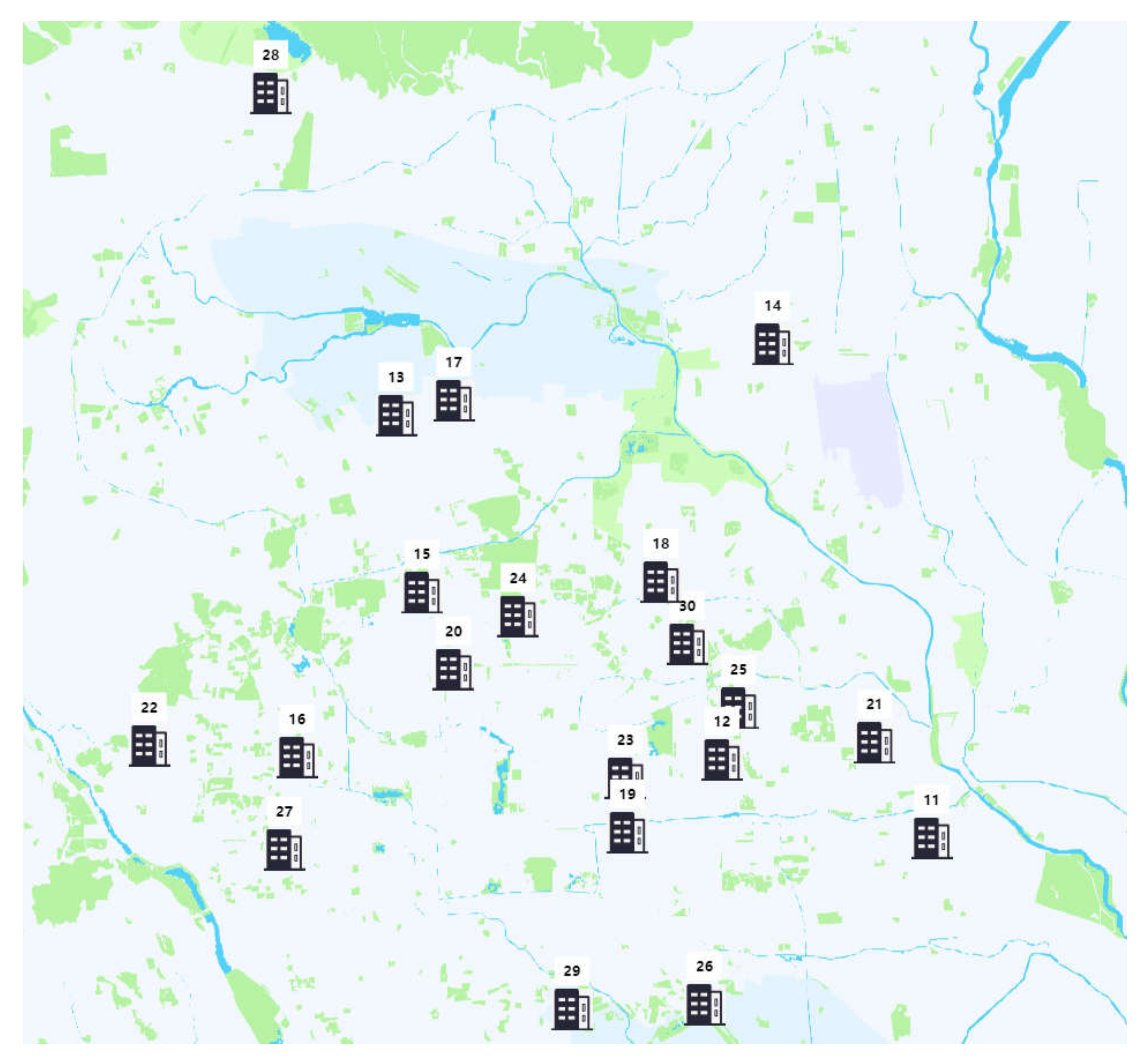
An e-commerce company, D, which focuses on the online pre-sale of community group purchasing products, has a distribution centre that serves a certain range of heads and has an agreement with them for in-store pick-up. The company gets the community purchase orders collected by the company’s heads by 10 pm the previous night. The company completes the transfer of goods through its own supply chain system and delivers them to the company’s shop heads within the agreed time frame so that customers in the community can recieve their orders without any problems. The company’s distribution centre is located near the Beijing Xinfadi vegetable Wholesale Market. To maintain customer information and the company’s interests without loss of generality, customer demand information is optimised and the distribution centre and the 30 demand points are located as shown in Figure 4.

5.1. Parameter Setting

Considering previous studies, we set the parameters of the SAA, ACA GA and SAACA as shown in

Table 2. Parameter setting table.

Parameter	Numerical Value
$M$: Number of ants	50
$\Omega$: number of iterations	100
$\alpha$: initial pheromone factor	1
$\beta$: heuristic factor	3
$\rho$: initial pheromone volatility factor	0.85
$Q$: initial pheromone value	5
$T_0$: initial temperature	100
$\Im$: cooling factor	0.99
$P_s$: probability of choosing a swap structure	0.2
$P_r$: probability of choosing the reversal structure	0.5
$P_i$: probability of choosing the insertion structure	0.3
$\upsilon$: maximum number of iterations (annealing algorithm)	2000
$N$: Number of populations	100
$P_c$: Crossover probability	0.9
$P_m$: Probability of variation	0.05
$G$: Generation gap	0.9

.

There are 30 communities to be served within the service area of a distribution centre. The location information and time windows of the distribution centre and the communities are collated as follows: Since users are not very sensitive to the time they choose community group purchases, there is a wide tolerance range of working hours, but the delivery must be completed within a hard-time window. At the same time, it must be considered that during loading, unloading, and handling, there are order verification processes and other operations, so during the distribution process of setting the corresponding service time according to the amount of goods, the planning of the distribution path is very important.

5.2. Algorithm Results

The SAA, a general-purpose optimisation algorithm, has theoretically probabilistic global optimisation performance. The ACA features distributed computing, positive information feedback, and heuristic searching. The advantages of both algorithms are combined here to propose an improved algorithm for solving the above community group buying problem. The solution process was computed on the same laptop computer equipped with an AMD R7 5800 H 3.20 GHz CPU and 16 GB of RAM. The distribution roadmap and total cost trends of the final global optimal solution obtained are shown below.

The actual latitude and longitude values of the points are normalised to obtain the coordinates of each point. The distribution centre is labelled as 0 and the 30 customer locations are labelled as 1–30, and the demand is rationalised according to the real data to set the demand for each customer point. Specific data information is shown in the

Table 3. Information on the needs of customers.

No.	Longitude	Latitude	Coordinates x	Coordinates y	Demand	Time Window	Service Time
0	116.347465	39.823758	24.26	2.35	0	[09, 20]	0
1	116.361222	40.036321	26.23	36.31	40	[10, 12]	0.1
2	116.322584	39.986339	20.70	28.33	45	[11, 13]	0.2
3	116.310073	39.918547	18.91	17.49	50	[11, 12]	0.2
4	116.342725	39.903466	23.58	15.09	40	[12, 14]	0.1
5	116.438126	39.872297	37.25	10.11	35	[11, 15]	0.1
6	116.372629	39.860298	27.87	8.19	40	[10, 14]	0.1
7	116.424175	39.930827	35.25	19.46	45	[10, 12]	0.2
8	116.45413	39.97696	26.83	0.33	50	[11, 14]	0.2
9	116.238929	39.899818	8.72	14.50	80	[10, 15]	0.4
10	116.471384	39.871168	42.01	9.93	45	[10, 16]	0.2
11	116.643538	39.887352	66.67	12.51	50	[15, 17]	0.2
12	116.518796	39.923086	48.80	18.22	45	[13, 15]	0.2
13	116.324892	40.079959	21.03	43.28	75	[15, 17]	0.4
14	116.548831	40.112143	53.10	48.42	60	[16, 17]	0.2
15	116.340279	39.999152	23.23	30.37	80	[15, 17]	0.4
16	116.265916	39.924242	12.58	18.41	35	[14, 17]	0.1
17	116.359216	40.086673	25.95	44.35	34	[16, 17]	0.1
18	116.482469	40.004037	43.60	31.15	58	[14, 17]	0.2
19	116.46251	39.889858	40.74	12.91	89	[13, 17]	0.5
20	116.359177	39.964364	25.94	24.81	60	[15, 17]	0.2
21	116.609571	39.930805	61.80	19.45	70	[11, 12]	0.3
22	116.178067	39.929568	0.00	19.25	35	[10, 12]	0.1
23	116.461371	39.914768	40.57	16.89	40	[11, 13]	0.1
24	116.397414	39.988556	31.41	28.68	65	[10, 13]	0.3
25	116.528565	39.946535	50.20	21.97	50	[10, 14]	0.2
26	116.508315	39.811369	47.30	0.37	86	[10, 12]	0.5
27	116.258358	39.882154	11.50	11.68	65	[15, 17]	0.3
28	116.250371	40.226344	10.35	66.67	75	[14, 17]	0.4
29	116.429564	39.809034	36.02	0.00	35	[10, 14]	0.1
30	116.498004	39.975869	45.82	26.65	45	[15, 17]	0.2

.

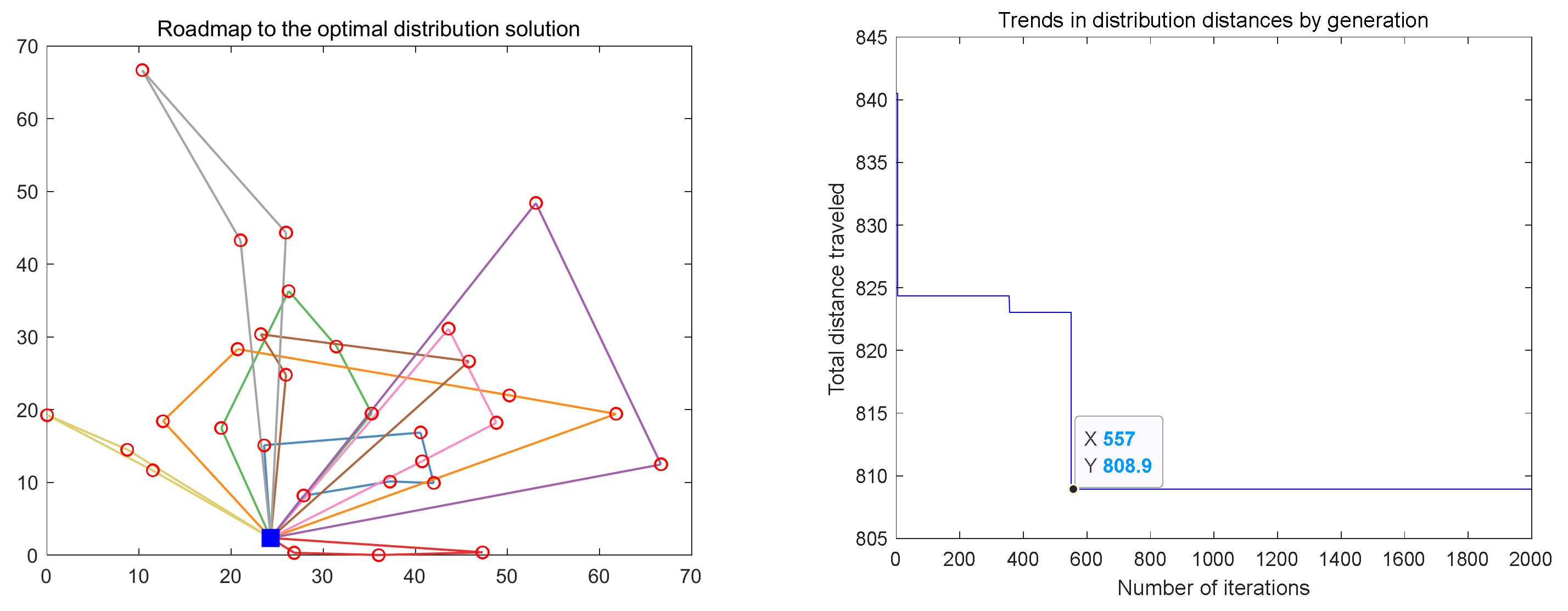
The improved ACA algorithm was used to solve the distribution problem with the parameters set in Table 2, and after 30 experiments, the optimal vehicle route map and shortest path trend diagram of which were selected is shown in Figure 5.

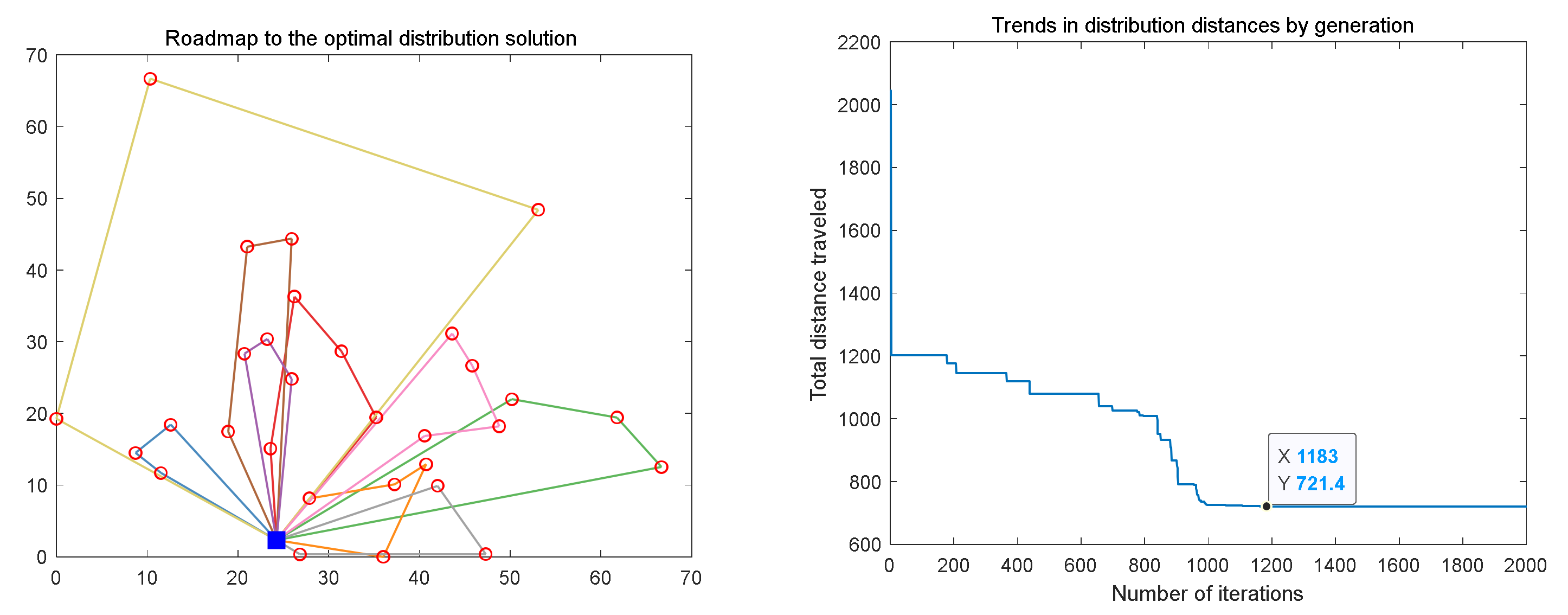
To verify the superiority of the improved algorithm, three other commonly used algorithms, the genetic algorithm, the simulated annealing algorithm, and the ant colony algorithm were introduced to solve the problem. The solution performance of the new algorithms was observed by comparing the computational results. The number of iterations of the three algorithms was unified to 2000, and after several trials, the vehicle route map and shortest route trend graphs obtained by the three algorithms under the optimal calculation scheme are shown in Figure 5, Figure 6, Figure 7 and Figure 8. From the optimal solution results of several algorithms, it can be obtained that the improved ACA can solve a more efficient distribution scheme, followed by the calculation efficiency of GA and SA, with the worst solution from ACA.

Based on 50 experiments, four algorithms were obtained, and the average value of the time required for the operation T, the average number of iterations of the optimal solution as $\overline{D}$, the shortest path as $Z_{\min }$, the average value of the shortest path as $\overline{Z}$, and the required vehicle $l$ were obtained, as shown in

Table 4. Comparison of improved ACA with other algorithms.

	$\mathit{T}$	$\overline{\mathit{D}}$	${\mathit{Z}}_{\mathbf{min}}$	$\overline{\mathit{Z}}$	$\mathit{l}$
GA	2926.25	1435	720.87	732.33	9
SAA	63.33	1237	721.40	728.77	9
ACA	598.67	653	808.90	818.93	9
SAAACA	113.82	987	700.10	712.35	9

. In terms of computation time, the SAA is the most efficient and can complete 2000 iterations in the shortest time, followed by the improved ACA, and finally, GA. while in terms of overall computation efficiency, the improved algorithm solves for the optimal result and can complete the computation in a shorter time, the number of iterations to reach the optimal solution is relatively top, low, and the algorithm’s stability is also relatively strong. Compared to ACA, the improved algorithm has great advantages in terms of computation time, computation results obtained, and stability. In comparison with the commonly used GA and SA, the improved ACA is superior in terms of accuracy and stability of the computed results. As shown in the table, the accuracy of the SAA and GA is similar, with the difference being that the SAA takes less time to compute. In addition, the traditional ACA is prone to early maturity and thus falls into a local optimum, but the improved algorithm has significantly improved the computation time and computation accuracy.

5.3. Comparative Analysis

To achieve a reliable comparison, two cases from the publicly available Solomon benchmark dataset were used, the 50-customer case and the 100-customer c101 case. As shown in

Table 5. Information on the needs of 50 customers.

Point of Demand	Position Coordinates x	Position Coordinates y	Demand	Time Window	Service Time
0	40	50	0	[09, 20]	0
1	62	80	54	[12, 16]	0.2
2	84	25	41	[12, 15]	0.2
3	55	15	27	[13, 17]	0.1
4	17	32	60	[13, 15]	0.2
5	69	91	49	[10, 13]	0.2
6	57	10	57	[10, 14]	0.2
7	49	45	60	[11, 15]	0.2
8	13	15	34	[13, 15]	0.1
9	72	75	37	[12, 16]	0.1
10	58	34	25	[11, 14]	0.1
11	44	85	36	[12, 16]	0.1
12	29	86	25	[10, 14]	0.1
13	74	92	52	[14, 17]	0.2
14	19	49	34	[14, 17]	0.1
15	95	66	49	[10, 12]	0.2
16	69	96	53	[10, 12]	0.2
17	60	95	44	[10, 12]	0.2
18	33	64	58	[12, 16]	0.2
19	19	53	29	[12, 15]	0.1
20	30	70	35	[11, 14]	0.1
21	67	39	29	[10, 13]	0.1
22	69	10	56	[10, 12]	0.2
23	84	68	58	[10, 12]	0.2
24	48	91	38	[11, 13]	0.1
25	91	25	35	[10, 14]	0.1
26	44	70	34	[11, 13]	0.1
27	79	18	33	[10, 14]	0.1
28	84	59	44	[12, 14]	0.2
29	52	60	58	[12, 14]	0.2
30	73	15	60	[10, 13]	0.2
31	13	93	31	[09, 12]	0.1
32	45	46	60	[10, 13]	0.2
33	23	43	36	[13, 16]	0.1
34	45	13	57	[11, 15]	0.2
35	98	69	55	[10, 12]	0.2
36	64	20	40	[11, 14]	0.1
37	93	23	34	[10, 14]	0.1
38	15	27	44	[12, 16]	0.2
39	29	51	49	[11, 13]	0.2
40	31	63	44	[12, 14]	0.2
41	96	87	57	[11, 13]	0.2
42	16	79	40	[12, 17]	0.1
43	30	93	31	[14, 17]	0.1
44	99	13	27	[15, 17]	0.1
45	18	82	56	[14, 17]	0.2
46	21	29	38	[13, 17]	0.1
47	36	24	35	[14, 17]	0.1
48	83	83	44	[10, 13]	0.2
49	36	73	47	[10, 14]	0.2
50	60	83	32	[12, 16]	0.1

, the 50-customer dataset was modified to bring the problem closer to reality, with modifications to customer location and goods demand, and variable service times given based on the amount of customer demand.

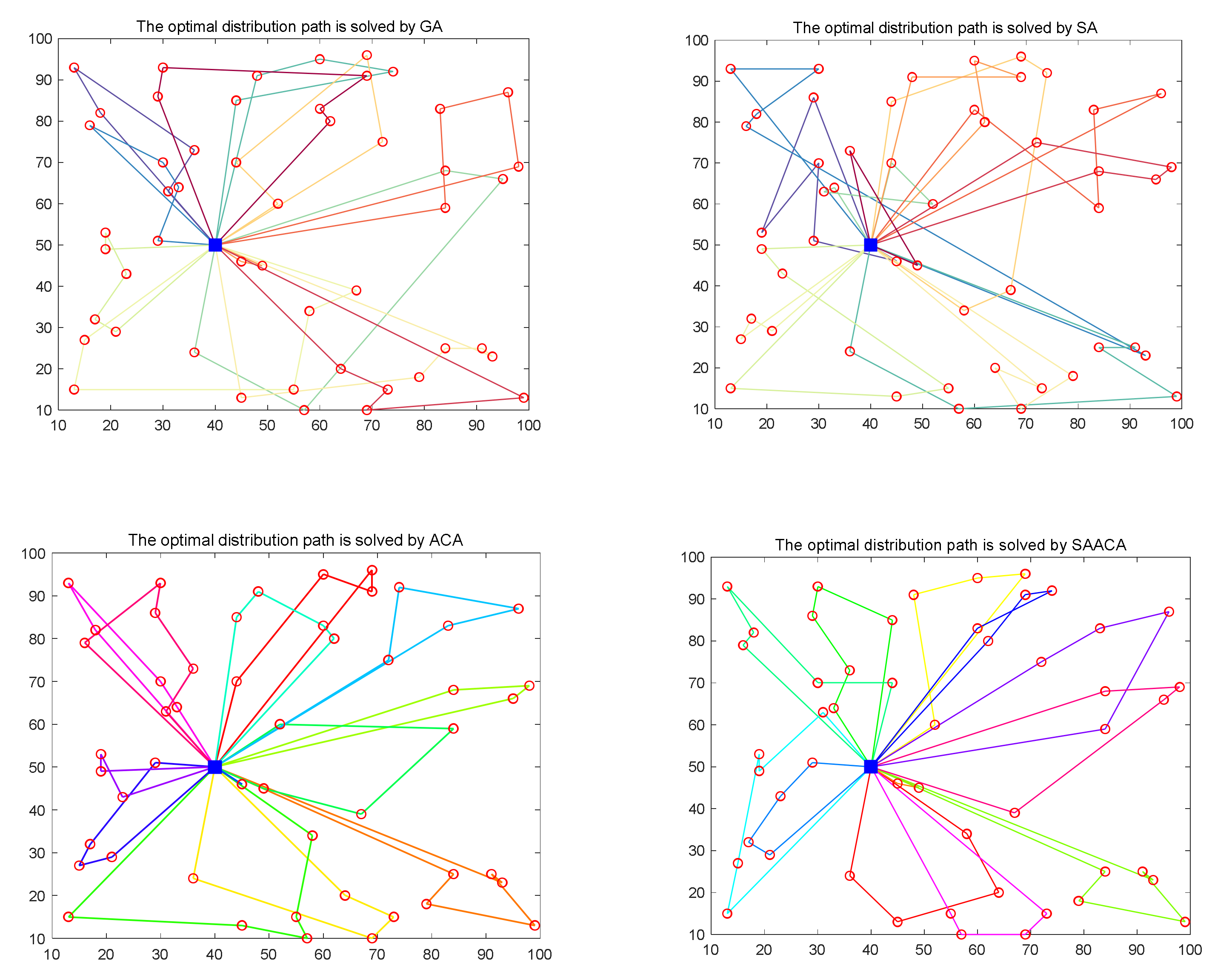
Each algorithm was uniformly set to 2000 iterations, and after 50 experiments, the conclusions shown in

Table 6. Comparison of improved ACA with other algorithms (50 customers).

	$\mathit{T}$	$\overline{\mathit{D}}$	${\mathit{Z}}_{\mathbf{min}}$	$\overline{\mathit{Z}}$	$\mathit{l}$
GA	5724.87	1337	1309.98	1349.33	12
SAA	80.52	1234	1308.03	1388.65	12
ACA	1244.76	1036	1659.80	1733.25	12
SAAACA	157.37	538	1272.21	1312.22	12

were obtained, and the optimal results were selected to obtain the optimal delivery paths for the four algorithms in the case of 50 customers as shown in Figure 9. From the figure, there are differences in the optimal delivery paths for the four algorithms. In terms of computation time, as the size of the computation increases, the time used by the GA increases most significantly, followed by the ACA, and the time of the new algorithm also increases. While the computation time of the SAA increases, it is still the fastest to complete the computation. In terms of accuracy, the advantage of the new algorithm is also evident. In particular, there is a dramatic improvement over the pre-improvement ACA, which achieves an accuracy not possible by the other three algorithms with a high level of stability. The performance of the GA and SA, on the other hand, is close in terms of both computational accuracy and stability.

With a benchmark dataset of 100 customer messages, we obtained the results in

Table 7. Comparison of improved ACA with other algorithms (100 customers).

	$\mathit{T}$	$\overline{\mathit{D}}$	${\mathit{Z}}_{\mathbf{min}}$	$\overline{\mathit{Z}}$	$\mathit{l}$
GA	550.44	70	828.94	852.32	10
SAA	87.57	1200	1004.48	1223.35	12
ACA	4285.57	1571	1255.81	1523.92	12
SAAACA	323.22	538	828.94	878.17	10

. Since the optimal solution to the problem is provided in the standard dataset, we can explore the performance of the algorithm by setting different numbers of iterations to different algorithms. Setting the number of iterations for GA to 100 provides the optimal result after an average of 68 iterations. The optimal results can also be obtained using the SAA and the improved ACA, the difference being that the improved ACA is slightly more stable, while the SAA is less stable. The SAA algorithm still has an undeniable advantage in terms of computation time, but the overall stability of the algorithm is lacking. The two GAs and the improved ACA, which provide exact solutions, are 41% better than the GA based on the actual running time required, although there is a significant difference in the number of iterations due to the algorithm’s own computational principles. For a larger customer base, the improved algorithm shows a significant advantage over the ACA in terms of both computational time and computational accuracy.

There is a relatively large difference in performance of the algorithm for GA in calculations with different sizes of data volumes, the main reason being that the service time considered in the traditional VRPTW problem is fixed. However, in the actual case in the article and in the modified dataset, the service time is based on variable service time for the volume of goods, which increases the difficulty of solving the problem. Therefore, the performance of the GA in the first two cases differ compared to the last case.

The improved ACA is vastly superior to SA, ACA, and GA when considering variable service times. The ACA and GA not only take a long time to compute but also tend to fall into local optimum solutions. The SAA has a great advantage in terms of computation time but is deficient in terms of accuracy and stability of the computation compared to the improved algorithm. By comparing the computational results using the standard dataset, it is found that the improved ACA is still well suited to the computational task and improves the computational time by 41% over the GA.

6. Summary

The problem of delivery in community group buying is modelled and analysed in this paper, considering the time window and variable service time in delivery. An improved ACA is proposed to solve the model by investigating the solution principles of SAA and ACA, and the computational performance of the improved ACA is explored by solving a benchmark dataset with the improved algorithm compared to several commonly used algorithms.

The improved algorithm is superior to the commonly used algorithms in terms of computation time and accuracy when solving problems under variable service times. The same advantage of the improved ACA is present in the comparison for the benchmark dataset, with a 41% improvement in computation time over the commonly used GA. The improved ACA has a unique advantage over the GA in computing problems with variable service times.

Although several experiments have been conducted to take an average, the presence of chance cannot be ruled out. Furthermore, although the improved algorithm has advantages in solving practical problems and computing for benchmark datasets, the increase in computation time is larger as the size of the data to be computed increases, which is still insufficient for handling large data, and the introduction of machine learning is considered in future research to improve computational efficiency.