1. Introduction
The operation and expansion of electricity systems have changed dramatically over the last couple of decades. Before the deregulation wave started in the 2000s, the decisions related to the electricity system were made by the system operator (SO), usually a public institution. The SO was the only decision-maker regarding installing new generation or transmission units to improve the system efficiency and guarantee its reliability. The development of a competitive market has introduced new actors (e.g., Generation Companies (GenCos) and retailers) that the SO must consider when solving Transmission Expansion Planning (TEP) and Generation Expansion Planning (GEP) problems [
1,
2]. According to the deregulation of power systems, new modeling trends have emerged to adjust TEP and GEP models to cope with new challenges while considering different viewpoints [
1,
3]. However, the framework of power systems is increasingly encompassing more dimensions (e.g., economic, technical, regulatory, corporate, and environmental), and planning models must take into account these new dimensions to avoid significant discrepancies between planning solutions and reality [
4].
In the context of global warming, planning models should consider environmental restrictions. These environmental-based restrictions might be related to public policies such as the share of Renewable Energy Sources (RES) present in the energy mix or to the level of security of supply to be maintained. Besides this, RES also introduce uncertainty regarding the availability of their resources. Therefore, TEP models should also consider RES production uncertainty.
In addition, the rise of new technologies (e.g., chemical storage, demand response, and hydrogen) as means of flexibility should also be accounted for through technical and regulatory restrictions. Moreover, given that energy mixes are foreseen to become extremely heterogeneous, TEP models should also consider a great level of technical details. For example, Ref. [
3] points out the need for details that TEP models should deal with according to Energy Storage Systems (ESS) to provide relevant insights. Nevertheless, investment models face a trade-off regarding the level of details of the electric power system considered, several uncertainties (e.g., fuel prices, water inflows, demand growth, strategic behavior, failures, new policies), and several dimensions surrounding the TEP problem.
However, since these emerging technologies have not yet been deployed, they are not considered in most regulatory frameworks and expansion plans. Although TEP models should include regulatory dimensions to enhance the representation of new challenges, TEP models could also assist the regulatory institutions in the design of new regulatory frameworks more conductive to sustainability. The contributions of this paper are the following. First, we identify the most relevant elements that are not included or insufficiently accounted for in TEP models. Then, we provide key insights to include them in planning exercises, including the main types of discrepancies that can be expected from disregarding them in the TEP process.
The main areas where these divergences lie have been identified as:
Technical: What human decisions have been made to simplify the planning problem? In particular, what physical phenomena have been approximated? What decisions have been simplified?
Regulatory: What current and new regulatory elements to consider in the operation of power systems (new legislation associated with the energy transition) may have a relevant impact on the investment plan?
Behavioural: To what extent are there behavioural phenomena that can have an impact on operation? In particular, is there a consideration of risk that should be incorporated to the analyses?
Each of these aspects of the human factor that we identify in transmission expansion can gave a deep impact on the resulting solution. However, it is extremely difficult to assess this impact. A suitable methodology would be: (1) Identify the most relevant human elements included in the problem. This had not been carried out in the literature. This paper performs a comprehensive analysis of the human elements involved in the problem and provides a list that can be used in practical projects. (2) Include the human factor in the formulation of the problem. We also provide formulation additions that can complement the basic formulation of the TEP problem (also provided) to incorporate these elements. (3) The parameters that describe these human components must be calibrated. This step is crucial to get relevant results; however, it is extremely difficult to carry out. Getting a good assessment of, for instance, how the different perspectives of stakeholders should be weighted against each other could take months of specialized work involving an interdisciplinary team including planners and the stakeholders themselves. This is why this paper stops at this step: we leave the calibration of the human factor to future work. (4) Solve the TEP problem with the most relevant human components included. This should include not only one instance of the problem but several of them, including different combinations of the additional equations and, if possible, sensitivity analyses on their parameters. As explained below, the result of this process should be a list of quasi-optimal, acceptably good solutions. (5) These acceptable solutions should be evaluated across all the relevant criteria, which may imply performing a series of simulations if the criteria were too complex to be included in the optimization model directly. Then, the best solution should be selected as the one to be implemented.
This paper is organized as follows.
Section 2 details the main structure of a TEP model and lists approaches and solution methods commonly used to solve the TEP problem (i.e., models and methods used for representing and solving the TEP problem: a simple formulation). In
Section 3 (i.e., The human behind the technical) we describe the human factors that lie behind the technical aspects of the model.
Section 4 dives deeper in the issues related to the human factor at the institutional scale, such as regulation and the legal framework that provides the context for the energy sector as a whole and the transmission network in particular. In
Section 5, we detail the individual attitudes and behaviours that influence energy planning. In
Section 3,
Section 4 and
Section 5 we propose modifications to the original formulation of the TEP problem that could be used to assess the impact of the human factor in transmission planning. Finally,
Section 6 summarises our main conclusions.
2. Models and Methods Used for Representing and Solving the TEP Problem: A Simple Formulation
2.1. Models
TEP is a complex problem where investment decisions have a long-standing impact on the whole system. Deciding the best transmission additions to the network is notoriously difficult. For this reason, optimization models such as openTEPES [
5] are used. These optimization models try to reflect the reality of the TEP problem. There are several modeling dimensions where these models diverge. A wide diversity of models make different modeling assumptions or use different solution methods. Their main features are shown below.
Time representation:
- -
Static: It focuses on one single expansion horizon.
- -
Dynamic: several time horizons are considered and solved simultaneously, with inter-temporal constraints linking the horizons.
- -
Sequentially static: several time horizons are considered, but instead of being solved simultaneously, they are solved sequentially.
Power flow formulation: Several power flow formulations can be used, with different implications.
- -
Transportation problem: A very crude description of the use of the network, which does not consider the physics of power flows. This is the one that is considered in most existing models [
5].
- -
DC Optimal Power Flow (DC OPF): An approximated linear form of the AC power flow.
- -
AC Optimal Power Flow (AC OPF): This would be the most accurate description of network physics, but its non-linearity means that it is impractical to include it in optimization models. When it is included indeed, it is usually approximated as Linear Problem (LP) relaxed into Second Order Conic (SOC), QC (Quadratic constraints), and SDP (Stochastic Dynamic Programming) to solve it. Besides, some meta-heuristic methods can be used to solve a non-linear AC OPF formulation. However, they typically do not work well in real-size case studies.
Decision dimension: The scope of the decisions taken into account for the problem can cover:
- -
Transmission lines
- -
Other technologies such as FACTS (Flexible AC Transmission Devices) and Phase-Shifting Transformers.
Uncertainty dimension: Several researchers have widely studied this dimension during the last decades because of its impact on the TEP problem. In the beginning, the works focused on deterministic approximations to solve the TEP problem due to the lack of computation resources. This approach has been changing until now, motivated by the increasing renewables shares and their uncertain nature. This uncertainty leads to fluctuating reserve capacities, and varying line power flows across the network; therefore, the TEP problem should include it. Some surveys, like [
1,
2], make references to this dimension and its importance. Note that the uncertainty approaches are the same as in other power system optimization problems, as presented, for instance, in [
6].
Reliability: Based on different international standards [
7,
8], a power system must operate in a such way that the outage of a single component does not interrupt supplying demand. Analyzing outage events in TEP models is a common practice called the N-1 criterion. Multiple studies have included this criterion in their mathematical formulations [
9,
10,
11,
12]. The application of N-1 analysis results in a list of congestions in the network, requiring a possible additional transmission investment. Modeling the N-1 criterion has an important impact on the size of the problem since restrictions related to the first and second Kirchhoff Law must be formulated for each contingency. This fact highlights the challenge of development methodologies to solve the problem with an acceptable computational burden.
In the following subsection, we present a stylized model for TEP, including its most relevant elements. This model is adapted from [
13] and is upgraded in the remaining sections of the paper to highlight the aspects of the TEP problem that are not usually considered in transmission planning projects. The section gets introduced with the notation of the model and then follows with the most relevant constraints and their interpretation. This model can be a good starting point for understanding the intricacies of the TEP problem. Later in the article, we will present the main human-factor issues that are not usually included in TEP studies and highlight where they would emerge in this model.
2.1.1. Notation
Sets: | Set of buses. |
| Set of circuits. |
| Set of generating units. |
| Set of branches, where . |
| Set of existing and candidate lines. |
| Set of alternative candidate lines |
| Set of load levels. |
| Set of weather scenarios. |
| Set of supergrid approach. |
Indices:
| i | Bus. |
| Line. |
| c | Circuit. |
| g | Generator (thermal, RES, or ESS). |
| n | Load level. |
| Time-step. Duration of each load level (e.g., 2 h). |
| i/k | Index for discharging/charging sample data. |
| t | Index for time step. |
| w | Index for weather scenario. |
| Index for supergrid approach. |
Functions:
| Network investment and operating cost. |
| Storage investment cost. |
System parameters:
| Base power. |
| Duration of each load level. |
| Energy not served cost. [€/ |
| Active power demand. |
| Price elasticity of demand, parameter only used in the additional equations. |
Generation System Parameters:
| Maximum and minimum active power generation. |
| Variable cost of a generator. Variable cost includes fuel, O&M and emission cost. [€/h, €/MWh] |
Transmission System Parameters:
| Annualized fixed cost of a candidate line or FACTS device respectively. [€] |
| Reactance. |
| Susceptance. (inverse value of the reactance). |
| Net transfer capacity (total transfer capacity multiplied by a security coefficient) of a line. |
| Maximum flow used in the Kirchhoff’s 2nd law constraint (e.g., disjunctive constraint for the candidate line). |
Continuous Variables:
| Load shedding. |
| Active power generation. |
| Voltage angle. |
| Active power flow. |
| Nodal prices. |
Binary Variables:
| Candidate line installed or not. |
2.1.2. A Standard Mathematical Formulation of the TEP Problem
Objective function: Transmission expansion planning aims to obtain a technically feasible expansion plan at a minimum cost for the end-users (those who ultimately pay for the assets of the energy system and their operation through the electricity bill). In this way, the objective function includes all possible costs in the mathematical model: investment, operating system that comprises the generation, and reliability. The decision-maker should assign the importance of each of these components. Equation (
1) represents the minimization of total (investment and operating) cost for the scope of the model.
Constraints:
The equation of generation-demand balance includes the balance with load demand and security of supply products (e.g., balancing services). Equation (
4) considers the balance of generation and demand at each node without ohmic losses [MW]
The flow of energy through existing elements follows physical rules. They are commonly modeled in a linear form using the voltage law equation (Kirchhoff’s second law). The Equation (
5) refers to the DC Power flow for existing and candidate lines (Kirchhoff’s second law) [rad]
Manufacturing industries produce equipment of different nominal capacities at different costs. The model considers this condition in the maximum flow constraints over each network element; its corresponding investment cost is represented in the objective function. Equations (
7)–(
11) are variable bounds for the transfer capacity in candidate transmission lines [p.u.]
Bounds on generation variables [MW]
Bounds on network variables [MW]
Voltage angle of the reference node fixed to 0 for each load level [rad]
2.2. Solution Methods
One of the first proposals for the TEP problem was presented in [
4,
14,
15,
16]. The authors focused on the determination of the expansion of the transmission network in simple cases using stylized descriptions of the power system (i.e., linear expressions). Mathematical simplifications were then necessary due to the limited computational resources during the 1970’s and 1980’s. Still, although they have the advantage of being simple and can be solved quickly, they cannot capture accurate power flows. In addition, they can only deal with continuous investment while transmission lines are discrete.
However, during the 1990’s and early 2000’s, several new, more accurate techniques to deal with the TEP were presented, for example, in references [
17,
18,
19,
20]. Mixed-Integer Linear Programming, which can incorporate both a DCPF and the discrete nature of the investment, is arguably the most extensively used method to solve the TEP problem. Currently, the TEP problem is being: (a) updated to incorporate a detailed representation of the power flows by using linearization and relaxation process within the ACPF [
21,
22,
23], and (b) integrated into another expansion planning problems [
24,
25,
26]. Alternatively, heuristic and meta-heuristics methods are also applied, as mentioned in [
27,
28,
29,
30,
31,
32]. Benders decomposition is especially interesting, as it exploits problem structure to get to a solution faster [
33]. In addition, some new techniques have been developed to reduce the problem size efficiently so that real-sized systems can be optimized [
34,
35].
The last few years have witnessed considerable growth in the number of software tools available to perform TEP. Many of these tools do not perform optimal planning but rather perform simulations of expansion solutions manually input by a planner. Some examples of these tools are DSATools, PowerWorld, PSLF, PSS/E, PSAT, and Matpower. In some cases, these tools can perform quite detailed analyses such as contingency analyses, transient stability, signal stability, or voltage stability. A full review can be found in [
36].
The most relevant tools that perform TEP are openTEPES, PLEXOS and TIMES. openTEPES is an open-source tool that performs TEP, GEP, and storage management, and which includes a DCPF [
5]. PLEXOS is a commercial tool that performs GEP, TEP, and a version of a Security-Constrained Unit Commitment [
37]. PLEXOS focuses on GEP and includes a rough description of transmission that considers the possibility of expanding the Net Transfer Capacity (NTC) among zones rather than specific transmission lines. TIMES, the family of models developed by IEA-ETSAP, also focuses on GEP with a rough description of transmission [
38].
OSeMOSYS has very similar characteristics to PLEXOS and TIMES, with the advantage of being open source [
39]. Similar open-source models with a very rough description of transmission are EMPIRE [
40], GENeSYS-MOD [
41], and Switch-Model [
42]. There is only one main tool with a more detailed description of the network than openTEPES and this is NetPlan, created by PSR [
43]. This tool focuses on optimizing only the network without considering generation or storage but with a higher level of detail. It does consider nodes and discrete investment in lines among them, with a DCPF in a stochastic setting. However, this tool is proprietary.
This section presented the core of TEP models and solving methods. Although the TEP model is detailed, the expansion planning requires refinement phases according to qualitative parameters (e.g., political decision, risk-aversion, business strategies, etc.) [
44]. The article is centered around the main dimensions of the problem as shown in
Figure 1.
3. The Human behind the Technical
In this section, we will review the human component that underlies the main decisions that seem to be technical but that include something else.
The main elements to consider are the new technologies that are included in the analysis or excluded from it and the assumptions made about the development of the generation sector in the future. In both cases, the human factor points to a subjective valuation of a technological solution.
3.1. New Technologies Considered
In a context where the energy landscape is likely to change, TEP models need to adapt to consider more details and new constraints. Although new technologies have not yet been fully deployed, their rapid development will enable them to participate in the operation of the electricity system. This section aims to list the new challenges that TEP models should consider according to new technologies.
3.1.1. Smart Elements
Growing demand and the increasing number of constraints to develop transmission projects (e.g., the protection of environmentally valuable spaces) result in a more congested electrical grid. New elements to mitigate this issue have arisen, such as smart valves [
45]. This technology can change dynamically the line impedance controlling its power flow. Another process that modifies the impedance of the line is Dynamic Line Rating (DLR), which modifies the capacity of the lines according to the weather: lower temperature or higher wind speed will allow for more power to be transmitted.
Probably the most relevant elements in this context are Flexible Alternating Transmission Devices (FACTs). In particular, we can consider Phase-Shifting Transformers (PSTs), which are able to decouple the voltage angle between two nodes connected by a line.
Constructively, these devices are located in the conductors of the transmission line; therefore, they do not require additional spaces, which is an issue for developing new transmission investments.
We can consider these elements by modifying the Second Kirchoff’s Law in Equation (
5) in the following manner:
where the meaning of the subsceptance can be modified to account for smart valves, with
being now a decision variable within a range rather than a static parameter.
DLR can be input in the line capacity equation by making the maximum power through the cable depend on a weather scenario, therefore making it
3.1.2. Energy Storage
Energy Storage Systems (ESSs) represent a challenge that needs to be included in TEP models for various reasons. First, ESSs can be seen as generating units when discharging and as load demand when charging, which should be included in the model of system operation. The fact that storage acts as a coupling between different time moments (i.e., how much energy stored remains depends on the energy was stored in the previous moment) complicates the model and requests a higher time resolution. Aside from this technical issue, the important reality about storage is that it can be used to offset the variability of renewables, hence allowing for a higher share while avoiding problems at the system level. Several issues are at play:
Lithium ion reserves, by 2040, could be in a critical state given the number of batteries that are planned to be installed worldwide [
46]. Although the trend in ESS costs is downwards, it is possible that in the future, costs will increase given the limited reserves. Thus, the uncertainty about the evolution of ESS costs should be a parameter bear in mind by TEP models and it will be deeply influenced by subjective assumptions. As an example of this growing concern, the US government recently commissioned a study on the risk that the state of material reserves may represent [
47].
Recent studies call for a better assessment of the cost of batteries to consider their long-term degradation [
48].
It is expected to be an important support for the integration of renewables. However, ESS’ ownership and operation may change their utility. To this end, TEP models could be useful to explore this multi-disciplinary issue [
49].
Including new technologies and storage can not only decrease the investment needs in traditional investment assets (transmission lines) but also minimize the environmental impact of the expansion plan, as the new technologies can be installed in a reduced area. In addition, distributed storage can increase the participation of consumers (or, prosumers) in the energy system.
According to [
50], we conduct some modifications to transmission expansion planning to consider energy storage. These modifications are listed below:
Additional Notation:
Functions:
| Storage investment cost. |
Storage Parameters:
| Variable cost of a generator. [€/ |
| Maximum energy and maximum power of an energy storage unit. |
| Efficiency of an energy storage unit. |
Continuous Variables:
| Discharging power of the storage unit. |
| Charging power of the storage unit. |
| Stored energy of a unit of energy in a period n. |
Binary Variables:
| Candidate storage unit installed or not (energy and power, respectively). |
Constraints:
where Equations (
16) and (
17) are the redefinition of the objective Functions (
1) and (
2). Equation (
18) is the redefinition of the demand balance constraint Equation (
4) considering the charge and discharge of the energy-storage units. Equation (
19) represents the storage unit efficiency. Equation (
20) is the inventory or state of charge of the storage unit. Finally, Equations (
21)–(
23) are the bounds of power and energy of every storage unit.
3.1.3. Hydrogen
Hydrogen-based technology has a significant potential to increase renewable resource shares in power systems. Recent studies have focused on its production, storage, applications, and challenges. In [
51], authors comment about four typical applications of integrating hydrogen into power systems:
Energy storage: Authors highlight that hydrogen has high energy storage capacity, a long storage period, and flexibility.
Power-to-gas: Hydrogen can be converted into methane and injected into the natural gas grid or stored, providing a balancing service to the energy market.
Co- and tri-generation: Fuel cells can be used as prime movers for combined heat and power (CHP) generation or combined cold and power (CCP) generation, known as co-generation, or to be used for combined cold heat and power (CCHP) generation, known as tri-generation.
Transportation: Authors highlight the expected growth of hydrogen-based transportation (around 36% of global vehicle sales in 2050).
According to the features mentioned above, it is necessary to model hydrogen-based storage in the transmission expansion problem to evaluate its effect on the power system as it was presented in [
52].
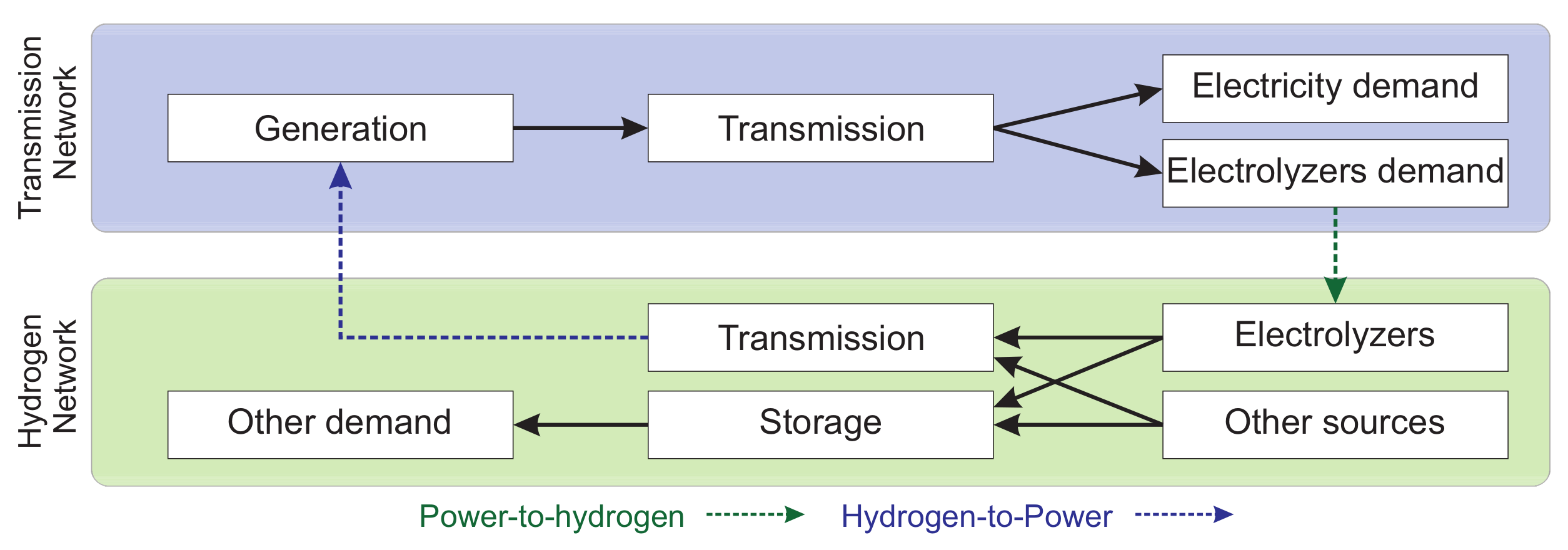
In this sense, a simplified hydrogen network within the TEP problem can be integrated according to the
Figure 2 by defining in a practicality way:
Subsets:
Set of generation units based on hydrogen:
Set of nodes of the hydrogen network:
Set of pipeline of the hydrogen network:
Indexes:
Index of generation units:
Index of nodes:
Index of pipelines:
Parameter:
Pipeline capacity:
Storage Capacity:
Efficiency power-to-hydrogen:
Efficiency hydrogen-to-power:
Hydrogen from another sources:
Hydrogen to another demand:
Maximum hydrogen charge
Variables:
hydrogen shedding
hydrogen flow
hydrogen stored
hydrogen charged
hydrogen spillage
Electrolyzer demand:
Constraints:
where Equation (
24) is the redefinition of the power balance Equation (
4), and Equation (
25) is the hydrogen balance. In addition, Equation (
26) is the inventory or state of charge of the stored hydrogen, and Equations (
27)–(
31) are the bounds of the hydrogen flow, shedding, inventory, charge, and spillage, respectively.
Figure 2.
Joint transmission and hydrogen operation.
Figure 2.
Joint transmission and hydrogen operation.
The joint planning of several energy carriers will lead to more efficient plans, with lowest investment costs for the same level of service. This additional efficiency will be higher the higher the synergies there are between the carriers. This means that, if the hydrogen network and technologies such as power-to-gas grow in importance, hydrogen should be included in the TEP planning process.
3.2. New Grid Framework: Smart-Grids/Distributed Generation
Distributed generation shifts the paradigm in power systems. Instead of large power generation units, it pushes for smaller units that are located near demand. This will require deep changes in the operation of the electricity system. In [
53], authors proposed a coordination scheme for the TSO-DSO coordination with microgrids within the TEP problem using the tri-level approach. Several TSO-DSO coordination models are defined and assessed in the literature, see [
54,
55]. In this sense, we propose the next alternatives to incorporate the TSO-DSO coordination within the TEP problem:
Two-stage approach: (a) First stage: solving the TSO-DSO coordination with microgrids, and then (b) Second stage: modifying the profile of the electricity demand to be used as a parameter to solve the TEP problem. This option could be suitable for large-scale problems, but it is probably not to get an optimal solution since it depends of iterations and couldn’t have a finite convergence.
Considering exchange variables on the power transformers at the border between the transmission and distribution network. It is suitable for medium-scale problems and consider the local flexibility within the TEP [
56], but it is complex to apply for solving large-scale problems.
Considering a tri-level [
53], it is a suitable way to consider the TSO-DSO coordination within the TEP problem; however, it is hard to be applied in large-scale problems, even for medium-scale due to the computational burden.
Geo-localization of power plants should be considered in TEP according to demand for using grid in an optimal way (transmission in a renewable-based power systems vs transmission in a thermal power-based power systems). This approach is already used for solving interconnection problem in wind offshore farms, creating HVDC grids to be interconnected to the current HVAC grids. The geo-localization could highlight the true costs of integrating new generation units on land. An alternative to connect small renewables to the bulk system is assessed in [
57].
Including distribution in the TEP process allows to get expansion plans that more accurately follow the needs of the system, avoiding over or underinvestment.
3.3. Critical Events
It is expected that by 2050 most of the electricity consumed will be produced from renewable resources. While this will mitigate the emissions from the energy sector, it brings other complications from a grid expansion planning point of view. Indeed, by increasing the system’s dependence on renewable resources such as wind, solar and water, it is necessary, when developing an expansion strategy, to consider the most critical events. These critical events can be related to demand, extreme climate conditions and other exceptional events [
58].
Moreover, according to [
58], critical events are related to unknowable and unknown uncertainties which are difficult to forecast. Therefore, it is common to design extreme strategic scenarios to further limit TEP outcomes. For example, in the Ten-Year Network Development Plan (TYNDP) 2022 Scenario Building Guidelines [
59], ENTSO-E builds ‘DunkelFlaute’ or anticyclonic gloom, as extreme scenarios for considering periods with with high load demand combined with low solar and wind generation. In this paper, since we propose a set of scenarios accounting for weather conditions,
w, it could be possible to create a subset considering critical periods such as low temperatures combined with low wind power output, and dry hydrological year.
The inclusion of critical events will generally lead to plans with a higher need for investment and better resilience to extreme scenarios.
4. The Human Factor at the Institutional Level
The main elements shaped by human-related factors at the institutional level have to do, on the one hand, with markets and regulation and, on the other, with the direct consideration of environmental constraints.
4.1. Regulation and Markets
The electric power industry is commonly divided into four activities: generation, transmission, distribution, and retailing. Usually, electric companies own the whole infrastructure from generation to distribution. Due to this structure, the electric industry was typically viewed as a natural monopoly. In many countries, the power industry experienced a significant shift towards the end of the 20th century: the deregulation of the power sector. Through a series of legal actions, the four processes composing electric power systems were unbundled and opened to competition with the possibility of new private actors joining the existing “incumbent” players. This reform began in England in 1990, migrating the monopoly structure of the market towards a competitive system.
A consequence of market liberalization is the diversity of different players in the power sector. On a broad level, we can identify diverse entities, such as generating companies (GENCOs), transmission companies (TRANSCOs), or the System Operator (SO). For this reason, it has been necessary to develop and complement the legal framework to seek efficiency and, at the same time, ensure fairness between different stakeholders.
Generation companies (GENCO): GENCOs own one or more generating units. GENCOs can bid the generating unit output into the competitive market.
Transmission companies (TRANSCO): TRANSCOs move power in large quantities from where this is produced to where it is consumed. The TRANSCO owns and maintains the transmission lines under the monopoly in some deregulated industries but does not operate them; in most countries, it is usual that an Independent System Operator (ISO) drives the operation of the electric network. The TRANSCO is paid for the use of its lines. The operation of the transmission system is not a competitive market.
System Operator (SO): The SO is an entity responsible for ensuring the reliability of the power system. The SO is an independent authority in some countries, and it does not participate in the electricity market trades and does not own electric infrastructure. SO is generally called Independent System Operator (ISO) in this case. In other ones, TRANSCOs are also system operators, and they are usually called Transmission System Operators (TSO). They have a regulatory framework to carry out the operation reliably and economically.
Traditionally, TSOs receive compensation for their investments, which are supposed to be the ones that optimally reduce system operating costs. This was a system that worked well when most of the investment was new transmission lines. However, for many emerging technologies, the operation of the network can be more expensive (even if the system as a whole becomes more efficient). This is specially true in the case of high levels of renewable penetration. Alternative remuneration models for TSOs, such as remunerating for both investment and operation costs, are currently being explored [
60].
Most models view TEP as cost minimization, where a central planner makes the most beneficial decisions for the whole electricity system [
61]. However, network investment has an intense impact on the generation market. For instance, authors in [
62] highlight that poor network design can lead to the formation of market power, which can result in a non-optimal operation.
Ideally, TEP models should take the competitive aspect of the generation market into account. In most cases, we assume that generation takes the first decision and that the network follows and must be optimized for the generation solution, but this is not always the case.
There are two main ways to include the stakeholders’ preferences in the model. The first one is through different levels in the optimization. For instance, Ref. [
63] considers three levels, one for TEP, one for GEP, and another for system operation. The other one is through a modified objective function for the problem. TSOs will minimize transmission investment, while generators will maximize their surplus, and consumers will try to reduce prices. All these can be input into a modified objective function.
where the coefficients in the equation represent the relative weights given to the objectives according to the importance attributed to the stakeholders.
A study related to this topic is carried out in [
64]. An Integrated Planned Approach (IPA), considering the transmission expansion and the generation in a perfect competition market, results in the most economical investment plan. However, this approach does not represent market liberalization.
In [
65], the authors evaluate different investment incentives on GEP in restructured power systems from a strategic generation company GENCOs perspective by using a bi-level mathematical model. Investment incentives are capacity payment and firm contract. In this case, the integration with transmission investments is missing.
In [
66] authors propose an integrated framework for developing plans considering coordinated generation and transmission investments. However, its mathematical formulation does not represent the whole transmission expansion model.
In summary, the fundamental objective of regulation is to find efficiency and, at the same time to ensure a competitive environment for different stakeholders. In the specific context of the transmission investment problem, regulation must provide proper incentives for investment but avoid over-investment and must encourage efficient operation but maintain system reliability [
62]. The omission of any relevant factors can result in divergences between investment plans’ decisions and the actual decision needed.
As explained, most works assume that generation investments lead and transmission investments follow [
67]. This means that TEP is calculated for one or several previously considered future evolution of the generation market. However, these future scenarios strongly depend on other policy ramifications.
Another interesting issue that depends on regulation is the remuneration of cross-border investment. When transmission lines are built between different countries, there tend to be countries and actors that benefit more from them, while others can even see a decrease in their profits and will request to be compensated for allowing the line. In this specific sense of the TEP, studies related to cross-border power interconnections demonstrate potential benefits by decreasing generation costs, changes in electricity prices, and reducing the end user’s payment. Building these lines that interconnect multiple countries has been proved even more efficient than national ones. Still, most times, there is a conflict and delays in the project due to the cost-benefit allocation among the countries involved. That is why the study of cross-border interconnection projects is essential, has a vast literature, and it helps to estimate how each country can contribute and how the building should reward it. Works like [
68,
69,
70,
71,
72] show how several theoretical concepts (i.e., cooperative game theory) can be applied to allocate the cost and benefits of cross-border investments.
Generation policy is also key for TEP, such as incentives towards RES at the European and national level, support for energy efficiency, or the weight given to national and European energy independence. It is interesting to note that this third group of factors is purely human, but at a collective level, reflecting social preferences about how much renewables or energy efficiency should be supported (which crystallizes in incentives for their construction) or how vital independence—also known as energy security—is also considered in the long-term planning. For instance, a scenario where high importance is placed on autonomy would never rely heavily on natural gas, given that most of it comes in imports from regions that could be considered geopolitically unstable. The human factor—not gas prices but how much Europe values independence—is a direct input for creating a panoramic energy strategy.
4.2. Environmental Protection at the Institutional Level
One of the issues that are faced by the construction of transmission corridors is the long delays that are introduced by the permitting process, which is mainly concerned with avoiding the installation of lines across environmentally protected areas [
73]. This means that the institutionally agreed definition of what land is worthy of protection and even what areas should be protected aesthetically is key when performing TEP. In some cases, the cost of building a line through aesthetically attractive areas can increase substantially, such as when alternative designs for the support towers are used or, even more, if underground installation is deemed necessary as opposed to the usual overhead line construction.
In addition, the institutional definitions of environmental concern also play a key role in the operation of hydropower, which is of the utmost importance in power systems planning because it deals with the most extreme scenarios of demand or renewables. In particular, the definition of minimum ecological flow is particularly relevant for the operation since it imposes a minimum production in hydroelectric power plants. The operational models must consider these generation requirements with other generation resources. The challenge is more significant when said coordination contemplates the interaction of cascading reservoirs. In short, the definition of minimum ecological flow is a restriction that takes away the flexibility to power system operation but is necessary to maintain the environmental sustainability.
The most appropriate way these constraints can be input into the model is through the restriction of candidate lines, where only the lines that do not cross potential areas are considered in the set of candidate lines []. In addition, the fact that underground cables may be necessary can be included as a modification in the cost of the lines, which can be input as a table. This would be represented in a modification of the investment cost parameter of lines [].
Including these elements in the planning process can decrease the social acceptance problems plaguing TEP projects and often delay their implementation.
5. The Human Factor at the Individual Level: Attitudes and Behaviour
This final section covers some of the aspects that have to do with attitudes and behaviour that start at the individual level and then get crystallized into the assumptions and goals of the planning process.
Because there is a high level of heterogeneity in the actors affected by the network planning process, we will first review the main list of stakeholders. It is the individual and institutional attitudes and behaviours of these groups that will impact the TEP solution.
Stakeholders that have the strongest interests in the transmission expansion planning and exert a driving force for network development are:
Consumers: For them, the desired transmission plan is the plan that reduces transmission constraints between demand and generation and provides the cheapest energy price. Network charges are also important for customers, and they prefer low network charges. They are also concerned with the reliability of the network.
Prosumers: From a prosumer’s viewpoint, the desired transmission plan is the plan that reduces transmission constraints and allows bidirectional power flows to switch between its consumer and generator behaviors. They are also interested in seeking a plan with a minimum network charge.
Generators: They are interested in removing the transmission constraints for dispatching generators and provides a competitive environment. Reliability is also important for power producers to sell their power without interruptions.
System operator: It seeks an investment plan that provides the most flexibility in the system operating, increasing network reliability, avoiding congestion, and reducing energy losses on the transmission.
Network owners: their objective is to maximize their revenue. In most regulatory frameworks, this implies increasing their assets under management as much as possible, hence favouring the most expensive transmission expansion plans.
Regulators: the desired plan for them is the plan which encourages competition, provides equity for all parties seeking network access, whilst the network reliability is maximized, minimizing operation cost and environmental impact.
Transmission planners should consider all of these viewpoints that usually are categorized as: economics, reliability, flexibility, network access and environmental impact. For this, several methodologies can be used, like cost-benefit analysis (CBA) and multi-criteria approach (MCA), used to consider all of these viewpoints transforming it into features to quantify the value of each network investment. The authors in [
74] propose a methodology to build expansion plans taking into account the stakeholders’ desires using fuzzy decision making. The authors in [
75] provide a general introduction of bilevel programming applications in transmission expansion planning.
When planning, the usual practice is to design several scenarios that will guide the process. These scenarios are open to subjective prioritization and assumptions that are deeply influenced by some of the human factors in Milfont’s scale [
76].
5.1. Austerity and Waste Avoidance vs. the Need to Display Social Status By Consumption
This is a cultural trait that varies widely across nations and has a deep impact on sustainability. The main form where this is included in the planning process is through the consideration of demand-response mechanisms.
In [
62], authors explain how demand roles have changed during the last decades. Before and after market liberalization, demand represented a critical parameter to consider. However, since the 2000s, demand has become an actor of electricity systems with the advancement of demand-response technology. Consumers can now reduce or shift their demand to avoid consuming at the peak-price hour. Therefore, there is a growing interest about considering a variety of technologies, available in future scenarios, onto the TEP.
In [
77], authors quantify the impact of demand response on transmission investment costs, and find a significant contribution when analysing real projects between 2010 and 2013.
Probably the most straightforward way of incorporating this is to consider an elastic demand rather than an inelastic one. For instance, we could use:
5.2. Inter-Generational Dependence
It is a variable that accounts for responsibility for past and future generations, beyond present self-interest. This is at play, for instance, in the acceptance or rejection of nuclear power plants, which create important issues with respect to the management of nuclear waste. This will be reflected in the costs assigned to generation, which would penalize problematic technologies, .
5.3. Confidence Given to Devices of the Market vs. the Need for Regulation and Institutions
This point is very relevant when designing market regulation. For instance, the remuneration of transmission is deeply affected by the attitudes towards market vs. regulated institutions.
Regulatory entities should propose legal frameworks to promote network investments. It is mandatory to carry out studies with a modified TEP model to evaluate these new devices. Usually, multilevel models represent this type of problem. The upper level represents a profit-maximization problem of an independent transmission company, whereas the lower one is a welfare maximization problem. In [
78], the authors propose a bilevel model to evaluate the H-R-G-V incentive mechanism; however, other instruments, such as presented in [
79], can be represented similarly.
5.4. Consideration of the Individual vs. the Community vs. the National or Supranational
The different accent given to each of these levels can lead to diverging actions and policies. For instance, the construction of a transmission line that might damage a particular region but highly benefit others would be determined by the specific balance of the national vs. suprantional interests.
The authors in [
80] show how important social and public acceptance are regarding new electric infrastructure, particularly new transmission networks. This work focused on Not-In-My-Backyard (NIMBY) attitudes adopted by communities and the “decide-announce-defend” (DAD) model implemented by governments. One of the most important conclusions is the inclusion of the community impacts (such as visual, health, or environmental) into the decision process.
We propose some alternatives to address this concern in a TEP model:
Include social and public acceptance constraints in the selection of candidate infrastructure. The results of this process are one of the inputs of a TEP model; therefore, the set of candidate inversions will change:
Include acceptance criteria for every candidate through an additional charge depending on preliminary social studies. This fact affects the benefits of a project and, therefore, produces different inversion plans; in this case, we can change the network investment function as follows:
Include acceptance criteria for every candidate through additional constraints. This way implies modeling other systems, for instance, environmental systems; a way to model this kind of constraint is by designing a measure for different geographical paths for every candidate inversion. In this case, we need to model the geographical system, and we must also carry out additional studies to establish referenced values of the measure. A way to model this concept is as follows:
where,
is a function to measure any acceptance criteria. This function depends on the line candidates.
is a binary variable representing the geographical path (
) of a candidate line. The parameter
is the acceptation level of the measure. Finally,
is the union of every line stretch.
Finally, suboptimal inversion plans can be proposed. The main feature of these alternative plans is to avoid candidates with low social acceptance. It would be desirable that their objective functional value will not be significantly high in comparison with a reference plan (a plan without social acceptance constraints).
5.5. The Importance of Independence/Autonomy Regarding Energy and Other Strategic Resources
This determines the network design that will be favoured, either one that serves very well the local interests but removes the accent from cooperation (i.e., a distributed generation model) or one where large investments in renewables in some areas are shared among a large region thanks to a strong, connected network such as the supergrid approach [
81].
The investments resulting from the GEP while considering the supergrid approach, tend to install generating units with larger capacity than the GEP considering the local point of view of each of the electricity systems (e.g., national electricity systems) [
82].
An alternative method for considering these two viewpoints is to propose several GEP scenarios with a more or less centralised vision. To differentiate between them, a first approach is to modify the prices given when the investment is required [
83]. In this study, we propose a set,
sg, of candidate generators and lines corresponding to the supergrid approach where the investment costs are different from the other candidates.
5.6. Perceptions of Social Risk and Responsibility
In state-of-the-art TEP, it is common to incorporate metrics such as Power Non Served to evaluate the risk of not supplying demand. However, the application of risk goes far beyond this.
The perception of social risk is the main element to consider when assessing the desirability of nuclear energy. In addition, it underlies the extreme-event assessment that is necessarily carried out in power systems operation and that must be incorporated, even if in a simplified manner, to the TEP process. Therefore, a practical way for considering social acceptability of futur projects (e.g., VRES, Nuclear, transmission lines) would be to explore scenarios where investment costs include the cost of social acceptance [
84].
6. Conclusions
In this paper, we identified the main elements of different dimensions related to the human factor (e.g., economic, technical, regulatory, corporate, and environmental) that are either neglected or insufficiently accounted for in current TEP models. Similarly, we showed the impact behind each dimension, classifying it into three broad groups: the human factor behind the technical, the human factor at the institutional level, and the human factor at the individual level. In the first group, we consider new technologies and critical events to be simulated, among others. In the second one, we group the energy market, regulation, environmental sustainability, and the institutions that handle these issues. Finally, in the last class, we add the different interests that exist for the various sector agents (e.g., consumers, prosumers, generators, system operators, network owners, and regulators). Because of these additional dimensions, the criteria and scenarios involved in TEP studies can change.
The human factor behind the technical
Technical factors such as the new technologies in power systems (e.g., smart elements, energy storage, electric vehicles, and hydrogen) can be included in the planning or not depending on their subjective evaluation by stakeholders. They result in different modifications in the formulation of the TEP model and the simulation of new critical events.
The human factor at the institutional level
The human factor in the institutions that handle energy markets, regulation, and environmental sustainability plays a key role in the decisions of new infrastructure and, therefore, on the TEP models used by analysts.
Advanced TEP models require to model the interactions between the electricity market and the operation of power systems. Expanding the TEP model allows us to evidence economic consequences (e.g., market power) by the expansion decisions under consideration. In other words, the TEP models should allow us to assess the competition level between the sector’s agents (consumers, prosumers, generators, system operators, network owners, and regulators). The regulatory framework is another key element of advanced TEP models. In this regard, these models must consider current regulatory schemes and the ability to assess new ones, such as demand response programs or financial elements for coordination of expansion.
Finally, there are additional environmental constraints that must be included in the model, such as geographical limitations for new lines or minimum flows.
The human factor at the individual level
Investments in new infrastructure show a high correlation with the interests of the actors in the electrical sector (such as consumers and prosumers). The transmission planner should consider these different viewpoints. For this, advanced TEP models should contemplate multi-objective functions or constraints representing some of the human factors on the Milfont scale.
We have also provided additional formulation that can be added to the fundamental TEP model presented to account for these elements.
This paper has presented an introduction to TEP, its importance for our global sustainability goals and how, in a problem that is apparently technical, the human factor is key and cannot be ignored. We have provided a comprehensive view of these issues and linked them to the human factors in Milfont’s scale. We hope this work helps frame the transmission expansion planning process in a more realistic manner that is better conducing to a more sustainable energy system.