Location Optimization of Fresh Agricultural Products Cold Chain Distribution Center under Carbon Emission Constraints
Abstract
1. Introduction
2. Literature Review
2.1. Carbon Emissions from Cold Chain Logistics
2.2. Location for Logistics Distribution Centers
2.3. Location for Cold Chain Logistics Distribution Centers
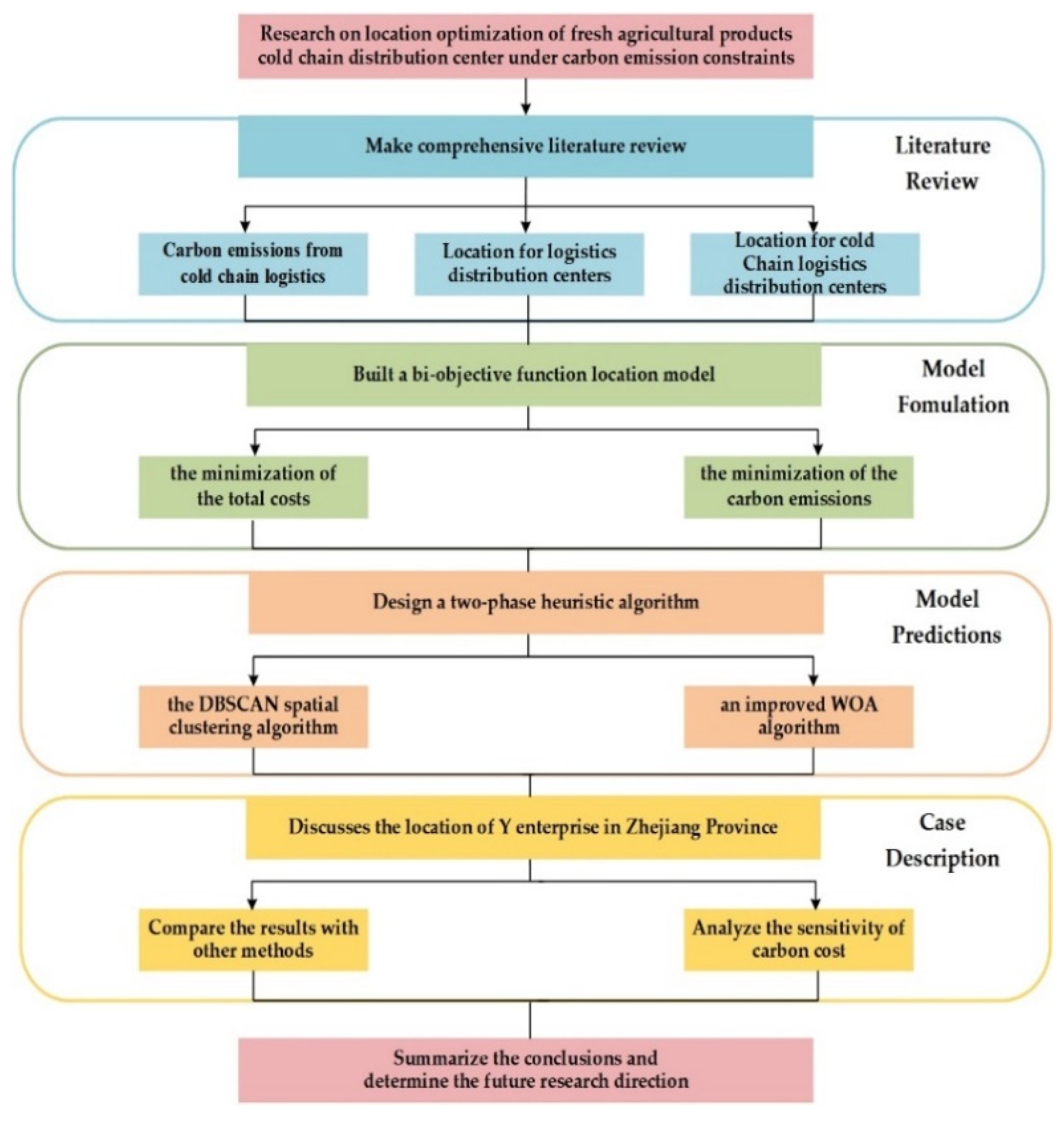
2.4. Research Framework and Summary of Ideas
- Question 1: How to build the location model of fresh agricultural products cold chain distribution center on the premise of considering carbon emissions?
- Question 2: How to design an optimization algorithm to solve the constructed model?
- Question 3: How to prove the correctness of the constructed model and algorithm through the solution of a case?
3. Model Formulation
3.1. Descriptions and Hypotheses of Location Selection
3.2. Symbols and Variables
3.3. Cost Analysis of the Location Selection for Cold Chain Distribution Centers
3.3.1. The Penalty Cost of Freshness
3.3.2. The Overall Carbon Emission Costs
- (1)
- The static carbon emissions of cold chain distribution centers
- (2)
- Dynamic carbon emissions during refrigerated vehicle transportation
3.4. Model Construction
4. Model Predictions
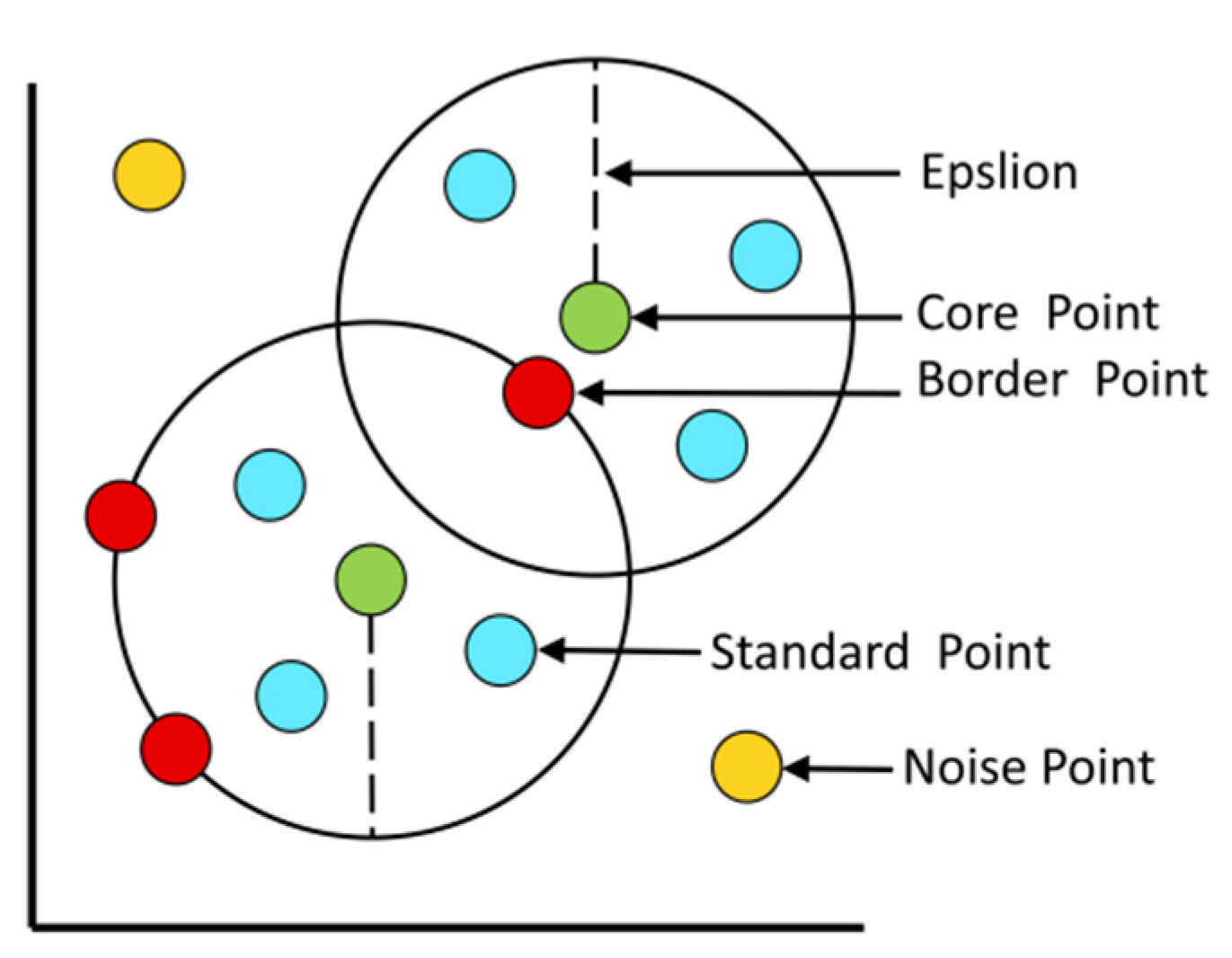
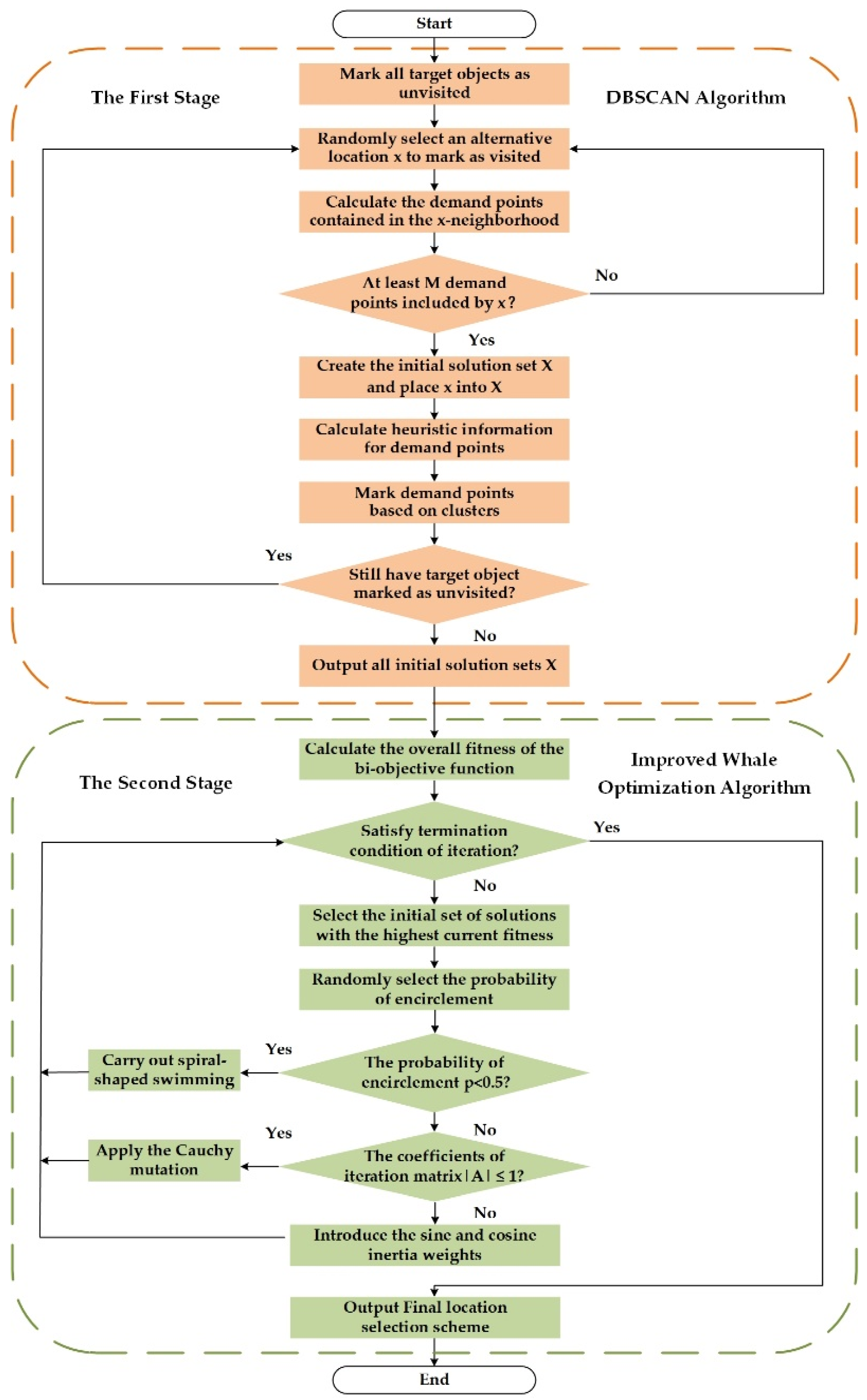
4.1. DBSCAN Spatial Clustering Algorithm for Initial Solution Clustering
4.1.1. Core Point Clustering
4.1.2. Border, Standard and Noise Point Clustering
4.2. Improved Whale Optimization Algorithm for Iterative Solution
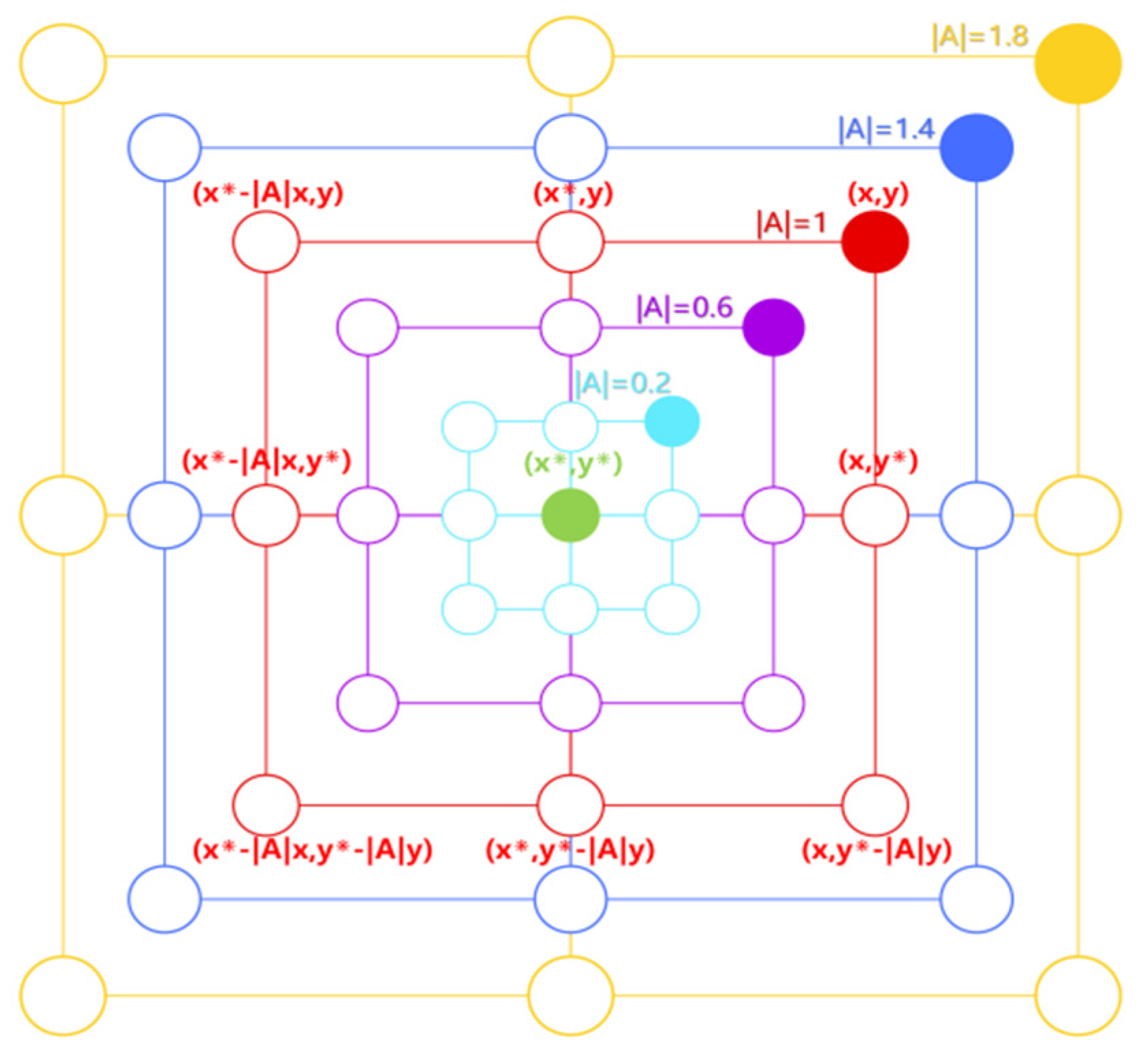
4.2.1. The Solution Process of the Basic Whale Optimization Algorithm
- (1)
- Encircling
- (2)
- Bubble-net attacking
- (3)
- Spiral-shaped hunting
4.2.2. Using Sort Matrices to Calculate the Overall Fitness of the Bi-objective Function
4.2.3. Adopting the Mutation-Induced Perturbation of the Cauchy Distribution
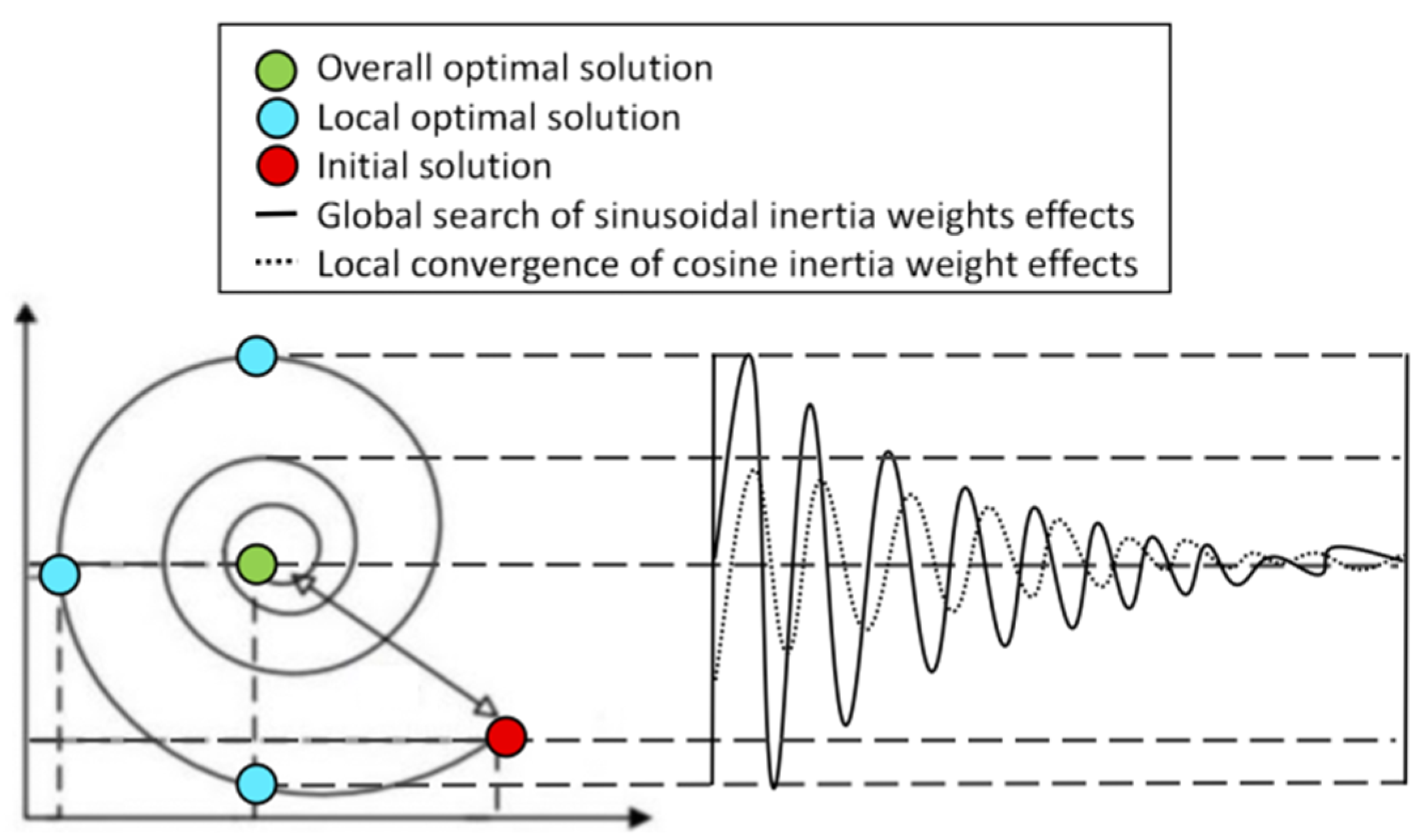
4.2.4. Introducing Sine and Cosine Inertia Weights
4.3. Solving Steps of Two-Stage Heuristic Algorithm
| Algorithm 1 First stage |
|
Import the necessary class library files Define key variables and parameters BEGIN Click the Start button Sign () function marks all objects as unvisited The random function Random () determines an alternative point as x Assign the x attribute to visited X = visited Calculate N demand points in x field If (N>=M) { Create solution set X X. add (x) Computational heuristic information Cluster() clustering algorithm marks demand points If (still target object unvisited) { Execute random function Random() module }else { Output all initial solution sets X } }else { Re-execute the random function Random() module } END |
| Algorithm 2 Second stage |
|
Import the necessary class library files Define key variables and parameters BEGIN According to the solution set X of the previous algorithm Calculate() calculate the overall fitness of the bi-objective function If (iteration termination condition satisfied) { Output program results } Else { The MAX() function selects the initial solution set with the highest fitness The Random() function randomly selects the corresponding probability P If (probability P<0.5) { Carry out spiral-shaped swimming Determine whether the iteration termination condition is satisfied Perform corresponding operations } Else { If (|A|<=1) { Apply the Cauchy mutation Determine whether the iteration termination condition is satisfied Perform corresponding operations } Else { Introduce the sine and cosine inertia weights Determine whether the iteration termination condition is satisfied Perform corresponding operations } } } END |
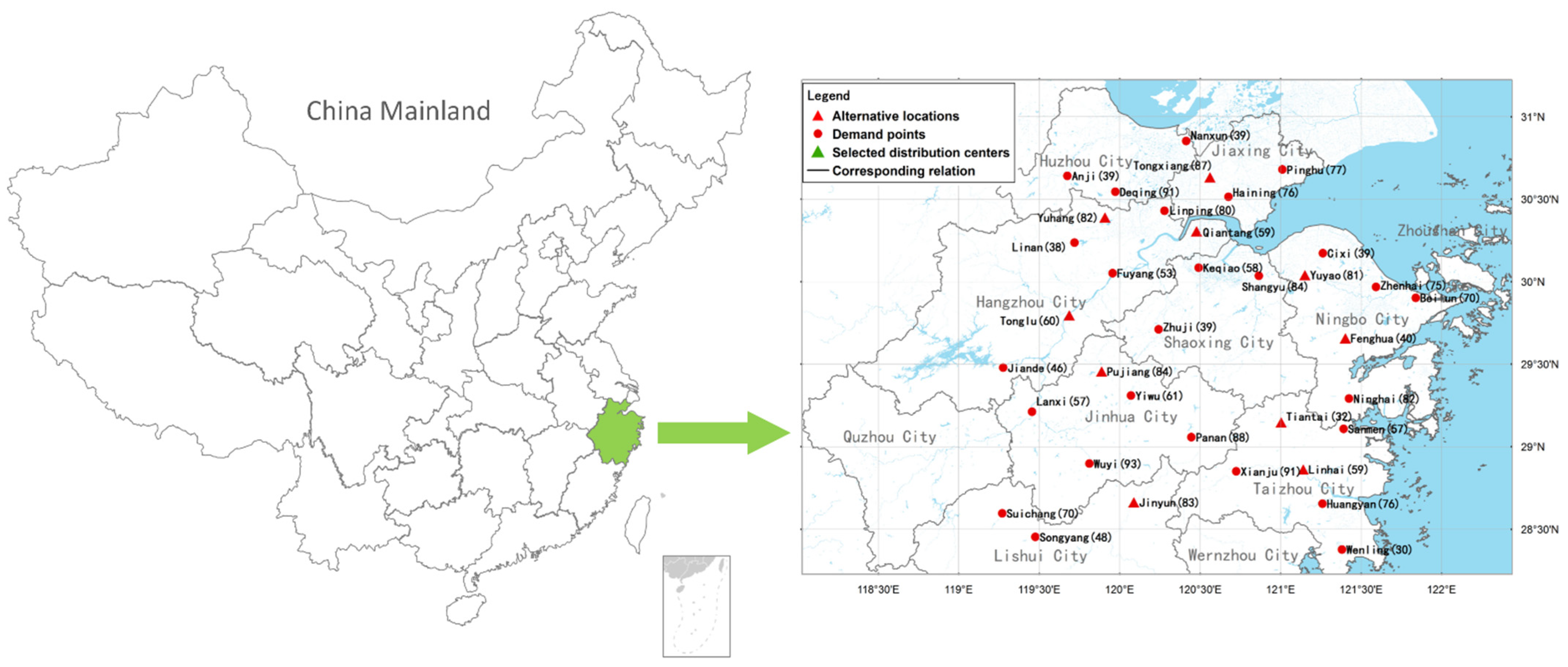
5. Case Description and Data Acquisition
6. Results and Discussion
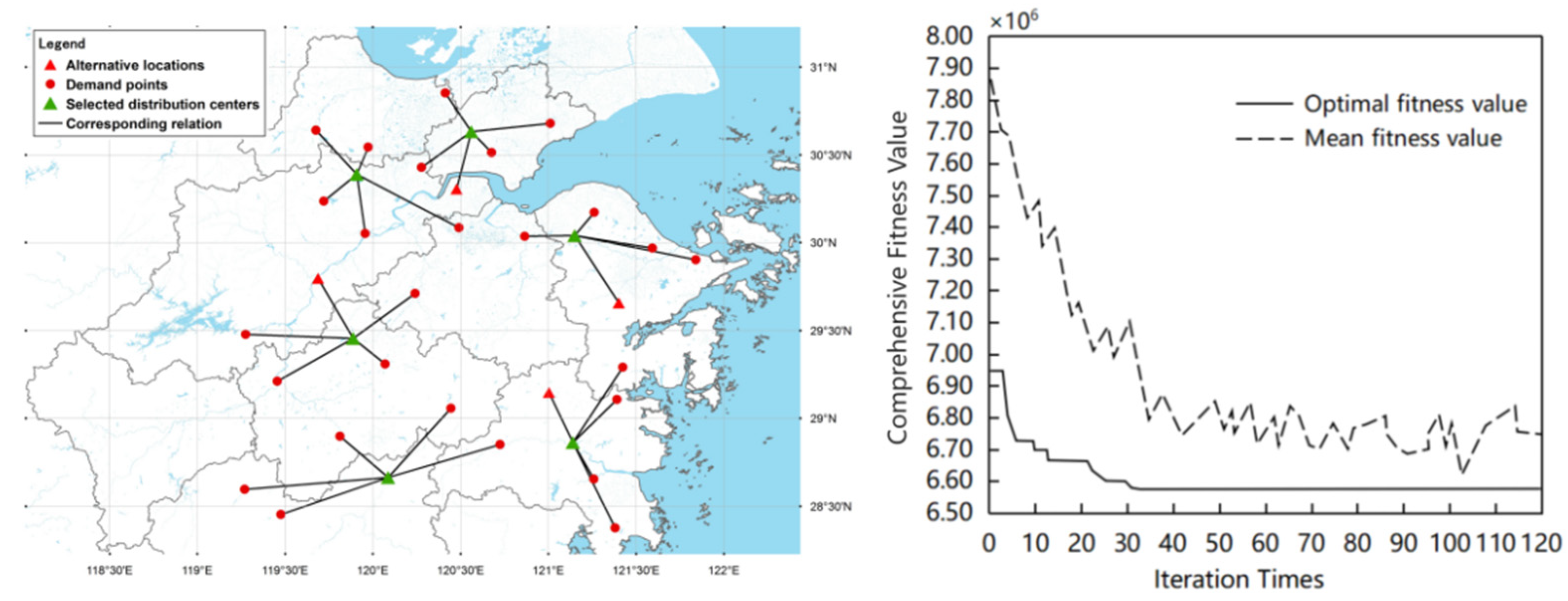
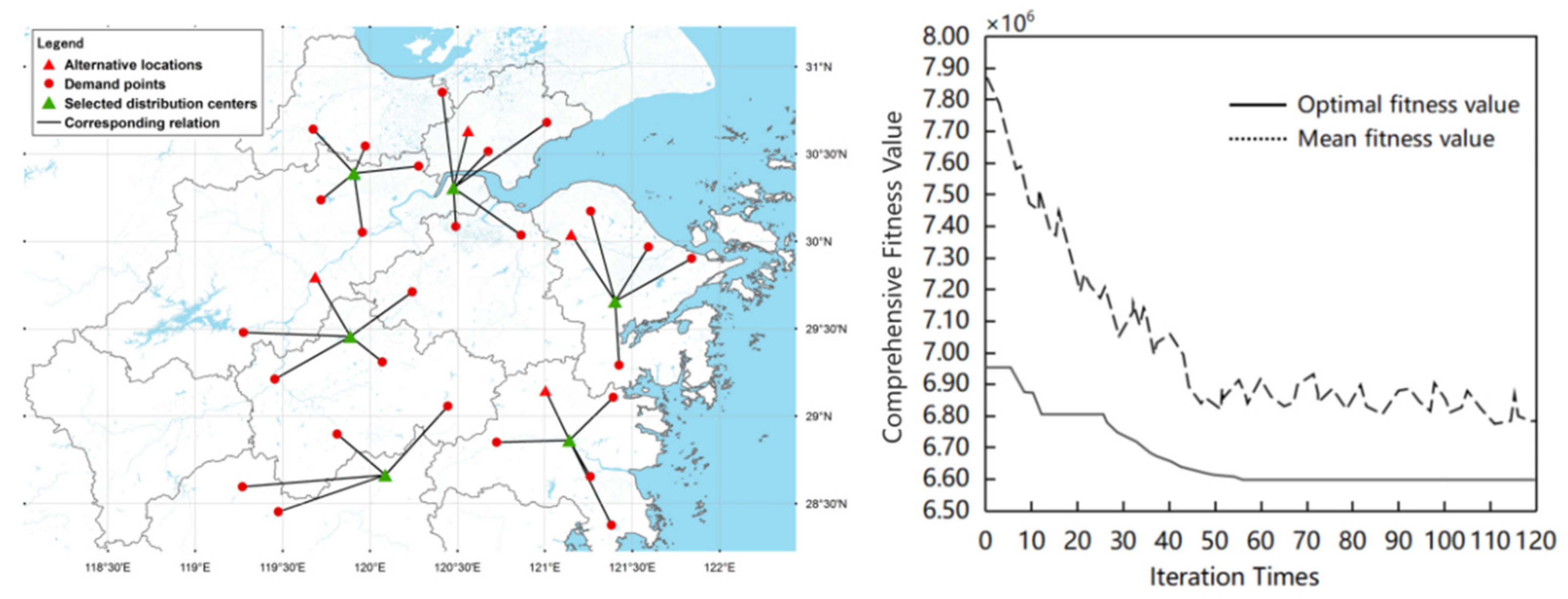
6.1. Contrastive Analysis of the Case Study
6.2. Sensitivity Analysis Based on the Cost per Unit of Carbon Emissions
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, H.J.; Chen, P.Y. A review of research on cold chain logistics and distribution of fresh agricultural products. Coop. Econ. Technol. 2022, 4, 93–95. [Google Scholar] [CrossRef]
- Luo, Y.; Peng, Y. Analysis on the development strategy of cold chain logistics of fresh agricultural products. Mod. Agric. Technol. 2022, 5, 203–204, 207. [Google Scholar]
- Mao, X.Y. Research on the development problems and solutions of fresh cold chain logistics in the post-epidemic era. China Storage Transp. 2022, 2, 185–187. [Google Scholar] [CrossRef]
- Yu, S.Z. Risk Assessment of Fresh Food E-Commerce Cold Chain Logistics. Master’s Thesis, Shijiazhuang Railway University, Shijiazhuang, China, 2021. [Google Scholar]
- Zhang, S. Research on Risk Identification, Evaluation and Countermeasures of Cold Chain Logistics of Fresh Agricultural Products. Master’s Thesis, Anhui University of Science and Technology, Hefei, China, 2020. [Google Scholar]
- Lord, H.E.; Taylor, J.D.; Finn, J.C.; Tsokos, N.; Jeffery, J.T.; Atherton, M.J.; Evans, S.F.; Bremner, A.P.; Elder, G.O.; Holman, C.D.A.J. A randomized controlled equivalence trial of short-term complications and efficacy of tension-free vaginal tape and suprapubic urethral support sling for treating stress incontinence. BJU Int. 2006, 98, 367–376. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.Y.; Chen, N.; Li, Y.H.; Yang, J. Research on optimization decision-making of urban cold chain logistics distribution system from the perspective of low carbon. Ind. Eng. Manag. 2022, 27, 56–64. [Google Scholar] [CrossRef]
- Duan, S.Y. Location-Path Research on Cold Chain Distribution of Fresh Agricultural Products Considering Carbon Trading. Master’s Thesis, Beijing Jiaotong University, Beijing, China, 2019. [Google Scholar]
- Pei, Y.H. Research on Location Selection of Cold Chain Distribution Center for Fresh Agricultural Products Based on Demand Forecast. Master’s Thesis, Chongqing Technology and Business University, Chongqing, China, 2016. [Google Scholar]
- Li, X.; Zhou, K. Multi-objective cold chain logistic distribution center location based on carbon emission. Environ. Sci. Pollut. Res. 2021, 28, 32396–32404. [Google Scholar] [CrossRef]
- Jiang, Y.M.; Wang, S.Y.; Ma, X.L. Research on the cold chain logistics system of agricultural products based on carbon optimization. Technol. Manag. Res. 2017, 37, 221–227. [Google Scholar]
- Tian, L.N. Optimization Analysis of Fruit Single-Stage Cold Chain Benefit Considering Carbon Emissions. Master’s Thesis, Southwest Jiaotong University, Chongqing, China, 2012. [Google Scholar]
- Benjaafar, S.; Li, Y.; Daskin, M. Carbon footprint and the management of supply chains: Insights from simple models. IEEE Trans. Autom. Sci. Eng. 2013, 10, 99–116. [Google Scholar] [CrossRef]
- Pan, Q.Q.; Gan, H.C. Research on optimization of cold chain logistics distribution path considering carbon emissions. Pract. Underst. Maths 2016, 46, 62–68. [Google Scholar]
- Li, H.D. Research on Inventory-Distribution Strategy of Fresh Food Supply Chain under Different Decision-Making Modes. Master’s Thesis, Beijing Jiaotong University, Beijing, China, 2020. [Google Scholar]
- Weber, A. Ueber Den Standort Der Industrien; Wentworth Press: London, UK, 1922. [Google Scholar]
- Hakimi, S.L. Optimum Locations of Switching Centers and the Absolute Centers and Medians of a Graph. Oper. Res. 1964, 12, 450–459. [Google Scholar] [CrossRef]
- Kayikci, Y. A conceptual model for intermodal freight logistics center location decisions. Procedia-Soc. Behav. Sci. 2010, 2, 6297–6311. [Google Scholar] [CrossRef]
- Fu, X.P.; Zou, J. Application of analytic hierarchy process in location selection of logistics center. World Shipp. 2002, 4, 23–24, 28. [Google Scholar]
- He, F.Z. Research and Application of Logistics Park Location Decision-Making. Master’s Thesis, Chongqing University, Chongqing, China, 2006. [Google Scholar]
- Zheng, Z.C.; Liu, X. The application of grey correlation degree and AHP in cold chain logistics distribution center location problem. Sci. Technol. Eng. 2009, 9, 1366–1369, 1374. [Google Scholar]
- Lu, X.C.; Zhan, H.S. Research on location selection of distribution center by gravity center method. J. North. Jiaotong Univ. 2000, 6, 108–110. [Google Scholar]
- Hua, G.W.; Yang, F.M.; Li, J.Q. Two two-objective competitive location problem models. Syst. Eng. Theory Pract. 2007, 1, 99–106. [Google Scholar]
- Li, Z.Y.; Lin, H.; Li, W. Layout of distribution center of fresh supermarket chain based on Baumol-Wolfe method. Logist. Technol. 2005, 7, 19–23. [Google Scholar]
- Erlebacher, S.J.; Meller, R.D. The interaction of location and inventory in designing distribution systems. IIE Trans. Inst. Ind. Eng. 2000, 32, 155–166. [Google Scholar] [CrossRef]
- Jiang, D.L.; Du, W. Location model of logistics distribution center based on genetic algorithm. Logist. Technol. 1997, 5, 3–6. [Google Scholar]
- Shen, B. Application of Improved Ant Colony Algorithm in Logistics Distribution. Master’s Thesis, Zhejiang University, Hangzhou, China, 2004. [Google Scholar]
- Yang, B. Research on Application of Tabu Search Algorithm in Refrigerated Supply Chain Distribution Network. Master’s Thesis, Shanghai Maritime University, Shanghai, China, 2005. [Google Scholar]
- Bai, S.; Liu, X. Research on Location of Cold Logistic Chains Distribution Centers Based on Grey Correlation Degree and AHP Method. In Proceedings of the 2008 IEEE International Conference on Service Operations and Logistics, and Informatics, Beijing, China, 12–15 October 2008; Volume 2, pp. 3027–3030. [Google Scholar]
- Pan, Q. Research on Location Selection of Cold Chain Distribution Center Based on Two-Level Planning Model. Master’s Thesis, Wuhan University of Technology, Wuhan, China, 2013. [Google Scholar]
- Montanari, R. Cold chain tracking: A managerial perspective. Trends Food Sci. Technol. 2008, 19, 425–431. [Google Scholar] [CrossRef]
- Demirtaş, N.; Tuzkaya, U.R. Strategic planning of layout of the distribution center: An approach for fruits and vegetables hall. Procedia-Soc. Behav. Sci. 2012, 58, 159–168. [Google Scholar] [CrossRef][Green Version]
- Li, X.; Wu, X.B.; Liu, Q. Location model of logistics distribution center based on variation and dynamic adaptive PSO. J. Dali Univ. 2021, 6, 12–16. [Google Scholar]
- Tang, X.F.; He, J.; Zhang, H. A two-stage site-routing problem considering carbon emissions and its algorithm. J. Southwest Jiaotong Univ. 2022, 4, 1–7. [Google Scholar]
- Li, J.J. Research on Location Selection of Cold Chain Logistics Distribution Center for Fresh Agricultural Products. Master’s Thesis, North Central University, Taiyuan, China, 2021. [Google Scholar]
- Yin, W.W. A case study on location selection of logistics distribution center. Logist. Eng. Manag. 2020, 42, 23, 68–71. [Google Scholar]
- Li, G.Q. Site Selection-Inventory-Path Integration Optimization and Research of Logistics System in Stochastic Environment. Master’s Thesis, Lanzhou Jiaotong University, Lanzhou, China, 2019. [Google Scholar]
- Wang, Y.Q.; Zhou, Y.; Zhang, R. Research on the equilibrium model of multi-level cold chain logistics network for agricultural products considering carbon emissions. J. Beijing Jiaotong Univ. 2017, 16, 99–107. [Google Scholar] [CrossRef]
- Wang, M. Research on Optimization Model and Algorithm of Fresh Product Logistics Distribution Considering Freshness. Master’s Thesis, Dalian University of Technology, Dalian, China, 2018. [Google Scholar]
- Ma, R.F. Research on the Equilibrium of Logistics Service Supply Chain Network Considering Carbon Emission and Carbon Emission Reduction Cost Allocation. Master’s Thesis, Qingdao University, Qingdao, China, 2021. [Google Scholar]
- Fei, X.D. Research on Vehicle Routing Problem in Cold Chain Logistics Distribution of Fresh Agricultural Products. Master’s Thesis, Beijing University of Posts and Telecommunications, Beijing, China, 2021. [Google Scholar]
- Hu, Y.L.; Zhu, Q.Y. Analysis on the revision of the waste volume of “IPCC 2006 Guidelines for National Greenhouse Gas Inventories” (2019 Revised Edition). Low Carbon World 2021, 11, 49–50. [Google Scholar] [CrossRef]
- Bowyer, D.P.; Akçelik, R.; Biggs, D.C. Guide to Fuel Consumption Analyses for Urban Traffic Management; Australian Road Research Board: Sydney, Australia, 1984. [Google Scholar]
- Zhao, Z.Q.; Zhang, L.T.; Wang, W.Z.; Hu, Z.B. Research on location selection of fresh agricultural products front warehouse based on customer demand distribution. Comput. Appl. Softw. 2021, 38, 107–113, 124. [Google Scholar]
- Sun, L.; Liang, Y.Q. An improved clustering algorithm integrating meshing and DBSCAN. Comput. Eng. Appl. 2022, 4, 1–9. [Google Scholar]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Dong, X.H. Research on Low-Carbon Distribution Path Selection of Fresh Agricultural Products Cold Chain Under Time-Varying Road Network. Master’s Thesis, Tianjin University of Technology, Tianjin, China, 2021. [Google Scholar]
- Shang, M.; Kang, J.Y.; Cao, J.W.; Wang, Z.P. Location strategy of logistics distribution center based on improved whale optimization algorithm. Comput. Appl. Softw. 2019, 36, 254–259. [Google Scholar]
- Qiu, X.G.; Wang, R.Z.; Zhang, W.G.; Zhang, Z.Z.; Zhang, Q. Improved whale optimization algorithm based on mixed strategy. Comput. Eng. Appl. 2022, 58, 70–78. [Google Scholar]
- Guo, Z.Z.; Wang, P.; Ma, Y.F.; Wang, Q.; Gong, C.Q. Whale optimization algorithm based on adaptive weights and cauchy variation. Microelectron. Comput. 2017, 34, 20–25. [Google Scholar] [CrossRef]
- Liu, Z.S.; Li, S. Positive co-chaos double string whale optimization algorithm. Comput. Eng. Appl. 2018, 54, 159–163, 212. [Google Scholar]
- Wang, Y.B. E-commerce logistics distribution path planning based on improved sine and cosine algorithm. J. Taiyuan Univ. 2021, 39, 68–74. [Google Scholar] [CrossRef]
- Shi, C.H.; Liu, H. Pharmaceutical logistics distribution path planning based on sine and cosine adaptive gray wolf optimization algorithm. Pract. Underst. Math. 2020, 50, 114–127. [Google Scholar]
- Ren, J. A review of research on cold chain logistics and distribution of fresh agricultural products in my country. Logist. Technol. 2022, 45, 150–152. [Google Scholar] [CrossRef]
- Zhang, D.Y. Research on the Supply Chain Model of Fresh Agricultural Products in enterprise Province. Master’s Thesis, Shanghai Academy of Social Sciences, Shanghai, China, 2018. [Google Scholar]
- Zhou, T.J.; Chen, X.L. Analysis on the accurate estimation of future carbon emission space under the temperature control target of the “Paris Agreement”. Proc. Chin. Acad. Sci. 2022, 37, 216–229. [Google Scholar] [CrossRef]
- Wu, H.J. Distribution route planning of agricultural product logistics enterprises based on greedy whale optimization algorithm. J. Lanzhou Inst. Technol. 2022, 29, 83–87. [Google Scholar]
- Tang, L.Q.; Ying, Z.Y.; Luo, Y. Base station location selection based on whale optimization and improved algorithm. Comput. Mod. 2020, 9, 100–105. [Google Scholar]
- Li, X.; Wu, X.B.; Tong, B.L. Particle swarm optimization algorithm based on dynamic adaptive variable parameters. J. Sichuan Univ. Light Chem. Ind. 2021, 34, 41–47. [Google Scholar]
- Gao, X.X. Several Particle Swarm Optimization Algorithms and Their Applications. Master’s Thesis, Northern University for Nationalities, Yinchuan, China, 2020. [Google Scholar]
- Hao, Y.T. Research on Cold Chain Coordination under Carbon Allowance Trading Mechanism. Master’s Thesis, North China Electric Power University, Beijing, China, 2021. [Google Scholar]
- Zheng, J.Z.; Hong, Y.W.; Xu, W.C.; Li, W.T.; Chen, Y.F. An effective iterated two-stage heuristic algorithm for the multiple Traveling Salesmen Problem. Comput. Oper. Res. 2022, 143, 105772. [Google Scholar] [CrossRef]
- He, L. Research on Dynamic Vehicle Routing Optimization Based on Two-Stage Heuristic Algorithm. Master’s Thesis, Chongqing University of Posts and Telecommunications, Chongqing, China, 2021. [Google Scholar]
- Luan, L. Research on Location Selection and Path Optimization of Cold Chain Distribution Center for Fresh Agricultural Products Based on Double-Layer Planning. Master’s Thesis, Beijing Jiaotong University, Beijing, China, 2019. [Google Scholar]
- Linfati, R.; Escobar, J.W.; Escalona, J. A two-phase heuristic algorithm for the problem of scheduling and vehicle routing for delivery of medication to patients. Math. Probl. Eng. 2018, 2018, 8901873. [Google Scholar] [CrossRef]
- Pan, L.G. Model Research on Low-Carbon Multimodal Transport Routing Problem Considering Time Window. Master’s Thesis, Nanjing University, Nanjing, China, 2020. [Google Scholar]
- Sun, J.P. Research on Route Optimization of Cold Chain Logistics Considering Traffic Congestion and Time Window Constraints. Master’s Thesis, North China Electric Power University, Beijing, China, 2021. [Google Scholar]




| Hypothetical Situations | Content |
|---|---|
| Supply and Demand | (1) the inventory of a single distribution center can satisfy the demand of covering demand points, and the inventory is equal to the sum of the demand of all demand points (2) the demand for fresh agricultural products at each demand point is fixed and will not fluctuate greatly in the short term |
| Transportation | (1) alternative locations are equipped with sufficient refrigerated vehicles for transport, regardless of shipping batches and fixed costs of vehicles (2) refrigerated vehicles travel at a constant speed, regardless of service time window constraints and vehicles routing |
| Carbon Emissions | (1) the site selection process involves static carbon emissions from distribution centers and dynamic carbon emissions from refrigerated vehicle transportation (2) carbon emissions from product decay are not considered |
| Freshness | (1) the freshness of fresh agricultural products is only related to the transportation time (2) the effect of temperature change on freshness is not considered |
| Parameters and Symbols | Meaning |
|---|---|
| n | the number of demand points of fresh agricultural products |
| m | the number of alternative locations for distribution centers |
| h | the number of distribution centers to be established |
| fi | the fixed reconstruction costs of the alternative location i for distribution centers |
| qij | the quantity of products provided by i to the demand point j |
| Dj | the quantity of products that j needs to provide |
| ci | the storage cost per unit of goods stored in i |
| dij | the straight-line distance between i and j |
| co | the fuel cost per unit distance during transportation |
| λ | the cost per unit of carbon emissions |
| ECi | the electric energy consumed by i |
| e1 | carbon emission factor per unit of electricity consumed |
| e2 | carbon emission factor per unit of diesel consumed |
| OPi | the amount of diesel consumed in daily storage operations in i |
| δ1 | the low calorific value of diesel |
| δ2 | carbon content per unit calorific value of diesel |
| δ3 | the carbon oxidation factor of diesel |
| VP | the diesel consumption per unit distance travelled by a refrigerated vehicle |
| Q0 | the weight of a refrigerated vehicle |
| Qmax | the maximum load of a refrigerated vehicle |
| β1 | the penalty cost for fresh agricultural products that do not meet the freshness requirements of the demand points |
| β2 | the negative penalty cost for fresh agricultural products that meet the freshness requirements of the demand points |
| R | the freshness of fresh agricultural products when delivered to the demand points |
| Φ | the sensitivity coefficient of freshness to time |
| Δt | the time needed for the transportation of fresh agricultural products to the point of demand |
| yi | a 0/1 variable. If a cold chain distribution center is established on i, yi is 1, otherwise, it is 0 |
| xij | a 0/1 variable. If i serves j, xij is 1, otherwise, it is 0 |
| a&b | the linear parameters |
| Object | Alternative | ||||
|---|---|---|---|---|---|
| Al(1) | Al(2) | Al(3) | ⋯ | Al(M) | |
| Obj1 | OR1(1) | OR1(2) | OR1(3) | ⋯ | OR1(M) |
| Obj2 | OR2(1) | OR2(2) | OR2(3) | ⋯ | OR2(M) |
| Demand Points | Longitude and Latitude Coordinates | Demanded Quantity/t | Demand Points | Longitude and Latitude Coordinates | Demanded Quantity/t |
|---|---|---|---|---|---|
| 1 Yuhang District | (120.30, 30.42) | 82 | 19 Anji County | (119.68, 30.63) | 39 |
| 2 Fuyang District | (119.95, 30.05) | 53 | 20 Pinghu City | (121.02, 30.70) | 77 |
| 3 Linan District | (119.72, 30.23) | 38 | 21 Haining City | (120.68, 30.53) | 36 |
| 4 Linping District | (120.30, 30.43) | 80 | 22 Tongxiang City | (120.57, 30.63) | 87 |
| 5 Qiantang District | (120.22, 30.26) | 59 | 23 Lanxi City | (119.45, 29.22) | 57 |
| 6 Jiande City | (119.28, 29.48) | 46 | 24 YiwuCity | (120.07, 29.30) | 61 |
| 7 Tonglu County | (119.67, 29.80) | 60 | 25 Wuyi County | (119.82, 28.90) | 93 |
| 8 Beilun District | (121.85, 29.93) | 70 | 26 Pujiang County | (119.88, 29.45) | 84 |
| 9 Zhenhai District | (121.72, 29.95) | 75 | 27 Pan’an County | (120.43, 29.05) | 88 |
| 10 Fenghua District | (121.40, 29.65) | 40 | 28 Huangyan District | (121.27, 28.65) | 76 |
| 11 Yuyao City | (121.15, 30.03) | 81 | 29 LInhai City | (121.12, 28.85) | 59 |
| 12 Cixi City | (121.23, 30.17) | 39 | 30 WenLingCity | (121.37, 28.37) | 30 |
| 13 Ninghai County | (121.43, 29.28) | 82 | 31 Sanmen County | (121.38, 29.12) | 57 |
| 14 Keqiao District | (120.50, 30.08) | 58 | 32 Tiantai County | (121.03, 29.13) | 32 |
| 15 Shangyu District | (120.87, 30.03) | 84 | 33 Xianju County | (120.73, 28.87) | 91 |
| 16 Zhuji City | (120.23, 29.72) | 39 | 34 Jinyun County | (120.07, 28.65) | 83 |
| 17 Nanxun City | (120.43, 30.88) | 39 | 35 Suichang County | (119.27, 28.60) | 70 |
| 18 Deqing County | (119.97, 30.53) | 91 | 36 Songyang County | (119.48, 28.45) | 48 |
| Alternative Location | Storage Cost per Unit of Goods ci/Dollar | Fixed Reconstruction Costs fi/10,000 Dollar | Electric Energy Consumption ECi/kw×h | Diesel Consumption OPi/kg |
|---|---|---|---|---|
| 1 Yuhang District | 137.22 | 5.40 | 2324 | 28 |
| 5 Qiantang District | 145.46 | 5.70 | 2033 | 36 |
| 7 Tonglu County | 110.97 | 7.50 | 2204 | 32 |
| 10 Fenghua District | 134.22 | 4.05 | 2341 | 34 |
| 11 Yuyao City | 130.47 | 3.15 | 2063 | 34 |
| 22 Tongxiang City | 138.72 | 6.15 | 2191 | 21 |
| 26 Pujiang County | 122.97 | 6.90 | 2304 | 35 |
| 29 LInhai City | 117.72 | 5.25 | 2100 | 21 |
| 32 Tiantai County | 127.47 | 4.65 | 2075 | 30 |
| 34 Jinyun County | 119.22 | 6.15 | 2394 | 39 |
| Variable | Value | Unit |
|---|---|---|
| the fuel cost per unit distance during transportation co | 0.27 | dollar/km |
| the speed of the vehicle v | 40 | km·h−1 |
| the diesel consumption of empty vehicles VP0 | 0.14 | kg·km−1 |
| the diesel consumption of fully-loaded vehicles VPmax | 0.16 | kg·km−1 |
| the weight of a refrigerated vehicle Q0 | 32,000 | kg |
| the maximum load of a refrigerated vehicle Qmax | 50,000 | kg |
| Constant | Value | Unit |
|---|---|---|
| carbon emission factor per unit of electricity consumed e1 | 0.5810 | tCO2·MW·h−1 |
| carbon emission factor per unit of diesel consumed e2 | 3.0959 | kg-CO2·kg−1 |
| the low calorific value of diesel δ1 | 42652 | kJ·kg−1 |
| carbon content per unit calorific value of diesel δ2 | 20.20 | t-C·TJ−1 |
| the carbon oxidation factor of diesel δ3 | 0.98 | unitless |
| the cost per unit of carbon emissions λ | 0.03 | dollar/kg·CO2 |
| the penalty cost when the freshness requirements are not met β1 | 119.97 | dollar |
| the negative penalty cost when the freshness requirements are met β2 | 119.97 | dollar |
| the sensitivity coefficient of freshness to time φ | 1.60 | unitless |
| Algorithm | THA | WOA | PSO |
|---|---|---|---|
| the location of the cold chain distribution center | (1, 11, 22, 26, 29, 34) | (1, 5, 10, 26, 29, 34) | (5, 7, 11, 22, 29, 34) |
| storage cost/dollar | 139,086.58 | 147,940.42 | 153,955.45 |
| transport costs/dollar | 33,929.22 | 38,137.20 | 42,663.09 |
| penalty costs of freshness/dollar | 10,805.16 | 12,938.69 | 14,041.38 |
| overall carbon emission/kg | 154,921 | 172,573 | 180,400 |
| overall carbon emission costs/dollar | 4414.17 | 4917.15 | 5140.15 |
| total costs of the location selection/dollar | 188,235.14 | 203,933.46 | 215,800.07 |
| the number of iterations | 32 | 57 | 78 |
| operation time/second | 17.4 | 35.2 | 48.6 |
| the Cost per Unit of Carbon Emissions λ/(Dollar/kg) | 0.02 | 0.03 | 0.04 | 0.05 | 0.06 |
|---|---|---|---|---|---|
| overall carbon emission costs/dollar | 4066.11 | 4414.17 | 4622.77 | 5420.58 | 5776.74 |
| the total costs of location selection/dollar | 183,987.13 | 188,235.14 | 183,944.84 | 188,871.58 | 189,597.71 |
| the difference in the total costs of location selection/dollar | −4248.01 | 0 | 4290.30 | 636.44 | 1362.57 |
| the proportion of the overall carbon emission costs in the total costs | 2.21% | 2.35% | 2.51% | 2.87% | 3.05% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Ran, H.; Dang, X. Location Optimization of Fresh Agricultural Products Cold Chain Distribution Center under Carbon Emission Constraints. Sustainability 2022, 14, 6726. https://doi.org/10.3390/su14116726
Wang H, Ran H, Dang X. Location Optimization of Fresh Agricultural Products Cold Chain Distribution Center under Carbon Emission Constraints. Sustainability. 2022; 14(11):6726. https://doi.org/10.3390/su14116726
Chicago/Turabian StyleWang, Hongzhi, Haojie Ran, and Xiaohong Dang. 2022. "Location Optimization of Fresh Agricultural Products Cold Chain Distribution Center under Carbon Emission Constraints" Sustainability 14, no. 11: 6726. https://doi.org/10.3390/su14116726
APA StyleWang, H., Ran, H., & Dang, X. (2022). Location Optimization of Fresh Agricultural Products Cold Chain Distribution Center under Carbon Emission Constraints. Sustainability, 14(11), 6726. https://doi.org/10.3390/su14116726





