An Injury-Severity-Prediction-Driven Accident Prevention System
Abstract
:1. Introduction
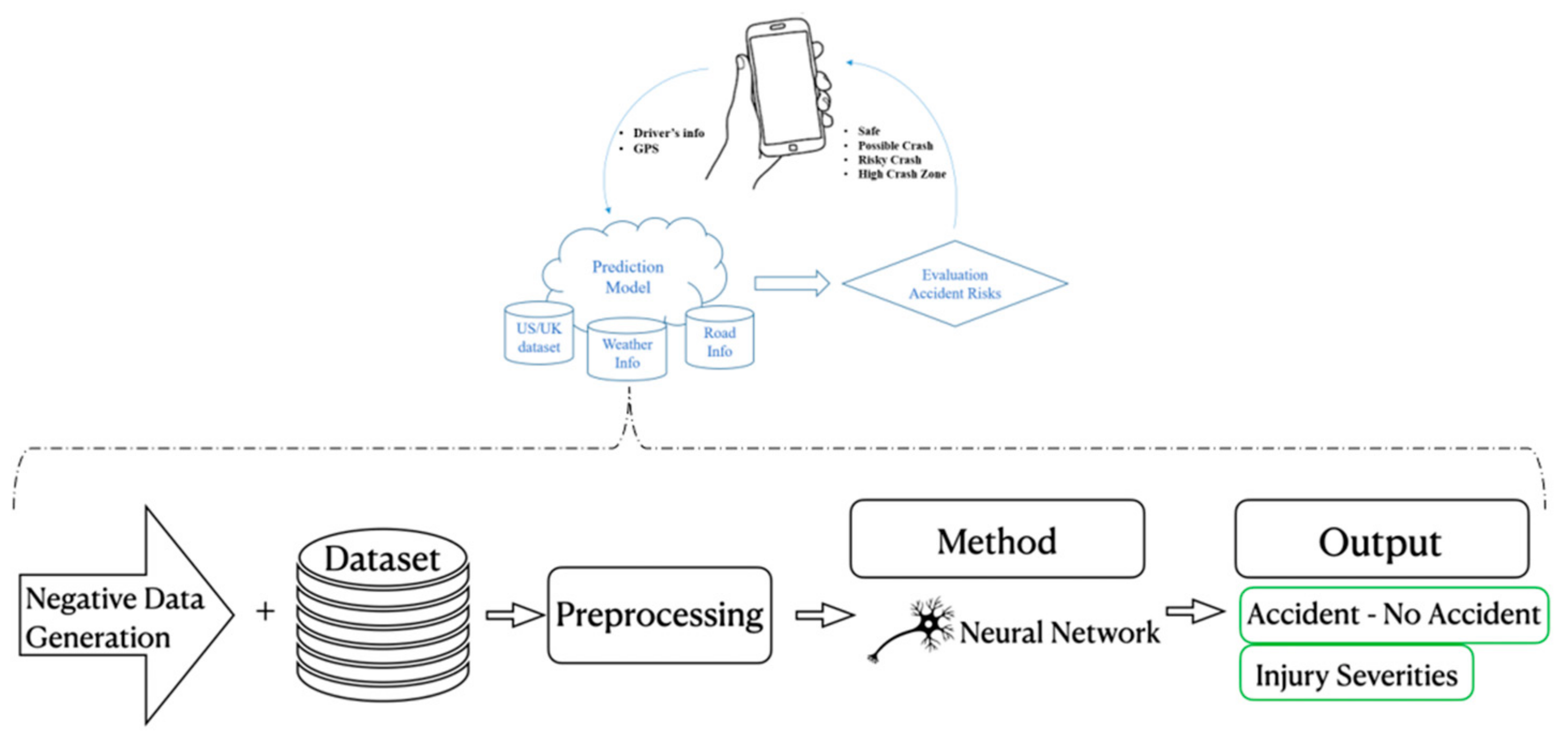
- A new framework to generate non-accident data based on the accident instances using the most contributing factors of traffic accidents. This will ensure a more balanced dataset and improve the predictive model in accident prevention systems for intelligent vehicles,
- A robust and more accurate NN prediction model to estimate injury severity compared to ordinal regression and other methods. With NN, we overcome the disadvantages of ordinal regression models (i.e., low robustness, not dealing with multicollinearity).
2. Literature Review
3. Methodology
3.1. Overview of Accident Prevention and Alert System
3.2. Ordinal Regression Models
3.3. Neural Network
3.4. Negative Data Generator
4. Experimental Results
4.1. Data Description
4.2. Feature Extraction and Negative Data Generation
4.3. Experimental Results, Comparisons, and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Variable | Description | |
|---|---|---|
| Atmospheric Condition | 1—Clear 2—Rain 3—Sleet 4—Snow | 5—Fog 6—Severe crosswinds 10—Cloudy |
| Holiday Related | 0—No Holiday 1—New Year 2—M. Luther King 3—JR Day 4—President’s Day 5—Memorial Day | 6—Independence Day 7—Labor Day 8—Veterans Day 9—Thanksgiving 10—Christmas |
| Light Condition | 1—Daylight 2—Dark 3—Dark-lighted | 4—Dawn 5—Dusk |
| Intersection Type | 1—Not intersection 2—Fourway 3—T-intersection 4—Y-intersection | 5—Traffic circle 6—Roundabout 10—L-intersection |
| Traffic Lane | 1–7—Actual number of lanes in a road | |
| Age | 001–120—Actual ages | |
| Person Type | 1—Driver 2—Passenger | |
| Sex | 1—Male 2—Female | |
| Travel Speed | 000–151—Reported speed up to 151 mph 998—Not Reported 999—Unknown | |
| Vehicle Make | 01–94—Actual make 97—Not reported | 98—Other make 99—Unknown make |
| Alcohol Involvement | 0—No 1—Yes | |
| Surface Condition | 1—Dry 2—Wet 3—Snow | 4—Ice 5—Sand |
| Surface Type | 1—Concrete 2—Asphalt 3—Brick | 4—Stone 5—Dirt |
Appendix B

References
- National Center for Statistics and Analysis. 2015 Motor Vehicle Crashes: Overview. Traffic Saf. Facts Res. Note 2016, 2016, 1–9. [Google Scholar]
- Han, S.; Wang, X.; Xu, L.; Sun, H.; Zheng, N. Frontal object perception for intelligent vehicles based on radar and camera fusion. In Proceedings of the 35th Chinese Control Conference (CCC), Chengdu, China, 27–29 July 2016. [Google Scholar] [CrossRef]
- Alicioglu, G.; Sun, B.; Ho, S.S. Assessing accident risk using ordinal regression and multinomial logistic regression data generation. In Proceedings of the International Joint Conference on Neural Networks (IJCNN), Glasgow, UK, 19–24 July 2020. [Google Scholar] [CrossRef]
- Severino, A.; Pappalardo, G.; Curto, S.; Trubia, S.; Olayode, I.O. Safety Evaluation of Flower Roundabout Considering Autonomous Vehicles Operation. Sustainability 2021, 13, 10120. [Google Scholar] [CrossRef]
- Macioszek, E. Roundabout Entry Capacity Calculation—A Case Study Based on Roundabouts in Tokyo, Japan, and Tokyo Surroundings. Sustainability 2020, 12, 1533. [Google Scholar] [CrossRef] [Green Version]
- Macioszek, E. The Comparison of Models for Critical Headways Estimation at Roundabouts. In Contemporary Challenges of Transport Systems and Traffic Engineering Lecture Notes in Networks and Systems; Macioszek, E., Sierpiński, G., Eds.; Springer: Cham, Switzerlands, 2017; Volume 2. [Google Scholar] [CrossRef]
- Thabtah, F.A.; Hammoud, S.; Kamalov, F.; Gonsalves, A. Data imbalance in classification: Experimental evaluation. Inf. Sci. 2020, 513, 429–441. [Google Scholar] [CrossRef]
- Mujalli, R.O.; Oña, J.D. A method for simplifying the analysis of traffic accidents injury severity on two-lane highways using Bayesian networks. J. Saf. Res. 2011, 42, 317–326. [Google Scholar] [CrossRef] [PubMed]
- Yuan, Z.; Zhou, X.; Yang, T.; Tamerius, J. Predicting traffic accidents through heterogeneous urban data: A case study. In Proceedings of the International Workshop on Urban Computing (KDD), Halifax, NS, Canada, 13–17 August 2017. [Google Scholar]
- Jeong, H.; Jang, Y.; Bowman, P.J.; Masoud, N. Classification of motor vehicle crash injury severity: A hybrid approach for imbalanced data. Accid. Anal. Prev. 2018, 120, 250–261. [Google Scholar] [CrossRef]
- Pérez-Ortiz, M.; Gutiérrez, P.A.; García-Alonso, C.R.; Salvador-Carulla, L.; Salinas-Perez, J.A.; Hervás-Martínez, C. Ordinal classification of depression spatial hot-spots of prevalence. In Proceedings of the 11th International Conference on Intelligent Systems Design and Applications, Cordoba, Spain, 22–24 November 2011. [Google Scholar] [CrossRef]
- Aci, C.; Ozden, C. Predicting the severity of motor vehicle accident injuries in Adana-Turkey using machine learning methods and detailed meteorological data. Int. J. Intell. Syst. Appl. Eng. 2018, 6, 72–79. [Google Scholar] [CrossRef]
- Wang, Y.; Ho, I.W. Joint Deep Neural Network Modelling and Statistical Analysis on Characterizing Driving Behaviors. In Proceedings of the IEEE Intelligent Vehicles Symposium (IV), Changshu, China, 26–30 June 2018. [Google Scholar] [CrossRef]
- Kahng, M.; Andrews, P.Y.; Kalro, A.; Chau, D. ActiVis: Visual Exploration of Industry-Scale Deep Neural Network Models. IEEE Trans. Vis. Comput. Graph. 2018, 24, 88–97. [Google Scholar] [CrossRef] [Green Version]
- Chatzimparmpas, A.; Martins, R.M.; Jusufi, I.; Kucher, K.; Rossi, F.; Kerren, A. The State of the Art in Enhancing Trust in Machine Learning Models with the Use of Visualizations. Comput. Graph. Forum 2020, 39, 713–756. [Google Scholar] [CrossRef]
- Azodi, C.B.; Tang, J.; Shiu, S. Opening the Black Box: Interpretable Machine Learning for Geneticists. Trends Genet. 2020, 36, 442–455. [Google Scholar] [CrossRef]
- Çodur, M.Y.; Tortum, A. An Artificial Neural Network Model for Highway Accident Prediction: A Case Study of Erzurum, Turkey. Promet-Traffic Transp. 2015, 27, 217–225. [Google Scholar] [CrossRef] [Green Version]
- Chong, M.; Abraham, A.; Paprzycki, M. Traffic accident analysis using machine learning paradigms. Informatica 2005, 29, 89–98. [Google Scholar]
- Iranitalab, A.; Khattak, A.J. Comparison of four statistical and machine learning methods for crash severity prediction. Accid. Anal. Prev. 2017, 108, 27–36. [Google Scholar] [CrossRef] [PubMed]
- Zhu, M.; Li, Y.; Wang, Y. Design and experiment verification of a novel analysis framework for recognition of driver injury patterns: From a multi-class classification perspective. Accid. Anal. Prev. 2018, 120, 152–164. [Google Scholar] [CrossRef]
- Pradhan, B.; Sameen, M.I. Modeling Traffic Accident Severity Using Neural Networks and Support Vector Machines. In Laser Scanning Systems in Highway and Safety Assessment; Springer: Cham, Switzerlands, 2020; pp. 111–117. [Google Scholar] [CrossRef]
- Delen, D.; Tomak, L.; Topuz, K.; Eryarsoy, E. Investigating injury severity risk factors in automobile crashes with predictive analytics and sensitivity analysis methods. J. Transp. Health 2017, 4, 118–131. [Google Scholar] [CrossRef]
- Liao, Y.; Zhang, J.; Wang, S.; Li, S.; Han, J. Study on Crash Injury Severity Prediction of Autonomous Vehicles for Different Emergency Decisions Based on Support Vector Machine Model. Electronics 2018, 7, 381. [Google Scholar] [CrossRef] [Green Version]
- Zeng, Q.; Huang, H. A stable and optimized neural network model for crash injury severity prediction. Accid. Anal. Prev. 2014, 73, 351–358. [Google Scholar] [CrossRef]
- Fernández-Navarro, F.; Campoy-Muñoz, P.; Paz-Marin, M.L.; Hervás-Martínez, C.; Yao, X. Addressing the EU sovereign ratings using an ordinal regression approach. IEEE Trans. Cybern. 2013, 43, 2228–2240. [Google Scholar] [CrossRef]
- Landschoot, S.; Waegeman, W.; Audenaert, K.; Haesaert, G.; Baets, B.D. Ordinal regression models for predicting deoxynivalenol in winter wheat. Plant Pathol. 2013, 62, 1319–1329. [Google Scholar] [CrossRef]
- Gao, X.; Feng, Y. Penalized weighted least absolute deviation regression. Stat. Its Interface 2018, 11, 79–89. [Google Scholar] [CrossRef]
- Xia, F.; Zhou, L.; Yang, Y.; Zhang, W. Ordinal regression as multiclass classification. Int. J. Intell. Control. Syst. 2007, 12, 230–236. [Google Scholar]
- Zahid, F.M.; Ramzan, S. Ordinal ridge regression with categorical predictors. J. Appl. Stat. 2012, 39, 161–171. [Google Scholar] [CrossRef] [Green Version]
- Aggarwal, C.C. Neural Networks and Deep Learning; Springer: Cham, Switzerlands, 2018. [Google Scholar] [CrossRef]
- Haykin, S. Neural Networks and Learning Machines, 3rd ed.; Prentice Hall: New York, NY, USA, 2009. [Google Scholar]
- Kalogirou, S.A. Solar Energy Engineering, 2nd ed.; Elsevier: Amsterdam, The Netherlands; Academic Press: Cambridge, MA, USA, 2014. [Google Scholar] [CrossRef]
- Ripley, B.D. Pattern Recognition and Neural Networks; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar] [CrossRef]
- Bottou, L. Stochastic Gradient Descent Tricks. In Neural Networks: Tricks of the Trade. Lecture Notes in Computer Science; Montavon, G., Orr, G.B., Müller, K.R., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; Volume 7700, pp. 421–436. [Google Scholar] [CrossRef] [Green Version]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. In Proceedings of the 3rd International Conference on Learning Representations, ICLR, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Williams, R. Generalized Ordered Logit/Partial Proportional Odds Models for Ordinal Dependent Variables. Stata J. 2006, 6, 58–82. [Google Scholar] [CrossRef] [Green Version]
- National Highway Traffic Safety Administration. Available online: https://www-fars.nhtsa.dot.gov (accessed on 18 February 2019).
- UK Transport for Greater Manchester. Available online: https://data.gov.uk/ (accessed on 20 December 2019).
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef] [Green Version]



| Studies | Class Descriptions | Algorithms | |
|---|---|---|---|
| [8] | Slight Injured Killed or Seriously Injured | Bayesian Networks | |
| [9] | Accident No Accident | SVM DT | RF NN |
| [10] | Fatal Injury Incapacitating Injury Non-Incapacitating Injury Possible Injury No Injury | Logistic Regression (LR) Gradient Boosting Model | NN DT Naïve Bayes |
| [12] | Non-Fatal Injury Fatal Injury | k-NN Naïve Bayes NN | DT SVM LR |
| [17] | No Injury Possible Injury Non-Incapacitating Injury Incapacitating Injury Fatal Injury | DT SVM Hybrid DT-Artificial NN | |
| [18] | Property Damage Only Possible Injury Visible Injury Fatal Injury | Multinomial Logit k-NN SVM | RF k-Means |
| [20] | No Injury Possible Injury Evident Injury Fatal Injury | RF NN | |
| US Accident Dataset (2015–2016) | UK Accident Dataset (2018) | |||
|---|---|---|---|---|
| Injury Severity | # of Accidents | Injury Severity | # of Accidents | |
| Class 0 | No apparent | 6405 (21.0%) | Slight | 8381 (57.4%) |
| Class 1 | Possible | 2697 (8.84%) | Serious | 4541 (31.1%) |
| Class 2 | Minor | 2967 (9.73%) | Fatal | 1671 (11.5%) |
| Class 3 | Serious | 1812 (5.95%) | ||
| Class 4 | Fatal | 8499 (27.8%) | ||
| Class 5 | No accident | 8104 (26.5%) | ||
| Non-Fatal Injury | Possible Injury | Minor Injury | Major Injury | Fatal Injury | |||||
|---|---|---|---|---|---|---|---|---|---|
| Light condition | 0.166 | Person type | 0.264 | Alcohol | 0.262 | Alcohol | 0.490 | Alcohol | 0.918 |
| Lane | 0.161 | Intersection type | 0.213 | Person type | 0.259 | Person type | 0.442 | Surface type | 0.099 |
| Intersection type | 0.064 | Sex | 0.189 | Surface condition | 0.122 | Surface type | 0.127 | Age | 0.013 |
| Holiday | 0.016 | Lane | 0.081 | Surface type | 0.099 | Sex | 0.106 | Vehicle make | 0.005 |
| Accident hour | 0.012 | Surface condition | 0.032 | Accident hour | 0.004 | Surface condition | 0.022 | Surface condition | 0.002 |
| Architecture | Hidden Layer | Neuron | Solver | Activation Function | MSE |
|---|---|---|---|---|---|
| 1 | 3 | 17 neuron each | SGD | ReLu | US dataset: 0.264 ± 0.040 a |
| UK dataset: 0.252 ± 0.078 | |||||
| 2 | 17 neuron each | SGD | Tanh | 0.258 ± 0.053 | |
| 0.297 ± 0.081 | |||||
| 3 | 17 neuron each | Adam | Tanh | 0.254 ± 0.038 | |
| 0.173 ± 0.016 | |||||
| 4 | 50 neuron each | SGD | Tanh | 0.283 ± 0.044 | |
| 0.208 ± 0.054 | |||||
| 5 | 100, 50, 25 | Adam | Tanh | 0.368 ± 0.026 | |
| 0.176 ± 0.027 | |||||
| 6 | 100, 50, 25 | SGD | Tanh | 0.311 ± 0.037 | |
| 0.183 ± 0.034 | |||||
| 7 | 5 | 25, 50, 50, 50, 100 | SGD | Tanh | 0.283 ± 0.035 |
| 0.236 ± 0.051 | |||||
| 8 | 100 neuron each | Adam | Tanh | 0.339 ± 0.030 | |
| 0.175 ± 0.024 |
| Data | Method | MSE | Class Accuracy | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Class 0 | Class 1 | Class 2 | Class 3 | Class 4 | Class 5 | ||||
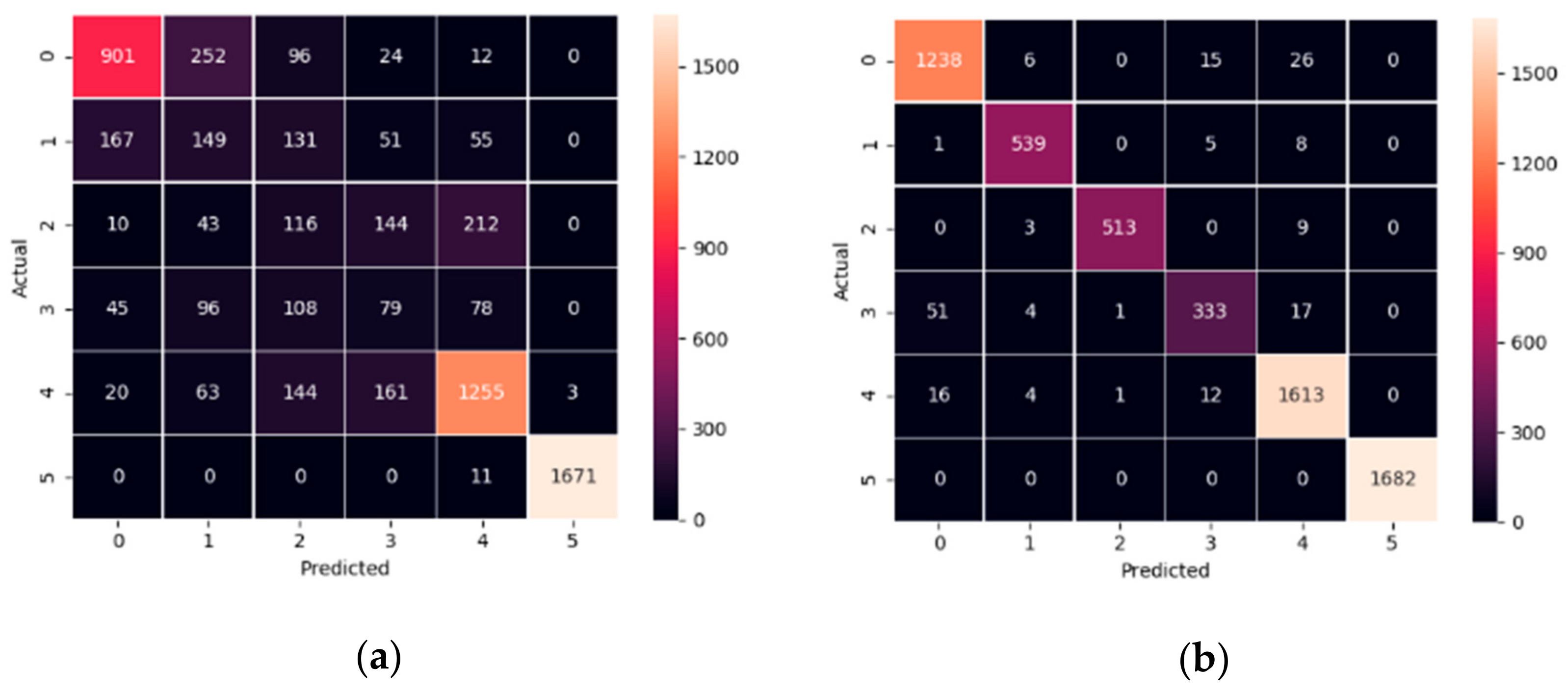
| US Dataset | NN | # 3 (Best) | 0.254 ± 0.038 | 0.963 * | 0.974 | 0.977 * | 0.820 | 0.979 * | 1.000 * |
| # 5 (Worst) | 0.368 ± 0.026 | 0.923 | 0.978 * | 0.977 | 0.834 * | 0.970 | 0.999 | ||
| OR Models | Ordinal Ridge | NB: 1.177 ± 0.097 | 0.178 | 0.262 | 0.289 | 0.426 | 0.238 | 0.703 | |
| B: 1.158 ± 0.094 | |||||||||
| LAD | 1.193 ± 0.106 | 0.332 | 0.255 | 0.321 | 0.426 | 0.237 | 0.829 | ||
| 1.174 ± 0.102 | |||||||||
| Logistic IT | 1.793 ± 0.189 | 0.927 | 0.000 | 0.000 | 0.000 | 0.917 | 0.997 | ||
| 1.686 ± 0.184 | |||||||||
| Logistic AT | 0.948 ± 0.135 | 0.701 | 0.269 | 0.220 | 0.195 | 0.762 | 0.993 | ||
| 0.928 ± 0.132 | |||||||||
| Other Methods | DT | 0.472 ± 0.136 | |||||||
| Linear SVM | 0.797 ± 0.067 | ||||||||
| LR | 0.773 ± 0.043 | ||||||||
| UK Dataset | NN | # 3 (Best) | 0.173 ± 0.016 | 0.833 * | 0.658 * | 0.969 | |||
| # 2 (Worst) | 0.297 ± 0.081 | 0.829 | 0.556 | 0.895 | |||||
| OR Models | Ordinal Ridge | NB: 0.372 ± 0.025 | 0.620 | 0.534 | 0.771 | ||||
| B: 0.363 ± 0.022 | |||||||||
| LAD | 0.585 ± 0.035 | 0.451 | 0.141 | 0.974 * | |||||
| 0.501 ± 0.092 | |||||||||
| Logistic IT | 0.438 ± 0.062 | 0.624 | 0.272 | 0.890 | |||||
| 0.426 ± 0.059 | |||||||||
| Logistic AT | 0.396 ± 0.022 | 0.620 | 0.430 | 0.831 | |||||
| 0.387 ± 0.023 | |||||||||
| Other Methods | DT | 0.205 ± 0.052 | |||||||
| Linear SVM | 0.387 ± 0.071 | ||||||||
| LR | 0.430 ± 0.038 | ||||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alicioglu, G.; Sun, B.; Ho, S.S. An Injury-Severity-Prediction-Driven Accident Prevention System. Sustainability 2022, 14, 6569. https://doi.org/10.3390/su14116569
Alicioglu G, Sun B, Ho SS. An Injury-Severity-Prediction-Driven Accident Prevention System. Sustainability. 2022; 14(11):6569. https://doi.org/10.3390/su14116569
Chicago/Turabian StyleAlicioglu, Gulsum, Bo Sun, and Shen Shyang Ho. 2022. "An Injury-Severity-Prediction-Driven Accident Prevention System" Sustainability 14, no. 11: 6569. https://doi.org/10.3390/su14116569
APA StyleAlicioglu, G., Sun, B., & Ho, S. S. (2022). An Injury-Severity-Prediction-Driven Accident Prevention System. Sustainability, 14(11), 6569. https://doi.org/10.3390/su14116569






