Abstract
Rock disasters caused by rock fractures seriously threaten the safe and sustainable mining of deep coal resources. The infrared thermal imaging of rock fractures has a non-uniform distribution. This is important information for the monitoring and early warning of rock mass instability. In this paper, the multi-fractal theory was introduced to analyze the infrared thermal image obtained from the uniaxial loading of sandstone, which is expected to provide quantitative indicators for the infrared monitoring of rock failure. The results show that the multi-fractal parameters (non-uniformity of temperature) and (frequency diversity of minimum and maximum temperature) can be used to describe the distribution of the thermal field; they are sensitive to the rock macro fracture. Both and are constant during the initial loading stage. When the samples yield and there is a failure in the later stage of loading, the and change abruptly. The sudden change in and can be regarded as the precursor to rock failure. The research results preliminarily show the feasibility and potential of multi-fractal analysis in rock mass disaster monitoring and early warning.
1. Introduction
China’s coal resources have gradually entered the deep stratum, due to the depletion of shallow resources. In the process of deep mining, coal and rock mass are in a more severe geomechanical environment of high geostress, high ground temperature and strong dynamic disturbance. Moreover, rock mass disasters (e.g., rockburst, roof caving) caused by rock fracture occur often [,,,], which seriously threatens the safety and sustainability of mining. To predict these disasters, various monitoring methods have been proposed and applied, such as acoustic emission (AE) [], electromagnetic radiation (EMR) [,] and infrared radiation (IRR) [,,,]. Among them, infrared technology is considered to be a potential method for monitoring rock mass instability; it assumes that the infrared radiation temperature (IRT) of the rock surface changes in the process of rock deformation and fracture [,,,,]. Infrared technology has the characteristics of being non-destructive, non-contact and observable. It is also widely used and studied in different rock engineering fields, such as roadway excavation [] and landslides [].
A large number of scholars have studied the characteristics of IRR in the rock loading process. Deng et al. [,] found that the IRT of rock increases with an increase in stress; an abnormal high or low temperature region on the infrared thermal image appears when the rock fractures. Wu et al. [,,,] explored the characteristics of the temperature–time curve and infrared thermal image in the rock loading process through different loading experiments (uniaxial compression, shear, impact, etc.). They took the abrupt change in average infrared radiation temperature (AIRT) and infrared thermal image as the precursor to rock failure. Moreover, the shear fracture of rock causes the IRT to rise and the tensile fracture causes the IRT to decrease. Freund [] studied the IRR during the loading process of granite and put forward the P-hole theory; he considered the electron flow in the rock as the source of IRR. Cao et al. found that the AIRT rate of rock before and after dilatancy changes [,]. Sun et al. [] compared the AE and IRR characteristics of rocks during the true triaxial loading and unloading experiments. Li et al. [] investigated the characteristics of IRR during the loading of coal containing gas. However, all the above research focused on the application and mechanism of infrared technology, while most descriptions of IRT and infrared thermal images are qualitative, which is not conducive to the further practical application of such technology to engineering.
Therefore, some work has been done to put forward the quantitative description method of IRR and to try to find the effective indicators for the early warning signs of rock mass instability. For instance, Liu et al. [] and Ma et al. [,] used variance, entropy, feature roughness and b-value to capture the evolution characteristics of infrared thermal images. Shen et al. [] adopted the method of critical slowing down to quantitatively analyze the maximum infrared radiation temperature (MaxIRT). In fact, when the rock fracture occurs, the infrared thermal image clearly shows areas of either abnormally high temperature (shear fracture zone) or abnormally low temperature (tensile fracture zone), and the temperature distribution is uneven. Moreover, the simultaneous existence of a high-temperature anomaly area and low-temperature anomaly area may cause little change in AIRT. Therefore, a better description of this infrared thermal image feature is very important and necessary. On the other hand, the multi-fractal theory can be used to describe the complexity and heterogeneity of data and it has been widely used in different disciplines [,,,]. Thus, it is possible to introduce the multi-fractal theory to the analysis of complicated infrared thermal images.
In this paper, the uniaxial compression test of sandstone samples was carried out and the IRR was collected simultaneously. The multi-fractal theory was introduced to quantitatively describe the infrared thermal image characteristics of the rock loading process, which is expected to provide new indicators and guidance for the monitoring and early warning signs of rock disasters.
2. Experimental Process and Analysis Method
2.1. Materials and Experimental System
According to the standards of the international society of rock mechanics (ISRM), standard samples of Φ 50 mm × 100 mm were prepared to carry out the uniaxial compression tests. The samples were made of red sandstone from the Linfen mining area, Shanxi Province. The density of the rock used is 2454.65 kg/m3. In order to ensure the homogeneity of the samples, the P-wave velocity of the samples was tested. The wave velocities of all samples are about 3.51 km/s and the homogeneity between samples is good.
The test system consists of two main parts: a loading system and an IRR data acquisition system. The loading system adopted the new SANS microcomputer-controlled electro-hydraulic servo pressure testing machine. The maximum load capacity is 3000 kN. The IRR data acquisition system adopted the Optris PI450 high-resolution infrared thermal imager. The optical resolution is 288 × 382 pixels; the temperature measurement range is −20~100 °C; the spectral range is 7.5~13 ; the frame frequency is 80 Hz; the field-of-view angle is 30° × 23°; and the thermal sensitivity is 0.04 k.
To reduce the interference of the external environment, all tests were carried out in an AFGP-II high-efficiency electromagnetic-shielding room. The infrared thermal imager was arranged 50 cm away from the sample and the infrared thermal image acquisition rate was set at 10 Hz. Before the test, the infrared thermal imager was turned on for about 30 min to preheat and the loading was started after the imager was stable. The loading rate was controlled as 400 N/s. Once loading was completed, the force, displacement and the IRR data were synchronously measured and stored. The test was finished upon the failure of the sandstone.
2.2. IRR Principle of Rock Fracture
Any object with a temperature higher than absolute zero (−273.15 °C) emits waves in a very wide wavelength range in the form of electromagnetic radiation. IRR is an electromagnetic wave in the wavelength range of 0.7–1000 and the part with a wavelength of 2.5–15 has a thermal effect. The IRR wave is collected by an infrared thermal imager and converted into temperature information according to the Stefan–Boltzmann law [,]:
where is the radiant energy intensity; is the emissivity; is a constant; and T is the absolute temperature (K). The principle is shown in Figure 1. Under the action of stress, the internal energy of rock transforms and causes IRR. The IRR can reflect the stress state of rock. The change in infrared radiation temperature is the comprehensive result of the thermoelastic effect, pore gas desorption and escape effect, fracture effect, friction thermal effect, heat transfer effect and environmental radiation effect [,].
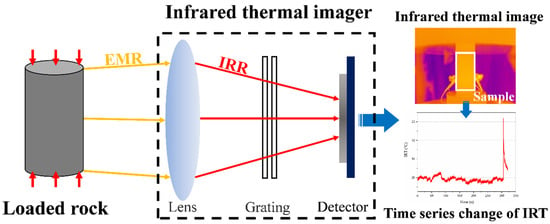
Figure 1.
Schematic diagram of infrared technology.
2.3. Multi-Fractal Theory
The upper left of Figure 2 shows the original infrared thermal image, which is essentially a matrix composed of IRT data. Each pixel corresponds to the IRT data of the corresponding position. If the optical resolution of the instrument is 288 × 382 pixels, the output result will be an IRT matrix T288×382 with the size of 288 × 382. The IRT matrix xm×n at the sample position (valid area) is extracted by MATLAB software, and the multi-fractal characteristics of the data in the matrix are analyzed according to the literature [,].
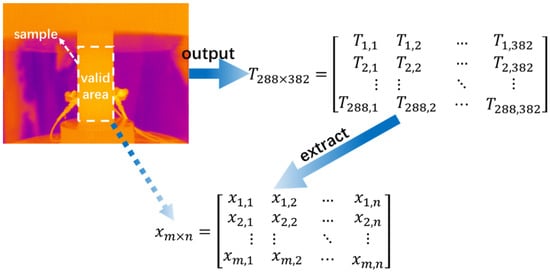
Figure 2.
Infrared thermal image data extraction process.
The matrix xm×n is divided into boxes of size . The probability density of the box subset (i, j) is . The probability distribution is calculated for each subset:
Among them, is the defined partition function, that is, the statistical moment. is the quality index, with . is a constant, called the singularity index, which controls the singularity of . It reflects the non-uniformity of the probability subset under different . means the frequency of the subset represented by in all subset sets and it is also the fractal dimension of subset .
The curve is the multi-fractal spectrum of the calculated matrix. The width of the spectrum reflects the differences among the distribution of temperature data. The larger the value of , the greater the non-uniformity of temperature and the more obvious the multi-fractal characteristics. The difference between the frequency of the lowest temperature data and that of the highest temperature data can be obtained by . A smaller value of represents a greater proportion of high temperature data and vice versa. indicates that the low temperature data dominates, while signifies the domination of high temperature data.
Therefore, the values of and can be used to describe the differences in infrared thermal images and the dominant temperature data, respectively. The evolution of these two multi-fractal indicators during the loading can be used to identify the characteristics of the thermal field.
3. Analysis and Discussion of Experimental Results
3.1. Time Series Change in IRT
Two typical samples were taken as examples for subsequent analysis, and their numbers were S-1 and S-2, respectively. Figure 3 shows the stress and strain of the two samples during the loading process, as well as the changes in MaxIRT, AIRT and the minimum IRT (MinIRT) on the surface of the samples. The loading process of rock can be roughly divided into three stages. I (Compaction stage): the primary pores are closed, the deformation is large and the deformation rate decreases gradually. II (Elastic deformation stage): the strain increases linearly with the increase in stress. III (Yield and failure stage): the strain increases unsteadily, and a large number of micro fractures gather to form macro fractures. When the stress reaches the peak value, the failure occurs.
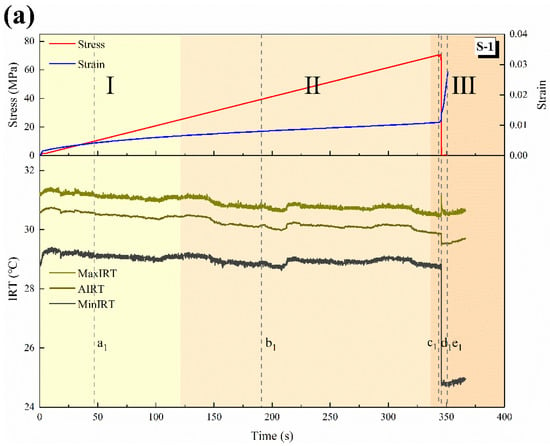
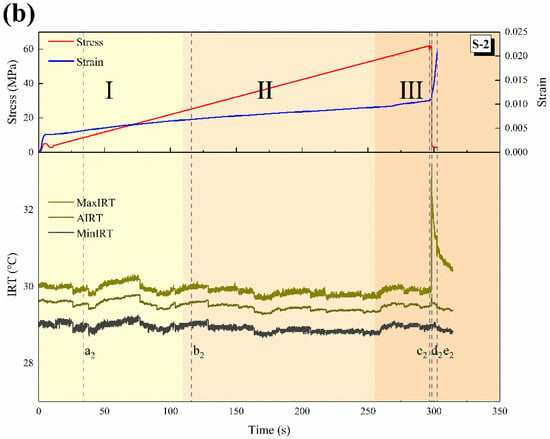
Figure 3.
Time series change in IRT: (a) S-1; (b) S-2. (Different color blocks distinguish stage I, II and III).
In the early stages (I and II) of loading, the changes in MaxIRT, AIRT and MinIRT are highly synchronous, which indicates that the surface temperature changes are uniform and integral. The initial MaxIRT, AIRT and MinIRT of sample S-1 are about 31.19 °C, 30.58 °C and 20.8 °C, respectively, and then the curves show a slow decline trend, but little change. The initial MaxIRT, AIRT, and MinIRT of sample S-2 are about 30.04 °C, 29.63 °C, and 29.02 °C, respectively, and then the curves are slightly inflected, but they are also basically unchanged. In most experiments, the IRT of the rock increases during the loading process, but occasionally the IRT continues to decrease, which may be caused by the exhaust gas after the rock pore is compressed []. The abnormal temperature fluctuation in the early stages of loading may be caused by changes to the microstructure inside the sample, such as the closure and propagation of microcracks caused by stress adjustment [].
In stage III, the specimens begin to show obvious macro fractures and the surface infrared temperature fields show local abnormal changes. In the moment of failure, the MaxIRT of sample S-1 increases from 30.54 °C to 31.16 °C and then gradually drops, while AIRT drops and MinIRT drops significantly. For sample S-2, MaxIRT significantly increased from 29.94 °C to 33.19 °C and then gradually cooled down, with AIRT being slightly increased, while MinIRT remained basically unchanged. This is related to the failure modes of different specimens, which will be discussed in more detail in the next section.
3.2. Multi-Fractal Analysis of Infrared Thermal Images
The infrared thermal images of two samples at several typical moments (a1-e1, a2-e2) were selected. The positions of different time points are shown in Figure 3. The multi-fractal characteristics of IRT field data at each time were calculated. Figure 4 and Figure 5a show the calculation results of sample S-1. The infrared thermal images in all the figures were redrawn by Surfer software. At the time of a1 (47.03 s), the is low, meaning that the degree of non-uniformity of the infrared temperature field data distribution is small, and is close to 0. With the loading process, the infrared temperature field changes as a whole. At the time of b1 (190.88 s), the values of and show little change. At c1 (343.45 s), the loading is close to the peak stress of the specimen, and a macro fracture occurs. The temperature field of the surface is in the abnormally high-temperature region and develops continuously. At d1 (345.73 s), the sample is destroyed, and there is an obvious shear fracture zone on the surface and some rock blocks fall off in the tensile fracture zone. The MaxIRT of the fracture zone is 31.16 °C and the temperature of the falling off area is the temperature of the background environment. In the process of c1-d1, the difference in infrared temperature distribution on the surface of samples gradually increases and increases. The performance of high temperature data is gradually dominant, so decreases. e1 (350.79 s) is the moment after the failure of the sample, at which time the temperature decreases, but the difference in the temperature distribution is still significant.
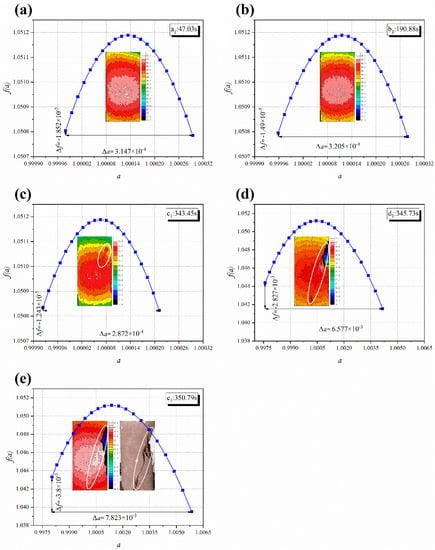
Figure 4.
Multi-fractal features of infrared thermal images at different time points of S-1: (a) a1; (b) b1; (c) c1; (d) d1; (e) e1.
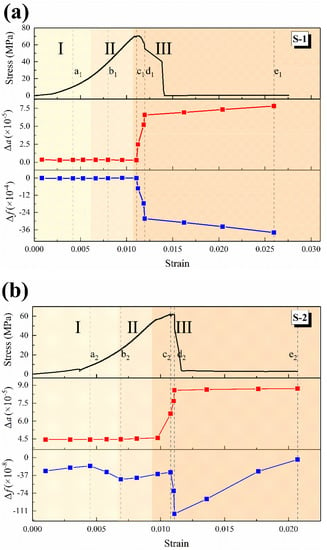
Figure 5.
Dynamic changes of multi-fractal indicators of infrared thermal image: (a) S-1; (b) S-2. (Different color blocks distinguish stage I, II and III).
Figure 5b and Figure 6 show the calculation results of sample S-2. Local shear failure occurs in the sample and the changing trend of and is similar to that of sample S-1. However, during the failure of the sample, the increase in and the decrease in are much lower than those of S-1. The reason may be that the falling off of some rocks increases the difference in the infrared temperature field distribution of S-1. The shear fracture area of S-1 is more serious, so the high temperature data performance is better, even if the increase in MaxIRT of S-2 is greater than that of S-1.
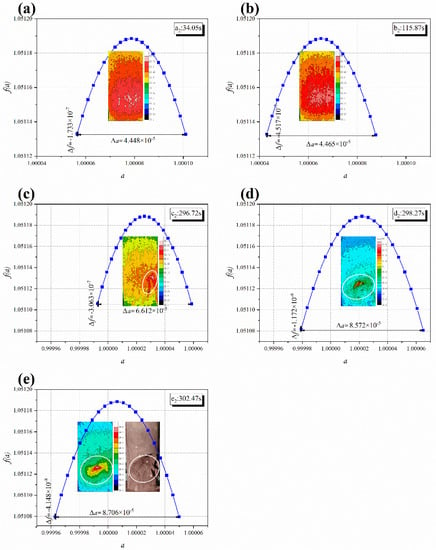
Figure 6.
Multi-fractal features of infrared thermal images at different time points of S-2: (a) a2; (b) b2; (c) c2; (d) d2; (e) e2.
In general, and are very sensitive to the macroscopic fracture of the rock. In the early stages of loading, the IRT of the sample surface changes uniformly as a whole and and are basically unchanged. Entering the yield and failure stage, the macro-fracture of the sample results in changes to and . This shows the validity of the indicators. The sudden change in and can be used as a precursor to the occurrence of rock disasters.
In addition, the experimental results show that the variations in and are closely related to the failure mode of the rock. Different fractures lead to different infrared temperature distributions. For example, due to the frictional thermal effect, the more severe the shear fracture, the better the high temperature data performance and the more uneven the overall temperature distribution. This results in an increase in and a decrease in . However, the failure mode of the rock is related to rock type, loading mode, water bearing state and so on. Therefore, we intend to carry out more experiments to establish a deeper relationship between rock fracture and multi-fractal indicators.
4. Conclusions
In this paper, a uniaxial compression experiment of sandstone is carried out and the infrared radiation is monitored at the same time. The multi-fractal theory was introduced to analyze infrared thermal images. The infrared thermal image of rock during loading has multi-fractal characteristics. The multi-fractal parameters (non-uniformity of temperature) and (frequency diversity of minimum and maximum temperature) are not sensitive to changes to the infrared thermal image in the early stage of loading, but are more sensitive to the macro fracture of rock. When the samples yield and fail in the later stage of loading, they have an obvious response. The sudden change to and can be regarded as the precursor of rock failure. The research results preliminarily show that the multi-fractal analysis of infrared thermal images can provide reference for the monitoring and early warning signs of rock mass disasters, which has great application value. In the future, we intend to establish a deeper relationship between multi-fractal indicators and rock fracture.
Author Contributions
Conceptualization, X.W.; writing—original draft preparation, B.M.; writing—review and editing, X.W.; methodology, H.L.; software, H.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ortlepp, W.D.; Stacey, T.R. Rockburst mechanisms in tunnels and shafts. Tunn. Undergr. Space Technol. 1994, 9, 59–65. [Google Scholar] [CrossRef]
- He, M.C.; Ren, F.Q.; Liu, D.Q. Rockburst mechanism research and its control. Int. J. Min. Sci. Technol. 2018, 28, 829–837. [Google Scholar] [CrossRef]
- Feng, X.J.; Ding, Z.; Ju, Y.Q.; Zhang, Q.M.; Ali, M. “Double Peak” of dynamic strengths and acoustic emission responses of coal masses under dynamic loading. Nat. Resour. Res. 2022, 31, 1705–1720. [Google Scholar] [CrossRef]
- Feng, X.J.; Ding, Z.; Hu, Q.J.; Zhao, X.; Ali, M.; Banquando, J.T. Orthogonal numerical analysis of deformation and failure characteristics of deep roadway in coal mines: A case study. Minerals 2022, 12, 185. [Google Scholar] [CrossRef]
- Li, H.R.; Qiao, Y.F.; Shen, R.X.; He, M.C.; Cheng, T.; Xiao, Y.M.; Tang, J. Effect of water on mechanical behavior and acoustic emission response of sandstone during loading process: Phenomenon and mechanism. Eng. Geol. 2021, 294, 106386. [Google Scholar] [CrossRef]
- Li, H.; Shen, R.; Wang, E.; Li, D.; Li, T.; Chen, T.; Hou, Z. Effect of water on the time-frequency characteristics of electromagnetic radiation during sandstone deformation and fracturing. Eng. Geol. 2020, 265, 105451. [Google Scholar] [CrossRef]
- Li, H.R.; Qiao, Y.F.; Shen, R.X.; He, M.C. Electromagnetic radiation signal monitoring and multi-fractal analysis during uniaxial compression of water-bearing sandstone. Measurement 2022, 196, 111245. [Google Scholar] [CrossRef]
- Shen, R.; Li, H.; Wang, E.; Chen, T.; Li, T.; Tian, H.; Hou, Z. Infrared radiation characteristics and fracture precursor information extraction of loaded sandstone samples with varying moisture contents. Int. J. Rock Mech. Min. Sci. 2020, 130, 104344. [Google Scholar] [CrossRef]
- Khan, N.M.; Ma, L.Q.; Cao, K.W.; Hussain, S.; Liu, W.; Xu, Y.J. Infrared radiation characteristics based rock failure indicator index for acidic mudstone under uniaxial loading. Arab. J. Geosci. 2022, 15, 343. [Google Scholar] [CrossRef]
- Cao, K.W.; Ma, L.Q.; Wu, Y.; Spearing, A.J.M.; Khan, N.M.; Hussain, S.; Rehman, F.U. Statistical damage model for dry and saturated rock under uniaxial loading based on infrared radiation for possible stress prediction. Eng. Fract. Mech. 2022, 260, 108134. [Google Scholar] [CrossRef]
- Tian, H.; Li, Z.H.; Shen, X.F.; Zang, Z.S.; Song, J.J.; Zhang, Q.C. Identification method of infrared radiation precursor information of coal sample failure and instability under uniaxial compression. Infrared Phys. Technol. 2021, 119, 103957. [Google Scholar] [CrossRef]
- Luong, M.P. Infrared thermovision of damage processes in concrete and rock. Eng. Fract. Mech. 1990, 35, 291–301. [Google Scholar] [CrossRef]
- Freund, F.T.; Takeuchi, A.; Lau, B.W.S.; Al-Manaseer, A.; Fu, C.C.; Bryant, N.A.; Ouzounov, D. Stimulated infrared emission from rocks: Assessing a stress indicator. Earth 2006, 2, 7–16. [Google Scholar]
- Wang, C.L.; Lu, Z.J.; Liu, L.; Chuai, X.S.; Lu, H. Predicting points of the infrared precursor for limestone failure under uniaxial compression. Int. J. Rock Mech. Min. Sci. 2016, 88, 34–43. [Google Scholar] [CrossRef]
- Gornyi, V.I.; Salman, A.G.; Tronin, A.A.; Shilin, B.V. Terrestrial outgoing infrared radiation as an indicator of seismic activity. Proc. Acad. Sci. USSR 1988, 301, 67–69. [Google Scholar]
- Sun, X.M.; Xu, H.C.; He, M.C.; Zhang, F. Experimental investigation of the occurrence of rockburst in a rock specimen through infrared thermography and acoustic emission. Int. J. Rock Mech. Min. Sci. 2017, 93, 250–259. [Google Scholar] [CrossRef]
- He, M.C.; Jia, X.N.; Gong, W.L.; Faramarzi, L. Physical modeling of an underground roadway excavation in vertically stratified rock using infrared thermography. Int. J. Rock Mech. Min. Sci. 2010, 47, 1212–1221. [Google Scholar] [CrossRef]
- Pappalardo, G.; Mineo, S.; Angrisani, A.C.; Di Martire, D.; Calcaterra, D. Combining field data with infrared thermography and DInSAR surveys to evaluate the activity of landslides: The case study of Randazzo Landslide (NE Sicily). Landslides 2018, 15, 2173–2193. [Google Scholar] [CrossRef]
- Deng, M.D.; Cui, C.Y.; Geng, N.G.; Zhi, Y.Q. Study on the infrared waveband radiation characteristics of rocks. J. Infrared Millim. Waves 1994, 13, 425–430. [Google Scholar]
- Deng, M.D.; Geng, N.G.; Cui, C.Y.; Zhi, Y.Q. The rule and characteristics of infrared radiation temperature along with stress of rock and their relation to AE rate. Northwestern Seismol. J. 1995, 17, 79–86. [Google Scholar]
- Wu, L.X.; Wang, J.Z. Infrared radiation features of coal and rocks under loading. Int. J. Rock Mech. Min. Sci. 1998, 35, 969–976. [Google Scholar] [CrossRef]
- Wu, L.X.; Cui, C.Y.; Geng, N.G.; Wang, J.Z. Remote sensing rock mechanics (RSRM) and associated experimental studies. Int. J. Rock Mech. Min. Sci. 2000, 37, 879–888. [Google Scholar] [CrossRef]
- Wu, L.X.; Liu, S.J.; Wu, Y.H.; Wang, C.Y. Precursors for rock fracturing and failure—Part I: IRR image abnormalities. Int. J. Rock Mech. Min. Sci. 2006, 43, 473–482. [Google Scholar] [CrossRef]
- Wu, L.X.; Liu, S.J.; Wu, Y.H.; Wang, C.Y. Precursors for rock fracturing and failure—Part II: IRR T-Curve abnormalities. Int. J. Rock Mech. Min. Sci. 2006, 43, 483–493. [Google Scholar] [CrossRef]
- Freund, F.T. Rocks that crackle and sparkle and glow: Strange pre-earthquake phenomena. J. Sci. Explor. 2003, 17, 37–71. [Google Scholar]
- Cao, K.W.; Ma, L.Q.; Zhang, D.S.; Lai, X.P.; Zhang, Z.T.; Khan, N.M. An experimental study of infrared radiation characteristics of sandstone in dilatancy process. Int. J. Rock Mech. Min. Sci. 2020, 136, 104503. [Google Scholar] [CrossRef]
- Ma, L.Q.; Khan, N.M.; Cao, K.W.; Rehman, H.; Salman, S.; Rehman, F.U. Prediction of sandstone dilatancy point in different water contents using infrared radiation characteristic: Experimental and machine learning approaches. Lithosphere 2021, 2021, 3243070. [Google Scholar] [CrossRef]
- Li, Z.; Yin, S.; Niu, Y.; Cheng, F.; Liu, S.; Kong, Y.; Sun, Y.; Wei, Y. Experimental study on the infrared thermal imaging of a coal fracture under the coupled effects of stress and gas. J. Nat. Gas Sci. Eng. 2018, 55, 444–451. [Google Scholar] [CrossRef]
- Liu, S.J.; Wei, J.L.; Huang, J.W.; Wu, L.X.; Zhang, Y.B.; Tian, B.Z. Quantitative analysis methods of infrared radiation temperature field variation in rock loading process. Chin. J. Rock Mech. Eng. 2015, 34, 2968–2976. [Google Scholar]
- Ma, L.Q.; Zhang, Y.; Cao, K.W.; Wang, Z.W. An experimental study on infrared radiation characteristics of sandstone samples under uniaxial loading. Rock Mech. Rock Eng. 2019, 52, 3493–3500. [Google Scholar] [CrossRef]
- Liu, W.; Ma, L.Q.; Sun, H.; Khan, N.M. Using the characteristics of infrared radiation b-value during the rock fracture process to offer a precursor for serious failure. Infrared Phys. Technol. 2021, 114, 103644. [Google Scholar] [CrossRef]
- Mandelbrot, B.B.; Passoja, D.E.; Paullay, A.J. Fractal Character of fracture surfaces of metals. Nature 1984, 308, 721–722. [Google Scholar] [CrossRef]
- Qiu, L.; Song, D.; He, X.; Wang, E.; Li, Z.; Yin, S.; Wei, M.; Liu, Y. Multifractal of electromagnetic waveform and spectrum about coal rock samples subjected to uniaxial compression. Fractals 2020, 28, 2050061. [Google Scholar] [CrossRef]
- Kong, X.; Wang, E.; Li, S.; Lin, H.; Xiao, P.; Zhang, K. Fractals and chaos characteristics of acoustic emission energy about gas-bearing coal during loaded failure. Fractals 2019, 27, 1950072. [Google Scholar] [CrossRef]
- Kong, B.; Wang, E.Y.; Li, Z.H.; Lu, W. Study on the feature of electromagnetic radiation under coal oxidation and temperature rise based on multifractal theory. Fractals 2019, 27, 1950038. [Google Scholar] [CrossRef]
- Cai, X.; Zhou, Z.; Tan, L.; Zang, H.; Song, Z. Water saturation effects on thermal infrared radiation features of rock materials during deformation and fracturing. Rock Mech. Rock Eng. 2020, 53, 4839–4856. [Google Scholar] [CrossRef]
- Luong, M.P. Introducing infrared thermography in soil dynamics. Infrared Phys. Technol. 2007, 49, 306–311. [Google Scholar] [CrossRef]
- Feng, J.J.; Wang, E.Y.; Huang, Q.S.; Ding, H.; Dang, L. Time-varying multifractal analysis of crack propagation and internal fracture process of coal under dynamic loading. Fractals 2021, 29, 2150089. [Google Scholar] [CrossRef]
- Li, H.; Shen, R.; Li, D.; Jia, H.; Li, T.; Chen, T.; Hou, Z. Acoustic emission multi-parameter analysis of dry and saturated sandstone with cracks under uniaxial compression. Energies 2019, 12, 1959. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).