1. Introduction
“Smart grid” is taken as an umbrella term for different technologies. Those technologies are considered alternatives to the traditional methods used to operate the power system. Some of these technologies are advanced metering infrastructure (AMI), demand response, outage management, wide-area measurement system (WAMS), active fault level monitoring, etc. In a smart grid, the power resources can be used efficiently [
1,
2]. A smart grid has a high dependence on the advanced communication infrastructure, as there is an exchange of a huge amount of data for the proper operation of such a complex network [
3,
4,
5]. In fact, the smart grid is taken as a network consisting of computers, as well as power infrastructure. All of these are used for monitoring and managing energy usage [
6,
7]. An automated and distributed energy network is created by the smart grid [
8]. Self-monitoring is carried out in the case of a smart grid, which makes the smart grid distinct from a traditional grid [
9]. Distributed power resources (DPR) can be accommodated in a smart grid [
10,
11].
In a power system, if there exists a mismatch between the generation and utilization of power, there will be a deviation of electrical quantities from their actual values. The two-way communication is carried out in a smart grid to have a safe and reliable power flow. That communication should be secure. Sometimes attackers hack these communication links to change the values of power flow in the power network. The hackers attack the power system to obtain different goals. Multiple purposes can be achieved by these attacks. Attacks can be used to obtain financial benefits; create technical problems, such as blackouts of power; and a combination of the two [
12,
13,
14,
15,
16,
17,
18].
Considering the target of attacks, they can be further divided into three types. The first category involves attacks that target availability. In these attacks, the aim of the attackers is to corrupt, block, or delay the communication in the power system. The second type is attacks that target integrity. In these types of attacks, the attackers try to illegally disrupt data exchange in the smart grid. The final category is attacks that target confidentiality. In these attacks, the attackers try to obtain unauthorized information from the smart network [
19].
1.1. Power System State Estimation
The power system state estimation (PSSE) technique is used for the detection of bad data received in the control room. All the received measurements are placed in a vector, which is denoted by
z. The measurement vector contains the real forward powers, reactive forward powers, real backward powers, reactive backward powers, real powers injected into all the buses, reactive powers injected into all buses, voltage magnitudes, and voltage angles [
20,
21,
22,
23]. The measurement vector
z and the state variable
x have the following relationship:
h(x) represents the non-linear function that gives the dependencies between measured values and the state variables, and it can be found using the power system topology. e represents random noise of Gaussian form with a zero mean and some known covariance.
In the case of AC state estimation (SE), the weighted least-squares method is adopted for solving the state variables with an objective function [
24,
25]:
where
W is the weighting matrix, as given in [
26]. This is an unconstrained optimization problem whose first-order optimality condition is given by:
Here,
H represents the Jacobian matrix and
is taken as the vector of the estimated states. An iterative process can be used for solving this non-linear equation [
27].
The non-linear function can be approximated by a linear function by using some DC assumptions. Those assumptions are given as follows:
The voltage magnitudes of all the buses are very close to each other and they are assumed to be “1 pu”.
The active power transmission through the transmission lines is taken as lossless, i.e., there are no losses in the transmission lines.
The value of reactive power injected into all the buses, as well as flowing through the transmission lines, is taken as zero.
There is a small difference in the voltage angles of two buses such that “Sin(δϕ) ≈ δϕ”
After applying the DC assumptions, we can rewrite the above equations in this form:
H is known as the Jacobian matrix of the power system topology. If the measurement vector has m values and the number of states is n, then the Jacobian matrix H will have an order of “m × n”. In (4), x contains the bus voltage angles. z contains the values of active powers flowing through the transmission lines and injected into all the buses.
The Jacobian matrix H is constant during each iteration of the linearization process. In the DC power flow model (4), the Jacobian matrix H is constant throughout. Equation (4) will be valid for each iteration of the linearization model (3). Therefore, the same notation is adopted for both the linearized model (3) and the DC power flow model (4).
The weighted least square (WLS) approach is used for estimating the states. In the WLS algorithm, the estimated state
can be written as follows [
19,
22]:
R represents the covariance matrix of
e. The estimated states, as well as the measurement vector
z, are used for the calculation of the measurement residue.
Then, the normalized
L2-norm is calculated for
r.
A comparison of
L(
r) is done with the threshold
τ for finding the presence of bad data. The
X2—test is used for the determination of the threshold
τ.
Bad data do not exist if the condition in (8) is satisfied. Similarly, when the condition is not satisfied, bad data exist in the system.
1.2. Stealth False Data Injection (FDI) Attack
A stealth attack is a special type of attack that bypasses the PSSE technique test. The residual test is not able to detect a stealth attack. This attack is also known as an unobservable attack or undetectable attack. In a stealth attack, the Jacobian matrix
H is fully known to the attacker.
H is used for the construction of an undetectable attack. Stealth false data injection (FDI) is given as follows [
17,
19,
22,
28,
29,
30]:
where
a represents the vector of false data that is added to the measurement vector
z. The attacker hacks the data from the communication line and injects the attack vector
a into it, where
a =
Hc.
The attack is done on the communication line by the attacker and all measurements of power are hacked. The Jacobian matrix H is determined with the help of those measurements of power. The whole power system topology can be understood with the help of H. The dependence of one power value on the other powers can be found using H. This leads the attacker to make an undetectable attack. In fact, it tells the attacker which specific values of power the attacker will have to change with one particular change in power. To understand the whole power network, the formation of the Jacobian matrix H is the most important component. The vector c is multiplied by matrix H and the resultant is added to the actual measurements when undertaking a stealth attack.
The stealth attack is executed against the PSSE in the power network and that is the attack of injecting false data into the system measurements. The state estimation technique is bypassed by the stealth attack [
31]. In case of an attack, the estimated state becomes:
The estimated state is changed in the case of a stealth attack. Now, the estimated state is equal to the original estimated state plus the addition of a constant vector
c. It is assumed that
c~N(0,
), where the false state variance is represented by
.
Therefore, the attack changes the state of the power system. The technique used in the system for bad data detection is bypassed by the stealth false data injection attack in this way:
The attacked residual is represented by . In the attack, the attacked residue is the same as that of the normal residue. Therefore, the technique of bad data detection using residue is bypassed by this attack and the defender is not able to detect the stealth attack.
1.3. Contributions
The key contributions of this study are the following:
It was shown that the bad data filter of the state estimation was only useful for detecting bad measurement data and could not efficiently detect a stealth FDI, making the system vulnerable to all such attacks.
A fixed dummy value model was proposed and it was shown that the false data attacks that went undetected by the bad data filter could be successfully detected.
Since the dummy value in the fixed dummy value model is kept fixed, the intruder may obtain a clue about it and may change the measurement, keeping the same dummy value, therefore causing this model to be vulnerable to FDI attacks. To address the vulnerability of the fixed dummy value model, another technique for the variable dummy value model was also proposed, which was shown to successfully counter such attacks.
In this work, a quasi-steady state system was assumed to carry out the AC state estimation model. Therefore, the dynamic model of the system is not discussed. For the AC state estimator, the Jacobian matrix H is obtained after the linearization of the measurement model at every iteration. Thus, Equation (5) is solved at each iteration until a stopping threshold is reached.
The organization of the rest of the paper is as follows.
Section 2 contains a brief literature review of the different methods and frameworks used for the detection of attacks.
Section 3 consists of the proposed model of the fixed dummy value model.
Section 4 discusses the simulations and results of DC state estimation, AC state estimation, and fixed dummy value model. The limitations of the fixed dummy value model are also given in that section.
Section 5 covers the variable dummy value model. The simulations and results of the variable dummy value model are present in
Section 6. Moreover,
Section 7 is devoted to the discussion of results and future work.
Section 8 contains the conclusion.
2. Literature Review
A large variety of methods and algorithms have been used for detecting stealth attacks. Machine learning methods achieved significant success in this area. In [
32], supervised learning based on recurrent neural networks (RNNs) was used for detecting FDI attacks. In [
16], three supervised machine learning classifiers, namely, SVM, k-nearest neighbor (kNN), and the extended nearest neighbor (ENN), were used. Different machine learning algorithms are proposed in [
28] for measurement classification. Measurements are classified as attacked or secure. Sparse logistic regression, SVM, and k-nearest neighbor methods were used in that study. Another technique was proposed in [
33] for the detection of FDI attacks, which used the Gaussian mixture model. The contribution in [
34] was based on unsupervised learning. Four machine learning methods, namely, a one-class SVM, local outlier factor, isolation forest, and robust covariance estimation, were employed for FDI attack detection. In [
35], a machine-learning-based scheme was used that employed ensemble learning. In ensemble learning, there is a use of multiple classifiers, and the decisions obtained by the individual classifiers are further classified. The proposed scheme used two ensembles. Supervised classifiers were used in the first ensemble and the unsupervised classifiers were employed in the second ensemble. Supervised learning was proposed in [
36], which used a two-layer hierarchical framework. The first layer distinguished the mode of operation, such as a normal state or cyberattack. The second layer classified the type of cyberattack. An approach based on machine learning was adopted in [
37] for cyber-attacks, which used an extremely randomized trees algorithm. In [
38], three machine learning techniques, namely, a support vector machine (SVM), k-nearest neighbor, and artificial neural network, were implemented for detecting FDI attacks. Each technique was used with three different feature selection techniques.
An extreme learning machine framework was used in [
39] for detecting FDI attacks. In [
40], auto-encoders were used for detecting FDI attacks. The hidden correlation structures were learned in the data by using auto-encoders. The correlation was learned in two dimensions, namely, the time and the spatial dimensions. Denoising auto-encoders were also used to clean the corrupted data. The approaches based on the auto-encoder neural network [
41] and attention-based auto-encoders [
42] were also used for the detection of attacks.
The contribution of [
15] distinguished the normal function of the power system from the function in which there was a stealth attack. The stealth attacks were detected by using two machine-learning-based techniques. In the first technique, supervised learning was used for a set of labeled data. That data was used for the training of a support vector machine (SVM). The second technique did not use any training data and the deviation of the measurements was detected. An anomaly detection algorithm was applied to detect stealth attacks.
Deep learning models were also used for the purpose of detecting FDI attacks. The deep neural network (DNN) model was used [
43] for the classification of cyber-attacks in a smart grid. Another deep learning-based method was proposed in [
44] to detect FDI attacks. The proposed approach consisted of a convolutional neural network (CNN) and a long short-term memory (LSTM) network for the detection of attacks. The data integrity attacks in AC power systems can be detected by using a deep Q-network detection (DQND) scheme proposed in [
45]. It is a deep reinforcement learning approach. A neural network model was used in [
46] for detecting false data. In this case, the residual elements obtained from state estimation were the inputs given to the perceptron model. An algorithm based on deep learning was proposed in [
47] to detect FDI attacks. The dimensionality reduction, as well as feature extraction from measurement datasets, was done by using auto-encoders. Then auto-encoders were integrated into an advanced generative adversarial network (GAN) framework, which was used for detecting the FDI attacks.
The methods based on machine learning had great success in the detection of FDI attacks. However, at the same time, they have certain limitations and drawbacks. The methods based on supervised learning need a labeled dataset. They are built on some conventional attack assumptions. Similarly, deep learning techniques also have some limitations. In these methods, there is a need for extensive training. More memory space is also required for deep learning methods.
The main aim of the detection frameworks is to protect the whole communication system against attacks. One of the key features of microgrids is a secure communication network. For the development of a communication network, its design has vital importance. For the deployment of a heterogeneous automation and monitoring system, a multi-layered architecture was proposed in [
48]. For the organization of hardware, as well as software equipment in an integrated manner, six functional layers were structured in the proposed architecture. In [
49], a clear description of a smart grid and the type of communication methods were given. The communication methods were explained based on their advantages and the lacking feature. The contribution of [
50] was based on the hybrid communication simulation model. In hybrid network architectures, both wireless and dedicated wired media are used. A suite of hybrid communication simulation models was developed for the validation of critical system design criteria.
A mathematical model of the power system was presented in [
51] and a robust security framework was proposed. A Kalman filter was used to estimate variables in the model. In [
52], an online data-driven algorithm was presented for detecting FDI attacks toward synchrophasor measurements. The proposed algorithm applied density-based LOF (local outlier factor) analysis for detecting anomalies in the data. Another method was proposed in [
53] in which the modeling of the system was done as a discrete-time linear dynamic system. There was the use of the Kalman filter for performing the state estimation (SE). A generalized cumulative sum algorithm achieved the quickest detection of the attacks. In [
18,
19], the economic impact due to stealth FDI attacks on the market operations in real-time was considered. The construction of a profitable attacking plan for the attacker was also shown. In [
20], it was explained that the attacker can construct the stealth FDI attack without knowing the structure of the system. The attacker can find the system structure and make an attack.
In [
54], a distributed state estimation method based on the alternating direction method of multipliers (ADMM) was presented for detecting cyber-attacks. In this case, the partitioning of regional subsystems was done using the K-means method. An online detection algorithm was proposed in [
55] for detecting cyber-attacks. The online estimation of the unknown and time-varying attack parameters was provided by the algorithm. The FDI attacks were detected by proposing an active data modification scheme in [
56]. In that scheme, there was an amendment of measurements and control data before they are transmitted through communication networks. In [
57], an FDI attack detection method was proposed that was based on the equivalent model of a load frequency control (LFC) system and a Kalman filter algorithm.
The work of [
21] formulated the problem of false data detection as a low-rank matrix recovery. Convex optimization was used for solving the problem. The adopted methodology normalized the combination of the
l1 norm and nuclear norm. This mixed norm optimization problem was solved using the augmented Lagrange method of multipliers in order to obtain a good convergence rate. In [
22], the false data detection problem was considered a matrix separation problem. FDI attacks are sparse in nature. To separate the states of the power system from the anomalies, a mechanism was developed. The problem was solved using two methods, namely, low-rank matrix factorization and nuclear norm minimization.
3. Proposed Model
The methods used in the literature for the detection of attacks are successful up to a certain limit. If the attacker knows the whole network of the smart grid and makes an attack, it becomes difficult to detect those attacks. Therefore, we proposed a new power system model for an AC power flow network that is safe against stealth FDI attacks and the control room is able to detect these attacks in an efficient manner. The introduced model was based on the concept of dummy value. The smart grid meters will transmit both values, i.e., the actual value and the dummy value. No additional transmission lines and no extra buses will be used. There is no need for any extra meters in the proposed model. The vulnerabilities of the communication networks in supervisory control and data acquisition (SCADA) systems in the smart grid, such as unsophisticated bugs or communication failures, were not considered in this work. The application of the measured value and the dummy value in this article did not consider the error caused by the measurement equipment itself or any other reason. In this work, the error due to parametric variation of the meter or any other unknown reason was not taken into consideration. However, it may be incorporated into our future work. Moreover, this work focused on false data injection attacks in which the intruder hacks the measurement vector and injects the attack vector into the measurement vector before it is received by the control room. Therefore, this study only considered targeted attacks.
The measurement vector for the AC power flow network contains the active and reactive powers injected into all the buses, active and reactive powers flowing through transmission lines in the forward direction, and active and reactive powers flowing in the backward direction. If a system has
b number of buses and
t number of transmission lines, then the measurement vector for the AC power flow network is given by
where
is the measurement vector at the
yth instant and
y = 1, 2, 3,…,
mt. Here,
mt represents the total number of instances.
and
are the vectors containing the active and reactive powers injected to all the buses at the
yth instant. Both vectors will have a dimension of 1 ×
b. Similarly,
and
denote vectors having the active and reactive powers flowing through all the transmission in the forward direction at the
yth instant. Both vectors have dimensions of 1 ×
t. Moreover,
and
represent the vectors of the active and reactive powers flowing through all the transmission lines in the backward direction at the
yth instant. The complete measurement vector will have a dimension of
m × 1. The state vector
x contains the voltage magnitudes and voltage angles of all the buses. However, the Jacobian matrix will have a dimension of
m ×
n, where
m is the total number of values in the measurement vector and
n is the total number of values in the state vector. The measurement vectors at all the instances can be placed together to obtain the measurement matrix as follows:
The dimensions of the measurement matrix are
mt ×
m. The measurement vector after implementing the proposed system will become like this:
The measurement vector containing the actual and dummy values is represented by
zdy. Here,
represents the first entry of the vector
and
is the
bth entry of the vector
. The dummy values of the power are present on the even indexes of the new measurement vector. The vectors of the dummy values containing the active and reactive powers injected to all the buses at the
yth instant are
and
. Similarly, other vectors containing dummy values of the active and reactive powers for transmission lines at the
yth instant are denoted by
,
,
, and
.
zdy will have dimensions of 2
m × 1. The measurement matrix after including the dummy values will be
This measurement vector will have dimensions of mt × 2m. The Jacobian matrix of the proposed system at the yth instant is represented by Hdy and its dimensions are 2m × n. There are different methods to find the Jacobian matrix. To make a stealth attack, it is necessary for the attacker to determine the Jacobian matrix. The attacker hacks both the dummy and actual values and creates a Jacobian matrix to attack the system.
Realistic data of the AC power flow network was used for implementing and evaluating the proposed model. For this purpose, the load curves of a transmission organization known as PJM, which serves 13 states of the United States and the District of Columbia, were taken as a reference to generate the data of the power flow network. These load curves were based on realistic data. Therefore, our generated data were very close to the realistic data of an AC power flow network. The data were generated for four different seasons, namely, summer, fall, winter, and spring, based on the standard realistic load curves given for each season.
The overall proposed model was divided into two scenarios. In the first scenario, a fixed dummy value was sent to the control room. However, in the second case, a variable dummy value was sent and it changed with the change of the actual value of power.
Fixed Dummy Value Model
In this case, a fixed dummy value, along with each of the actual values, was sent to the control room. The dummy value of the power was not dependent on the load. It did not vary with the variation in load or variation in the actual value of power. In the fixed dummy value model, to select the dummy value of a particular power, the average value was calculated from all the actual measured values that occurred for that value at all the instances. That average value was selected as the dummy value of power. In this case, the dummy values were determined by taking the mean of the last year’s worth of historical measurement data, i.e., real-time measured values are stored from the past year and utilized for the calculation of fixed dummy values based on Equations (18)–(21). Later, these values were inserted into the memory of the meters and were simply appended or added to all the newly acquired measurements accordingly. It should be noted that the dummy value will no longer change with the newly acquired measurements. The calculation of the fixed dummy value was done by using these formulas:
In (18), represents the lth entry of the dummy values vector . denotes the lpth entry of the sth historical measurement vector. is the total number of instances for which the historical measurement vectors are obtained. To calculate the first entry of the dummy measurement vector , the sum of the first entries of all the historical measurement vectors is calculated and then divided by the total number of instances for which those historical measurement vectors are obtained. Similarly, the second entry of the dummy values vector can be calculated by finding the mean of the second entries of historical measurement vectors. The same procedure is adopted for finding all the entries of and the dummy values of all the active powers injected into the buses are calculated in this way. In (19), denotes the lth entry of the dummy values vector , and represents the lqth entry of the sth historical measurement vector. gives the total number of historical measurement vectors. The lth entry of the dummy values vector is found by calculating the mean of the lqth entry of historical measurement vectors. By using this procedure, the dummy values of all the reactive powers injected into the buses can be calculated. In (20) and (21), and represent the lth entry of each of the dummy measurement vectors and , respectively. and denote the lpvth and lqvth entries of the sth historical measurement vector, respectively. The lth entry of each of the dummy measurement vectors and is calculated by finding the mean of the lpvth and lqvth entries of historical measurement vectors, respectively. Therefore, the dummy values of the active and reactive powers flowing through all the transmission lines can be calculated by using Equations (20) and (21), respectively.
By applying Equations (18)–(21), the dummy values are calculated at a single instant by using historical measurement vectors and then those calculated dummy values are kept the same for all the instances, i.e., the dummy values do not change for the other instances. In fact, in the fixed dummy value model, the dummy values depend only on the historical measurement values and they do not depend on the real-time measurement values.
and
can also be calculated using this method and all the dummy values are selected in this way. These dummy values are placed in
, which is embedded in the meters. These values are also placed in another vector
d present in the control room. When the system is hacked by the attacker, 2
m power values will be obtained by the attacker in
instead of
m values. In the next step, the Jacobian matrix will be constructed by the attacker and a stealthy attack will be done in this way:
Here,
denotes the measurement vector received in the control room at the
yth instant. For the detection of an attack, a comparison is made between the dummy values obtained from
and those dummy values set by the control room. The following equation is used in the control room to detect the attack:
where
u = 1, 2, 3…,
m and
Here
d(u) denotes the
uth entry of the dummy values vector
d, which is selected and set by the defender. Meanwhile,
denotes the
vth entry of the received measurement vector. In the case of a secure system:
where
u = 1,2, 3,…,
m.
During the case of no attack, .
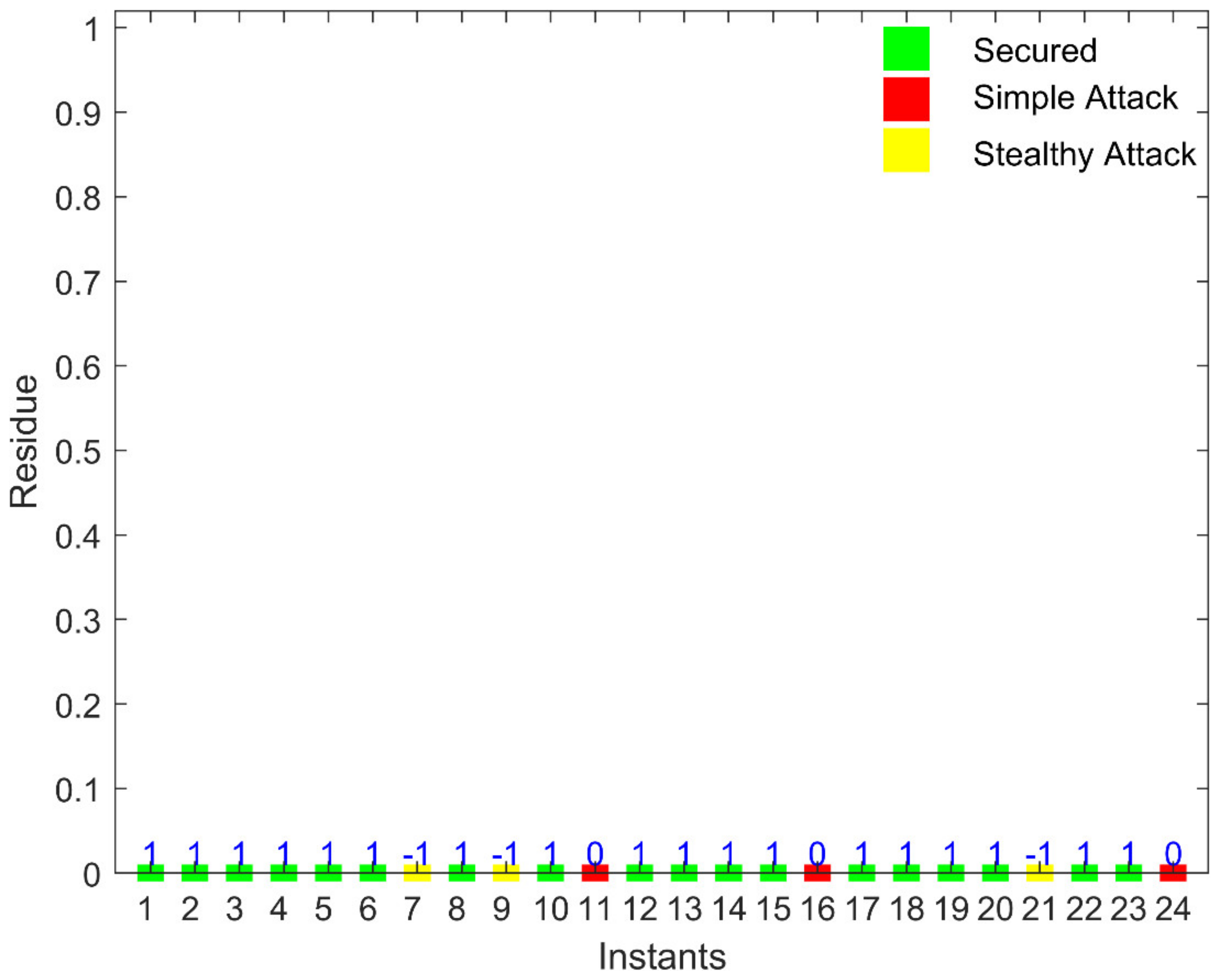
To launch an attack, the attacker changes the actual and dummy values according to the construction of the stealth attack. As the dummy values are fixed, they should not change for a secure system. Therefore, for an attack, the value of will come out to be greater than zero and the attack will be detected in this way.
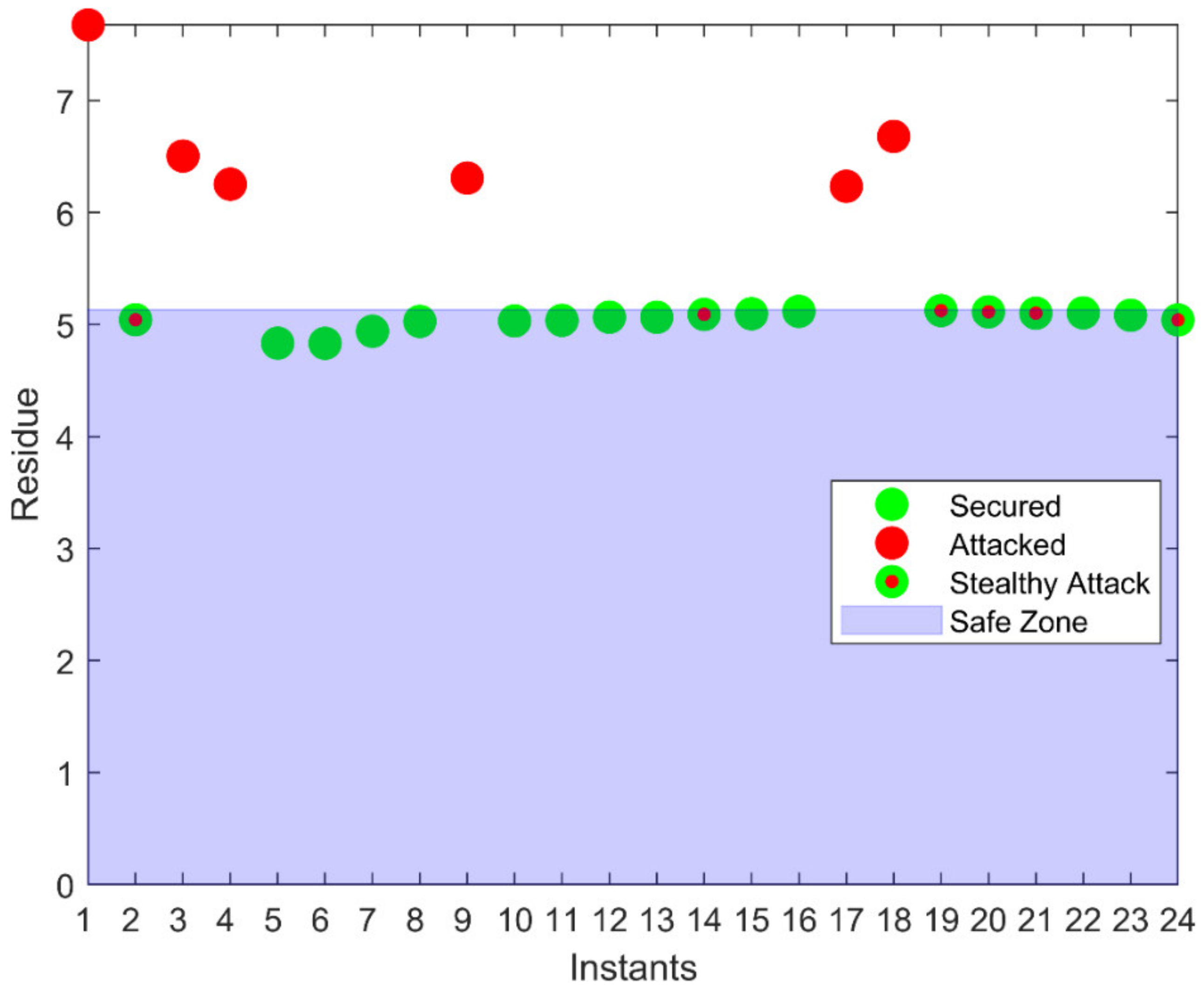
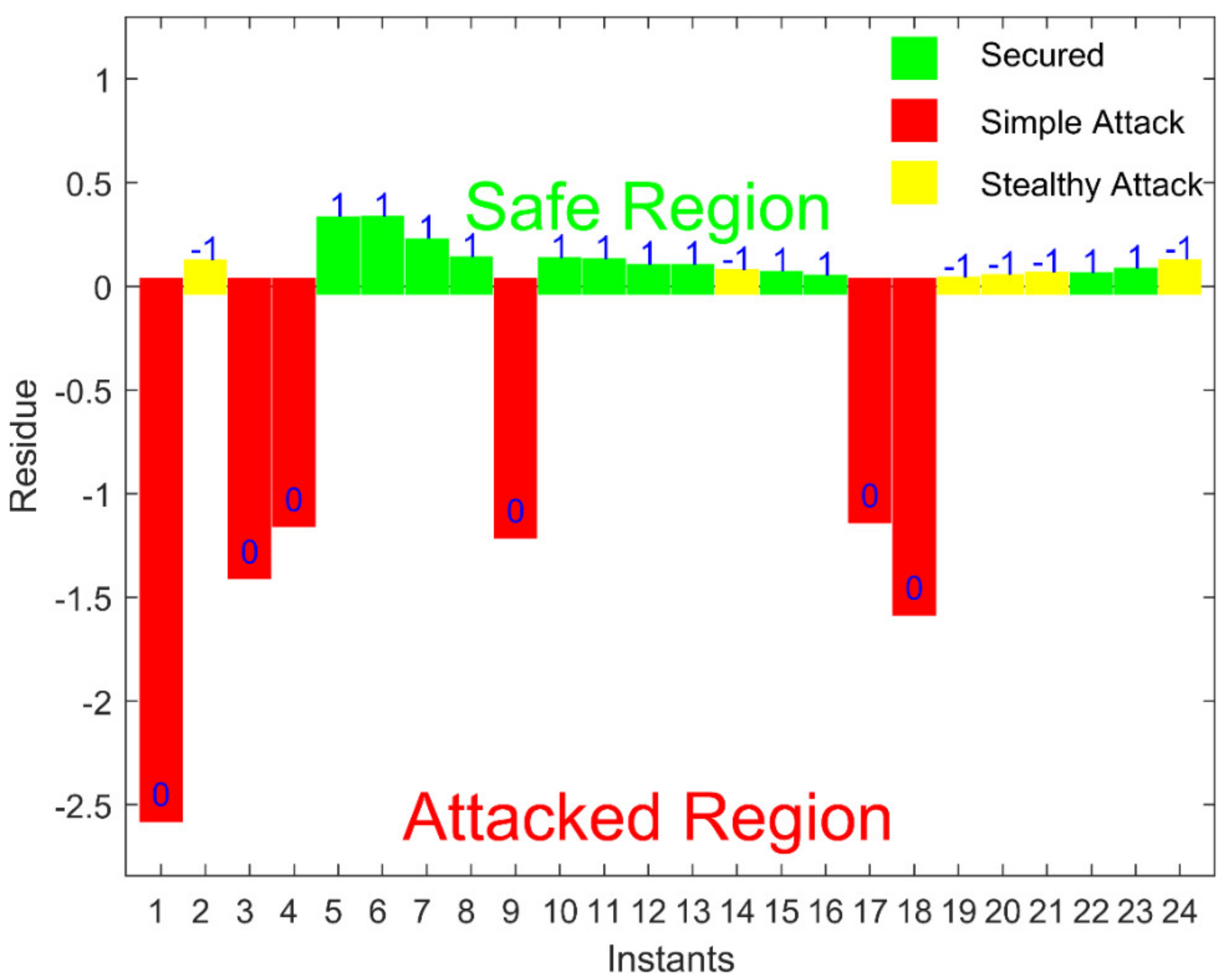
The conventional technique for bad data detection (BDD), such as DC state estimation (SE), fails to detect a stealth FDI attack. Moreover, AC SE is also bypassed by this attack. However, our model with a fixed dummy value was capable enough to detect the FDI attacks in the AC power flow network and all the attacks could be detected by the control room.
5. Variable Dummy Value Model
In the proposed model with a fixed dummy value, the attacker may attack the system by remaining undetected because the dummy value is fixed for all instances. Therefore, the dummy value should vary to protect the system against attacks. For this purpose, the model with a variable dummy value was introduced. In this scenario, the dummy value will change at every instant, and it will depend on the actual value, as well as some other values of the power in the system. Therefore, the dummy value of the power changes with the change in either of those values on which it depends. In the variable dummy value model, a linear function is implemented for the calculation of the dummy value and that function uses the actual measured value of that meter and the measured value of some other meter that has a relationship with that actual value. The function is only known to the control room. In the fixed dummy value model, the calculated dummy values are embedded into the meters. Similarly, in the variable dummy value model, the function used for the calculation of dummy values is embedded into the meters. This work assumed that the intruder does not have access to the meters, i.e., the intruder only has access to the measurements sent to the control room. The following functions are used in the case of the variable dummy value model for the calculation of dummy values for buses:
where
and
represent the
ith entries of the dummy values vectors
and
, respectively.
and
denote the
ith entries of
and
, respectively. Similarly,
and
represent the active power and reactive power flowing through the first transmission line connected to the
ith bus at the
yth instant, respectively.
,
,
,
,
, and
are the constants that have to be learned to calculate the dummy values. Similarly, the calculation of the dummy values of the active and reactive powers flowing through the transmission lines can be done by using the following functions:
and denote the ith entries of vectors and , respectively, which contain the dummy values of powers flowing through the transmission lines in the forward direction at yth instant. and represent the active power and reactive power injected into ith bus at yth instant, respectively. and belong to and , respectively. Similarly, and show the ith entries of vectors and , respectively, which have the dummy values of the active power and reactive power flowing through transmission lines in the backward direction. Constants are also used in the equations proposed for the calculation of dummy values.
The Equations (25)–(30) are used for finding the dummy values at the yth instant. In the variable dummy value model, the dummy values depend on the real-time measurement values. As the real-time measurement values are used for the calculation of the dummy values, the dummy values change at every instant in this case.
There is a key point to consider while selecting the dummy value, which is that the dummy value of a meter should be close to its actual value. There should not be too much difference between the actual and dummy value such that the attacker can find the dummy value and construct an undetectable attack. Therefore, when these linear functions are implemented for the calculation of the dummy value, we may obtain a dummy value that is far away from its actual value. The reason for this is that these dummy values depend on two different values of the power and there might be a high variance in the values of a certain meter depending upon the load connected to a bus. If the variance of either of the two actual values is high for a whole day, the dummy value will not be close to the actual value.
This problem may be minimized due to the selection of appropriate values of the constants. The selection of constants is done in such a way that all dummy values of a specific power for the whole day must remain close to the actual value of that power. For this purpose, a machine-learning technique, namely, multivariate linear regression (MLR), was used for finding the best values of the constants. The procedure of MLR to find the constants of the equation used to calculate the dummy values of the active power injected to all the buses is explained here. In this case, the hypothesis is written as
Here,
is a function of
that is parameterized using
.
represents the
kth input vector, where
k = 1, 2, 3, …, b and
= [1
]
T.
denotes the
kth parameter vector and
= [
]
T.
,
and
are the constants to be learned for each dummy value of the active power injected into the buses. Therefore, for each dummy value, a different vector of constants is used. Depending upon the hypothesis, the cost function for the multivariate linear regression can be written as
Here,
mt represents the total number of instances, i.e., the total number of training examples in this case.
represents the output of the
yth training example of the active power injected to the
kth bus. We must minimize the cost function so that we obtain the best values of the parameters. For this purpose, the gradient descent algorithm was applied, which is based on the update rule. The gradient descent can be written as
represents the fth entry of the kth parameter vector. denotes the fth entry of the kth input vector at the yth instant. The β’s are calculated again and again, and those parameters are used to calculate the cost. The above process is repeated until convergence occurs. When the cost converges, this produces the best values of the parameters.
By adopting the same procedure, the constants for the remaining equations are also found and those constants are put in their respective functions to calculate the dummy values of the active and reactive power. Then, these functions are embedded into the meters for the calculation of the dummy values. The meters measure the actual values of power and then use those functions to calculate the dummy values of power to send them to the control room. These functions are only known to the control room.
In the control room, to detect the FDI attacks, these functions are used to recalculate the dummy value by using the actual values obtained from the measurement vector. Then, the recalculated dummy value is compared with the dummy value obtained from the measurement vector for attack detection. The following equations are used in the control room to compare the calculated dummy values and received dummy values of active and reactive powers injected into all the buses:
The measurement vector received in the control room at the
yth instant is
. Here,
and
represent the
jth entries of the received vectors
and
, respectively, which contain the dummy values of the active power and reactive power received in the control room at the
yth instant.
and
denote the
jth entries of the received vectors
and
, respectively, which contain the actual values of the active power and reactive power received in the control room at the
yth instant.
and
are taken from the received measurement vector.
and
represent the
jth entries of the residue vectors
and
, respectively, which contain the residues for the active and reactive powers injected into the buses at the
yth instant. Similarly, the equations for calculating the residues for the forward and backward powers flowing through the transmission lines are given by:
In these equations, the dummy and actual values are obtained from the received measurement vector in the control room.
,
,
and
represent the
jth entries of the residue vectors
,
,
, and
, respectively, which contain the residues for the active and reactive powers flowing through the transmission lines in the forward and backward directions at the
yth instant. The overall residue at the
yth instant is calculated using
If the total residue has some value other than zero, the system is considered attacked. The attacker hacks the measurement vector and sends the vector to the control room after making the attack. As the attacker does not know which are the dummy values, the attacker will attack dummy values too. The attacker also does not know about the relationship used to calculate the dummy value. As a result, the attack is easily detected in the control room, as the value of r will not be equal to zero.
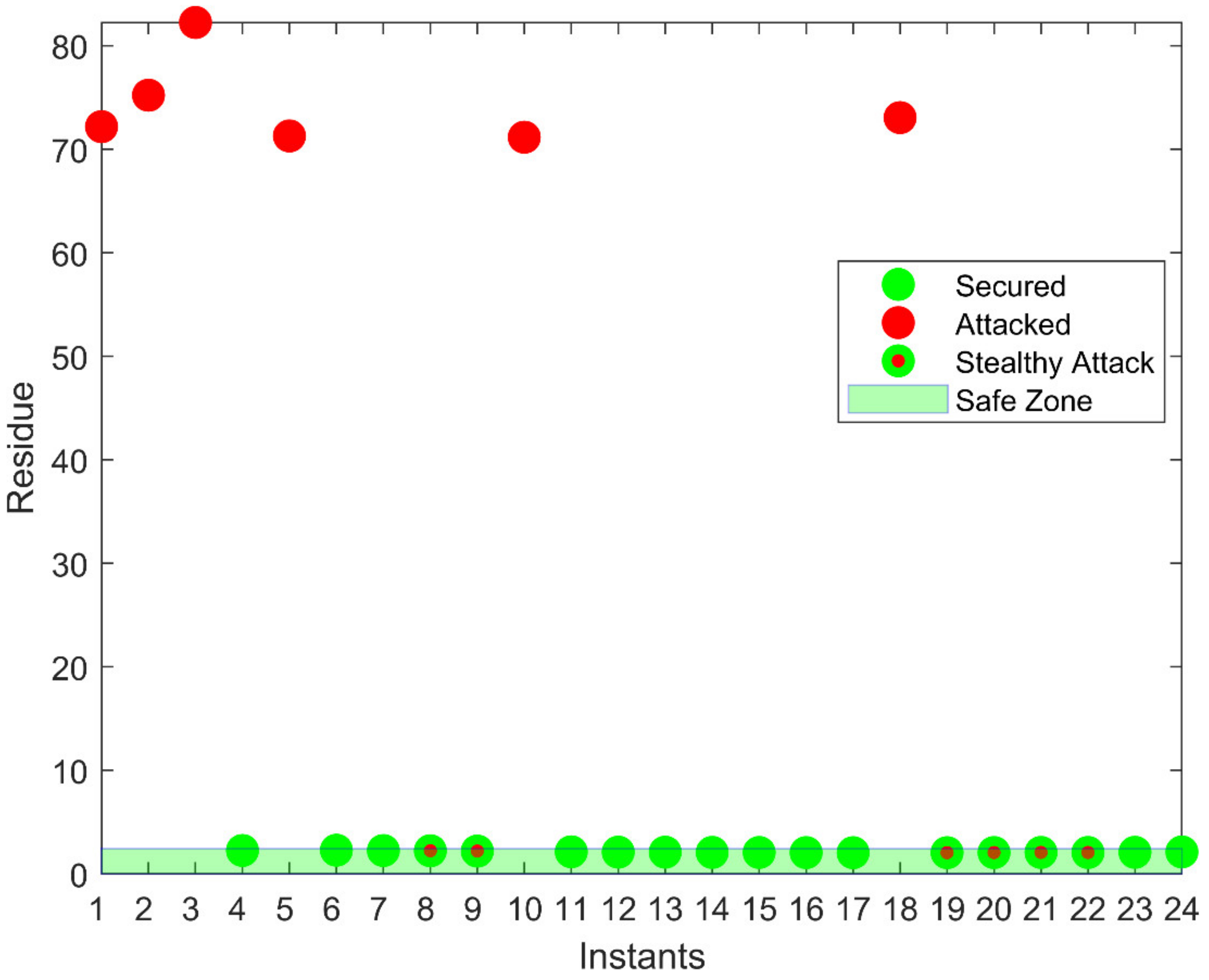
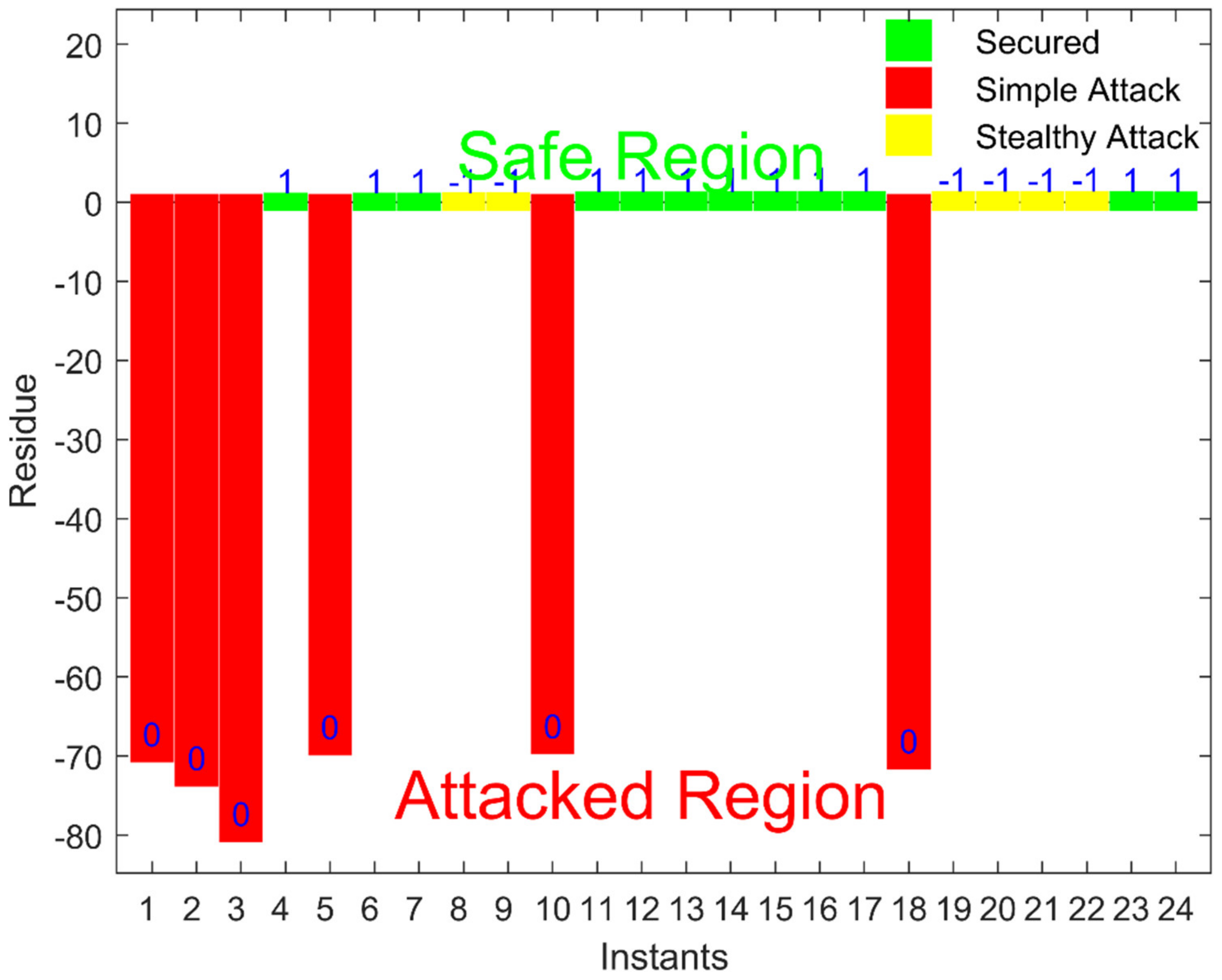
This proposed model of the variable dummy value can tackle the limitations of the fixed dummy value model and the stealth FDI attacks can be detected in an efficient way.
7. Discussion
Stealth false data injection attacks create huge damage to a power system. Such kinds of attacks should be detected for a smooth and reliable power flow in a smart grid. The proposed model was applied for the detection of such attacks. The model was based on a dummy measurement. The meters in the smart grid send the actual measurement and the dummy measurement. There are two techniques in the proposed model, namely, the fixed dummy value model and the variable dummy value model.
Both techniques were validated through the experimental results. The first technique of the fixed dummy value model could detect FDI attacks. However, at the same time, this technique has some limitations. When the attacker does not attack the dummy value of measurement, i.e., only the actual measurement is attacked, the control room is not able to detect that attack. The second technique of the proposed model, such as the variable dummy value model overcomes the limitation and the FDI attacks that were left unnoticed by the fixed dummy value model were detected by the variable dummy value model, as validated by the results.
The proposed model does not require the installation of any extra buses or transmission lines. There is no need to install any extra meters. Therefore, the model can be effectively applied to a smart grid and is economically efficient. From the viewpoint of long-term operation, the proposed model can be applied to make a smart grid more protected and secured. In the future, an extension of this work can be done to practically implement the model for a smart grid, which will protect the smart grid from FDI attacks. Some other methods can be adopted to set the dummy values of the power in the future. The probability of launching the attack can be minimized in this way.