Abstract
Energy efficiency has become a major concern for manufacturing companies not only due to environmental concerns and stringent regulations, but also due to large and incremental energy costs. Energy-efficient scheduling can be effective at improving energy efficiency and thus reducing energy consumption and associated costs, as well as pollutant emissions. This work reviews recent literature on energy-efficient scheduling in job shop manufacturing systems, with a particular focus on metaheuristics. We review 172 papers published between 2013 and 2022, by analyzing the shop floor type, the energy efficiency strategy, the objective function(s), the newly added problem feature(s), and the solution approach(es). We also report on the existing data sets and make them available to the research community. The paper is concluded by pointing out potential directions for future research, namely developing integrated scheduling approaches for interconnected problems, fast metaheuristic methods to respond to dynamic scheduling problems, and hybrid metaheuristic and big data methods for cyber-physical production systems.
1. Introduction
According to the 2021 U.S. Energy Information Administration’s International Energy Outlook, the industrial sector, including refining, mining, manufacturing, agriculture, and construction, accounts for more than 50% of end-use energy consumption. Although it dropped by a few percentage points in 2020, due to the effects of the COVID-19 pandemic, energy consumption is projected to increase from its current 245 quadrillion British thermal units (BTUs) to over 360 quadrillion BTUs in 2050 (a 45% increase) [1].
Due to a steady increase in both energy demand and environmental awareness, the industrial sector faces additional challenges, including stricter regulations and volatile energy costs. Thus, manufacturing companies need to reduce their energy consumption, which can be accomplished through the use of new equipment and better process and product design. However, researchers have proved energy-efficient scheduling to be an effective way of reducing energy consumption. Additionally, energy-efficient scheduling has the advantage of not requiring a significant investment, if at all, which is particularly relevant for small and medium enterprises [2,3,4,5,6].
Scheduling is the process of allocating scarce resources to tasks over time, and it is one of the success factors of a manufacturing system since it may have a considerable impact on the system performance. Energy-efficient scheduling attempts to lower energy consumption while providing the same level of service.
In recent years, several researchers have addressed energy-efficient scheduling problems, some by imposing energy-related constraints or objectives [7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22] and others by extending the scope of problem decisions to include equipment status [23,24,25,26,27,28,29], equipment working speed [30,31,32,33,34], and time slot allocation [35,36,37,38]. We review all works on energy-efficient job shop scheduling problems, regardless of how energy consumption is approached (optimized or restricted) and how energy consumption is changed (equipment status or working speed).
The purpose of this work is to provide a comprehensive review of the main research efforts and achievements regarding energy-efficient scheduling in job shop manufacturing systems, with an emphasis on metaheuristic approaches. Additionally, it can be further regarded as an essential update and extension of existing reviews, providing a structured guideline for future practices and research. Lastly, it also aims at facilitating solution comparisons in future work by creating a publicly available library of benchmark instances of energy-efficient job shop scheduling problems.
Scheduling problems in manufacturing systems are, in general, NP-hard; thus, their energy-efficient versions are also NP-hard [39]. Exact optimization approaches can only solve efficiently small-sized problem instances. Therefore, most of the literature proposes (meta)heuristic solution approaches.
Although there is a large number of interesting manufacturing scheduling problems, this review focuses on the job shop manufacturing environment, as a large and important segment of the industry uses such a shop floor type. The classical job shop scheduling problem (JSP) comprises a set of jobs and a set of machines. Each job consists of a sequence of manufacturing operations that must be processed in a given order. The JSP considers that each operation must be processed on a given machine. In contrast, in the flexible job shop scheduling problem (FJSP), there are several machines that can process each operation of each job. Therefore, to solve the FJSP, one also has to determine which machine processes each operation (i.e., job routing).
The increasing number of publications concerned with sustainable manufacturing has led to the publication of several reviews. As described in [3], early reviews focus on concepts and technologies, and more recent ones address (i) specific aspects of energy-aware production planning, such as power load scheduling [40], electric storage systems [41], smart grid [42], and waste minimization [43]; (ii) specific approaches, such as approaches in multi-objective environments [44], simulation [45], and machine learning [46]; (iii) sustainable practices [43,47,48]; or (iv) general manufacturing systems [3,4,5,6,44].
The contributions of this work can be summarized as follows: (i) to collect in a single source all recent relevant contributions to energy-efficient scheduling in job shop manufacturing systems, (ii) to summarize current research findings, (iii) to outline the significance of the work done in a range of contexts, (iv) to identify possible future research directions, and (v) to create and make available to the research community a web-library with existing data sets that can be used as benchmark instances in future studies.
The remainder of this work is organized as follows. Section 2 describes the scope of this review and the criteria used to select the papers. In Section 3, we provide a brief analysis of the 172 papers reviewed, and in Section 4, we discuss the different features incorporated in recent energy-efficient scheduling research. Section 5 presents solution approaches developed for energy-efficient scheduling problems in job shop environments. Moreover, in Section 6, we provide a review of the literature benchmark problem instances. Finally, literature gaps, topics for future research, and some conclusion remarks are presented in Section 7.
2. Review Scope and Methodology
Scheduling problems involving energy have been increasingly attracting the attention of researchers and practitioners. Due to the large volume of literature, we focus on the papers published in English that explicitly address energy efficiency and propose scheduling methods within job shop manufacturing systems. In other words, the papers considering sustainability objectives other than energy efficiency are outside the scope of this work. (For a detailed breakdown of the various research clusters regarding sustainable manufacturing, the reader is referred to [5,43]). Also out of the scope of this review are works tackling higher levels of decision making (mid- and long-term), such as logistics, supply chain management, and business management, even if focusing on energy efficiency. (A review on such works can be found in [49]). Finally, our search is limited to journal papers and book chapters, thus excluding publications in the form of conference proceedings.
The review process used consists of the following six stages:
- i.
- scope definition—described in the previous paragraphs;
- ii.
- keywords definition—extracted from recent literature (review and research papers) by a heuristic search;
- iii.
- structured search (data gathering)—bibliographic databases were searched using the keywords found in stage ii (in a generic format and considering both American and English spellings) and considering the date range 2011–2022;
- iv.
- data structuring and organizing—the sets of records resulting from the structured search were then combined, screened, and cleaned as explained below;
- v.
- search expansion (additional data gathering by backward/forward reference search)— works citing and works cited by the set of works resulting from stage iv were added, and the new set of records was then subject to structuring and organizing (stages iv and v were repeated several times until the set of records remained unchanged); and
- vi.
- bibliography classification and analysis—reported in the following sections.
We searched for published papers, dating back to 2011 (note that although we considered the papers published in and after 2011, the first relevant papers were published in 2013), that included in the title, in the abstract, or in the list of keywords the following combinations of generic keywords (stage ii):
- (“*machin*” or “production*” or “operation*”, “manufactur*” or “job-shop*” or “jobshop*” or “job shop*”, or “flexib*”)
- And (“schedul*” or “planning”)
- And (“optimization*” or “optimisation*” or “*heuristic*”)
- And (“energy*” or “sustainab*” or “tariff*” or “*carbon*” or “*green*”)
These keywords were selected so as to gather specifically energy-efficient manufacturing scheduling works. The search was conducted on the two most well-established bibliographic databases: Web of Science™ and Scopus®. To avoid missing relevant papers due to varying authors’ keyword choices, papers were also gathered through backward/forward reference search, including from the most recent review papers [2,3,4,5].
The literature search was performed in March 2022. In the first search (stage iii), we collected 2179 and 2088 entries from the bibliographic databases Web of Science™ and Scopus®, respectively.
The data structuring and organizing stage involves several steps. We started by combining the two sets of results and removing the duplicated entries (through their Digital Object Identifier (DOI), title, or abstract similarity), after which we were left with 2820 papers. The first round of the screening process allowed for the exclusion of about 1050 papers by automatically eliminating papers outside the scope of this work, that is, papers mentioning a form of “flow shop”, “single machine”, “parallel machine”, “supply chain”, or “logistic” in the title or abstract. In the second round of the screening, by reading the title and skimming the abstracts, we excluded about 1500 papers. Thus, at the end of stage iv, there were 270 records.
Then, based on these 270 works, we performed backward and forward reference search (stage v), added the records found to the 270 existing ones, removed duplicates, and screened the newly found records by reading the title and skimming the abstracts (stage iv), and repeated the process (stages iv and v) whenever new records were found. The number of papers that went through the final data structuring and organizing round, in which all papers were fully read, was 310. Before moving on to the final stage of the review process—bibliography classification and analysis—we excluded another 131 papers; therefore, we were left with 179 papers. Since seven of these papers are reviews, we ended up with 172 papers to be further synthesized, analyzed, and reported on. This is almost four times the number of JSP and FJSP papers reviewed in the most recently published literature reviews [2,3,4]. Moreover, of these 172 papers, 115 have been published since 2019.
All papers are listed in Supplementary Materials attached to this paper. Although we have analyzed and synthesized all 172 papers to draw conclusions, we review and describe in detail a selected subset, which includes the most recent and most cited ones.
3. Literature Analysis
The first works on energy-efficient scheduling problems date back to the 1990s [4,5,6]. However, energy-efficient scheduling has only recently become the subject of systematic research. Figure 1 depicts the number of papers published, between 2013 and the first quarter of 2022, on the energy-efficient job shop problem and its variants (here and hereafter collectively designated as EEJSPs). As can be seen, the number of publications has been growing quickly, particularly since 2018. Between 2013 and 2018, a total of 57 such papers were published, while between 2019 and the first quarter of 2022, this number has gone up to 115 (more than doubling in half of the time).
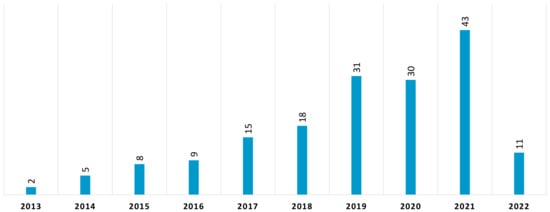
Figure 1.
Number of publications, per year, on energy-efficient scheduling problems in job shop manufacturing systems. (Early view publications were assigned to 2022.)
The 172 papers have been published in 82 journals and two different books. However, only 15 journals have published three or more papers on EEJSPs. Overall, these 15 journals have published 89 papers, more than half of the papers found. Table 1 reports the list of journals and the number of papers published in each journal, including only those journals that have published three or more papers.

Table 1.
Publication source titles with at least three papers published between 2013 and 2022 (first quarter) on energy-efficient scheduling problems in job shop manufacturing systems.
We have also analyzed the usage of keywords by extracting the author keywords from each of the papers. The 32 most repeated keywords and the number of works that use them are depicted in Figure 2. (Please note that we have merged similar keywords and different versions of the same keyword, such as singular and plural and different spellings, usage of hyphenation, etc.). As expected, “flexible job shop scheduling problem” and “job shop scheduling problem” are among the most used keywords, being first and third, respectively. Regarding energy efficiency scheduling, four different keywords are used in the literature, namely “energy-efficient scheduling”, “energy-saving scheduling”, “energy-aware scheduling”, and “energy-conscious scheduling”, with the most common, by far, being “energy-efficient scheduling” (used more frequently than all other three combined). Three other keywords are used for this purpose, namely: “low carbon scheduling”, “green scheduling”, and “sustainable manufacturing”; however, they are mainly used in works concentrated on environmental and/or social objectives. The second most used keyword is “multi-objective optimization”, which is due to the fact that the most used approach to energy efficiency is considering two or more objectives. Among the objectives considered, the ones that are most frequently included as keywords are energy consumption and carbon emissions. Finally, several of the keywords refer to solution approaches.
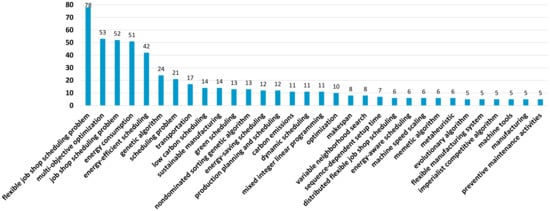
Figure 2.
Keyword usage (including only those keywords found in at least five works).
Of the papers reviewed, 90 propose mathematical programming models, most being mixed-integer linear programming (MILP) models. There are, however, a few that propose constraint programming (CP) and dynamic programming (DP) models. The mathematical models are almost always introduced just to formally define the problem. Hence, they are rarely solved, even for small-sized problem instances (see, e.g., [29]). Regarding the proposed solution approach, 149 of the papers reviewed propose at least one metaheuristic. This is not surprising, as EEJSPs are NP-hard in the strong sense (for further details, see Section 5).
The papers are classified according to six criteria: shop floor type, energy efficiency strategy, scheduling objectives, additional scheduling features, and (metaheuristic) solution approach (see Table A1). A full classification of the reviewed papers, extending the concise version given in Table A1, is provided as a Supplementary Excel Spreadsheet.
4. Features of the Papers on EEJSPs
A job shop environment is characterized by having several machines that are used to process the operations of several jobs. Thus, each job must pass through (at least some of) these machines. To solve the JSP, one needs to find the sequence of operations in each machine, as well as the processing starting time of each operation. While in the JSP, the job route (i.e., the sequence of machines that each job has to go through) is predefined, in the FJSP, one also has to determine the machine on which each operation is processed. Thus, one also has to determine the assignment of operations to machines.
Most of the papers reviewed (about two-thirds) consider a multi-objective version of the JSP or FJSP in which one of the objectives is energy related (typically, energy consumption, energy costs, carbon emissions, or peak power consumption). Thus, in these works, solving the problem requires the usual decisions (job sequencing and operation start/completion time for the JSP, and also job routing for the FJSP). Then, the goodness of a solution is evaluated by combining time- and energy-related performance measures. The remaining one-third also incorporates additional problem features that lead to additional decision-making variables, namely: machine status, whenever machines can be turned off; machine processing speed, whenever the processing speed can be chosen; and time slot allocation, whenever the scheduling horizon is divided into slots according to energy prices. This section classifies the papers reviewed in terms of the main features impacting the decision-making process.
4.1. Shop Floor
The shop floor type is the main feature when distinguishing problem type. This review only considers job shop environments. Nevertheless, whenever relevant, we clearly distinguish the JSP from the FJSP, since the latter encompasses the additional flexibility of choosing the machine that processes each operation. Therefore, there is more room to search for better strategies with regard to energy consumption. As illustrated in Figure 3, about two-thirds of the papers (113 out of 172) consider job routing flexibility. Additionally, it can also be seen that the number of papers on energy-efficient FJSP is growing faster than that of energy-efficient JSP, particularly in the most recent years. The main reasons for such a trend are likely to be (i) the new advancements in manufacturing technology (also related to the development of Industry 4.0) and (ii) the natural opportunities that the job routing choice provides regarding energy efficiency (different machines may have different characteristics, such as processing time, power consumption, etc.).
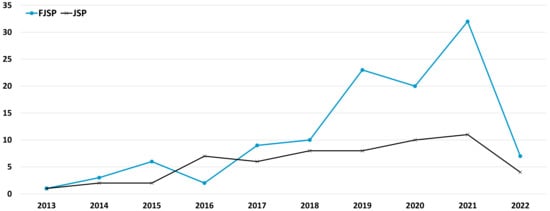
Figure 3.
Number of publications, per year, addressing energy-efficient JSPs and FJSPs.
4.2. Strategies for Energy Efficiency
In the EEJSPs literature, three main strategies have been used to improve energy efficiency, namely: (i) control machines working speed (speed adjustment), (ii) schedule tasks under time-dependent energy prices (time of use, real-time pricing, and critical peak pricing), and (iii) switch machines to a power-saving mode while idle (e.g., turning them off). While under the first and second strategies, one needs to balance energy consumption and production time (e.g., makespan, tardiness, and earliness), under the third strategy, energy savings from resorting to the use of a power-saving mode need to be balanced with energy requirements to restart and warm up the resources.
The first strategy acts on power consumption, which clearly impacts processing energy consumption. Additionally, it may also impact non-processing energy consumption, as speeding up or slowing down a machine while processing an operation may reduce its idle time or the idle time of the machine processing the next operation of the corresponding job. Moreover, speeding up or slowing down a machine while processing an operation impacts the operation completion time, which in turn may impact the job completion time, and even the completion time of the whole set of jobs (makespan).
In contrast, the third strategy addresses non-processing energy consumption only. The additional decisions of switching machines into a power-saving mode between consecutive operations result solely from whether the energy consumption during the idle time is larger than that required for warming up the machine. Such a strategy does not affect completion times.
The second strategy is related to energy supply characteristics, in particular its price. Scheduling under variable prices may have different impacts, depending on the chosen performance metric (i.e., objective function). For example, minimizing energy consumption and minimizing energy costs can lead to quite different schedules. A change in the consumption pattern by shifting electricity usage from a high-cost period to a low-cost period can lead to cost savings, even if the total energy consumption remains the same. This strategy needs to account for completion times, as shifting electricity usage implies delaying operation completion time.
Out of the 172 papers reviewed (59 on the JSP and 113 on the FJSP), 113 papers take energy efficiency into consideration just by including either an energy-related objective function or energy-related constraints. The remaining 59 papers incorporate at least one of the above-mentioned energy efficiency strategies. Indeed, six papers consider two such strategies simultaneously. Furthermore, energy efficiency strategies are more popular in works on the JSP than on the FJSP; they are considered in 31 JSP papers (53% of the 59 such papers) and in 28 FJSP papers (25% of the 113 such papers). This is most likely due to the FJSP’s built-in energy-saving opportunities (see Section 4.1 for further details). Figure 4 summarizes these observations. Recall that six publications, one on the JSP and five on the FJSP, include two strategies each. Since we provided the number of publications incorporating each of the three strategies, these six papers are counted twice.
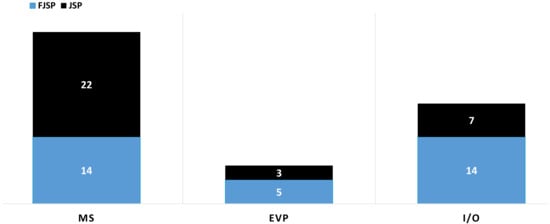
Figure 4.
Number of JSP and FJSP publications incorporating energy-efficient strategies (MS—machine speed adjustment, I/O—turn-on and turn-off status, EVP—energy variable price).
In the remainder of this subsection, we discuss only the 59 papers that incorporate energy efficiency strategies.
Several authors have resorted to the speed adjusting strategy; however, only machine processing speed (MS) has been considered (see, e.g., [24,30,31,33,50,51,52,53]). The exception is the work in [54] that considers simultaneously adjusting the machine processing speed and the vehicle traveling speed. By adjusting the working speed of some resources, one may reduce energy consumption without impacting productivity. For example, non-critical resources (resources finishing their activities ahead of time) can perform some of their activities at a lower speed without impacting the job completion time or makespan, while reducing the energy consumption associated with those activities. Additionally, by reducing the processing speed of some activities, a reduction in nonproductive energy consumption may also be accomplished, since the idle time of those and/or other resources may be reduced. (Usually, performing activities at a lower speed requires a lower power demand and thus lower energy consumption). Machine speed adjustment stands out, by far, as the most used energy-saving strategy. About 60% of the papers, addressing either a JSP or a FJSP version extending its original scope, consider adjusting the machine processing speed (22 regarding the JSP and 14 the FJSP).
Electricity suppliers have been adopting time-varying pricing schemes to incentivize users to shift electricity consumption from high-demand periods to lower-demand ones, improving the reliability and efficiency of the electrical power grids, as well as reducing carbon emissions in electricity generation. Therefore, a new trend in the research on EEJSPs, which optimizes energy costs by taking advantage of such incentives, has emerged [35,36,38]. Researchers usually resort to discrete time formulations that divide the scheduling horizon into time slots with equal duration, each having a predefined energy cost. Manufacturing activities are then allocated to and scheduled in these slots such that the total energy cost is minimized. However, under time-dependent energy prices, lower energy costs may be accomplished by changing the demand pattern rather than by consuming less energy. Hence, researchers typically simultaneously consider a time-related objective. This line of work is very recent, and it has been considered in only eight papers (three on the JSP and five on the FJSP).
The third strategy has been considered in 21 papers. Some of these papers include decisions on turning machines off while idle (e.g., [24,25,26,27,28,29,55,56,57]), and others on switching them to a stand-by mode (e.g., [58,59,60,61]). These works balance the energy saved from not having the machines running idle with that required to restart or warm up the machines, depending on whether the machines are switched off or switched to a power-saving mode, respectively. In order to do so, most authors consider a switch on time and a switch on power consumption, which are then used to compute a switch on energy consumption (e.g., [23,24,27,28,29]). Some of these works even consider that the switch on time and power depend on whether the machine was previously on a standby mode or switched off (e.g., [26,61]). Other authors pre-calculate, for each machine, a break-even time period for which turning the machine off and on is economically justifiable. Then, for each machine, whenever the time between two consecutive operations (i.e., the time between starting an operation and ending its immediate predecessor on the same machine) exceeds the break-even time, the machine is switched off (e.g., [25,56,57]). A few of these papers are more realistic, as they also include machine transition states such as warming up and ramping down, often through the consideration of sequence-dependent setup times (SDST) [35,62].
4.3. Energy Efficiency Objective Functions
The most common approach to the EEJSPs is to solve the JSP or the FJSP while optimizing an energy-related objective function. However, a few papers address energy efficiency concerns by imposing an upper limit on the total energy consumption (e.g., [21,22,34,63,64]) or on the peak power consumption (e.g., [65,66,67,68]). Of the 172 papers reviewed, 163 consider energy-related objective function(s). Although some of them also incorporate energy efficiency strategies, most find solutions to the original problem (JSP or FJSP) and then use an energy-related performance measure to evaluate the quality of the solutions found (113 papers).
Overall, four different energy objective functions have been considered, namely: E—total energy consumption, —total energy cost, —total carbon emissions, and —peak power consumption. Most of these 163 papers, about two-thirds, minimize the total energy consumption. In contrast, just two papers [69,70] minimize the peak power consumption. The minimization of the total energy cost and of the total carbon emissions have been considered more recently. Nevertheless, they already account for about 16% and 14% of the 163 papers, respectively.
To calculate the total energy consumption of the manufacturing system, researchers consider three to five types of consumption, namely machine processing energy (P), machine idle energy (), machine setup energy (S), job transport energy (), and indirect energy (), as well as energy associated with auxiliary equipment [71,72,73,74,75,76], coolant and lubricant [77], and keeping room temperature constant and lighting [29,78].
The calculation of the energy consumption is very similar for the different types of consumption, mainly differing on the values used for the parameters. The mathematical expression for the total energy consumption, considering all five consumption types, is provided in Equation (1).
where M is the set of machines; is the set of operations to be processed on machine ; and are, respectively, the power consumption of machine m when processing operation j, when idle, and when being setup for operation j; and , and are the corresponding times. The energy required to transport the job to have operation j processed includes the empty travel energy to pickup the job (from the position where the vehicle finished its last task to the position where the job’s previous operation was processed) and the loaded travel energy to deliver the job to where operation j is to be processed. Thus, and are, respectively, the empty and loaded travel times associated with operation j, and and are the vehicles’ power requirements when traveling empty and loaded, respectively. We assume that the vehicles are equipped with automatic start-stop technology; thus, there is no consumption while idle. (Note that, usually, all vehicles have the same power requirements, which do not depend on the job being transported). The indirect power consumption is constant throughout the completion time of all jobs .
The calculation of the energy costs and the calculation of the carbon emissions are typically based on the total energy consumed, as given in Equations (2) and (3), where and are, respectively, the coefficients that convert the consumed energy into carbon emissions and monetary units.
Regarding peak power consumption, the two works that minimized it do not provide any mathematical expression for . However, it should be as given in Equation (4), or at least similar, since it calculates the maximum instantaneous power consumption considering all five types of consumption.
where and are binary variables that take the value 1 if at time t machine m is processing operation j, is idle, or is being set up to process an operation j, respectively, and zero otherwise. Similarly, and are binary variables that take the value 1 if at time t vehicle v is traveling loaded or empty, respectively, and zero otherwise. (Recall that we are assuming the vehicles to be equipped with automatic start-stop technology).
Figure 5 shows the classification of the 161 papers addressing EEJSPs by optimizing energy-related objective functions regarding the objective function considered (E, , and , the problem addressed (JSP and FJSP), and the type of energy consumption included (P, , S, , and ). (Note that most authors consider just some of the energy consumption types.) The papers on peak power consumption are excluded from this figure, since there are only two [69,70] and both consider only processing energy consumption. Figure 5 has three circles: the innermost circle depicts, in parentheses, the number of papers considering each of the energy efficiency objective functions; the middle circle shows the number of papers on the JSP and on the FJSP for each of the objectives considered in the inner circle; and the outer circle depicts the percentage of papers that consider each of the energy consumption types for each problem type (middle circle) and each objective function (inner circle). Note that since several papers consider more than one energy consumption type, the total percentage value for each category is greater than 100%, and that the percentages refer to the 161 papers being analyzed in this subsection.
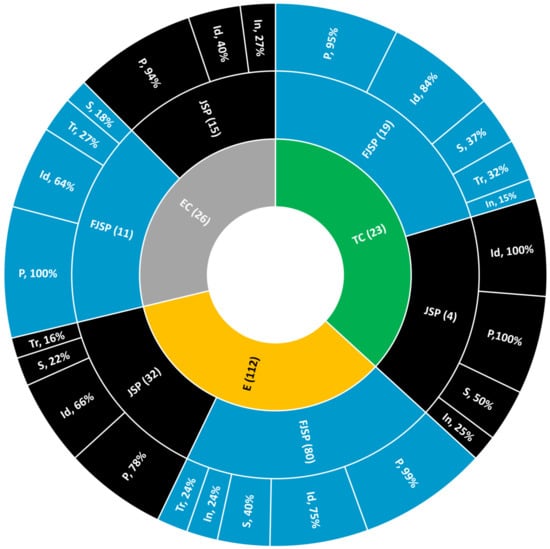
Figure 5.
Paper classification regarding energy efficiency objective functions and their components for JSPs and FSJPs. (The areas are not to scale.)
Ascan be seen in Figure 5, almost all works consider machine processing energy (P). Its minimization is mainly tackled through speed adjustment in JSPs (e.g., [30,33,79,80,81]) and through job routing in FJSPs (e.g., [7,8,9,10,11,13,14,15,16,63,82]).
The second most commonly considered energy consumption type is machine idle energy, that is, the energy consumed by machines when they are running idle or when they are switched to a standby mode [7,23,24,26,30,31]. Quite often, machines that are idle between consecutive operations are not turned off. On the one hand, frequently turning machines on and off leads to additional degradation. On the other hand, some machines require a non-negligible setup time and/or cost when turned back on.
Setup energy is quite often disregarded as, typically, setup times are either disregarded or accounted for in the operation processing times. However, some studies consider setup times explicitly, as well as the associated energy consumption [35,50,62]. Additionally, some authors consider that setup energy consumption (S) includes not only the energy required to exchange tools and machine settings between consecutive operations, but also the energy required to change the state of the machines (e.g., warming up and ramping down) [11,24,25,26].
The energy required to transport the jobs around the shop floor is also accounted for by six papers addressing the JSP and by 28 papers addressing the FJSP. However, since no limitation and/or scheduling decisions are considered, job transport time is equivalent to sequence-dependent setup time, and thus the job transport energy could be considered as setup energy (e.g., [11,16,73,83,84,85,86]). Nevertheless, there are a few exceptions. Some authors [37,38,85,87,88,89,90,91,92] schedule transport and take into account the energy required to load/unload vehicles, and others [93,94,95,96,97,98] consider the energy required to transport the jobs between geographically distributed facilities.
Finally, the least considered energy consumption type is indirect energy, which is usually due to auxiliary equipment (e.g., [14,29,80,99]). Some works consider the indirect energy consumption to be proportional to the makespan, and thus a single objective function is used to minimize the makespan and the energy consumption (e.g., [72,76,100]).
Figure 6 depicts the yearly evolution of the number of papers that consider each of the five energy consumption types. It is clear that the number of publications considering energy consumption has been growing significantly. In particular, the number of papers considering the energy consumed by transport resources has grown quite impressively; the number of such studies published in 2021 is almost the same as those published over the previous four years. In contrast, the number of papers considering indirect energy consumption has recently been decreasing.
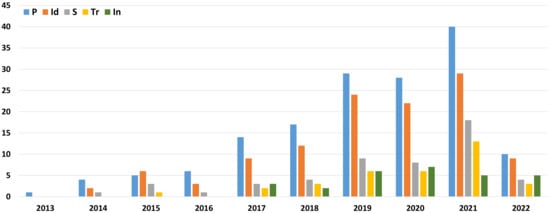
Figure 6.
Number of papers published, per year, that include each of the five energy consumption types.
4.4. Other Objective Functions
About 81% of the reviewed papers include more than one objective function, thus addressing a multi-objective version of the problem. The objective functions considered include an energy efficiency objective function and at least one additional objective function. The latter is typically related to performance objectives (e.g., makespan, earliness, or tardiness) and/or to economic objectives (e.g., production costs).
The makespan () is the time required to complete all operations of all jobs and is the most frequently considered objective function. In fact, it is optimized in about 64% of the reviewed papers (e.g., [7,24,26,32,33]). A closely related objective that is sometimes considered is the total processing time, which is given by the sum, over all jobs and all operations, of the operation processing time (e.g., [8,101]).
The second most frequently considered objective is the tardiness, which measures the difference between the job due date and the job completion time. About 20% of the reviewed papers optimize some form of tardiness, namely: total tardiness (T) (e.g., [9,63,102,103,104]), total weighted tardiness () (e.g., [21,23,25,30,105]), total weighted tardiness and earliness () [59,69,97], tardiness cost () [86,106], mean tardiness () [107], and maximum tardiness () [108,109].
Regarding economic objectives, the most frequently considered one is the total production cost (), which is optimized in about 13% of the studies. The costs accounted for include costs of human resources [13,35,110,111], raw materials [73,112], maintenance [73,113], transportation [88], and processing [97,114,115]. Other economic objectives include penalty costs associated with earliness and/or tardiness [22,97,106], machine under- and over-utilization [38], and customer dissatisfaction [116].
Besides the performance and economy objectives, a few other objectives have been considered, although in just a very small number of papers. These include machine performance goals such as machines workload () [16,31,35], rescheduling disruption () [57,103], machines’ fault probability () [117], and system reliability () [8,51]; product-related goals such as work in process () [16], raw material usage () [64], quality and defective rate (Q) [19,22], and customer satisfaction () [35]; and social objectives, included mainly through working conditions such as noise level (N) [32,101,118], ergonomic risk () [119], and vibration () [101].
Although some works simultaneously include environmental (energy), economic (makespan), and social (noise) objectives, not many do so. This is further discussed in Section 5.4.
4.5. Additional Scheduling Problems
As seen, most of the reviewed papers address the EEJSP by just including additional objectives. Thus, the problem being solved is still the JSP or the FJSP. Nevertheless, energy-efficient solutions are obtained, as the objective functions include at least one energy metric. In contrast, some works extend the scope of the addressed problem by considering additional problem features that require additional decision making. We have already discussed the works that do so by adjusting machine speed, by switching the machine status, or by considering time slots with different prices. Here, we discuss works that include, simultaneously, decisions on other resources or other activities.
Problems simultaneously scheduling machines and workers consider several workers with different skills. Additionally, due to the complexity of the machines, each worker can only operate a subset of the existing machines. Furthermore, each operation may require different worker skills, thus not all workers can perform all operations. Finally, each operation can only be processed on a subset of the existing machines. Therefore, when scheduling an operation, one has to look for an available machine among the ones that can process the operation and also for an available worker that can perform the operation and can operate the chosen machine. Although workers do not impose energy consumption, they may impose constraints on the operations schedule, which in turn may lead to a higher energy consumption. Such problems have been addressed while minimizing processing energy consumption [13,15,119,120] and while minimizing carbon emissions [111].
Another line of research considers problems in which both the machines that process the operations and the vehicles that transport the jobs have to be scheduled simultaneously. The transportation imposes its own additional energy requirements, as vehicles need to move around the shop floor. Transportation may also lead to a more energy-consuming schedule due to the required synchronization of machines and vehicles [37,87,88,90,94]. The vast majority of the studies either disregard transportation or consider that transport time is included in the processing time; consequently, a job can be processed on the next machine immediately after its completion on the previous one. Others assume a transport time between the machines and also that the job can be transported immediately after the completion of the operation. Such an assumption implies the existence of an unlimited number of vehicles, which is unrealistic. Energy consumption associated with transportation cannot be ignored, and it can be optimized by a proper scheduling scheme.
The performance of machines degrades, naturally, as a result of aging and wear, which leads to a decrease in performance (quality and speed) and reliability (faults and failures). Thus, some authors consider preventive maintenance, which has to be scheduled together with the manufacturing operations [8,73,87,105]. The purpose of such integration is twofold: to maintain the performance of machines at an acceptable level (which also reduces the energy consumption), and to minimize the energy consumed by maintenance activities.
Other subproblems that impact the total energy consumption have been considered, although less frequently: layout optimization (LOP) [86,89]—machine location (and reallocation) is determined at the same time that the manufacturing operations are scheduled; job process planning (JPP) [14]—job routing is chosen from a set of predefined job routes; batch scheduling (BS) [62]—machines are set up to process a batch of similar operations; and distributed manufacturing scheduling (DMS) [93,94,98,121,122]—operations may be processed on machines that are located in different factories, which are geographically distributed. Among these, we highlight the last two, since they address non-identical factories and consider the three pillars of sustainability (economic, social, and environmental), thus complying with the triple bottom line principle.
5. Solution Approaches
Energy-efficient job shop problems are NP-hard in the strong sense since they extend a well-known NP-hard problem, the JSP [39]. Thus, exact methods may not be able to obtain an optimal solution within a reasonable amount of (computation) time. Additionally, they may not even be able to find a feasible solution, particularly in the presence of problem instances of a realistic size. Therefore, the majority of the studies propose approximate solution methods that are capable of finding good quality solutions quickly, but do not ensure optimality.
The solution approaches proposed include heuristics, metaheuristics, and hybrid metaheuristics. While heuristics exploit problem-dependent information to find a good solution to a specific problem, metaheuristics are general algorithms that can be applied to a broad range of problems.
5.1. Heuristic Methods
Heuristic methods are designed for a specific problem and take advantage of the problem characteristics as well as previous experience with the problem. They are capable of finding feasible solutions very quickly, which are often reasonably good. Hence, heuristics may be used on their own to find feasible solutions quickly; this is particularly relevant in the presence of a very short time-frame or deadline. On the other hand, they may be used together with or embedded in other optimization algorithms. Metaheuristic approaches frequently resort to heuristics to generate initial solutions and/or to try to improve the solutions they found. The latter results in hybrid metaheuristics (see Section 5.3).
In the papers reviewed, heuristics have been proposed for dynamic EEJSPs, as these involve finding schedules in real time in response to uncertainties in customer demand, resource availability, energy disruptions, and more. Quite often, researchers designate such approaches as real-time reactive scheduling. The progress in the Internet of manufacturing things (IoMT) is facilitating the availability of information, particularly in real time; hence, dynamic scheduling (DS) has recently been capturing more research attention. About 14% of the papers reviewed propose DS approaches, which were implemented by resorting to heuristic methods (5 papers were published in 2018 or earlier, and 19 were published in and after 2019). DS has been implemented by using two main strategies to react to real-time events: full schedule reconstruction [21] and specific schedule changes addressing only the disrupted resources and impacted tasks (e.g., [57,92,123,124]).
For example, in [123], a reactive heuristic is used to identify the disrupted resources (machines or vehicles) and to reassign the impacted tasks. The authors reassign each impacted task to the (possible) resource that cumulatively satisfies: (i) smallest operating time or earliest completion time, (ii) lowest energy consumption, and (iii) smallest slack time and highest energy consumption during idle time. Another reactive heuristic is proposed in [57]. In this case, the need for dynamic scheduling is due to the arrival of new jobs. Whenever a new job arrives, its operations are tentatively inserted into the machines’ idle time, shifting the previously assigned operations to a later time if necessary and possible without compromising the makespan; otherwise, they are sequenced as the last tasks of the machines.
An alternative and interesting approach to deal with uncertainty is to model it explicitly by resorting, for example, to fuzzy numbers. Fuzzy arithmetic is a powerful tool to introduce uncertainty into mathematical models. Some of the reviewed papers, though not many, use triangular fuzzy numbers to model uncertainty regarding processing times [104,125,126] and setup times and defective product rate [37]. On the other hand, in [127], the uncertainty associated with delivery times is modeled through trapezoidal fuzzy numbers. A recent discussion on sources of uncertainty in scheduling can be found in [128], although for a different problem. They propose a multi-attribute fuzzy decision-making approach to the disassembly scheduling problem under uncertainty. This problem has a relevant impact on the environment since it allows one to obtain parts or sub-assemblies from end-of-life products.
Several of the metaheuristics proposed (see Section 5.2) resort to a heuristic to obtain initial solutions rather than generate them randomly. Recall that metaheuristics are general purpose algorithms and do not take advantage of the problem characteristics. Thus, having good initial solutions typically enhances their performance. Many authors have used heuristics, mainly constructive heuristics, to obtain initial solution(s). For example, [80] proposes a whale optimization algorithm (WOA) for the JSP with speed-adjustable machines. An initial population of solutions is obtained by combining some randomly generated solutions with solutions obtained by dispatch rules. The latter are randomly selected from the following four: (i) schedule (the first available operation of) the job with the largest remaining processing time, (ii) schedule (the first available operation of) the job with the most operations remaining, (iii) schedule (the first available operation of) the job with the shortest total processing time, and (iv) schedule (the first available operation of) the job with the longest total processing time. The processing speed is always randomly assigned to the each operation.
5.2. Metaheuristics
Metaheuristics are high-level iterative processes that guide the search over the solution space. They may consider a single solution or a collection of solutions (population of solutions). Single-solution metaheuristics are trajectory-based, while multiple solution ones can mainly be divided into evolutionary-based and nature-inspired. The latter are sometimes categorized as bio-inspired (e.g., ant colony optimization), human-based (e.g., imperialistic competitive algorithm), swarm-based (e.g., particle swarm optimization), physics/chemistry-based (e.g., electromagnetism), and other less known and less used categories. The search process is stochastic in nature, and its efficiency and effectiveness are closely related to a trade-off between exploitation (intensive search of a promising area) and exploration (wide search of the solution space in the search of new areas).
Single-solution metaheuristics iteratively modify a single candidate solution in the hope of finding a better solution in its neighborhood. Thus, this type of algorithm is exploitation-oriented and can get trapped into a local optimum. However, they are all enhancements of the basic local search procedure since they are probabilistic in nature. On the one hand, the modification to apply to the candidate solution is probabilistic, and on the other hand, worse candidate solutions are sometimes accepted. Simulated annealing (SA) [129], one of the most well-known single-solution metaheuristics, borrows concepts from the physical annealing of metals. To find a new solution, SA moves in the search space by taking steps of a random but constrained size from the candidate solution. If the new solution is better than the candidate one, then it replaces the candidate one. A worse solution is probabilistically accepted; the acceptance probability is a function of how long the algorithm has been run for and of how much worse the new solution is. Other well-known single-solution metaheuristics are iterated local search (ILS) [130], variable neighborhood search (VNS) [131], and Tabu search (TS) [132].
Over the years, many evolutionary-based metaheuristics have been proposed. Among the most popular and best performing are genetic algorithms (GAs) [133]. A GA evolves a population of solutions along several generations through natural selection and genetics. Solutions are randomly selected for reproduction in order to produce offspring (new solutions), which inherit the characteristics of the parents. The offspring are then added to the next generation. Although the selection is random, following on Darwin’s theory of natural evolution, better solutions are given a higher probability of being chosen for reproduction. By doing so, the characteristics of good solutions are more likely to be preserved as new solutions are obtained by copying the genes of the parents. A crossover operator is used to defined which genes are inherited from which parent. Additionally, some solutions are changed through mutation in order to maintain diversity and prevent premature convergence.
Nature-inspired metaheuristics search the solution space by imitating natural phenomena such as the behavior and interaction in bird flocking, fish schooling, foraging bees, flower pollination, and so on. Many such algorithms have been proposed and used in a variety of applications. The literature on this type of metaheuristic is rapidly expanding. One of the most popular nature-inspired metaheuristics is particle swarm optimization (PSO) [134], which was originally devised for continuous optimization problems. PSO works with a collection of solutions, termed particles, that are moved around the search space by changing the position and velocity of each particle. The movement of each particle is influenced by its own experience (its best previous position) and the experience of its neighbors (the best previous position in the neighborhood), moving the swarm toward the best solutions.
Metaheuristics are proposed in 149 of the 172 reviewed papers. Evolutionary-based metaheuristics are the most popular, with 64% of the papers proposing them, followed by nature-inspired metaheuristics, which are proposed in 29% of the papers. Single-solution metaheuristics are proposed in 7% of the papers.
Overall, the papers reviewed propose 38 different metaheuristics to find solutions to EEJSPs. Although in some papers more than one metaheuristic is implemented, we only count one metaheuristic per paper—the one proposed and described in detail.
Figure 7 shows the metaheuristics proposed, as well as the number of papers proposing each one of them (including only those proposed in two or more papers). Genetic algorithms are by far the most used metaheuristic; over 53% of the proposed metaheuristics are GAs. Additionally, there are over 13 times more papers proposing GAs than papers proposing imperialistic competitive algorithms, the second most proposed approach.
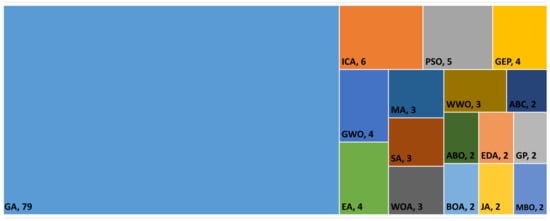
Figure 7.
Metaheuristics proposed for EEJSPs and number of papers proposing them (including only those proposed in two or more papers). (The list of abbreviations provides the full name of every algorithm.)
Hybrid metaheuristics have also been proposed for EEJSPs, and they are discussed next.
5.3. Hybrid Metaheuristics
Over the years, many metaheuristic algorithms combining various algorithmic components have been reported. Such algorithms are commonly referred to as hybrid metaheuristics. The main motivation behind the hybridization of different algorithms is to exploit the complementary character of different optimization strategies, thus taking advantage of their synergies. In fact, the hybridization of metaheuristics is a widespread practice, especially in what concerns the use of local search methods within population-based metaheuristics, regardless of whether they are evolutionary-based or nature-inspired. Metaheuristics, although good at exploring the search space and identifying areas with high-quality solutions, are usually less effective at exploiting the accumulated search experience, that is, at finding the best solutions within these high-quality areas. Therefore, local search is used to refine the solutions that are generated during the search process, as its strength is the capability of quickly searching the vicinity of a given solution.
Hybrid metaheuristics are proposed in almost 17% of the reviewed papers, the most common being the hybridization of GAs and local search procedures. For example, Zhang and Chiong [30] embed an ILS procedure within a multi-objective GA (moGA) to minimize and E in a JSP with speed-adjustable machines. The GA evolves the population of solutions through the usual genetic operators, and at each generation, the ILS attempts to improve the generation’s best solutions by searching for better ones in their neighborhood using three different strategies. At each generation, the solutions are partitioned into a series of Pareto ranks, and then solutions in each rank are sorted. Let set B consist of the solutions in the top half, and let and be, respectively, the median values of and E of the solutions in set B. Set B is partitioned into four subsets, namely: , which consists of the solutions with at least as good as the median value and E worse than the median value (i.e., and ); , which consists of the solutions with and ; , which consists of the solutions with and ; and , which consists of the solutions with and . Then, the neighborhood of the solutions in subset (biased toward ) is explored through a heuristic in which the sequence of a pair of operations on a critical machine are swapped while their processing speeds remain unchanged. To attempt to improve the solutions in subset (biased toward E), the processing speed of non-critical operations is decreased. The two heuristics are applied sequentially to the solutions in subset , and no local search is applied to the solutions in subset . A similar idea is pursued in [16], which divides the population into four subsets, each associated with the best solutions regarding each of the four objective functions considered, and attempts to find better solutions in each subset by improving the corresponding objective. In [135], two local search strategies are used: one to change the operation starting time to cheaper periods (under EVP prices) and another to insert a random operation of a tardy job into an earlier position.
Similar strategies have been proposed in [8] for the FJSP, in [24,53] for the FJSP with speed-adjustable machines, and in [93] for the JSP with speed-adjustable machines. In all of them, a GA is used to find and rank feasible solutions and to evolve the populations. Then, at each generation, the neighborhood of the best solutions is searched for in an attempt to find better solutions. While [8] resorts to an SA algorithm that randomly selects an operation to be reinserted at a random position and randomly swaps the selected elements of two operations, [24] reassigns critical operations (operations of a last completed job) to machines that can process them sooner and slows down non-critical operations as long as the makespan remains unaffected; and [93] swaps two operations on a critical machine (a last finishing machine), increases the processing speed of a randomly selected critical operation, and decreases the processing speed of a randomly selected operation of a first complete job. A different strategy for hybridizing local search is proposed in [63], which hybridizes an ICA and a VNS algorithm. Since, in the problem they address, an energy upper limit is imposed, generating feasible solutions can be quite time consuming. Therefore, the ICA finds good solutions, while disregarding the energy upper limit (i.e., solutions with good makespan values that may be infeasible regarding the energy limit). The VNS is then used to search for solutions that comply with the energy upper limit, in the neighborhood of the set of non-dominated solutions.
Dai et al. [11] propose a different approach to hybridize a GA, a PSO, and an SA, as the PSO and the SA are used within and as a replacement for the genetic operators, respectively. The GA crossover operator uses the PSO information-sharing mechanism to generate offspring that inherit some genes from the best global solution and the remaining ones from the parents. The mutation operator is replaced by a simulated annealing algorithm. Other examples include hybridizing GA and PSO [10,74], PSO and SA [86], and GA and TS [95], among others.
5.4. Multi-Objective Algorithms
In single-objective optimization, we seek to find an optimal solution, and the superiority of a solution over other solutions is easily determined by comparing their objective function values. In contrast, in multi-objective optimization, we are looking for a set of solutions (rather than just one). These solutions define the best trade-offs between conflicting objectives. The goodness of a solution is determined by the concept of dominance. A solution dominates another solution if it is strictly better in at least one objective, and not worse in any of the remaining objectives. Ideally, we would like to find the Pareto-optimal set, that is, all solutions of the entire feasible decision space that are non-dominated. Usually, however, that is not possible. Thus, the objective becomes to find a set of diverse solutions that approximate the Pareto-optimal front, which is the boundary defined by the Pareto-optimal set.
From the 172 papers reviewed, 139 consider a multi-objective version of the problem tackled. The number of objective functions considered ranges from two to five. However, most papers consider either two or three. The most common multi-objective problem versions consider the minimization of the total energy consumption E and of the makespan (about 32% of the papers). Nevertheless, other combinations of objective functions have been considered. Table 2 reports the combinations of objective functions used in multi-objective approaches, as well as how many papers used each one (including only combinations used in three or more papers).

Table 2.
Number of papers considering multi-objective functions combining non-energy-related functions (Objother) with energy-related functions (ObjEE) (including only those considered in at least three papers).
Some of the objectives reported in Table 2 are used in just two or three papers, with each calculating them in a different way. Hence, readers wishing to find out more about how they are calculated are referred to those works: —machines workload [16,31,35], —rescheduling disruption [57,103], Q—quality and defective rate [19,22], and N—noise level [32,101,118]. The mathematical expressions for the other objectives are provided in Equations (5) to (9). (Here, only the new notation is defined; for the remaining notation, see Section 4.3).
where and are, respectively, the cost of machine m when processing operation j and when idle; is the operational cost of vehicle v; is the travel time required by job j; is the cost of the raw material required to produce job j; L is the set of human resources; is the cost associated with collaborator l; is the set of maintenance activities; and is the costs associated with maintenance activity a.
Over 94% of the solution approaches proposed for multi-objective EEJSPs are metaheuristic. The remaining ones propose game theory [12,136,137], simulation [28,138,139,140,141], multi-agent systems [17], constraint programming [142,143], MIP-based heuristics [144,145], and deep learning methods [124].
Over the years, many methods have been proposed to approximate the Pareto front. Some of these methods scalarize the objectives and obtain a single objective function by adding the objective functions, usually pre-multiplied by a weight. An optimal solution to this single-objective problem is Pareto optimal to the multi-objective problem. An approximation of the Pareto front is obtained by solving a series of single-objective problems, with different weights. Although such a strategy is simple and easy to implement, it does have some major drawbacks. On the one hand, it cannot be ensured that the chosen weights produce a Pareto-optimal solution in a desired region of the objective space. On the other hand, two different sets of weights may not produce two different Pareto-optimal solutions. Hence, a uniformly distributed set of Pareto-optimal solutions cannot be ensured. Additionally, if the objective space is non-convex, then some Pareto-optimal solutions will not be found.
Almost 36% of the proposed multi-objective (MO) metaheuristics use a scalarized objective function obtained by the sum, the weighted sum, or the normalized weighted sum of the original objective functions (e.g., [7,8,9,10,20,32,33,79,118]). Other methods of finding Pareto solutions that resort to single-objective problems include the analytical hierarchy process (AHP) method, in which the weights are determined by the decision maker [95], and the lexicographic method [15,71], in which the objectives are considered one at a time in the order of importance given by the decision maker. Thus, in the lexicographic method, the problem is solved for the most important objective, and then for the second most important objective, with an additional constraint imposing the previously attained value for the first objective, and so on, until all objectives have been considered or just one optimal solution exists.
Solution approaches considering all objectives simultaneously but independently have become the current trend, and in this regard, evolutionary algorithms have been taking the lead. This is not a surprise since they have the advantage of dealing with a set of possible solutions (the so-called population), which allows one to find several solutions of the Pareto-optimal set in a single “run” of the algorithm (instead of having to perform a series of separate runs). The most commonly proposed multi-objective evolutionary algorithms (MOEAs) are variants of the NSGA-II proposed in [146]. NSGA-II uses an explicit diversity-preserving strategy together with an elite-preservation strategy, which are implemented by: (i) classifying the solutions into a number of mutually exclusive equivalent non-dominated sets (NDS); (ii) determining the crowding distance (CD) of the solutions in each NDS, which is given by half of the perimeter of the enclosing cuboid with the nearest neighboring solutions in the same front; and (iii) selecting solutions by a crowding tournament, in which a solution wins if it has a better rank or a better crowding distance if they have the same rank. Some of the approaches proposed just rank the solutions, typically using the non-dominated sets (see, e.g., [18,31,93]); however, most approaches also use CD to sort the solutions with the same rank (see, e.g., [16,19,23,24,25,26,56,147]). Other metaheuristics resorting to NDS and CD include ICA [120], PSO [88], and GWO [148].
There are, however, other sorting mechanisms. For example, Deb and Jain [149] resort to the reference point direction (RPD), and May et al. [26] to the density estimator (Dens). In the RPD, solutions in the direction of a larger number of reference points (ideally provided by the decision maker) are better, while in the Dens, the goodness of the solutions is provided by the summation of the Euclidean distance between the solution and all other solutions with the same rank. The combination of NDS and RPD procedures is mainly used in NSGA-III (see, e.g., [35,101,119,150]) and in ICA [84,108].
Figure 8 summarizes the methods used to address multi-objective EEJSPs, as well as the mechanisms used to rank and sort solutions, when addressing all objectives independently but simultaneously.
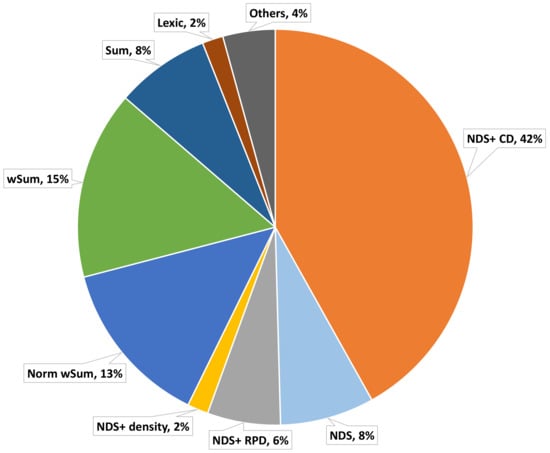
Figure 8.
Multi-objective solution methods: ranking and sorting mechanisms for evaluating solutions under multiple objectives and scalarization methods to convert the several objectives into a single one (Sum—summation, wSum—weighted sum, Norm wSum—normalized wSum, Lexic—lexicographic).
After finding a final set of solutions, the quality of the solutions has to be evaluated and, whenever possible, compared with the Pareto front. Although several performance metrics have been proposed over the years, the solutions to EEJSPs have rarely been evaluated or compared by resorting to such metrics. To the best of our knowledge, only 13 papers report such evaluations. The metrics used include the generational distance (GD) and inverted generational distance (IGD), which measure the convergence of the solutions to a reference Pareto front [11,104,105,111,148,150]; the hyper volume (HV), which measures the size of the dominated space according to some reference points [50,73,74,105,110]; and the spread, which evaluates the diversity and uniformity of the solutions [50,105,148,150]. One possible reason behind the very small number of papers reporting such metrics may be the lack of reference solutions. This problem can be obviated if researchers use the same problem instances in their computational experiments. The existence and availability of (benchmark) problem instances are discussed next.
6. Problem Instances and Data Sets
The quality of the solutions obtained by metaheuristic approaches can only be analyzed or inferred by comparing the solutions they found with either optimal solutions or the solutions found by other approaches. Optimal solutions are usually not available. A few mathematical models were proposed for EEJSPs; however, most were not solved. On the one hand, EEJSPs are NP-hard problems, and thus only small-sized instances may be solved to optimality. On the other hand, the multi-objective nature of EEJSPs increases problem complexity, as it requires solving the models several times in order to approximate the Pareto front.
Comparisons with the results of previous works can seldom be found. The main reasons for this are the incompatibility and unavailability of the data used for testing, since authors use problem instances that are either randomly generated, randomly adapted from instances of closely related problems, or specific case-studies. Additionally, authors do not typically make the problem instances they use publicly available. Hence, the comparison of a newly proposed (meta)heuristic with previously proposed ones requires the implementation of all of them, as well as performing computational experiments with all (meta)heuristics on the same set of problem instances. This is no easy task. First, some authors do not provide all details of the methods they propose. Second, since there are some differences in the definition of the addressed problems, the approaches would have to be adapted so that all could solve the same problem. Third, since no previous comparison between the proposed methods exists, there is no information on which one(s) to select (i.e., on the best performing ones). Finally, the computational burden quickly becomes prohibitive. Therefore, no comparisons are usually reported.
One simple step that can be taken to help remedy the lack of comparisons is to “force” authors to make the data of the instances they consider publicly available; fewer than half of the reviewed papers do so. Moreover, in addition to the value of the objective functions, authors should report the computational effort. Another important step would be to create a library of such problem instances, together with the best known solutions (schedule and value of the objective functions). This would be a manageable and relatively simple task if all authors contribute with the data and solutions of the instances used. We have started such a process and urge researchers to contribute.
We have created a web-library for the EEJSP (locate at https://fastmanufacturingproject.wordpress.com/eejsp-library) and have already uploaded some data sets that can be used as benchmark problem instances in future studies. In our selection, we consider the problem instances for which the full data set is provided either in the corresponding paper or in an online database. We strongly encourage authors to provide additional data sets and corresponding solutions, for example, by contacting us.
The problem instances being used in the literature include case studies, randomly generated instances, and instances adapting well-known benchmark problem instances previously proposed for other related problems. However, only a minority of the reviewed papers, 41 out the 172 reviewed, feature adapted benchmark instances. Several authors introduce and discuss specific case studies on problems that can be cast as energy-efficient (flexible) job shop problems. The problem instances associated with such studies involve the FJSP [10,19,56], the FJSP and tool allocation [7], the FJSP and WoS [13], the FJSP with TrT [11,18,20], the FJSP with LOP and TrS [89], the DS FJSP [106], and the JSP with TrT [116].
Random problem instances have been proposed for energy-efficient (flexible) job shop problems. Following, we list the problems they have been proposed for as well as the works proposing them: FJSP [32], FJSP including I/O machine status [55], FJSP with TrT [11], FJSP with TrS [90], FJSP considering DS [57], DS FJSP [14], JSP [60,118], JSP with TrT [64], and JSP and MaS [51].
Regarding adapted energy-efficient JSP instances, they have been adapted mainly from the JSP instances originally proposed by Adams et al. [151] (abz5~abz9), Fisher and Thompson [152] (ft06, ft10, and ft20), Lawrence [153] (la01~la40), and Applagate and Cook [52] (orb01~orb10). Different authors adapted them in different ways and by adding additional data, typically randomly generated, as in the following examples: energy consumption for each operation [70], energy consumption for each operation at different speed levels [30,33,50,80,114], energy consumption for each operation and for turn on/off actions [23,25,26], energy consumption for each operation and each maintenance activity and a due date for each job [105], and energy consumption for each operation at different speed levels and a due date for each job [30].
Finally, the FJSP instances commonly adapted are those originally proposed by Brandimarte [154] (mk01~15), Dauzere-Péres and Paulli [155] (dp1~18), Kacem et al. [156] (Kacem), and Hurink et al. [157] (Hurink). To adapt them, additional parameters have to be considered, as in the following examples: [22,24,31,84] generate energy consumption for each operation at different speed levels, [29] generates energy consumption for each operation and for turn on-off actions, [16] generates energy consumption for each operation and for transport tasks, [97,98] generate energy consumption for each operation and DMS data, and [15] generates energy consumption for each operation and workers’ capabilities data.
Table 3 summarizes the benchmark instances considered and already included in EEJSP Library. This table has six columns: the first one provides the paper reference; the second and third columns provide, respectively, the energy efficiency objective function (ObjEE) and additional objective function(s) if considered (Objother); the next two columns report the energy efficiency strategy (EE strategy) used (refer to Section 4.2) and the additional scheduling problems (Features) considered (refer to Section 4.5); lastly, the problem instances column provides information on the origin of the instances considered (original instance when adapted, “App” when based on a real-world application, and “Rnd Ins” when randomly generated).

Table 3.
Benchmark problem instances for EEJSPs.
As stated earlier, not many works can be found that compare the results they obtain with the results of previous works. Additionally, most of the works reporting comparisons do so for only some features, as the problem definitions and/or objective functions are not exactly the same. For example, Abedi et al. [105] compare their results with those of Essafi et al. [158] and Salido et al. [33]. However, there is no direct comparison between Pareto fronts with either of the two works, as they do not share the same combination of objective functions. Instead, the comparison addresses a single objective function at a time, with each work: the total weighted tardiness is compared with that of Essafi et al. [158], and the energy consumption is compared with that of Salido et al. [33]. As far as we know, the only exceptions are the works reported in [33,142,143]. The first two compare the Pareto fronts, regarding trade-offs between makespan and energy consumption, obtained by a moGA and a CP model for four sets of problem instances. The authors extend the previous work by incorporating a local search algorithm into the moGA, improving its performance [33].
7. Conclusions
Metaheuristics have been used to find high-quality solutions to a large number of complex problems in a wide range of application areas (e.g., manufacturing scheduling, molecular modeling, inventory allocation, project scheduling, maritime operations, network flows, and many others). The scientific community has shown them to be a viable, and often superior, alternative to more traditional (exact) methods, in particular when tackling combinatorial optimization problems. Moreover, metaheuristics are more flexible than more traditional (exact) methods, since they are problem independent, and thus can be adapted to fit the needs of almost any real-life optimization problem. Additionally, they can be used to find a “good enough” solution in a computation time that is “small enough”. However, metaheuristics are not able to ensure the optimality of the solutions they find. On the contrary, exact methods can theoretically ensure optimality if allowed to run long enough. Nevertheless, often they are not able to find an optimal solution in a reasonable amount of time, and sometimes not even a feasible one.
This work reviews metaheuristic approaches proposed, in the last decade, for the energy-efficient job shop scheduling problem and its variants (EEJSPs). EEJSPs are NP-hard as they are extensions of the JSP, which has been proven NP-hard. A further complexity associated with EEJSPs arises from the fact that energy efficiency is usually optimized along with other objective function(s), such as makespan, tardiness, production costs, and so on. Since frequently conflicting objective functions are considered, one no longer looks for an optimal solution, which may not even exist. Instead, we look for a set of solutions that defines the best trade-offs between the conflicting objectives (i.e., a set of non-dominated solutions). Metaheuristics are particularly suited to address this type of problem, as most of them evolve a set of candidate solutions, rather than a single solution.
Manufacturing systems often employ several resource types, such as workers, machines, and vehicles. In such systems, two or more resource types usually collaborate to perform the activities. Therefore, resources should be scheduled simultaneously. Although research on JSPs integrating more than one resource type has been reported in the literature, integrated EEJSPs are yet to be addressed. This is a very important avenue of research, since the impact of scheduling collaborative resources separately is even more relevant in EEJSPs. For example, consider a manufacturing environment in which the jobs need to be transported around the shop floor. In addition to the direct increase in energy consumption required by the transport vehicles, machines may have longer idle times as they may have to wait for the delivery of jobs, and vehicles may also have idle times as they may have to wait for the completion of operations, thus impacting not only productivity, resource utilization, completion time, and production costs, but also energy consumption. Other examples include preventive maintenance activities, which need to be scheduled at the same time as manufacturing activities.
Many technological developments have been achieved over the years. Regarding manufacturing systems, the most recent such developments have led to the existence of intelligent manufacturing systems—Industry 4.0. Industry 4.0, also called the Internet of manufacturing things, is closely tied with the digitalization of industrial processes and equipment, cyber-physical systems, and the capability of gathering and processing data and information in real time. Once the extracted data and information are transformed into useful knowledge by resorting to, for example, machine learning methods, it can be used to improve the efficiency and quality of the scheduling solutions. Future research is needed in at least two different directions, namely: (i) how to transform the data and information collected into knowledge and (ii) how to use the collected information and derived knowledge to improve the efficiency and quality of the scheduling solutions. Regarding the former, the main issues that require further research are the communication and cooperation of the different types of data sources, that is, how to handle the increasing variety of smart components and equipment and how to integrate the information coming from different sources in a consistent and homogeneous way. Regarding the latter, the information obtained and the knowledge derived can be used to increase scheduling efficiency and robustness. The better and more reliable information available can be used, on the one hand, to predict changes in the system (e.g., resource breakdowns, energy disruption, worker’s fatigue, etc.), and on the other hand, to adapt the existing schedules to cope with such changes.
One way of taking advantage of the information and produced knowledge (i.e., information on unexpected events and predictions) is to reschedule the activities ensuring feasibility, producing more robust and effective schedules. (The need for rescheduling can also come from considering the arrival of new jobs during the planning horizon.)
Another way of adapting to such events is to control the resources in real time, for example, adjusting the speed of some of the resources. Moreover, resource control in real time may also be used to improve energy efficiency, slowing down resources that would complete their tasks ahead of time or switching resources to a standby mode in the presence of increased idle times.
Another interesting direction is to directly address the uncertainty regarding, for example, processing times, energy supply, energy consumption, availability of resources, and so on. This involves the development of new optimization tools such as robust optimization, simheuristics, stochastic models, and fuzzy logic, among others. Robust optimization methods typically optimize the worst possible outcomes considering solutions that are feasible, regardless of data and uncertain parameters. Simheuristics add a simulation layer to the metaheuristics that allows the optimization component to deal with scenarios under uncertainty. Stochastic models optimize the problem in several stages based on the current known state of the system and correct the decisions at successive stages, once more reliable data becomes available. Fuzzy logic creates an approximation mechanism to incorporate the uncertainties into other optimization tools (e.g., exact methods and metaheuristics). Although these solution approaches are particularly relevant for EEJSPs, they have rarely been proposed.
The incorporation of new problem characteristics, such as the ones discussed above, leads to new problem versions that are even more complex. Hence, new faster and more robust approaches are of the utmost importance.
Almost all papers reviewed simultaneously consider economic and energy objective functions. Only a few consider the three pillars of sustainability (economic, environmental, and social). For example, three papers consider the makespan (economic objective), total energy consumption (energy objective), and noise (social objective). Given the small presence of the social pillar in the papers reviewed and the growing importance of the subject, research on job shop problems that also includes social objectives is identified as a main future research topic.
Despite the fact that the number of studies solving EEJSPs is growing fast, specifically in the past three years, the number of cross-references is quite low. According to the data extracted from Scopus® in March 2022, the H-index for EEJSP papers is 35; however, only 6 papers published in or after 2019 are among the top 35 most highly cited papers. This may be a sign that the EEJPs research community is not fully aware of the rich literature on EEJSPs, specifically with regard to work published in the most recent years.
Many papers are covered in this review, but it may miss some relevant and important studies. However, not all data are precisely recorded in the two databases used in this work. Additionally, we have disregarded studies that have been published in conference proceedings. Finally, some of the papers may use different terminology or may describe the problem and/or the solution approaches in a different way, and thus may not have been found through our searches.
Supplementary Materials
The following are available online at https://www.mdpi.com/article/10.3390/su14106264/s1.
Author Contributions
The work was shared as follows: J.M.R.C.F. contributed to formal analysis, investigation, and writing—original draft preparation; S.M.H. contributed with article conceptualization, methodology, validation, formal analysis, investigation, visualization, writing—original draft and editing; and D.B.M.M.F. contributed to conceptualization, validation, writing—review and editing, supervision, project administration, and funding acquisition. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by ERDF—European Regional Development Fund through the Operational Programme for Competitiveness and Internationalisation—COMPETE 2020 Programme, and by national funds through the Portuguese funding agency FCT—Fundação para a Ciência e a Tecnologia, within projects POCI-01-0145-FEDER-031821-PTDC/EGE-OGE/31821/2017 and POCI-01-0145-FEDER-031447-PTDC/EEI-AUT/31447/2017.
Data Availability Statement
The publications reviewed in this work and their classified data are available as a Supplementary Excel Spreadsheet.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ABC | Artificial bee colony |
| ABO | African buffalo optimization. |
| ACO | Ant colony optimization |
| AHP | Analytical hierarchy process |
| AMO | Animal migration optimization |
| BA | Bees algorithm |
| Bat | Bat optimization algorithm |
| BBO | Biogeography-based optimization |
| BOA | Bacterial foraging optimization algorithm |
| BS | Batch scheduling |
| BSA | Backtracking search algorithm |
| Makespan | |
| CD | Crowding distance |
| CP | Constraint programming |
| CSO | Cat swarm optimization |
| Total completion time of the jobs | |
| Customer satisfaction | |
| DEA | Differential evolution algorithm |
| Dens | Density estimator |
| DMS | Distributed manufacturing scheduling |
| DP | Dynamic programming |
| DS | Dynamic sheduling |
| E | Energy consumption |
| EA | Evolutionary algorithm |
| Energy cost | |
| EDA | Estimation of distribution algorithm |
| EEJSP | Energy-efficient job shop scheduling problem |
| EMA | Electromagnetism-like mechanism algorithm |
| EVP | Energy variable price |
| FA | Firefly algorithm |
| FFO | Fruit fly optimization |
| FJSP | Flexible job shop scheduling problem |
| GA | Genetic algorithm |
| GD | Generational distance |
| GEP | Gene expression programming |
| GP | Genetic programming |
| GRASP | Greedy randomized adaptive search procedure |
| GSO | Glow-worm swarm optimization |
| GWO | Grey wolf optimization |
| HSA | Harmony search algorithm |
| HV | Hyper volume |
| I/O | On/off |
| ICA | Imperialist competitive algorithm |
| Idle time energy consumption | |
| IGD | Inverted generational distance |
| ILS | Iterated local search |
| Indirect energy consumption | |
| IoMT | Internet of manufacturing things |
| JA | Jaya algorithm |
| JPP | Job process planning |
| JSP | Job shop schedulin problem |
| Labour cost | |
| Lexic | Lexicographic |
| Learn | Learning methods |
| LOP | Layout optimization problem |
| MA | Memetic algorithm |
| MaS | Maintenance scheduling |
| MBO | Migrating birds optimization |
| MILP | Mixed-integer linear programming |
| MIP | Mixed integer programming |
| Total machine workload | |
| Mean machine workload | |
| Maximum machine workload | |
| moEA | Multi-objective EA |
| moGA | Multi-objective GA |
| moPSO | Multi-objective PSO |
| MS | Machine speed |
| N | Noise |
| NDS | Non-dominated sets |
| NPA | Nested partitions algorithm |
| NSGAII | Non-dominated sorting GA II |
| P | Processing energy consumption |
| Total production cost | |
| Peak power consumption | |
| PSO | Particle swarm optimization |
| Q | Quality |
| QEA | Quantum evolution algorithm |
| RD | Rescheduling disruptions |
| Reliability | |
| Raw material consumption | |
| RPD | Reference point direction |
| S | Setup energy consumption |
| SA | Simulated annealing |
| SDST | Sequence-dependent setup time |
| Simul | Simulation |
| SPEAII | Strength Pareto evolutionary algorithm II |
| Sum | Summation of the objective functions |
| wSum | Summation of weighted objective functions |
| Norm wSum | Summation of weighted normalized objective functions |
| SFLA | Shuffled frog-leaping algorithm |
| T | Total tardiness |
| Mean tardiness | |
| Total carbon emission | |
| Transportation energy consumption | |
| Cost of total tardiness | |
| Total tardiness and earliness | |
| Maximum tardiness | |
| TrT | Transport Time |
| TrS | Transport scheduling |
| TS | Tabu search |
| Total weighted tardiness | |
| Total weighted tardiness and earliness | |
| VNS | Variable neighborhood search |
| Work in progress | |
| WOA | Whale optimization algorithm |
| WoS | Worker scheduling |
| WWO | Water wave optimization |
Appendix A

Table A1.
Classification of the papers cited.
Table A1.
Classification of the papers cited.
| Ref | Floor | ObjEE | P | Id | S | T | In | Objother | MO App | Sol App | EE Strategy | Features |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2022 | ||||||||||||
| [92] | FJSP | E | ✓ | ✓ | ✓ | ✓ | wSum | Learn+GP | TrS; DS | |||
| [51] | JSP | ✓ | ; | NDS+ CD | NSGAII+Simul | MS | MaS | |||||
| [60] | JSP | ✓ | ✓ | ✓ | ✓ | FA | EVP; I/O | |||||
| [55] | FJSP | E | ✓ | ✓ | ✓ | ✓ | GEP | I/O | ||||
| [75] | FJSP | E | ✓ | ✓ | ✓ | ✓ | ; | EMA | ||||
| [76] | FJSP | E | ✓ | ✓ | ✓ | ✓ | AMO | |||||
| [53] | FJSP | E | ✓ | ✓ | ✓ | NDS+ CD | NSGAII | MS | ||||
| [124] | FJSP | ✓ | ✓ | ; | Ensemble deep forest | DS | ||||||
| [138] | JSP | E | ✓ | ✓ | ; | Norm wSum | Simul | DS | ||||
| [104] | JSP | E | ✓ | ✓ | ; T | NDS | moGA | |||||
| [125] | JSP | E | ✓ | NDS+ CD | NSGAII | |||||||
| 2021 | ||||||||||||
| [50] | JSP | E | ✓ | ✓ | ✓ | ; T | Fuzzy RPD | GA | MS | SDST | ||
| [150] | FJSP | ✓ | ✓ | ; | NDS+ RPD | NSGAIII | ||||||
| [89] | FJSP | E | ✓ | ✓ | ✓ | ✓ | ✓ | NDS+ CD | NSGAII | LOP; TrS | ||
| [88] | FJSP | E; | ✓ | ✓ | NDS+ CD | moPSO | TrS | |||||
| [94] | FJSP | E | ✓ | ✓ | ✓ | EDA+VNS | DMS; TrS | |||||
| [87] | FJSP | E | ✓ | ✓ | NDS+ CD | GA+DEA | MaS; TrS | |||||
| [120] | FJSP | E | ✓ | ✓ | ✓ | ; N | NDS+ CD | ICA | WoS; TrT | |||
| [95] | FJSP | ✓ | ✓ | ✓ | ; ; Q | Fuzzy AHP | GA+TS | DMS; TrT | ||||
| [59] | JSP | E | ✓ | ✓ | ; | NDS+ RPD | NSGAIII | I/O | ||||
| [81] | JSP | E | ✓ | ✓ | NDS+ CD | MA | MS | |||||
| [112] | FJSP | ✓ | ; | NDS+ CD | NSGAII+QEA | |||||||
| [97] | FJSP | ✓ | ✓ | ✓ | ✓ | ; ; | NDS+ Dens | moGA | DMS; TrT; SDST | |||
| [106] | FJSP | ✓ | ✓ | NDS+ CD | NSGAII | DS | ||||||
| [109] | FJSP | E | ✓ | ✓ | ; | NDS+ CD | NSGAII | MS | ||||
| [110] | JSP | E | ✓ | ✓ | ✓ | ; T; | Fuzzy RPD | moEA | MS | WoS | ||
| [135] | JSP | ✓ | NDS+ CD | NSGAII | EVP | |||||||
| [84] | FJSP | E | ✓ | ✓ | ✓ | ✓ | ; T | NDS | ICA | MS | SDST; TrT | |
| [119] | FJSP | E | ✓ | ✓ | ; | NDS+ RPD | NSGAIII | WoS | ||||
| [83] | FJSP | E | ✓ | ✓ | , | NDS+ CD | NSGA-II+VNS | TrT | ||||
| [85] | FJSP | E | ✓ | ✓ | ✓ | ✓ | NDS+ CD | NSGA-II+LS | TrT | |||
| [90] | FJSP | E | ✓ | ✓ | wSum | SA | TrS | |||||
| [67] | JSP | ✓ | MIP | MS | ||||||||
| [77] | FJSP | ✓ | ✓ | ✓ | ✓ | , T | NDS+ CD | NSGA-II | JPP | |||
| [91] | JSP | E | ✓ | ✓ | ✓ | NDS | GWO | TrS | ||||
| [117] | FJSP | E | ✓ | ; | NDS+ CD | NSGA-II | ||||||
| [74] | FJSP | E | ✓ | ✓ | ✓ | ✓ | NDS | PSO+GA | ||||
| [107] | FJSP | E | ✓ | ✓ | NDS+ CD | GP | DS | |||||
| [137] | FJSP | E | ✓ | ✓ | ✓ | , | Game theory | DS; DMS | ||||
| [140] | JSP | E | ✓ | ✓ | ; | Simul | DS; MaS; SDST | |||||
| 2020 | ||||||||||||
| [93] | JSP | E | ✓ | ✓ | NDS | moEA | MS | DMS | ||||
| [105] | JSP | E | ✓ | NDS+ CD | MA | MS | MaS | |||||
| [98] | FJSP | E | ✓ | ✓ | ; | NDS+ CD | NSGAII | DMS; TrT | ||||
| [103] | JSP | ✓ | T; | Norm wSum | GA | MS | DS | |||||
| [57] | FJSP | E | ✓ | ✓ | ✓ | ; | NDS+ CD | BSA | I/O | DS | ||
| [123] | FJSP | E | ✓ | ✓ | wSum | PSO | DS | |||||
| [86] | FJSP | ✓ | ✓ | Sum | PSO+LS; PSO+SA | LOP; TrT | ||||||
| [58] | FJSP | E | ✓ | ✓ | NDS+ CD | NSGAII | I/O | DS | ||||
| [73] | FJSP | E | ✓ | ✓ | ✓ | ✓ | ✓ | ; T; | NDS+ CD | NSGAII | MaS; TrT | |
| [111] | FJSP | ✓ | ✓ | ; | NDS+ CD | MA | WoS | |||||
| [70] | JSP | ✓ | NDS+ CD | NSGAII | ||||||||
| [78] | FJSP | E | ✓ | ✓ | ✓ | ✓ | MBO | WoS | ||||
| [96] | FJSP | E | ✓ | ✓ | ✓ | SFLA | DMS | |||||
| [136] | FJSP | E | ✓ | ✓ | ✓ | ; | wSum | Game theory | DS; JPP | |||
| [61] | FJSP | ✓ | ✓ | ✓ | ; | NDS+ CD | ABC | MS; I/O | ||||
| [127] | FJSP | E | ✓ | ✓ | ✓ | ; | GA+AIA | |||||
| [126] | JSP | E | ✓ | NDS+ CD | NSGAII | |||||||
| 2019 | ||||||||||||
| [11] | FJSP | E | ✓ | ✓ | ✓ | ✓ | NDS+ CD | GA+SA+PSO | TrT | |||
| [63] | FJSP | ✓ | ✓ | ; T | NDS+ CD | ICA+VNS | ||||||
| [20] | FJSP | E | ✓ | ✓ | wSum | GA+GSO | TrT | |||||
| [148] | FJSP | E | ✓ | ✓ | NDS+ CD | GWO | MS | |||||
| [35] | FJSP | ✓ | ✓ | ✓ | ; ; | NDS+ RPD | NSGAIII | I/O; EVP | WoS; SDST | |||
| [114] | JSP | ✓ | ✓ | Sum | WOA | MS | ||||||
| [115] | JSP | ✓ | Sum | Bat | MS | |||||||
| [101] | FJSP | ✓ | ✓ | ✓ | ; ; N | NDS+ CD | NSGAII; NSGAIII | |||||
| [108] | FJSP | E | ✓ | ✓ | ; ; | NDS+ RPD | ICA | |||||
| [100] | JSP | E | ✓ | ✓ | GEP | EVP | ||||||
| [116] | JSP | ✓ | ✓ | ; | Sum | GA | TrT | |||||
| [37] | FJSP | ✓ | ✓ | ; T | Fuzzy Sum | NSGAII | EVP | TrS; WoS | ||||
| [56] | FJSP | E | ✓ | ✓ | NDS+ CD | NSGAII | ||||||
| [27] | FJSP | E | ✓ | ✓ | ✓ | ✓ | MILP | I/O | ||||
| [68] | JSP | ✓ | ✓ | MILP | EVP | |||||||
| [141] | FJSP | E | ✓ | ✓ | ✓ | ; ; Q | Simul | DS | ||||
| [145] | JSP | ✓ | Sum | MILP | ||||||||
| 2018 | ||||||||||||
| [24] | FJSP | E | ✓ | ✓ | ✓ | ; | NDS+ CD | NSGAII | MS; I/O | |||
| [9] | FJSP | ✓ | ✓ | T | Norm wSum | GA | ||||||
| [10] | FJSP | E | ✓ | ✓ | wSum | GA; GA+PSO | ||||||
| [13] | FJSP | E | ✓ | ; | wSum rank | GA | WoS | |||||
| [80] | JSP | ✓ | ✓ | ✓ | WOA | MS | ||||||
| [82] | FJSP | ✓ | ✓ | CSO | ||||||||
| [102] | JSP | ✓ | T | Sum | GWO | |||||||
| [72] | JSP | E | ✓ | ✓ | GA | DS | ||||||
| [113] | JSP | ✓ | ✓ | ✓ | ; | Norm wSum | GA | |||||
| [38] | FJSP | ✓ | ✓ | ; Q | wSum | GA+ACO | EVP | TrS | ||||
| [17] | FJSP | E | ✓ | ✓ | ; | Multi-agent Sys | DS | |||||
| 2017 | ||||||||||||
| [8] | FJSP | ✓ | ; | Norm wSum | GA+SA | MaS | ||||||
| [31] | FJSP | E | ✓ | ✓ | NDS | SFLA | MS | |||||
| [32] | FJSP | E | ✓ | ; N | Norm wSum | GA | MS | |||||
| [29] | FJSP | E | ✓ | ✓ | ✓ | GEP | I/O | |||||
| [18] | FJSP | ✓ | ✓ | ✓ | NDS | FFO | TrT | |||||
| [79] | JSP | E | ✓ | Norm wSum | GA+LS | MS | DS | |||||
| [118] | JSP | E | ✓ | ; N | Norm wSum | GA | MS | |||||
| [71] | FJSP | E | ✓ | ✓ | ✓ | ; | Lexic | ILS | ||||
| [36] | FJSP | ✓ | ✓ | wSum | BBO | EVP; MS | ||||||
| [65] | JSP | ✓ | GRASP | |||||||||
| [64] | JSP | E | ✓ | ✓ | ✓ | ✓ | wSum | GA | TrT | |||
| [12] | FJSP | E | ✓ | ✓ | ✓ | ; | Game theory | DS; SDST | ||||
| [139] | JSP | E | ✓ | Simul | MS | |||||||
| [144] | JSP | ✓ | ✓ | - | MILP | MS | SDST; BS; Inventory | |||||
| 2016 | ||||||||||||
| [30] | JSP | E | ✓ | ✓ | NDS+ Dens | moGA+ILS | MS | |||||
| [33] | JSP | E | ✓ | Norm wSum | GA | MS | ||||||
| [25] | JSP | E | ✓ | ✓ | NDS+ CD | NSGAII | I/O | |||||
| [21] | JSP | E | ✓ | ; | GA | DS | ||||||
| [22] | FJSP | E | ✓ | ; ; Q; | BA | |||||||
| [147] | FJSP | E | ✓ | NDS+ CD | NSGAII | |||||||
| [66] | JSP | ✓ | MIP | |||||||||
| [142] | JSP | E | ✓ | wSum | CP | MS | ||||||
| [143] | JSP | E | ✓ | Norm wSum | GA | MS | ||||||
| 2015 | ||||||||||||
| [26] | JSP | E | ✓ | ✓ | Dom + Dens | moGA; SPEAII | I/O | |||||
| [7] | FJSP | E | ✓ | ✓ | Norm wSum | NPA | Tools | |||||
| [14] | FJSP | E | ✓ | ✓ | GA+SA | JPP | ||||||
| [15] | FJSP | ✓ | ✓ | Lexic | VNS | WoS | ||||||
| [16] | FJSP | ✓ | ✓ | ; ; | NDS+ CD | NSGAII | TrT | |||||
| [34] | JSP | ✓ | ✓ | ✓ | GA+SA | MS | ||||||
| [62] | FJSP | E | ✓ | ✓ | HSA | I/O | BS; SDST | |||||
| 2014 | ||||||||||||
| [23] | JSP | E | ✓ | NDS+ CD | NSGAII | |||||||
| [19] | FJSP | E | ✓ | ; ; Q | NDS+ CD | NSGAII | ||||||
| [69] | JSP | ✓ | ; | wSum | TS | |||||||
| [28] | FJSP | E | ✓ | ✓ | Simul | I/O | DS |
References
- U.S. Energy Information Administration. International Energy Outlook 2021; EIA: Washington, DC, USA, 2021.
- Para, J.; Del Ser, J.; Nebro, A.J. Energy-Aware Multi-Objective Job Shop Scheduling Optimization with Metaheuristics in Manufacturing Industries: A Critical Survey, Results, and Perspectives. Appl. Sci. 2022, 12, 1491. [Google Scholar] [CrossRef]
- Bansch, K.; Busse, J.; Meisel, F.; Rieck, J.; Scholz, S.; Volling, T.; Wichmann, M.G. Energy-aware decision support models in production environments: A systematic literature review. Comput. Ind. Eng. 2021, 159, 107456. [Google Scholar] [CrossRef]
- Gao, K.; Huang, Y.; Sadollah, A.; Wang, L. A review of energy-efficient scheduling in intelligent production systems. Complex Intell. Syst. 2020, 6, 237–249. [Google Scholar] [CrossRef]
- Akbar, M.; Irohara, T. Scheduling for sustainable manufacturing: A review. J. Clean. Prod. 2018, 205, 866–883. [Google Scholar] [CrossRef]
- Gahm, C.; Denz, F.; Dirr, M.; Tuma, A. Energy-efficient scheduling in manufacturing companies: A review and research framework. Eur. J. Oper. Res. 2016, 248, 744–757. [Google Scholar] [CrossRef]
- He, Y.; Li, Y.; Wu, T.; Sutherland, J.W. An energy-responsive optimization method for machine tool selection and operation sequence in flexible machining job shops. J. Clean. Prod. 2015, 87, 245–254. [Google Scholar] [CrossRef]
- Mokhtari, H.; Hasani, A. An energy-efficient multi-objective optimization for flexible job-shop scheduling problem. Comput. Chem. Eng. 2017, 104, 339–352. [Google Scholar] [CrossRef]
- Piroozfard, H.; Wong, K.Y.; Wong, W.P. Minimizing total carbon footprint and total late work criterion in flexible job shop scheduling by using an improved multi-objective genetic algorithm. Resour. Conserv. Recycl. 2018, 128, 267–283. [Google Scholar] [CrossRef]
- Wang, H.; Jiang, Z.; Wang, Y.; Zhang, H.; Wang, Y. A two-stage optimization method for energy-saving flexible job-shop scheduling based on energy dynamic characterization. J. Clean. Prod. 2018, 188, 575–588. [Google Scholar] [CrossRef]
- Dai, M.; Tang, D.; Giret, A.; Salido, M.A. Multi-objective optimization for energy-efficient flexible job shop scheduling problem with transportation constraints. Robot. Comput.-Integr. Manuf. 2019, 59, 143–157. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, J.; Liu, Y. Game theory based real-time multi-objective flexible job shop scheduling considering environmental impact. J. Clean. Prod. 2017, 167, 665–679. [Google Scholar] [CrossRef]
- Gong, G.; Deng, Q.; Gong, X.; Liu, W.; Ren, Q. A new double flexible job-shop scheduling problem integrating processing time, green production, and human factor indicators. J. Clean. Prod. 2018, 174, 560–576. [Google Scholar] [CrossRef]
- Dai, M.; Tang, D.; Xu, Y.; Li, W. Energy-aware integrated process planning and scheduling for job shops. J. Eng. Manuf. 2015, 229, 13–36. [Google Scholar] [CrossRef]
- Lei, D.; Guo, X. An effective neighborhood search for scheduling in dual-resource constrained interval job shop with environmental objective. Int. J. Prod. Econ. 2015, 159, 296–303. [Google Scholar] [CrossRef]
- Zhang, C.; Gu, P.; Jiang, P. Low-carbon scheduling and estimating for a flexible job shop based on carbon footprint and carbon efficiency of multi-job processing. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2015, 229, 328–342. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, Y.; Liu, Y.; Wu, N. Multiagent and bargaining-game-based real-time scheduling for internet of things-enabled flexible job shop. IEEE Internet Things J. 2018, 6, 2518–2531. [Google Scholar] [CrossRef]
- Liu, Q.; Zhan, M.; Chekem, F.O.; Shao, X.; Ying, B.; Sutherland, J.W. A hybrid fruit fly algorithm for solving flexible job-shop scheduling to reduce manufacturing carbon footprint. J. Clean. Prod. 2017, 168, 668–678. [Google Scholar] [CrossRef]
- Jiang, Z.; Le, Z.; E, M. Study on multi-objective flexible job-shop scheduling problem considering energy consumption. J. Ind. Eng. Manag. 2014, 7, 589–604. [Google Scholar] [CrossRef][Green Version]
- Liu, Z.; Guo, S.; Wang, L. Integrated green scheduling optimization of flexible job shop and crane transportation considering comprehensive energy consumption. J. Clean. Prod. 2019, 211, 765–786. [Google Scholar] [CrossRef]
- Zhang, L.; Li, X.; Gao, L.; Zhang, G. Dynamic rescheduling in FMS that is simultaneously considering energy consumption and schedule efficiency. Int. J. Adv. Manuf. Technol. 2016, 87, 1387–1399. [Google Scholar] [CrossRef]
- Xu, W.; Shao, L.; Yao, B.; Zhou, Z.; Pham, D.T. Perception data-driven optimization of manufacturing equipment service scheduling in sustainable manufacturing. J. Manuf. Syst. 2016, 41, 86–101. [Google Scholar] [CrossRef]
- Liu, Y.; Dong, H.; Lohse, N.; Petrovic, S.; Gindy, N. An investigation into minimising total energy consumption and total weighted tardiness in job shops. J. Clean. Prod. 2014, 65, 87–96. [Google Scholar] [CrossRef]
- Wu, X.; Sun, Y. A green scheduling algorithm for flexible job shop with energy-saving measures. J. Clean. Prod. 2018, 172, 3249–3264. [Google Scholar] [CrossRef]
- Liu, Y.; Dong, H.; Lohse, N.; Petrovic, S. A multi-objective genetic algorithm for optimisation of energy consumption and shop floor production performance. Int. J. Prod. Econ. 2016, 179, 259–272. [Google Scholar] [CrossRef]
- May, G.; Stahl, B.; Taisch, M.; Prabhu, V. Multi-objective genetic algorithm for energy-efficient job shop scheduling. Int. J. Prod. Res. 2015, 53, 7071–7089. [Google Scholar] [CrossRef]
- Meng, L.; Zhang, C.; Shao, X.; Ren, Y. MILP models for energy-aware flexible job shop scheduling problem. J. Clean. Prod. 2019, 210, 710–723. [Google Scholar] [CrossRef]
- Pach, C.; Berger, T.; Sallez, Y.; Bonte, T.; Adam, E.; Trentesaux, D. Reactive and energy-aware scheduling of flexible manufacturing systems using potential fields. Comput. Ind. 2014, 65, 434–448. [Google Scholar] [CrossRef]
- Zhang, L.; Tang, Q.; Wu, Z.; Wang, F. Mathematical modeling and evolutionary generation of rule sets for energy-efficient flexible job shops. Energy 2017, 138, 210–227. [Google Scholar] [CrossRef]
- Zhang, R.; Chiong, R. Solving the energy-efficient job shop scheduling problem: A multi-objective genetic algorithm with enhanced local search for minimizing the total weighted tardiness and total energy consumption. J. Clean. Prod. 2016, 112, 3361–3375. [Google Scholar] [CrossRef]
- Lei, D.; Zheng, Y.; Guo, X. A shuffled frog-leaping algorithm for flexible job shop scheduling with the consideration of energy consumption. Int. J. Prod. Res. 2017, 55, 3126–3140. [Google Scholar] [CrossRef]
- Yin, L.; Li, X.; Gao, L.; Lu, C.; Zhang, Z. A novel mathematical model and multi-objective method for the low-carbon flexible job shop scheduling problem. Sustain. Comput. Inform. Syst. 2017, 13, 15–30. [Google Scholar] [CrossRef]
- Salido, M.A.; Escamilla, J.; Giret, A.; Barber, F. A genetic algorithm for energy-efficiency in job-shop scheduling. Int. J. Adv. Manuf. Technol. 2016, 85, 1303–1314. [Google Scholar] [CrossRef]
- Tang, D.; Dai, M. Energy-efficient approach to minimizing the energy consumption in an extended job-shop scheduling problem. Chin. J. Mech. Eng. 2015, 28, 1048–1055. [Google Scholar] [CrossRef]
- Gong, X.; De Pessemier, T.; Martens, L.; Joseph, W. Energy-and labor-aware flexible job shop scheduling under dynamic electricity pricing: A many-objective optimization investigation. J. Clean. Prod. 2019, 209, 1078–1094. [Google Scholar] [CrossRef]
- Zhang, H.; Dai, Z.; Zhang, W.; Zhang, S.; Wang, Y.; Liu, R. A new energy-aware flexible job shop scheduling method using modified biogeography-based optimization. Math. Probl. Eng. 2017, 2017, 7249876. [Google Scholar] [CrossRef]
- Far, M.H.; Haleh, H.; Saghaei, A. A fuzzy bi-objective flexible cell scheduling optimization model under green and energy-efficient strategy using Pareto-based algorithms: SATPSPGA, SANRGA, and NSGA-II. Int. J. Adv. Manuf. Technol. 2019, 105, 3853–3879. [Google Scholar]
- Hemmati Far, M.; Haleh, H.; Saghaei, A. A flexible cell scheduling problem with automated guided vehicles and robots under energy-conscious policy. Sci. Iran. 2018, 25, 339–358. [Google Scholar] [CrossRef]
- Garey, M.R.; Johnson, D.S.; Sethi, R. The complexity of flowshop and jobshop scheduling. Math. Oper. Res. 1976, 1, 117–129. [Google Scholar] [CrossRef]
- Cui, H.; Zhou, K. Industrial power load scheduling considering demand response. J. Clean. Prod. 2018, 204, 447–460. [Google Scholar] [CrossRef]
- Weitzel, T.; Glock, C.H. Energy management for stationary electric energy storage systems: A systematic literature review. Eur. J. Oper. Res. 2018, 264, 582–606. [Google Scholar] [CrossRef]
- Rathor, S.K.; Saxena, D. Energy management system for smart grid: An overview and key issues. Int. J. Energy Res. 2020, 44, 4067–4109. [Google Scholar] [CrossRef]
- Le Hesran, C.; Ladier, A.L.; Botta-Genoulaz, V.; Laforest, V. Operations scheduling for waste minimization: A review. J. Clean. Prod. 2019, 206, 211–226. [Google Scholar] [CrossRef]
- Giret, A.; Trentesaux, D.; Prabhu, V. Sustainability in manufacturing operations scheduling: A state of the art review. J. Manuf. Syst. 2015, 37, 126–140. [Google Scholar] [CrossRef]
- Garwood, T.L.; Hughes, B.R.; Oates, M.R.; O’Connor, D.; Hughes, R. A review of energy simulation tools for the manufacturing sector. Renew. Sustain. Energy Rev. 2018, 81, 895–911. [Google Scholar] [CrossRef]
- Narciso, D.A.; Martins, F. Application of machine learning tools for energy efficiency in industry: A review. Energy Rep. 2020, 6, 1181–1199. [Google Scholar] [CrossRef]
- Renna, P.; Materi, S. A literature review of energy efficiency and sustainability in manufacturing systems. Appl. Sci. 2021, 11, 7366. [Google Scholar] [CrossRef]
- Waltersmann, L.; Kiemel, S.; Stuhlsatz, J.; Sauer, A.; Miehe, R. Artificial Intelligence Applications for Increasing Resource Efficiency in Manufacturing Companies—A Comprehensive Review. Sustainability 2021, 13, 6689. [Google Scholar] [CrossRef]
- Biel, K.; Glock, C.H. Systematic literature review of decision support models for energy-efficient production planning. Comput. Ind. Eng. 2016, 101, 243–259. [Google Scholar] [CrossRef]
- He, L.; Chiong, R.; Li, W.; Dhakal, S.; Cao, Y.; Zhang, Y. Multiobjective Optimization of Energy-efficient Job-Shop Scheduling with Dynamic Reference Point-based Fuzzy Relative Entropy. IEEE Trans. Ind. Inform. 2021, 18, 600–610. [Google Scholar] [CrossRef]
- Amelian, S.S.; Sajadi, S.M.; Navabakhsh, M.; Esmaelian, M. Multi-objective optimization for stochastic failure-prone job shop scheduling problem via hybrid of NSGA-II and simulation method. Expert Syst. 2022, 39, e12455. [Google Scholar] [CrossRef]
- Applagate, D.; Cook, W. A computational study of the job-shop scheduling instance. ORSA J. Comput. 1991, 3, 49–51. [Google Scholar]
- Wei, Z.; Liao, W.; Zhang, L. Hybrid energy-efficient scheduling measures for flexible job-shop problem with variable machining speeds. Expert Syst. Appl. 2022, 197, 116785. [Google Scholar] [CrossRef]
- Homayouni, S.M.; Fontes, D.B.M.M. A MILP Model for Energy-Efficient Job Shop Scheduling Problem and Transport Resources. In Advances in Production Management Systems. Artificial Intelligence for Sustainable and Resilient Production Systems. APMS 2021, Proceedings of the IFIP International Conference on Advances in Production Management Systems, Nantes, France, 5–9 September 2021; Springer: Cham, Switzerland, 2021; pp. 378–386. [Google Scholar]
- Rakovitis, N.; Li, D.; Zhang, N.; Li, J.; Zhang, L.; Xiao, X. Novel approach to energy-efficient flexible job-shop scheduling problems. Energy 2022, 238, 121773. [Google Scholar] [CrossRef]
- Zhang, Z.; Wu, L.; Peng, T.; Jia, S. An improved scheduling approach for minimizing total energy consumption and makespan in a flexible job shop environment. Sustainability 2019, 11, 179. [Google Scholar] [CrossRef]
- Caldeira, R.H.; Gnanavelbabu, A.; Vaidyanathan, T. An effective backtracking search algorithm for multi-objective flexible job shop scheduling considering new job arrivals and energy consumption. Comput. Ind. Eng. 2020, 149, 106863. [Google Scholar] [CrossRef]
- Li, Y.; He, Y.; Wang, Y.; Tao, F.; Sutherland, J.W. An optimization method for energy-conscious production in flexible machining job shops with dynamic job arrivals and machine breakdowns. J. Clean. Prod. 2020, 254, 120009. [Google Scholar] [CrossRef]
- Wei, H.; Li, S.; Quan, H.; Liu, D.; Rao, S.; Li, C.; Hu, J. Unified Multi-Objective Genetic Algorithm for Energy Efficient Job Shop Scheduling. IEEE Access 2021, 9, 54542–54557. [Google Scholar] [CrossRef]
- Xu, E.; Li, Y.; Liu, Y.; Du, J.; Gao, X. Energy saving scheduling strategy for job shop under TOU and tiered electricity price. Alex. Eng. J. 2022, 61, 459–467. [Google Scholar] [CrossRef]
- Li, Y.; Huang, W.; Wu, R.; Guo, K. An improved artificial bee colony algorithm for solving multi-objective low-carbon flexible job shop scheduling problem. Appl. Soft Comput. 2020, 95, 106544. [Google Scholar] [CrossRef]
- Garcia-Santiago, C.; Del Ser, J.; Upton, C.; Quilligan, F.; Gil-Lopez, S.; Salcedo-Sanz, S. A random-key encoded harmony search approach for energy-efficient production scheduling with shared resources. Eng. Optim. 2015, 47, 1481–1496. [Google Scholar] [CrossRef]
- Lei, D.; Li, M.; Wang, L. A two-phase meta-heuristic for multiobjective flexible job shop scheduling problem with total energy consumption threshold. IEEE Trans. Cybern. 2018, 49, 1097–1109. [Google Scholar] [CrossRef]
- Xu, J.; Wang, L. A feedback control method for addressing the production scheduling problem by considering energy consumption and makespan. Sustainability 2017, 9, 1185. [Google Scholar] [CrossRef]
- Kemmoe, S.; Lamy, D.; Tchernev, N. Job-shop like manufacturing system with variable power threshold and operations with power requirements. Int. J. Prod. Res. 2017, 55, 6011–6032. [Google Scholar] [CrossRef]
- Samukawa, T.; Suwa, H. An optimization of energy-efficiency in machining manufacturing systems based on a framework of multi-mode RCPSP. Int. J. Autom. Technol. 2016, 10, 985–992. [Google Scholar] [CrossRef]
- Carlucci, D.; Renna, P.; Materi, S. A Job-Shop Scheduling Decision-Making Model for Sustainable Production Planning with Power Constraint. IEEE Trans. Eng. Manag. 2021, 1–10. [Google Scholar] [CrossRef]
- Masmoudi, O.; Delorme, X.; Gianessi, P. Job-shop scheduling problem with energy consideration. Int. J. Prod. Econ. 2019, 216, 12–22. [Google Scholar] [CrossRef]
- Ichoua, S.; Pechmann, A. Production scheduling for sustainable manufacturing systems. Key Eng. Mater. 2014, 572, 235–238. [Google Scholar] [CrossRef]
- Gondran, M.; Kemmoe, S.; Lamy, D.; Tchernev, N. Bi-objective optimisation approaches to Job-shop problem with power requirements. Expert Syst. Appl. 2020, 162, 113753. [Google Scholar] [CrossRef]
- Plitsos, S.; Repoussis, P.P.; Mourtos, I.; Tarantilis, C.D. Energy-aware decision support for production scheduling. Decis. Support Syst. 2017, 93, 88–97. [Google Scholar] [CrossRef]
- Feng, Y.; Wang, Q.; Gao, Y.; Cheng, J.; Tan, J. Energy-efficient job-shop dynamic scheduling system based on the cyber-physical energy-monitoring system. IEEE Access 2018, 6, 52238–52247. [Google Scholar] [CrossRef]
- An, Y.; Chen, X.; Zhang, J.; Li, Y. A hybrid multi-objective evolutionary algorithm to integrate optimization of the production scheduling and imperfect cutting tool maintenance considering total energy consumption. J. Clean. Prod. 2020, 268, 121540. [Google Scholar] [CrossRef]
- Ren, W.; Wen, J.; Yan, Y.; Hu, Y.; Guan, Y.; Li, J. Multi-objective optimisation for energy-aware flexible job-shop scheduling problem with assembly operations. Int. J. Prod. Res. 2021, 59, 7216–7231. [Google Scholar] [CrossRef]
- Qu, M.; Zuo, Y.; Xiang, F.; Tao, F. An improved electromagnetism-like mechanism algorithm for energy-aware many-objective flexible job shop scheduling. Int. J. Adv. Manuf. Technol. 2022, 119, 4265–4275. [Google Scholar] [CrossRef]
- Jiang, T.; Zhu, H.; Liu, L.; Gong, Q. Energy-conscious flexible job shop scheduling problem considering transportation time and deterioration effect simultaneously. Sustain. Comput. Inform. Syst. 2022, 35, 100680. [Google Scholar] [CrossRef]
- Wen, X.; Wang, K.; Li, H.; Sun, H.; Wang, H.; Jin, L. A two-stage solution method based on NSGA-II for Green Multi-Objective integrated process planning and scheduling in a battery packaging machinery workshop. Swarm Evol. Comput. 2021, 61, 100820. [Google Scholar] [CrossRef]
- Li, H.; Zhu, H.; Jiang, T. Modified migrating birds optimization for energy-aware flexible job shop scheduling problem. Algorithms 2020, 13, 44. [Google Scholar] [CrossRef]
- Salido, M.A.; Escamilla, J.; Barber, F.; Giret, A. Rescheduling in job-shop problems for sustainable manufacturing systems. J. Clean. Prod. 2017, 162, S121–S132. [Google Scholar] [CrossRef]
- Jiang, T.; Zhang, C.; Zhu, H.; Gu, J.; Deng, G. Energy-efficient scheduling for a job shop using an improved whale optimization algorithm. Mathematics 2018, 6, 220. [Google Scholar] [CrossRef]
- Lu, C.; Zhang, B.; Gao, L.; Yi, J.; Mou, J. A Knowledge-Based Multiobjective Memetic Algorithm for Green Job Shop Scheduling with Variable Machining Speeds. IEEE Syst. J. 2021, 16, 844–855. [Google Scholar] [CrossRef]
- Jiang, T.; Deng, G. Optimizing the low-carbon flexible job shop scheduling problem considering energy consumption. IEEE Access 2018, 6, 46346–46355. [Google Scholar] [CrossRef]
- Han, Y.; Chen, X.; Xu, M.; An, Y.; Gu, F.; Ball, A.D. A multi-objective flexible job-shop cell scheduling problem with sequence-dependent family setup times and intercellular transportation by improved NSGA-II. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2021, 16, 844–855. [Google Scholar] [CrossRef]
- Li, M.; Lei, D. An imperialist competitive algorithm with feedback for energy-efficient flexible job shop scheduling with transportation and sequence-dependent setup times. Eng. Appl. Artif. Intell. 2021, 103, 104307. [Google Scholar] [CrossRef]
- Zhang, H.; Xu, G.; Pan, R.; Ge, H. A novel heuristic method for the energy-efficient flexible job-shop scheduling problem with sequence-dependent set-up and transportation time. Eng. Optim. 2021, 15, 1–22. [Google Scholar] [CrossRef]
- Ebrahimi, A.; Jeon, H.W.; Lee, S.; Wang, C. Minimizing total energy cost and tardiness penalty for a scheduling-layout problem in a flexible job shop system: A comparison of four metaheuristic algorithms. Comput. Ind. Eng. 2020, 141, 106295. [Google Scholar] [CrossRef]
- Wang, H.; Sheng, B.; Lu, Q.; Yin, X.; Zhao, F.; Lu, X.; Luo, R.; Fu, G. A novel multi-objective optimization algorithm for the integrated scheduling of flexible job shops considering preventive maintenance activities and transportation processes. Soft Comput. 2021, 25, 2863–2889. [Google Scholar] [CrossRef]
- Barak, S.; Moghdani, R.; Maghsoudlou, H. Energy-efficient multi-objective flexible manufacturing scheduling. J. Clean. Prod. 2021, 283, 124610. [Google Scholar] [CrossRef]
- Li, H.; Duan, J.; Zhang, Q. Multi-objective integrated scheduling optimization of semi-combined marine crankshaft structure production workshop for green manufacturing. Trans. Inst. Meas. Control 2021, 43, 579–596. [Google Scholar] [CrossRef]
- Li, J.Q.; Du, Y.; Gao, K.Z.; Duan, P.Y.; Gong, D.W.; Pan, Q.K.; Suganthan, P. A hybrid iterated greedy algorithm for a crane transportation flexible job shop problem. IEEE Trans. Autom. Sci. Eng. 2021, 1–18. [Google Scholar] [CrossRef]
- Zhou, B.; Lei, Y. Bi-objective grey wolf optimization algorithm combined Levy flight mechanism for the FMC green scheduling problem. Appl. Soft Comput. 2021, 111, 107717. [Google Scholar] [CrossRef]
- Li, Y.; Gu, W.; Yuan, M.; Tang, Y. Real-time data-driven dynamic scheduling for flexible job shop with insufficient transportation resources using hybrid deep Q network. Robot. Comput.-Integr. Manuf. 2022, 74, 102283. [Google Scholar] [CrossRef]
- Jiang, E.D.; Wang, L.; Peng, Z.P. Solving energy-efficient distributed job shop scheduling via multi-objective evolutionary algorithm with decomposition. Swarm Evol. Comput. 2020, 58, 100745. [Google Scholar] [CrossRef]
- Du, Y.; Li, J.q.; Luo, C.; Meng, L.l. A hybrid estimation of distribution algorithm for distributed flexible job shop scheduling with crane transportations. Swarm Evol. Comput. 2021, 62, 100861. [Google Scholar] [CrossRef]
- Xu, W.; Hu, Y.; Luo, W.; Wang, L.; Wu, R. A multi-objective scheduling method for distributed and flexible job shop based on hybrid genetic algorithm and tabu search considering operation outsourcing and carbon emission. Comput. Ind. Eng. 2021, 157, 107318. [Google Scholar] [CrossRef]
- Meng, L.; Ren, Y.; Zhang, B.; Li, J.Q.; Sang, H.; Zhang, C. MILP Modeling and Optimization of Energy-Efficient Distributed Flexible Job Shop Scheduling Problem. IEEE Access 2020, 8, 191191–191203. [Google Scholar] [CrossRef]
- Liu, Q.; Gui, Z.; Xiong, S.; Zhan, M. A principal component analysis dominance mechanism based many-objective scheduling optimization. Appl. Soft Comput. 2021, 113, 107931. [Google Scholar] [CrossRef]
- Luo, Q.; Deng, Q.; Gong, G.; Zhang, L.; Han, W.; Li, K. An efficient memetic algorithm for distributed flexible job shop scheduling problem with transfers. Expert Syst. Appl. 2020, 160, 113721. [Google Scholar] [CrossRef]
- Meng, L.; Zhang, C.; Zhang, B.; Ren, Y. Mathematical modeling and optimization of energy-conscious flexible job shop scheduling problem with worker flexibility. IEEE Access 2019, 7, 68043–68059. [Google Scholar] [CrossRef]
- Zhang, L.; Li, Z.; Królczyk, G.; Wu, D.; Tang, Q. Mathematical modeling and multi-attribute rule mining for energy efficient job-shop scheduling. J. Clean. Prod. 2019, 241, 118289. [Google Scholar] [CrossRef]
- Coca, G.; Castrillón, O.D.; Ruiz, S.; Mateo-Sanz, J.M.; Jiménez, L. Sustainable evaluation of environmental and occupational risks scheduling flexible job shop manufacturing systems. J. Clean. Prod. 2019, 209, 146–168. [Google Scholar] [CrossRef]
- Jiang, T.; Zhang, C.; Zhu, H.; Deng, G. Energy-efficient scheduling for a job shop using grey wolf optimization algorithm with double-searching mode. Math. Probl. Eng. 2018, 2018, 8574892. [Google Scholar] [CrossRef]
- Luo, J.; El Baz, D.; Xue, R.; Hu, J. Solving the dynamic energy aware job shop scheduling problem with the heterogeneous parallel genetic algorithm. Future Gener. Comput. Syst. 2020, 108, 119–134. [Google Scholar] [CrossRef]
- Pan, Z.; Lei, D.; Wang, L. A Bi-Population Evolutionary Algorithm with Feedback for Energy-Efficient Fuzzy Flexible Job Shop Scheduling. IEEE Trans. Syst. Man Cybern. Syst. 2021, 1–13. [Google Scholar] [CrossRef]
- Abedi, M.; Chiong, R.; Noman, N.; Zhang, R. A multi-population, multi-objective memetic algorithm for energy-efficient job-shop scheduling with deteriorating machines. Expert Syst. Appl. 2020, 157, 113348. [Google Scholar] [CrossRef]
- Ayyoubzadeh, B.; Ebrahimnejad, S.; Bashiri, M.; Baradaran, V.; Hosseini, S.M.H. Modelling and an improved NSGA-II algorithm for sustainable manufacturing systems with energy conservation under environmental uncertainties: A case study. Int. J. Sustain. Eng. 2021, 14, 255–279. [Google Scholar] [CrossRef]
- Xu, B.; Mei, Y.; Wang, Y.; Ji, Z.; Zhang, M. Genetic programming with delayed routing for multiobjective dynamic flexible job shop scheduling. Evol. Comput. 2021, 29, 75–105. [Google Scholar] [CrossRef]
- Li, M.; Lei, D.; Xiong, H. An imperialist competitive algorithm with the diversified operators for many-objective scheduling in flexible job shop. IEEE Access 2019, 7, 29553–29562. [Google Scholar] [CrossRef]
- Ahangar, N.K.; Khalili, M.; Tayebi, H. The Three-Objective Optimization Model of Flexible Workshop Scheduling Problem for Minimizing Work Completion Time, Work Delay Time, and Energy Consumption. Teh. Glas. 2021, 15, 76–83. [Google Scholar] [CrossRef]
- Li, W.; He, L.; Cao, Y. Many-Objective Evolutionary Algorithm with Reference Point-Based Fuzzy Correlation Entropy for Energy-Efficient Job Shop Scheduling with Limited Workers. IEEE Trans. Cybern. 2021, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Zhu, H.; Deng, Q.; Zhang, L.; Hu, X.; Lin, W. Low carbon flexible job shop scheduling problem considering worker learning using a memetic algorithm. Optim. Eng. 2020, 21, 1691–1716. [Google Scholar] [CrossRef]
- Ning, T.; Huang, Y. Low carbon emission management for flexible job shop scheduling: A study case in China. J. Ambient Intell. Humaniz. Comput. 2021. [Google Scholar] [CrossRef]
- Liao, W.; Wang, T. Promoting green and sustainability: A multi-objective optimization method for the job-shop scheduling problem. Sustainability 2018, 10, 4205. [Google Scholar] [CrossRef]
- Jiang, T.; Zhang, C.; Sun, Q.M. Green job shop scheduling problem with discrete whale optimization algorithm. IEEE Access 2019, 7, 43153–43166. [Google Scholar] [CrossRef]
- Lu, Y.; Jiang, T. Bi-population based discrete bat algorithm for the low-carbon job shop scheduling problem. IEEE Access 2019, 7, 14513–14522. [Google Scholar] [CrossRef]
- Liao, W.; Wang, T. A Novel Collaborative Optimization Model for Job Shop Production–Delivery Considering Time Window and Carbon Emission. Sustainability 2019, 11, 2781. [Google Scholar] [CrossRef]
- Sui, Z.; Li, X.; Yang, J.; Liu, J. Data-driven fault-aware multi-objective optimization for flexible job-shop scheduling problem. In Artificial Intelligence in China; Springer: Berlin/Heidelberg, Germany, 2021; pp. 261–269. [Google Scholar]
- Yin, L.; Li, X.; Gao, L.; Lu, C.; Zhang, Z. Energy-efficient job shop scheduling problem with variable spindle speed using a novel multi-objective algorithm. Adv. Mech. Eng. 2017, 9, 1687814017695959. [Google Scholar] [CrossRef]
- Hongyu, L.; Xiuli, W. A survival duration-guided NSGA-III for sustainable flexible job shop scheduling problem considering dual resources. IET Collab. Intell. Manuf. 2021, 3, 119–130. [Google Scholar] [CrossRef]
- Peng, Z.; Zhang, H.; Tang, H.; Feng, Y.; Yin, W. Research on flexible job-shop scheduling problem in green sustainable manufacturing based on learning effect. J. Intell. Manuf. 2021, 1–22. [Google Scholar] [CrossRef]
- Lu, C.; Gao, L.; Gong, W.; Hu, C.; Yan, X.; Li, X. Sustainable scheduling of distributed permutation flow-shop with non-identical factory using a knowledge-based multi-objective memetic optimization algorithm. Swarm Evol. Comput. 2021, 60, 100803. [Google Scholar] [CrossRef]
- Fathollahi-Fard, A.M.; Woodward, L.; Akhrif, O. Sustainable distributed permutation flow-shop scheduling model based on a triple bottom line concept. J. Ind. Inf. Integr. 2021, 24, 100233. [Google Scholar] [CrossRef]
- Nouiri, M.; Bekrar, A.; Trentesaux, D. An energy-efficient scheduling and rescheduling method for production and logistics systems. Int. J. Prod. Res. 2020, 58, 3263–3283. [Google Scholar] [CrossRef]
- Zhou, G.; Chen, Z.; Zhang, C.; Chang, F. An adaptive ensemble deep forest based dynamic scheduling strategy for low carbon flexible job shop under recessive disturbance. J. Clean. Prod. 2022, 337, 130541. [Google Scholar] [CrossRef]
- Afsar, S.; Palacios, J.J.; Puente, J.; Vela, C.R.; González-Rodríguez, I. Multi-objective enhanced memetic algorithm for green job shop scheduling with uncertain times. Swarm Evol. Comput. 2022, 68, 101016. [Google Scholar] [CrossRef]
- González-Rodríguez, I.; Puente, J.; Palacios, J.J.; Vela, C.R. Multi-objective evolutionary algorithm for solving energy-aware fuzzy job shop problems. Soft Comput. 2020, 24, 16291–16302. [Google Scholar] [CrossRef]
- Shi, D.; Zhang, B.; Li, Y. A multi-objective flexible job-shop scheduling model based on fuzzy theory and immune genetic algorithm. Int. J. Simul. Model. 2020, 19, 123–133. [Google Scholar] [CrossRef]
- Yuan, G.; Yang, Y.; Tian, G.; Fathollahi-Fard, A.M. Capacitated multi-objective disassembly scheduling with fuzzy processing time via a fruit fly optimization algorithm. Environ. Sci. Pollut. Res. 2022. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Lourenço, H.R.; Martin, O.C.; Stützle, T. Iterated local search. In Handbook of Metaheuristics; Springer: Berlin/Heidelberg, Germany, 2003; pp. 320–353. [Google Scholar]
- Mladenović, N.; Hansen, P. Variable neighborhood search. Comput. Oper. Res. 1997, 24, 1097–1100. [Google Scholar] [CrossRef]
- Glover, F. Tabu search—Part I. ORSA J. Comput. 1989, 1, 190–206. [Google Scholar] [CrossRef]
- Goldberg, D.E.; Holland, J.H. Genetic algorithms and machine learning. In Proceedings of the 6th Annual Conference on Computational Learning Theory, Santa Cruz, CA, USA, 26–28 July 1988. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Kurniawan, B.; Song, W.; Weng, W.; Fujimura, S. Distributed-elite local search based on a genetic algorithm for bi-objective job-shop scheduling under time-of-use tariffs. Evol. Intell. 2021, 14, 1581–1595. [Google Scholar] [CrossRef]
- Wang, J.; Yang, J.; Zhang, Y.; Ren, S.; Liu, Y. Infinitely repeated game based real-time scheduling for low-carbon flexible job shop considering multi-time periods. J. Clean. Prod. 2020, 247, 119093. [Google Scholar] [CrossRef]
- Wang, J.; Liu, Y.; Ren, S.; Wang, C.; Wang, W. Evolutionary game based real-time scheduling for energy-efficient distributed and flexible job shop. J. Clean. Prod. 2021, 293, 126093. [Google Scholar] [CrossRef]
- Cai, L.; Li, W.; Luo, Y.; He, L. Real-time scheduling simulation optimisation of job shop in a production-logistics collaborative environment. Int. J. Prod. Res. 2022. [Google Scholar] [CrossRef]
- Raileanu, S.; Anton, F.; Iatan, A.; Borangiu, T.; Anton, S.; Morariu, O. Resource scheduling based on energy consumption for sustainable manufacturing. J. Intell. Manuf. 2017, 28, 1519–1530. [Google Scholar] [CrossRef]
- Gupta, S.; Jain, A. Assessing the effect of reliability-based maintenance approach in job shop scheduling with setup time and energy consideration using simulation: A simulation study. Smart Sci. 2021, 9, 283–304. [Google Scholar] [CrossRef]
- Wang, H. Manufacturing workshop multi-objective dynamic scheduling problem and model establishment. Acad. J. Manuf. Eng. 2019, 17, 92–97. [Google Scholar]
- Salido, M.A.; Escamilla, J.; Barber, F.; Giret, A.; Tang, D.; Dai, M. Energy efficiency, robustness, and makespan optimality in job-shop scheduling problems. Artif. Intell. Eng. Des. Anal. Manuf. 2016, 30, 300–312. [Google Scholar] [CrossRef]
- Escamilla, J.; Salido, M.A.; Giret, A.; Barber, F. A metaheuristic technique for energy-efficiency in job-shop scheduling. Knowl. Eng. Rev. 2016, 31, 475–485. [Google Scholar] [CrossRef]
- Giglio, D.; Paolucci, M.; Roshani, A. Integrated lot sizing and energy-efficient job shop scheduling problem in manufacturing/remanufacturing systems. J. Clean. Prod. 2017, 148, 624–641. [Google Scholar] [CrossRef]
- Hassani, Z.I.M.; Barkany, A.E.; Abbassi, I.E.; Jabri, A.; Darcherif, A.M. New model of planning and scheduling for job-shop production system with energy consideration. Manag. Prod. Eng. Rev. 2019, 10, 89–97. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Yang, X.; Zeng, Z.; Wang, R.; Sun, X. Bi-objective flexible job-shop scheduling problem considering energy consumption under stochastic processing times. PLoS ONE 2016, 11, e0167427. [Google Scholar] [CrossRef]
- Luo, S.; Zhang, L.; Fan, Y. Energy-efficient scheduling for multi-objective flexible job shops with variable processing speeds by grey wolf optimization. J. Clean. Prod. 2019, 234, 1365–1384. [Google Scholar] [CrossRef]
- Deb, K.; Jain, H. An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, part I: Solving problems with box constraints. IEEE Trans. Evol. Comput. 2013, 18, 577–601. [Google Scholar] [CrossRef]
- Sun, X.; Wang, Y.; Kang, H.; Shen, Y.; Chen, Q.; Wang, D. Modified Multi-Crossover Operator NSGA-III for Solving Low Carbon Flexible Job Shop Scheduling Problem. Processes 2021, 9, 62. [Google Scholar] [CrossRef]
- Adams, J.; Balas, E.; Zawack, D. The shifting bottleneck procedure for job shop scheduling. Manag. Sci. 1988, 34, 391–401. [Google Scholar] [CrossRef]
- Fisher, H.; Thompson, G.L. Probabilistic learning combinations of local job-shop scheduling rules. In Industrial Scheduling; Prentice Hall: Hoboken, NJ, USA, 1963; pp. 225–251. [Google Scholar]
- Lawrence, S. Resouce Constrained Project Scheduling: An Experimental Investigation of Heuristic Scheduling Techniques; Supplement; Graduate School of Industrial Administration, Carnegie-Mellon University: Pittsburgh, PA, USA, 1984. [Google Scholar]
- Brandimarte, P. Routing and scheduling in a flexible job shop by tabu search. Ann. Oper. Res. 1993, 41, 157–183. [Google Scholar] [CrossRef]
- Dauzère-Pérès, S.; Paulli, J. An integrated approach for modeling and solving the general multiprocessor job-shop scheduling problem using tabu search. Ann. Oper. Res. 1997, 70, 281–306. [Google Scholar] [CrossRef]
- Kacem, I.; Hammadi, S.; Borne, P. Approach by localization and multiobjective evolutionary optimization for flexible job-shop scheduling problems. IEEE Trans. Syst. Man Cybern. Part C Appl. Rev. 2002, 32, 1–13. [Google Scholar] [CrossRef]
- Hurink, J.; Jurisch, B.; Thole, M. Tabu search for the job-shop scheduling problem with multi-purpose machines. Oper.-Res.-Spektrum 1994, 15, 205–215. [Google Scholar] [CrossRef]
- Essafi, I.; Mati, Y.; Dauzère-Pérès, S. A genetic local search algorithm for minimizing total weighted tardiness in the job-shop scheduling problem. Comput. Oper. Res. 2008, 35, 2599–2616. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).