Safety Risk Assessment of Air Traffic Control System Based on the Game Theory and the Cloud Matter Element Analysis

Abstract

With the ever-increasing demand for air traffic over the years, safety risk assessment has become significant in maintaining the operational safety of the air transport system for long-term development towards sustainability. This paper conducts a safety risk assessment of the air traffic control (ATC) system based on game theory and cloud matter element analysis. The safety risk of the ATC system is evaluated from four aspects, including human, machine, environment, and management. The Nash equilibrium is introduced from game theory to weigh the indicators. The cloud matter element assessment adopts the cloud model from fuzzy sets and probability theory to replace the certain value in conventional matter element theory, which takes the randomness, ambiguity, and incompatibility of the indicators into consideration. In this sense, the safety risk level of the ATC system can be evaluated by calculating the correlation degree of the standard cloud matter element between the indicators and the risks. This paper expands the research scope by introducing and combing game theory and cloud matter element analysis. Furthermore, the applicability and the robustness of the method are examined with a case study of the ATC system, which enriches the existing literature and points out the direction for future work.

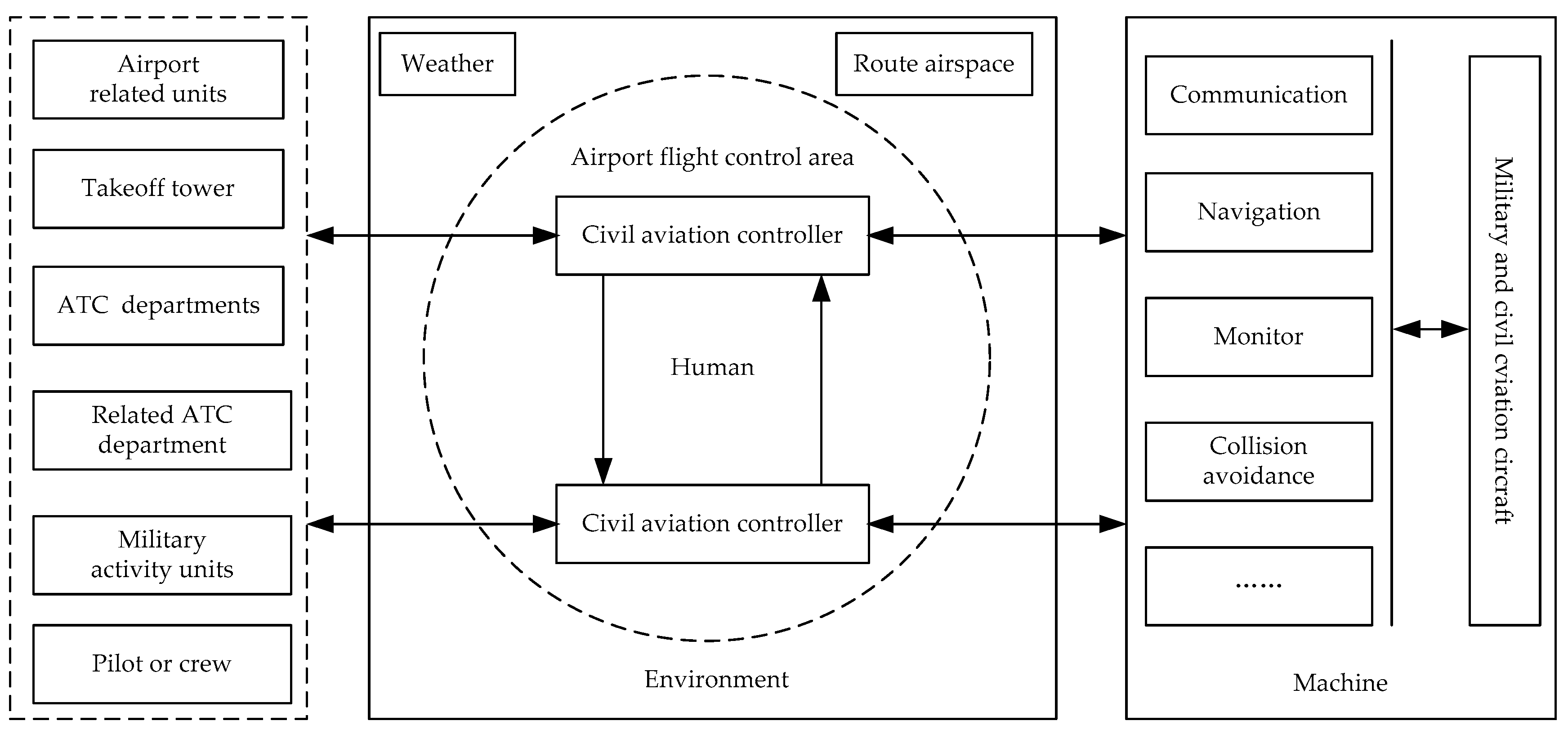
1. Introduction

Operational safety has always been pursued by the air transport industry as one of its primary goals towards development and sustainability. Although the air traffic control (ATC) system guides aircrafts’ daily operation, it also accompanies the safety of the air transport industry [1]. Moreover, it has been found that skill-based errors (e.g., memory lapses and attention failures) made by air traffic controllers lead to incidents and accidents in the air transport industry [2].

The International Civil Aviation Organization (ICAO) claims that the global air traffic demand will continue to grow in the long run. Therefore, the ever-increasing number of flights will impose more pressure on air traffic flow, which will further congest the airspace and lead to an ultra-high-density operational status. Meanwhile, the workloads of air traffic controllers would increase simultaneously following the growing demand for air traffic [3]. Since the daily operation of air traffic will be more complicated than ever, the ATC system is required to take the initiative and deal with the upcoming pressure on the safety risks. To this end, the ICAO stresses the cruciality of implementing a safety management system (SMS) in the units that provide ATC services [4]. Furthermore, the ICAO has released Annex 19 Safety Management to improve the safety management level worldwide [5]. Although those ICAO publications provide a roadmap for member states to enhance their air traffic control systematically, they also raise the question of how to measure and assess the safety risk level properly in a constantly changing industry.

The safety risk level assessment identifies the weaknesses in the ATC system, reflects the operational status of the system, and highlights future work for improvement. Subsequently, it has become an essential part of the safety management system.

Attention has been found to improve the safety risk level of the ATC system toward the sustainable and safe development of air transportation [6]. Precisely, Friedman and Carterette proposed the concept of the SHELL model, using software, hardware, environment, and liveware to clarify the scope of human factors in the aviation industry [7]. In accordance with the SHELL model, Hawkins analyzed the human factors in the air transport field to gain insights into the relationships between the aviation system and the human component [8]. Ternov and Akselsson conducted disturbance effect barrier (DEB) analysis to identify weaknesses that could lead to insufficient protection in the ATC system [9]. Leveson proposed an accident cause model based on the System-Theoretic Accident Model and Processes (STAMP), which analyzed the risk in the ATC system and expanded the current accident causality [10]. Subotie et al. primarily investigated the performance of controllers and assessed the interaction between equipment failure and human reliability in the system [11]. By identifying and analyzing different types of errors made by air traffic controllers, Shorrock suggested that the decision-making of a controller is dependent on whether operational safety can be achieved [12]. Kirwan et al. collected human error data in the ATC system and assessed human reliability before giving suggestions about how to improve the safety level systematically [13]. Chang illustrated the air traffic safety situation in Taiwan with statistical measurements [14].

Regarding assessment approaches, Saaty proposed the analytic hierarchy process (AHP) in the 1970s, which is a multi-criteria decision-making method combining qualitative and quantitative methods [15]. Since then, AHP has been applied to many decision-making areas. For instance, Ding and Wang established a safety early-warning indicator system for the ATC system using the AHP method [16]. Shyur applied the proportional hazard model for the first time to analyze the accidents and safety indicators in the aviation field. It was concluded that human error is the major cause of safety risk accidents in the ATC system [17].

Other methods have been introduced into the air transport industry as well. For example, Du et al. and Zhang et al. assessed the safety risks in ATC systems with the fuzzy comprehensive assessment method [18,19]. Vismari and Camargo measured the safety level of the ATC system through a random Perti network [20]. Wen built a gray multi-level model for an air traffic safety risk assessment [21]. Yang simulated the possible scenarios and predicted the safety risks of the ATC system, taking the system dynamics into consideration [22]. Liu et al. and Zhang et al. applied the matter element extension theory to evaluate the safety status of the ATC system [23,24]. Yuan et al. assessed the operational safety level of the ATC system based on the evidence synthesis theory [25]. Zhao and Wan analyzed the operational risks of the ATC system by introducing the set pair method [26]. Wang et al. proposed a trajectory-based landing risk assessment method using Bayesian update, and they claimed that their model can predict the occurrence of landing accidents [27]. Hu et al. proposed a risk-based operational safety bound for unmanned air traffic to enhance operational safety [28,29].

Although the above-mentioned papers provided techniques that have been widely applied in the aviation industry, they have their defects and limitations. To be more specific, references [6,7,8,9,10,11,12,13] revealed the safety risk levels qualitatively rather than quantitatively, and the quantitative methods in references [14,15,16,17,18,19,20,21,22,23,24,25,26] have defects and deficiencies. For instance, the applicability of those statistics methods highly depends on the incident and accident data sample. Since the sample should be consistent with the safety management level, it limits the application of the mathematical statistics method in the ATC field. The AHP requires judgment calls from the professionals and experts, implying that the results could be affected by their knowledge and experience in safety and risk assessment. Additionally, the AHP can only assess a limited number of indicators; otherwise, the calculation process would be time-consuming. Additionally, the accuracy of the fuzzy comprehensive assessment method can be easily affected by the reviewer. Besides, the system dynamics methods require accurately predetermined parameters to achieve objective results, which is not easy to achieve in the real world. Regarding the proportional risk model, the indicators are static instead of time-varying. In other words, those indicators can hardly reveal the operational safety trend of the ever-changing ATC system. Although the Perti network theory does not reveal the ambiguity of the ATC safety management level, the determination of the whitening weight function in the grey clustering method lacks certain theoretical bases. The matter element extension model determines the level of the assessment object based on the maximum membership principle. Nonetheless, the assessment matter element information may be lost, which may lead to errors. The lack of theoretical basis makes the evidence synthesis theory controversial, and the possibility of exponential explosion in calculation further questions its rationality and validity. Lastly, the set pair theory continues to develop. The way it determines the difference coefficient between [−1, 1] is simple and rough, and cannot fully demonstrate the evolutionary laws of a system. Regarding references [27,28,29], the Bayesian-based method is not ideal for the civil aviation industry since it requires the prior probability and more data, and the risk-based dynamic tropic operational safety bound has only been tested on unmanned air traffic, which is less complex than civil aviation.

The ATC system is a complex scheme. There are considerable qualitative indicators and ambiguous information that should be carefully evaluated. However, the above-mentioned conventional methods tend to leave some of the critical information behind due to the gray characteristics of the risk assessment of the ATC system. To fill the gap, this study proposes a safety risk assessment model for the ATC system and contributes to the previous literature.

This paper contributes to the sustainable development of air transport by introducing game theory [30,31,32,33] into the weighing system for the initial indicator assessments. To overcome the ambiguity and randomness of the indicators, the cloud model [34,35,36] is applied to solve the conversion of uncertain knowledge between qualitative and quantitative measurements. Furthermore, this paper introduces the matter element model [37,38,39] to explore the internal characteristics of those indicators and obtain an in-depth understanding of their incompatibility. Lastly, this study replaces the certain value in the conventional matter element theory with the cloud model to build a cloud matter element assessment [40,41,42] for safety risk assessment of the ATC system. Generating the assessment cloud of the indicators, this study presents a comprehensive safety risk assessment using the correlation function of the matter element theory. Consequently, this study expands the research scope to game theory and cloud matter element analysis, which contributes to the previous literature on the sustainable development of interdisciplinarity.

2. Model Specification

2.1. Indicator Selection and Classification

The ATC system guides military and civil aircrafts flying at high speeds. When an incident or accident occurs, the stakeholders have a narrow time window to execute the contingency plan. The consequence of an accident (e.g., collision) would be severe and devastating. Subsequently, for safe and effective operation, all participants in the ATC system must maintain relatively high standards, including humans (e.g., air traffic controllers, crew members), machines (e.g., aircrafts, ATC systems, and the navigation systems), and environments (e.g., weather, airspace en route).

Figure 1 demonstrates the human–machine–environment relationship with a special focus on the ATC system in the terminal area. It can be seen that the air traffic controllers are extremely important in the whole ATC system. To fulfill their roles, the controllers need information from other stakeholders, including ATC departments, civil and military aviation authorities, local airports, and equipment such as the Automatic Dependent Surveillance-Broadcast and various surveillance radars. The controllers need to process all the information before giving instructions to crews. Accordingly, the controllers may feel considerable pressure from the role and the responsibility behind the scenes. As anything can go wrong and result in catastrophic consequences in the system, it would be of great value to obtain an in-depth understanding of the critical factors systematically beforehand.

The safety risk assessment of the ATC system is recognized as a sophisticated project. The key to accomplishing this mission is to properly identify the indicators for evaluation. The indicators should be scientifically reasonable, comparable, and feasible, and can be used to reflect the safety risk level of the ATC system objectively and fairly.

Table 1. The safety risk assessment indicators for the ATC system.

Target	Criterion	Indicator	Score
ATC system (N)	Human (N1)	Controller’s professional dedication spirit (N11)	90
		Controller’s safety responsibility awareness (N12)	88
		Controller’s health status (N13)	84
		Controller’s expertise (N14)	86
		Controller’s communication skills (N15)	78
		Controller’s decision-making ability (N16)	75
		New controller’s training status (N17)	63
	Equipment (N2)	Maintenance (N21)	87
		Reliability (N22)	82
		Condition (N23)	71
		Operation management (N24)	70
		Back-up equipment (N25)	83
	Environment (N3)	Pros and cons of the flight procedure design (N31)	82
		Flight meteorological conditions (N32)	78
		Air traffic flow status (N33)	73
		Airspace (N34)	78
		Control information (N35)	83
	Management (N4)	Rationality of regulation (N41)	90
		Safety culture of air traffic control (N42)	82
		Technical training institutionalization (N43)	71
		Execution of the management system (N44)	64
		Clarity of institutional responsibilities (N45)	72
		Information exchange effectiveness (N46)	77
		Job satisfaction (N47)	72
		Brain drain (N48)	83

lists the safety risk assessment indicators adopted in this paper, which evaluate the safety risk level of the ATC system from four aspects, including human (air traffic controllers), equipment (equipment and facilities), environment (working environment of the ATC system), and management (safety management of the ATC system). Those indicators were selected based on previous investigations and studies [18,19,20,21,22,23,24,25], interviews with ATC safety management experts, and ICAO documents, such as the Safety Management Manual (DOC 9859) [43]. Other documents and requirements implemented by the Civil Aviation Administration of China (CAAC) were also taken into account, including the Air Traffic Control Safety Audit [44] and the Air Traffic Service Safety Assessment System [45].

As discussed in Section 1, the AHP decomposes complex problems into various constituent factors and groups them with a hierarchical structure according to their dominance relationships. Hence, this study classified the 25 indicators into a three-level hierarchical structure. As illustrated in Table 1, the top layer in the first column is the target layer, representing the object of this research. The criterion layer in the second column shows the four aspects of the assessment, which are human, equipment, environment, and management. The third column represents the indicator layer, which consists of the 25 indicators from the above-mentioned four criteria. In this sense, the ATC authority could evaluate the safety risk level of the ATC system directly and take initiative for further improvements.

2.2. The Indicator Weighting Process

The indicator weighting process is the key to safety risk assessment. In general, indicator weighting methods consist of subjective and objective ones [46]. The subjective weighting approach largely relies on the knowledge and experience of the experts. In other words, a less experienced expert may jeopardize the whole assessment. On the other hand, objective weighting methods are usually data-driven, which produces results with better accuracy and reliability. However, some of the extreme values in the collected dataset may put it in doubt. Subsequently, this paper proposes a combination of both subjective and objective methods to overcome their shortcomings and reflect the relationships between the weighted indicators objectively. First, the AHP is carried out as a subjective approach, since it largely depends on the judgment of experts to determine the hierarchy of the factors. Next, the ordered weighted averaging (OWA) method is adopted as the objective one to reduce the flaws of the expert judgments. Lastly, the results from the AHP and OWA approaches are combined with game theory.

2.2.1. The AHP-Based Weighting Process

The basic steps of AHP include establishing a multi-level hierarchy, scoring and comparing, building a judgment matrix, finding the maximum eigenvalue and eigenvector, normalizing, and checking for consistency.

As shown in Table 1, this research developed a three-level hierarchical structure, which consists of four criteria and 25 indicators. Eight experienced experts scored each of those indicators from 0 to 100. Table 1 presents the average results of those scores for each indicator.

After that, the relative importance of those indicators was determined by the experts. During this process, experts were invited to use the pairwise comparison approach to decide the relative importance of the indicators in the same layer and build an $n$ -dimensional judgment matrix. In this sense, the value in the matrix, scored from 1 to 9, reflects the expert’s understanding of indicators’ relative importance (see

Table 2. The meanings of the scores in the pairwise comparison matrix.

${\mathit{a}}_{\mathit{i}\mathit{j}}$	Meaning
1	Both indicators are equally important.
3	One factor is slightly more important than the other.
5	One factor is more important than the other.
7	One factor is significantly more important than the other.
9	One factor is extremely more important than the other.
2, 4, 6, 8	Those scores represent the intermediate states among the above adjacent scores.
Reciprocal	$a_{ij}$ denotes the relative importance of indicator $i$ to indicator $j$, whereas the relative importance of indicator $j$ to indicator $i$ can be expressed as $a_{ji}$, where $a_{ji}=1/a_{ij}$.

).

Equation (1) represents the judgment matrix. It is noticeable that the relative importance equals 1, when compared with the indicator itself. In other words, $a_{ii}=1$. The relative importance values on the opposite side of the diagonal are reciprocals, where $a_{ji}=1/a_{ij}$.

$$A= [\begin{array}{ccc}\begin{array}{cc}1& a_{12}\\ \frac{1}{a_{12}}& 1\end{array}& \begin{array}{c}\cdots \\ \cdots \end{array}& \begin{array}{c}{a}_{1n}\\ a_{2n}\end{array}\\ \begin{array}{cc}⋮ & ⋮\end{array}& ⋮& ⋮\\ \begin{array}{cc}\frac{1}{a_{1n}}& \frac{1}{a_{2n}}\end{array}& \cdots & 1\end{array}] .$$

(1)

Equation (2) denotes the calculation of the maximum eigenvalue ${\lambda }_{max}$ and eigenvector $W$ in the judgment matrix, where the value of $W$ represents the relative importance of the indicator $n$.

$$AW=\lambda W$$

(2)

Then, the eigenvector $W_i$ can be normalized with Equation (3) in order to obtain the weight for each indicator. Equation (4) denotes the normalized eigenvector, which is the weight vector of the set of layers.

$${\mu }_i=\raisebox{1ex}{$W_i$}\!\left/ \!\raisebox{-1ex}{${{\displaystyle \sum }}_{i=1}^n{W}_i$}\right.$$

(3)

$$\mu ={\left({\mu }_1, {\mu }_2,\dots , {\mu }_n\right)}^T$$

(4)

Lastly, the consistency and assigned weights are checked with Equations (5) and (6) as follows:

$$CI=\left({\lambda }_{max}-n_k\right)/\left(n_k-1\right)$$

(5)

$$CR=CI/RI$$

(6)

where ${\lambda }_{max}$ denotes the maximum eigenvalue of the judgment matrix, and $n_k$ denotes the order of the consistency check matrix. $CI$ represents the consistency index, whereas $CR$ stands for the consistency ratio. $RI$ (random index) denotes the average random consistency index, which can be found in

Table 3. The values of the random index.

Order of Matrix	1	2	3	4	5	6	7	8	9
$RI$	0	0	0.52	0.89	1.12	1.26	1.36	1.41	1.46

. The consistency of the judgment matrix is acceptable only when $CR<0.10$, otherwise the judgment matrix should be properly revised. For the first- and second-order matrices, the $CR$ always equals 0.

2.2.2. The OWA-Based Weighting Process

To reduce the possible flaws of experts’ subjective judgments, this section introduces the ordered weighted averaging (OWA) operator as a tool to deal with the aggregating multicriteria and the overall decision-making. The family of OWA operators was proposed by Yager in 1988 [47]. The OWA operator has received great attention, and it has been widely applied in different disciplinary contexts, such as decision-making under uncertainty, fuzzy systems, information retrieval systems, and data mining [48,49,50,51]. Unlike AHP, the OWA method assigns extreme values to the fewer influence areas to reduce the drawbacks of the subjective opinions and improve the objectivity of the weights.

The OWA operator assumes $F:R^n\to R$, if

$$F\left(a_1, a_2, \dots , a_n\right)={{\displaystyle \sum }}_{j=1}^n{\mu }_j·b_j$$

(7)

where the weight vector $\mu ={\left(a_1, a_2,\dots , a_n\right)}^T$ is only associated with $F$, whereas ${\mu }_j\in [0,1]$ and ${\displaystyle \sum }_{j=1}^n{\mu }_j=1$. $b_i$ denotes the $j^{th}$ largest element in the array $\left(a_1, a_2, \dots , a_n\right)$, and $R$ represents the set of real numbers. $F$ denotes an $n-$ dimensional OWA operator.

The OWA operator first arranges the original array $\left(a_1, a_2, \dots , a_n\right)$ in a descending order from largest to smallest and builds a new array $\left(b_0, b_1, \dots , b_{n-1}\right)$, before calculating the weights. In this sense, ${\mu }_j$ is only associated with the position of $b_i$.

The OWA operator enhances the same judgments by assigning a larger weight and avoids the flaws of the extreme values. The OWA-based weighting process can be described as follows:

This approach first invites $n$ experts to score the indicator $C_i$ to build the original array $\left(a_1, a_2, \dots , a_n\right)$. Then the array can be reorganized into $\left(b_0, b_1, \dots , b_{n-1}\right)$. The value of the weight vector can be calculated with Equation (8) based on the position of $b_{\mathrm{i}}$.

$${\partial }_{j+1}=\frac{C_{n-1}^j}{{{\displaystyle \sum }}_{k=0}^{n-1}{C}_{n-1}^k}=\frac{C_{n-1}^j}{2^{n-1}}, j=0, 1,\dots ,n-1$$

(8)

Next, the weighting vector ${\partial }_{j+1}$ is used in the process of weighting experts’ judgments, calculating the absolute weight value $\overline{{\mu }_j}$ as follows:

$$\overline{{\mu }_j}={{\displaystyle \sum }}_{j=1}^n{\partial }_j·b_j$$

(9)

Lastly, Equation (10) calculates the actual weight ${\mu }_{\mathrm{j}}$ of the indicator $C_i$.

$${\mu }_j=\frac{\overline{{\mu }_j}}{{{\displaystyle \sum }}_{j=1}^n\overline{{\mu }_j}}, j=1, 2,\dots ,n$$

(10)

2.2.3. The Game Theory-Based Combined Weighting Process

To obtain a more objective and reasonable weight, this study introduced game theory to combine the results from the above-mentioned methods and reduce their possible drawbacks. As one type of decision theory, game theory determines one’s choice of action after taking all possible alternatives available to an opponent playing the same game into account. More importantly, it details the procedure and principles by which action should be taken rather than how a game should be played.

Although Neumann and Morgenstern laid the foundations of classical game theory [52], game theory transformed social science over the next several decades after, most notably, John Nash and the Nash equilibrium [53]. The Nash equilibrium, representing a profile of strategies adopted by a set of agents, is based on the Bayesian rationality criterion according to maximizing one’s respective payoff [30,31,32,33].

Consequently, the game theory-based combined weighting process can be described as a decisive game in which each weighting method participates as the player. As a result, the combined weighting vector represents rational decision-making among individual weighting methods. By applying the Nash equilibrium to the weighting process, this paper aimed to identify an equilibrium solution between subjective and objective weighting approaches. The game theory calculation steps with two or more participants are as follows [33]:

Step 1: Assuming that there are $L$ methods to weigh $n$ indicators. The weight vector sets can be written as ${\mu }_i=\left\{{\mu }_{i1}, {\mu }_{i2},\dots ,{\mu }_{in}\right\}\left(i=1, 2,\dots ,L\right)$. Hence, Equation (11) denotes the linear combined weight vector composed of $L$ different weight vectors.

$$\mu ={{\displaystyle \sum }}_{i=1}^L{\alpha }_i{\mu }_i^T {\alpha }_i>0, {{\displaystyle \sum }}_{i=1}^L{\alpha }_i=1$$

(11)

where $\mu$ denotes one of the possible combined weight vectors, whereas $\left\{\mu ={\displaystyle \sum }_{i=1}^L{\alpha }_i{\mu }_i^T\right\}$ represents the whole set. ${\alpha }_i$ denotes the linear combined coefficient of the $i^{th}$ weighted method.

Step 2: Equation (12) represents a cross-programming model with multiple objective functions as follows:

$$min\left|\right|{{\displaystyle \sum }}_{i=1}^L{\alpha }_i{\mu }_i^T-{\mu }_j\left|\right|{}_2 j=1, 2,\dots , L$$

(12)

By minimizing the deviation between $\mu$ and ${\mu }_i$ with Equation (12), the most satisfying weight vector ${\mu }^{\prime }$ of all the possible weight vector sets $\mu$ can be identified.

Step 3: Equation (13) denotes the condition of the optimal first-order derivative in Equation (12), based on the differentiation property of the matrix. Meanwhile, Equation (14) represents the corresponding system of the linear equations. Based on that, the weight coefficient ${\alpha }_i$ can be calculated.

$${{\displaystyle \sum }}_{i=1}^L{\alpha }_i{\mu }_j{\mu }_i^T={\mu }_j{\mu }_i^T$$

(13)

$$\left|\begin{array}{cc}\begin{array}{cc}{\mu }_1{\mu }_1^T& {\mu }_1{\mu }_2^T\\ {\mu }_2{\mu }_1^T& {\mu }_2{\mu }_2^T\end{array}& \begin{array}{cc}\cdots & {\mu }_1{\mu }_L^T\\ \cdots & {\mu }_2{\mu }_L^T\end{array}\\ \begin{array}{cc}⋮& ⋮\\ {\mu }_L{\mu }_1^T& {\mu }_L{\mu }_2^T\end{array}& \begin{array}{cc}\ddots & ⋮\\ \cdots & {\mu }_L{\mu }_L^T\end{array}\end{array}\right|\left|\begin{array}{c}\begin{array}{c}{\alpha }_1\\ \begin{array}{c}{\alpha }_2\\ ⋮\end{array}\end{array}\\ {\alpha }_L\end{array}\right|=\left|\begin{array}{c}\begin{array}{c}{\mu }_1{\mu }_1^T\\ \begin{array}{c}{\mu }_2{\mu }_2^T\\ ⋮\end{array}\end{array}\\ {\mu }_L{\mu }_L^T\end{array}\right|$$

(14)

Step 4: By normalizing ${\alpha }_i$ with Equation (15), the combined weight can be obtained with Equation (16).

$${{\alpha }_i}^{\prime }=\frac{{\alpha }_i}{{{\displaystyle \sum }}_{i=1}^L{\alpha }_i}$$

(15)

$${\mu }^{\prime }={{\displaystyle \sum }}_{i=1}^L{{\alpha }_i}^{\prime }{\mu }_i^T$$

(16)

2.3. The Cloud Matter Element Model Specification

2.3.1. The Cloud Model

Based on fuzzy sets and probability theory, Li et al. proposed the cloud model in the 1990s [34]. It can transform the uncertainty of qualitative and quantitative values with subordinate cloud, digital feature, cloud generator, and related calculation rules. Quantifying the randomness and ambiguity effectively, the cloud model makes up for the shortcomings of traditional methods and improves the assessment accuracy with more convenience in the calculation [34].

The cloud model can be expressed as $\left(E_x, E_n,H_e\right)$, where $E_x$ represents the mathematic expectation, $E_n$ denotes the entropy, and $H_e$ denotes the hyper-entropy.

2.3.2. The Matter Element Model

Matter element theory is an interdisciplinary subject, absorbing ideas from systems science, thinking science, and mathematics [34]. It can be represented by an ordered triple $R=\left(N, C, V\right)$, where $N$ denotes the name of the object, $C$ denotes the characteristic, and $V$ denotes the value. Those three parameters describe the basic features of the objects, constituting the matter element.

This theory evaluates the objects by generating a standard matter element based on the ideal value of each feature and comparing it with the matter element of the object. Through matter element transformation, it converts contradictory problems into compatible problems for comprehensive evaluation. Subsequently, this approach is suitable for existing objects or objects with ideal or standard values [37].

This study chose matter element theory for two reasons. First of all, a large number of indicators is selected, which may inevitably cause contradictions. Additionally, the matter element theory is of great value in evaluating criteria and classifying the security risk levels.

2.3.3. The Cloud Matter Element Model

In conventional matter element theory, $V$ denotes a certain value. This means that the matter element theory does not consider the ambiguity and randomness of the object. However, this issue can be solved by introducing the cloud model to replace $V$. In other words, the cloud $\left(E_x, E_n,H_e\right)$ will substitute $V$, which constitutes a new ordered triple $R=\left(N, C, \left(E_x, E_n,H_e\right)\right)$. Thus, the new cloud matter element of “name, characteristic, cloud value” is expressed as follows:

$$R= [\begin{array}{cc}N& \begin{array}{cc}{C}_1& \left(E_{x1}, E_{n1},H_{e1}\right)\\ C_2& \left(E_{x2}, E_{n2},H_{e2}\right)\end{array}\\ \begin{array}{c}\\ \\ \end{array}& \begin{array}{cc}⋮& ⋮\\ C_n& \left(E_{xn}, E_{nn},H_{en}\right)\end{array}\end{array}]$$

(17)

where $E_n$ denotes the fuzziness of the safety risk level limit, and $H_e$ represents the possible randomness of the safety risk assessment sample.

2.3.4. The Five-Level Risk Structure and the Standard Cloud Parameters

Considering the characteristics of operational safety in the ATC system, experts suggest using a five-level risk structure for the assessment based on the Civil Aviation Air Traffic Management Safety Management System (SMS) Construction Instruction Manual and ICAO DOC 9859 [43,54] (see the first two columns in

Table 4. Five-level safety risk classification and the standard cloud benchmark parameters.

Value	Safety Risk Level	Standard Cloud Parameters for Benchmark
		${\mathit{E}}_{\mathit{x}\mathit{s}}$	${\mathit{E}}_{\mathit{n}\mathit{s}}$	${\mathit{H}}_{\mathit{e}\mathit{s}}$
[0, 30)	I (very low safety)	15.0000	5.0000	0.5000
[30, 60)	II (low safety)	45.0000	5.0000	0.5000
[60, 70)	III (general safety)	65.0000	1.6667	0.5000
[70, 85)	IV (high safety)	77.5000	2.5000	0.5000
[85, 100)	V (very high safety)	92.5000	2.5000	0.5000

). Therefore, Equations (18)–(20) calculate the standard cloud parameters for the benchmark.

$$E_{xs}=\frac{x_{max}+x_{min}}{2}.$$

(18)

$$E_{ns}=\frac{x_{max}-x_{min}}{6}.$$

(19)

$$H_{es}=l$$

(20)

where $x_{max}$ and $x_{min}$ represent the upper and lower limits of the safety risk level, respectively, in the first column in Table 4, and $l$ denotes a constant. This study chose an $l$. equal to 0.5000 as the fuzzy threshold of the indicator. The standard cloud parameters for the benchmark are listed in the last three columns in Table 4.

2.3.5. The Correlation Degree of the Safety Risk Level

This section uses the cloud matter element model to determine the correlation degree between the indicator and the safety risk level. Precisely, assuming the indicator value ($x$) as a cloud droplet, it generates a random number ${E_n}^{\prime }$ following the normal distribution, which has a mathematic expectation $E_x$ and a standard deviation $H_e$. Then, Equation (21) calculates the correlation degree $k$ of the indicator value $x$ corresponding to the safety risk level.

$$k=exp(-\frac{{\left(x-E_x\right)}^2}{2{\left({E_n}^{\prime }\right)}^2})$$

(21)

2.3.6. The Safety Risk Level Assessment for the ATC System

Based on the above-mentioned discussion, the cloud matter element weighted correlation degree of the indicator layers can be determined before calculating the correlation degree to each safety risk level. The correlation degree for an indicator can be expressed as follows:

$$K_j\left(N_f\right)={{\displaystyle \sum }}_{i=1}^{n_f}{{\mu }_{fi}}^{\prime }{K}_j\left(N_{fi}\right)$$

(22)

where $K_j\left(N_f\right)$ denotes the correlation degree of the $f^{th}$ criterion layer to the $j^{th}$ safety risk level, and $K_j\left(N_{fi}\right)$ represents the correlation degree of the $i^{th}$ indicator in the $f^{th}$ criterion layer to the $j^{th}$ safety risk level. ${{\mu }_{fi}}^{\prime }$ is the combined weighted value of the $i^{th}$ indicator in the $f^{th}$ criterion layer. $N_f$ expresses the number of indicators of the indicator layer from the $f^{th}$ criterion layer.

In the following step, this study calculated the comprehensive correlation degree $K_j\left(N\right)$ of each safety risk level for the target layer, which denotes the cloud matter element of the safety risk in the ATC system. Equation (23) expresses the correlation degrees of different safety risk levels based on the principle of the maximum membership degree. The safety risk level in the ATC system can be expressed with each $j$ corresponding to the maximum correlation degree $max K_j\left(N\right)$ accordingly.

$$K_j\left(N\right)={{\displaystyle \sum }}_{f=1}^n{{\mu }_f}^{\prime }{K}_j\left(N_f\right)$$

(23)

3. The Safety Risk Assessment for the ATC System

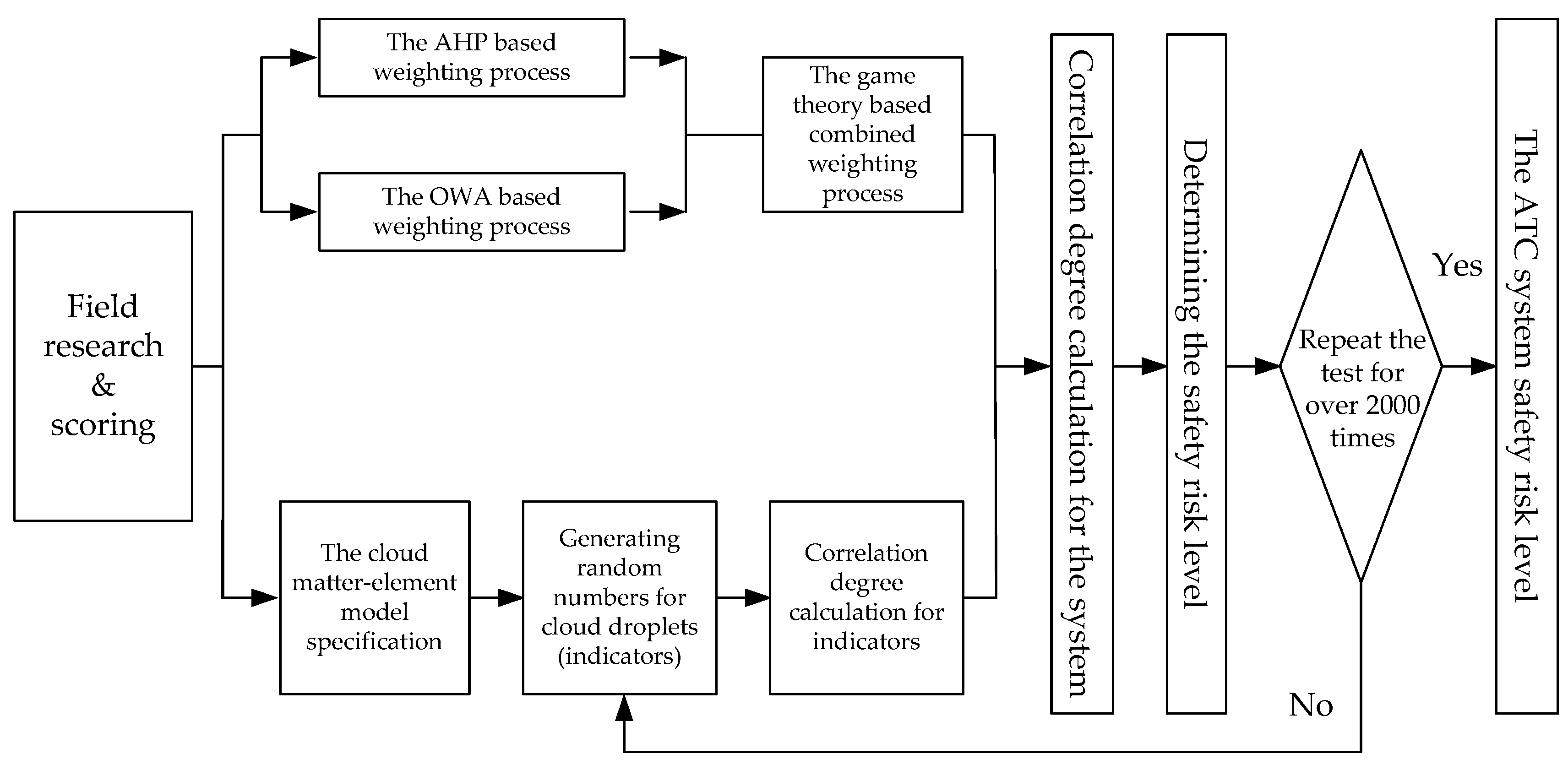
Figure 2 reveals the safety risk assessment process for the ATC system. The assessment started with experts conducting field research on the safety risk management status of the ATC units. In this study, eight experts were invited to an ATC unit in China to examine the applicability and the robustness of the proposed method. After scoring each indicator listed in Table 1, a game theory-based cloud matter element assessment model was introduced for the analysis and evaluation. As discussed in the model specification, this research first combined weights using game theory before multiplying with the cloud matter element matrix to calculate the correlation degree of the respective indicator. The result represents the quantitative outcomes of the safety risk degree, showing the safety risk in the ATC system.

3.1. The Combined Weighting Processes

3.1.1. The AHP-Based Weighting Process

This study invited eight experts to an ATC unit in China and scored each of the indicators listed in Table 1. Based on the above discussion in Section 2.2.1, the AHP-based weighting process required the experts to conduct a pairwise comparison and build a matrix for the indicators (see Table 2).

This study took the criterion layer as an example to demonstrate the AHP calculating process. Based on the experts’ opinions, the judgment matrix of the four criteria could be written as:

$$A= [\begin{array}{ccc}\begin{array}{cc}1& 2\\ 1/2& 1\end{array}& \begin{array}{c}3\\ 2\end{array}& \begin{array}{c}2\\ 1\end{array}\\ \begin{array}{cc}1/3& 1/2\end{array}& 1& 1/2\\ \begin{array}{cc}1/2& 1\end{array}& 2& 1\end{array}]$$

Then, the maximum eigen root and eigenvector of the matrix were calculated with Equation (2), where ${\lambda }_{max}=4.0104$ and $W= [1.6925 0.9087 0.4901 0.9087]$. Equation (3) calculated the weights ($\mu$) of the criteria (see the second column in

Table 5. The combined weights for the criterion layer.

Criterion	Weight
	AHP-Based Weight	OWA-Based Weight	Game Theory-Based Combined Weight
Human (N1)	0.4231	0.3155	0.3892
Equipment (N2)	0.2272	0.2488	0.2340
Environment (N3)	0.1225	0.1887	0.1434
Management (N4)	0.2272	0.2470	0.2334

). Since the $CR \left(0.0039\right)$ was less than 0.10, the judgment matrix passed the consistency test. Similarly, the second column in

Table 6. The combined weights for the indicator layer.

Indicator	Weight
	AHP-Based Weight	OWA-Based Weight	Game Theory-Based Combined Weight
Controller’s professional dedication spirit (N11)	0.2577	0.1809	0.2355
Controller’s safety responsibility awareness (N12)	0.2577	0.1779	0.2347
Controller’s health status (N13)	0.1381	0.1597	0.1443
Controller’s expertise (N14)	0.1381	0.1497	0.1414
Controller’s communication skills (N15)	0.0942	0.1104	0.0989
Controller’s decision-making ability (N16)	0.0694	0.1274	0.0861
New controller’s training status (N17)	0.0449	0.0940	0.0591
Maintenance (N21)	0.1579	0.2051	0.1706
Reliability (N22)	0.2976	0.2285	0.2790
Condition (N23)	0.2976	0.2323	0.2801
Operation management (N24)	0.1579	0.1923	0.1671
Back-up equipment (N25)	0.0890	0.1417	0.1032
Pros and cons of the flight Procedure design (N31)	0.4162	0.2428	0.3756
Flight meteorological conditions (N32)	0.1611	0.2172	0.1742
Air traffic flow status (N33)	0.0986	0.1822	0.1182
Airspace (N34)	0.2618	0.2242	0.2530
Control information (N35)	0.0624	0.1336	0.0791
Rationality of regulation (N41)	0.2400	0.1638	0.2152
Safety culture of ATC (N42)	0.1476	0.1466	0.1467
Technical training institutionalization (N43)	0.1476	0.1475	0.1470
Execution of the management system (N44)	0.2400	0.1630	0.2150
Clarity of institutional responsibilities (N45)	0.0936	0.0994	0.0951
Information exchange effectiveness (N46)	0.0614	0.1158	0.0817
Job satisfaction (N47)	0.0411	0.0974	0.0587
Brain drain (N48)	0.0288	0.0666	0.0406

illustrates the AHP-based weighting results for the indicator layers from N1 to N4.

3.1.2. The OWA-Based Weighting Process

Regarding the OWA-based weights, this study still took the criterion layer as an example to demonstrate the calculating process.

Firstly, the eight experts scored the criteria with multiples of 0.5, ranging from 0 to 5, to evaluate their relative importance (see

Table 7. The relative importance of the criteria (raw data scored by experts).

N	Expert 1	Expert 2	Expert 3	Expert 4	Expert 5	Expert 6	Expert 7	Expert 8
N1	5.0	4.5	5.0	4.5	5.0	5.0	5.0	5.0
N2	4.5	3.5	4.0	3.5	4.0	3.5	4.5	4.0
N3	3.5	2.5	3.0	2.5	3.0	3.0	3.0	3.0
N4	4.5	3.5	4.0	3.5	4.0	3.5	4.0	4.0

). The higher the score, the more important the criterion.

Then, the scores were reorganized in descending order and four new datasets built as follows:

$$b_1=\left(5.0 5.0 5.0 5.0 5.0 5.0 4.5 4.5\right)$$

$$b_2=\left(4.5 4.5 4.0 4.0 4.0 3.5 3.5 3.5\right)$$

$$b_3=\left(3.5 3.0 3.0 3.0 3.0 3.0 2.5 2.5\right)$$

$$b_4=\left(4.5 4.0 4.0 4.0 4.0 3.5 3.5 3.5\right)$$

Next, the set of weight vectors were calculated based on Equation (8), where $\partial =\left(0.0078 0.0547 0.1641 0.2734 0.2734 0.1641 0.0547 0.0078\right)$. Lastly, Equations (9) and (10) calculated the absolute weight value of the four criteria (see the third column in Table 5). Likewise, the third column in Table 6 illustrates the OWA-based weighting results for the indicator layers.

3.1.3. The Game Theory-Based Combined Weighting Process

The game theory-based combined weights were obtained with the weight vector from the AHP and OWA operator in the first two steps. Take the criterion layer as an example. First, the weight vectors ${\mu }_1=\left(0.4231 0.2272 0.1225 0.2272\right)$ and ${\mu }_2=\left(0.3155 0.2488 0.1887 0.2470\right)$ represent the AHP- and OWA-based weights, respectively (see the second and third columns of Table 6). According to Equations (13) and (14), the weight coefficient for the AHP method (${\alpha }_1$) equaled 1.7149, whereas the weight coefficient for the OWA method (${\alpha }_2$) equaled 0.7893. After normalizing with Equation (15), ${{\alpha }_1}^{\prime } =0.6848$ and ${{\alpha }_2}^{\prime } =0.3152$. The combined weights for the criteria are listed in the last column of Table 6, based on Equation (16). Table 7 reveals the combined weights for the indicator layer, which were calculated with an identical process.

3.2. The Safety Risk Level Assessment for the ATC System

The safety risk correlation degrees of each indicator for each safety risk level cloud were determined by Equation (21) (see

Table 8. The correlation degrees for indicators in different safety risk levels.

Indicator			Level
	I	II	III	IV	V
Controller’s professional dedication spirit (N11)	0.0000	0.0000	0.0000	0.0000	0.6065
Controller’s safety Responsibility awareness (N12)	0.0000	0.0000	0.0000	0.0001	0.1979
Controller’s health status (N13)	0.0000	0.0000	0.0000	0.0340	0.0031
Controller’s expertise (N14)	0.0000	0.0000	0.0000	0.0031	0.0340
Controller’s communication skills (N15)	0.0000	0.0000	0.0000	0.9802	0.0000
Controller’s decision-making ability (N16)	0.0000	0.0000	0.0000	0.6065	0.0000
New controller’s training status (N17)	0.0000	0.0015	0.4868	0.0000	0.0000
Maintenance (N21)	0.0000	0.0000	0.0000	0.0007	0.0889
Reliability (N22)	0.0000	0.0000	0.0000	0.1979	0.0001
Condition (N23)	0.0000	0.0000	0.0015	0.0340	0.0000
Operation management (N24)	0.0000	0.0000	0.0111	0.0111	0.0000
Back-up equipment (N25)	0.0000	0.0000	0.0000	0.0889	0.0007
Pros and cons of the flight procedure design (N31)	0.0000	0.0000	0.0000	0.1979	0.0001
Flight meteorological conditions (N32)	0.0000	0.0000	0.0000	0.9802	0.0000
Air traffic flow status (N33)	0.0000	0.0000	0.0000	0.1979	0.0000
Airspace (N34)	0.0000	0.0000	0.0000	0.9802	0.0000
Control information (N35)	0.0000	0.0000	0.0000	0.0889	0.0007
Rationality of regulation (N41)	0.0000	0.0000	0.0000	0.0000	0.6065
Safety culture of ATC (N42)	0.0000	0.0000	0.0000	0.1979	0.0001
Technical training Institutionalization (N43)	0.0000	0.0000	0.0015	0.0340	0.0000
Execution of the management system (N44)	0.0000	0.0007	0.8353	0.0000	0.0000
Clarity of institutional responsibilities (N45)	0.0000	0.0000	0.0001	0.0889	0.0000
Information exchange effectiveness (N46)	0.0000	0.0000	0.0000	0.9802	0.0000
Job satisfaction (N47)	0.0000	0.0000	0.0001	0.0889	0.0000
Brain drain (N48)	0.0000	0.0000	0.0000	0.0889	0.0007

and Figure 3). Based on Equation (22), the correlation degrees of four criteria layers to the five safety risk level clouds were calculated. Lastly,

Table 9. The comprehensive correlation results.

Indicator			Level			Maximum Value	Level
	I	II	III	IV	V
Human (N1)	0.0000	0.0000	0.0112	0.0601	0.0757	0.0757	V
Equipment (N2)	0.0000	0.0000	0.0005	0.0178	0.0036	0.0178	IV
Environment (N3)	0.0000	0.0000	0.0000	0.0746	0.0000	0.0746	IV
Management (N4)	0.0000	0.0000	0.0421	0.0299	0.0306	0.0421	III
Comprehensive correlation	0.0000	0.0001	0.0538	0.1824	0.1099	0.1824	IV

and Figure 4 demonstrate the comprehensive correlation degree of the corresponding safety risk level cloud of the ATC unit calculated based on Equation (23).

As shown in Table 9, the maximum comprehensive correlation degree of the ATC unit was 0.1824. Although the safety risk assessment level of the ATC unit fell into Level IV, the unit maintained a relatively high level of safety. In other words, the operational safety of ATC can be guaranteed. The results are consistent with the actual safety risk level of the ATC unit, thus verifying the applicability of the proposed method.

Moreover, it is noticeable that the N1 was in Level V, which was the highest level among all indicators and one step away from Level IV. this reveals the vulnerability of manpower and reminds the authority to pay attention to the training of new controllers.

The safety risk level for N2 fell into Level IV. Although the equipment maintained a relatively high level of operational safety, the safety risk level could be further enhanced by improving the operation and management equipment.

The safety risk level for N3 was Level IV, indicating that the superior environment helps the ATC unit to maintain its high level of safety. However, there is still room for improvement.

The comprehensive correlation degree of safety risk level in the management field was the worst compared with other indicators. Therefore, the safety risk level for N4 fell into Level III. Among all the indicators in N4, the execution of the management system (N44) showed the worst result, which sounds the alarm to authorities to maintain constant monitoring of ATC units.

3.3. Model Comparison

To examine the effectiveness of the proposed method, this research conducted a comparative analysis with the fuzzy comprehensive assessment method and the gray multi-level assessment method (see

Table 10. The comparative analysis among three methods.

Indicator	Safety Risk Level
	Cloud Matter Element Analysis	Fuzzy Comprehensive Assessment	Gray Multi-Level Assessment
Human (N1)	V	V	V
Equipment (N2)	IV	IV	IV
Environment (N3)	IV	IV	IV
Management (N4)	III	III	III
Comprehensive correlation	IV	IV	IV

). The results of the cloud matter element analysis are consistent with those of the other two methods, verifying the applicability of the proposed method in assessing the safety risk of the ATC system.

However, the fuzzy method only considers the objective weight and leaves the subjective one behind, which reduces the creditability of the results. In contrast, the gray method only considers the subjective weight. By combining the weights based on game theory, the proposed cloud matter element model fills the gap of the previous approaches and provides results with more reliability and rationality.

4. Conclusions

To assess the safety risk level in the ATC system, this paper proposed a game theory-based cloud matter element assessment method. This approach first calculates the weight based on AHP and OWA operators. Then, it combines both results by introducing the idea of game theory to avoid the drawbacks of each method. Last but not least, the combined weights are adopted in the cloud matter element assessment and the safety risk level in the ATC system is evaluated. The contributions and the novelty of this paper are listed below:

(1)

This paper establishes a cloud matter element model and applies the method to the safety risk assessment of the ATC system, which fills the gap in the existing literature by solving the ambiguity, randomness, and incompatibility of indicators in the system. More precisely, the indicator selection and scoring process, purely based on the experts’ experience, tends to be qualitative and brings ambiguity and randomness into this research. Therefore, this study introduces the cloud model to deal with the fuzziness and randomness of the indicators. Specifically, the cloud model transforms the qualitative problems into quantitative ones, which reveals the logical relationship and deduction law of the conversion between quantitative and qualitative variables.

(2)

Game theory is introduced to determine the combined weights of the indicators. With the help of the Nash equilibrium, this paper obtains indicators that are more scientific and reasonable compared with previous approaches.

(3)

This paper verifies the applicability of the cloud matter element model in assessing the safety risk in the ATC system. Furthermore, this method not only obtains the overall safety risk level, but also identifies the safety risk level of each indicator in the criterion and indicator layer. Consequently, the authorities and stakeholders can take initiative and continue monitoring the whole system with a special focus on certain indicators.

(4)

The aggregated frameworks of the cloud matter element model consider this research to be novel and unique. It provides new insights into safety risk assessment in the ATC system. Besides, the decision-making method proposed in this paper exhibits a certain universality, which could be used for decision-making in other fields.

However, the initial weights of the indicators are determined based on experts’ opinions, thus creating uncertainty in the results. Furthermore, the safety risk assessment involves a large number of indicators. the aviation industry is a fast-changing sector, so the indicator system established in this paper needs continual monitor and modification based on the analysis, which highlights the direction of future work.