An MFD Construction Method Considering Multi-Source Data Reliability for Urban Road Networks

Abstract

Road network traffic management and control are the key mechanisms to alleviate urban traffic congestion. With this study, we aimed to characterize the traffic flow state of urban road networks using the Macroscopic Fundamental Diagram (MFD) to support area traffic control. The core property of an MFD is that the network flow is maximized when network traffic stays at an optimal accumulation state. The property can be used to optimize the temporal and spatial distribution of traffic flow with applications such as gating control. MFD construction is the basis of these MFD-based applications. Although many studies have been conducted to construct MFDs, few studies are dedicated to improving the accuracy considering the reliability of different sources of data. To this end, we propose an MFD construction method using multi-source data based on Dempster–Shafer evidence (DS evidence) theory considering the reliability of different data sources. First, the MFD was constructed using VTD and CSD, separately. Then, the fused MFD was derived by quantifying the reliability of different sources of data for each MFD parameter based on DS evidence theory. The results under real data and simulated data show that the accuracy of the constructed MFDs was greatly improved considering the reliability of different data sources (the maximum MFD estimation error was reduced by 22.3%). The proposed method has the potential to support the evaluation of traffic operations and the optimization of signal control schemes for urban traffic networks.

1. Introduction

Road network traffic management and control based on the traffic supply–demand relationship are important means to actively alleviate urban traffic congestion and improve the operational efficiency of road traffic systems. Characterizing the traffic flow state of urban road networks is a fundamental problem to understand the traffic supply–demand relationship. In this study, we characterize the traffic flow state of urban road networks using the Macroscopic Fundamental Diagram (MFD), which has the following advantages: it can dynamically describe the traffic state of the road network, and it can be readily obtained with traffic flow data from existing detectors, etc. The existence of MFD has been confirmed in many cities around the world [1]. The core property of MFD is that the network traffic flow is maximized when network traffic stays at an optimal accumulation state (the network traffic flow remains maximum with increasing network traffic density). The property can be applied in gating control, traffic safety, congestion tolls, etc. [2,3,4,5,6]. The construction of an MFD is the basis of MFD-based applications.

Generally, there are three types of data to construct MFDs: cross-sectional data of traffic flow (CSD), vehicle trajectory data (VTD), and both sources of data. The general method to construct an MFD is the weighted average method for CSD and Edie’s method for VTD. However, MFD construction based on CSD is greatly affected by the location of detectors, and that based on VTD has high requirements for the penetration rate and the balanced spatial distribution of probe vehicles. Few multi-source data-based methods consider the different reliability of different sources of data, and the method that estimates different parameters of MFD with different data sources may lead to inconsistencies between the two parameters. In view of this, an MFD fusion method that can take advantage of different sources of data is needed.

Considering the different reliability of estimating ATF and ATD using CSD and VTD, we developed an MFD construction method based on the Dempster–Shafer evidence (DS evidence) theory using multi-source data. Firstly, the MFDs based on CSD and VTD were constructed separately. Secondly, the weight of CSD and VTD for ATF and ATD were separately estimated using DS evidence theory, and then the fusion MFD was derived and evaluated. The proposed method aims to improve the accuracy of MFD construction by making full use of different sources of data. To this end, the contributions of this paper can be described as follows: (1) an MFD construction method was proposed considering the difference in penetration of probe vehicles with different origins and destinations (OD); (2) a fusion method for MFD construction was proposed considering the different reliability of different sources of data.

The rest of our paper is organized as follows: Section 2 is the literature review of MFD construction, Section 3 proposes the methodology for MFD construction, Section 4 is the case study, Section 5 is the implementation of the proposed method, and the conclusions and discussion are in Section 6.

2. Literature Review

The construction of an MFD is the basis of MFD-based applications. Regarding the different data sources, three types of data were included for MFD construction: cross-sectional data of traffic flow (CSD), vehicle trajectory data (VTD), and both sources of data. The studies on MFD construction are introduced as follows.

MFD construction based on CSD (such as loop detector data, microwave vehicle detector) derives the average traffic density (ATD) and average traffic flow (ATF) of the road network through aggregating links’ traffic density and traffic flow. Geroliminis and Daganzo [1] used loops and microwave detectors to detect traffic flow and occupancy, and derived the road network MFD considering the length of links. Limited by the cost of detector deployment, a cross-sectional vehicle detector is usually fragmented in the road network. How to detect cross-sectional traffic flow based on spatially fragmented vehicle detectors, and thus accurately construct an MFD, has become a problem that must be solved. In response to this problem, Ortigosa and Menendez [7] sought to find the optimal link combination by minimizing the difference of MFD derived from traffic flow data aggregated by partial links and all links based on VISSIM simulation; their results show that 25% of vehicle detectors can make the difference less than 15%.

However, the location of the cross-sectional vehicle detector has a significant impact on the estimation of ATD. Buisson and Ladier [8] divided the CSD into three categories according to the distance between the detector and the downstream signalized intersections, and then constructed MFD using the three types of data. They found that the closer the detector is to the downstream signalized intersections, the higher the slope of the rising section of the MFD obtained by these detectors. Courbon and Leclercq [9] conducted a comparative analysis of MFD construction based on VTD and CSD, and found that the accuracy of a constructed MFD depends on the distribution of loop detectors in the road network. Leclercq [10] pointed out that only using CSD to construct an MFD leads to inaccuracy, as the CSD cannot accurately capture the average traffic speed or density. In addition, Leclercq believes that the accuracy of MFD construction is significantly improved when estimating traffic flow using CSD and estimating traffic speed using VTD compared with the single use of the loop detector data. Tilg et al. [11] systematically evaluated two main analytical approximation methods to derive the MFD for arterial roads and urban networks, and the results revealed that the availability of signal data can improve the analytical approximation of the MFD.

The MFD construction using VTD is generally obtained by expanding the travel time and travel distance of probe vehicles, and the estimation of the penetration rate has to depend on CSD. Earlier studies assumed that the probe vehicles were evenly distributed in a road network. Geroliminis and Daganzo [1] used the position coordinates provided by taxis’ GPS, along with the effective travel information of the taxis to estimate the effective travel time and travel distance, and the CSD was used to estimate the taxis’ penetration rate. Nagle and Gayah [12] assumed that the probe vehicles’ penetration rate was constant among all OD pairs, using the probe vehicles’ proportion at fixed vehicle detectors to approximately estimate the penetration rate. Ambühl and Menendez [13] assumed that the loop detectors are evenly distributed in different positions of links, and constructed MFD with CSD and VTD; their results showed that the error of the constructed MFD was smaller for multi-source data than that of single-source data. In addition, the study also analyzed MFD construction errors under different penetration rates and loop detectors’ coverage rates. Considering the different penetration rate among different ODs, some scholars proposed new methods that can improve the rationality of MFD construction [14,15,16,17,18,19]. Du et al. [14] proposed a weighted average penetration rate estimation method for OD pairs based on fixed vehicle detectors and taxi GPS data. The simulation results show that the accuracy of the proposed method is higher than that of the unified penetration rate.

With the development of traffic detection technology, the coverage rate of fixed vehicle detectors and the penetration rate of probe vehicles on the urban roads have been significantly improved. Considering the characteristics of different data sources, some scholars proposed to estimate different parameters of MFD with different sources of data. Leclercq [10] pointed out that the accuracy of a constructed MFD will be greatly improved by using loop detector data to estimate ATF and by using VTD to estimate ATD, compared to using loop detector data to construct an MFD. Ji et al. [20] proposed to use CSD to estimate ATF, and use VTD to estimate the ATD. The accuracy of constructed MFDs using multi-source data has been improved. However, most of the studies assumed that the penetration rate was evenly distributed around the road network. A summary of the data type, data source, and the MFD construction methods of representative research is given in

Table 1. Summary of representative research.

The Type of Data	Data Sources	Method	Representative Research
Cross-sectional data of traffic flow	Loops and microwave detectors	Weighted average method	Geroliminis and Daganzo [1]
	VISSIM simulation	Weighted average method	Ortigosa and Menendez [7]
	Loop detectors	Unweighted average method	Buisson and Ladier [8]
	Simulation	Weighted average method	Courbon and Leclercq [9]
	Simulation	Weighted average method	Leclercq [10]
Vehicle trajectory data	Taxi GPS	Edie’s method	Geroliminis and Daganzo [1]
	Simulation	Edie’s method	Courbon and Leclercq [9]
	Simulation	Edie’s method	Leclercq [10]
	Mobile probe data	Edie’s method	Nagle and Gayah [12]
Multi-source data	Loop detectors data and floating car data	Weighted average method, Edie’s method, and fusion algorithm considering network coverage of each data type	Ambühl and Menendez [13]
	Loop detector data and floating car data from simulation	Weighted average method, Edie’s method, and Bayesian fusion method	Saffari et al. [16]
	Loop detectors and taxi GPS	Weighted average method, Edie’s method	Ji et al. [20]
	Microwave vehicle detectors, automatic license plate recognition equipment, taxi GPS	Weighted average method, Edie’s method, and DS evidence theory fusion method	This article

.

3. Materials and Methods

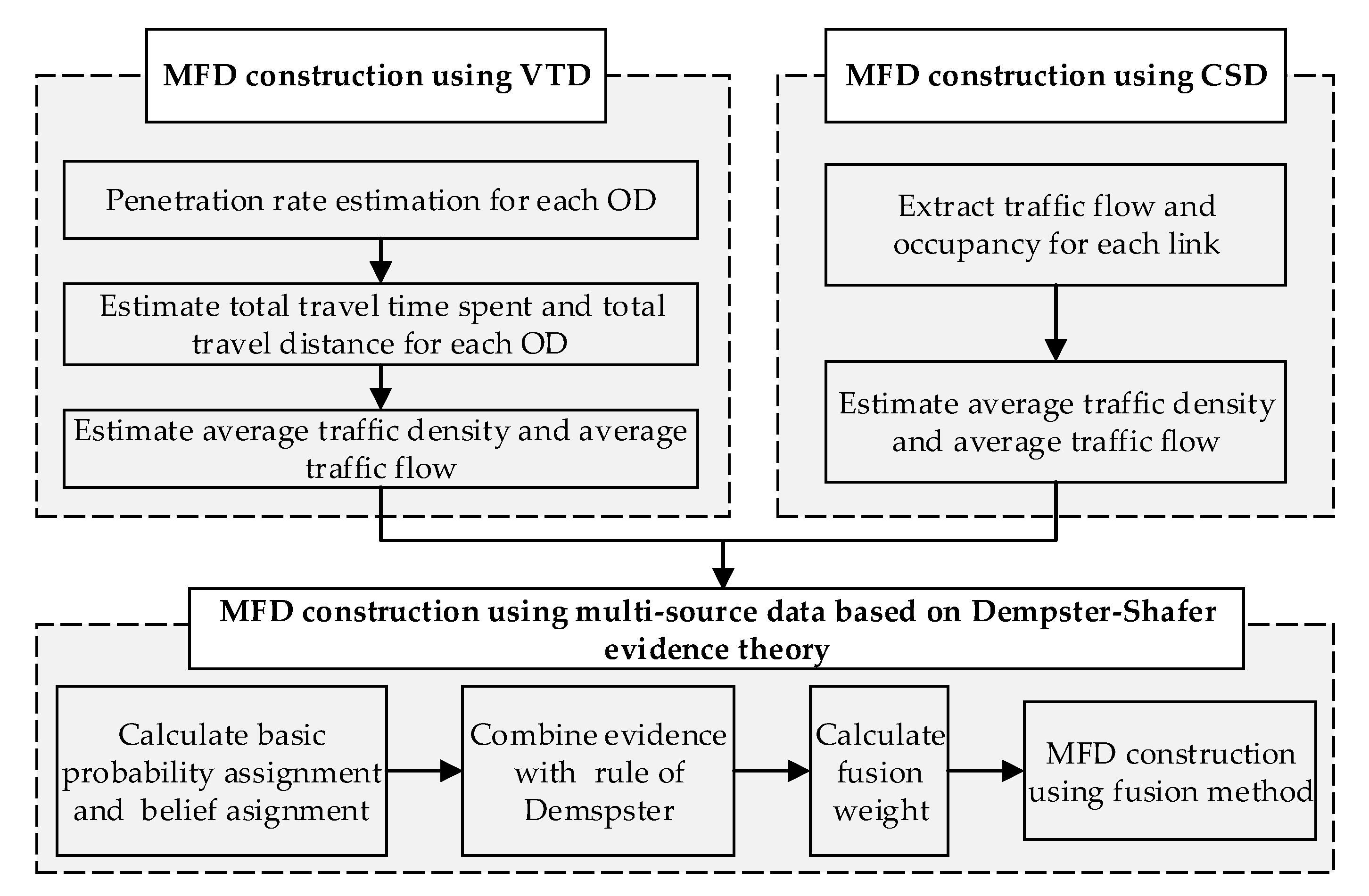
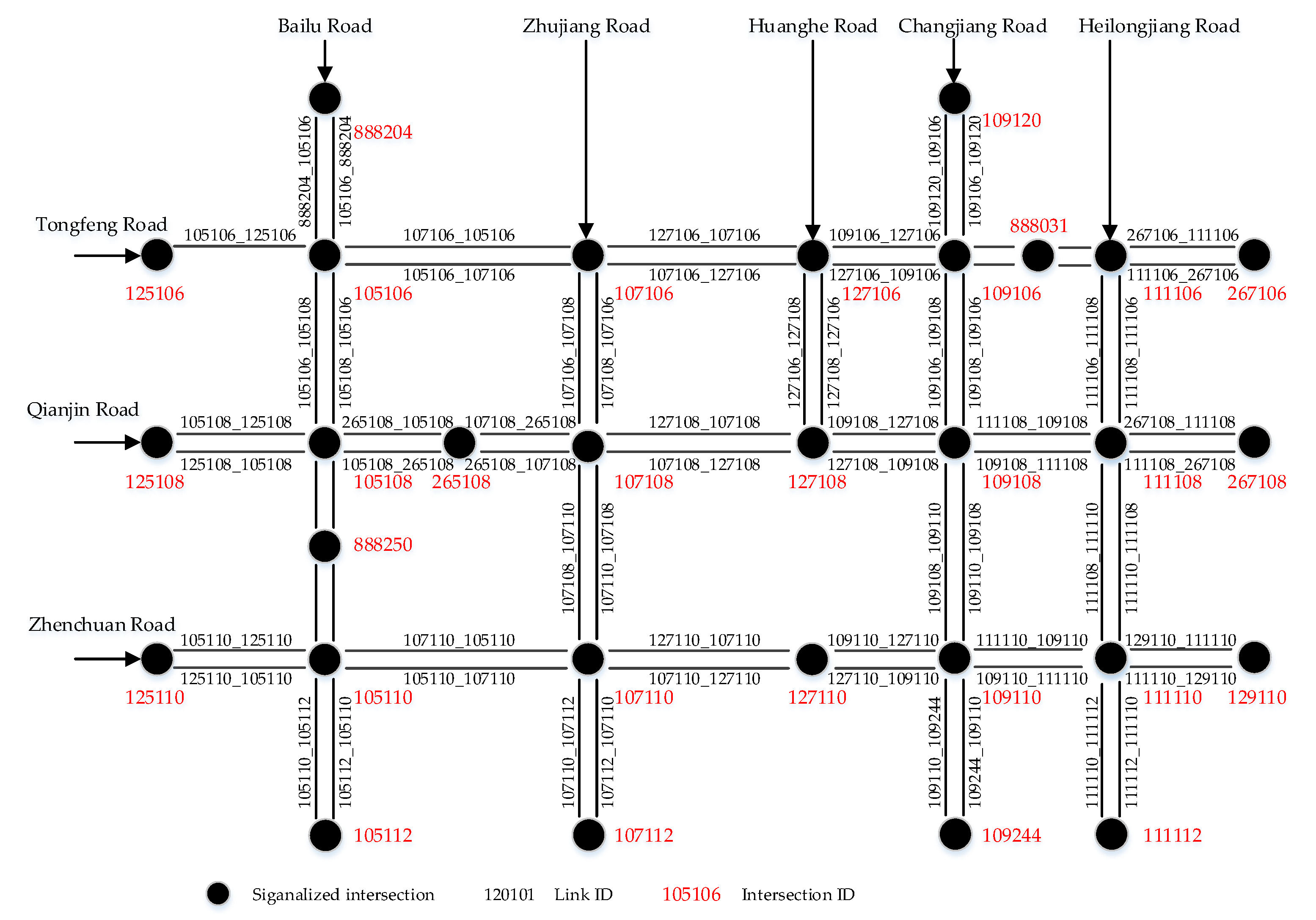
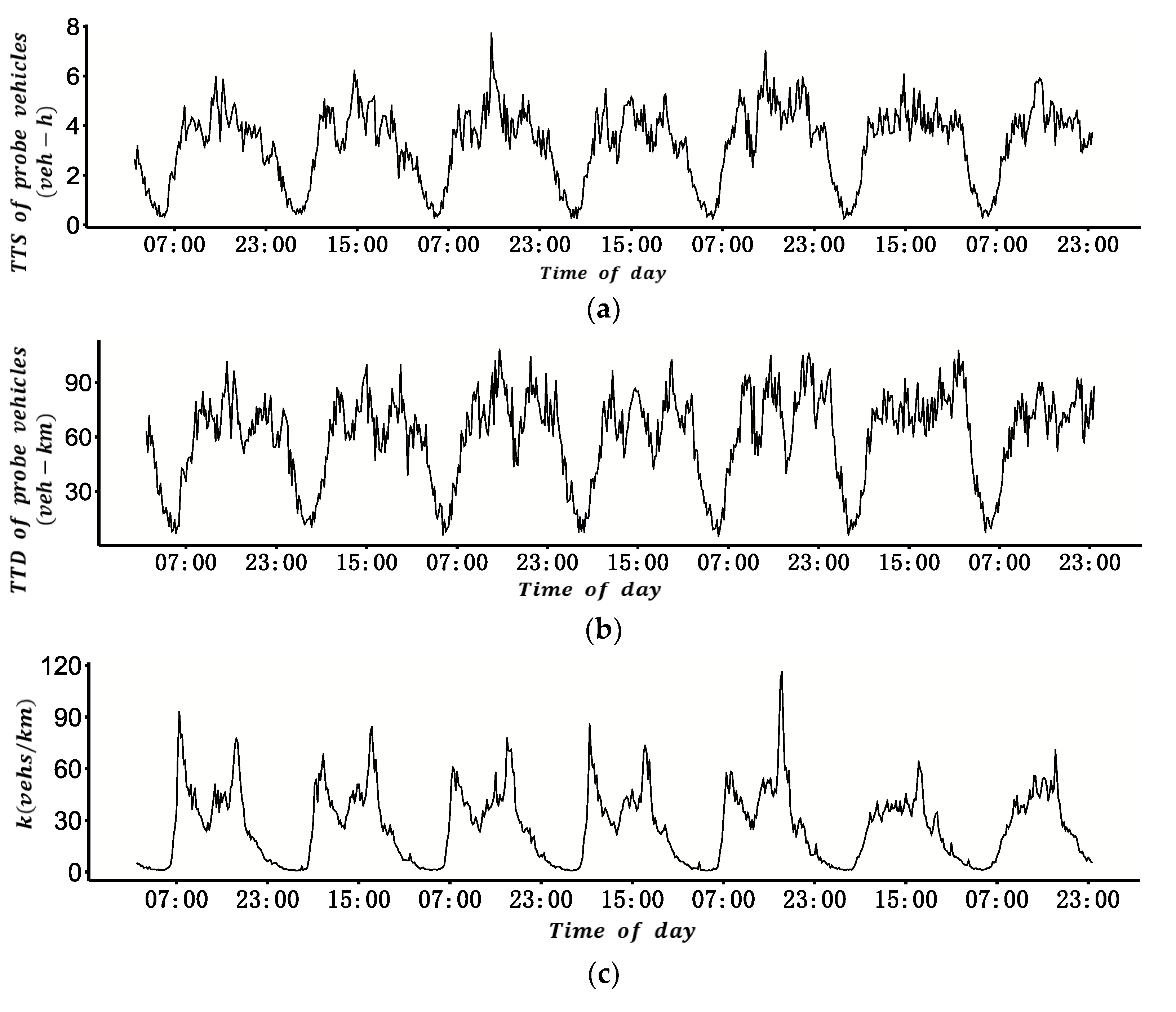
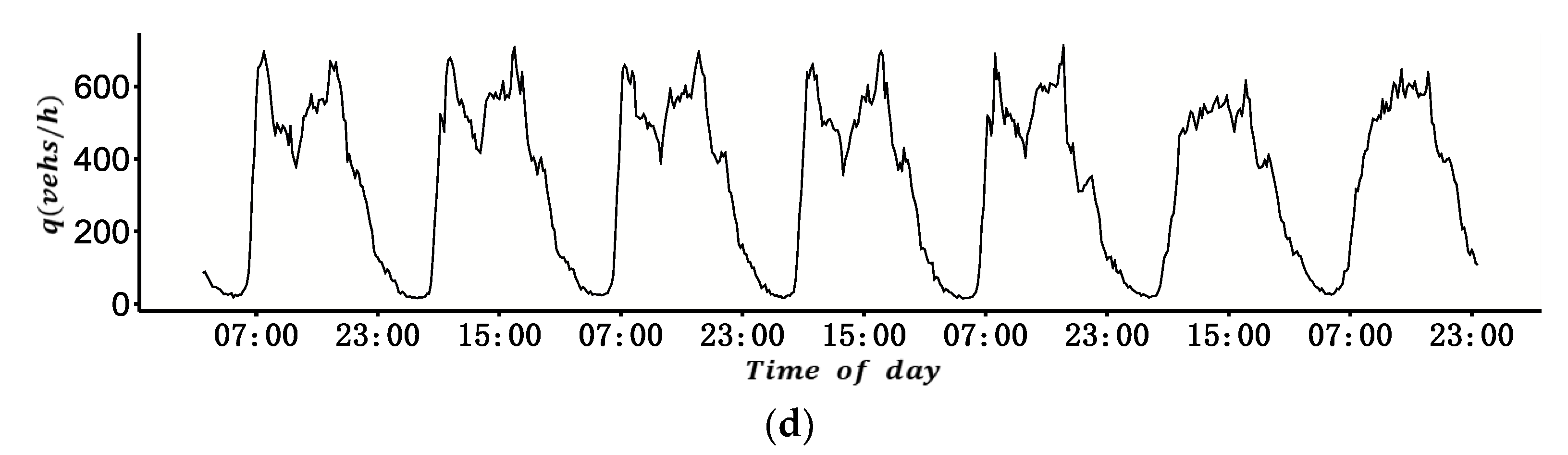
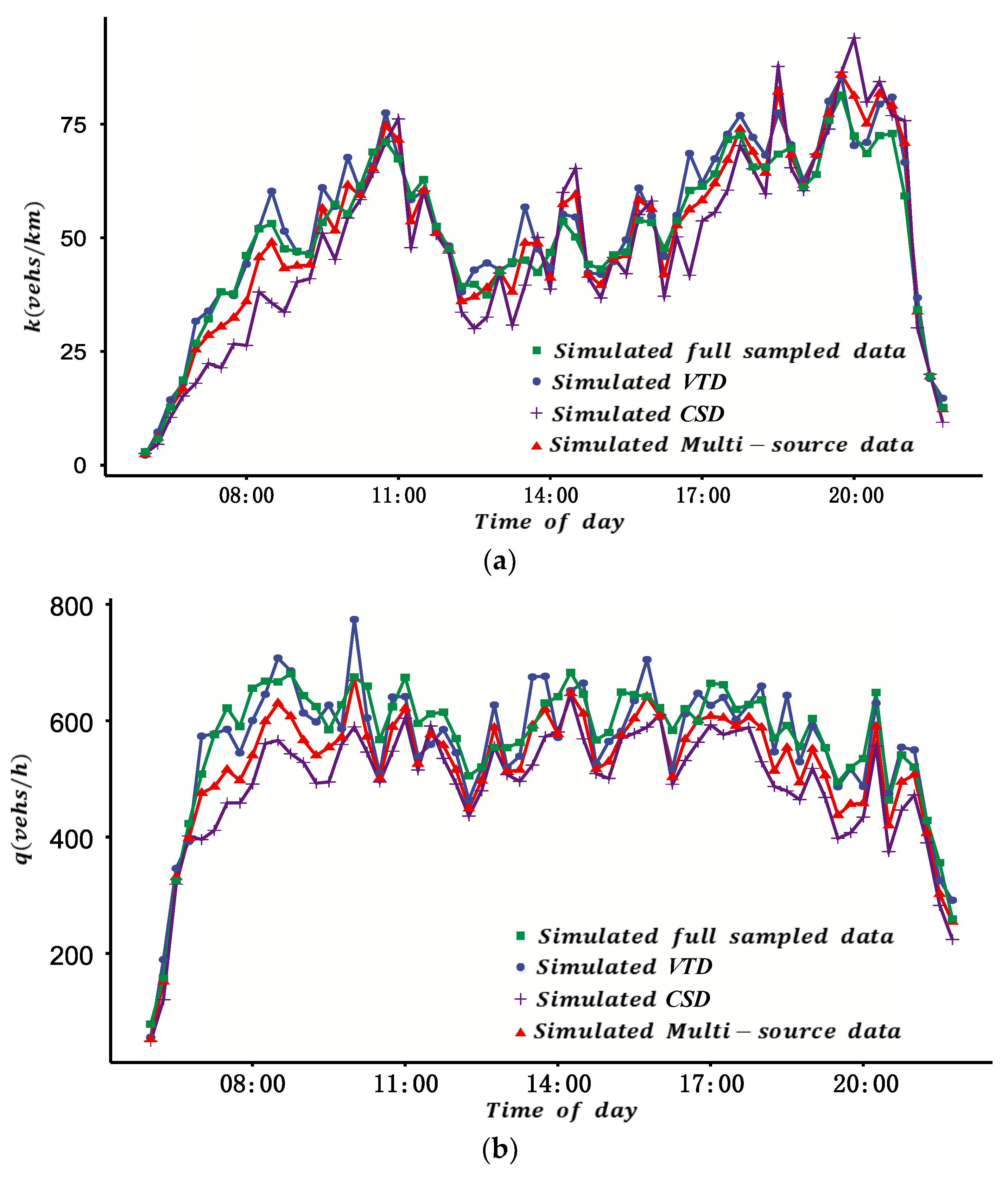
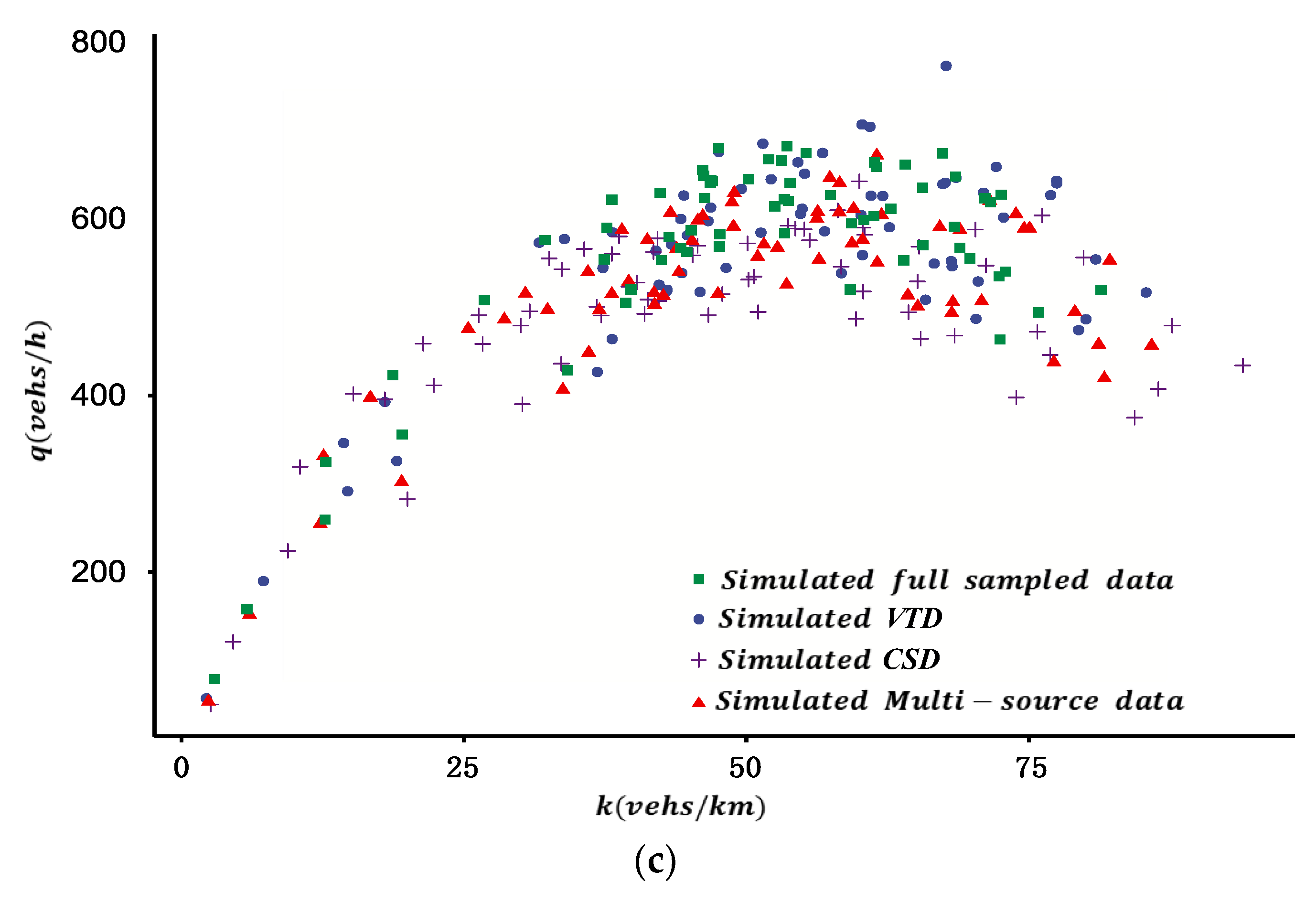
Considering the reliability of different data sources, an MFD construction method is proposed using multi-source data. The framework of the study is shown in Figure 1. The abbreviations in Figure 1 are listed in Appendix (Abbreviations). Firstly, the MFD was constructed based on VTD by estimating the total travel distance (TTD) and total travel time spent (TTS) of all vehicles considering the different penetration rates of probe vehicles in different ODs. Secondly, drawing on existing research, the MFD was constructed based on CSD. Finally, considering the different reliability of different sources of data, the two types of data were fused, and the MFD was constructed based on the DS evidence theory. The contents of each part are described as follows.

(1)

MFD construction using VTD

VTD has the advantages of wide spatial coverage and high estimation accuracy of the ATD of the road network, but it also has disadvantages such as a low penetration rate and uneven spatial distribution of probe vehicles. Because of this, firstly, the probe vehicle’s penetration rate of each OD in each period was estimated by the proportion of probe vehicles detected by automatic license plate recognition (ALPR) equipment between each OD. Secondly, the travel time and travel distance of all probe vehicles in each period of each OD in the road network were calculated. Thirdly, the total travel time and total travel distance of all vehicles in each period for the road network were derived from the estimated penetration rate. Finally, the ATD and the ATF of the test site were calculated.

(2)

MFD construction using CSD

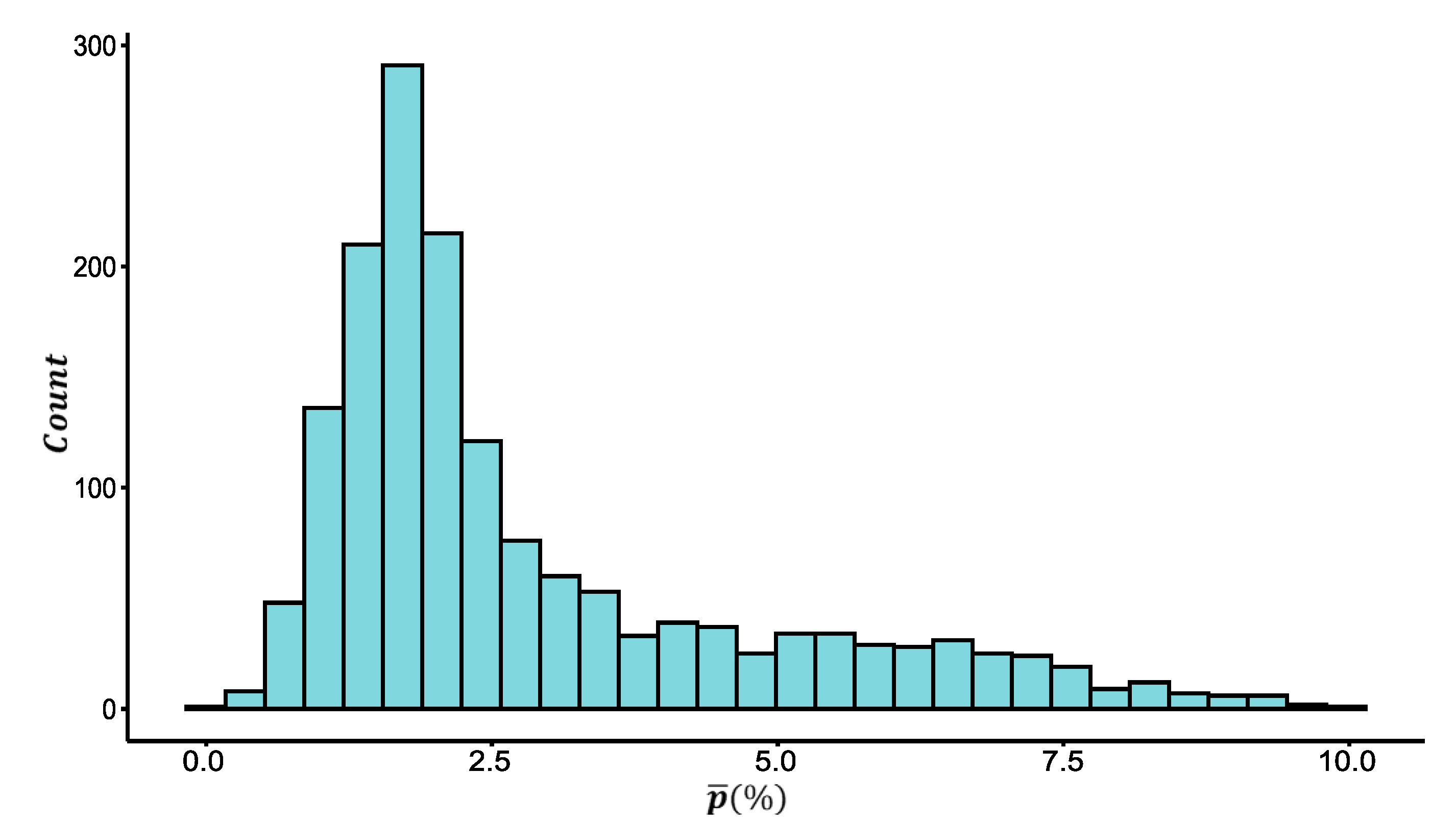
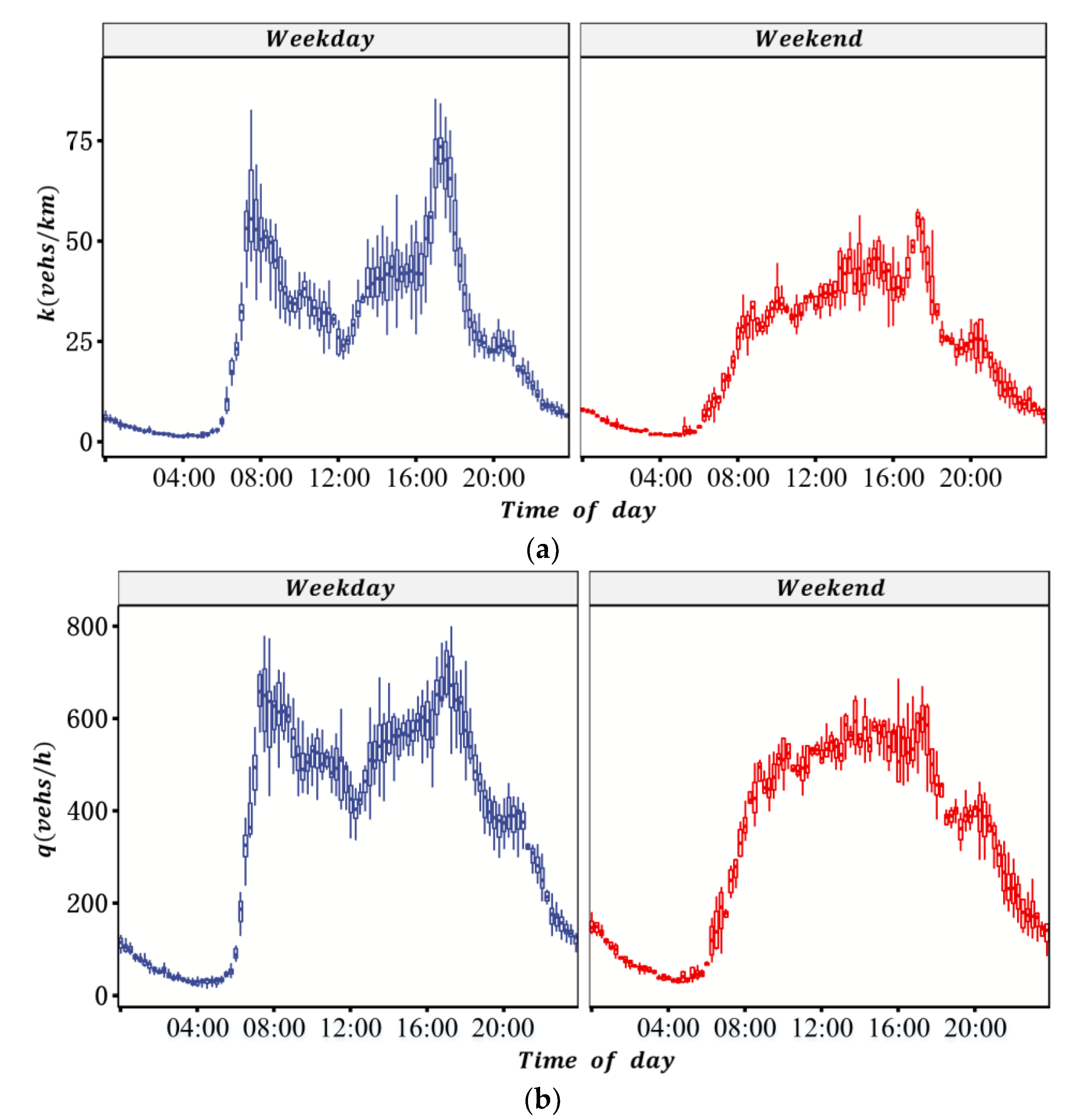
The traffic flow data for a location of a link are collected by fixed vehicle detectors (such as microwave, video, etc.). The ATF derived from the CSD can accurately reflect the traffic flow of a road networks when the spatial coverage of fixed vehicle detectors is sufficient (such as more than 25% in reference [7]). In view of this, referring to the research of Ortigosa et al. [7], the basic idea of our study is to use link length as weight, and aggregate the links’ traffic density and traffic flow using the CSD to construct an MFD.

(3)

MFD construction using multi-source data based on DS evidence theory

Because of the low penetration rate and disequilibrium spatial distribution of probe vehicles, and the insufficient coverage of fixed vehicle detectors in real road networks, the reliability of the two sources of data in the estimation of ATD and ATF is different. Furthermore, there may be inconsistencies if estimating ATD and ATF with different sources of data. Because of this, it is proposed to quantify the fusion weight of different sources of data by their reliability based on the DS evidence theory, and then construct an MFD with the fusion method. The basic idea to determine the fusion weight is introduced as follows: (1) Establish the recognition framework of the DS evidence model based on estimated ATF and ATD for the two sources of data. (2) Quantify the reliability of each source of data for ATF and ATD based on the means and variances of historical data for multiple days; on this basis, calculate the basic probability distribution and basic trust distribution. (3) Synthesize the evidence and calculate the fusion weight of different sources of data based on the Dempster synthesis rule.

3.1. MFD Construction Using VTD

According to Edie’s [21] definition, the parameters of MFD are ATF and ATD, which are linearly related to total travel distance (TTD) and total travel time spent (TTS) of all vehicles, respectively. The specific definitions are shown as Equations (1) and (2),

$$q=\frac{TTD}{L\Delta }$$

(1)

$$k=\frac{TTS}{L\Delta }$$

(2)

where q (vehs/h) and k (vehs/km) are ATF and ATD of network traffic, respectively. $TTD$(veh-km) and $TTS$(veh-h) are total travel distance and total travel time spent of all vehicles during the research period in the test site, respectively; and $L$(km) is the length of the test site. $\Delta$ is the research period, considering the time-varying characteristics of road network traffic; the research period in this paper is 0.25 h.

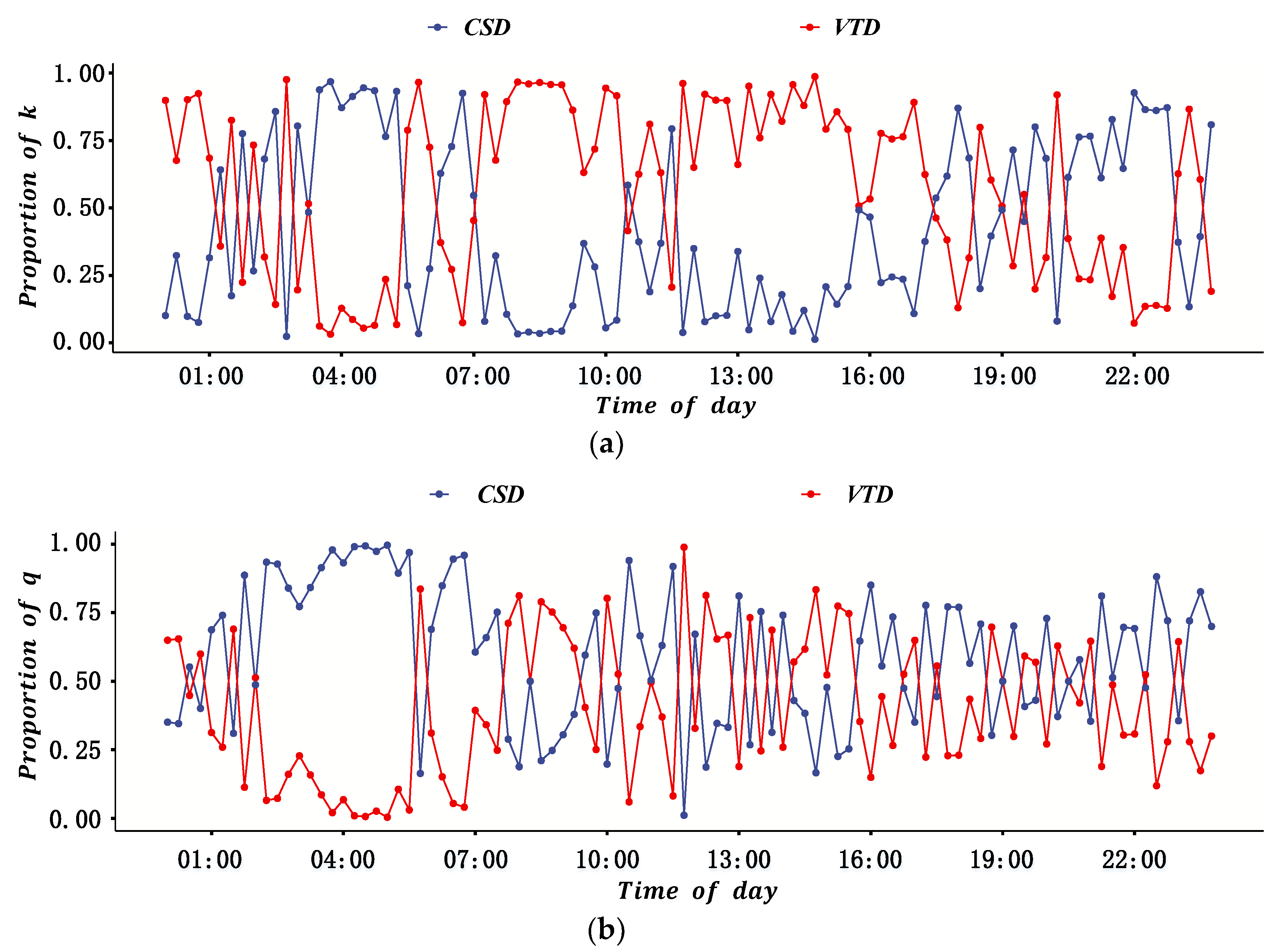
To estimate the total vehicle travel time and total vehicle travel distance, MFD construction using VTD assumed that the number of probe vehicles is sufficiently large and the penetration rate was homogeneous in all areas of a road network. However, these assumptions are inconsistent with the actual situation. Taking taxis as an example, their distribution often varies greatly in different ODs, and their trips are usually more frequent in the central business district of a city. Given this, we intend to construct an MFD using VTD considering the difference in the penetration rate of probe vehicles between different ODs. The method involves two key issues: first, estimating different OD penetration rates of probe vehicles, and second, estimating the total travel time and total travel distance of all vehicles with the penetration rate.

For the first issue, the penetration rate was estimated based on the vehicle identity and location information collected by probe vehicles, supplemented by traffic flow data collected by ALPR. Then, the penetration rate was estimated as the proportion of probe vehicles detected by ALPR detectors between different ODs. The estimation method [14] is shown in Equation (3):

$$p_{ij}\left(t\right)=\mathcal{F}{N}_{ij}\left(t\right)/\mathcal{L}{N}_{ij}\left(t\right)$$

(3)

where $O_i$ and $D_j$ are the first link (link $i$) and last link (link $j$) installed with ALPR detectors that the probe vehicles passed by, respectively; $p_{ij}\left(t\right)$ is the penetration rate of $O_i{D}_j$ during period $t$; and $\mathcal{F}{N}_{ij}\left(t\right)$ (vehs) and $\mathcal{L}{N}_{ij}\left(t\right)$ (vehs) denote the count of detected probe vehicles and the count of all detected vehicles from ALPR detectors for $O_i{D}_j$ during period $t$.

For ODs without ALPR detectors or probe vehicles, the penetration rate was calculated as the proportion of probe vehicles detected by all ALPR detectors in a road network during period $t$. The specific method is shown in Equation (4).

$$\overline{p}\left(t\right)=\mathcal{F}N\left(t\right)/\mathcal{L}N\left(t\right)$$

(4)

where $\overline{p}\left(t\right)$ is the averaged penetration rate for the road network during period $t$, and$\mathcal{F}N\left(t\right)$ (vehs) and $\mathcal{L}N\left(t\right)$ (vehs) are the counts of probe vehicles and all vehicles detected by ALPR detectors during period $t$, respectively.

With the estimated penetration rate, the total travel time and total travel distance were derived by the sum of the expanded travel time and travel distance of each OD. According to Edie’s definition 20, the travel time and travel distance were converted into the ATD and ATF, respectively. For example, the network traffic flow during period $t$ is equal to the number of times of all vehicles running on the road network during period $t$. The specific method is shown in Equations (5) and (6).

$$q^{\mathcal{F}}\left(t\right)=\frac{{{\displaystyle \sum }}_{i=1}^m{{\displaystyle \sum }}_{j=1}^{n}tt{d}_{ij}\left(t\right)/p_{ij}\left(t\right)}{L\Delta }$$

(5)

$$k^{\mathcal{F}}\left(t\right)=\frac{{{\displaystyle \sum }}_{i=1}^m{{\displaystyle \sum }}_{j=1}^{n}tt{s}_{ij}\left(t\right)/p_{ij}\left(t\right)}{L\Delta }$$

(6)

where $q^{\mathcal{F}}\left(t\right)$ (vehs/h) and $k^{\mathcal{F}}\left(t\right)$ (vehs/km) represent the ATF and ATD, respectively, based on VTD during period $t$; $tt{d}_{ij}^{\mathcal{F}}\left(t\right)$ (km) and $tt{s}_{ij}^{\mathcal{F}}\left(t\right)$ (h) denote all probe vehicles’ travel distance and travel time, respectively, of $O_i{D}_j$ in the road network during period $t$; and$m$ and $n$are the count of the first and last links, respectively, installed with ALPR detectors that the probe vehicles passed by during period $t$.

3.2. MFD Construction Using CSD

Generally, detectors are installed in the middle of links of the urban network road in China; therefore, the MFD constructed with CSD is conducted through estimating the ATF and ATD with link length as weight [7]. The specific method is shown in Equations (7) and (8),

$$q^{\mathcal{M}}\left(t\right)={{\displaystyle \sum }}_{i=1}^W{q}_i^{\mathcal{M}}\left(t\right)\ast \left(l_i^{\mathcal{M}}/{{\displaystyle \sum }}_{i=1}^W{l}_i^{\mathcal{M}}\right)$$

(7)

$$k^{\mathcal{M}}\left(t\right)={{\displaystyle \sum }}_{i=1}^W{k}_i^{\mathcal{M}}\left(t\right)\ast \left(l_i^{\mathcal{M}}/{{\displaystyle \sum }}_{i=1}^W{l}_i^{\mathcal{M}}\right)$$

(8)

where $q^{\mathcal{M}}\left(t\right)$ (vehs/h) and $k^{\mathcal{M}}\left(t\right)$ (vehs/km) represent the ATF and ATD, respectively, of the road network based on CSD during period $t$; $q_i^{\mathcal{M}}\left(t\right)$ (vehs/h) and $k_i^{\mathcal{M}}\left(t\right)$ (vehs/km) represent traffic flow and traffic density, respectively, of the $i$-th link installed with fixed vehicle detectors during period $t$; $l_i^{\mathcal{M}}$ is the length of the $i$-th link installed with fixed vehicle detector; and$W$ is the number of fixed vehicle detectors in road networks.

3.3. A Fusion Method for MFD Construction Using Multi-Source Data

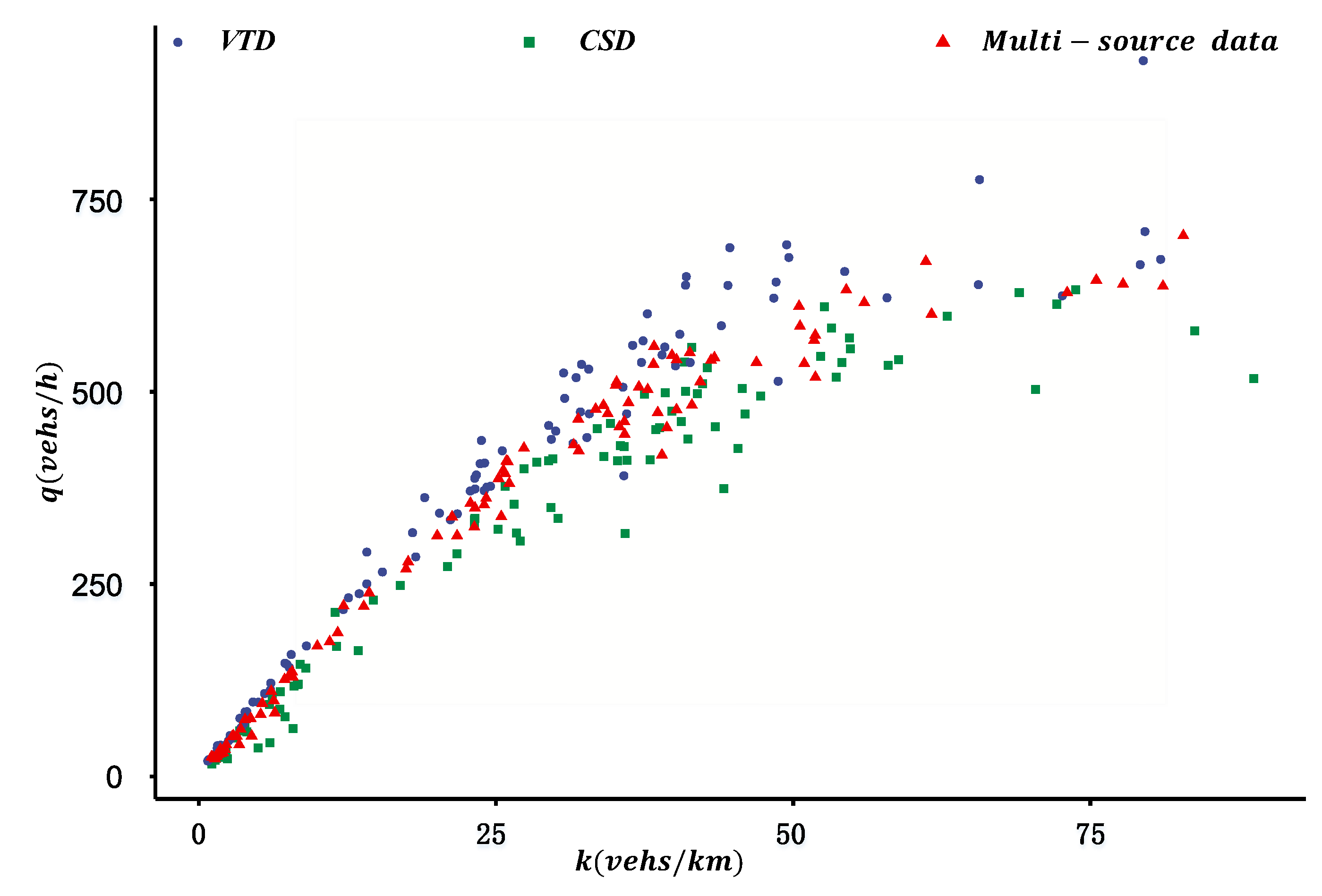
It is theoretically possible to estimate ATF and ATD of road networks based on VTD or CSD. To accurately estimate MFD, some studies [10] used different sources of data to estimate different parameters. However, the assumptions for estimating ATF and ATD with different data sources are different. For ATD estimation, it is generally assumed that the probe vehicles’ amount is sufficient and spatial distribution is uniform. For ATF estimation, it is usually assumed that the traffic flow achieved from detectors is representative. Therefore, there may be inconsistencies in the parameters of MFD using different sources of data to estimate different parameters. Considering the different reliability of different data sources, the basic framework of the fusion method for MFD construction under multi-source data is shown in Equations (9) and (10):

$$q\left(t\right)=\alpha \left(t\right)\ast q^{\mathcal{F}}\left(t\right)+\left[1-\alpha \left(t\right)\right]\ast q^{\mathcal{M}}\left(t\right)$$

(9)

$$k\left(t\right)=\beta \left(t\right)\ast k^{\mathcal{F}}\left(t\right)+\left[1-\beta \left(t\right)\right]\ast k^{\mathcal{M}}\left(t\right)$$

(10)

where $q\left(t\right)$ (vehs/h) and $k\left(t\right)$ (vehs/km) denote the ATF and ATD with fusion method in$t$, respectively. The meanings of $q^{\mathcal{F}}\left(t\right)$, $q^{\mathcal{M}}\left(t\right), k^{\mathcal{F}}\left(t\right)$, and $k^{\mathcal{M}}\left(t\right)$ are the same as in Equations (5)–(8). $\alpha \left(t\right)$ and $\left[1-\alpha \left(t\right)\right]$ are the weight of VTD and CSD for traffic flow estimation in$t$, respectively. $\beta \left(t\right)$ and $\left[1-\beta \left(t\right)\right]$ are the weight of VTD and CSD for traffic density estimation in$t$, respectively.

The core of the fusion method is to determine the weight of the two types of data. The weights were achieved using the ATF, ATD, and their variance distribution (reliability) for different periods during multiple days based on the DS evidence theory [22]. Taking the estimation of $\alpha \left(t\right)$ for ATF in $t$ as an example, the specific process is described as follows.

First, we establish the recognition framework $\Theta \left(t\right)$ of the DS evidence inference model based on the two types of data; the specific description is shown as Equation (11):

$$\Theta \left(t\right)=\left\{q^{\mathcal{M}}\left(t\right),q^{\mathcal{F}}\left(t\right)\right\}$$

(11)

where$q^{\mathcal{M}}\left(t\right)$ and $q^{\mathcal{F}}\left(t\right)$ denote the estimated weight of CSD and VTD for ATF in $t$, respectively.

Since $q^{\mathcal{M}}\left(t\right)$ and $q^{\mathcal{F}}\left(t\right)$ come from different sources of data, they can be considered mutually exclusive. Thus, the power set $2^{{\Vert \Theta \left(t\right)\Vert }_0}$ composed of all elements in $\Theta \left(t\right)$ is shown in Equation (12):

$$\left\{\begin{array}{c}{2}^{{\Vert \Theta \left(t\right)\Vert }_0}=\left\{\varnothing ,X_1\left(t\right),X_2\left(t\right),X_3\left(t\right)\right\}\hfill \\ X_1\left(t\right)=\left\{q^{\mathcal{M}}\left(t\right)\right\}\hfill \\ X_2\left(t\right)=\left\{q^{\mathcal{F}}\left(t\right)\right\}\hfill \\ X_3\left(t\right)=\left\{q^{\mathcal{M}}\left(t\right)\cup q^{\mathcal{F}}\left(t\right)\right\}\hfill \end{array}\right.$$

(12)

where $\varnothing$ is the empty set; $\Theta {\left(t\right)}_0$ is $\mathrm{L}-0$ norm of $\Theta \left(t\right)$, namely, the non-zero element of $\Theta \left(t\right)$; and $X_1\left(t\right), X_2\left(t\right), \mathrm{and} X_3\left(t\right)$ are non-empty sub-collections of $\Theta \left(t\right)$, $X_1\left(t\right)$ (vehs/h), and $X_2\left(t\right)$ (vehs/h), respectively. The first two denote the decision of ATF based on CSD and VTD, while $X_3\left(t\right)$ is an uncertain decision, which means it cannot determine the decision between $X_{1t}$ and $X_{2t}$.

Secondly, DS evidence theory involves two important concepts: basic trust distribution (also known as evidence function) and the Dempster evidence synthesis rule. The basic trust distribution is an indicator to quantify the support degree for a certain decision (namely, the evidence of each decision). The evidence synthesis rule is a comprehensive analysis rule of pieces of evidence corresponding to each decision. Let $\mathrm{s}$: $2^{{\Vert \Theta \left(t\right)\Vert }_0}\to \left[0,1\right]$, meaning that the basic trust distribution $\mathrm{s}$ is a mapping $2^{{\Vert \Theta \left(t\right)\Vert }_0}\to \left[0,1\right]$, which needs to satisfy the requirements described in Equation (13):

$$\left\{\begin{array}{c}{s}_i\left(\varnothing \right)=0\hfill \\ {{\displaystyle \sum }}_{X_j\left(t\right)\subset 2^{{\Vert \Theta \left(t\right)\Vert }_0}}{s}_i\left(X_j\left(t\right)\right)=1\end{array}\right. i=1,2;j=1,2,3$$

(13)

where $i$ is the $i$-th evidence provided by the $i$-th type of data, and $j$ is the $j$-th decision. The meanings of $\varnothing$ and ${\Vert \Theta \left(t\right)\Vert }_0$ are the same as in Equation (12).$s_i\left(X_j\left(t\right)\right)$ represents the degree of support for the decision $X_j\left(t\right)$ provided by the $i$-th type of data evidence, which is equal to the basic trust distribution of decision $X_j\left(t\right)$. The basic trust value of the empty set is 0, and the sum of the trust of the other subset is equal to 1.

The basic trust distribution is determined by the basic probability distribution function $p_i\left(X_j\left(t\right)\right)$ of the decision $X_j\left(t\right)$ under each type of data; the specific method is shown in Equation (14).

$$s_i\left(X_j\left(t\right)\right)=p_i\left(X_j\left(t\right)\right)/{\displaystyle \sum }_{j=1}^3{p}_i\left(X_j\left(t\right)\right),i=1,2$$

(14)

where the meaning of $s_i\left(X_j\left(t\right)\right)$ is the same as in Equation (13), and $p_i\left(X_j\left(t\right)\right)$ is the basic probability distribution function of decision $X_j\left(t\right)$ under different types of data.

Assuming that $p_i\left(X_j\left(t\right)\right)$ satisfies ${\phi }_i\left(v\right)\sim N\left({\mu }_i\left(t\right),{\sigma }_i^2\left(t\right)\right)$, where ${\mu }_i\left(t\right)$ and ${\sigma }_i^2\left(t\right)$ represent the mean and variance (i = 1, 2) of ATF ${\phi }_i\left(v\right)$ during period $t$ for the historical data of the $i$-th type of data, $p_i\left(X_j\left(t\right)\right)$ can be calculated according to Equation (15) [22]:

$$\left\{\begin{array}{c}{p}_i\left(\varnothing \right)=0\hfill \\ p_i\left(X_1\left(t\right)\right)={{\displaystyle \int }}_{{\mu }_1\left(t\right)-1/2}^{{\mu }_1\left(t\right)+1/2}\frac{1}{\sqrt{2\pi }{\sigma }_i\left(t\right)}exp\left\{-\frac{1}{2}{\left(\frac{v-{\mu }_i\left(t\right)}{{\sigma }_i\left(t\right)}\right)}^2\right\}dv\hfill \\ p_i\left(X_2\left(t\right)\right)={{\displaystyle \int }}_{{\mu }_2\left(t\right)-1/2}^{{\mu }_2\left(t\right)+1/2}\frac{1}{\sqrt{2\pi }{\sigma }_i\left(t\right)}exp\left\{-\frac{1}{2}{\left(\frac{v-{\mu }_i\left(t\right)}{{\sigma }_i\left(t\right)}\right)}^2\right\}dv\hfill \\ p_i\left(X_3\left(t\right)\right)=\frac{1}{2\pi {\sigma }_i{}^2\left(t\right)}\left\{\begin{array}{c}{{\displaystyle \int }}_{{\mu }_1\left(t\right)-1/2}^{{\mu }_1\left(t\right)+1/2}exp\left\{-\frac{1}{2}{\left(\frac{v-{\mu }_i\left(t\right)}{{\sigma }_i\left(t\right)}\right)}^2\right\}dv\\ \times {{\displaystyle \int }}_{{\mu }_2\left(t\right)-1/2}^{{\mu }_2\left(t\right)+1/2}exp\left\{-\frac{1}{2}{\left(\frac{v-{\mu }_i\left(t\right)}{{\sigma }_i\left(t\right)}\right)}^2\right\}dv\end{array}\right\}\hfill \end{array}\right.$$

(15)

where $\left[{\mu }_i\left(t\right)-1/2,{\mu }_i\left(t\right)+1/2\right]$ are the integral intervals to calculate $p_i\left(X_1\left(t\right)\right)$ with given ${\phi }_i\left(v\right)$. Moreover, $p_i\left(X_1\left(t\right)\right)$,$p_i\left(X_2\left(t\right)\right)$, and $p_i\left(X_3\left(t\right)\right)$ represent the occurrence probability of decisions $X_1\left(t\right)$, $X_2\left(t\right)$, and $X_3\left(t\right)$, respectively, under the evidence provided by different types of data.

Based on the basic trust assignment $s_i\left(X_j\left(t\right)\right)$ of the decision $X_j\left(t\right)$, the evidence synthesis is conducted with the basic probability assignments of multiple types of evidence using the Dempster evidence synthesis rule [22]. The specific method is shown in Equation (16):

$$s\left(X\right)=\left\{\begin{array}{cc}{K}_D\ast {\displaystyle {\displaystyle \sum }_{X_j\left(t\right)\cap X_j\left(t\right)=X}}{s}_1\left(X_j\left(t\right)\right)s_2\left(X_j\left(t\right)\right)& X\ne \varnothing \\ 0& X=\varnothing \end{array}\right.$$

(16)

where $j=1,2,3$, $s\left(X\right),X\subset 2^{\Vert \Theta {\left(t\right)\Vert }_0}$ is synthetic trust distribution, and $X_j\left(t\right)$ is the decision provided by the evidence of the $j$-th type of data. $1/K_D$ is the conflict coefficient between evidence provided by different types of data, calculated as $1/K_D=1-{\displaystyle \sum }_{X_j\left(t\right)\cap X_j\left(t\right)=\varnothing }{s}_1\left(X_j\left(t\right)\right)s_2\left(X_j\left(t\right)\right)$; the closer $1/K_D$ is to 0, the greater the degree of conflict between the evidence provided by different data sources is, and when $1/K_D=0$, the sum under the Dempster evidence synthesis rule does not exist.

Finally, the fusion weight is determined by the synthetic trust distribution; the method to calculate the weight for $q^{\mathcal{F}}\left(t\right)$ is shown in Equation (17):

$$\alpha \left(t\right)=\frac{s\left(X_2\left(t\right)\right)}{s\left(X_1\left(t\right)\right)+s\left(X_2\left(t\right)\right)}$$

(17)

where, the meaning of $\alpha \left(t\right)$ is the same as in Equation (9), and $s\left(X_1\left(t\right)\right)$, $s\left(X_2\left(t\right)\right),$ and $s\left(X_3\left(t\right)\right)$ represent the synthetic trust distribution of each decision under the evidence provided by each type of data. The abbreviations and variables used in the paper are listed in the Abbreviations.

4. Case Study

The road network in the central urban area of Kunshan was selected as the test site. The test site consists of 71 links and 18 intersections, including links that are prone to traffic congestion, such as Qianjin Road, Bailu Road, and Zhenchuan Road. The data were provided by a real-time monitoring system of urban road traffic conditions in Kunshan city. The system integrates data collected by microwave vehicle detectors, automatic license plate recognition (ALPR) equipment, GPS-equipped taxis, etc. There are 54 sets of ALPR equipment and 33 sets of microwave vehicle detectors. Figure 2 shows the distribution of various devices, and Figure 3 shows the abstract topology of the test site. The data used in our study were from 3 January 2018 to 20 January 2018.

4.1. Data Preprocessing for VTD

The VTD (from the taxis in Kunshan city) consists of the vehicle license plate, time, longitude, latitude, vehicle speed, driving direction, etc. The data are updated every 20 s. An example of the data is shown in

Table 2. Examples of GPS-equipped taxi travel data.

License_ Plate	Date_Key	Time_Key	Status	Latitude	Longitude	Speed	Direction
***** ZF	20180104	07:32:04	0	31.391811	120.959656	5	WB
***** ZF	20180104	07:32:24	0	31.392311	120.959145	25	NB
***** ZF	20180104	07:32:44	0	31.39361	120.959045	27	NB
***** ZF	20180104	07:33:04	0	31.394411	120.959045	17	NB
***** ZF	20180104	07:33:24	0	31.395313	120.959045	15	NB
***** ZF	20180104	07:33:44	0	31.39561	120.959045	0	NB
***** ZF	20180104	07:34:04	1	31.395512	120.959045	3	NB
***** ZF	20180104	07:35:04	1	31.39592	120.962555	16	EB
***** ZF	20180104	07:36:04	1	31.394623	120.96416	18	SB

To protect travelers’ privacy, only part of the license number is displayed in the table, others were replaced by *****.

. After map-matching, there are about 1500 taxis in the study area every day.

The preprocessing for VTD mainly includes the followings steps [23,24]: (1) Given the error of the satellite’s positioning, the VTD is matched with links’ positions. (2) Considering that taxis may stop for a long time to pick up and drop off, or wait for customers, these trajectory points with long-term parking were marked as abnormal data. (3) Considering the spatio-temporal continuity of trajectory data, the discontinuous links between two adjacent points were marked as abnormal data, and abnormal changes in the distance between the downstream intersection and two adjacent points in the same link were also marked as abnormal data. (4) Based on the valid trajectory data, each OD’s count of taxis and each OD’s taxi travel time and travel distance were calculated.

4.2. The Data Preprocessing for ALPR Data

Kunshan city’s ALPR data were collected when vehicles passed stop lines at road intersections. The data consist of ALPR equipment’s ID, date, vehicle license plates, passing time, passing lane, etc. (an example is shown in

Table 3. Examples of automatic license plate recognition (ALPR) data.

ID	Date_Key	Time_Key	License_Plate	Lane
1995	20180104	07:13:00	***** 70	1
710	20180104	07:13:00	***** 1N	3
664	20180104	07:13:00	***** 79	2
459	20180104	07:13:00	***** 27	1
870	20180104	07:13:00	***** 1K	1
220	20180104	07:13:00	***** 17	3
156	20180104	07:13:00	***** U9	3
856	20180104	07:13:00	***** 29	1
1888	20180104	07:13:00	***** PC	1
1940	20180104	07:13:00	unrecognized	1

To protect travelers’ privacy, only the last two digits of the license number are displayed in the table, others were replaced by *****.

). Among them, the equipment’s ID is the unique identification of each device, the passing time represents the time when the vehicle passes the stop line of the entrance, and the passing lane represents the lane where the vehicle was located. Affected by equipment failure, data transmission failure, image recognition quality, etc., there may be problems such as unrecognized vehicle number plates and duplicate records. In view of this, the ALPR data were preprocessed, including time regularization, removal of duplicate records, removal of unrecognized data [25,26], etc. It should be noted that the ALPR data are only used to extract the traffic flow of link; the vehicle trajectory reconstruction is not considered to construct an MFD. The main reasons include three aspects: (1) limited by the cost, ALPR equipment’s coverage is limited, and the vehicle trajectory obtained after vehicle license plate matching is fragmented in time and space; (2) the inflow and outflow of vehicles between the ALPR equipment is serious; and (3) the ALPR equipment in our study only covers the straight and left-turn lane groups.

4.3. The Preprocessing for Microwave Detector Data

Kunshan city’s microwave vehicle detectors are mostly installed in the middle of the links. The traffic flow data of a lane were collected every 30 s. The data consist of the equipment ID, lane ID, date, time, flow, speed, time occupancy, etc. (see

Table 4. Examples of microwave vehicle detector data.

ID	Lane_ID	Date_Key	Time_Key	Flow	Speed	Occupancy
14752043516	2	20180104	07:01:30	11	45	0.13
14752043516	2	20180104	07:02:00	8	41	0.11
14752043516	2	20180104	07:04:00	9	52	0.09
14752043516	2	20180104	07:06:00	7	60	0.08
14752043516	2	20180104	07:07:30	0	0	0
14752043516	2	20180104	07:08:00	3	59	0.02
14752043516	2	20180104	07:09:00	10	55	0.09
14752043516	2	20180104	07:09:30	3	54	0.05
14752043516	2	20180104	07:10:00	1	48	0.01
14752043516	2	20180104	07:11:00	6	45	0.08
14752043516	2	20180104	07:11:30	13	47	0.13

for a sample of the data). In the table, the device ID is the unique identification of each microwave detector, the flow rate is the number of vehicles passing through a detector in a lane within 30 s, the speed is the average speed of all vehicles passing a detector in a lane within 30 s, and the time occupancy rate is time occupancy of a lane over 30 s.

Due to the equipment transmission failure and equipment failure, some microwave data are abnormal. In view of this, the microwave detector data are preprocessed. The preprocessing consists of a data validity test and data aggregation. The data validity test was conducted referring to Ref. [27], aiming to identify abnormal data. Data aggregation includes two aspects: temporal aggregation and spatial aggregation of traffic flow data. Temporal aggregation refers to the aggregation of traffic flow data from the original 30 s interval to the period required for the study, and spatial aggregation refers to aggregate traffic flow of lanes to links and aggregate traffic flow of sections to links [27]. The period for MFD construction is 15 min in our study.

5. Results

This section consists of three parts: a case study, results, and the evaluation. The specific contents are introduced as follows.

5.1. Results of Key Parameters of MFD Construction Using Multi-Source Data

The key parameters of the proposed method for MFD construction include TTS and TTD of probe vehicles, probe vehicles’ penetration rate, and ATF and ATD of the road network of CSD.

The estimation of TTS and TTD of probe vehicles directly affects the accuracy of the MFD. Figure 4a,b shows the travel time and total travel distance of all probe vehicles in a 15 min period from 8 to 14 January 2018 without expansion. January 8 to 12 are weekdays, and 13 and 14 January are weekends.

Figure 4a,b shows that the changing trend of all probe vehicles’ travel time and travel distance every 15 min for the test site during the peak period is similar. The variation in the two parameters between different periods is larger on weekdays, while the changes on weekends are relatively minor. The main reason is that there are many commuting trips at the test site on weekdays, and the travel time and travel distance of all probe vehicles are quite different during peak and off-peak periods. However, on weekends, there are fewer commuting vehicles and there are no obvious morning and evening peaks. The results are consistent with the actual traffic. Figure 4c,d shows the time series of ATF and ATD based on the CSD of the test site from 8 to 14 January 2018. It shows that the ATF and ATD of the test site on weekdays have obvious morning and evening peaks, and are significantly larger than those on weekends. Considering that there are many commuting trips on weekdays, the results of the case study are consistent with the actual traffic.

Table 5. The penetration rate of some ODs from 7:00 a.m. to 7:15 a.m. from 3 January to 20 January 2018.

Time	Link ID of Origin and Destination	Penetration
07:00:01–07:15:00	105106_105108-888250_105110	5.71%
07:00:01–07:15:00	105106_107106-107106_127106	14.29%
07:00:01–07:15:00	105110_107110-107110_127110	4.60%
07:00:01–07:15:00	107110_105110-127110_107110	2.44%
07:00:01–07:15:00	109106_109108-109108_109110	3.51%
07:00:01–07:15:00	109106_109108-109110_127110	11.11%
07:00:01–07:15:00	111108_111110-111110_111112	2.94%
07:00:01–07:15:00	125110_105110-105110_107110	3.06%
07:00:01–07:15:00	125110_105110-107110_127110	4.55%
07:00:01–07:15:00	129110_111110-111110_111112	5.26%

shows the penetration rate of probe vehicles in some ODs from 7:00 a.m. to 07:15 a.m. from 3 January 2018 to 20 January 2018. The link IDs of origins and destinations in the table are the same as those in the road network topology in Figure 3. It shows that the penetration rate of probe vehicles in different ODs is significantly different, which reflects the uneven spatial distribution of probe vehicles.

Figure 5 shows the statistical distribution of the probe vehicles’ penetration rate at each period from 3 January to 20 January 2018. The horizontal axis represents the average penetration rate of the test site in each period, and the vertical axis represents the period’s frequency corresponding to specific penetration rate. It shows that the median penetration rate in the test site is about 2%. Ref. [28] estimated the penetration rate of probe vehicles in the central urban area of Kunshan to be 1.8% during off-peak periods and about 1.5% during the peak period. Since the central area of Kunshan where congestion is frequently presented is selected in our study, more probe vehicles’ trips are presented, so the penetration rate is slightly higher. The estimated results for the penetration rate in our study are consistent with Ref. [28].

Figure 6 shows the boxplot of each period’s penetration rate for weekdays and weekends within 18 days. It can be seen from the figure that the penetration rates at certain periods have obvious differences. Specifically, the penetration rate is relatively high and has a large range from 8:00 p.m. to 6:00 a.m. the next day, while it is relatively low and has a small range from 6:00 a.m. to 8:00 p.m. Judging from the changing trend between weekdays and weekends, the penetration rate also seems different at certain periods. Specifically, the penetration rate has relatively obvious peaks on weekdays. Considering that taxis (probe vehicles) travel frequently at night compared to social vehicles, and that social vehicles generally present at other periods, the penetration rate of probe vehicles is higher at night. In addition, since social vehicle travel at night is lesser and more unstable, its impact on the penetration rate of probe vehicles is greater. The results of the case study are consistent with the actual traffic.

Based on the estimated key parameters, MFD construction under multi-source data was conducted. Considering the stability of fusion weight estimation under different sources of data, the dynamic fusion weights of different periods were estimated. The results of dynamic fusion weights for weekdays are shown in Figure 7.

In Figure 7, the blue and red dots represent the fusion weights of each parameter in each period under CSD and VTD, respectively. It reveals that the fusion weights of the MFD parameters in different periods are significantly different. For the fusion weight estimation of ATD of the test site (Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7a), the weight of the VTD is greater in most periods, and the overall weight is 0.637 on weekdays. For the fusion weight estimation of ATF of the test site (Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7b), the weight of the CSD is slightly larger in most periods (the weight of VTD in some periods is larger; the reason may be that the fixed vehicle detector has detected the queue at these periods, and fixed vehicle data reliability is lower compared to VTD), and the overall weight is 0.551 on weekdays. The estimation of ATD is more accurate using VTD compared with CSD because the spatial coverage of the probe vehicle data is wider, and the estimation of traffic density is easily affected by the location of fixed detectors. However, the sample size is not large enough and the penetration rate is not sufficient; therefore, the estimation for ATF is more accurate using CSD compared with VTD. The results of the case study are consistent with the qualitative analysis results of the two types of data.

5.2. Results of MFD Construction Based on Multi-Source Data

In this section, we focus on the analysis of the constructed MFDs. Figure 8 shows the ATF and the ATD of the test site estimated by VTD, CSD, and multi-source data. Taking the MFD on 4 January 2018 as an example, Figure 8a,b shows the estimated ATD and ATF under different sources of data for the test site. In the figure, the blue round scatter points, green square scatter points, and red triangle scatter points represent the estimated ATD and ATF based on VTD, CSD, and multi-source data in each period, respectively.

Figure 8 shows that the constructed MFDs under different sources of data are consistent, and the change trends of ATD and ATF of the test site under the three types of data are similar. The ATD of the test site under different data sources is similar in most periods. However, the estimated ATF of the test site based on VTD is significantly higher in some periods (such as morning peak and evening peak).

Figure 9 is the boxplot of the ATD and ATF of the test site for each period on weekdays and weekends within 18 days. It is shown that the median ATD and median ATF are significantly different between weekdays and weekends. The ATD of the test site during peak hours on weekdays can reach 75 vehicles/km, and the ATF is about 700 vehicles/h; the ATD during peak hours on weekends is about 50 vehicles/km, and the ATF is about 600 vehicles/h. The distance between the upper and lower edges of the ATF and ATD in the boxplot at each period on weekends is significantly smaller than that in the same period on weekdays, and the ATD and ATF of the test site on weekends have no obvious morning and evening peaks.

Figure 10 shows the scatter plots of the constructed MFDs using different types of data. In the figure, the blue circles, green squares, and red triangles represent the constructed MFDs based on the VTD, CSD, and multi-source data for each period, respectively. It can be seen from the figure that there are many abnormal points in the MFD under the VTD, and the ATF of the test site in some periods is significantly higher. It is concluded that the ATF estimation using VTD is less stable. The estimation of ATF based on the CSD has small fluctuations, but the estimation of the ATD has large fluctuations. The stability of the estimation of the ATD and the ATF under the multi-source data is between VTD and CSD.

Figure 11 shows the scatter plot of the constructed MFDs of weekdays and weekends under multi-source data. In the figure, the horizontal axis and the vertical axis represent the ATD and ATF of the test site (blue dots for weekdays, red dots for weekends), respectively. It is shown that there is a significant difference in the MFD between weekdays and weekends. The range of ATD and ATF on weekdays is significantly wider. Most of the points whose ATD is greater than 60 vehicles/km or traffic flow is greater than 600 vehicles/hour come from weekdays. Given that there is indeed a large number of commuting trips at the test site on weekdays, the results of the case study are consistent with the actual traffic.

The results in Figure 11 reveal that the traffic state of the test site is not over-saturated (with the increasing ATD, ATF shows a downward trend), which may be related to the heterogeneity of the traffic flow of links in the test site. The heterogeneity is general in actual urban traffic networks. Moreover, the evaluation of the proposed method is difficult to realize with real data. Therefore, it is intended to analyze MFD with an over-saturated state and evaluate the performance of the proposed method using simulated data.

5.3. The Evaluation of Constructed MFD’s Accuracy Based on Traffic Simulation

Because of the difficulty of evaluating the accuracy of the proposed method based on real traffic data, the actual traffic of the test site was simulated based on Q-PARAMICS (Quadtone Parallel Microscopic Simulator), and the VTD, CSD, and ALPR data were output. On this basis, the MFD under different sources of data is constructed based on the simulation data, and the accuracy of the proposed method is evaluated. Also based on the test site, the simulated road network is shown in Figure 12 (considering the comparability of the MFD constructed from the actual data and the simulated data, the simulated road network is consistent with the actual one). Based on the traffic flow data of links and intersections that can be observed in 15 min, this paper refers to the method of Ref. [29] to calibrate parameters such as traffic demand and the link’s traffic capacity for traffic simulation. The start time of the simulation is 06:00:00, and the duration is 16 h.

To evaluate the accuracy of the MFD construction method, the CSD for every 5 min and all vehicles’ trajectory data with 0.5 s’ updated frequency were extracted based on traffic simulation. The examples of extracted data are shown in

Table 6. The sample of simulated CSD.

Detector ID	Time	Link Length (m)	Link Flow (Vehs/15 min)
D108124	6:45:00	206	96
D108127	6:45:00	391	176
D108128	6:45:00	361	202
D108129	6:45:00	303	157
D108224	6:45:00	206	106
D108227	6:45:00	391	252
D108228	6:45:00	361	244

and

Table 7. The sample of simulated VTD.

Time	Vehicle ID	Origin ID	Destination ID	Lane	x	y
6:00:01	637893	61	40	1	5738.87	5261.87
6:00:01	637894	89	118	1	5326.12	4727.6
6:00:01	637893	61	40	1	5735.73	5261.81
6:00:01	637894	89	118	1	5329.26	4727.72
6:00:02	637893	61	40	1	5731.97	5261.75
6:00:02	637894	89	118	1	5333.02	4727.87
6:00:02	637894	89	118	1	5337.4	4728.04

(the vehicle position coordinates in the VTD are from the traffic simulation software). It is worth noting that the actual simulated road network is larger than that shown in Figure 12, and the vehicles’ ODs are not limited to the selected area.

To evaluate the accuracy of the proposed method, MFDs of 10 scenarios were constructed with the penetration rate of probe vehicles (5% to 10%) and the coverage rate of fixed vehicle detectors (15% to 90%) and then compared with the MFD under all vehicles’ data. Referring to the research of Saffari et al. [30], the root mean square error between partial samples and full samples was selected as the accuracy evaluation index, and the calculation method is shown in Equation (18):

$$RMSE\left(q,k\right)=\sqrt{\frac{{{\displaystyle \sum }}_{t=1}^T\left[{\left(\frac{q_t^P-q_t^S}{Q}\right)}^2+{\left(\frac{k_t^P-k_t^S}{k_{max}}\right)}^2\right]}{T}}$$

(18)

where $RMSE\left(q,k\right)$ is the root mean square error for ATF and ATD of the test site; $q_t^P$ and $q_t^S$ (vehs/h) denote the ATF derived from simulated full-sample data and simulated multi-source data during period $t$, respectively; $k_t^P$ and $k_t^S$ (vehs/km) are ATD derived from simulated full-sample data and simulated multi-source data during period $t$, respectively; $T$ is the count of periods; Q (vehs/h) is the network traffic capacity; $k_{max}$ (vehs/km) is the maximum ATD, referring to the research of Saffari et al. [30]; and $k_{max}$ is approximated as the mean of the first three maximum ATDs.

Table 8. The error of the constructed MFDs under different sources of data.

Scenario	Error (%)				Improvement of Error (%)
	I	II	III	IV	I	II	III
1	14.8%	7.8%	7.8%	7.7%	7.1%	0.1%	0.1%
2	21.6%	20.4%	18.4%	13.8%	7.8%	6.6%	4.6%
3	21.6%	12.5%	15.5%	10.6%	11.0%	1.9%	4.9%
4	16.7%	39.5%	29.9%	21.8%	−5.1%	17.7%	8.1%
5	16.7%	18.1%	17.1%	12.9%	3.8%	5.2%	4.2%
6	16.7%	7.7%	13.5%	9.6%	7.1%	−1.9%	3.9%
7	14.8%	12.7%	10.2%	9.4%	5.4%	3.3%	0.8%
8	21.6%	48.5%	33.7%	26.2%	−4.6%	22.3%	7.5%
9	21.6%	25.3%	18.6%	21.0%	0.6%	4.3%	−2.4%
10	16.7%	24.4%	19.1%	16.3%	0.4%	8.1%	2.8%

shows the errors of the constructed MFDs with different data sources in each scenario. The improvement in the table refers to the difference between the errors of the current method and the proposed method (MFD fusion construction), and I, II, III, and IV represent MFD construction using simulated CSD, simulated VTD, different sources of data, and simulated multi-source data, respectively. It can be seen from the table that the error of the proposed method is smaller (with a minimum of 7.7%) than that of other methods. For the same scenario, compared with MFD construction using simulated CSD, the error of the constructed MFD is reduced by 11% based on the fusion method. Furthermore, for the same scenario, compared with MFD construction using simulated VTD, the error of the constructed MFD is reduced by 22.3% based on the fusion method. Compared with MFD construction through estimating different parameters separately, the error of the constructed MFD is reduced by 8.1% based on the fusion method. The errors of Scenario 4 and Scenario 8 are as high as 39.5% and 48.5% for simulated VTD, respectively, which reflects the instability of MFD construction based on simulated VTD.

Taking the scenario in which probe vehicles’ penetration rate is 10% and fixed vehicle detectors’ coverage rate is 15% as an example, Figure 13 shows the results of a constructed MFD based on different sources of data. In the figure, the scatter points with blue circles, green squares, purple plus signs, and red triangles represent the estimated traffic density and traffic flow derived from the simulated VTD, simulated full sample data, simulated CSD, and simulated multi-source data for each period, respectively. It can be seen from the figure that the MFD under various data sources is generally consistent. The changing trends of MFD under the three sources of data in different periods are the same, and the values are similar, which confirms the rationality of the proposed method.

The results in Figure 13 reveal that the accuracy of estimated ATF is higher based on simulated CSD compared with that derived from simulated VTD, but the accuracy of estimated ATD is not accurate enough based on simulated CSD. The results also reveal that the MFD under multi-source data integrates the advantages of the two types of data, and the accuracies of estimated ATF and ATD are between those derived from the other two types of data. In addition, like the results of real data, the estimated ATF under the simulated VTD is significantly higher in some periods, and the error is large. In general, the accuracy and stability of MFD construction by the fusion method under multi-source data are higher.

6. Conclusions and Discussion

In this study, we proposed an MFD construction method based on multi-source data, as follows: First, estimate the travel time and travel distance of probe vehicles of each OD, and estimate the probe vehicles’ penetration rate of each OD with the percentage of probe vehicles collected by fixed vehicle detectors. On this basis, the vehicles’ travel time and travel distance are expanded, and then the average traffic density and average traffic flow are estimated. Secondly, the traffic density and traffic flow of each link are collected, and the MFD under cross-sectional traffic flow data is constructed. Finally, considering the historical distribution characteristics of the average traffic density and average traffic flow in each period for different data sources, the reliability of each data source is quantified. On this basis, the MFD under multi-source data is constructed based on DS evidence theory.

Taking the congested area of Kunshan city, Jiangsu province, as the test site, the results for actual and simulated scenarios were analyzed, and the performance of the proposed method was evaluated. The results of the case study show that the changing trends of MFD in different periods under the three data sources are the same, and the values are similar, confirming the reliability of the proposed method. The results also show the high accuracy (with a minimum error of 7.7%) of the constructed MFD under multi-source data. For the same scenario, the MFD construction error of the fusion method has a maximum reduction of 11% compared with that only using cross-sectional traffic flow data, a maximum reduction of 22.3% compared with that only using vehicle trajectory data, and a maximum reduction of 8.1% compared with that based on estimates of different parameters using different data sources. In summary, the proposed method can significantly improve the accuracy of constructed MFDs by combining the advantages of the two types of data. It provides potential to support the evaluation of traffic operation and the optimization of the signal control schemes for urban traffic networks. However, due to the limitations of data availability, the accuracy of the proposed method cannot be evaluated in cities with severe congestion (such as Beijing), whose descending part of MFD would present. In the future, the impact factors that affect the accuracy of constructed MFDs will be investigated through comparative analysis. Additionally, more field validation works are needed to validate the effectiveness of the proposed method.