Abstract
The coordinated development of companies and ecological protection are possible only with increasing environmental awareness. Therefore, this study aims to investigate how companies can achieve sustainable development. It is found that the scientific implementation of the vehicle scheduling problem (VSP) for just-in-time (JIT) delivery in the raw material procurement logistics of iron and steel companies can reduce the carbon emissions in the VSP process and, taking into account the negative correlation between weather conditions and PM10, can effectively reduce PM10. On this basis, a multiobjective optimization model is constructed with the objectives of minimizing carbon emissions and PM10 along with the traditional objective of cost optimization. A greedy algorithm with high computational efficiency and an embedded genetic algorithm (GA) is used to further improve the response time of the VSP. Verification shows that in practice, the model enables companies to effectively reduce not only logistics costs but also PM10 and carbon emissions; in theory, the model expands the applicability of JIT to all value-added activities, exploring all value-added activities in different spatial and temporal dimensions to achieve the optimal combination of company cost, environmental effects, and weather dimensions.
1. Introduction
In 2019, United Nations Secretary-General Guterres stated that without drastic measures to reverse the trend of carbon emissions, we will continue to experience deadly and disastrous heatwaves, storms, and pollution. As a major carbon emitter, China has pledged to reduce carbon emissions per unit gross domestic product (GDP) by more than 65% by 2030 from those in 2005. The steel industry is a key factor in China’s carbon emission control. For HBIS Group Chengsteel Company (hereinafter referred to as Chengsteel), realizing pollution and emission reduction will determine the future survival and fate of the company. In terms of procurement logistics, due to its location in inland mountainous areas, 100% of vanadium containing iron powder, 30% of imported ore powder, 10% of coke, and 100% of the auxiliary materials purchased by the company need to be transported by road. Road transport is the mode of transport with the highest percentage of emissions. This study takes the procurement logistics of vanadium-titanium iron powder as the research object and employs the “door-to-door” feature of automobile transportation to realize “loading and unloading” scheduling from suppliers to factories through the implementation of the vehicle scheduling problem (VSP) for just-in-time (JIT) delivery to reduce the carbon emissions and logistics costs from the waiting time for vehicle loading and unloading as well as reshipment between storage stockyards [1]. In addition, through the analysis of the impact of weather changes on PM10, the functional relationship between weather changes and the PM10 cost target is established. Finally, a comprehensive multiobjective optimization model of logistics cost, carbon emissions, and PM10 cost is constructed [2].
With the JIT-VSP, JIT delivery is completed by vehicle scheduling, where the manufacturer’s supply requirements for each piece of goods from the supplier are within an acceptable time range, there is a designated location, and the quantity requested is available in the current inventory. Under multitask and multiconstraint conditions, the supplier completes all transportation tasks through vehicle scheduling according to the carrying capacity of vehicles [3]. Admittedly, JIT-VSPs are common, but more constraints may be added according to the actual conditions. To address the uncertainty in factors such as supply chain operation, the perishability of transported products, and the termination of partnerships, [4] establish cross-warehouse facilities between suppliers and manufacturers to improve the effectiveness of product distribution. Ref. [5] consider the scheduling of returning vehicles for recycling packaging materials to achieve JIT supply chain sustainability. Ref. [6] discuss the internal JIT-VSP and establish that the exact number of parts can be delivered to the workstation in time through the tractor with carrying capacity constraints.
A review of the VSP-related literature finds that some scholars have not clearly distinguished between the JIT-VSP and time window VSP (TWVSP). Ref. [7] argue that the VSP based on cross-transfer facilities to meet customers’ required time windows (TWs) should be viewed as a TWVSP. Facing the same problem, [4] define it as a JIT-VSP. This issue occurs because the understanding of the JIT concept is not sufficiently thorough. This study distinguishes the two different concepts through comparative analysis. The basic objective of JIT is to reduce inventory, and the strategy to achieve the objective is to quickly respond to customers’ demands [5]. However, the focus of JIT is to take the means to solve the problems exposed by reducing inventory: production streamline, production equalization, and resource allocation rationalization [8]. The ultimate objective is to improve production efficiency by solving problems and eliminating all waste. Therefore, the ultimate objective of the JIT-VSP is to maximize profits, while the focus of the TWVSP is to meet the needs of customers.
Based on the JIT-VSP of procurement logistics in iron and steel firms, the first objective of this study is to reduce the logistics cost, including vehicle operation cost, inventory cost, as well as intermediate inventory loading and unloading cost; the second and third objectives are to reduce the carbon emission and PM10 costs of vehicles [9], respectively, and the comprehensive optimal objective is achieved by the greedy algorithm with an embedded genetic algorithm (GA) [10]. This study contributes to JIT theory and company management. Specifically, the contributions to the JIT production system are as follows: (1) the implementation of the JIT-VSP can reduce emissions and improve the ecological environment; (2) JIT can not only eliminate all non-value-added activities but also create all valuable activities; (3) JIT can enable core firms and upstream firms to “maximize profits” and achieve a win-win outcome. Through one-year cost analysis, (1) the cost of vehicles used by the firm is significantly reduced, (2) the annual carbon emissions are reduced and the PM10 fines are significantly reduced, and (3) the comprehensive target cost is 50,178,635 RMB, amounting to a reduction of 16,282,459 RMB compared with 66,461,094 RMB before optimization. The rest of this article is organized as follows: Section 2 briefly reviews the relevant literature; the mathematical model is constructed, and the algorithm flow is introduced in Section 3; Section 4 describes the problem, introduces a case, and verifies it; Section 5 presents the theoretical and managerial implications of the present study; and Section 6 gives conclusions.
2. Literature Review
2.1. JIT and VSP
JIT is an extension of the Toyota Production System and has been adopted to address the issue of receiving goods from suppliers as needed for reducing inventory holding costs or increasing inventory turnover. However, most researchers treat the ideas of JIT and lean production as interchangeable. The difference between these two ideas is that JIT is production-oriented based on a company, while lean production is customer-oriented. Therefore, studies applied the JIT concept in different fields to promote a company’s performance through the implementation of continuous improvements and problem-solving in their organization [11,12]. Several studies attempted to adopt the JIT concept to reduce the lead time and inventories through integration with VSPs [13]. In a recent application, [14] attempted to utilize JIT considerations in dealing with the COVID 19 pandemic to balance economical and managerial aspects. Several studies highlighted that JIT may be able to control the consumer food waste by generating adaptive interventions [15,16].
The wide applicability of the VSP has attracted many scholars to engage in research in the related fields. Compared with static VSP, the dynamic VSP can adjust the response to external changes in real-time, improving the degree of freedom of decision-making. For example, in a travel plan, the itinerary of tourists may change midway, which causes the originally planned schedule to become suboptimal or even infeasible [17]. The VSP is closely related to the urban public transport system. Urban public transport systems are difficult to model because of their multicriteria characteristics [18]. Due to the environmental protection benefits and low cost of electric vehicles, the number of electric buses is gradually increasing in traditional public transport systems, so traditional public transport dispatching systems are no longer suitable for the current demand [19,20]. Based on the research of single depots, the multidepot VSP is more widely applicable [21,22].
The ultralong distance JIT-VSP of multinational corporations is a new challenge. To increase the coordination and consistency between manufacturing plants and suppliers, [23] set up a transfer station at a wharf. Overseas suppliers store parts and components in the transfer station, and the vehicles realize container distribution according to the production plan of the factory. To solve the VSP of parts distribution in an automobile assembly line, a JIT distribution mode for a parts supermarket was designed [4]. The past research on the JIT-VSP focuses more on solving the problem of how to meet the production demand on time and rarely connects JIT-VSP with the ecological environment for discussion. The impact of JIT on atmospheric suspended particle emissions is even less often studied.
It is increasingly difficult to solve mathematical models of the JIT-VSP with increasing complexity. Default solvers and exact algorithms can solve only some small-scale problems in a limited time. To solve some large-scale problems in practical applications, heuristic algorithms are used to obtain approximate solutions [24]. To solve the VSP based on a JIT automobile assembly line, taking the total penalty of punctual advance and delay time as constraints in the model design and minimization of the inventory level of the production line as the optimization objective, an improved discrete artificial bee colony metaheuristic algorithm was developed [25]. An example showed that the improved algorithm improves the mining ability of the metaheuristic algorithm. In addition, the time penalty of punctuality can be taken as the optimization objective. Aiming at the JIT-VSP of sending parts to an assembly plant, a multiobjective model was constructed by minimizing the number of vehicles and the total waiting time, and the approximate solution was obtained by using the algorithm of large-scale neighborhood search. An example showed that the solution speed is fast and that the result is much better than that of the solver. The JIT-VSP with cross warehouse facilities is another a problem often faced by manufacturing companies. Taking the minimization of the VSP cost as the optimization objective, a delayed start parallel evolutionary algorithm was designed. An example showed that the performance of the improved hybrid heuristic algorithm is superior to that of the general metaheuristic algorithm for solving the JIT-VSP [4].
2.2. Proposed Methods
Greedy algorithms always make the best choice when solving a problem. In other words, without considering the overall optimization, the algorithm obtains the local optimal solution. Greedy algorithms have been successfully applied to various scheduling problems [26,27]. Iterative greedy (IG) algorithms are simple random metaheuristic algorithms. This type of algorithm starts with an initial solution and then tries to improve the current solution through three main stages of iteration (destruction, construction, and acceptance); this can be applied to the workshop scheduling problem with different processing capabilities and unrelated parallel machines. A simple and effective IG algorithm can be used to further improve the quality of the solution. The greedy algorithm has the advantage of a fast operation speed but is easily trapped in local optima. Therefore, more studies use hybrid algorithms combining global search and greedy algorithms to obtain better solutions. An improved particle swarm optimization algorithm combined with a greedy algorithm was introduced for multirobot task allocation strategy optimization [28]. Aiming at the task allocation problem of a multi-intelligent system, with careful consideration of the constraints of space, time, and energy consumption in a multi-intelligent system, a distributed algorithm combining the multiobjective evolutionary algorithm D-NSGA3 and the greedy algorithm was used to search for an optimal solution.
Compared with precise algorithms, heuristic algorithms find a “near-optimal” solution within an acceptable time range. Therefore, researchers prefer to use heuristic algorithms to solve practical problems. In particular, the GA is an effective metaheuristic algorithm that can be used to solve operation management problems such as facility layout problems, supply network design problems, scheduling problems, prediction problems, and inventory control problems [29] and shows good performance in scheduling problems such as process planning and scheduling integration [30,31,32]. The GA can find a better solution in an acceptable time range in the field of operations research, so the GA is the designated algorithm tool by default [33]. An efficient and order-aware hybrid GA was applied to solve the vehicle routing problem with carrying capacity in the Internet of Things [34]. The algorithm improves the initialization strategy and designs the crossover operator for specific problems. Combined with the characteristics of production continuity in iron and steel firms, this study requires rapid scheduling response, so the greedy algorithm with the embedded GA are used to solve it.
3. Materials and Methods
3.1. Objective Function
In the objective function of Equation (1), is the minimized target cost of ten weather characteristics during [35]. is the logistics cost during , including the cost to use the scheduled vehicles, the penalty cost of violating the left TW, the vehicle transportation cost, the inventory cost increase according to the relative humidity level, the inventory cost increase according to the rainfall level, and the water content transportation cost; is the cost of carbon emissions during , including those from waiting for unloading and transportation [36]; and is the PM10 penalty function generated by transportation during .
3.2. Constraints
Equation (2) describes the transportation when vehicle is assigned to the mineral occurrence under weather conditions with a relative humidity level ; Equation (3) expresses the transportation when vehicle is assigned to the mineral occurrence under weather conditions with a rainfall level ; Equation (4) expresses the transportation when vehicle is assigned to the mineral occurrence under weather conditions with a rainfall level . Since the water content in iron powder increases during the transportation process, the inventory is increased accordingly. Equation (5) determines the total transportation distance when the weather relative humidity or rainfall is determined; Equation (6) is the constant carrying capacity of vehicle ; Inequality (7) expresses the situation when the procurement plan for iron powder is much greater than the vehicle carrying capacity; Inequality (8) expresses the situation where the total transportation batch of vehicles is greater than 1; Equation (9) is the time expression of vehicle when it departs from the loading & unloading stockyard, reaches the mineral occurrence , and returns to the loading & unloading stockyard; Equation (10) expresses the constraint of the update of the inventory in the loading & unloading stockyard; Inequality (11) expresses the constraint of the inventory of the loading & unloading stockyard; Inequality (12) expresses the situation when the transportation volume of mineral occurrence is greater than or equal to the planned procurement volume of mineral occurrence .
3.3. Algorithm Process Flow
Taking the beneficiation of vanadium-titanium iron powder as the starting point, the iron powder is transported to the loading & unloading stockyard by automobiles, sent to the sintering stockyard by conveyor belt, sent to the sintering machines by conveyor belt, and finally sintered. Figure 1 is the algorithm process flow chart.
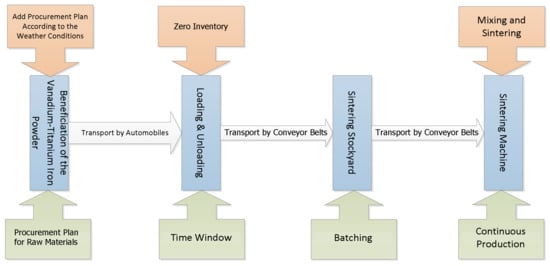
Figure 1.
Algorithm process flow chart.
3.4. Coding Design
This study takes the load capacity of a vehicle as one production unit. According to the production cycle of each production unit and the procurement plan of vanadium-titanium iron powder, a two-dimensional (2D) matrix of production units is established. First, a list composed of the starting time of production of each mineral occurrence is used as the initial code, and the initial population is generated by random combination. While scheduling a vehicle, the earliest completed production unit in the 2D matrix is determined as the transportation unit of this vehicle, and it is matched with the transportation route in the decoding process.
Equation (13) shows the 2D matrix of the production unit. indicates the completion time of the first production unit of mineral occurrence 1, and so on. is the completion time of the production unit of mineral occurrence ; is the completion time of the last production unit.
3.5. Decoding Process
- 1.
- Complete the vehicle scheduling for the procurement plan (weather conditions with relative humidity of 0–39%).
Randomly generate the initial population, determine the transportation task of each mineral occurrence according to the procurement plan, arrange the mineral occurrences to begin production, and set the loading & unloading TW. Check the current inventory of the loading & unloading stockyard, and determine the number of schedulable vehicles before decoding. Complete the matching process between the earliest completion time of the production unit and the vehicle in the 2D matrix of the production unit, and obtain the time at which the vehicle returns to the loading & unloading stockyard. Update the current inventory of each loading & unloading stockyard. According to the loading & unloading TW and the arrival time at the stockyard, calculate the penalty function value of the transportation. The specific steps are as follows:
- Step 1 Set the parameters and initial conditions
First, set the minimum number of vehicles used and various parameters to generate the initial population, and establish the 2D matrix of production unit. Generate the current inventory list of each loading & unloading stockyard and the unloading time of each vehicle.
- Step 2 Update the current inventory and vehicle unloading time list
- Step 3 Determine vehicle scheduling, and arrange vehicle transportation
- ○
- Step 3.1 Determine vehicle scheduling
If the vehicles are in the initial state, randomly select a vehicle to start scheduling. If vehicles are in the process of executing tasks, sort and compare the unloading times of all schedulable vehicles according to the greedy algorithm, and take the vehicle with the current earliest unloading time. Determine the iron powder to be transported , match with the earliest finished production unit in the 2D matrix of the production unit that has not been transported, and record vehicle ’s departure time from the stockyard. Record the vehicle loading time according to Equation (14) and the vehicle arrival time at the stockyard according to Equation (15). Use Equation (16) to calculate the unloading time of the vehicle, and add the data into the unloading time list. Additionally, increase the unit transportation volume, and suspend the elements of the production unit corresponding to the production unit that has completed transportation in the 2D matrix of the production unit.
- ○
- Step 3.2 Calculate the TW penalty function
Compare the current left TW with and, calculate the value of the TW penalty function.
- Step 4 Determine whether the transportation task is completed in the current TW
Calculate the current updated inventory and the maximum inventory of this procurement plan according to Equation (17). If the current TW is lower than the maximum inventory, return to step 2. Otherwise, complete transportation task of mineral occurrence within the current TW.
- Step 5 Supply sintering batch
According to the mixing ratio of sintering raw materials, take the materials from the loading & unloading stockyard and send them to the sintering stockyard through the belt, and calculate the current stock of each loading & unloading warehouse according to Equation (10). Return to step 2, and execute the vehicle scheduling task in the next TW.
- 2.
- Add procurement plan and vehicle scheduling according to the relative humidity or rainfall level of that day.
- Step 6 Determine the relative humidity level (weather condition with relative humidity of 40–100%), and carry out vehicle scheduling
If it is not rainy, determine the relative humidity level , increase the inventory of loading & unloading stockyard accordingly, then perform steps 2 and 3.
- Step 7 Determine the rainfall level of the day and dispatch vehicles
If it is rainy and snowy, according to the -level of rainfall, increase the inventory of loading & unloading stockyard accordingly. Additionally, since the rainfall level reaches , the water content increases; thus, increase the transportation volume; accordingly, perform steps 2 and 3.
- Step 8 Calculate the objective function value
Calculate the objective function value of the number of dispatched vehicles . Then, add another vehicle, and return to Step 1. Until all available vehicles are dispatched, calculate the objective function value of the number of dispatched vehicles is, then compare and take . Figure 2 presents the entire computation procedures.
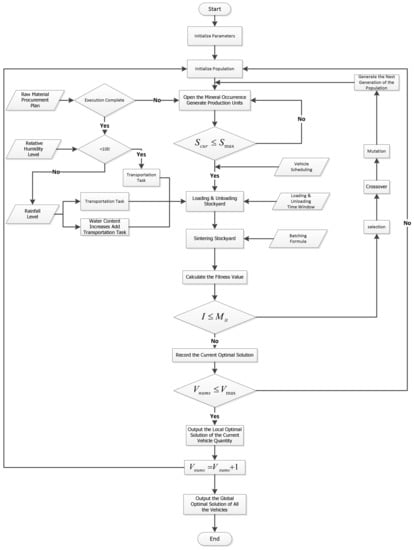
Figure 2.
Algorithm flow chart.
In the flowchart, is the inventory of the loading & unloading stockyard in the current period, the maximum stock for the procurement plan, is the maximum number of iterations of the GA, is the maximum number of dispatchable vehicles, and is the number of vehicles at present.
4. Results
4.1. Case Information
This study takes Chengsteel as an example. The proven reserves of vanadium-titanium magnetite in the Chengde area reach 5.537 billion tons mainly distributed within 100 km around Chengsteel. Nearly 200 concentrators can provide vanadium-titanium iron powder for Chengsteel. The Nanshan stockyard of Chengsteel is responsible for the unloading storage production, supply of iron powder.
Due to the limitations of process equipment and technology, the company faces following problems:
- 1.
- The size of the stockyard is small
Chengsteel is located in a mountainous area, and the stockyard area is small, which does not match the sintering production capacity of Chengsteel, resulting in a multitude of problems. For example, the distance between stockpiles is too small, which often causes material mixing and affects the batching accuracy, the classification of iron powder types is too rough, and the components fluctuate greatly.
- 2.
- The material handling method is outdated
The production and material supply of the stockyard adopts forklift loading & unloading and automobile transportation. The reshipment cost is high.
- 3.
- Weather factors have a great influence
Iron powder is stacked in the open air, and the inventory can be seriously damaged. In the cold in wintertime, the surface iron powder containing water is frozen into blocks, so this iron powder cannot be used for further production; when it rains in summer, the moisture content of iron powder increases from 5 to 10%, affecting the batching accuracy. It has been demonstrated that the implementation of JIT deliveries of iron powder can effectively reduce the cost, improve the efficiency, reduce the damage to goods, and improve the sintering quality.
4.2. Analytical Result
Complete the vehicle scheduling for the procurement plan (weather conditions with relative humidity of 0–39%).
- 1.
- Set parameters and generate initial conditions
After several test trials, the parameters of the algorithm are chosen as follows: population size 30, crossover probability 0.3, mutation probability 0.01, and maximum number of iterations 1000 [37]; and the model parameters are set as follows: production unit 80 tons, vehicle weight 15 tons, minimum number of vehicles 5, maximum number of vehicles 20, loading time 13 min, unloading time 10 min; driving speed 60 km/h.
According to the time taken for processing one production unit at each mineral occurrence provided in Table 1, generate a 2D matrix of the production units in the Section 3.4 coding design according to the purchase plan. Set the purchase cycle to 24 h. From time zero, randomly generate the processing time of the mineral occurrence to generate the initial code, and then generate the initial population.

Table 1.
Symbol definitions.
- 2.
- Vehicle scheduling starts from the minimum number of vehicles
Convert the time from the transportation distance and vehicle speed in Table 2, and carry out the vehicle scheduling of each vehicle according to the greedy algorithm. Record the time when the vehicle arrives at the stockyard, and compare it with the TW of the loading and unloading stockyard, currently in Table 3. Calculate the unloading time of the vehicle and the TW penalty function value of the current vehicle. In addition, within the current TW, according to determine the stock of the material warehouse, and circularly dispatch transportation.

Table 2.
Mineral Occurrence Data.

Table 3.
Loading and Unloading Stockyard TW.
- 3.
- Calculate the sintering batch supply and annual comprehensive cost before optimization
Complete transportation scheduling within the current TW. Carry out sintering mixing according to the batching formula in Table 4, and supply the sintering stockyard. Calculate the current stock of each material warehouse according to . Cycle the vehicle scheduling of the next TW until the procurement plan of one production cycle is completed.

Table 4.
Annual Comprehensive Cost before Optimization.
Add procurement plan and dispatch vehicles according to the weather characteristics.
- 1.
- Statistically analyze the weather data
Statistical analysis shows that the average value of the correlation coefficient r between HR and PM10 of relative humidity in Beijing from 2019 to 2021 is −0.59, indicating that there is a negative correlation between HR and PM10. In this study, the weather characteristics of relative humidity and rainfall in Beijing are classified into 10 levels based on relevant classification criteria.
- 2.
- Calculate the probability distribution function value of relative humidity and rainfall in a year
A data set of the relative humidity and rainfall (rain and snow) in Beijing from 2018 to 2020 is collected. According to the statistical analysis of the data, the relative humidity distribution of nonrainfall weather in Beijing follows a normal distribution with and , and the rainfall follows an exponential distribution with . The distribution probability is calculated according to the full probability formula. Table 5 shows grading division and probability distribution function values of weather characteristics.

Table 5.
Grading Division and Probability Distribution Function Values of Weather Characteristics.
- 3.
- Add procurement plan and vehicle scheduling
According to the weather characteristic values, carry out vehicle scheduling after the procurement plan is added to increase the inventory, and calculate the time penalty function value of each vehicle schedule. After completing the vehicle scheduling for one procurement cycle, gradually increase the number of vehicles, and then carry out vehicle scheduling for another procurement cycle until the scheduling of the maximum number of vehicles is completed. Ultimately, the cumulative statistical table of time penalty function under weather characteristic value in Table 6 is generated. The data in the gray cells in the table are the cumulative minimum values of the TW penalty under the current weather characteristic values.

Table 6.
Cumulative Values of the Time Penalty Function under Different Weather Characteristic Values (units: minutes).
- 4.
- Calculate the objective function value
Table 7 shows the annual logistics costs calculated based on under different weather characteristic values. The data in the gray cells in the table are the annual logistics costs minimum values under the current weather characteristic values. Figure 3 shows local near-optimal solution obtained with the combination of logistics cost and vehicle quantity under different weather characteristic values.). Table 8 is based on the annual carbon emissions according to under different weather characteristic values, the data in the gray cells in the table are the annual carbon emissions minimum values under the current weather characteristic values. Figure 4 shows local near-optimal solution obtained with the combination of carbon emissions and vehicle quantity under different weather characteristic values. Appendix A shows the annual PM10 fines, calculated based on Table 4 lists the annual comprehensive cost before optimization, and Table 9 lists the annual comprehensive cost after optimization. The data in the gray cells in the table represent the minimum values under the current weather characteristic values. Figure 5 shows near-optimal solution obtained with the combination of annual comprehensive cost and vehicle quantity under different weather characteristic values).

Table 7.
Annual Logistics Costs under Different Weather Characteristic Values (units: RMB).
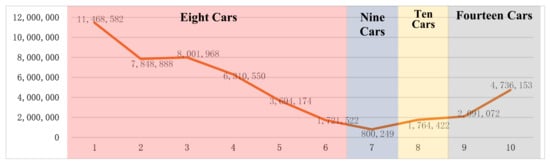
Figure 3.
Local near-optimal solution obtained with the combination of logistics cost and vehicle quantity under different weather characteristic values.

Table 8.
Annual Carbon Emissions under Different Weather Characteristic Values (units: ton).
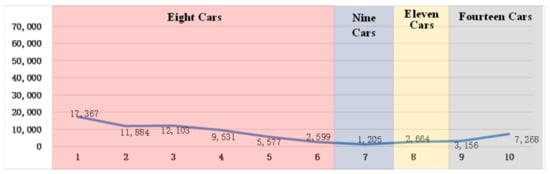
Figure 4.
Local near-optimal solution obtained with the combination of carbon emissions and vehicle quantity under different weather characteristic value.

Table 9.
Annual Comprehensive Cost under Different Weather Characteristic Values (units: RMB).
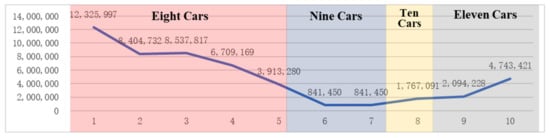
Figure 5.
Near-optimal solution of the comprehensive cost .
5. Implications
This section presents the theoretical and management implications of this study from the analysis of the test results.
5.1. Theoretical Implications
Previous studies on the JIT-VSP mostly focused on controlling the vehicle cost and time cost while satisfying the time constraints of downstream processes but ignored the inventory problem under JIT. Based on the core idea of JIT “pull”, this study takes inventory minimization as the production constraint of downstream processes. The implementation of the JIT-VSP has a direct impact on the carbon emissions of the dispatching vehicles. Compared with the continuous improvement concept of eliminating all non-value-added activities, this new solution creatively puts forward the idea of constantly exploring all value-added activities and reasonably dispatches vehicles according to the impact of weather changes on PM10. An example shows that the implementation of JIT can achieve the objective of “zero inventory” for downstream companies and upstream companies at the same time and ultimately is mutually beneficial.
Production JIT argues that inventory is proof of an unreasonable production system design, uncoordinated production processes, and poor production operation. Realizing “zero inventory” not only eliminates waste in inventory but also improves the external production efficiency, which is a reason why “zero inventory” is a primary objective of JIT. Previous studies focused only on JIT supply to meet demand, that is, the external appearance of JIT, while ignoring the core concept of JIT production.
While vehicle scheduling meets JIT production, it can reduce vehicle waiting time or vehicle driving distance by improving the connection of various production links to reduce carbon emissions. Technology creates value. In the dimensions of space and time, exploring all value-added activities is essential. According to the environment and weather changes in the area where a company is located, this study associates vehicle scheduling with multiple weather factors to realize added value in the dimensions of time and space. The JIT-VSP is implemented to realize the optimal combination of firm cost, environmental factors and three-dimensional weather conditions.
In previous studies, the JIT production models based on supply chain strategies focus on the interests of core companies while ignoring the contributions of relevant upstream suppliers. They often sacrifice the interests of suppliers to achieve the production and operation objectives of core companies. Based on actual conditions, in this study, upstream firms are used as a link in the production of core firms to implement JIT for joint continuous improvement; thus, everyone benefits.
5.2. Managerial Implications
Logistics costs represent the largest cost in procurement and transportation. The logistics cost after optimization is 48,437,582 RMB, which is 2,827,234 RMB lower than the logistics cost (51,264,816 RMB) before optimization, shown in Table 4 and Table 8. In particular, the reduction in vehicle use cost is the main factor reducing the logistics cost. Before the optimization, the company used 24 vehicles. After the optimization, 8 vehicles can complete the same transportation task in 90% of the cases in a year.
Carbon emissions and atmospheric particulate matter from iron powder transportation are the main pollutants in procurement. After the implementation of the JIT-VSP, according to Table 7, the annual carbon emissions are 73,354 tons, whereas the carbon emissions before optimization are 76,729 tons, amounting to a reduction in carbon emissions after optimization of 3375 tons. According to Appendix A, the PM10 fines after optimization are 2,643,264 RMB, amounting to a reduction of 24.1% compared with the 3,484,290 RMB before optimization.
According to Table 7, 73,354 tons/year of annual carbon emissions are generated during the transportation of iron powder, a reduction of 3351 tons/year after the optimization compared with the annual carbon emissions of 76,705 tons/year before the optimization; this reduction is achieved by decreasing the vehicle waiting time for unloading. The implementation of JIT-VSP improves the efficiency of the connection between processes and thus reduces the vehicle waiting time for unloading to a certain extent, thereby achieving the effect of carbon emission reduction.
Atmospheric particulate matter is a major pollutant in the transportation of iron powder. Referring to Appendix A, the PM10 penalty cost after the optimization is 2,643,264 RMB/year, a 24.1% reduction compared with 3,484,290 RMB/year before the optimization, indicating that the implementation of JIT-VSP substantially lowers the emissions of atmospheric particulate matter during the transportation of iron powder.
The objective of the model is to optimize the combination of logistics cost, carbon emission and PM10 fines. Referring to Table 4 and Table 9, the comprehensive target cost is 50,178,635 RMB, amounting to a reduction by 16,282,459 RMB compared with the 66,461,094 RMB before optimization. In the vehicle scheduling description of Figure 5, the values of 1–5, 6–7, 8 and 9–10 are taken according to the weather characteristics, and the corresponding numbers of scheduled vehicles are 8–11 and 14, respectively.
6. Conclusions
The consequences of various types of environmental pollution have demonstrated to the world that national action to reduce pollution and emissions is urgently needed. The iron & steel industry is a major emitter and a key target for emission control in China. Based on the annual output of 8 million tons of steel, Chengsteel needs more than 16 million tons of raw fuel. At present, 1/3 of the raw fuel still needs to be transported by automobile. In addition, 100% of the tailings produced by smelting are transported by automobile, and the total annual automobile transportation volume is more than 10 million tons. Moreover, the carbon emissions of trucks are more than ten times, even dozens of times, those of cars. Therefore, it is of great practical significance to study the carbon emissions and suspended particulate matter emissions of the carrier vehicles operated by Chengsteel.
Different from the previous studies on JIT-VSP, this study focuses on the core idea of JIT “pull”, determines the unreasonable designs, uncoordinated production processes, and poor production operations in the production system through the implementation of the strategy of gradually reducing inventory, and gradually improves and perfects them [39]. In addition, the implementation of the JIT-VSP can reduce the vehicle retention time, reduce the vehicle driving distance and reduce carbon emissions by improving the connection of all production links. Based on the classical JIT theory, this study creatively proposes exploring all value-added activities and realizing the optimal combination of firm cost, environmental factors and weather conditions in the dimensions of space and time. It is empirically verified that compared with the comprehensive objective of the company without implementation of optimization, when 24 vehicles are used, the cost is reduced after optimization, when 8 vehicles are used for 90% of the year, the carbon emissions are reduced by 4.3%, and the PM10 is reduced by 24.1%, thus achieving the effect of comprehensive optimization.
Empirical verification reveals an enormous gap between the optimized comprehensive cost and the optimal cost target. For example, the carbon emissions due to vehicle waiting time for unloading is 14,087 tons/year, accounting for 19.2% of the total carbon emissions; the logistics cost due to vehicle waiting time for unloading is 5,073,500 RMB, accounting for 9.55% of the total logistics cost. The gap from the optimal comprehensive cost target suggests that there remains significant room for improvement in future research.
The implementation of the JIT-VSP on vanadium-titanium iron powder reveals an important discovery after a period of application. Vanadium-titanium iron powder is produced continuously and in batches. If the corresponding batch is purchased, the chemical composition of iron powder is relatively stable. Adopting JIT-VSP’s “loading and unloading” and “zero inventory” management models from suppliers to manufacturers further stabilizes the sinter ingredients and improves the sinter quality and realizes quality tracking of vanadium-titanium iron powder from the supplier to the manufacturer. If the blast furnace conditions fluctuate, it is easier to find the cause from the source. Second, the implementation of the JIT-VSP not only improves the use efficiency of vehicles but also alleviates the traffic congestion in the stockyard, making the links such as vehicle entry, weight inspection and sampling smoother.
This study only takes the JIT-VSP of vanadium-titanium iron powder from Chengsteel as a verification example to demonstrate through production practice the contribution of the proposed method toward sustainable firm development. Under the pressure of the state policy on environmental protection, the test method has been quickly applied to practical production. Therefore, further verification will be performed in the follow-up study using a comparative model to address the limitations of this study in verifying the test method. This study takes the JIT-VSP of vanadium-titanium iron powder from Chengsteel as an example for verification purpose. If it is applied to other raw fuels and auxiliary materials such as imported ore, coke, and fluorite, further study should be carried out in combination with the constraints (e.g., purchase and transportation conditions, production process performance, storage mode, and mixed transportation) of each raw fuel and auxiliary material. In addition, how to improve the recovery rate and recovery quality and reduce environmental pollution for steel recyclable tailings (e.g., sinter return, blast furnace slag, gas ash, and steel slag) is a more complicated and comprehensive problem in the application of JIT-VSP in circular supply chain. Considering the very high resource consumption of iron and steel firms and their serious threat to the environment, how to deal with recyclable tailings, wastewater, and waste in a scientific and reasonable way is also an urgent problem to be addressed as a next step.
Author Contributions
Conceptualization, B.Q.; Data curation, S.L.; Investigation, B.Q.; Methodology, K.-J.W.; Supervision, S.L.; Writing—original draft, B.Q.; Writing—review & editing, K.-J.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Fines under Different Weather Characteristic Values (units: RMB).
Table A1.
Fines under Different Weather Characteristic Values (units: RMB).
| Characteristic Values | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Number of Cars | |||||||||||
| 8 | 840,048 | 543,960 | 523,746 | 389,088 | 213,528 | 92,898 | 39,996 | 0 | 0 | 0 | |
| 9 | 840,048 | 543,960 | 523,746 | 389,088 | 213,528 | 92,898 | 39,996 | 0 | 0 | 0 | |
| 10 | 840,048 | 543,960 | 523,746 | 389,088 | 213,528 | 92,898 | 39,996 | 0 | 0 | 0 | |
| 11 | 840,048 | 543,960 | 523,746 | 389,088 | 213,528 | 92,898 | 39,996 | 0 | 0 | 0 | |
| 12 | 840,048 | 543,960 | 523,746 | 389,088 | 213,528 | 92,898 | 39,996 | 0 | 0 | 0 | |
| 13 | 840,048 | 543,960 | 523,746 | 389,088 | 213,528 | 92,898 | 39,996 | 0 | 0 | 0 | |
| 14 | 840,048 | 543,960 | 523,746 | 389,088 | 213,528 | 92,898 | 39,996 | 0 | 0 | 0 | |
| 15 | 840,048 | 543,960 | 523,746 | 389,088 | 213,528 | 92,898 | 39,996 | 0 | 0 | 0 | |

Table A2.
Case Parameters.
Table A2.
Case Parameters.
| Freight (RMB/ton-kilometer) | 0.21 |
| Carbon Emissions (kg/ton-kilometer) | 0.47 |
| Carbon Emissions Cost (US$/ton) | 24 |
| Vehicle Load(ton) | 80 |
| Vehicle Body Weight (ton) | 15 |
| PM10 Fines (RMB/each transport) | 111 |
References
- Dulebenets, M.A. An Adaptive Polyploid Memetic Algorithm for scheduling trucks at a cross-docking terminal. Inf. Sci. 2021, 565, 390–421. [Google Scholar] [CrossRef]
- Liu, Z.Z.; Wang, Y.; Huang, P.Q. AnD, A many-objective evolutionary algorithm with angle-based selection and shift-based density estimation. Inf. Sci. 2020, 509, 400–419. [Google Scholar] [CrossRef] [Green Version]
- Boysen, N.; Briskorn, D.; Emde, S. Just-in-time vehicle scheduling with capacity constraints. IEEE Trans. 2016, 48, 134–145. [Google Scholar] [CrossRef]
- Dulebenets, M.A. A Delayed Start Parallel Evolutionary Algorithm for just-in-time truck scheduling at a cross-docking facility. Int. J. Prod. Econ. 2019, 212, 236–258. [Google Scholar] [CrossRef]
- Tseng, S.H.; Wee, H.M.; Reong, S.; Wu, C.I. Considering JIT in assigning task for return vehicle in green supply chain. Sustainability 2019, 11, 6464. [Google Scholar] [CrossRef] [Green Version]
- Emde, S.; Schneider, M. Just-in-time vehicle routing for in-house part feeding to assembly lines. Transp. Sci. 2018, 52, 657–672. [Google Scholar] [CrossRef]
- Ladier, A.L.; Alpan, G. Cross-docking operations, Current research versus industry practice. Omega 2016, 62, 145–162. [Google Scholar] [CrossRef]
- Pinto, J.L.Q.; Matias, J.C.O.; Pimentel, C.; Azevedo, S.G.; Govindan, K. Introduction to lean and just-in-time manufacturing. In Just In Time Factory; Springer: Cham, Switzerland, 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Dulebenets, M.A.; Pasha, J.; Kavoosi, M.; Abioye, O.F.; Ozguven, E.E.; Moses, R.; Boot, W.R.; Sando, T. Multiobjective optimization model for emergency evacuation planning in geographical locations with vulnerable population groups. J. Manag. Eng. 2020, 36, 4019043. [Google Scholar] [CrossRef]
- Fathollahi-Fard, A.M.; Dulebenets, M.A.; Hajiaghaei-Keshteli, M.; Tavakkoli-Moghaddam, R.; Safaeian, M.; Mirzahosseinian, H. Two hybrid meta-heuristic algorithms for a dual-channel closed-loop supply chain network design problem in the tire industry under uncertainty. Adv. Eng. Inform. 2021, 50, 101418. [Google Scholar] [CrossRef]
- Alcaraz, J.L.G.; Macías, A.A.M.; Luevano, D.J.P.; Fernández, J.B.; López, A.D.J.G.; Macías, E.J. Main benefits obtained from a successful JIT implementation. Int. J. Adv. Manuf. Technol. 2016, 86, 2711–2722. [Google Scholar] [CrossRef]
- Chakrabarty, R.; Roy, T.; Chaudhuri, K.S. An examination of inventory and production costs in the models with stock out risk under JIT system. Int. J. Bus. Forecast. Mark. Intell. 2017, 3, 259–269. [Google Scholar] [CrossRef]
- Apornak, A.; Hezaveh, M.A. Extension of the model of manufacturing supply chain quality management, an empirical study. Int. J. Product. Qual. Manag. 2019, 28, 417–437. [Google Scholar] [CrossRef]
- Milewski, D. Managerial and Economical Aspects of the Just-In-Time System “Lean Management in the Time of Pandemic”. Sustainability 2022, 14, 1204. [Google Scholar] [CrossRef]
- Nahum-Shani, I.; Smith, S.N.; Spring, B.J.; Collins, L.M.; Witkiewitz, K.; Tewari, A.; Murphy, S.A. Just-in-time adaptive interventions (JITAIs) in mobile health, key components and design principles for ongoing health behavior support. Ann. Behav. Med. 2018, 52, 446–462. [Google Scholar] [CrossRef] [Green Version]
- Roe, B.E.; Qi, D.; Beyl, R.A.; Neubig, K.E.; Apolzan, J.W.; Martin, C.K. A Randomized Controlled Trial to Address Consumer Food Waste with a Technology-aided Tailored Sustainability Intervention. Resour. Conserv. Recycl. 2022, 179, 106121. [Google Scholar] [CrossRef]
- Ozbaygin, G.; Savelsbergh, M. An iterative re-optimization framework for the dynamic vehicle routing problem with roaming delivery locations. Transp. Res. Part B Methodol. 2019, 128, 207–235. [Google Scholar] [CrossRef]
- Anokić, A.; Stanimirović, Z.; Davidović, T.; Stakić, Đ. Variable neighborhood search based approaches to a vehicle scheduling problem in agriculture. Int. Trans. Oper. Res. 2020, 27, 26–56. [Google Scholar] [CrossRef] [Green Version]
- Teng, J.; Chen, T.; Fan, W.D. Integrated approach to vehicle scheduling and bus timetabling for an electric bus line. J. Transp. Eng. Part A Syst. 2020, 146, 4019073. [Google Scholar] [CrossRef]
- Wang, C.; Guo, C.; Zuo, X. Solving multi-depot electric vehicle scheduling problem by column generation and genetic algorithm. Appl. Soft Comput. 2021, 112, 107774. [Google Scholar] [CrossRef]
- Kulkarni, S.; Krishnamoorthy, M.; Ranade, A.; Ernst, A.T.; Patil, R. A new formulation and a column generation-based heuristic for the multiple depot vehicle scheduling problem. Transp. Res. Part B Methodol. 2018, 118, 457–487. [Google Scholar] [CrossRef]
- Zhou, G.J.; Xie, D.F.; Zhao, X.M.; Lu, C. Collaborative optimization of vehicle and charging scheduling for a bus fleet mixed with electric and traditional buses. IEEE Access 2020, 8, 8056–8072. [Google Scholar] [CrossRef]
- Schwerdfeger, S.; Boysen, N.; Briskorn, D. Just-in-time logistics for far-distant suppliers, scheduling truck departures from an intermediate cross-docking terminal. OR Spectr. 2018, 40, 1–21. [Google Scholar] [CrossRef]
- Peng, Y.; Zeng, T.; Han, Y.; Xia, B. Scheduling just-in-time transport vehicles to feed parts for mixed model assembly lines. Discret. Dyn. Nat. Soc. 2020, 2020, 2939272. [Google Scholar] [CrossRef]
- Zhou, B.; Peng, T. Scheduling the in-house logistics distribution for automotive assembly lines with just-in-time principles. Assem. Autom. 2017, 37. [Google Scholar] [CrossRef]
- Benavides, A.J.; Ritt, M. Two simple and effective heuristics for minimizing the makespan in non-permutation flow shops. Comput. Oper. Res. 2016, 66, 160–169. [Google Scholar] [CrossRef]
- Arroyo, J.E.C.; Leung, J.Y.T.; Tavares, R.G. An iterated greedy algorithm for total flow time minimization in unrelated parallel batch machines with unequal job release times. Eng. Appl. Artif. Intell. 2019, 77, 239–254. [Google Scholar] [CrossRef]
- Kong, X.; Gao, Y.; Wang, T.; Liu, J.; Xu, W. Multi-robot task allocation strategy based on particle swarm optimization and greedy algorithm. In Proceedings of the IEEE 8th Joint International Information Technology and Artificial Intelligence Conference (ITAIC), Chongqing, China, 24–26 May 2019; pp. 1643–1646. [Google Scholar] [CrossRef]
- Katoch, S.; Chauhan, S.S.; Kumar, V. A review on genetic algorithm, past, present, and future. Multimed. Tools Appl. 2021, 80, 8091–8126. [Google Scholar] [CrossRef]
- Yuce, B.; Fruggiero, F.; Packianather, M.S.; Pham, D.T.; Mastrocinque, E.; Lambiase, A.; Fera, M. Hybrid Genetic Bees Algorithm applied to single machine scheduling with earliness and tardiness penalties. Comput. Ind. Eng. 2017, 113, 842–858. [Google Scholar] [CrossRef]
- Arakaki, R.K.; Usberti, F.L. Hybrid genetic algorithm for the open capacitated arc routing problem. Comput. Oper. Res. 2018, 90, 221–231. [Google Scholar] [CrossRef]
- Karakatič, S. Optimizing nonlinear charging times of electric vehicle routing with genetic algorithm. Expert Syst. Appl. 2021, 164, 114039. [Google Scholar] [CrossRef]
- Lee, C.K.H. A review of applications of genetic algorithms in operations management. Eng. Appl. Artif. Intell. 2018, 76, 1–12. [Google Scholar] [CrossRef]
- Lin, N.; Shi, Y.; Zhang, T.; Wang, X. An effective order-aware hybrid genetic algorithm for capacitated vehicle routing problems in internet of things. IEEE Access 2019, 7, 86102–86114. [Google Scholar] [CrossRef]
- Zhao, H.; Zhang, C. An online-learning-based evolutionary many-objective algorithm. Inf. Sci. 2020, 509, 1–21. [Google Scholar] [CrossRef]
- Pasha, J.; Dulebenets, M.A.; Fathollahi-Fard, A.M.; Ian, G.; Lau, Y.Y.; Singh, P.; Liang, B. An integrated optimization method for tactical-level planning in liner shipping with heterogeneous ship fleet and environmental considerations. Adv. Eng. Inform. 2021, 48, 101299. [Google Scholar] [CrossRef]
- Wang, C.; Shi, H.; Zuo, X. A multi-objective genetic algorithm based approach for dynamical bus vehicles scheduling under traffic congestion. Swarm Evol. Comput. 2020, 54, 100667. [Google Scholar] [CrossRef]
- Ricke, K.; Drouet, L.; Caldeira, K.; Tavoni, M. Country-level social cost of carbon. Nat. Clim. Change 2018, 8, 895–900. [Google Scholar] [CrossRef]
- Rabbani, M.; Oladzad-Abbasabady, N.; Akbarian-Saravi, N. Ambulance routing in disaster response considering variable patient condition, NSGA-II and MOPSO algorithms. J. Ind. Manag. Optim. 2022, 18, 1035. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).