Reservoir Operation Sequence- and Equity Principle-Based Multi-Objective Ecological Operation of Reservoir Group: A Case Study in a Basin of Northeast China
Abstract
:1. Introduction
2. Material and Methods
2.1. Multi-Objective Ecological Operation Model
2.1.1. Objective Function
- Maximize WSGR
- 2.
- Maximize EFS
2.1.2. Constraints
- Water balance constraint:
- 2.
- Reservoir outflow and water supply constraints:
- 3.
- Reservoir storage capacity constraint:
- 4.
- Channel overflow capacity constraints:
2.1.3. Reservoir Operation Sequence (ROS) and Equity Principle (EP)
- Reservoir Operation Sequence (ROS)
2.2. Equity Principle (EP)
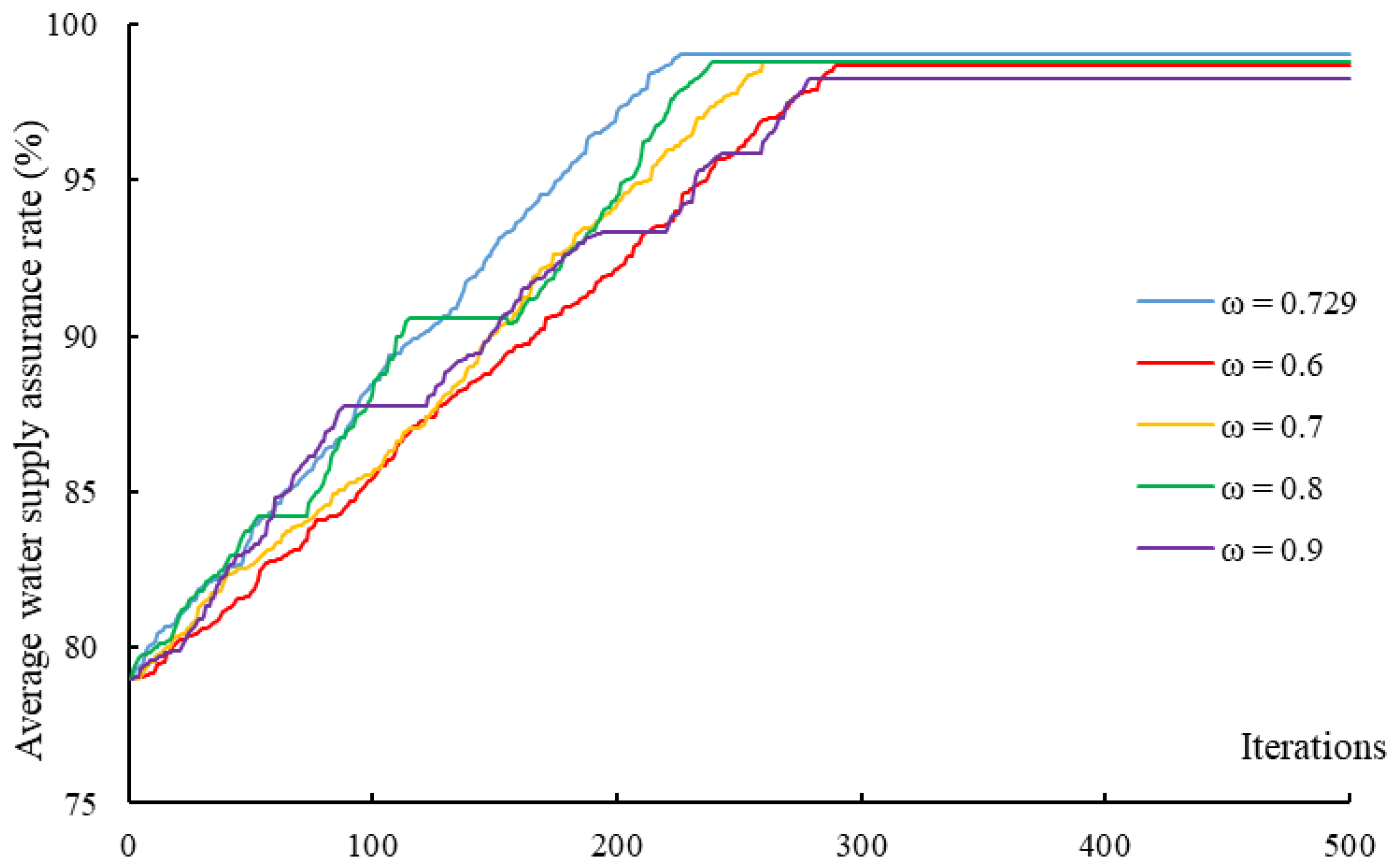
2.2.1. Optimisation Algorithm
2.2.2. Data Input
2.3. Case Study
2.3.1. Study Area and Data
2.3.2. Calculation of Ecological Flow
2.3.3. Scheduling Network Generalisation
2.3.4. Scheduling Schemes Setting
3. Results
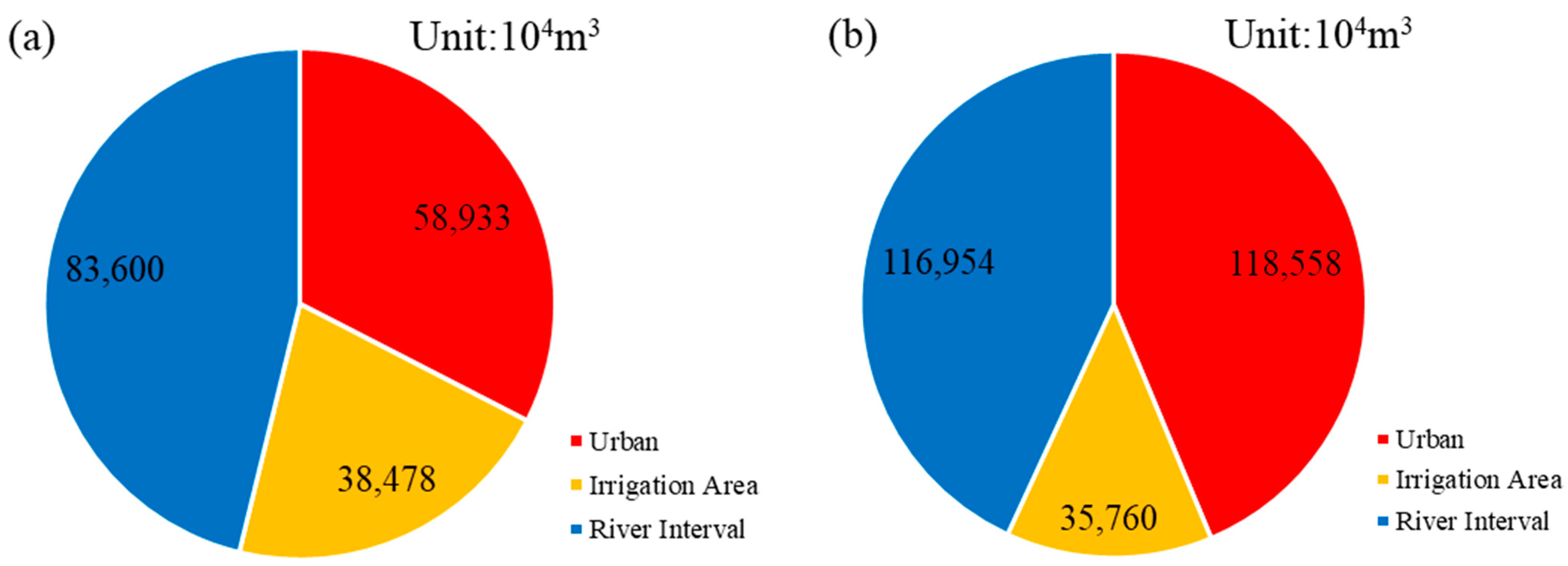
3.1. Water Demand Prediction
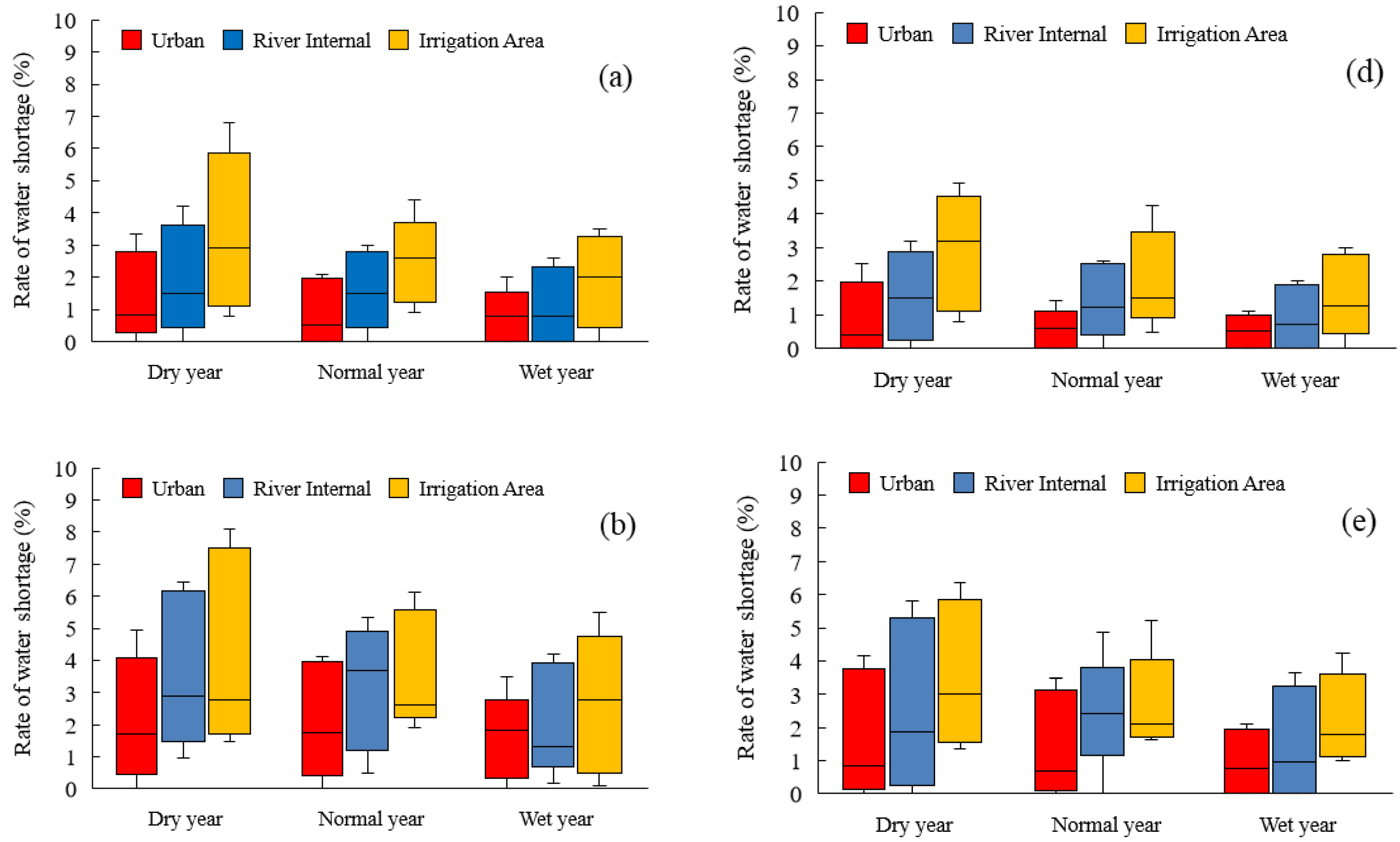
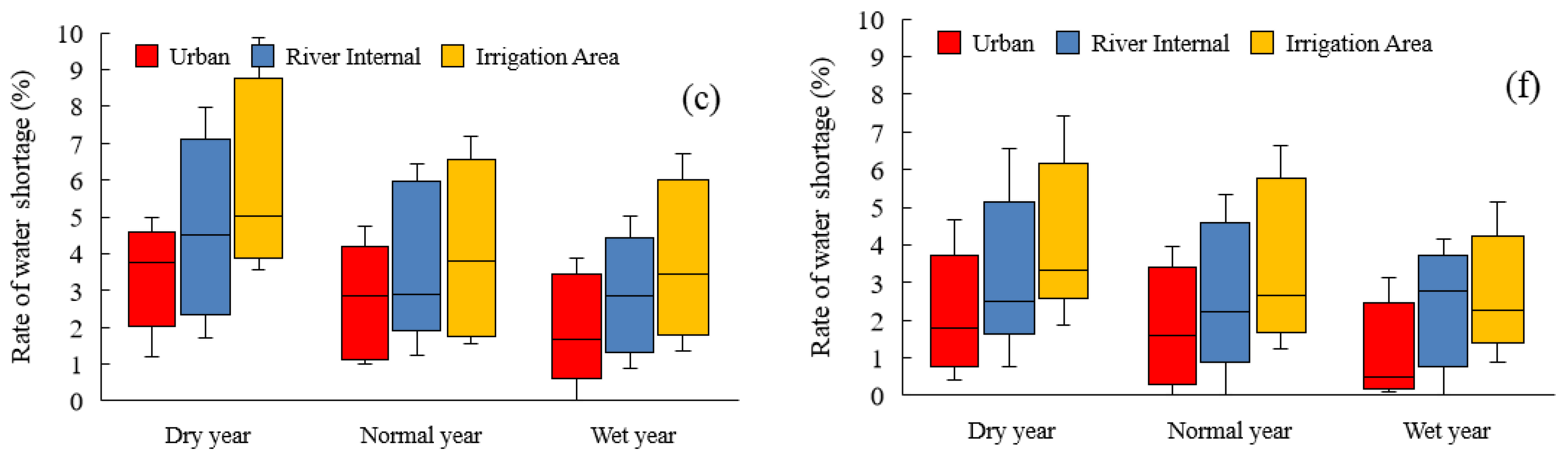
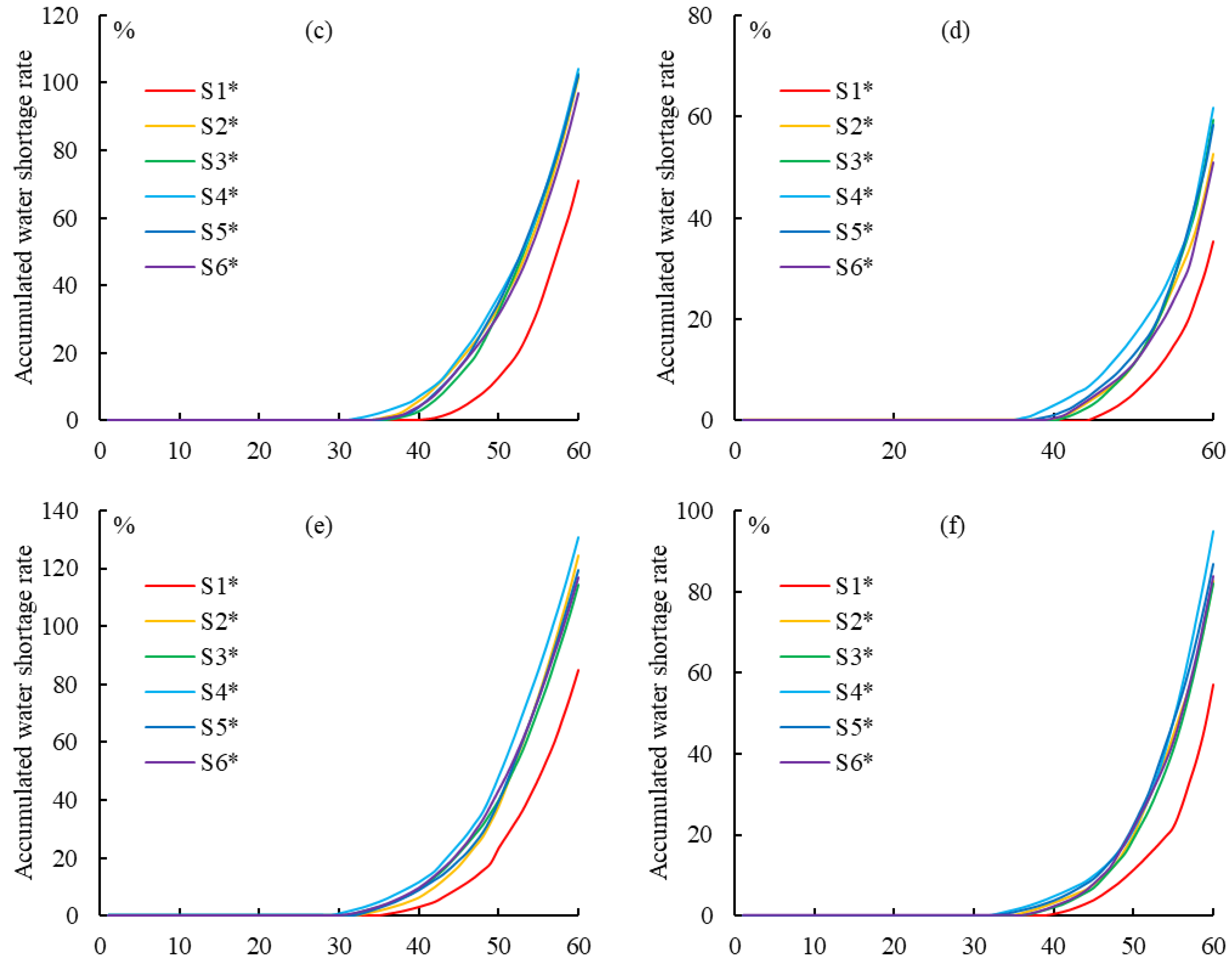
3.2. Supply-Demand Balance Analysis
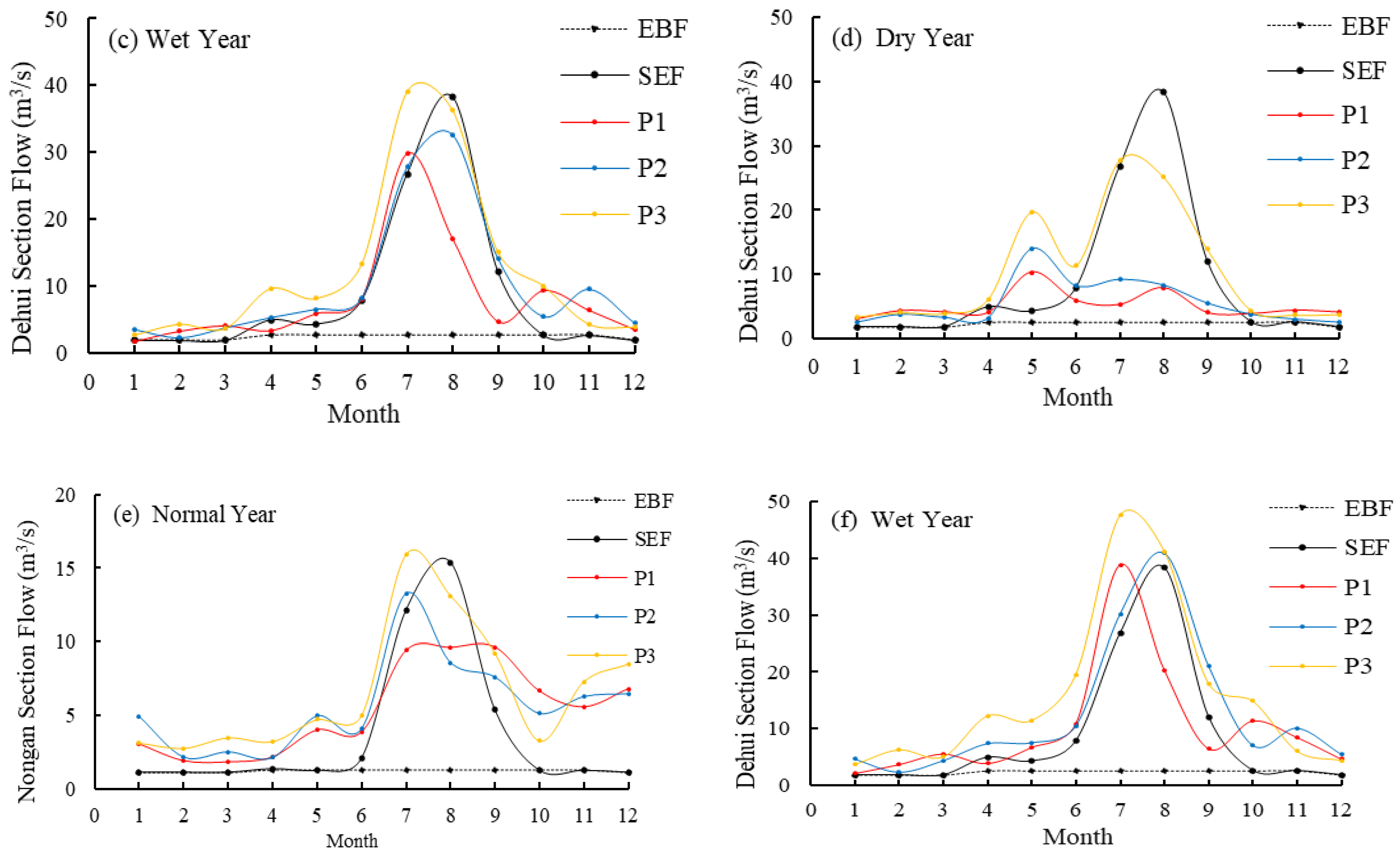
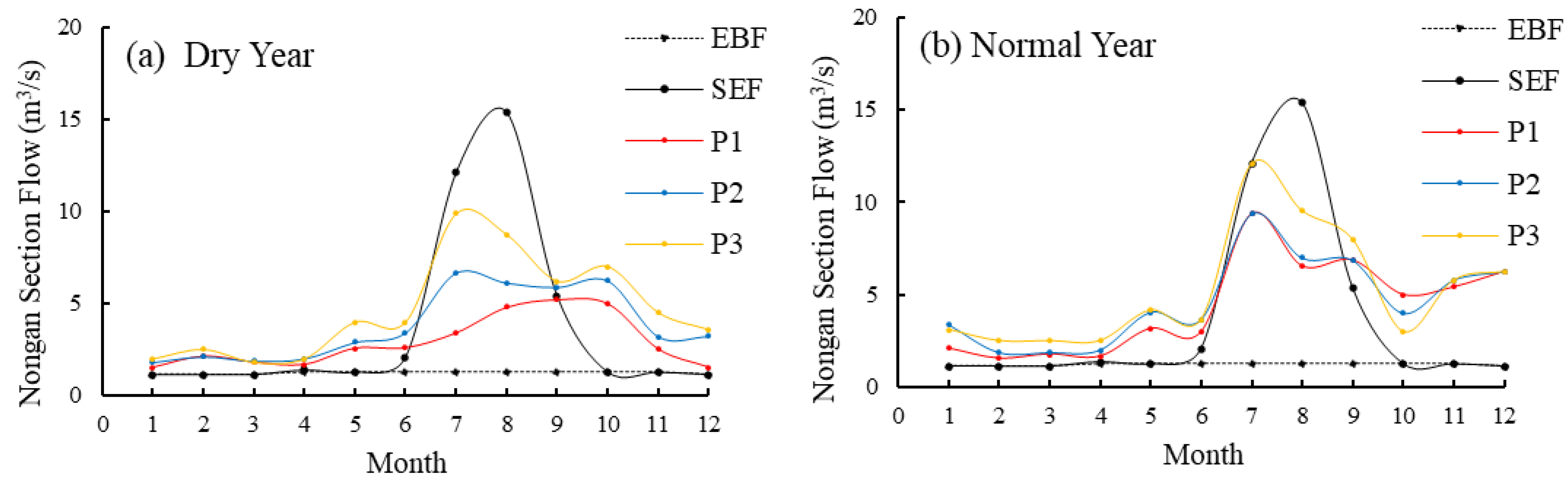
3.3. Runoff of River Section
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wan, W.; Guo, X.; Lei, X.; Jiang, Y.; Wang, H. A Novel Optimization Method for Multi-Reservoir Operation Policy Derivation in Complex Inter-Basin Water Transfer System. Water Resour. Manag. 2017, 32, 31–51. [Google Scholar] [CrossRef]
- Mengistu, B.; Alemu, H.; Kassa, M.; Zelalem, M.; Abate, M.; Bitewulign, B.; Magge, H. An innovative intervention to improve respectful maternity care in three Districts in Ethiopia. BMC Pregnancy Childbirth 2021, 21, 541. [Google Scholar] [CrossRef] [PubMed]
- Gui, Z.H.; Chen, X.H.; He, Y.H. Spatiotemporal analysis of water resources system vulnerability in the Lancang River Basin, China. J. Hydrol. 2021, 601, 126614. [Google Scholar] [CrossRef]
- Wu, X.; Shen, X.; Li, J. Spatiotemporal Distribution of Drought and Humidity in China Based on the Pedj Drought Index (PDI). Sustainability 2022, 14, 4546. [Google Scholar] [CrossRef]
- Shen, X.; Wu, X.; Xie, X.; Ma, Z.; Yang, M. Spatiotemporal Analysis of Drought Characteristics in Song-Liao River Basin in China. Adv. Meteorol. 2017, 2017, 3484363. [Google Scholar] [CrossRef]
- Shen, X.; Wu, X.; Xie, X.; Wei, C.; Li, L.; Zhang, J. Synergetic Theory-Based Water Resource Allocation Model. Water Resour. Manag. 2021, 35, 2053–2078. [Google Scholar] [CrossRef]
- Liu, B.; Wang, Y.; Xia, J.; Quan, J.; Wang, J. Optimal water resources operation for rivers-connected lake under uncertainty. J. Hydrol. 2021, 595, 125863. [Google Scholar] [CrossRef]
- Fillmore, H.; Singletary, L. Climate data and information needs of indigenous communities on reservation lands: Insights from stakeholders in the Southwestern United States. Clim. Change 2021, 169, 1–22. [Google Scholar] [CrossRef]
- Mahjouri, N.; Ardestani, M. A game theoretic approach for interbasin water resources allocation considering the water quality issues. Environ. Monit. Assess. 2009, 167, 527–544. [Google Scholar] [CrossRef]
- Chang, L.-C.; Chang, F.-J. Multi-objective evolutionary algorithm for operating parallel reservoir system. J. Hydrol. 2009, 377, 12–20. [Google Scholar] [CrossRef]
- Zhang, T.; Hu, T.; Guo, X.; Chen, Z.; Zheng, Y. Solving high dimensional bilevel multiobjective programming problem using a hybrid particle swarm optimization algorithm with crossover operator. Knowl.-Based Syst. 2013, 53, 13–19. [Google Scholar] [CrossRef]
- Ashofteh, P.; Haddad, O.B.; Loáiciga, H.A. Evaluation of climatic-change impacts on multiobjective reservoir operation with multiobjective genetic programming. J. Water Resour. Plan Manag. 2015, 141, 4015030. [Google Scholar] [CrossRef] [Green Version]
- Heydarizad, M.; Minaei, M.; Ichiyanagi, K.; Sori, R. The effects of local and regional parameters on the delta O-18 and delta H-2 values of precipitation and surface water resources in the Middle East. J. Hydrol. 2021, 600, 126485. [Google Scholar] [CrossRef]
- Espa, P.; Brignoli, M.L.; Crosa, G.; Gentili, G.; Quadroni, S. Controlled sediment flushing at the Cancano Reservoir (Italian Alps): Management of the operation and downstream environmental impact. J. Environ. Manag. 2016, 182, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Arthington, A.H.; Bhaduri, A.; Bunn, S.E.; Jackson, S.E.; Tharme, R.E.; Tickner, D.; Young, B.; Acreman, M.; Baker, N.; Capon, S.; et al. The Brisbane Declaration and Global Action Agenda on Environmental Flows. Front. Environ. Sci. 2018, 6, 45. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.Q.; Liu, P.; Wang, H.; Lei, X.H.; Yin, J.B. Adaptive reservoir flood limited water level for a changing environment. Environ. Earth Sci. 2017, 76, 743. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, P.; Dou, M.; Li, H.; Ming, B.; Gong, Y.; Yang, Z. Reservoir ecological operation considering outflow variations across different time scales. Ecol. Indic. 2021, 125, 107582. [Google Scholar] [CrossRef]
- Benjankar, R.; Tonina, D.; McKean, J.A.; Sohrabi, M.M.; Chen, Q.; Vidergar, D. Dam operations may improve aquatic habitat and offset negative effects of climate change. J. Environ. Manag. 2018, 213, 126–134. [Google Scholar] [CrossRef]
- Gao, S.; Liu, P.; Pan, Z.; Ming, B.; Guo, S.; Cheng, L.; Wang, J. Incorporating reservoir impacts into flood frequency distribution functions. J. Hydrol. 2018, 568, 234–246. [Google Scholar] [CrossRef]
- Sabzi, H.Z.; Rezapour, S.; Fovargue, R.; Moreno, H.; Neeson, T.M. Strategic allocation of water conservation incentives to balance environmental flows and societal outcomes. Ecol. Eng. 2018, 127, 160–169. [Google Scholar] [CrossRef]
- Needham, J.T.; Watkins, D.W.; Lund, J.R.; Nanda, S.K. Linear Programming for Flood Control in the Iowa and Des Moines Rivers. J. Water Resour. Plan. Manag. 2000, 126, 118–127. [Google Scholar] [CrossRef] [Green Version]
- Kim, Y.-G.; Sun, B.-Q.; Kim, P.; Jo, M.-B.; Ri, T.-H.; Pak, G.-H. A study on optimal operation of gate-controlled reservoir system for flood control based on PSO algorithm combined with rearrangement method of partial solution groups. J. Hydrol. 2020, 593, 125783. [Google Scholar] [CrossRef]
- Ji, C.-M.; Xie, W.; Yu, S.; Zhu, X.-L. Application of virus particle swarm optimization algorithm in economic operation of hydropower station. In Proceedings of the 2010 Sixth International Conference on Natural Computation, Yantai, China, 10–12 August 2010; Volume 5, pp. 2595–2599. [Google Scholar] [CrossRef]
- Bayat, B.; Mousavi, S.J.; Namin, M.M. Optimization–simulation for short-term reservoir operation under flooding conditions. J. Water Supply Res. Technol. 2011, 60, 434–447. [Google Scholar] [CrossRef]
- Hasebe, M.; Nagayama, Y. Reservoir operation using the neural network and fuzzy systems for dam control and operation support. Adv. Eng. Softw. 2002, 33, 245–260. [Google Scholar] [CrossRef]
- Rubio, F.; Rodríguez, I. Water-Based Metaheuristics: How Water Dynamics Can Help Us to Solve NP-Hard Problems. Complexity 2019, 2019, 4034258. [Google Scholar] [CrossRef]
- Unver, O.I.; Mays, L.W. Model for real-time optimal flood control operation of a reservoir system. Water Resour. Manag. 1990, 4, 21–46. [Google Scholar] [CrossRef]
- Simonovic, S.P.; Savić, D.A. Intelligent Decision Support and Reservoir Management and Operations. J. Comput. Civ. Eng. 1989, 3, 367–385. [Google Scholar] [CrossRef]
- Feng, Z.K.; Niu, W.J.; Cheng, C.T. Optimizing electrical power production of hydropower system by uniform pro-gressive optimality algorithm based on two-stage search mechanism and uniform design. J. Clean. Prod. 2018, 190, 432–442. [Google Scholar] [CrossRef]
- Fu, G. A fuzzy optimization method for multicriteria decision making: An application to reservoir flood control operation. Expert Syst. Appl. 2008, 34, 145–149. [Google Scholar] [CrossRef]
- Chang, L.-C. Guiding rational reservoir flood operation using penalty-type genetic algorithm. J. Hydrol. 2008, 354, 65–74. [Google Scholar] [CrossRef]
- Peng, Y.; Wang, G.; He, B. Optimal operation of cascade reservoirs based on generalized ant colony optimization method. In Proceedings of the 2010 Sixth International Conference on Natural Computation, Yantai, China, 10–12 August 2010. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar] [CrossRef]
- Shi, Y.; Eberhart, R.C. Empirical study of particle swarm optimization. In Proceedings of the 1999 congress on evolutionary computation-CEC99, Washington, DC, USA, 6–9 July 1999; Volume 3, pp. 1945–1950. [Google Scholar]
- Clerc, M.; Kennedy, J. The particle swarm—explosion, stability, and convergence in a multidimensional complex space. IEEE Trans. Evol. Comput. 2002, 6, 58–73. [Google Scholar] [CrossRef] [Green Version]
- Cheng, B.; Li, H. Agricultural economic losses caused by protection of the ecological basic flow of rivers. J. Hydrol. 2018, 564, 68–75. [Google Scholar] [CrossRef]
- Fu, Y.; Leng, J.; Zhao, J.; Na, Y.; Zou, Y.; Yu, B.; Fu, G.; Wu, W. Quantitative calculation and optimized applications of ecological flow based on nature-based solutions. J. Hydrol. 2021, 598, 126216. [Google Scholar] [CrossRef]
- Yang, Z.; Yang, K.; Hu, H.; Su, L. The Cascade Reservoirs Multi-Objective Ecological Operation Optimization Considering Different Ecological Flow Demand. Water Resour. Manag. 2018, 33, 207–228. [Google Scholar] [CrossRef]
- Tennant, D.L. Ohio Division of Wildlife, UInstream Flow Regimens for Fish, Wildlife, Recreation and Related Environ-mental Resources. Fisheries 1976, 1, 6–10. [Google Scholar] [CrossRef]
- Chen, L.; McPhee, J.; Yeh, W.W.-G. A diversified multiobjective GA for optimizing reservoir rule curves. Adv. Water Resour. 2007, 30, 1082–1093. [Google Scholar] [CrossRef]
- Wang, H.; Li, F.; Wang, G.; Qiu, J. Shrinking Pareto Fronts to Guide Reservoir Operations by Quantifying Competition Among Multiple Objectives. Water Resour. Res. 2022, 58, e2021WR029702. [Google Scholar] [CrossRef]
- Wu, C.; Wang, Y.B.; Ji, J.; Liu, P.; Li, L.P.; Feng, M.Y. Deriving reservoir operating rules considering ecological demands of multiple stations. In Proceedings of the Institution of Civil Engineers-Water Management; Thomas Telford Ltd.: London, UK, 2022; Available online: https://doi.org/10.1680/jwama.21.00009 (accessed on 8 May 2022).
- Doretto, A.; Espa, P.; Salmaso, F.; Crosa, G.; Quadroni, S. Considering mesohabitat scale in ecological impact as-sessment of sediment flushing. Knowl. Manag. Aquat. Ecosyst. 2022, 423, 2. [Google Scholar] [CrossRef]
- Yuan, B.; Guo, M.J.; Wu, W.; Zhou, X.D.; Li, M.J.; Xie, S.G. Spatial and Seasonal Patterns of Sediment Bacterial Com-munities in Large River Cascade Reservoirs: Drivers, Assembly Processes, and Co-occurrence Relationship. Microb. Ecol. 2022, 1–18. [Google Scholar]
- Pander, J.; Casas-Mulet, R.; Geist, J. Hydropeaking impairs upstream salmonid spawning habitats in a restored Danube tributary. River Res. Appl. 2022. ahead of print. [Google Scholar] [CrossRef]
- Sedighkia, M.; Datta, B.; Fathi, Z. Linking ecohydraulic simulation and optimization system for mitigating economic and environmental losses of reservoirs. J. Water Supply Res. Technol. 2022, 71, 229–247. [Google Scholar] [CrossRef]
- Cyriac, R.; Rastogi, A.K. An Overview of the Applications of Particle Swarm in Water Resources Optimization. In Proceedings of Seventh International Conference on Bio-Inspired Computing: Theories and Applications (Bic-Ta 2012); Springer: Berlin/Heidelberg, Germany, 2012; Available online: https://link.springer.com/chapter/10.1007/978-81-322-1041-2_4 (accessed on 8 May 2022).
- Liu, W.L.; Liu, L.N.; Dong, Z.C. On the Use of Multi-Objective Particle Swarm Optimization for Allocation of Water Re-sources. In Proceedings of the 2013 Ninth International Conference on Natural Computation (Icnc), Shenyang, China, 23–25 July 2013; pp. 612–617. [Google Scholar]
- Wang, Y.; Wu, P.; Zhao, X.; Jin, J. Water-Saving Crop Planning Using Multiple Objective Chaos Particle Swarm Optimization for Sustainable Agricultural and Soil Resources Development. Clean Soil Air Water 2012, 40, 1376–1384. [Google Scholar] [CrossRef]
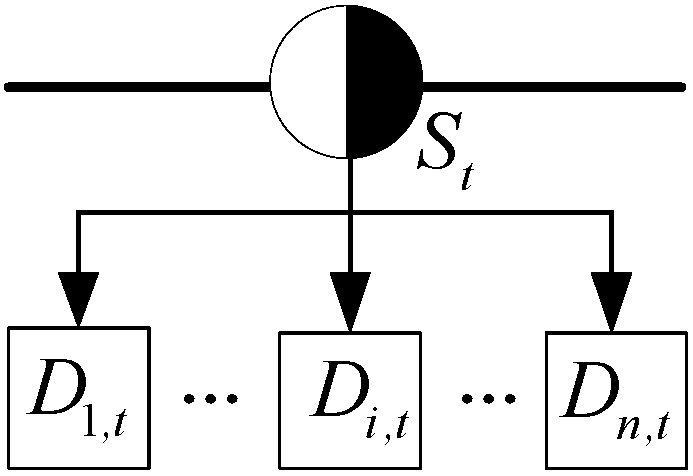







| Mode | Schematic Diagram * | Reservoir Operation Sequence |
|---|---|---|
| A | 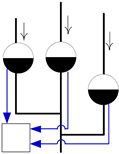 | The water supply sequence is based on the utilisable reservoir storage capacity, from small to large. |
| B | 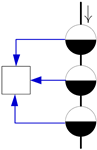 | The water supply sequence depends on the reservoir locations, which proceed successively from the downstream reservoir to the upstream reservoir. |
| C | 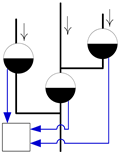 | The two tandem reservoirs on the right are equivalent to a reservoir, and the utilisable capacity of the equivalent reservoir is equal to the sum of the reservoir’s utilisable capacity in the series system. Thus, the equivalent reservoir forms a parallel system with the remaining reservoirs, and the water supply sequence is determined according to the operation rules of Mode A. Additionally, the water supply sequence of the series reservoirs follows Mode B. |
| D |  | The two upstream parallel reservoirs are equivalent to a reservoir. Thus, the equivalent reservoir forms a series system with the remaining reservoirs, and the water supply sequence of the reservoirs is determined according to the operation rules of Mode B. Additionally, the water supply sequence of the parallel reservoirs follows Mode A. |
 .
.| Year | Scenario Description | Ecological Scheduling Scheme | No. |
|---|---|---|---|
| 2015 | Before the water supply of Central Jilin Water Supply Project | Reservoir group operation not considering ecological flow | P1 |
| Reservoir group operation considering ecological base flow | P2 | ||
| Reservoir group operation considering ecological suitable flow | P3 | ||
| 2030 | After the water supply of Central Jilin Water Supply Project | Reservoir group operation not considering ecological flow | P1 |
| Reservoir group operation considering ecological base flow | P2 | ||
| Reservoir group operation considering ecological suitable flow | P3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, X.; Shen, X.; Wei, C.; Xie, X.; Li, J. Reservoir Operation Sequence- and Equity Principle-Based Multi-Objective Ecological Operation of Reservoir Group: A Case Study in a Basin of Northeast China. Sustainability 2022, 14, 6150. https://doi.org/10.3390/su14106150
Wu X, Shen X, Wei C, Xie X, Li J. Reservoir Operation Sequence- and Equity Principle-Based Multi-Objective Ecological Operation of Reservoir Group: A Case Study in a Basin of Northeast China. Sustainability. 2022; 14(10):6150. https://doi.org/10.3390/su14106150
Chicago/Turabian StyleWu, Xu, Xiaojing Shen, Chuanjiang Wei, Xinmin Xie, and Jianshe Li. 2022. "Reservoir Operation Sequence- and Equity Principle-Based Multi-Objective Ecological Operation of Reservoir Group: A Case Study in a Basin of Northeast China" Sustainability 14, no. 10: 6150. https://doi.org/10.3390/su14106150
APA StyleWu, X., Shen, X., Wei, C., Xie, X., & Li, J. (2022). Reservoir Operation Sequence- and Equity Principle-Based Multi-Objective Ecological Operation of Reservoir Group: A Case Study in a Basin of Northeast China. Sustainability, 14(10), 6150. https://doi.org/10.3390/su14106150






