1. Introduction
Sustainability is an important topic for the world today, and incorporating sustainability practices into supply chain networks has attracted wide attention from the industry and academia [
1]. Sustainable supply chains emphasize that while coordinating the critical organizational business for improving the long-term financial performance, supply chain participants are requested to achieve the organization’s social, environmental and economic goals [
2]. Therefore, in addition to considering economic goals of cost reduction and profit increase, firms should also take social and environmental performance into account [
3], including customer well-being, energy consumption and emissions, when making management decisions in order to achieve sustainable development.
With the development of information technologies and the popularity of e-commerce, most commodity distribution firms, especially firms with multi-echelon distribution networks, retained the traditional offline distribution channels while establishing online channels, forming a dual-channel distribution mode with the coexistence of online and offline channels [
4,
5], where each channel has separate inventory, operation system and commercial teams [
6]. Although this decentralized management can broaden the sale approaches to some extent, it often leads to a higher operational cost, an overall increase in inventory and a decrease in operational efficiency and customer service level [
6,
7,
8], which are caused by the following two aspects. Firstly, each node of the network mostly holds an online and offline independent inventory rather than a shared inventory to meet customers’ online and offline needs, increasing the holding cost and wasting the inventory resources [
6]. Secondly, the proximity-based assignment principle of online orders allows excessive orders to be pooled in the lower echelon nodes of the distribution network (for example, stores), which not only exacerbates the risk of stock-outs at the lower nodes [
9] but also causes firms to replenish inventory by increasing the frequency of replenishment, causing the waste of transportation resources and increasing the emissions [
10]. Moreover, the consideration of the second aspect will in turn affect the inventory of each node in the first aspect. As a result, there is an urgent need for firms to seek new modes to pursue sustainable development.
Recently, the omni-channel distribution mode has increasingly attracted the attention of many scholars because it can provide customers with consistent goods and services by effectively integrating inventory, customer and other information data from all sales channels [
11,
12]. For this mode, optimizing the above-mentioned inventory and online order allocation problems will, on the one hand, enable the firm to integrate the resources of various channels to reduce operational costs and thus provide customers with high service and quality products, improve customer satisfaction and increase sales profits [
13], thus achieving economic sustainability; on the other hand, the firm will reduce land occupation by reducing inventory holdings and reduce the emissions by optimizing the order fulfillment mode [
14], thus achieving environmental sustainability. Therefore, it is of great importance for firms with multi-echelon distribution networks to make joint decisions of inventory optimization (IO) and order allocation (OA) in omni-channel.
For the IO in multi-echelon distribution networks, there is an increasing number of studies focusing on the methods of online and offline inventory sharing within nodes (referred to as inventory sharing) and lateral transshipment between nodes [
15,
16,
17,
18]. The inventory-sharing method aims to achieve optimal system-wide holdings at a given service level by integrating online and offline inventory [
19], which can reduce the overall inventory level within nodes but cannot avoid the risk of its own stock-outs. The lateral transshipment method refers to stock movements between nodes in the same echelon of the supply chain network by transshipping the available inventory of one node to meet the shortage at another node [
20], which prevents the loss of offline orders of store nodes and is also environmentally friendly [
21]. However, most of the existing research has focused on one or the other, while it is still relatively rare to integrate inventory sharing and lateral transshipment to optimize inventory level in omni-channel multi-echelon distribution networks (OMDN).
As for OA in multi-echelon distribution networks, current studies have focused on the issue of the selection of fulfillment node for each order [
9,
22,
23]. The existing studies find that the selection of upper echelon nodes can reduce the unit inventory cost and replenishment frequencies but increase the order delivery time and return risk due to the longer delivery distance; while the selection of lower echelon nodes can reduce the order delivery distance and time but increase the unit inventory cost and replenishment cost. Currently, although there is some existing literature exploring the way of order allocation, the studies about how to integrate multi-dimensional factors related to order fulfillment costs among different echelon nodes in OMDN, including the inventory replenishment, holding, order delivery distance and time to achieve optimal order allocation is less common.
More importantly, while the issues of IO and OA relate to the storage and transportation of goods and have a significant impact on the sustainability of the supply chain [
10], there is little literature on the exploration of both in an omni-channel multi-echelon and multi-node network.
To address the above-mentioned research gaps, we innovatively propose a joint model of inventory optimization and order allocation for OMDN, aiming to achieve cost-efficient and sustainable omni-channel operations. Firstly, from the perspective of IO, an inventory integrated policy is explored for online and offline inventory sharing within nodes and lateral transshipment between nodes; from the aspect of OA, an order allocation mechanism is designed for the minimum cost under the influence of multiple factors (inventory replenishment, holding, order delivery distance and time) among different echelon nodes of the network. Then, a joint optimization model is developed and solved by genetic algorithm (GA). Finally, based on an example analysis, the effectiveness of the proposed inventory and order allocation strategy is verified by comparing the alternative strategies and more insights are showed on the analysis of the system parameters.
3. Problem Description and Modelling
This section will describe the problem context and then develop a joint optimization model.
3.1. Problem Description
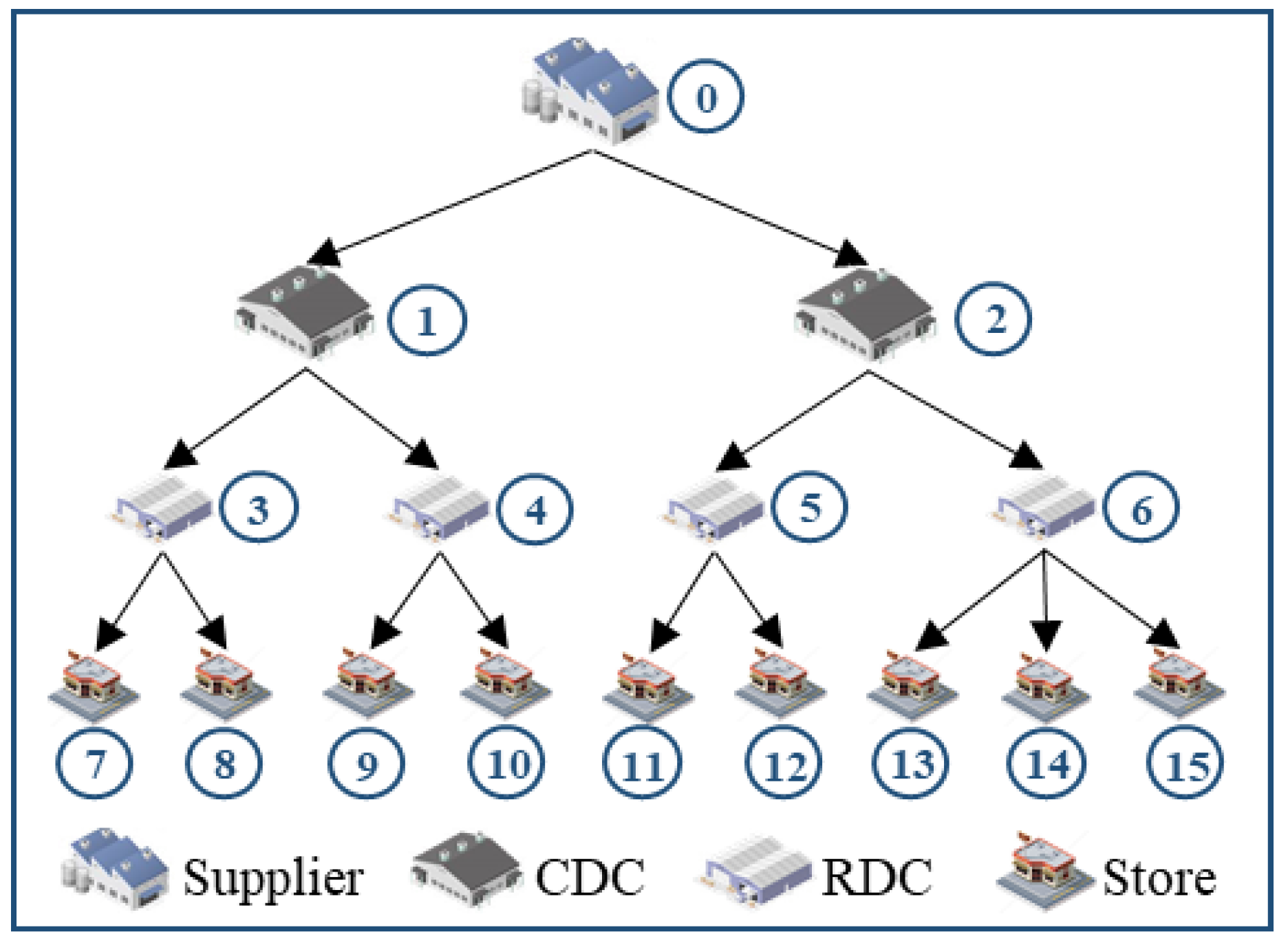
This paper considers a three-echelon distribution network of a B&M firm in mainland China, consisting of external suppliers, a set of central distribution centers (CDCs), regional distribution centers (RDCs) and stores. As illustrated in
Figure 1a, each echelon node holds two types of inventory and is replenished by their upper nodes; and suppliers out the scope of the paper are mainly for supplying to the CDCs. An operational time horizon is considered (for example, weekly, monthly) and is divided into a set of control periods (for example, daily). At a given period, the network faces offline demand from consumers purchasing in stores, which is met by offline inventory in stores; and it also faces online demand from consumers ordering online, which is collected at a certain time point and then satisfied by the online inventory of the closest node to the customer (including CDCs, RDCs and stores). Unmet offline and online demand is accounted for as out-of-stock losses. In addition, the replenishment demand from RDCs and stores are responded to by the replenishment inventory of the CDCs and RDCs. However, in this dual-channel mode, the online and offline inventory in the nodes operate independently, and online orders are assigned to the closest nodes, which often leads to the problem of high inventory holding at each node and high order fulfillment costs between distribution networks. Therefore, how to optimally manage the inventory at each node and optimally allocate the online orders to reduce the total cost of the distribution network is an urgent issue to be solved.
This paper proposed an inventory integration policy of inventory sharing within nodes and lateral transshipment between nodes from the perspective of IO. As illustrated in
Figure 1b, the online and offline replenishment inventory at each node is integrated into one type of inventory and replenished by upper echelon nodes. Moreover, when the inventory of a store is unavailable, it can request lateral transshipment from other stores. An order allocation mechanism for the minimum cost under the influence of multiple factors is adopted from the aspect of OA: the online orders are assigned to the node with minimum cost affected on replenishment cost, inventory holding cost, order delivery cost, and time penalty cost for the loss of some online orders due to longer order delivery time.
Given the above inventory and order joint strategy, we will answer the following questions at each decision opportunity: (1) the optimal allocation node for online orders in each period; (2) the optimal inventory replenishment amount for each node in each period; (3) the optimal inventory transshipment amount in case of insufficient inventory in store nodes in each period.
3.2. Problem Assumptions and Parameter Definitions
The notation of the parameters used in the model in this paper is shown in
Table 1 and the problem assumptions are given as follows:
- (1)
A single kind of product with the same quality and price is considered;
- (2)
The online and offline demands of each node are stochastic and independent and follow a normal distribution;
- (3)
Each node adopts a periodic review policy and the replenishment between different echelons had the lead time;
- (4)
Each node has a different distribution region, and the distribution region between nodes of the same echelon does not overlap, and between different echelon nodes the upper nodes will cover the whole region of lower replenishment nodes;
- (5)
We measure the location and the shortest delivery time of online customers by the closest node in the distribution range and choose the node with minimum cost within distribution networks to fulfill online orders;
- (6)
Except suppliers, each echelon node in the distribution network has the inventory capacity limit;
- (7)
Lateral transshipments are only conducted after the realization of actual demands: we adopt an emergency transshipment policy;
- (8)
For offline orders, it only occurs stock-out when the store node requests lateral transshipment and still cannot be satisfied; for online orders, it occurs stock-out only when the node whose total cost including the stock-out cost is still the lowest. The loss will be calculated at that node.
3.3. The Omni-Channel Multi-Echelon Joint Optimization Model
In this paper, we study the joint problem of inventory optimization and order allocation for OMDN, which can be described as follows: for each period t and known online and offline demand in OMDN with a set of CDCs (w), RDCs (u) and stores (k), making joint decisions of the allocation node for online orders, the replenishment amount of each node and the transshipment node and amount between store nodes to minimize the total cost in OMDN.
Based on the inventory optimization model in Firoozi et al. [
33], the model of this paper is formulated as follows:
Objective function: Equation (1) minimizes the total system cost (TC) including the cost of stores, RDCs and CDCs.
Analysis model: Equations (2)–(4) give the detailed cost component of stores, RDCs and CDCs, where:
The cost of Replenishment (CR): the online and offline inventory sharing within nodes is considered: the offline demand replenishment quantity and the online demand replenishment quantity are combined into a uniform replenishment quantity .
The cost of Transshipment (CT): when the store node k is out-of-stock, it can request lateral transshipment from other store nodes and the inventory are priority to meet offline demand.
The cost of Holding (CH): the average inventory in each period t is half of the sum of the inventory after replenishment at the beginning of the period and the remaining inventory at the end of the period.
The cost of Fulfillment (CF): the delivery cost and the time penalty cost of the online orders assigned to the node to satisfy are included. For the order allocation mechanism, except from the replenishment and storage factors of the node’s inventory, we consider the costs associated with the following factors:
Order delivery cost: the delivery distance affects the assignment of online orders. The unit delivery cost (
) is a linear function of the delivery distance. The related formula is
, where
and
are the fixed and variable unitary delivery cost from site
n to site
(
n = =
), respectively [
23,
33];
Time penalty cost: we assume that when an online order is allocated from the closest node to other ones for fulfillment, the delivery time is subsequently extended, which will cause some customers who are sensitive to the delivery time to abandon their intended purchase, thus incurring an order loss. Referring to DeValve et al. [
39], we set a time penalty coefficient
when allocating online orders, which will be defined as the order loss rate.
The cost of Stock-out (CS): when the online and offline orders cannot be met, the nodes incur out-of-stock losses, where the out-of-stock losses of the store nodes include online and offline orders, and the CDCs and RDCs only incur online order losses.
Constraints: Equations (5)–(7) indicate the inventory on hand in store nodes, RDCs and CDCs, respectively, by balancing the flows in and out of the site for each period. More specifically, the inventory on hand of store nodes in each period is the summation of inventory on hand in the last period t-1, the received inventory from RDCs and other store nodes minus the inventory transshipped to other stores, the inventory fulfilling offline orders and online orders allocated to it. Similarly, the inventory on hand ( in each period is the summation of inventory on hand in the last period t-1, the received inventory from upper echelons minus the inventory sent to the lower stages (CDCs for RDCs and RDCs for stores) and the inventory fulfilling online order allocated to them. Equation (8) indicates the offline demand balance of store nodes, which means offline orders can be satisfied by the node’s own inventory and the inventory transshipped from other nodes, and shortage occurs if it cannot be satisfied. Equations (9)–(11) represent the online demand balance of each node, meaning that the online orders can be allocated to any node within the distribution network to satisfy, and shortage occurs if it cannot be satisfied. Constraints (12)–(14) indicate that the number of nodes assigned for the online demand can have more than 1. Constraint (15) checks that a given node can satisfy any given online orders only when the allocation decision variable is set to 1. Moreover, constraint (16) limits the inventory capacity of each node. Finally, binary and non-negative restricts are given by constrains (17) and (18).
4. The GA-Based Solution Approach
As mentioned above, the joint optimization model of OMDN is intractable due to the inherent combinatorial complexity to make optimal inventory and order allocation decisions. Given that GA has better performance in solving a nonlinear mixed-integer programming model in the supply chain [
46,
47,
48], we decided to use GA to find near-optimal solutions. The specific steps are as follows:
Since there are two different types of variables in the model, real variables
and
and binary variables
, we set up two genomes in the GA, corresponding to the two types of variables and using real and binary encoding methods. Taking the store node as an example, its chromosome coding composition is shown as follows:
- (2)
Initializing
The constraints (5)–(18) in the model of this paper are tightly restricted. If we choose not to initialize the population randomly in the feasible domain, it will generate a large number of infeasible solutions and reduce the efficiency of the algorithm. Therefore, in order to alleviate this problem, we initialize the population of individuals under the considered constraints. For example, when initializing the decision variable , the individuals are initialized in groups of variables, and the inventory of each node is randomly generated within the node inventory capacity interval [0,].
- (3)
Fitness function
We use the objective function as the fitness function, which is represented by the equation: , where denotes the value obtained by substituting the value of the variable corresponding to the gene of the i individual in the population into the model; denotes the smallest fitness value in the current population; and denotes the fitness value of the i individual.
- (4)
Selection
In this paper, a roulette strategy is used for the selection of individuals, which was calculated as: , where denotes the fitness value of the i individual; NP denotes the number of individuals in the population; and denotes the probability of an individual being selected for inheritance to the next generation.
- (5)
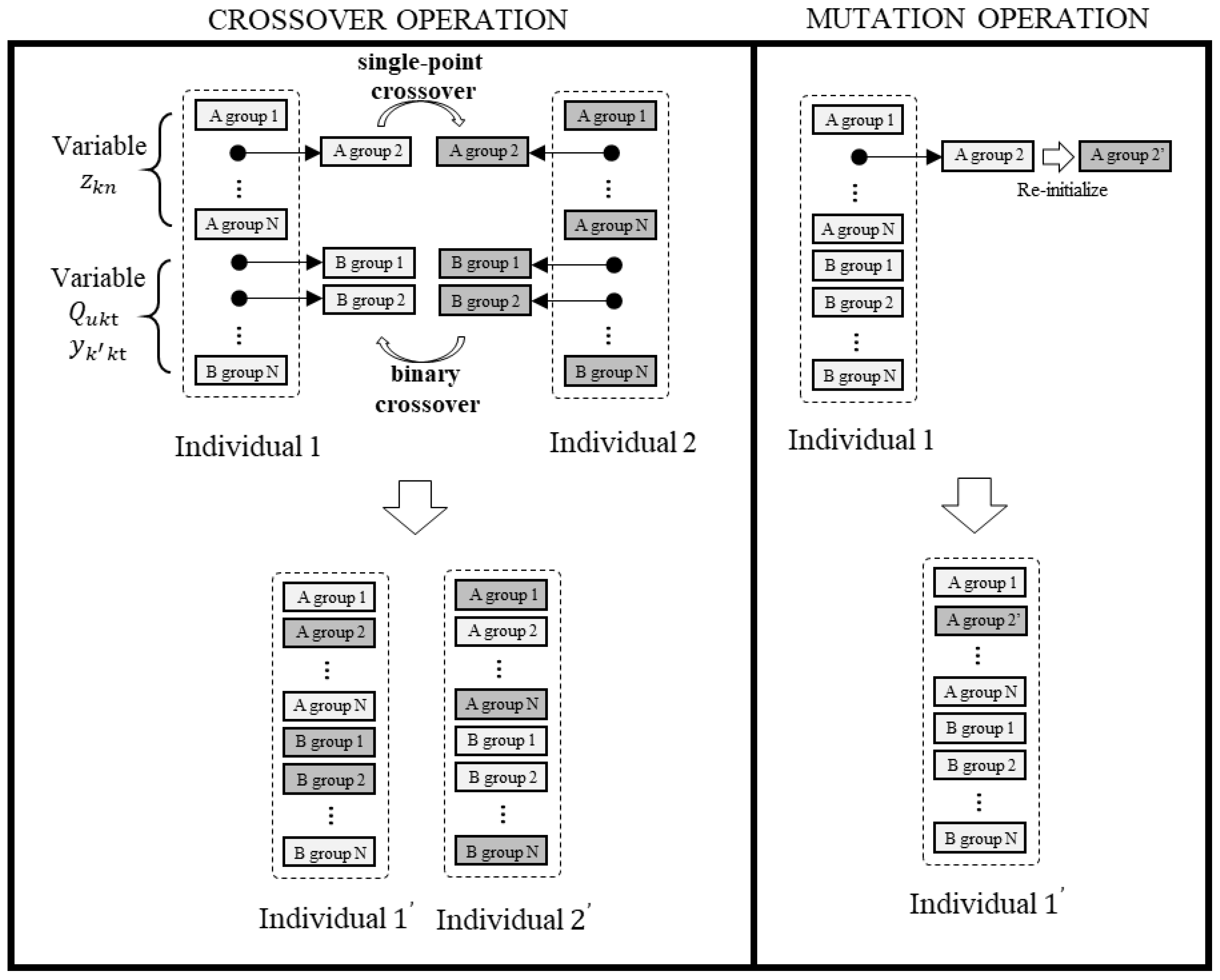
Crossover and mutation
The model in this paper involves binary and real variables, and we decide to use the single-point crossover method for binary variables and the simulated binary crossover method for real variables and set the crossover probability
. The mutation is a disturbance to the population mode, thus improving the local search capability and preventing prematureness and convergence of the results, and we set the mutation probability
. The specific crossover and mutation process is shown in
Figure 2.
6. Conclusions
This section presents the main conclusions of the paper, along with the theoretical contributions, and further presents the limitations and suggestions for future research.
6.1. Concluding Remarks
Sustainable supply chains are currently attracting increasing attention. In addition to economic sustainability, the environmental and social sustainability are also important aspects that firms cannot ignore when seeking to develop. Therefore, in order to achieve cost-efficient and sustainable omni-channel operations, it is crucial for firms with multi-echelon distribution networks to systematically address the issues of inventory optimization and order allocation. To this end, we propose an inventory integrated policy for online and offline inventory sharing within nodes and lateral transshipment between nodes from the perspective of inventory optimization, and an order allocation mechanism for the minimum cost under the influence of multiple factors from the aspect of order allocation. Moreover, we construct a joint optimization model of inventory and order for the omni-channel multi-echelon distribution network, which is solved by GA.
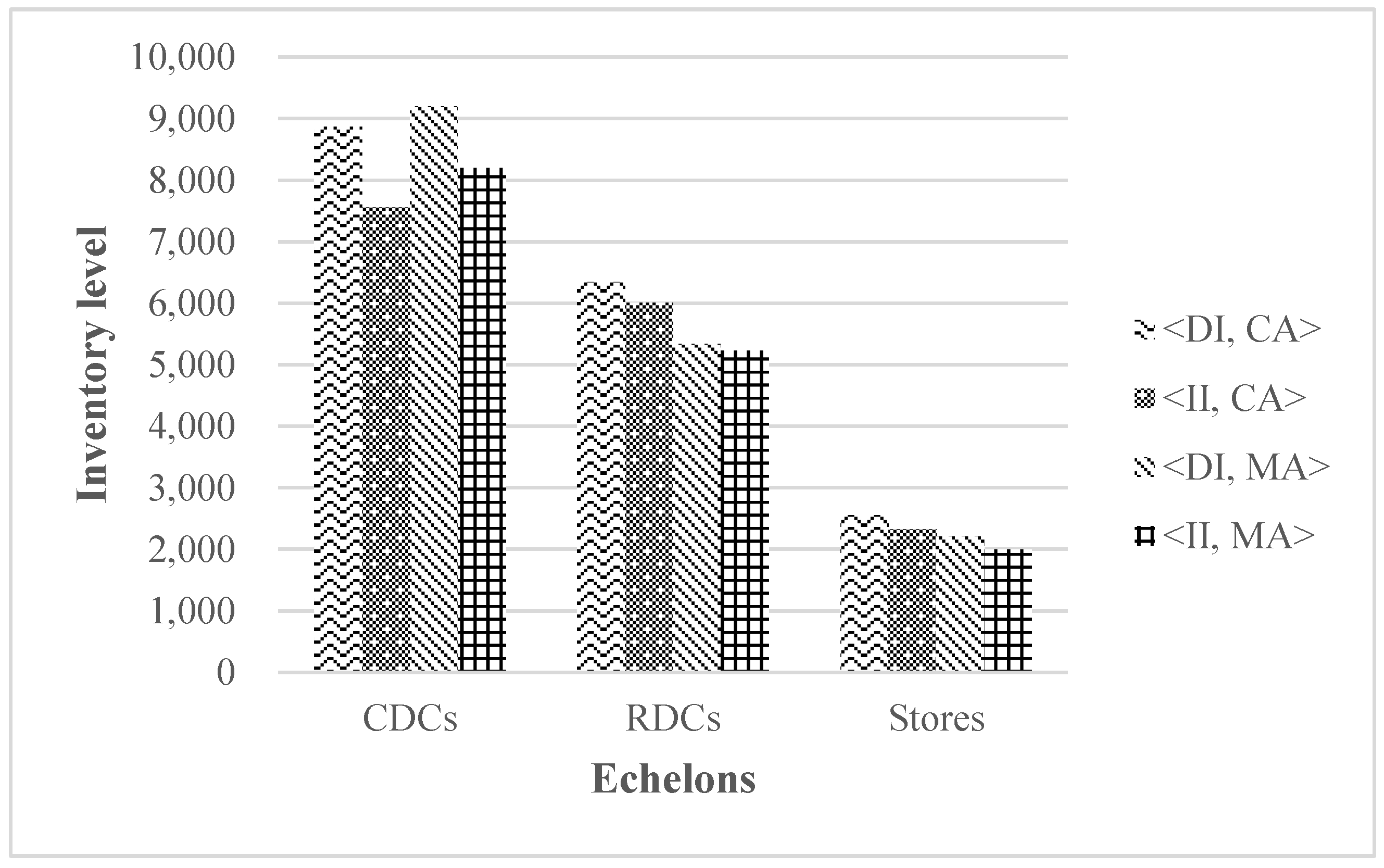
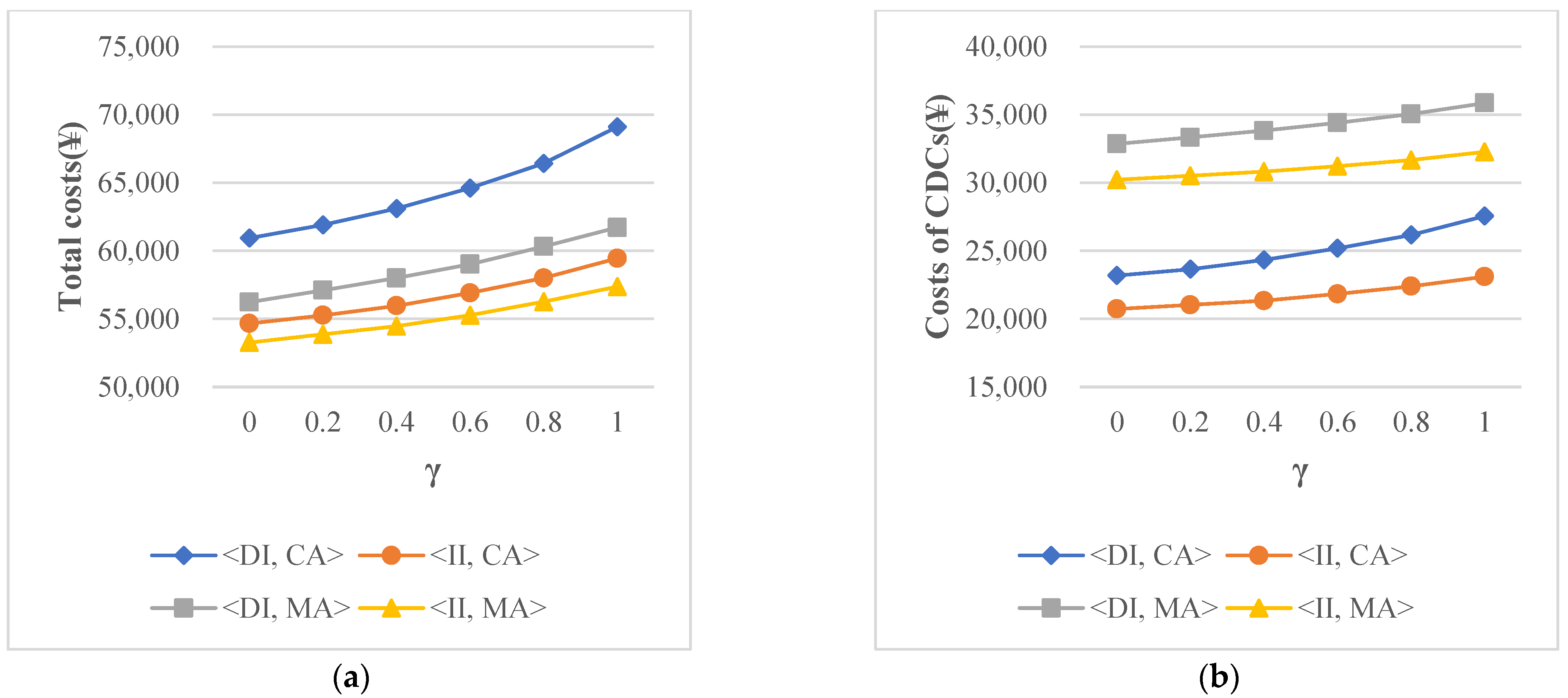
The numerical results demonstrate that the proposed joint strategy can effectively improve economic, social, and environmental sustainability. Particularly, the joint strategy can reduce the total operational cost and improve the customer service level. Moreover, another important finding is that the inventory integration policy is economically and environmentally sustainable due to the reduction in wasted inventory resources and transportation, making the cost advantage of using only this option more significant than that of using only order allocation mechanism. Moreover, through sensitivity analysis of demand fluctuation ratio and time penalty coefficient, it is also found that the joint strategy of our study can effectively mitigate the impact of demand uncertainty and customer delivery time sensitivity on the operational cost of the network, achieving the social and economic sustainability. When market demand is volatile and customers are not sensitive to order delivery times, firms are willing to transfer orders to upper echelons for fulfillment, thereby reducing out-of-stocks as well as lowering total costs. On the contrary, when the market demand is less volatile and customers are sensitive to delivery times, firms will take advantage of the proximity of RDCs and stores to customers and transfer most of orders to lower echelons to improve their competitiveness.
6.2. Theoretical Contributions
To the best of our knowledge, there is less literature on both inventory management and order allocation issues in OMDN. We propose a joint strategy and construct a joint optimization model to make optimal inventory and order allocation decisions for OMDN to further enrich the research on omni-channel operations. More importantly, the exploration of omni-channel operations of our study provides a new direction for the sustainable supply chain, which is a key area of sustainability improvement. The theoretical contributions of this paper are mainly in the following two aspects: (1) we introduce both inventory sharing and lateral transshipment into the inventory optimization for exploration, enriching the research on inventory decision-making in omni-channel and the multi-echelon inventory theory; (2) we also further explore the minimum-cost allocation for online orders under the influence of multiple factors, which provides a novel vision for optimal order allocation decision in multi-echelon distribution networks and further enriches supply chain control theory.
6.3. Research Limitations and Future Directions
In this paper, only a few nodes of the firm are selected for the validation of the experiment, which is relatively simple compared to the reality. Therefore, multiple nodes can be selected for future validation. It is worth noting that the model in this paper mainly measures economic sustainability but lacks quantitative measures of environmental and social sustainability. Therefore, environmental and social dimensions of sustainability could be considered in the model in the future. Next, one kind of online demand is only considered in this paper, online shipping, but a popular mode of omni-channel fulfillment is in-store pickups. Therefore, an optimization model that includes multiple kinds of online demands can be considered in the future to make the model more relevant to the actual needs of enterprises and provide them with a useful basis for decision making. In addition, the data used in this paper are based on the history record of the firm, but firms often encounter various dynamic uncertainties in reality, such as supply interruptions, transportation delays, etc., which will have a certain impact on the operation of the firm. Therefore, this paper can use big data, digital twin and other information technologies to get the real-time information data to provide real-time visual guidance for the operation of the enterprise distribution network.