Analysis of the Spatial Effect of Capital Misallocation on Agricultural Output—Taking the Main Grain Producing Areas in Northeast China as an Example
Abstract
:1. Introduction
2. Materials and Methods
2.1. Research Methods
2.1.1. Spatial Autocorrelation Test
2.1.2. Econometric Model Construction
2.2. Variable Selection
2.2.1. Dependent Variable
2.2.2. Independent Variables
2.2.3. Control Variables
2.2.4. Other Variables
2.3. Data Sources
3. Results
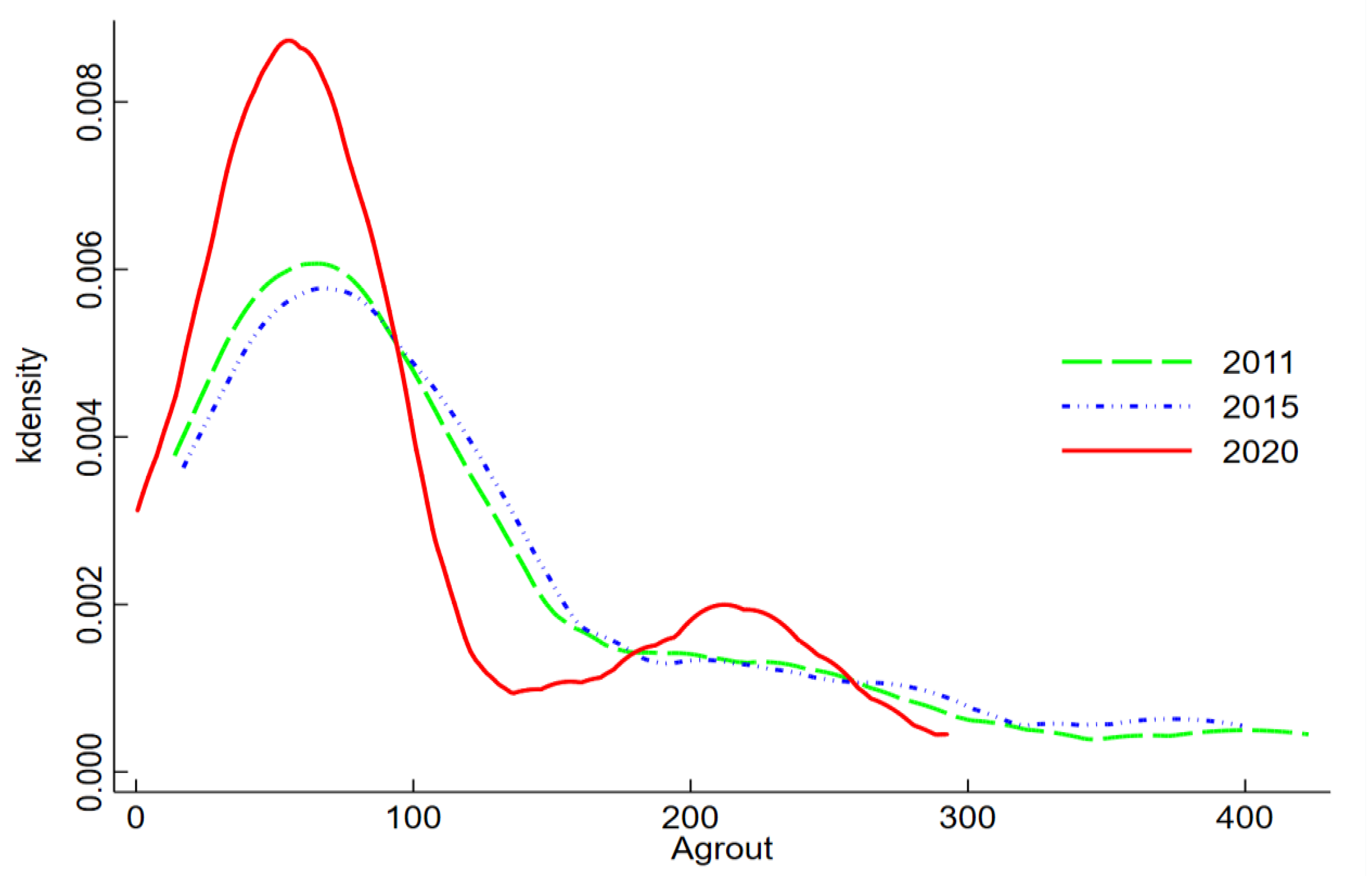
3.1. Dynamic Evolution of Agricultural Output
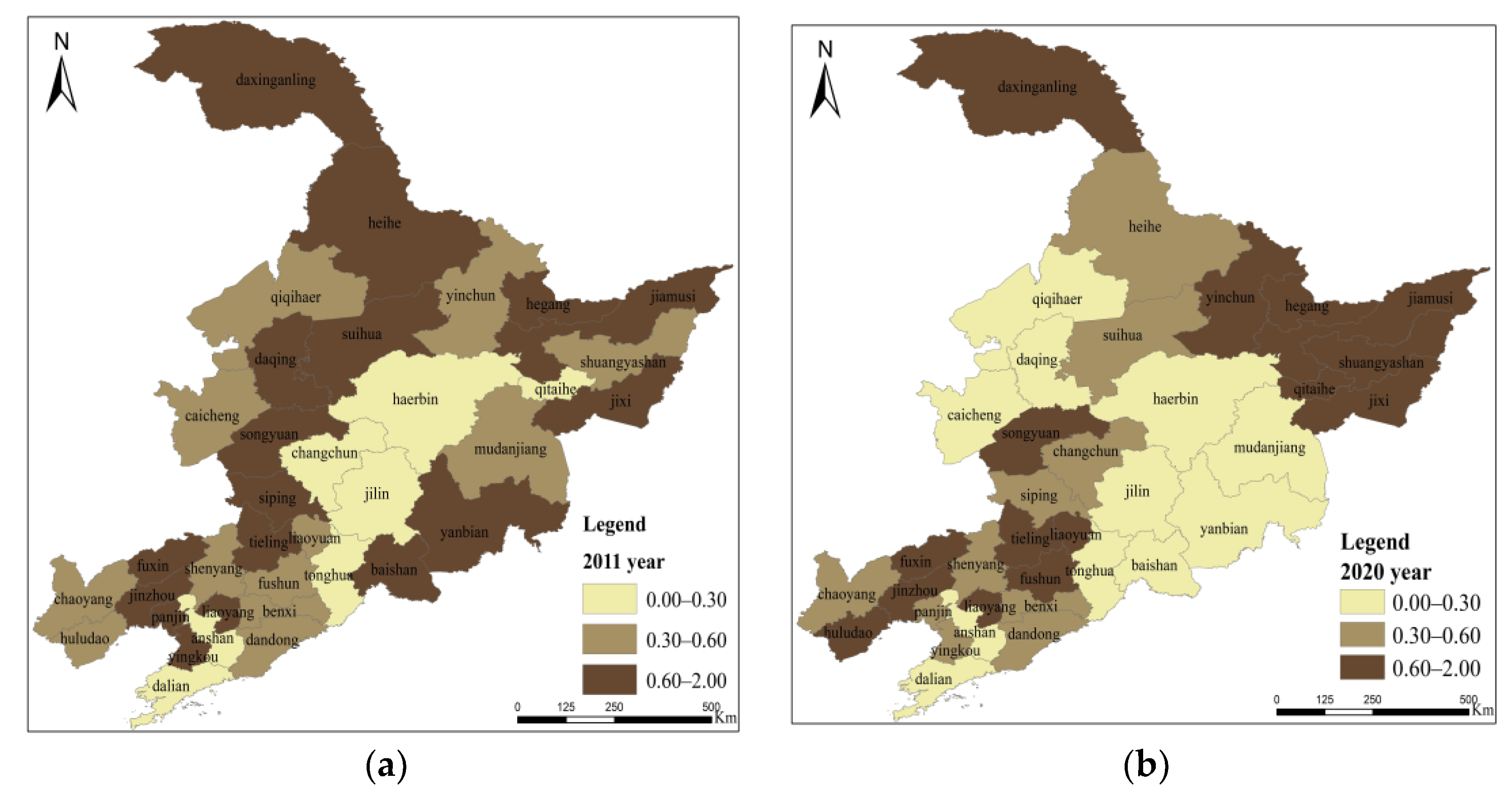
3.2. Spatial-Temporal Evolution Analysis of Agricultural Capital Misallocation
3.3. Spatial Inspection and Selection
3.4. Analysis of Spatial Effect Decomposition
3.5. Robustness Test
3.5.1. Shorten the Time Window
3.5.2. Winsorize
3.5.3. Replace the Dependent Variable
3.5.4. Replace the Weight
3.6. Further Analysis
3.6.1. Mechanism Test of Agricultural Industry Upgrade
3.6.2. Mechanism Test of Agricultural Technology Progress
4. Discussion
5. Conclusions and Suggestions
- (1)
- During the sample period, agricultural output capacity showed a declining trend, and the spatial difference was decreasing, but the polarization was obvious. The degree of agricultural capital misallocation decreased, but the spatial agglomeration was significant, showing a spatial distribution pattern of “low in the middle and high in the north and south”;
- (2)
- The inhibition effect of capital misallocation on agricultural output growth has a significant spatial spillover effect. On average, every 1 unit of increase in capital misallocation will reduce the local agricultural output by 16.00% and neighboring agricultural output by 1.80%;
- (3)
- The negative impact of capital misallocation on agricultural output can be weakened through the optimization and upgrading of the agricultural industry and agricultural technology, and the agricultural industry upgrade has a significant spatial spillover effect, but the spillover effect of agricultural technology progress is not obvious.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jaacks, L.M.; Veluguri, D.; Serupally, R.; Roy, A.; Prabhakaran, P.; Ramanjaneyulu, G. Impact of the COVID-19 pandemic on agricultural production, livelihoods, and food security in India: Baseline results of a phone survey. Food Secur. 2021, 13, 1323–1339. [Google Scholar] [CrossRef]
- Pu, M.; Zhong, Y. Rising concerns over agricultural production as COVID-19 spreads: Lessons from China. Glob. Food Secur. 2020, 26, 100409. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Chen, C.; Xu, S.; Xu, B. Measurement of capital allocation efficiency in emerging economies: Evidence from China. Technol. Forecast. Soc. Change 2021, 171, 120954. [Google Scholar] [CrossRef]
- Beckman, J.; Countryman, A.M. The Importance of Agriculture in the Economy: Impacts from COVID-19. Am. J. Agric. Econ. 2021, 103, 1595–1611. [Google Scholar] [CrossRef] [PubMed]
- Gollin, D.; Udry, C. Heterogeneity, Measurement Error, and Misallocation: Evidence from African Agriculture. J. Polit. Econ. 2021, 129, 1–80. [Google Scholar] [CrossRef]
- Aragona, F.M.; Restucciabc, D.; Rud, J.P. Are small farms really more productive than large farms? Food Policy 2022, 106, 102168. [Google Scholar] [CrossRef]
- Rogerson, R.R. Policy distortions and aggregate productivity with heterogeneous establishments. Rev. Econ. Dyn. 2008, 11, 707–720. [Google Scholar]
- Brandt, L.; Tombe, T.; Zhu, X. Factor Market Distortions Across Time, Space and Sectors in China. Rev. Econ. Dyn. 2013, 16, 39–58. [Google Scholar] [CrossRef] [Green Version]
- Zheng, H.Y.; Ma, W.L. The role of resource reallocation in promoting total factor productivity growth: Insights from China’s agricultural sector. Rev. Dev. Econ. 2021, 25, 2350–2371. [Google Scholar] [CrossRef]
- Zhu, J.; Li, T.X.; Lin, D.Y.; Zhong, F.N. Thinking after “Nine Continuous Increases”: Contribution and Future Potential Analysis of Grain Internal Structure Adjustment. Issues Agric. Econ. 2013, 34, 36–43. [Google Scholar]
- Shen, Z.Y.; Tomas, B.; Chen, X.L.; Valdmanis, V. Green growth and structural change in Chinese agricultural sector during 1997–2014. China Econ. Rev. 2018, 51, 83–96. [Google Scholar] [CrossRef]
- Han, H.; Li, H.; Zhao, L. Determinants of Factor Misallocation in Agricultural Production and Implications for Agricultural Supply-side Reform in China. China World Econ. 2018, 26, 22–42. [Google Scholar] [CrossRef]
- Zheng, H.Y.; Li, G.C.; Zhou, X.S. Factor mismatch and loss of agricultural output in China. J. Nanjing Agric. Univ. Soc. Sci. Ed. 2019, 19, 143–153. [Google Scholar]
- Adamopoulos, T.; Brandt, L.; Leight, J.; Restuccia, D. Misallocation, Selection and Productivity: A Quantitative Analysis with Panel Data from China; National Bureau of Economic Research: Cambridge, MA, USA, 2017; No. 23039. [Google Scholar]
- Zhu, X.; Shi, Q.H.; Gai, Q.E. Factor Allocation Distortion and Agricultural Total Factor Productivity. Econ. Res. 2011, 46, 86–98. [Google Scholar]
- Skevas, T.; Wu, F.; Guan, Z. Farm Capital Investment and Deviations from the Optimal Path. J. Agric. Econ. 2018, 69, 561–577. [Google Scholar] [CrossRef]
- Stephen, A.; Loren, B.; Diego, R. Market constraints, misallocation, and productivity in Vietnam agriculture. Food Policy 2020, 94, 101840. [Google Scholar]
- Chen, X.B. Resource allocation, total factor productivity and the vision of agricultural economic growth. Reform 2012, 35, 82–90. [Google Scholar]
- Adamopoulos, T.; Diego, R. The Size Distribution of Farms and International Productivity Differences. Am. Econ. Rev. 2014, 104, 1667–1697. [Google Scholar] [CrossRef] [Green Version]
- Hsieh, C.T.; Klenow, P. Misallocation and Manufacturing TFP in China and India. Q. J. Econ. 2009, 124, 1403–1448. [Google Scholar] [CrossRef] [Green Version]
- Aoki, S. A simple accounting framework for the effect of resource misallocation on aggregate productivity. J. Jpn. Int. Econ. 2012, 26, 473–494. [Google Scholar] [CrossRef] [Green Version]
- Anselin, L.; Lowenberg, D.B.J. A Spatial Econometric Approach to the Economics of Site-Specific Nitrogen Management in Corn Production. Am. J. Agric. Econ. 2004, 86, 675–687. [Google Scholar] [CrossRef]
- Liu, S.; Wang, X.Z.; Yang, M.Y.; Wang, Z.L. The Impact of Financial Market Development on Agricultural Factor Misallocation: Household-Level Evidence from China. Math. Probl. Eng. 2021, 2021, 9997438. [Google Scholar] [CrossRef]
- Wu, W.W.; Bao, K.X.; Zhang, Y.H. An Empirical Study on the Mismatch Measurement and Influencing Factors of Agricultural Production Factors in Jiangxi Province. Resour. Environ. Yangtze River Basin 2020, 29, 1005–1015. [Google Scholar]
- Tobler, W.R. A Computer Movie Simulating Urban Growth in the Detroit Region. Econ. Geogr. 1970, 46, 234–240. [Google Scholar] [CrossRef]
- Chen, Z.; Zhu, H.; Zhao, W.; Zhao, M.; Zhang, Y. Spatial Agglomeration of China’s Forest Products Manufacturing Industry: Measurement, Characteristics and Determinants. Forests 2021, 12, 1006. [Google Scholar] [CrossRef]
- Echevarria, C. A Three-factor Agricultural Production Function: The Case of Canada. Int. Econ. J. 1998, 12, 63–75. [Google Scholar] [CrossRef]
- Wu, Y.M. Calculation of Input-Output Elasticity of China’s Regional Agricultural Production Factors—Empirical Based on Spatial Econometric Model. China Rural Econ. 2010, 26, 25–37. [Google Scholar]
- Wang, F.; Liu, Y.F.; Kong, X.S.; Chen, Y.Y.; Pan, J.W. Spatial-temporal evolution and influencing factors of grain yield at county level in China. Econ. Geogr. 2018, 38, 142–151. [Google Scholar]
- Chen, Y.F.; Li, X.D. Spatial-temporal patterns and influencing factors of grain yield change in China. Trans. Case 2013, 29, 1–10. [Google Scholar]
- Han, C.G.; Zhang, L. Does the Internet improve resource mismatch in China: A test based on dynamic Spatial Dubin model and threshold model. Explor. Econ. Probl. 2019, 40, 43–55. [Google Scholar]
- Zhao, Y.W.; LV, H.M. Construction and Regional Differences Research on Evaluation System of Rural Well-off Construction. Agric. Econ. Issues 2016, 37, 9–15. [Google Scholar]
- Li, G.C. Green productivity revolution in China’s agriculture: 1978–2008. Econ. Q. 2014, 13, 537–558. [Google Scholar]
- Zhang, J.; Wu, G.Y.; Zhang, J.P. Estimation of China’s Interprovincial Material Capital Stock: 1952–2000. Econ. Res. 2004, 68, 35–44. [Google Scholar]
- Wang, X.B.; Yamauchi, F.; Otsuka, K.; Huang, J.K. Wage Growth, Landholding, and Mechanization in Chinese Agriculture. World Dev. 2016, 86, 30–45. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Luo, X.W.; Liao, J.; Hu, L.; Zang, Y.; Zhou, Z.Y. Improving the level of agricultural mechanization to promote sustainable agricultural development. Chin. J. Agric. Eng. 2016, 32, 1–11. [Google Scholar]
- Zhou, Z.; Kong, X.Z. Effect evaluation and policy direction of agricultural mechanization on Grain output in China. China Soft Sci. 2019, 34, 20–32. [Google Scholar]
- Jiang, Y. China’s water security: Current status, emerging challenges and future prospects. Environ. Sci. Policy 2015, 54, 106–125. [Google Scholar] [CrossRef]
- Fang, Q.X.; Ma, L. Green T R, Yu Q, Wang T D, Ahuja L R. Water resources and water use efficiency in the North China Plain: Current status and agronomic management options. Agric. Water Manag. 2010, 97, 1102–1116. [Google Scholar] [CrossRef]
- Chen, X.W.; Chen, Y.Y.; Zhang, J.J. A Quantitative Study on the Impact of China’s Rural Population Aging on Agricultural Output. China Popul. Sci. 2011, 36, 39–46. [Google Scholar]
- Gai, Q.E.; Zhu, X.; Shi, Q.H. The impact of labor transfer on China’s agricultural production. Econ. Q. 2014, 13, 1147–1170. [Google Scholar]
- Chen, L.S.; Zhang, D. Empirical analysis on agricultural investment since China’s reform and opening-up. Chin. Rural Econ. 2004, 20, 40–46. [Google Scholar]
- Chen, Y.; Kuang, G.L. Review on the theoretical core and research ideas of “industrial upgrading”. Reform 2009, 22, 85–89. [Google Scholar]
- Chen, Y.E.; Chen, W. Research on the relationship between agricultural mechanization, industrial upgrading and agricultural carbon emissions: Empirical analysis based on dynamic panel data model. Agric. Technol. Econ. 2018, 37, 122–133. [Google Scholar]
- Gao, M.; Song, H.Y. Spatial convergence and functional zone difference of grain production technical efficiency: Also on spatial ripple effect of technological diffusion. Manag. World 2014, 30, 83–92. [Google Scholar]
- Yang, X.Y.; Qiao, C.X. Spatial differences and convergence of agricultural industrial structure optimization and upgrading. J. South China Agric. Univ. Soc. Sci. Ed. 2022, 21, 67–80. [Google Scholar]
- Wei, H.K. The Structural Contradiction of China’s Agricultural Development and Its Policy Transformation. China Rural Econ. 2017, 33, 2–17. [Google Scholar]
- Lesage, J.; Pace, R.K. Introduction to Spatial Econometrics, 1st ed.; CRC Press: Boca Raton, FL, USA, 2009; pp. 45–75. [Google Scholar]
- Luo, Y.M.; Fan, L.M. Spatial Characteristics of Income-Increasing Effects of China’s Rural Infrastructure: An Empirical Study Based on Spatial Correlation and Spatial Heterogeneity. Manag. World 2012, 38, 71–87. [Google Scholar]
- Su, X.S.; Xu, L. Catastrophe Effect and Risk Assessment of China’s Grain Market-Simulation Analysis Based on Partial Equilibrium Model. Agric. Technol. Econ. 2021, 40, 18–32. [Google Scholar]
- Liu, Q.; Yang, Q.Z. The evolution of my country’s agricultural production model during the transition period. Rural Econ. 2013, 31, 46–48. [Google Scholar]
- Liu, D.; Zhu, X.; Wang, Y. China’s agricultural green total factor productivity based on carbon emission: An analysis of evolution trend and influencing factors. J. Clean. Prod. 2020, 278, 123692. [Google Scholar] [CrossRef]
- Bai, J.H.; Wang, Y.; Jiang, F.X.; Li, J. Flow of research and development factors, spatial knowledge spillover and economic growth. Econ. Res. 2017, 52, 109–123. [Google Scholar]
- Gan, C.H.; Zheng, R.G.; Yu, J.J. The impact of China’s industrial structure changes on economic growth and volatility. Econ. Res. 2011, 46, 4–16. [Google Scholar]
- Dong, J.C.; Feng, T.; Li, J.J. The impact of factor mismatch between regions in China on the quality of economic development: An empirical test based on a chained multiple mediation effect model. Financ. Trade Res. 2020, 31, 1–12. [Google Scholar]
- Jin, F.; Jin, R.X. Analysis of the Spatial Effect of Fiscal Supporting Agriculture Affecting the Change of Agricultural Industrial Structure. Res. Financ. Issues 2020, 42, 82–91. [Google Scholar]
- Wei, W.; Wen, C.C.; Cui, Q.; Xie, W. The impact of agricultural technology progress on agricultural energy use and carbon emissions: Analysis based on GTAP-E model. Agric. Technol. Econ. 2018, 37, 30–40. [Google Scholar]
- Yang, M.; Yang, F.; Sun, C. Factor market distortion correction, resource reallocation and potential productivity gains: An empirical study on China’s heavy industry sector. Energy Econ. 2018, 69, 270–279. [Google Scholar] [CrossRef]
- Fan, G.; Wang, X.; Ma, G. The Contribution of Marketization to China’s Economic Growth. China Econ. 2012, 7, 4. [Google Scholar]
- Gao, S.P.; Liu, P. Credit Collateral in rural financial system: Dilemma and outlet. Financ. Res. 2009, 51, 64–72. [Google Scholar]
- Hou, T.; Du, Y.K. Performance Evaluation of Agricultural Loans from the Perspective of Industrial Comparison. J. China Agric. Univ. 2017, 22, 180–191. [Google Scholar]
- Xin, B.H.; Lian, Y.H.; Tao, J. The Bargaining Power Measurement of Lenders and Lenders in my country’s Rural Lending Market—Analysis Based on Bilateral Stochastic Boundary Model. Agric. Technol. Econ. 2014, 32, 64–73. [Google Scholar]
- Wang, X.; Shao, S.; Li, L. Agricultural inputs, urbanization, and urban-rural income disparity: Evidence from China. China Econ. Rev. 2019, 55, 67–84. [Google Scholar] [CrossRef]
| Variable Type | Variable | Obs | Mean | Min | Max |
|---|---|---|---|---|---|
| Dependent variable | Agrout | 360 | 108.71 | 0.57 | 430.06 |
| Independent variable | Miscap | 360 | 0.64 | 0.01 | 2.25 |
| Control variables | Area | 360 | 640.52 | 58.00 | 2746.82 |
| Mechan | 360 | 292.19 | 15.24 | 1636.43 | |
| Fertilizer | 360 | 12.69 | 0.33 | 48.56 | |
| Labor | 360 | 50.40 | 1.50 | 152.20 | |
| Irrigation | 360 | 0.32 | 0.01 | 1.06 | |
| Other variables | Upgrade | 360 | 0.68 | 0.16 | 0.93 |
| Tech | 360 | 33.57 | 10.01 | 59.53 |
| Test Indicator | Test Method | Statistical Value | p-Value |
|---|---|---|---|
| LM test | LM test no spatial error | 32.94 | 0.001 |
| LM test no spatial lag | 40.70 | 0.001 | |
| Robust LM test | Robust LM test no spatial error | 26.90 | 0.001 |
| Robust LM test no spatial lag | 34.65 | 0.001 | |
| Wald test | Wald test spatial lag | 45.54 | 0.001 |
| Wald test spatial error | 41.61 | 0.001 | |
| LR test | LR test spatial lag | 41.29 | 0.001 |
| LR test lag spatial error | 38.48 | 0.001 | |
| Hausman test | Hausman test | 12.50 | 0.052 |
| Variable | Spatial Fixed Effect | Time Fixed Effect | Spatial-Temporal Fixed Effect | |||
|---|---|---|---|---|---|---|
| Coefficient | t-Value | Coefficient | t-Value | Coefficient | t-Value | |
| Miscap | −0.390 *** | [−7.37] | −0.218 *** | [−8.42] | −0.160 *** | [−7.22] |
| lnArea | 1.025 *** | [5.70] | −0.193 * | [−1.89] | 1.087 *** | [6.37] |
| lnMechan | −0.434 *** | [−3.09] | 0.171 | [1.41] | −0.398 *** | [−2.92] |
| lnFertilizer | −0.051 | [−0.40] | 0.171 | [1.61] | 0.015 | [0.12] |
| lnLabor | 0.572 * | [1.82] | 0.516 *** | [6.16] | 0.210 | [0.68] |
| Irrigation | 0.228 | [0.66] | −0.401 ** | [−1.99] | 0.637 * | [1.85] |
| WMiscap | −0.028 | [−0.26] | 0.0136 | [0.22] | −0.073 *** | [−6.91] |
| WlnArea | −0.888 *** | [−3.05] | −0.782 *** | [−3.38] | 0.012 | [0.04] |
| WlnMechan | 0.209 | [0.81] | 0.715 *** | [2.69] | 0.421 | [1.43] |
| WlnFertilizer | 0.268 | [1.29] | −0.055 | [−0.29] | 0.269 | [1.31] |
| WlnLabor | 0.322 | [0.50] | 0.008 | [0.04] | −0.444 | [−0.67] |
| WIrrigation | −2.050 *** | [−3.68] | −1.939 *** | [−4.88] | −0.692 | [−1.15] |
| ρ | −0.023 | [−0.33] | −0.129 * | [−1.74] | −0.257 *** | [−3.38] |
| sigma2 | 0.145 *** | [13.42] | 0.324 *** | [13.39] | 0.126 *** | [13.33] |
| R-squared | 0.420 | 0.556 | 0.290 | |||
| log-l | −163.504 | −308.702 | −141.293 | |||
| N | 360 | 360 | 360 | |||
| Variable | Miscap | lnMechan | lnFertilizer | Irrigation | lnArea | lnLabor |
|---|---|---|---|---|---|---|
| Direct effects | −0.160 *** | 0.415 *** | −0.001 | 0.671 ** | 1.091 *** | 0.246 |
| [−6.68] | [3.08] | [−0.01] | [2.06] | [6.55] | [0.80] | |
| Indirect effects | −0.018 *** | −0.460 * | 0.231 | −0.688 | −0.026 | −0.426 |
| [−3.56] | [−1.85] | [1.30] | [−1.36] | [−0.92] | [−0.78] | |
| Total effect | −0.178 *** | 0.045 | 0.231 | −0.017 | 0.965 *** | −0.170 |
| [−4.48] | [0.20] | [1.26] | [−0.03] | [3.23] | [−0.28] |
| Type | Miscap | lnMechan | lnFertilizer | Irrigation | lnArea | lnLabor | |
|---|---|---|---|---|---|---|---|
| Shorten the time window | Direct effects | −0.665 *** | −0.620 *** | 0.064 | 0.321 | 0.852 *** | −0.107 |
| [−7.00] | [−2.89] | [0.38] | [0.64] | [3.78] | [−0.24] | ||
| Indirect effects | −0.126 * | 0.723 * | 0.303 | −0.170 | −0.099 | 0.199 | |
| [−1.93] | [1.73] | [1.24] | [−0.24] | [−0.30] | [0.24] | ||
| Total effects | −0.791 *** | 0.103 | 0.367 | 0.151 | 0.753 ** | 0.092 | |
| [−3.43] | [0.24] | [1.46] | [0.18] | [2.11] | [0.10] | ||
| Winsorize | Direct effects | −0.269 *** | −0.286 * | −0.041 | 0.543 * | 1.067 *** | 0.184 |
| [−5.84] | [−2.38] | [−0.41] | [1.85] | [7.48] | [0.75] | ||
| Indirect effects | −0.014 * | 0.168 | 0.142 | −1.057 ** | −0.362 * | −0.746 * | |
| [−1.84] | [0.80] | [0.95] | [−2.24] | [−1.69] | [−1.70] | ||
| Total effects | −0.283 *** | −0.118 | 0.101 | −0.514 | 0.705 *** | −0.562 | |
| [−3.90] | [−0.56] | [0.66] | [−0.93] | [2.95] | [−1.09] | ||
| Replace the dependent variable | Direct effects | −0.126 *** | 0.117 ** | −0.072 | 0.123 | 0.719 *** | 0.487 *** |
| [−5.59] | [2.02] | [−1.44] | [0.88] | [10.06] | [3.60] | ||
| Indirect effects | −0.015 * | 0.085 | 0.142 | −0.626 ** | −0.192 | −0.248 | |
| [−1.78] | [0.68] | [1.63] | [−2.44] | [−1.56] | [−0.89] | ||
| Total effects | −0.141 *** | 0.202 | 0.07 | −0.503 | 0.527 *** | 0.239 | |
| [−2.75] | [1.48] | [0.71] | [−1.62] | [3.66] | [0.70] | ||
| Economic distance weight | Direct effects | −0.367 *** | −0.225 * | −0.051 | 0.759 ** | 1.117 *** | 0.400 |
| [−7.94] | [−1.83] | [−0.48] | [2.55] | [7.14] | [1.47] | ||
| Indirect effects | −0.166 ** | 1.863 *** | −0.572 | 0.631 | −1.311 | 1.766 | |
| [−2.35] | [2.62] | [−0.83] | [0.49] | [−1.36] | [1.19] | ||
| Total effects | −0.533 | 1.638 ** | −0.623 | 1.401 | −0.195 | 2.166 | |
| [−1.34] | [2.29] | [−0.90] | [1.08] | [−0.20] | [1.42] | ||
| Independent Variable | Dependent Variable: Agrout | |||||
|---|---|---|---|---|---|---|
| Miscap | −0.180 *** [−12.82] | −0.036 [−0.48] | ||||
| Upgrade | −0.629 *** [−4.95] | |||||
| Miscap × Upgrade | 0.168 *** [10.19] | |||||
| Tech | −0.007 [−0.63] | |||||
| Miscap × Tech | 0.009 *** [7.14] | |||||
| W × Miscap | −0.183 [−0.94] | −0.203 [−1.01] | ||||
| W × Upgrade | −0.535 [−0.88] | |||||
| W × Miscap × Upgrade | 0.241 * [1.66] | |||||
| W Tech | 0.018 [0.74] | |||||
| W × Miscap × Tech | 0.004 [1.11] | |||||
| Decomposition of interaction term | Direct effects | Indirect effects | Total effects | Direct effects | Indirect effects | Total effects |
| 0.174 *** [9.96] | 0.066 * [1.72] | 0.240 *** [5.19] | 0.001 *** [7.36] | 0.005 [1.60] | 0.006 [1.25] | |
| Control variables | YES | YES | ||||
| ρ | −0.261 *** [−3.43] | −0.198 *** [−2.58] | ||||
| sigma2 | 0.098 *** [13.33] | 0.108 *** [13.36] | ||||
| N | 360 | 360 | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, S.; Chen, H.; Tran, T.T.; Wang, H. Analysis of the Spatial Effect of Capital Misallocation on Agricultural Output—Taking the Main Grain Producing Areas in Northeast China as an Example. Sustainability 2022, 14, 5782. https://doi.org/10.3390/su14105782
Qin S, Chen H, Tran TT, Wang H. Analysis of the Spatial Effect of Capital Misallocation on Agricultural Output—Taking the Main Grain Producing Areas in Northeast China as an Example. Sustainability. 2022; 14(10):5782. https://doi.org/10.3390/su14105782
Chicago/Turabian StyleQin, Shuai, Hong Chen, Tuyen Thi Tran, and Haokun Wang. 2022. "Analysis of the Spatial Effect of Capital Misallocation on Agricultural Output—Taking the Main Grain Producing Areas in Northeast China as an Example" Sustainability 14, no. 10: 5782. https://doi.org/10.3390/su14105782
APA StyleQin, S., Chen, H., Tran, T. T., & Wang, H. (2022). Analysis of the Spatial Effect of Capital Misallocation on Agricultural Output—Taking the Main Grain Producing Areas in Northeast China as an Example. Sustainability, 14(10), 5782. https://doi.org/10.3390/su14105782






