Abstract
Smart cities have a significant impact on the future of renewable energies as terms such as sustainability and energy saving steadily become more common. In this regard, both wind and hydrokinetic compact-size turbines can play important roles in urban communities by providing energy to nearby consumption points in an environmentally suitable manner. To evaluate the operation of a Darrieus turbine rotor as a wind or hydro microgenerator, a series of wind tunnel and water current flume tests were performed. Power and characteristic curves were obtained for all test conditions. In the wind tests, all curves seemed to be identical, which means that the turbine rotor works properly under open-field conditions. Two blockage correction equations were applied to the water channel tests that were performed under blockage values ranging from 0.2 to 0.35 to estimate the operational behavior in open water. Finally, it has been demonstrated that, with the condition of maintaining the Reynolds number between experiments in the wind tunnel and water flume, the turbine wind characteristics represents the its operation in open-water conditions.
1. Introduction
Significant progress has been made in generating electricity from sustainable renewable resources, such as the improvement in solar panels performance [1] or the installation of offshore wind arrays [2]. In 2020, the outbreak of the COVID-19 pandemic tested the strength of the world’s electricity system. During the first semester and coinciding with the hardest months of the disease and with confinements, the demand for world energy suffered a notable setback with a decrease of 5%, mainly due to the interruption of industrial activity [3]. However, the demand of renewable energy increased by 1%, showing great resilience despite the reduction in overall demand. Thus, the renewable energy sector has shown an extraordinary ability to adapt to this new situation, contributing more than 18% of that which was envisaged in 2019. A variety of factors, such as their independence from the transport of resources (they are located where the resource is available) or their installation at isolated locations, are the main reasons of this extraordinary resilience [4].
In this way, recent studies have estimated that green energy will increase by 10% in 2021, 3% more than expected, because of the resumption of projects that had previously been blocked due to the effects of the pandemic. As a consequence, more than a hundred million dollars, mainly in Europe, United States, China, and India, will be invested to build these facilities so that the ultimate target of zero emissions can be reached by 2030 [5].
A portion of this investment is allocated to research and development of hydrokinetic turbines at ocean currents. These systems harness the great potential that exists in those locations, which in the case of marine currents, is estimated at 800 TWh/year worldwide [3]. This hydrokinetic power is also predictable over time, and its energetic use can be compatible with other needs such as water supply [6].
With regard to smart cities, there have been inroads in the development of microgeneration using turbines [7]. In this work, the proposed rotor is designed to be used in water and wind, giving competitive advantages by reducing its cost and facilitating its manufacture, since it does not require specific changes (in the design) to adapt to the working fluid. This is possible due to the use of lift-based rotors, the installation of permanent magnet generators, and the development of much more efficient electronic control systems [8]. The system is simple, so that the visual impact and cost are minimized, making it very attractive to be installed in urban environments [9]. Figure 1 shows the dual proposal composed by water and wind turbines using the same rotor design to harness both resources. In this case, the energy is used to supply electricity and other services to a city.
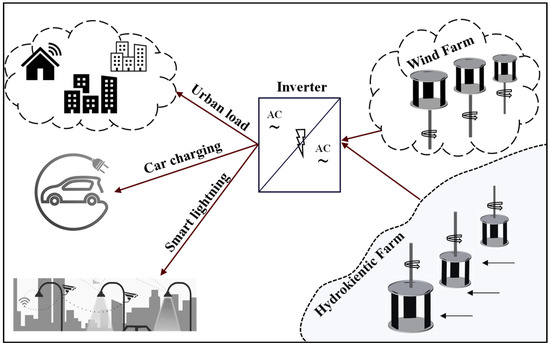
Figure 1.
Integration of hydrokinetic and wind turbines for urban systems.
Hydrokinetic turbines use the kinetic term of the current, not requiring the creation of potential elevations, so not only the installation requires less initial investment but also the environmental impact is minimized [10]. Thus, the power obtained by these turbines will mainly depend on the water velocity, together with the area swept by their blades, the fluid density, and the conversion efficiency of the equipment.
Hydrokinetic turbines can be classified into two large groups depending on the direction of the flow and the axis of rotation: axial turbines (flow and axis are parallel) and crossflow turbines (flow and axis are perpendicular). Nowadays, crossflow turbines are those that generate more interest [11]. This is mainly because these rotors, although not as efficient as axial ones, have a much simpler mechanical coupling system that reduces the construction costs and facilitates installation and maintenance activities [12]. One of the most frequently used crossflow rotor designs is Darrieus type with different configurations: Squirrel Cage (SC), H, and curved [13] (Figure 2). These designs are based on aerodynamical profiles used in the wind industry [14].
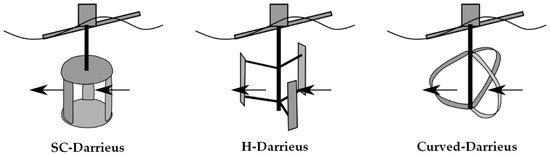
Figure 2.
Different designs of Darrieus rotors [15].
Crossflow rotors can be divided in accordance with the axis position in horizontal and vertical axis turbines. Although horizontal turbines have been used mainly for shallow-water conditions [16], vertical rotors allow for greater use of the cross-sectional area of the water current when they are arranged in farms or arrays, allowing for the production of energy under low-velocity conditions [17]. Additionally, because their dimensions rarely exceed 2 m in height and diameter, they have a reduced effect on the environment or river-maritime traffic [18].
The use of vertical axis water turbines under low-velocity and shallow-water conditions is possible due to the appearance of the blockage phenomenon [19]. Under these circumstances, three simultaneous phenomena appear: an increase in the fluid velocity around the rotor, high pressure changes across the rotor, and the appearance of longitudinal pressure gradients associated with boundary layer conditions [20].
Until now, blockage has been studied from two different points of view: the energetic use of the blockage effect and the development of mathematical corrections to extrapolate results (with blockage existence) to open-field conditions. In the first case, the design of the devices is studied, such as the accelerator or the deflectors used to induce blockage conditions into the water stream current [10]. In the second instance, different numerical methodologies are developed to eliminate the effects of blockage that inherently appear in experimental tests and to extrapolate that behavior to open-field conditions [21].
More specifically, most accelerators studies have tested different designs, observing the increases in the extracted power for the same hydrodynamic conditions. Some examples are the results presented by [22,23]. In the case of blocking corrections, the development of numerical expressions to correct these effects are mainly based on the application of the simple actuator disc theory and the use of empirical coefficients. The results presented by [20,24,25] show the value of the corrected open-field velocity from a theoretical study of energy, while [21,26] provide empirical correction coefficients based on laboratory tests.
The study of blockage in crossflow turbines under confined and open-field conditions have been approached. These studies have been carried out using wind and water tunnels, sometimes even simultaneously. On the one hand, some confined flow studies such as the one carried out by Hossein et al. [27], analyzed the effects of blockage and the position of the water free surface on the energy extracted by the rotor. It concludes that there is a clear relationship between both aspects since there is a change in the hydrodynamic operation of the acting forces. This study was approached using a high-speed camera and a torque meter. Additionally, of interest is the work presented by Bachant et al. [28] in which a comparison was made between Gorlov and Savonius rotors under blockage conditions. In this case, the study concludes that Gorlov turbines are more recommended when blockage coefficient is low (<20%).
On the other hand, open-field studies, such as those carried out by Banerjee et al. [29] and Consul et al. [30], have analyzed how certain parameters such as solidity or wake appearance affect the power extraction. Finally, some studies have been made using both wind and water tunnels. For example, the studies presented by [31,32] carried out tests with wind turbines, obtaining power measurements and analyzing the flow characteristics around the blades in a wind tunnel using PIV (Particle Image Velocimetry) techniques. It was then possible to quantify the detachment effect so the blade design could be adjusted.
Other studies such as the one carried by [33,34] tested axial turbines in wind and water tunnels to study in which fluid the chosen designs were more suitable. Furthermore, in the work presented by [35], a Darrieus tidal turbine was studied in similar infrastructure. Wind experiments were used to study the starting and dynamic torque, and the suitability of different blade geometries. After that, the water tunnel was used to verify the dynamic torque values and to obtain the maximum tip speed ratio of the turbine under low flow conditions. Finally, in the studies carried out by [36,37], an accurate study of blockage effects was carried out considering those produce by the wake phenomenon. Thus, it was possible to quantify the effect that the presence of the rotor produces on other turbines specially when they are arranged in arrays. However, none of these publications address the study of blockage conditions by testing the turbine under different fluids and by focusing only on differences in power parameters.
This article presents an analysis of the power stage of a vertical axis turbine (squirrel cage-Darrieus type) with straight blades manufactured with the help of additive manufacturing technology (3D printing). Wind tests are used to obtain the behavior of the turbine at open-field conditions, while water experiments represent blockage conditions. Finally, both situations are analyzed separately so the results are contrasted.
The article is structured as five main sections: introduction, theoretical bases of the experiments (in both wind and water), materials and methods (including descriptions of the rotor, wind tunnel, water flume, and testing procedure), results and discussion, and finally the conclusions.
2. Theoretical Bases
There is a marked difference between the theoretical bases that describe the experimental tests at the wind tunnel and the water flume since the turbine is subjected to the influence of two different fluids (air and water). However, the operation of the turbine is analogous in both cases, meaning that the results are comparable when the Reynolds numbers are equal in wind and water scenarios, which implies that the wind speed should be ten times greater than the water velocity.
2.1. Wind Bases
The experimentation of the turbine in the wind tunnel is based on the application of the actuator disk theory. In these circumstances, the flow is incompressible, and homogeneous, stationary and the rotor has an infinite number of blades, inducing a uniform thrust in all of them. The upstream velocity is progressively reduced as it approaches the disc, reaching its minimum value once the fluid has passed through it due to wake effects [38]. Additionally, far away from the disk (upstream and downstream), the static pressure of the air is equal to the atmospheric pressure () (Figure 3).
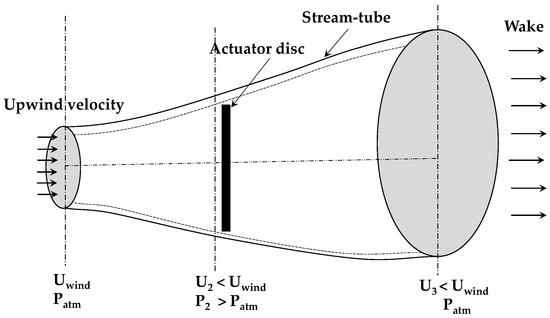
Figure 3.
Actuator disk theory at a wind tunnel [39].
Thus, as the wind approaches the rotor, there is a decrease in its speed since energy is driven out by the turbine. By applying the linear momentum conservation equation, the power produced by the turbine depends on the wind density, the area swept by blades, the cubic value of wind velocity, and the power coefficient of the rotor. At maximum power conditions (), the power coefficient is limited to 0.59, which corresponds to the Betz limit [40].
2.2. Water Bases
The turbine testing conditions inside the water flume follows the one-dimensional actuator disc model that was put forward by Houlsby et al. [41]. The rotor acts as a hydrokinetic turbine in conditions of uniform and subcritical flow. More specifically, the following are considered:
- The disc is submerged in water and under blockage conditions.
- Two different zones with uniform flow are distinguished upstream and downstream of the disc.
- A mixing zone also appears due to turbulence phenomena, being located just after the disc.
These conditions are produced in the hydrodynamic water flume using a water gate that is situated downstream from the rotor. Furthermore, since the channel is made of glass (low roughness) and the slope is practically horizontal, a constant velocity profile can be assumed (Figure 4).

Figure 4.
Actuator disk scheme at a water channel [42].
It should be noted that the calculation of power in water turbines is executed by applying the same expression as wind turbines but that, due to the appearance of blockage conditions, the power coefficient is not limited by the Betz law [43].
2.3. Testing Parameters
In both installations, the characterization of the power stage is performed by applying two dimensionless coefficients: tip speed ratio and power coefficient. Other parameters including the hydraulic and mechanical power are also calculated. The following equations are used:
where λ is the relation between the velocity at the tip of the blade and the fluid speed (dimensionless), is the rotational speed of the turbine (rad/s), is the radius of the rotor (m), is the fluid velocity (m/s), is the power coefficient (dimensionless), is the mechanical power (W), is the fluid density (kg/m3), is the area swept by blades (m2), is the hydraulic power (W), and is the torque measured by the torque meter (N). The blockage coefficient is defined as the ratio between the turbine area and the channel section:
where is the blockage ratio (dimensionless), is the channel section (m2), is the height of the rotor (m), is the width of the channel (m) and is the height of the water free surface (m).
Clearly, the wind and water tests differ, not only because two different fluids have been used. In this case, the tests conducted at the water flume are influenced by the blockage so it is necessary to extrapolate the confined results to the open-field conditions. With that in mind, mathematical expressions must be applied to obtain the velocity in open-field conditions. Although, there are many different formulations, in this case, the corrections proposed by Gauvin et al. [21] (Equations (6) and (7)) and Werle [25] (Equation (8)) have been applied because they are suitable for low blockage coefficients [44].
where is the water velocity at open-field conditions (m/s), is an empirical factor (dimensionless), is the tip speed ratio at open-field conditions (dimensionless), and is the power coefficient at open-field conditions (dimensionless). , , and are the experimental measured values in the water flume (confined conditions).
3. Materials and Methods
3.1. Rotor Description
The designed rotor has a height and radius of h = 0.15 m and R = 0.075 m, respectively, with three blades spaced at 120 degrees. A NACA-0015 standard profile with a chord of c = 0.05 m was used, so its solidity was that of 2. This blade profile was selected for its good behavior under low flow velocity conditions, far superior to asymmetric profiles [45]. Moreover, a decided was taken to use a three-bladed rotor because there are more advantageous in terms of cost and efficiency [46]. Figure 5 shows the characteristics and fabrication process of the turbine.

Figure 5.
(a) Geometric characteristics of the turbine. (b) Blade fabrication process using a 3D printer.
The turbine and its coupling system were built using 3D additive manufacturing technology, with the Polylactic Acid (PLA) being the selected material. The behavior of PLA under conditions of dynamic stress has been exemplary. Its endurance when working with water is unquestionable, whilst it is readily pliable so that pieces can be adjusted to complex profiles such as NACA-0015 [47]. For both experiments, the shaft diameter was set at 10 mm.
3.2. Wind Tunnel Description
The wind tunnel has a total length of 13.75 m and a discharge section of 0.68 × 0.68 m2, working as an open-air admission circuit and under subsonic conditions. In addition, the discharge section where the turbine was tested is fully open and does not imply blockage. The air movement was produced by an axial fan with a diameter of 1.2 m and a power of 30 kW, controlled by an electronic power inverter that allows maximum wind speeds of up to 35.5 m/s.
The characteristics of the wind tunnel are shown in Figure 6, where (1) is the honeycomb panels controlling admission, (2) is the axial fan, (3) is the diffuser section, (4) is the stilling chamber, and (5) is the testing section.
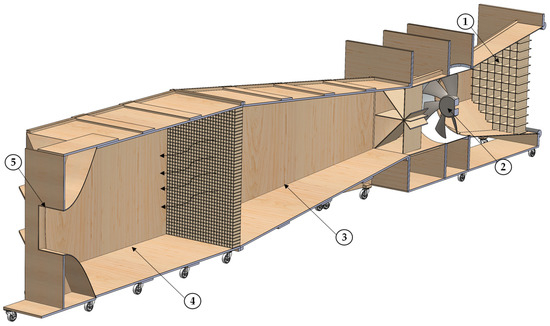
Figure 6.
Wind tunnel configuration (sectional-view).
To reduce turbulent phenomena, the wind tunnel has a stilling chamber and lengthwise honeycomb panels throughout the facility. Additionally, the installation has different sensors that allow for the parametrization of test conditions. More specifically, Pitot tubes, and differential and digital manometers are available, so wind speed and pressure are known.
The rotor was tested in the tunnel using a portable aluminum structure where the rotor and measurement instruments were included. The rotational axis was joined above and below by two high-performance radial bearings, and the rotor was placed between them. Both the torque meter and electric brake were placed in the upper part. Figure 7 shows the rotor placed at the wind tunnel, where (1) is the power supply devices, (2) is the tested turbine, (3) is the data acquisition system, (4) is the aluminum structure, and (5) is the digital manometer.

Figure 7.
(a) Different devices used during a wind test. (b) The turbine at the testing section.
3.3. Water Flume Description
The water current flume has a rectangular section with a length of 1.5 m, a height of 0.55 m, and a width of 0.3 m, with the floor and walls being made of laminated glass, thus allowing the tests to be recorded. The flow movement was generated by a hydraulic pumping system with a total power of 30 kW that can move a maximum flow rate of 600 m3/h. Both pumps were controlled by two electronic inverters. The whole system works as a close circuit, suctioning the water from a recirculation tank of 5 m3 and driving it upwards to the hydraulic testing channel. At the end of the channel, a metallic gate controlled by a gear system was installed to induce low-velocity hydrokinetic conditions.
The description of the water flume is shown in Figure 8, where (1) is the hydraulic pumps, (2) is the electronic system, (3) is the reassuring tank, (4) is the channel test section including torque sensor and rotor, (5) is the water gate, and (6) is the suction tank.

Figure 8.
Water flume including the turbine rotor.
To test the turbine, a water-resistant methacrylate box was designed and built. This structure has in its submerged part a waterproof radial bearing that allows for the rotation of the axis in optimal conditions. In the upper part and out of the water current, a lid is available as the location of the torque meter and the electric brake. It should be noted that this structure can be easily installed and removed thanks to the anchoring system based on slide clamps.
3.4. Testing Procedure
To study the power stage of the described turbine, a high-precision torque meter was used together with an electromagnetic brake. This procedure was used both in the wind tunnel and in the water current flume. The torque transducer used was an integrated high-precision torque and rotational speed sensor (Magtrol TS-103, 0.5 Nm of rated torque, accuracy <0.1% and 15,000 rpm max. speed, accuracy <0.015%) calibrated in accordance with the standards of the Swiss Federal Institute of Metrology (METAS).
This device allows for measurements of torque, rotational speeds, and relative position of the blades with data-taking frequencies up to 80 data per second, thereby collecting a good range of sampling. All collected data were sent to a database for further processing. The variation in the braking force was directly controlled by a power supply device. The characterization procedure (Figure 9) started with an initial measurement where no braking force was applied, so the rotor had its maximum rotational speed but did not generate power.
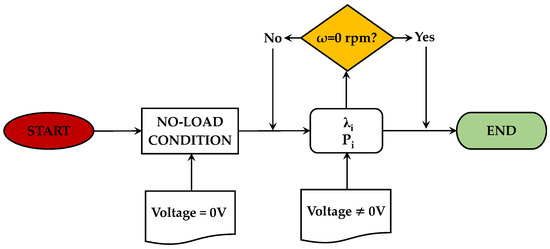
Figure 9.
Experimental test procedure.
This step is called “no-load condition”. Subsequently, the resistive torque of the electric brake was sequentially changed, in different “i” steps, through voltage variations at the power supply device, obtaining different extracted powers (Pi) and tip speed ratios (λi).
The turbine was tested at different wind and water velocities as well as various blockage conditions (see Table 1). In fact, this rotor was tested for flow velocities higher than 10 m/s, reaching 20 m/s and proved stability, reliability, and durability, but it should be borne in mind that these higher velocities are somewhat rare, particularly in an urban environment, indicating that our research is largely focused on real-world performance and on not an artificial one.

Table 1.
Different wind and water testing conditions.
4. Results and Discussion
During the different tests, continuous measurements of the parameters, including torque and angular velocity, were carried out. Thus, it was possible to check if the turbine reached stability before starting the power test in each point, thereby minimizing discontinuities. After loading the turbine rotor, it proved preferable to wait and watch the rotational speed variation of the turbine rotor before recording the results to ensure that the turbine was working under stable conditions. Figure 10 illustrates the stability condition during one of the proposed tests.
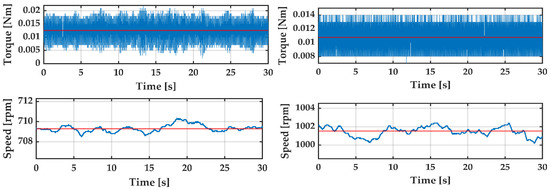
Figure 10.
Stability conditions for low and high rotational speeds test conditions at a wind speed of 8 m/s.
The variation in the power output with the rotational speed of the turbine rotor for different upstream wind velocities are shown in Figure 11. All tested speeds show the same tendency. When loading the turbine rotor, the rotational speed decreased and the output power increased dramatically until reaching the maximum power point. After that, the power output started to decline up until it reached the point where the turbine stopped and was not able to produce more power. In fact, for high flow velocities, the power curve was almost complete after reaching the MPP, but for low velocities, the power curve nearly reached the MPP and does not reach the completion point. This is due to the power-to-friction ratio, since for high flow velocity, the turbine is able to produce power to overcome the friction and to pass the MPP. On the other hand, for low velocities, the rotor is not able to pass this point and to characterize this part of the power curve.
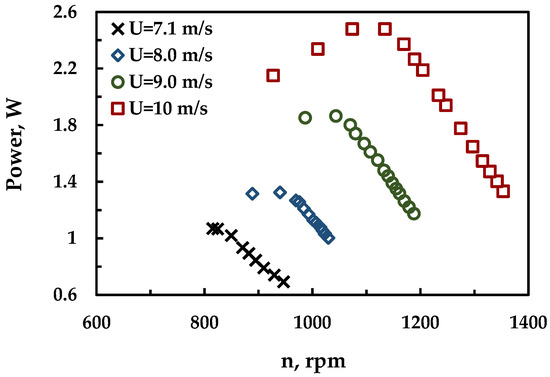
Figure 11.
Wind tunnel power curves at different upstream velocities.
By tracking the maximum power point MPP variation with the upstream wind velocity (Figure 12), it was found that the maximum power increases approximately with the cube of the upstream wind velocity, as Equation (3) indicates, to reach its maximum value of 2.5 W at a wind velocity of 10 m/s.
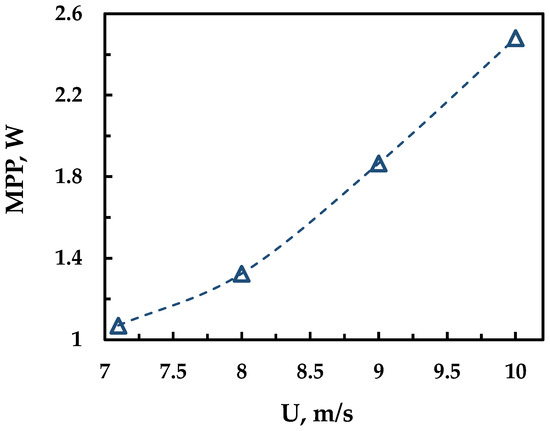
Figure 12.
Maximum power point variation with wind velocities.
The characteristic curve of the turbine inside the wind tunnel is shown in Figure 13. The rotor is observed as working in a stable range of approximately 0.13, this being the maximum point reached at a of 1.1. Additionally, all curves seem to be identical, which means that the turbine rotor works properly under open-field conditions without the existence of other factor such as blockage. In fact, the value of tip speed ratio is considered paltry compared with other similar turbines; this is due to the high solidity value that was selected in the proposed rotor to allow for self-starting under low flow velocities.
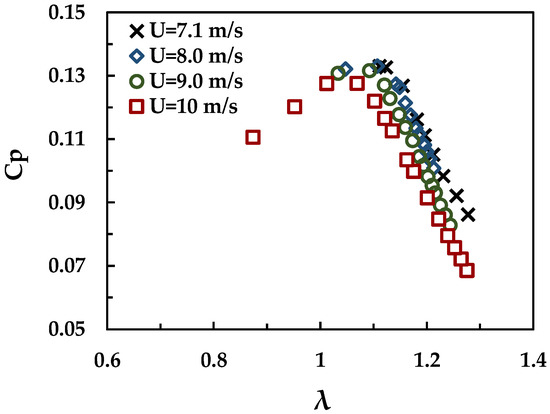
Figure 13.
Characteristic curve for the turbine rotor at different wind velocities.
To study the effects of blockage conditions and their correction to open-field behavior, the turbine was tested in the open-surface water flume. Four tests were carried out for similar velocities and different blockage values ranging from 0.2 to 0.34. Figure 14a shows the variation in the characteristic curves with blockage. Different curves were obtained for the same rotor, while for wind tests, only one curve was drawn. This is due to the existence of flow blockage conditions that affect the rotor performance. By increasing the blockage value, the performance curves shifted to higher values of tip speed ratios and power coefficients. This is a direct consequence of the flow acceleration around the turbine rotor while the blockage increased. As shown in Figure 14b, with a turbine rotor blockage value of 6.8% inside the wind tunnel, which is considered an open-field condition, the maximum power coefficient value is of 0.13. By increasing the blockage value from 6.8% to 34.1%, the maximum power coefficient increased to reach its maximum value of 0.97.
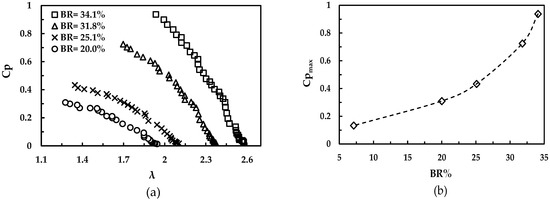
Figure 14.
(a) Characteristic curves at different water blockage values and (b) variation in Cpmax with Blockage ratio.
The extrapolation of blockage to open-field conditions was performed using the flow velocity of 0.71 m/s with a of 0.2. Under these conditions, the rotor works at Reynolds number of 3.5 × 104 approximately, so that results between wind and water can be compared. After applying the formulation of Gauvin et al. and Werle, the of 0.92 m/s and 0.875 m/s were extracted, respectively. Figure 15 compares the results: obtained at wind tunnel, confined water flume, and calculated for an open field (open waters) with the blockage corrections (Werle and Gauvin) and with the results of the experiments carried out by Patel et al. [45] using the same profile and solidity in open waters.
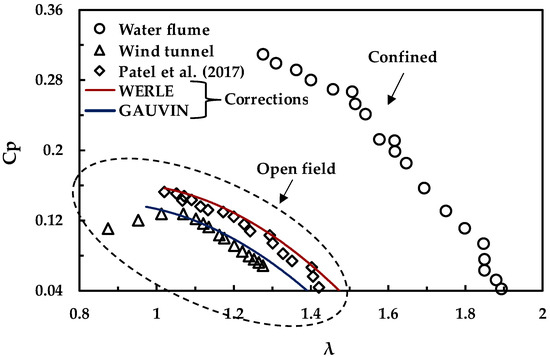
Figure 15.
Turbine characteristic curves in wind tunnel and water flume (Re = 3.5 × 104 approximately).
The peak power coefficient for the confined flow condition reached a value of 0.31, while in the wind tunnel, the obtained value is 0.13, which demonstrates the effect of blockage on the energy extraction. In fact, the corrected results (Werle and Gauvin) are quite similar to the results obtained from the wind tunnel and Patel et al. [45] tests (validating the results obtained). However, Werle’s formulations gives slightly higher results, reaching a value of nearly 0.16. Moreover, the tip speed ratio that corresponds to the maximum power coefficient values coincide in all open-field cases being greater than 1.
Therefore, maintaining the Reynolds number value between experiments in a wind tunnel (no blockage) and a water flume (with blockage), which is wind velocity approximately 10 times water velocity, demonstrates that the wind power characteristic obtained is similar to the one that corresponds to open-water conditions.
5. Conclusions
The combined use of hydrokinetic and wind turbines farms is considered a modern development in the energy sector for urban communities and smart cities that will be able to provide energy to nearby consumption points. The use of a vertical-axis crossflow turbine design is considered one of the best options from the economic and technical points of view.
A compact Darrieus turbine designed to operate in both water and air was presented and tested in a wind tunnel and water flume. The wind tunnel tests reproduced real open-field conditions at four wind velocities varying from 7 to 10 m/s. Power curves were obtained for each tested wind velocity, showing that the maximum power point increases approximately with the cube of the upstream wind velocity, up to a value of 2.5 W at a wind velocity of 10 m/s.
Characteristic curves for the rotor inside the wind tunnel at different upstream wind velocities seem to be identical, which means that the turbine rotor works properly under open-field conditions without blockage.
The turbine was tested at an open-surface water flume for different blockage values ranging from 0.2 to 0.34. Increasing the blockage value shifts the performance curves to higher values of tip speed ratios and power coefficients due to the flow acceleration around the turbine rotor while the blockage increased, reaching a value of 0.97 for a blockage ratio of 0.34.
The curves obtained in the wind tunnel (open field conditions) are similar to those obtained in the water current flume (confined conditions) as long as the same Reynolds number is maintained and the blockage corrections are applied. That opens the door to accurately estimating the power characteristics for different water current scenarios (blockage and velocities) from the results obtained in a wind tunnel or vice versa.
Author Contributions
Conceptualization, A.G.-Y.; methodology, E.B.-M.; software, A.F.-J.; validation, A.G.-Y., A.F.-J.; formal analysis, E.B.-M., E.Á.-Á.; investigation, A.G.-Y.; resources, R.E.-V.; data curation, R.E.-V.; writing—original draft preparation, A.G.-Y.; writing—review and editing, E.Á.-Á.; visualization, A.G.-Y.; supervision, E.B.-M.; project administration, R.E.-V. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Acknowledgments
The authors would like to express their gratitude to the Egyptian Cultural Affairs and Missions Sector (the Egyptian Ministry of Higher Education and Scientific Research) along with Port Said University and to the project HYDROCIMAR II financed by the Institute of Economic Development of the Principality of Asturias (Spain).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Espejo-Marín, C.; Aparicio-Guerrero, A.E. La Producción de Electricidad con Energía Solar Fotovoltaica en España en el Siglo XXI. Cuad. Sobre Vico 2020, 66–93. [Google Scholar] [CrossRef]
- Díaz, H.; Soares, C.G. Review of the current status, technology and future trends of offshore wind farms. Ocean Eng. 2020, 209, 107381. [Google Scholar] [CrossRef]
- IEA. Energy Technology Perspectives 2020. Available online: https://www.iea.org/reports/energy-technology-perspectives-2020 (accessed on 8 May 2020).
- REN21. Renewables 2020 Global Status Report 2020. Available online: https://www.ren21.net/gsr-2020/ (accessed on 8 May 2020).
- IRENA. Global Renewables Outlook: Energy Transformation 2050; 2020. Available online: https://www.irena.org/publications/2020/Apr/Global-Renewables-Outlook-2020#:~:text=Global%20Renewables%20Outlook%3A%20Energy%20transformation%202050,-April%202020&text=The%20Global%20Renewables%20Outlook%20shows,challenges%20faced%20by%20different%20regions (accessed on 8 May 2020).
- Oreste, F.; Vittorio, M.G.; Francesco, P. Numerical assessment of the vulnerability to impact erosion of a pump as turbine in a water supply system. J. Hydroinformat. 2020, 22, 691–712. [Google Scholar] [CrossRef]
- Malael, I.; Gherman, G.B.; Porumbel, I. Increase the Smart Cities Development by Using an Innovative Design for Vertical Axis Wind Turbine. In Proceedings of the 27th DAAAM International Symposium on Intelligent Manufacturing and Automation, Vienna, Austria, 26–29 October 2016; pp. 506–513. [Google Scholar]
- Alvarez, E.A.; Rico-Secades, M.; Corominas, E.; Huerta-Medina, N.; Guitart, J.S. Design and control strategies for a modular hydroKinetic smart grid. Int. J. Electr. Power Energy Syst. 2018, 95, 137–145. [Google Scholar] [CrossRef]
- Yuan, Z.; Wang, W.; Fan, X. Back propagation neural network clustering architecture for stability enhancement and harmonic suppression in wind turbines for smart cities. Comput. Electr. Eng. 2019, 74, 105–116. [Google Scholar] [CrossRef]
- Mohammadi, S.; Hassanalian, M.; Arionfard, H.; Bakhtiyarov, S. Optimal design of hydrokinetic turbine for low-speed water flow in Golden Gate Strait. Renew. Energy 2020, 150, 147–155. [Google Scholar] [CrossRef]
- Lee, J.H.; Park, S.; Kim, D.H.; Rhee, S.H.; Kim, M.-C. Computational methods for performance analysis of horizontal axis tidal stream turbines. Appl. Energy 2012, 98, 512–523. [Google Scholar] [CrossRef]
- Consul, C.A.; Willden, R.H.J.; Ferrer, E.; Mcculloch, M.D. Influence of Solidity on the Performance of a Cross-Flow Turbine. In Proceedings of the 8th European Wave and Tidal Energy Conference, Uppsala, Sweden, 7–10 September 2009; pp. 484–493. [Google Scholar]
- Khan, M.; Bhuyan, G.; Iqbal, M.; Quaicoe, J. Hydrokinetic energy conversion systems and assessment of horizontal and vertical axis turbines for river and tidal applications: A technology status review. Appl. Energy 2009, 86, 1823–1835. [Google Scholar] [CrossRef]
- Kaprawi, S.; Santoso, D.; Sipahutar, R. Performance of combined water turbine darrieus-savonius with two stage savonius buckets and single deflector. Int. J. Renew. Energy Res. 2015, 5, 217–221. [Google Scholar]
- Vermaak, H.J.; Kusakana, K.; Koko, S.P. Status of micro-hydrokinetic river technology in rural applications: A review of literature. Renew. Sustain. Energy Rev. 2014, 29, 625–633. [Google Scholar] [CrossRef]
- Le Hocine, A.E.B.; Lacey, R.J.; Poncet, S. Multiphase modeling of the free surface flow through a Darrieus horizontal axis shallow-water turbine. Renew. Energy 2019, 143, 1890–1901. [Google Scholar] [CrossRef]
- Balduzzi, F.; Zini, M.; Molina, A.C.; Bartoli, G.; De Troyer, T.; Runacres, M.C.; Ferrara, G.; Bianchini, A. Understanding the Aerodynamic Behavior and Energy Conversion Capability of Small Darrieus Vertical Axis Wind Turbines in Turbulent Flows. Energies 2020, 13, 2936. [Google Scholar] [CrossRef]
- Sinagra, M.; Sammartano, V.; Aricò, C.; Collura, A.; Tucciarelli, T. Cross-flow Turbine Design for Variable Operating Conditions. Procedia Eng. 2014, 70, 1539–1548. [Google Scholar] [CrossRef]
- Yosry, A.G.; Fernández-Jiménez, A.; Álvarez-Álvarez, E.; Marigorta, E.B. Design and characterization of a vertical-axis micro tidal turbine for low velocity scenarios. Energy Convers. Manag. 2021, 237, 114144. [Google Scholar] [CrossRef]
- Glauert, H. Wind Tunnel Interference on Wings, Bodies and Airscrews. Aeronaut. Res. Comm. 1933, 1566, 1–52. [Google Scholar]
- Gauvin-Tremblay, O.; Dumas, G. Two-way interaction between river and deployed cross-flow hydrokinetic turbines. J. Renew. Sustain. Energy 2020, 12, 034501. [Google Scholar] [CrossRef]
- Schluntz, J.; Willden, R. The effect of blockage on tidal turbine rotor design and performance. Renew. Energy 2015, 81, 432–441. [Google Scholar] [CrossRef]
- Vennell, R. Exceeding the Betz limit with tidal turbines. Renew. Energy 2013, 55, 277–285. [Google Scholar] [CrossRef]
- Bahaj, A.; Molland, A.; Chaplin, J.; Batten, W. Power and thrust measurements of marine current turbines under various hydrodynamic flow conditions in a cavitation tunnel and a towing tank. Renew. Energy 2007, 32, 407–426. [Google Scholar] [CrossRef]
- Werle, M.J. Wind Turbine Wall-Blockage Performance Corrections. J. Propuls. Power 2010, 26, 1317–1321. [Google Scholar] [CrossRef]
- Soerensen, H.C.; Weinstein, A. Ocean Energy: Position Paper for IPCC. In Proceedings of the Scoping Meeting on Renewable Energy Sources and Climate Change Mitigation, Lübeck, Germany, 20–25 January 2008; pp. 93–102. [Google Scholar]
- Birjandi, A.H.; Bibeau, E.L.; Chatoorgoon, V.; Kumar, A. Power measurement of hydrokinetic turbines with free-surface and blockage effect. Ocean Eng. 2013, 69, 9–17. [Google Scholar] [CrossRef]
- Bachant, P.; Wosnik, M. Performance measurements of cylindrical- and spherical-helical cross-flow marine hydrokinetic turbines, with estimates of exergy efficiency. Renew. Energy 2015, 74, 318–325. [Google Scholar] [CrossRef]
- Kolekar, N.; Vinod, A.; Banerjee, A. On Blockage Effects for a Tidal Turbine in Free Surface Proximity. Energies 2019, 12, 3325. [Google Scholar] [CrossRef]
- A Consul, C.; Willden, R.H.J.; McIntosh, S.C. Blockage effects on the hydrodynamic performance of a marine cross-flow turbine. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2013, 371, 20120299. [Google Scholar] [CrossRef] [PubMed]
- Brochier, G.; Fraunie, P.; Beguier, C.; Paraschivoiu, I. Water channel experiments of dynamic stall on Darrieus wind turbine blades. J. Propuls. Power 1986, 2, 445–449. [Google Scholar] [CrossRef]
- Fujisawa, N.; Shibuya, S. Observations of dynamic stall on Darrieus wind turbine blades. J. Wind. Eng. Ind. Aerodyn. 2001, 89, 201–214. [Google Scholar] [CrossRef]
- Sherry, M.; Sheridan, J.; Jacono, D.L. Horizontal Axis Wind Turbine Tip and Root Vortex Measurements. Exp. Fluids 2013, 54, 3. [Google Scholar] [CrossRef]
- Iungo, G.V.; Viola, F.; Camarri, S.; Porté-Agel, F.; Gallaire, F. Linear stability analysis of wind turbine wakes performed on wind tunnel measurements. J. Fluid Mech. 2013, 737, 499–526. [Google Scholar] [CrossRef]
- Hiraki, K.; Wakita, R.; Inoue, M. Improvement of straight-bladed vertical-axis water turbine for tidal current power generation. In Proceedings of the 9th ISOPE Pacific/Asia Offshore Mechanics Symposium (PACOMS-2010), Busan, Korea, 14–17 November 2010; pp. 169–174. [Google Scholar]
- Shahsavarifard, M.; Bibeau, E.L.; Chatoorgoon, V. Effect of shroud on the performance of horizontal axis hydrokinetic turbines. Ocean Eng. 2015, 96, 215–225. [Google Scholar] [CrossRef]
- Jeong, H.; Lee, S.; Kwon, S.-D. Blockage corrections for wind tunnel tests conducted on a Darrieus wind turbine. J. Wind. Eng. Ind. Aerodyn. 2018, 179, 229–239. [Google Scholar] [CrossRef]
- Ruiz, S.N. Aerogeneradores de Media Potencia; CIEMAT: Madrid, Spain, 2020. [Google Scholar]
- Betz, A. Der Maximum der theoretisch möglichen Ausnutzung des Windesdurch Windmotoren. Z. Gesamte Turbinenwes 1920, 26, 307–309. [Google Scholar]
- Nishino, T.; Willden, R.H.J. The efficiency of an array of tidal turbines partially blocking a wide channel. J. Fluid Mech. 2012, 708, 596–606. [Google Scholar] [CrossRef]
- Draper, S.; Houlsby, G.T.; Oldfield, M.L.G.; Borthwick, A.G.L. Modelling tidal energy extraction in a depth-averaged coastal domain. IET Renew. Power Gener. 2010, 4, 545. [Google Scholar] [CrossRef]
- Houlsby, G.T.; Vogel, C.R. The power available to tidal turbines in an open channel flow. Proc. Inst. Civ. Eng. Energy 2017, 170, 12–21. [Google Scholar] [CrossRef]
- Espina-Valdés, R.; Fernández-Jiménez, A.; Francos, J.F.; Marigorta, E.B.; Álvarez-Álvarez, E. Small cross-flow turbine:Design and testing in high blockage conditions. Energy Convers. Manag. 2020, 213, 112863. [Google Scholar] [CrossRef]
- Álvarez-Álvarez, E.; Rico-Secades, M.; Fernández-Jiménez, A.; Espina-Valdés, R.; Corominas, E.L.; Calleja-Rodríguez, A.J. Hydrodynamic water tunnel for characterization of hydrokinetic microturbines designs. Clean Technol. Environ. Policy 2020, 22, 1843–1854. [Google Scholar] [CrossRef] [PubMed]
- Patel, V.; Eldho, T.; Prabhu, S. Experimental investigations on Darrieus straight blade turbine for tidal current application and parametric optimization for hydro farm arrangement. Int. J. Mar. Energy 2017, 17, 110–135. [Google Scholar] [CrossRef]
- Burton, T.; Jenkins, N.; Sharpe, D.; Bossanyi, E. Wind Energy Handbook; John Wiley & Sons, Ltd.: Chichester, UK, 2011. [Google Scholar]
- Calignano, F.; Lorusso, M.; Roppolo, I.; Minetola, P. Investigation of the Mechanical Properties of a Carbon Fibre-Reinforced Nylon Filament for 3D Printing. Machines 2020, 8, 52. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).