Outdoors Evacuation Routes Algorithm Using Cellular Automata and Graph Theory for Uphills and Downhills
Abstract
1. Introduction
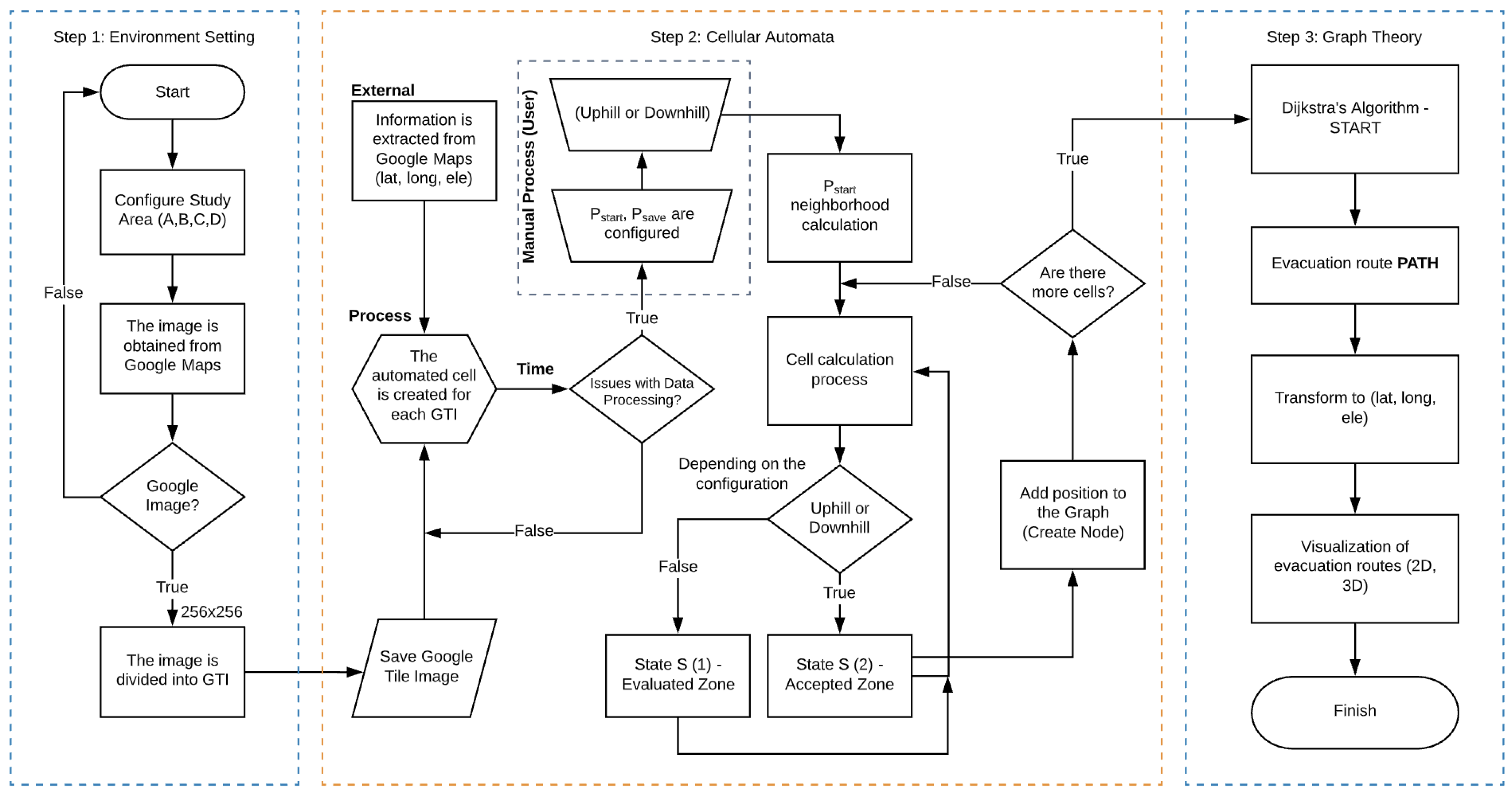
2. Methodology
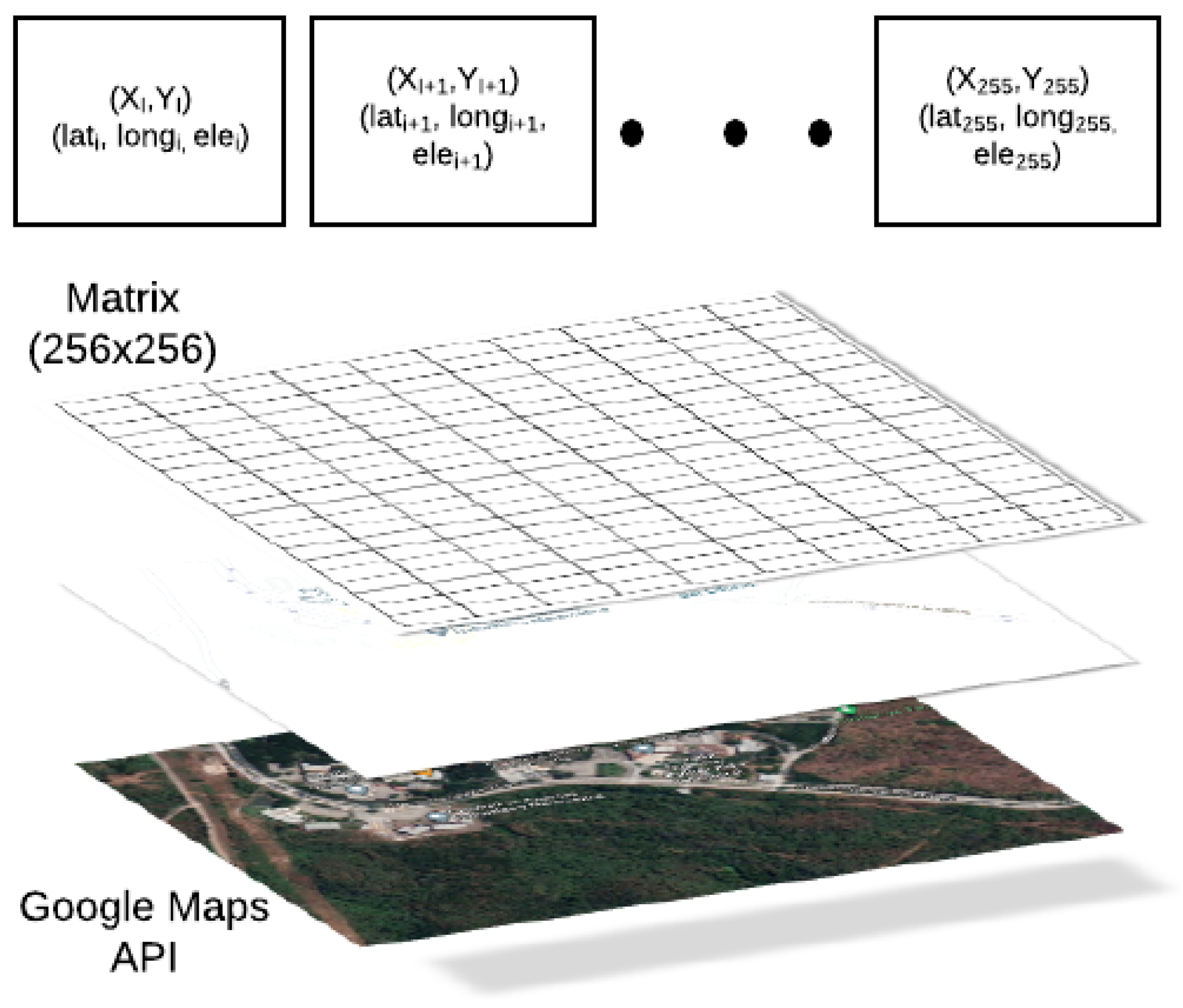
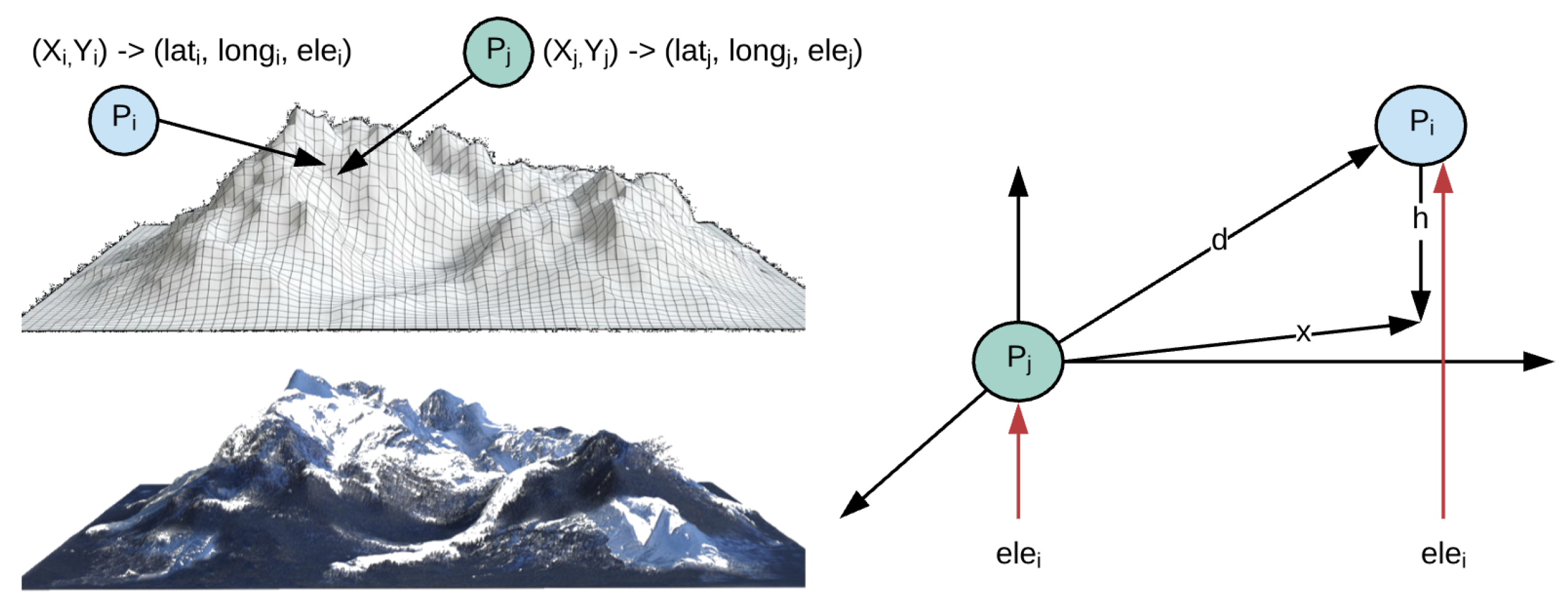
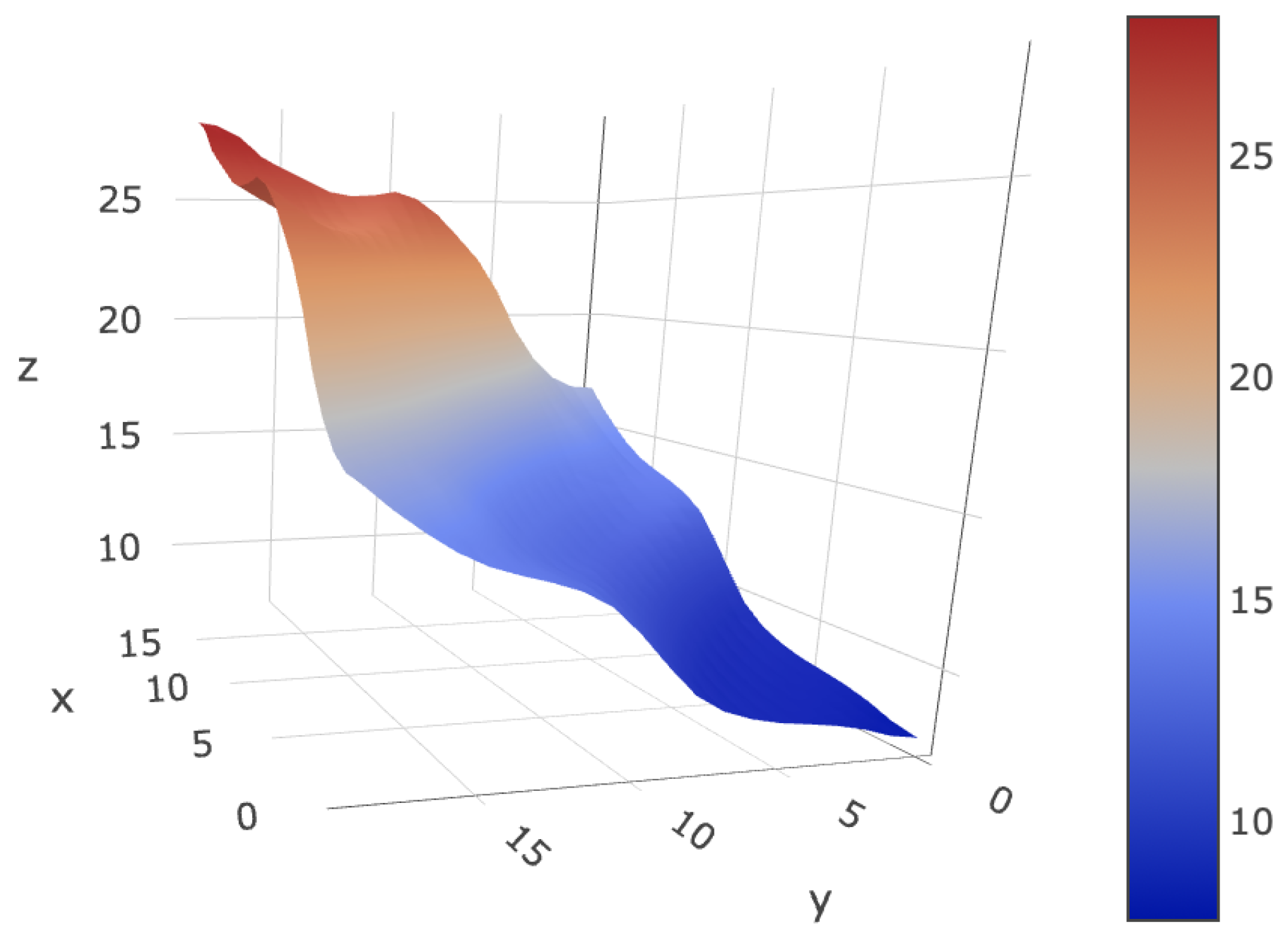
2.1. Geographical Information
- Latitude , Longitude , and Elevation : The geographical coordinates used refer to Google Maps with the cellular automata. A precision of eight digits is used so that the evaluation points are not so distant in the cellular automata.
- : Positions in the matrix are used for the user’s movement in the cellular automata, i.e., positions are used to create evacuation routes.
- States S: This is a finite non-empty set of states used in cellular automata. Each state changes depending on the user’s location and if it has been evaluated in the route calculation.
2.2. Cellular Automata
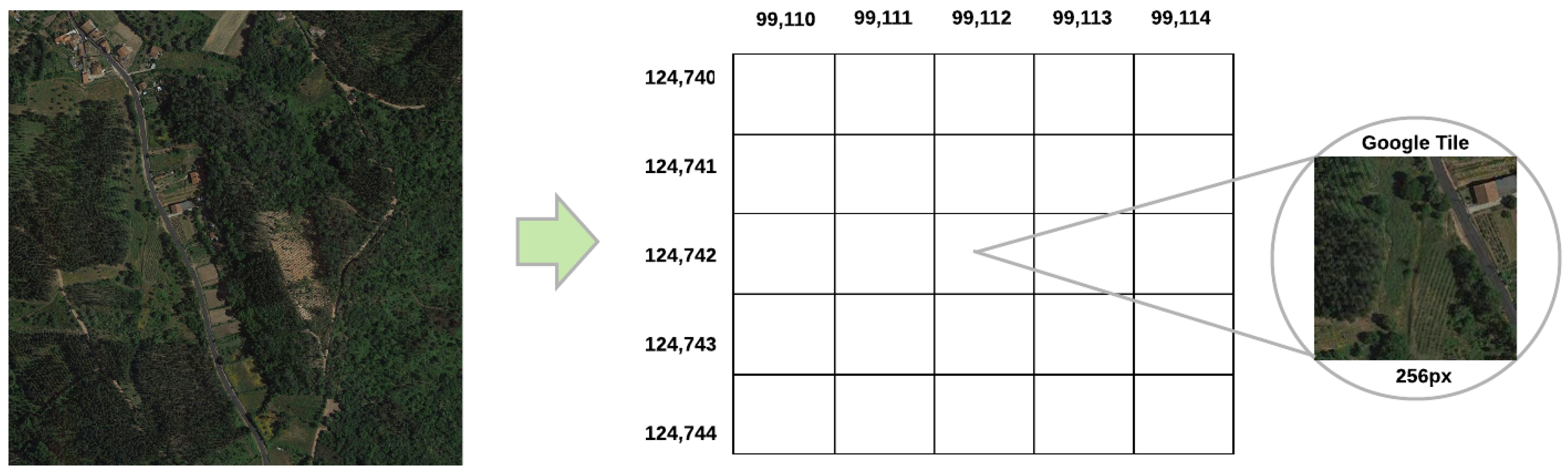
- Network Infrastructure: The cells in a CA are usually rectangular or square, although they can have other topologies, but always with a finite-dimensional. This CA case is 256 × 256.
- State S: There is a finite set of states in a CA; each cell must be in a defined state. The set of states on the different cells will help us to identify the possibility that there is a path through the cells.
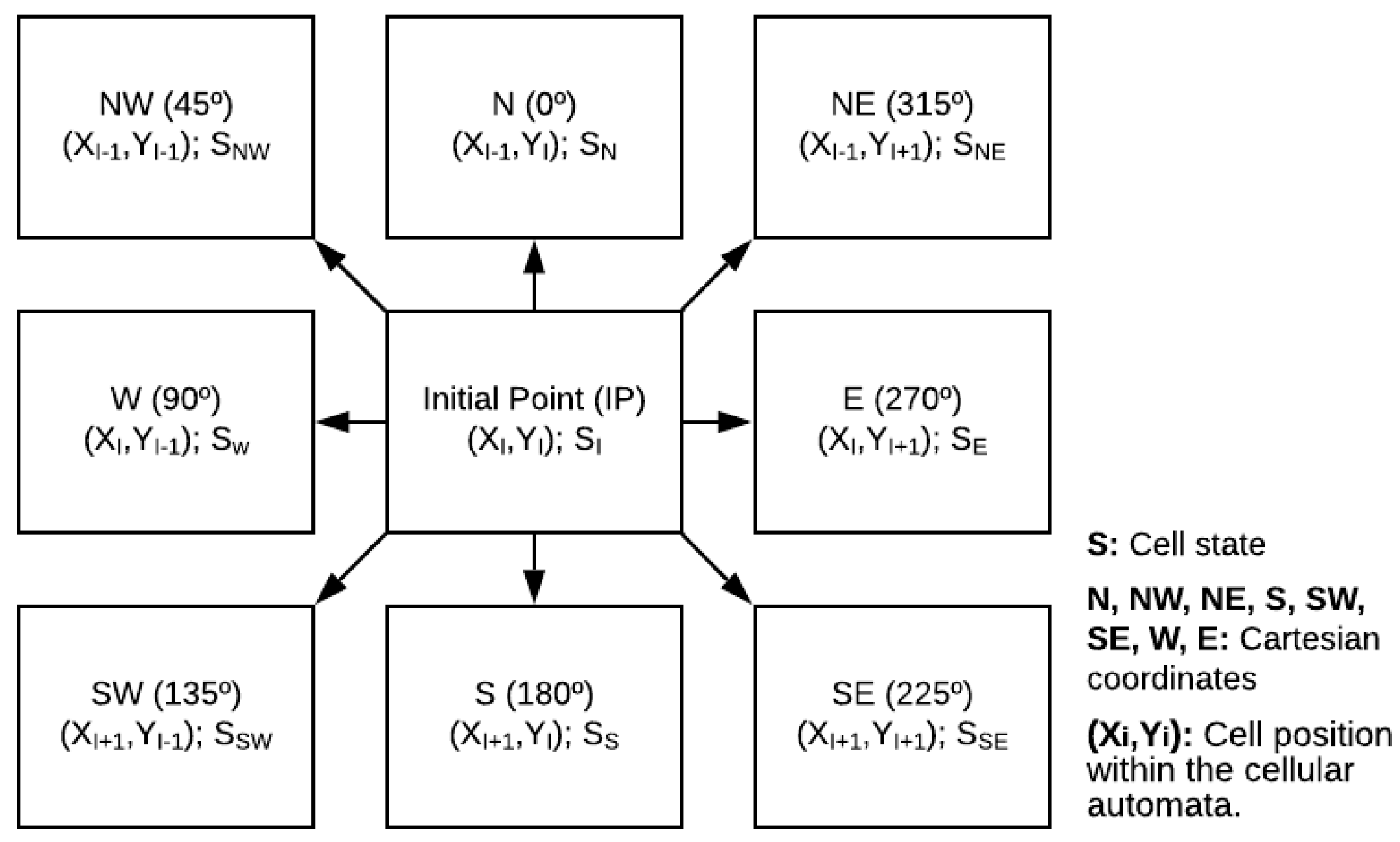
- , , , , , , , and : They are labels of the cellular automaton states to show the user the direction of their evacuation route.
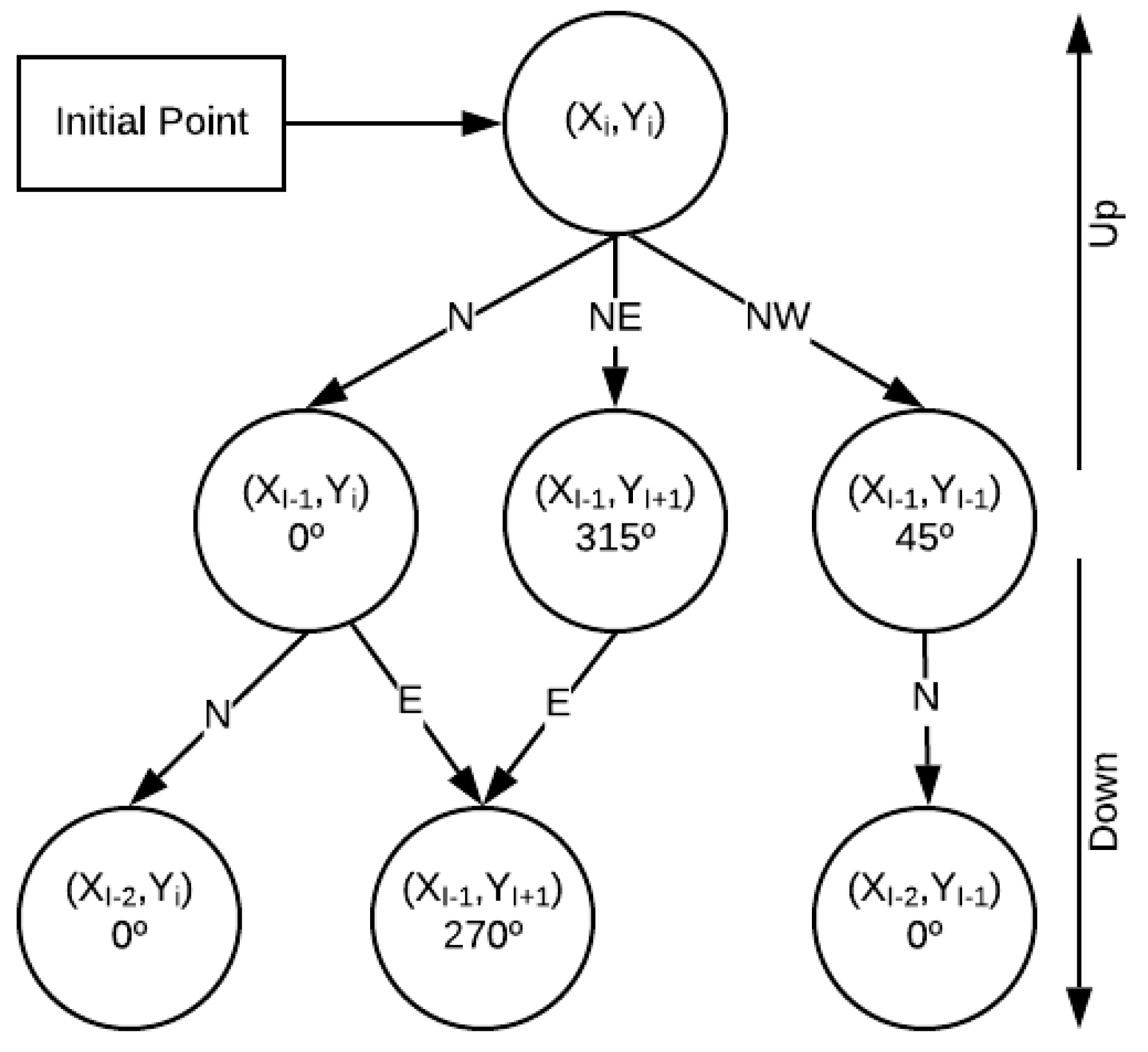
- Cell neighborhood: Each cell will have a neighborhood, usually defined by the developer; for two-dimensional structures, Moore and von Neumann schemes are the most used. Each cell’s status and those of neighboring cells within the neighborhood will depend on the transition rules that will be applied in each case [30]. A general scheme is shown in Figure 2.
- : Cell position within the cellular automata. The position is considered as the initial position, and the surrounding positions as its neighborhood.
- Transition rules: Each cell in the CA has applied a rule, which determines its state based on its state in time and on the state of its neighbors in time T.
- Empty Zone (0): Initial state of the cell.
- Evaluated Zone (1): If the cell is previously evaluated but is not considered acceptable in the final route.
- Accepted Zone (2): When the cells around a cell () are analyzed and it presents a lower slope with respect to the initial cell (considering if the person is walking downhill).
2.3. Evacuation Routes
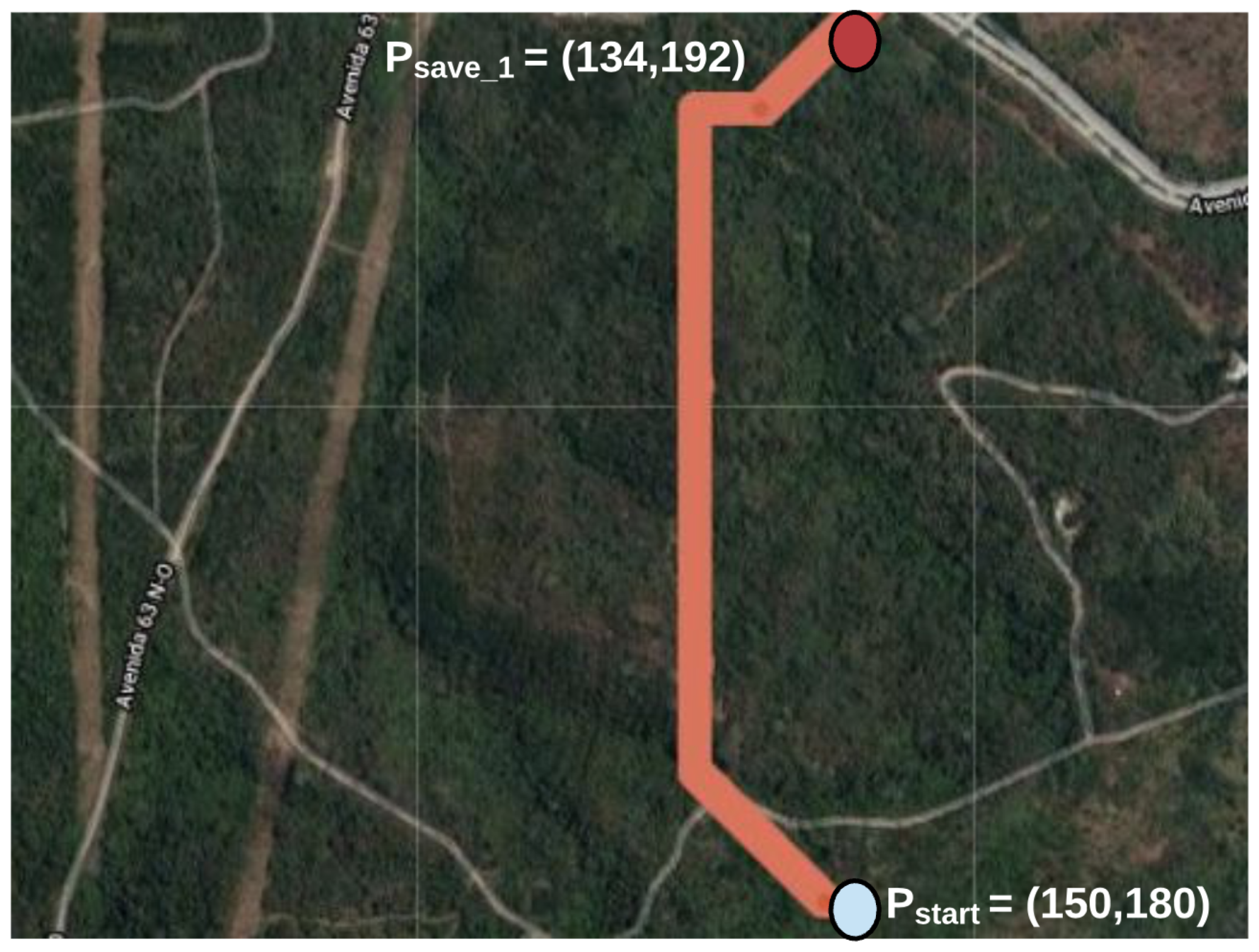
- : Initial starting point (when the user starts walking).
- : These points are the final position where the user is going; they are used to know the graph’s optimal evacuation route.
- : Labels on the edges to know the direction of evacuation routes.
| Algorithm 1: Evacuation Routes Algorithm |
 |
3. Case Study
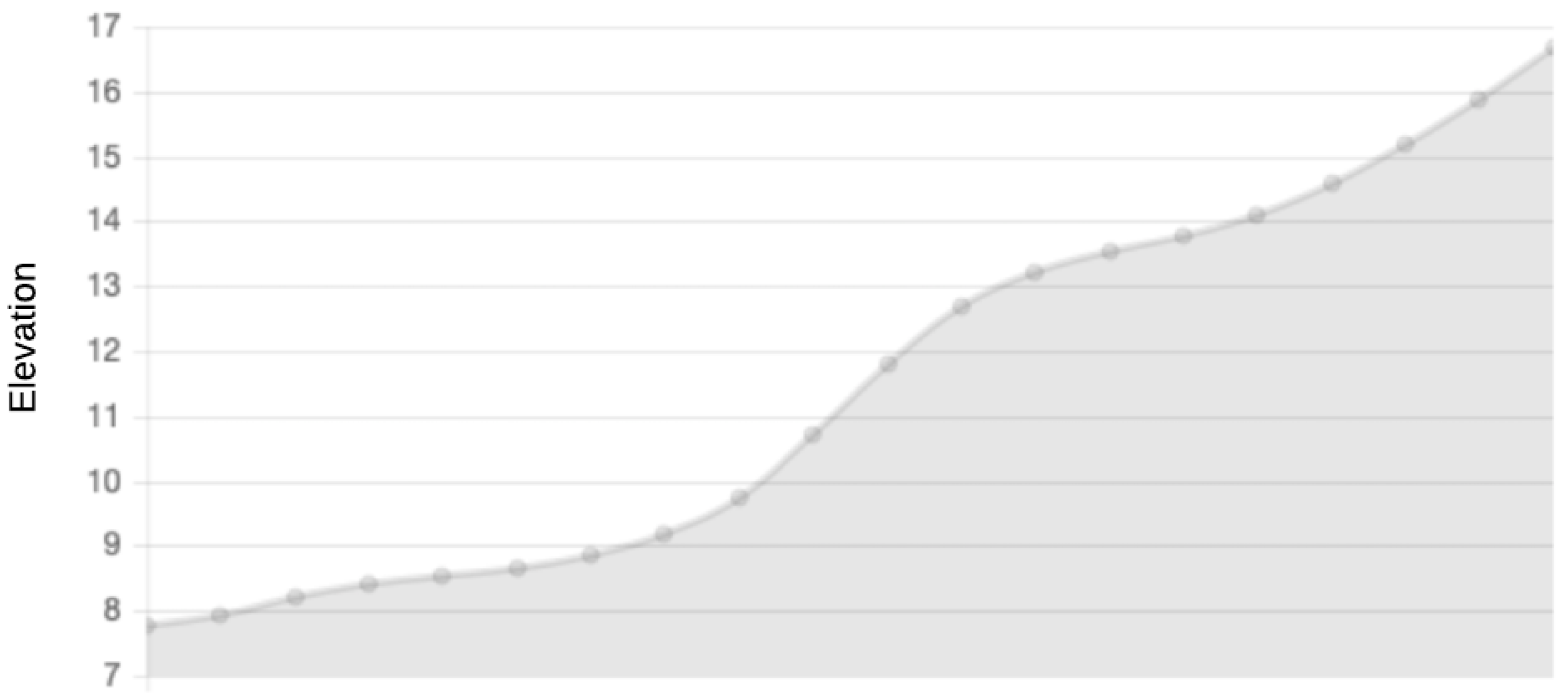
4. Results and Discussion
- PATH:
- -> (149,179) -> (148,178) -> (147,179) -> (146,180) -> (145,181) -> (144,182) -> (143,183) -> (142,184) -> (141,185) -> (140,186) -> (138,187) -> (138,188) -> (137,189) -> (136,190) -> (135,191) -> .
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Appendix A. Evacuation Routes Flowchart
References
- Onorati, T.; Malizia, A.; Diaz, P.; Aedo, I. Modeling an ontology on accessible evacuation routes for emergencies. Expert Syst. Appl. 2014, 41, 7124–7134. [Google Scholar] [CrossRef]
- Yoo, B.; Choi, S.D. Emergency evacuation plan for hazardous chemicals leakage accidents using GIS-based risk analysis techniques in South Korea. Int. J. Environ. Res. Public Health 2019, 16, 1948. [Google Scholar] [CrossRef]
- Mostafizi, A.; Wang, H.; Cox, D.; Dong, S. An agent-based vertical evacuation model for a near-field tsunami: Choice behavior, logical shelter locations, and life safety. Int. J. Disaster Risk Reduct. 2019, 34, 467–479. [Google Scholar] [CrossRef]
- Ping, P.; Wang, K.; Kong, D. Analysis of emergency evacuation in an offshore platform using evacuation simulation modeling. Phys. Stat. Mech. Appl. 2018, 505, 601–612. [Google Scholar] [CrossRef]
- Chen, X.; Li, T.; Ruan, L.; Xu, K.; Huang, J.; Xiong, Y. Research and application of fire risk assessment based on satellite remote sensing for transmission line. In Proceedings of the World Congress on Engineering and Computer Science, San Francisco, CA, USA, 23–25 October 2015; pp. 21–23. [Google Scholar]
- Gershon, R.R.; Kraus, L.E.; Raveis, V.H.; Sherman, M.F.; Kailes, J.I. Emergency preparedness in a sample of persons with disabilities. Am. J. Disaster Med. 2013, 8, 35–47. [Google Scholar] [CrossRef] [PubMed]
- Kowalski-Trakofler, K.M.; Vaught, C.; Scharf, T. Judgment and decision making under stress: An overview for emergency managers. Int. J. Emerg. Manag. 2003, 1, 278–289. [Google Scholar] [CrossRef]
- Kobes, M.; Helsloot, I.; De Vries, B.; Post, J.G. Building safety and human behaviour in fire: A literature review. Fire Saf. J. 2010, 45, 1–11. [Google Scholar] [CrossRef]
- Li, J.j.; Zhu, H.Y. A risk-based model of evacuation route optimization under fire. Procedia Eng. 2018, 211, 365–371. [Google Scholar] [CrossRef]
- Taneja, L.; Bolia, N.B. Network redesign for efficient crowd flow and evacuation. Appl. Math. Model. 2018, 53, 251–266. [Google Scholar] [CrossRef]
- Al-Fares, M.; Sun, Z.; Cruickshank, H. High survivable routing protocol in self organizing wireless sensor network. Iaeng Int. J. Comput. Sci. 2009, 36, 147–156. [Google Scholar]
- Oyola, A.; Romero, D.G.; Vintimilla, B.X. A Dijkstra-based algorithm for selecting the Shortest-Safe Evacuation Routes in dynamic environments (SSER). In International Conference on Industrial, Engineering and Other Applications of Applied Intelligent Systems; Springer: Berlin/Heidelberg, Germany, 2017; pp. 131–135. [Google Scholar]
- Velásquez, W.; Alvarez-Alvarado, M.S.; Munoz-Arcentales, A.; López-Pernas, S.; Salvachúa, J. Body Mass Index in Human Gait for Building Risk Assessment Using Graph Theory. Sensors 2020, 20, 2899. [Google Scholar] [CrossRef] [PubMed]
- Munoz-Arcentales, A.; Yánez-Pazmino, W.; Velásquez Vargas, W. Proposal of a communication structure model for activating reactive signaling in an emergency evacuation systems. In Proceedings of the 2017 IEEE 7th Annual Computing and Communication Workshop and Conference (CCWC), Las Vegas, NV, USA, 9–11 January 2017; pp. 1–5. [Google Scholar]
- González, A.; Velásquez, W. Event Viewer Design of a Wireless Indoor Sensor Network used in Emergencies. In Proceedings of the 2018 1st International Conference on Computer Applications &Information Security (ICCAIS), Riyadh, Saudi Arabia,, 4–6 April 2018; pp. 1–5. [Google Scholar]
- Calligaris, C.; Devoto, S.; Zini, L.; Cucchi, F. An integrated approach for investigations of ground-subsidence phenomena in the Ovaro village (NE Italy). In EuroKarst 2016, Neuchâtel; Springer: Berlin/Heidelberg, Germany, 2017; pp. 71–77. [Google Scholar]
- Pratiwi, A.; Riyanto, S.; Listyaningrum, R.; Aji, G. The Shortest Path Finder for Tsunami Evacuation Strategy using Dijkstra Algorithm. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2020; Volume 854, p. 012035. [Google Scholar]
- Jeong, D.; Kim, M.; Song, K.; Lee, J. Planning a Green Infrastructure Network to Integrate Potential Evacuation Routes and the Urban Green Space in a Coastal City: The Case Study of Haeundae District, Busan, South Korea. Sci. Total Environ. 2021, 761, 143179. [Google Scholar] [CrossRef]
- Herrera, G.; Rodríguez, G. Resiliencia y turismo: El caso de la ciudad de Ba nos de Agua Santa-Ecuador. HOLOS 2016, 3, 229–250. [Google Scholar] [CrossRef]
- Pei, H.; Zhang, S.; Borana, L.; Zhao, Y.; Yin, J. Slope stability analysis based on real-time displacement measurements. Measurement 2019, 131, 686–693. [Google Scholar] [CrossRef]
- Desai, A. The Zigzag Way; Houghton Mifflin Harcourt: New York, NY, USA, 2004. [Google Scholar]
- Wang, L.; Liu, M.; Meng, B. Incorporating topography in a cellular automata model to simulate residents evacuation in a mountain area in China. Phys. Stat. Mech. Appl. 2013, 392, 520–528. [Google Scholar] [CrossRef]
- Birn-Jeffery, A.V.; Higham, T.E. The Scaling of Uphill and Downhill Locomotion in Legged Animals. Integr. Comp. Biol. 2014, 54, 1159–1172. [Google Scholar] [CrossRef] [PubMed]
- Rajput, S.R.; Kale, K. A Review Paper on GIS Web-System to Support Emergency Situations in Urban Areas and Provide Services. Int. J. Comput. Sci. Eng. 2015, 3, 345–350. [Google Scholar]
- Wang, Y.; Zou, Y.; Henrickson, K.; Wang, Y.; Tang, J.; Park, B.J. Google Earth elevation data extraction and accuracy assessment for transportation applications. PLoS ONE 2017, 12, e0175756. [Google Scholar] [CrossRef] [PubMed]
- Velásquez, W.; Munoz-Arcentales, A.; Bohnert, T.M.; Salvachúa, J. Wildfire Propagation Simulation Tool using Cellular Automata and GIS. In Proceedings of the 2019 International Symposium on Networks, Computers and Communications (ISNCC), Istanbul, Turkey, 18–20 June 2019; pp. 1–7. [Google Scholar]
- Ilachinski, A. Cellular Automata: A Discrete Universe; World Scientific Publishing Company: Singapore, 2001. [Google Scholar]
- Pelechano, N.; Malkawi, A. Evacuation simulation models: Challenges in modeling high rise building evacuation with cellular automata approaches. Autom. Constr. 2008, 17, 377–385. [Google Scholar] [CrossRef]
- Yuan, W.; Tan, K.H. An evacuation model using cellular automata. Phys. Stat. Mech. Appl. 2007, 384, 549–566. [Google Scholar] [CrossRef]
- Lo, S.C. Speeding up Multi-lane Traffic Cellular Automata Simulation. Iaeng Int. J. Appl. Math. 2018, 48, 1–6. [Google Scholar]
- Hernandez-Becerrjl, A.; Nakano-Miyatake, M.; Perez-Meana, H.M.; Bucio, A.; Ramirez-Tachiquin, M. A parallel authenticated encryption sharing scheme based on cellular automata. In Proceedings of the World Congress on Engineering and Computer Science, San Francisco, CA, USA, 22–24 October 2014; Volume 1. [Google Scholar]
- Shirinivas, S.; Vetrivel, S.; Elango, N. Applications of graph theory in computer science an overview. Int. J. Eng. Sci. Technol. 2010, 2, 4610–4621. [Google Scholar]
- Permana, S.; Bintoro, K.; Arifitama, B.; Syahputra, A. Comparative analysis of pathfinding algorithms a*, dijkstra, and bfs on maze runner game. IJISTECH Int. J. Inf. Syst. Technol. 2018, 1, 1. [Google Scholar] [CrossRef]
- Velásquez, W.; Munoz-Arcentales, A.; Rodriguez, J.S. A case study: Ingestion analysis of wsn data in databases using docker. In Proceedings of the 2018 1st International Conference on Computer Applications &Information Security (ICCAIS), Riyadh, Saudi Arabia, 4–6 April 2018; pp. 1–6. [Google Scholar]
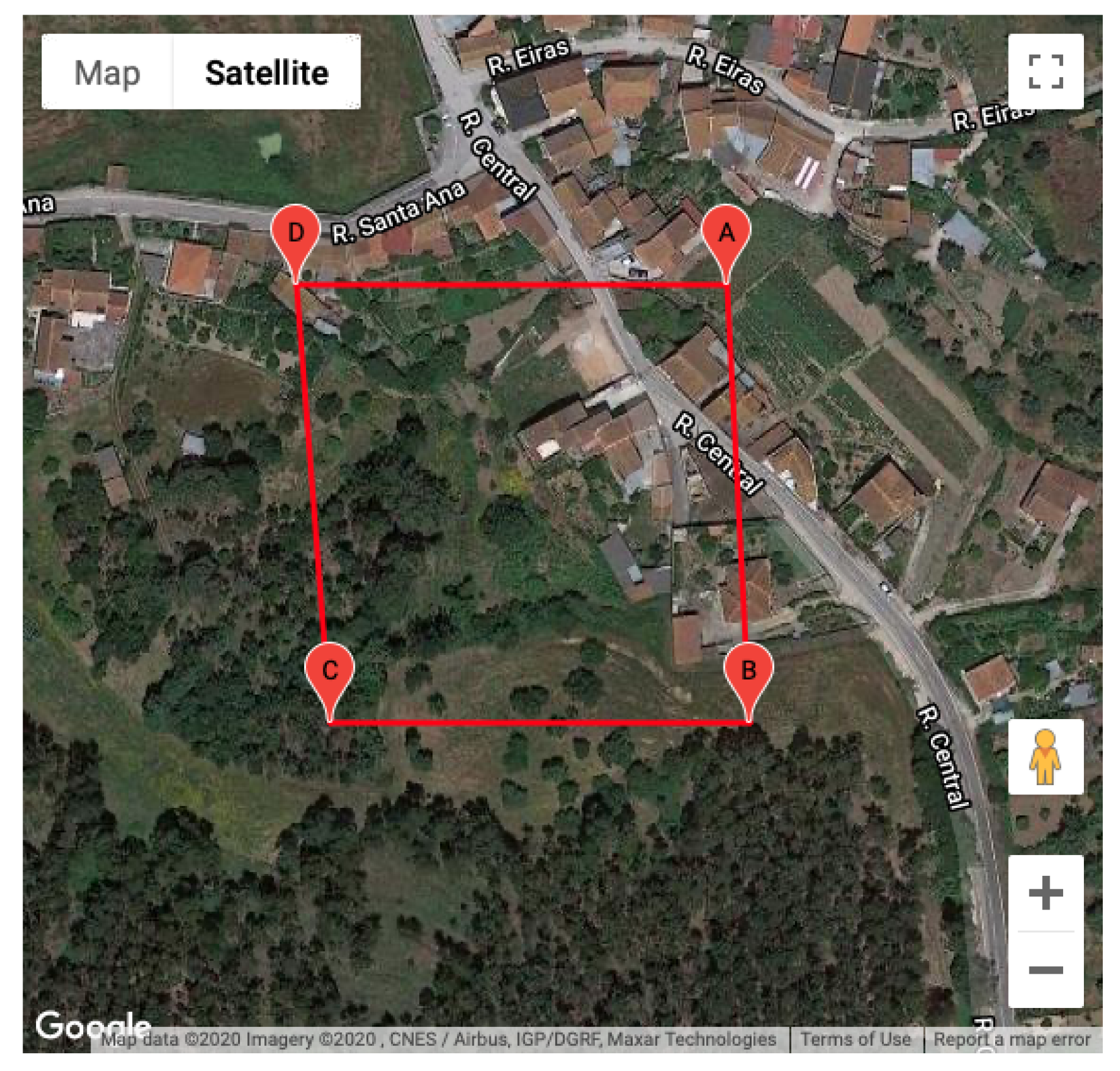
| Point | Latitude | Longitude | Elevation |
|---|---|---|---|
| A | 40.13897826 | 7.77376699 | |
| B | 40.13802564 | 16.68270111 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Velasquez, W.; Alvarez-Alvarado, M.S. Outdoors Evacuation Routes Algorithm Using Cellular Automata and Graph Theory for Uphills and Downhills. Sustainability 2021, 13, 4731. https://doi.org/10.3390/su13094731
Velasquez W, Alvarez-Alvarado MS. Outdoors Evacuation Routes Algorithm Using Cellular Automata and Graph Theory for Uphills and Downhills. Sustainability. 2021; 13(9):4731. https://doi.org/10.3390/su13094731
Chicago/Turabian StyleVelasquez, Washington, and Manuel S. Alvarez-Alvarado. 2021. "Outdoors Evacuation Routes Algorithm Using Cellular Automata and Graph Theory for Uphills and Downhills" Sustainability 13, no. 9: 4731. https://doi.org/10.3390/su13094731
APA StyleVelasquez, W., & Alvarez-Alvarado, M. S. (2021). Outdoors Evacuation Routes Algorithm Using Cellular Automata and Graph Theory for Uphills and Downhills. Sustainability, 13(9), 4731. https://doi.org/10.3390/su13094731






