Total Investment in Fixed Assets and the Later Stage of Urbanization: A Case Study of Shanghai
Abstract
1. Introduction
2. Literature Review
3. Materials and Method
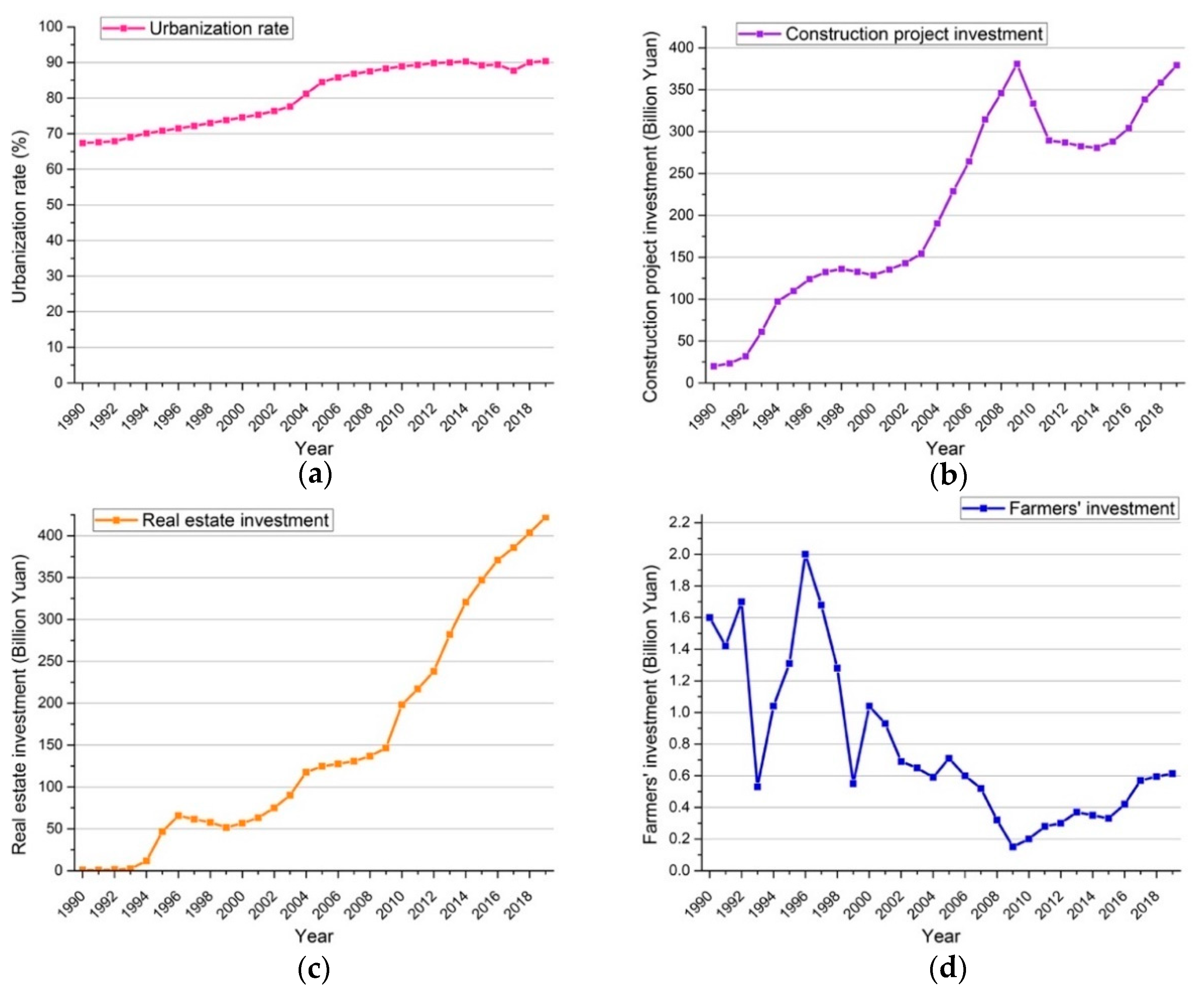
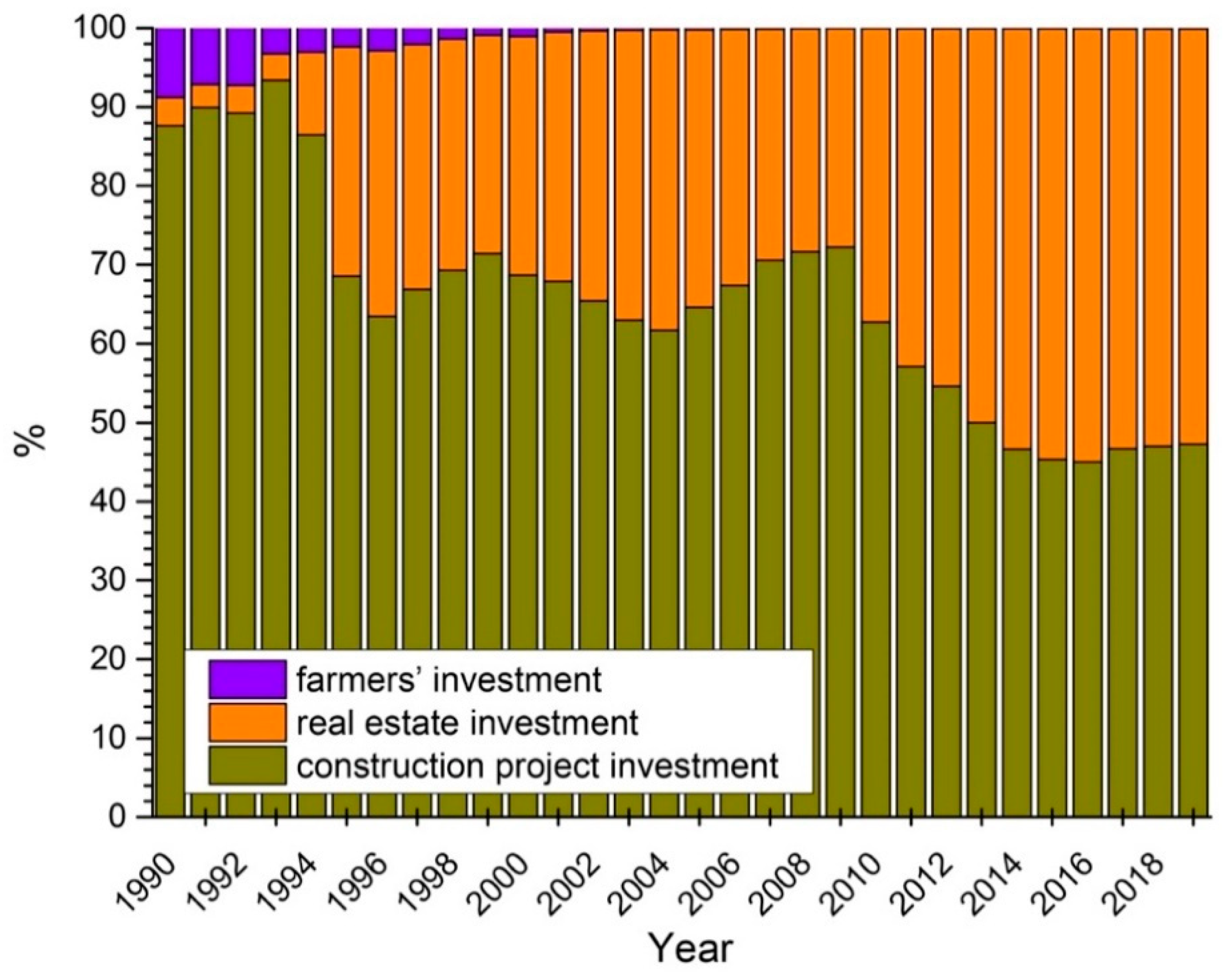
3.1. Data Source
3.2. Econometric Methodology
3.2.1. Unit Roots Test
3.2.2. Johansen Co-Integration Test
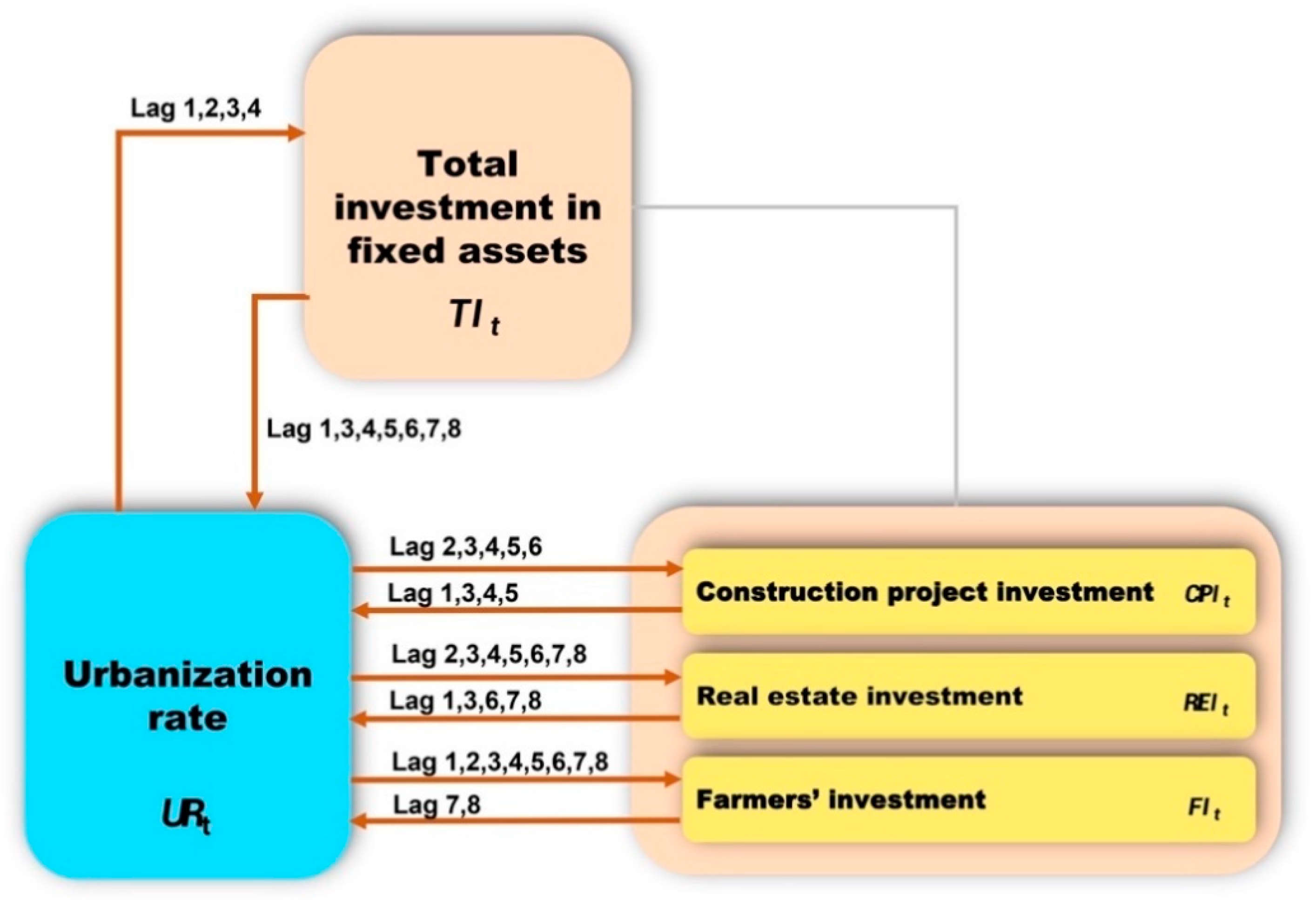
3.2.3. VAR Model and Granger Causality Test
3.2.4. Impulse Response Functions and Variance Decomposition
4. Empirical Results
4.1. Descriptive Statistics Analysis
4.2. Results of Stationarity Test
4.3. Results of Co-Integration Test
4.4. Results of Granger Causality Test
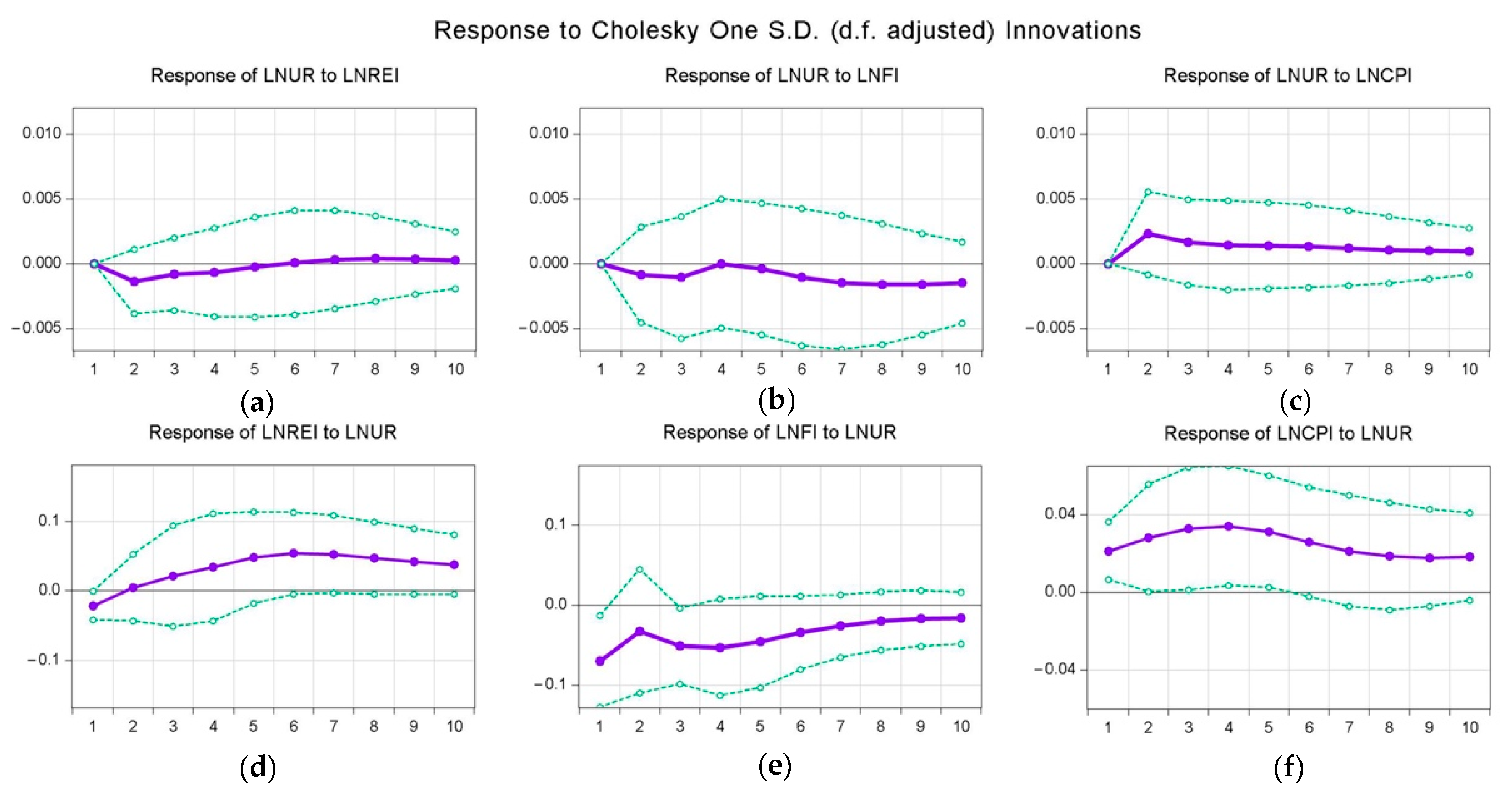
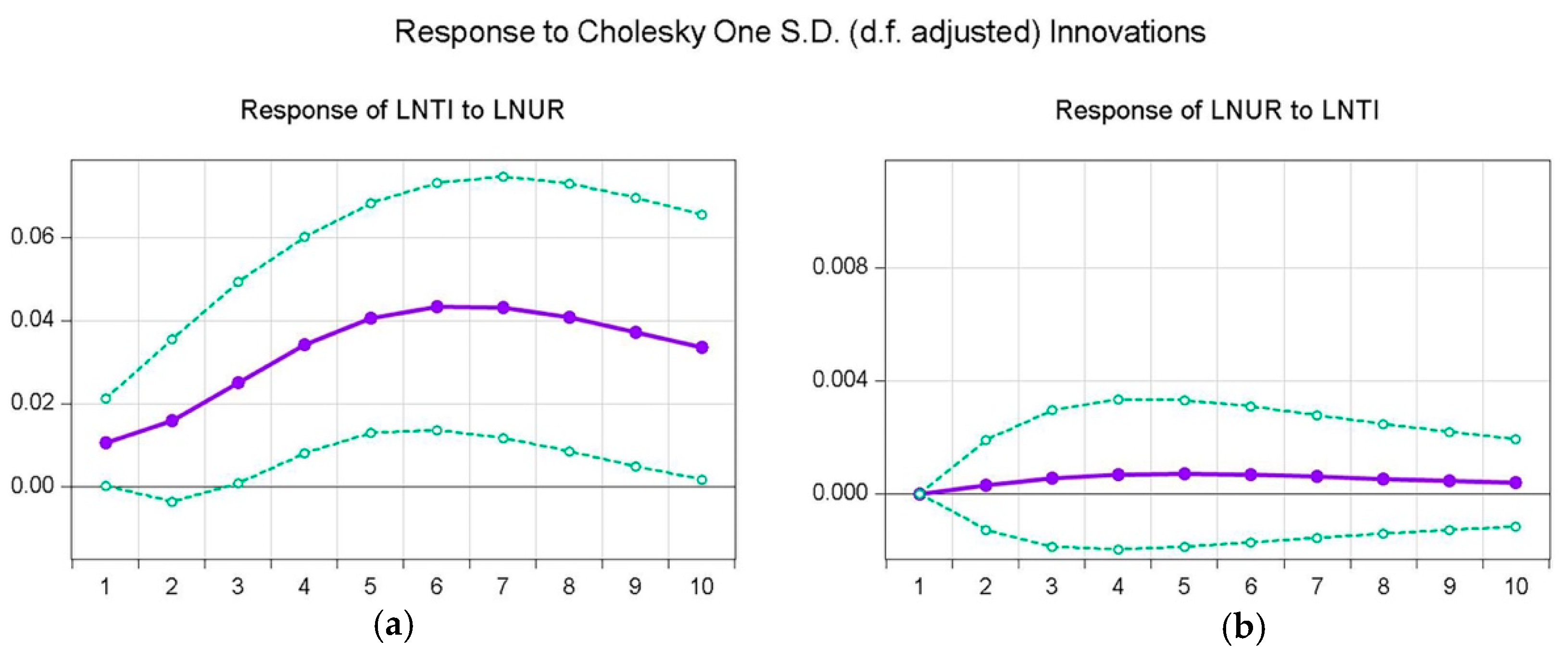
4.5. Impulse Response Analysis
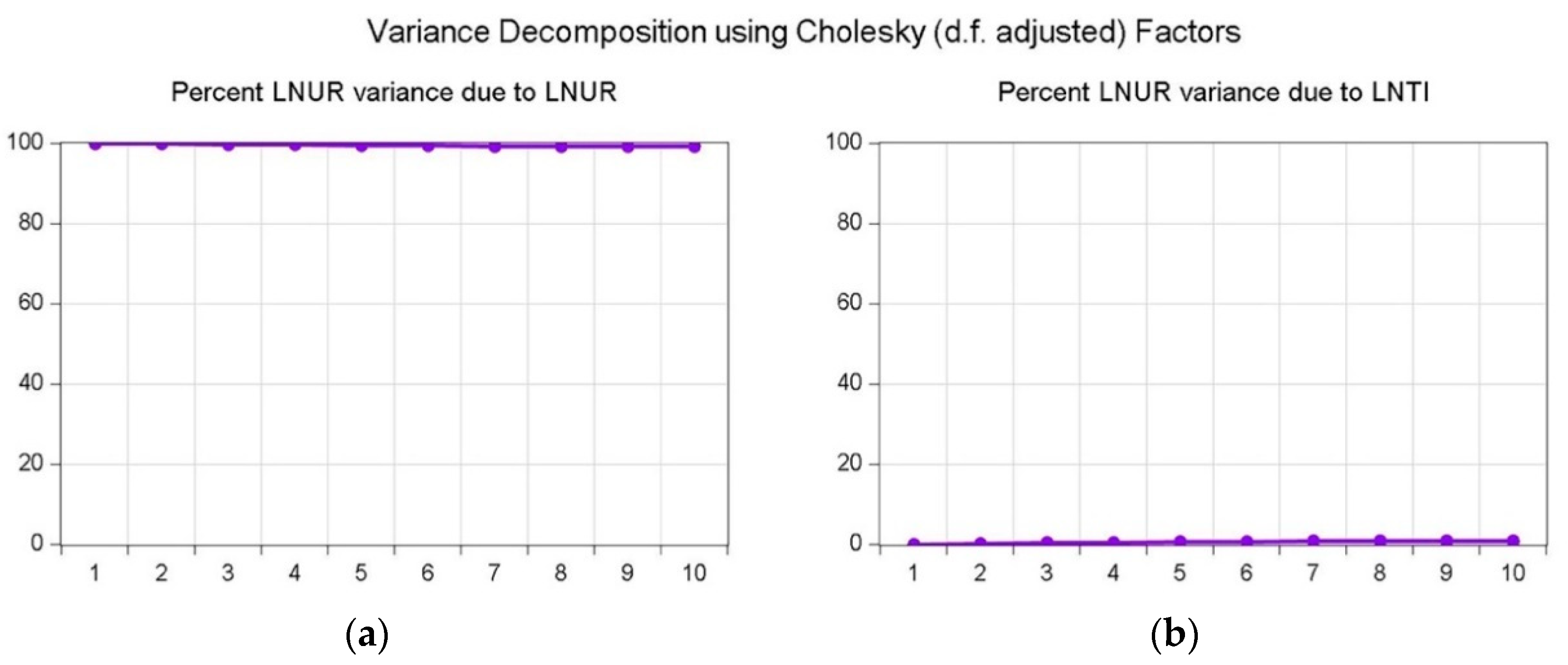
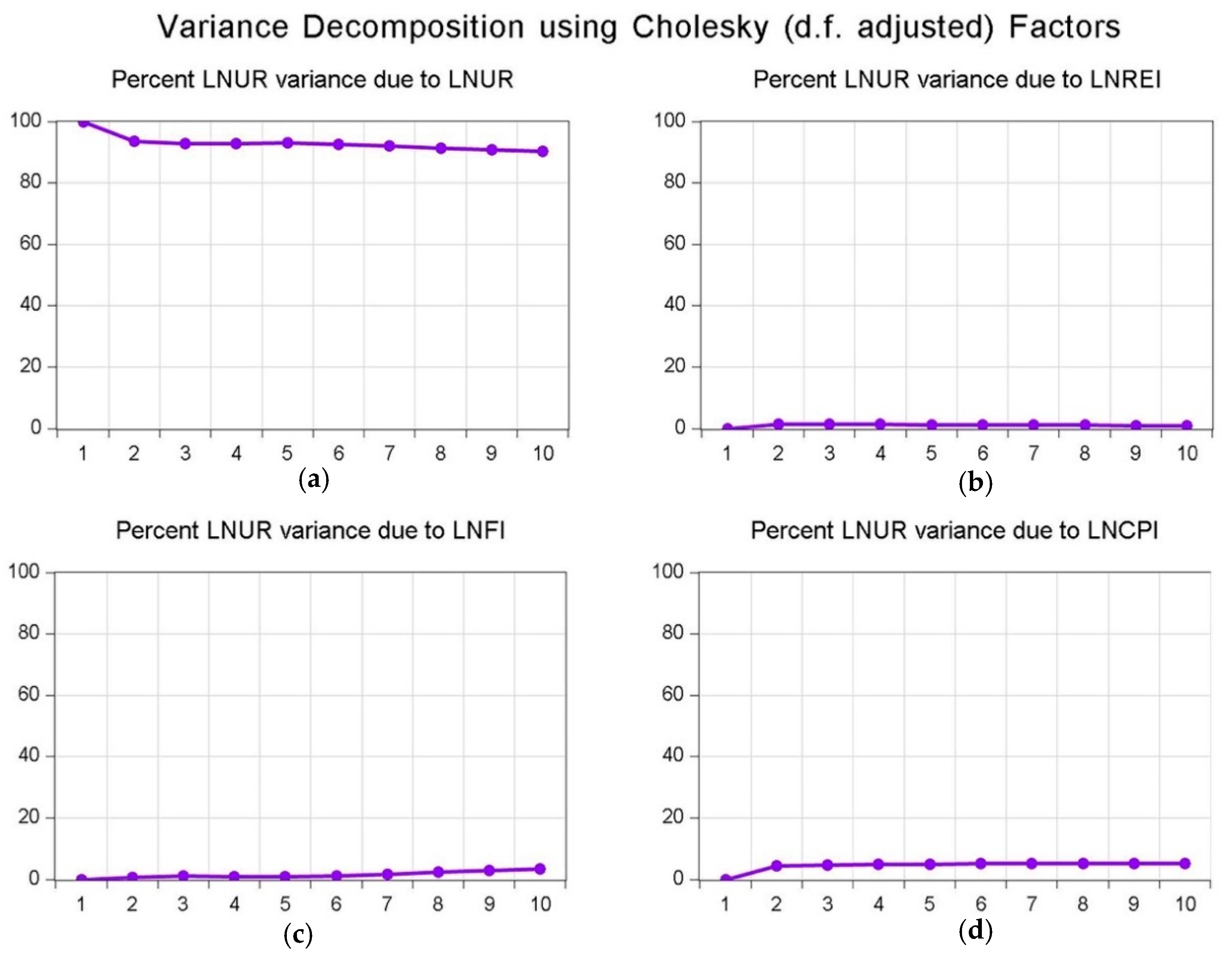
4.6. Variance Decomposition Analysis
5. Discussion and Conclusions
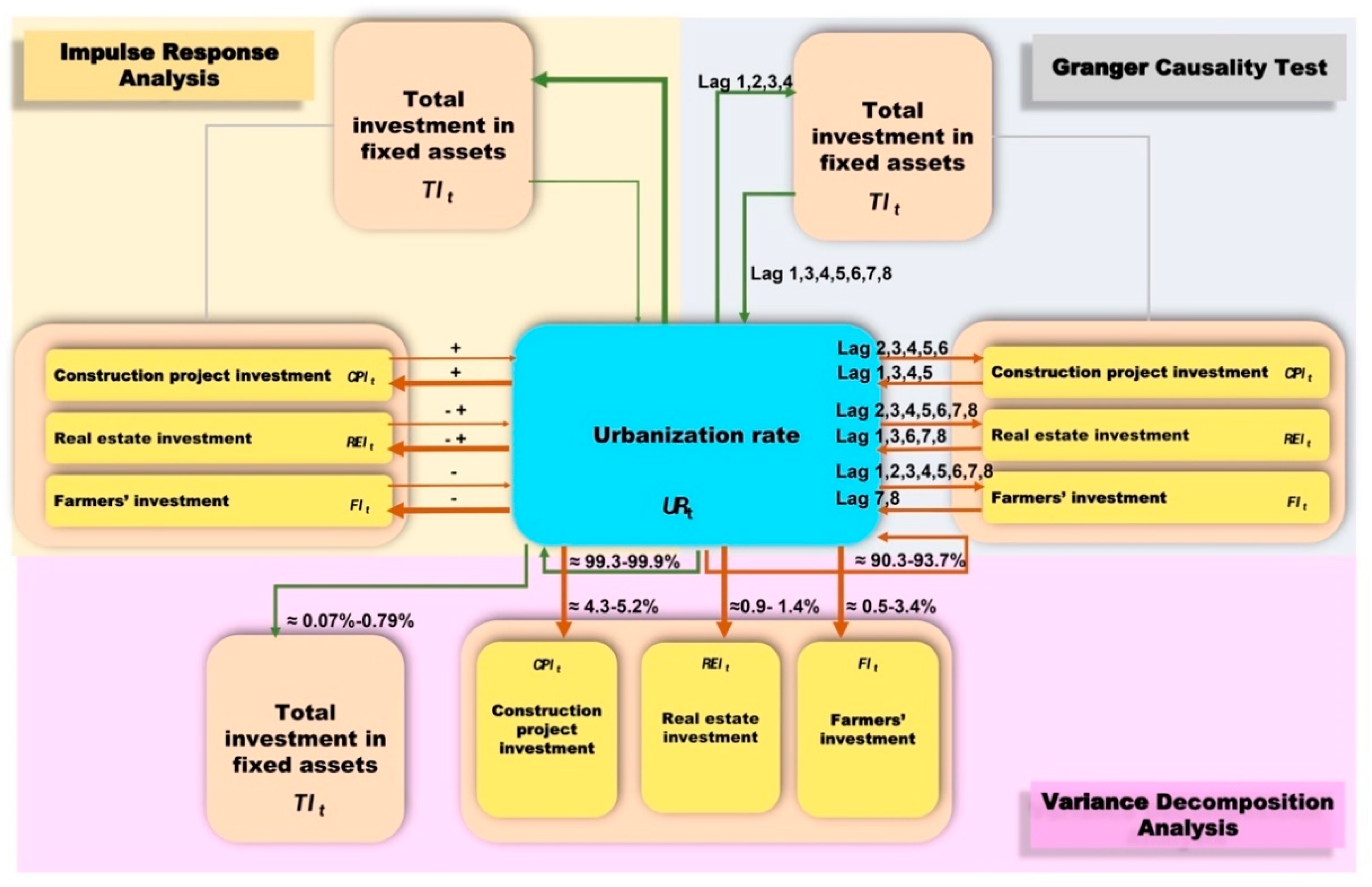
- Both Group (, , , and ) and Group (, ) have a long-term co-integration relationship among the studied variables, and construction project investment plays an important role in promoting the urbanization rate in the studied period.
- Granger causality shows that both Group (, , , and ) and Group (, ) have a bilateral Granger causal relationship; however, the urbanization rate has more Granger causal impact on the studied variable both in Group (, , and ) and Group (, ).
- The impulse response analysis illustrates that the urbanization rate has a positive impact on the total investment in fixed assets in the short term and long term. A similar conclusion is found in [21], that is, government investment policy has substantially affected Egypt and its sustainable development.
- Variance decomposition analysis reveals that the urbanization rate in Group (, , , and ) and Group (, ) accounts for the majority of percentage impacts, and the total investment in fixed assets and its three categories contribute a small minority to the urbanization rate.
6. Policy Implication
- Strengthen the rational total investment in fixed assets. According to our results, the total investment in fixed assets has a one-direction Granger relationship with urbanization rate and a bilateral Granger relationship in the long term. Notably, urbanization is a process that needs time to comply with economic factors, such as the total investment in fixed assets. Thus, the city would not benefit from the higher urbanization rate. Similarly, the total investment in fixed assets also needs a process that would convert its investment into related beneficial interests of the city. Therefore, a rational investment strategy is necessary to ensure the healthy development of urbanization through, for example, conceptual infrastructure planning and investment project appraisal schemes. A similar implication can be found in [57].
- Set a more flexible policy on construction project investment. Generally, construction project investment is a critical factor that plays a substantial role as a drive of urban development. In addition, our results demonstrate a one-way Granger relationship between construction project investment and urbanization rate. Therefore, policymakers must balance the two indicators, for example, the related population policy and construction project investment policy, which can be implemented according to the current condition to solve urban problems (i.e., gentrification, polarization, and urban renewal) caused by urbanization [2].
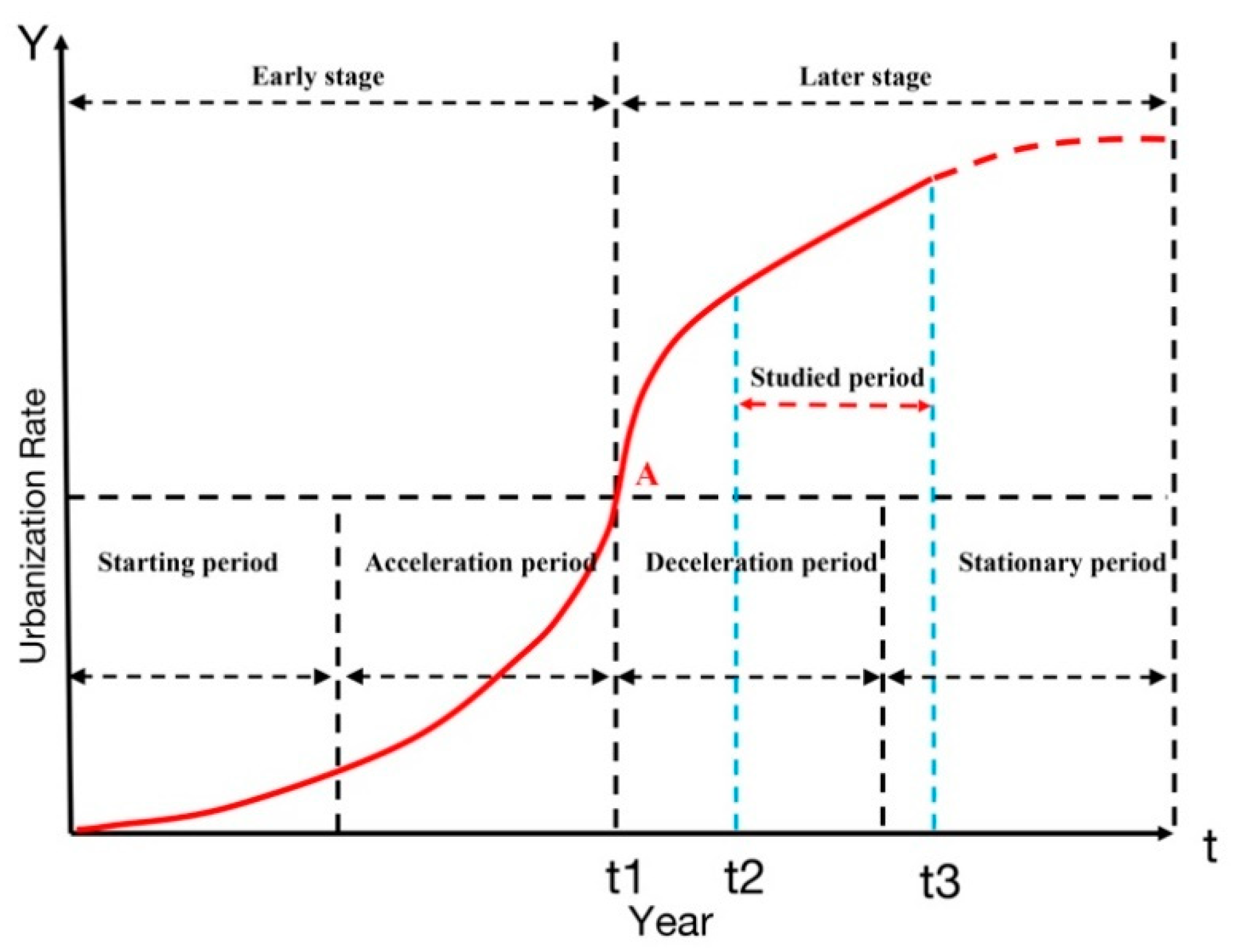
- More rationally guide the development of the real estate industry. Theoretically, based on the characteristics of the other countries’ urbanization experience, urbanization can be divided into four stages: initial, acceleration, deceleration, and stable.Similarly, the development of the real estate industry follows similar laws of urbanization development, summarized as four stages: formation, growth, maturity, and decline. However, the relationship between urbanization and the real estate industry should be harmonious, or it may cause serious economic problems. Notably, the real estate industry has developed rapidly since the commercial housing reform in Shanghai in 1998. However, the real estate industry has always been the economic pillar of Shanghai and has been criticized for its “excessively high housing price,” the “real estate bubble,” and other problems of the society. Moreover, according to our research, there is a bilateral direction of Granger causality between the real estate industry and urbanization, indicating that the two factors have a close relationship. Therefore, Shanghai should guide the rational development of the real estate industry in the later stage of urbanization. More specifically, the government should coordinate land financing policy [12] and eliminate the negative externalities of the policy, for example, the polarization effect and high housing prices; thus, the government must more practically manage the related social, economic, or environmental problems caused by real estate investment.
- Promote rural revitalization and coordinate the development of urbanization through scientific planning.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
- Unit root test.
- ADF testTable A1. ADF test.
Include in Test Equation Variables ADF Test Statistic Test Critical Value Prob.* (5% Level) Level Intercept 1 ln(TI) −2.974150 −3.012363 0.0539 2 ln(CPI) −3.007464 −3.012363 0.0505 3 ln(REI) −1.420050 −3.004861 0.5538 4 ln(FI) −1.901596 −2.976263 0.3266 5 ln(UR) −1.355025 −2.976263 0.5888 Intercept and trend 1 ln(TI) −0.252700 −3.644963 0.9865 2 ln(CPI) −1.271979 −3.644963 0.8668 3 ln(REI) −4.679380 −3.595026 0.0048 4 ln(FI) −2.459441 −3.587527 0.3437 5 ln(UR) −0.067273 −3.587527 0.9928 None 1 ln(TI) 3.398008 −1.956406 0.9995 2 ln(CPI) 0.778335 −1.954414 0.8754 3 ln(REI) 2.492405 −1.956406 0.9953 4 ln(FI) −1.093929 −1.953858 0.2413 5 ln(UR) 2.789532 −1.953858 0.9979 First difference Intercept 1 ln(TI) −6.059505 −2.998064 0.0000 2 ln(CPI) −2.094011 −2.981038 0.2484 3 ln(REI) −8.306588 −2.998064 0.0000 4 ln(FI) −5.777930 −2.981038 0.0001 5 ln(UR) −2.093889 −2.986225 0.2485 Intercept and trend 1 ln(TI) −4.879820 −3.644963 0.0043 2 ln(CPI) −4.235406 −3.644963 0.0159 3 ln(REI) −6.881178 −3.622033 0.0001 4 ln(FI) −5.746140 −3.595026 0.0004 5 ln(UR) −2.566373 −3.603202 0.2969 None 1 ln(TI) −1.380192 −1.954414 0.1516 2 ln(CPI) −1.808925 −1.954414 0.0676 3 ln(REI) −1.989104 −1.954414 0.0465 4 ln(FI) −5.843456 −1.954414 0.0000 5 ln(UR) −1.668758 −1.955020 0.0892 * MacKinnon (1996) one-sided p-values. - PP testTable A2. PP test.
Include in Test Equation Variables PP Test Statistic Test Critical Value Prob. * (5% Level) Level Intercept 1 ln(TI) −3.312157 −2.976263 0.0243 2 ln(CPI) −3.682527 −2.976263 0.0104 3 ln(REI) −2.661924 −2.976263 0.0937 4 ln(FI) −1.860863 −2.976263 0.3447 5 ln(UR) −1.307643 −2.976263 0.6111 Intercept and trend 1 ln(TI) −2.397368 −3.587527 0.3725 2 ln(CPI) −2.393708 −3.587527 0.3742 3 ln(REI) −1.940834 −3.587527 0.6059 4 ln(FI) −2.459441 −3.587527 0.3437 5 ln(UR) −0.327360 −3.587527 0.9853 None 1 ln(TI) 2.056535 −1.953858 0.9883 2 ln(CPI) 1.703675 −1.953858 0.9754 3 ln(REI) 1.134348 −1.953858 0.9293 4 ln(FI) −1.137367 −1.953858 0.2258 5 ln(UR) 2.473166 −1.953858 0.9955 First difference Intercept 1 ln(TI) −1.982617 −2.981038 0.2921 2 ln(CPI) −2.168164 −2.981038 0.2218 3 ln(REI) −2.562258 −2.981038 0.1134 4 ln(FI) −5.982451 −2.981038 0.0000 5 ln(UR) −4.333654 −2.981038 0.0023 Intercept and trend 1 ln(TI) −2.624646 −3.595026 0.2732 2 ln(CPI) −2.640510 −3.595026 0.2670 3 ln(REI) −3.060382 −3.595026 0.1362 4 ln(FI) −5.963815 −3.595026 0.0003 5 ln(UR) −4.602260 −3.595026 0.0058 None 1 ln(TI) −1.579302 −1.954414 0.1058 2 ln(CPI) −1.765214 −1.954414 0.0738 3 ln(REI) −2.158700 −1.954414 0.0321 4 ln(FI) −5.890789 −1.954414 0.0000 5 ln(UR) −3.550310 −1.954414 0.0010 * MacKinnon (1996) one-sided p-values. - DF GLS testTable A3. DF GLS test.
Include in Test Equation Variables DF GLS Test Statistic Test Critical Value (5% Level) Level Intercept 1 ln(TI) −0.131325 −1.95502 2 ln(CPI) −1.086410 −1.954414 3 ln(REI) −0.735425 −1.955020 4 ln(FI) −1.624687 −1.953858 5 ln(UR) −1.150360 −1.955020 Intercept and trend 1 ln(TI) −4.177963 −3.190000 2 ln(CPI) −3.193654 −3.190000 3 ln(REI) −2.093001 −3.190000 4 ln(FI) −2.676590 −3.190000 5 ln(UR) −1.442210 −3.190000 First difference Intercept 1 ln(TI) −1.744151 −1.954414 2 ln(CPI) −2.116516 −1.954414 3 ln(REI) −9.221668 −1.956406 4 ln(FI) −5.899968 −1.954414 5 ln(UR) −1.968365 −1.955020 Intercept and trend 1 ln(TI) −5.179672 −3.190000 2 ln(CPI) −4.189617 −3.190000 3 ln(REI) −2.770603 −3.190000 4 ln(FI) −5.980730 −3.190000 5 ln(UR) −2.593204 −3.190000 - KPSS testTable A4. KPSS test.
Include in Test Equation Variables KPSS Test Statistic
(LM-Stat.)Test Critical Value (5% Level) Level Intercept 1 ln(TI) 0.635611 0.463000 2 ln(CPI) 0.609767 0.463000 3 ln(REI) 0.586319 0.463000 4 ln(FI) 0.552366 0.463000 5 ln(UR) 0.630447 0.463000 Intercept and trend 1 ln(TI) 0.148130 0.146000 2 ln(CPI) 0.155706 0.146000 3 ln(REI) 0.149842 0.146000 4 ln(FI) 0.110950 0.146000 5 ln(UR) 0.116601 0.146000 First difference Intercept 1 ln(TI) 0.326506 0.463000 2 ln(CPI) 0.348473 0.463000 3 ln(REI) 0.283457 0.463000 4 ln(FI) 0.146240 0.463000 5 ln(UR) 0.286196 0.463000 Intercept and trend 1 ln(TI) 0.090225 0.146000 2 ln(CPI) 0.083030 0.146000 3 ln(REI) 0.074952 0.146000 4 ln(FI) 0.094182 0.146000 5 ln(UR) 0.171965 0.146000
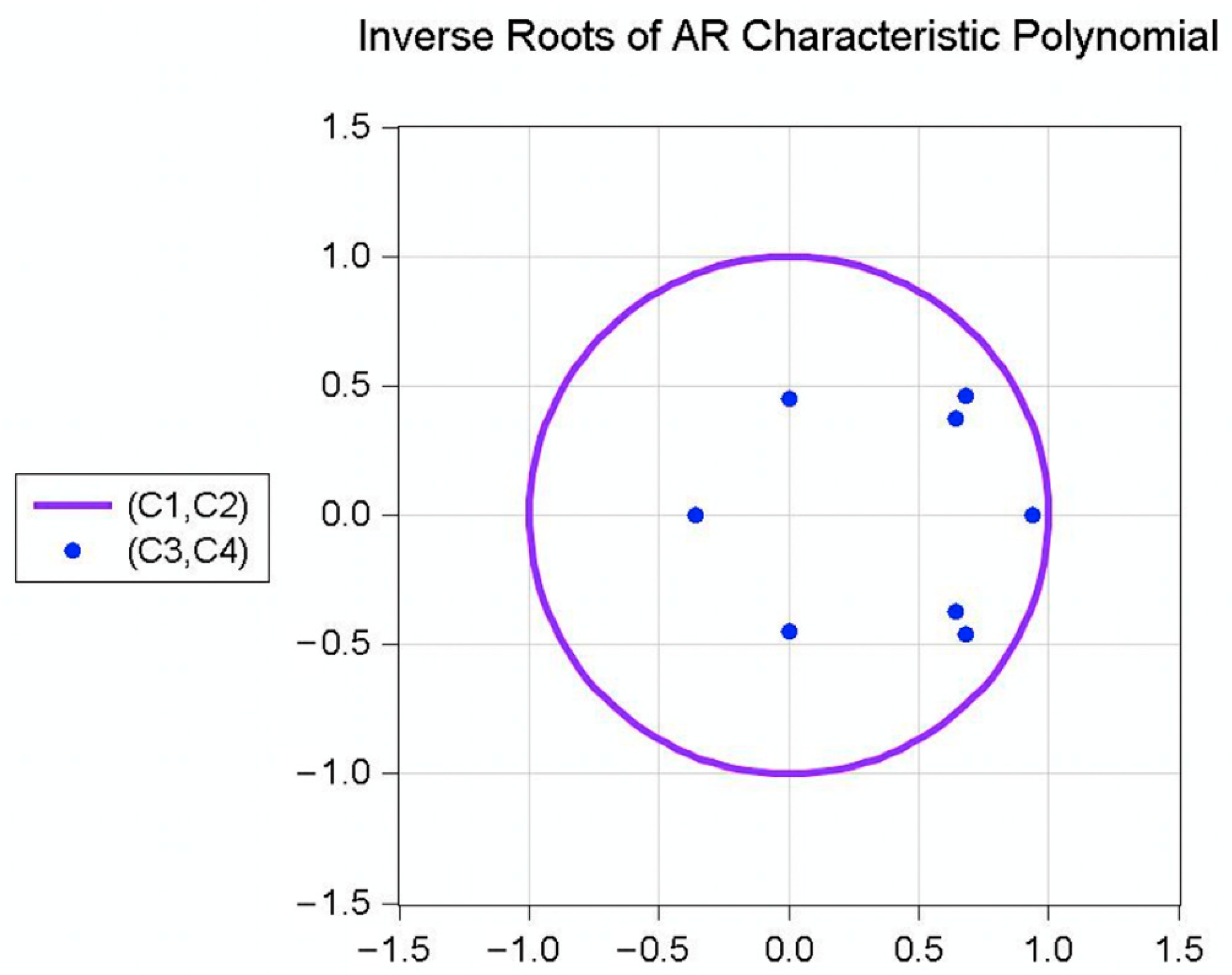
- VAR model stability test
- Lag length CriteriaTable A5. The optimal lag length test results.
Endogenous Variables: LNUR LNREI LNFI LNCPI Lag LogL LR FPE AIC SC HQ 0 107.3996 NA 2.13 × 10−9 −8.616631 −8.420289 −8.564541 1 190.6542 131.8198 8.03 × 10−12 −14.22118 −13.23947 −13.96073 2 224.7761 42.65236 * 2.02 × 10−12 −15.73134 −13.96426 * −15.26253 3 247.1822 20.53895 1.70 × 10−12 * −16.26518 −13.71273 −15.58802 4 273.5519 15.38233 1.74 × 10−12 −17.12933* −13.79151 −16.24380 * Endogenous variables: LNUR LNTI 0 69.43158 NA 4.04 × 10−6 −6.743158 −6.643585 −6.72372 1 117.7289 82.10542 4.84 × 10−8 −11.17289 −10.87417 −11.11458 2 126.0379 12.46350 * 3.20 × 10−8 * −11.60379 −11.10592 * −11.5066 3 128.7788 3.563223 3.78 × 10−8 −11.47788 −10.78087 −11.34182 4 131.0546 2.503410 4.85 × 10−8 −11.30546 −10.40931 −11.13053 5 136.7627 5.137205 4.67 × 10−8 −11.47627 −10.38096 −11.26245 6 137.7866 0.716748 7.90 × 10−8 −11.17866 −9.884206 −10.92597 7 145.8918 4.052623 7.75 × 10−8 −11.58918 −10.09558 −11.29762 8 157.9017 3.602975 7.24 × 10−8 −12.39017* −10.69743 −12.05973 * Endogenous variables: LNCPI LNUR 0 71.68151 NA 3.23 × 10−6 −6.968151 −6.868578 −6.948713 1 109.4189 64.15355 1.11 × 10−7 −10.34189 −10.04317 −10.28358 2 118.8922 14.21001 * 6.54 × 10−8 * −10.88922 −10.39136 * −10.79203 3 122.6084 4.831030 7.00 × 10−8 −10.86084 −10.16383 −10.72478 4 127.2259 5.079235 7.11 × 10−8 −10.92259 −10.02643 −10.74765 5 132.6427 4.875137 7.06 × 10−8 −11.06427 −9.968966 −10.85046 6 134.5060 1.304267 1.10 × 10−7 −10.8506 −9.556144 −10.5979 7 136.5102 1.002104 1.98 × 10−7 −10.65102 −9.157418 −10.35945 8 153.0950 4.975459 1.17 × 10−7 −11.90950 * −10.21676 −11.57906 * Endogenous variables: LNUR LNFI 0 50.94417 NA 2.57 × 10−5 −4.894417 −4.794844 −4.87498 1 83.34779 55.08616 1.51 × 10−6 −7.734779 −7.43606 −7.676466 2 84.98780 2.460008 1.94 × 10−6 −7.49878 −7.000914 −7.401591 3 87.31935 3.031019 2.39 × 10−6 −7.331935 −6.634923 −7.195871 4 88.61514 1.425366 3.38 × 10−6 −7.061514 −6.165355 −6.886574 5 92.24668 3.268384 4.01 × 10−6 −7.024668 −5.929362 −6.810853 6 107.4306 10.62873 1.65 × 10−6 −8.143058 −6.848606 −7.890368 7 125.0243 8.796877 6.24 × 10−7 −9.502434 −8.008835 −9.210868 8 160.3043 10.58400* 5.69 × 10−8 * −12.63043 * −10.93769 * −12.29999 * Endogenous variables: LNUR LNREI 0 53.23147 NA 2.04 × 10−5 −5.123147 −5.023573 −5.103709 1 107.0701 91.52568 1.40 × 10−7 −10.10701 −9.808291 −10.0487 2 112.5153 8.167730 1.24 × 10−7 −10.25153 −9.75366 −10.15434 3 117.7268 6.774992 1.14 × 10−7 −10.37268 −9.675666 −10.23661 4 119.7344 2.208402 1.50 × 10−7 −10.17344 −9.277284 −9.998503 5 136.9797 15.52072 * 4.57 × 10−8 −11.49797 −10.40266 −11.28415 6 143.5897 4.627038 4.42 × 10−8 −11.75897 −10.46452 −11.50628 7 148.7749 2.592569 5.81 × 10−8 −11.87749 −10.38389 −11.58592 8 175.3801 7.981562 1.26 × 10−8 * −14.13801 * −12.44526 * −13.80757 * * indicates lag order selected by the criterion. LR: sequential modified LR test statistic (each test at 5% level). FPE: Final prediction error. AIC: Akaike information criterion. SC: Schwarz information criterion. HQ: Hannan-Quinn information criterion - JJ testTable A6. Co-integration test.
Variables Group JJ Co-Integration
ConfigurationCo-Integration Equation
NumberLog Likelihood Value Trace Test Max-Eigenvalue Test LNUR and LNTI no intercept or trend in test VAR; Lags interval (in first differences): 1 to 1 1 1 152.0092 LNUR and LNCPI, LNREI, LNFI no intercept or trend in test VAR; Lags interval (in first differences): 1 to 1 1 1 193.6514 - Granger causality testTable A7. Granger causality test result.
Lag Length Urbanization Rate and Total Investment in Fixed Assets Urbanization Rate and Construction Project Investment Urbanization Rate and Real Estate Investment Urbanization Rate and Farmers’ Investment Null Hypothesis F-Statistic p-Value Accept/
RejectConclusion Null Hypothesis F-Statistic p-Value Accept/
RejectConclusion Null Hypothesis F-Statistic p-Value Accept/
RejectConclusion Null Hypothesis F-Statistic p-Value Accept/
RejectConclusion 1 ≠> 0.95 0.34 R ≥ ≠> 1.69 0.21 R ≥ ≠> 0.77 0.39 R ≥ ≠> 5.27 0.03 R ≥ 1 ≠> 0.8 0.38 R ≥ ≠> 0.5 0.49 A ≠> ≠> 0.19 0.66 A ≠> ≠> 0.04 0.84 A ≠> 2 ≠> 0.14 0.86 A ≠> ≠> 0.45 0.64 A ≠> ≠> 0.34 0.71 A ≥ ≠> 3.02 0.07 R ≥ 2 ≠> 9.37 0 R ≥ ≠> 3.89 0.04 R ≥ ≠> 3.66 0.04 R ≥ ≠> 0.09 0.92 A ≠> 3 ≠> 1.9 0.16 R ≥ ≠> 1.63 0.22 R ≥ ≠> 0.66 0.59 R ≥ ≠> 2.46 0.1 R ≥ 3 ≠> 7.23 0 R ≥ ≠> 4.86 0.01 R ≠> 2.23 0.12 R ≥ ≠> 0.23 0.88 A ≠> 4 ≠> 1.34 0.3 R ≥ ≠> 1.29 0.32 R ≥ ≠> 0.43 0.78 A ≠> ≠> 2.82 0.06 R ≥ 4 ≠> 1.37 0.29 R ≥ ≠> 1.69 0.2 R ≥ ≠> 14.2 0 R ≥ ≠> 0.25 0.91 A ≠> 5 ≠> 0.75 0.6 R ≥ ≠> 0.97 0.47 R ≥ ≠> 0.45 0.81 A ≠> ≠> 1.6 0.23 R ≥ 5 ≠> 0.55 0.74 A ≠> ≠> 1.19 0.37 R ≠> 6.62 0 R ≥ ≠> 0.16 0.97 A ≠> 6 ≠> 0.78 0.61 R ≥ ≠> 0.52 0.78 A ≠> ≠> 1.08 0.44 R ≥ ≠> 5.02 0.02 R ≥ 6 ≠> 0.44 0.83 A ≠> ≠> 1.05 0.45 R ≠> 2.5 0.11 R ≥ ≠> 0.57 0.75 A ≠> 7 ≠> 0.94 0.54 R ≥ UR ≠> 0.3 0.93 A ≠> ≠> 0.92 0.55 R ≥ ≠> 6.06 0.02 R ≥ 7 ≠> 0.58 0.75 A ≠> ≠> 0.59 0.75 A ≠> ≠> 2.67 0.13 R ≥ ≠> 1.63 0.28 R ≥ 8 ≠> 0.93 0.59 R ≥ UR ≠> 0.46 0.83 A ≠> ≠> 2.79 0.22 R ≥ ≠> 10.08 0.04 R ≥ 8 ≠> 0.26 0.94 A ≠> ≠> 0.34 0.9 A ≠> ≠> 11.01 0.04 R ≥ ≠> 3.36 0.17 R ≥ - Impulse response function analysisTable A8. Impulse response function analysis result of Group (, , and ).
Response of LNUR: Period LNUR LNREI LNFI LNCPI 1 0.008015 0.000000 0.000000 0.000000 (0.00111) (0.00000) (0.00000) (0.00000) 2 0.007424 −0.001344 −0.000835 0.002355 (0.00229) (0.00124) (0.00185) (0.00160) 3 0.006740 −0.000817 −0.001057 0.001661 (0.00226) (0.00141) (0.00236) (0.00166) 4 0.005870 −0.000669 2.39E−06 0.001433 (0.00218) (0.00171) (0.00249) (0.00172) 5 0.005507 −0.000256 −0.000388 0.001391 (0.00208) (0.00193) (0.00254) (0.00167) 6 0.004987 9.76E−05 −0.001033 0.001346 (0.00211) (0.00201) (0.00265) (0.00158) 7 0.004529 0.000333 −0.001445 0.001203 (0.00207) (0.00190) (0.00259) (0.00146) 8 0.004191 0.000402 −0.00159 0.001090 (0.00200) (0.00165) (0.00233) (0.00129) 9 0.003953 0.000366 −0.001581 0.001016 (0.00193) (0.00135) (0.00195) (0.00109) 10 0.003759 0.000277 −0.001454 0.000963 (0.00189) (0.00109) (0.00157) (0.00090) Response of LNREI: Period LNUR LNREI LNFI LNCPI 1 −0.021352 0.050006 0.000000 0.000000 (0.01024) (0.00693) (0.00000) (0.00000) 2 0.004724 0.055465 −0.071406 0.050022 (0.02428) (0.02024) (0.01846) (0.01266) 3 0.021578 0.049850 −0.104369 0.061358 (0.03640) (0.02913) (0.03148) (0.02220) 4 0.034252 0.034144 −0.076669 0.049433 (0.03881) (0.02893) (0.03889) (0.02755) 5 0.048198 0.019811 −0.045606 0.033325 (0.03291) (0.02846) (0.03992) (0.02656) 6 0.054488 0.011126 −0.029232 0.018094 (0.02957) (0.02910) (0.03853) (0.02476) 7 0.052776 0.006943 −0.022126 0.005269 (0.02800) (0.02850) (0.03916) (0.02311) 8 0.047439 0.004342 −0.018585 −0.002232 (0.02600) (0.02578) (0.03815) (0.02179) 9 0.041997 0.001767 −0.016069 −0.003654 (0.02363) (0.02184) (0.03352) (0.01967) 10 0.037861 −0.001002 −0.012863 −0.00066 (0.02151) (0.01822) (0.02756) (0.01649) Response of LNFI: Period LNUR LNREI LNFI LNCPI 1 −0.070103 −0.009286 0.135964 0.000000 (0.02844) (0.02670) (0.01885) (0.00000) 2 −0.032795 0.034758 0.009469 −0.007008 (0.03859) (0.02216) (0.03418) (0.02987) 3 −0.051116 0.043485 −0.0504 −0.012088 (0.02356) (0.02032) (0.03346) (0.02007) 4 −0.052888 0.039885 −0.058855 −0.025699 (0.03005) (0.02250) (0.03215) (0.02133) 5 −0.04586 0.022481 −0.040059 −0.024572 (0.02866) (0.02281) (0.03554) (0.02250) 6 −0.034499 0.005305 −0.019324 −0.017462 (0.02281) (0.02208) (0.03446) (0.02165) 7 −0.025916 −0.007593 0.002268 −0.009639 (0.01949) (0.02136) (0.02998) (0.01886) 8 −0.019954 −0.013841 0.018508 −0.003767 (0.01816) (0.02021) (0.02832) (0.01626) 9 −0.01687 −0.014011 0.025670 −0.00043 (0.01738) (0.01770) (0.02747) (0.01580) 10 −0.016266 −0.010069 0.024340 0.000185 (0.01604) (0.01462) (0.02505) (0.01563) Response of LNCPI: Period LNUR LNREI LNFI LNCPI 1 0.021433 −0.004447 −0.01131 0.032548 (0.00743) (0.00679) (0.00657) (0.00451) 2 0.028201 −0.006838 −0.005661 0.043433 (0.01383) (0.01037) (0.01248) (0.00998) 3 0.032984 −0.004054 0.003783 0.037967 (0.01573) (0.01118) (0.01579) (0.01157) 4 0.034250 0.001798 0.002753 0.026742 (0.01538) (0.01204) (0.01707) (0.01203) 5 0.031342 0.008494 −0.007333 0.013502 (0.01436) (0.01292) (0.01718) (0.01153) 6 0.026088 0.012557 −0.017562 0.002152 (0.01413) (0.01363) (0.01771) (0.01083) 7 0.021456 0.012505 −0.023114 −0.004478 (0.01429) (0.01345) (0.01818) (0.01066) 8 0.018772 0.008894 −0.022676 −0.005843 (0.01380) (0.01229) (0.01776) (0.01060) 9 0.018018 0.003566 −0.017313 −0.003345 (0.01252) (0.01075) (0.01602) (0.00986) 10 0.018456 −0.001428 −0.009603 0.000901 (0.01125) (0.00948) (0.01362) (0.00841) Cholesky Ordering: LNUR LNREI LNFI LNCPI. Standard Errors: Analytic, The standard errors are marked in parentheses.Table A9. Impulse response function analysis result of Group (, ).Response of LNUR: Period LNUR LNTI 1 0.007795 0.000000 (0.00108) (0.00000) 2 0.007575 0.000307 (0.00211) (0.00079) 3 0.007027 0.000552 (0.00218) (0.00121) 4 0.006589 0.000687 (0.00220) (0.00133) 5 0.006245 0.000722 (0.00228) (0.00129) 6 0.005952 0.000687 (0.00237) (0.00120) 7 0.005682 0.000614 (0.00242) (0.00109) 8 0.005415 0.000531 (0.00244) (0.00098) 9 0.005144 0.000456 (0.00243) (0.00087) 10 0.004871 0.000399 (0.00242) (0.00077) Response of LNTI: Period LNUR LNTI 1 0.010648 0.025808 (0.00527) (0.00358) 2 0.015947 0.035379 (0.00980) (0.00567) 3 0.025087 0.033296 (0.01215) (0.00717) 4 0.034156 0.025147 (0.01302) (0.00780) 5 0.040534 0.015488 (0.01384) (0.00782) 6 0.043394 0.007214 (0.01488) (0.00782) 7 0.043130 0.001613 (0.01575) (0.00797) 8 0.040723 −0.001224 (0.01618) (0.00799) 9 0.037249 −0.001894 (0.01621) (0.00764) 10 0.033580 −0.001234 (0.01599) (0.00694) Cholesky Ordering: LNUR LNTI. Standard Errors: Analytic, The standard errors are marked in parentheses. - Variance decomposition analysisTable A10. Variance decomposition analysis result of Group (, ).
Variance Decomposition of LNUR: Period S.E. LNUR LNTI 1 0.007795 100.0000 0.000000 2 0.010874 99.92033 0.079668 3 0.012959 99.76276 0.237236 4 0.014554 99.58902 0.410983 5 0.015854 99.44595 0.554046 6 0.016948 99.35094 0.649055 7 0.017886 99.29944 0.700557 8 0.018695 99.27812 0.721876 9 0.019395 99.27393 0.726070 10 0.020001 99.27756 0.722442 Cholesky Ordering: LNUR LNTI.Table A11. Variance decomposition analysis result of Group (, , and ).Variance Decomposition of LNUR: Period S.E. LNUR LNREI LNFI LNCPI 1 0.008015 100.0000 0.000000 0.000000 0.000000 2 0.011287 93.68445 1.416877 0.546892 4.351780 3 0.013318 92.90239 1.394456 1.022664 4.680485 4 0.014640 92.95874 1.362949 0.846329 4.831987 5 0.015710 93.01351 1.210128 0.796065 4.980294 6 0.016570 92.66779 1.091239 1.104283 5.136685 7 0.017284 92.04011 1.040078 1.713907 5.205907 8 0.017893 91.36200 1.020946 2.388455 5.228599 9 0.018424 90.77305 1.002354 2.988863 5.235735 10 0.018887 90.34507 0.975413 3.436823 5.242690 Cholesky Ordering: LNUR LNREI LNFI LNCPI.
References
- Chaolin, G. Urbanization. In International Encyclopedia of Human Geography, 2nd ed.; Kobayashi, A., Ed.; Elsevier: Oxford, UK, 2020; pp. 141–153. [Google Scholar]
- Guan, X.; Wei, H.; Lu, S.; Dai, Q.; Su, H. Assessment on the urbanization strategy in China: Achievements, challenges and reflections. Habitat. Int. 2018, 71, 97–109. [Google Scholar] [CrossRef]
- Northam, R.M.J.R. Urban Geography; Wiley: Hoboken, NJ, USA, 1979; Volume 23, pp. 430–444. [Google Scholar]
- Chu, Y.-W. China’s new urbanization plan: Progress and structural constraints. Cities 2020, 103, 102736. [Google Scholar] [CrossRef]
- Perry, D.C. Infrastructure Investment. In International Encyclopedia of the Social & Behavioral Sciences, 2nd ed.; Wright, J.D., Ed.; Elsevier: Oxford, UK, 2015; pp. 116–118. [Google Scholar]
- Cheng, M.; Lu, Y. Investment efficiency of urban infrastructure systems: Empirical measurement and implications for China. Habitat. Int. 2017, 70, 91–102. [Google Scholar] [CrossRef]
- Tian, L.; Ge, B.; Li, Y. Impacts of state-led and bottom-up urbanization on land use change in the peri-urban areas of Shanghai: Planned growth or uncontrolled sprawl? Cities 2017, 60, 476–486. [Google Scholar] [CrossRef]
- Maparu, T.S.; Mazumder, T.N. Transport infrastructure, economic development and urbanization in India (1990–2011): Is there any causal relationship? Transp. Res. Part A Policy Pract. 2017, 100, 319–336. [Google Scholar] [CrossRef]
- Grafe, F.-J.; Mieg, H.A. Connecting financialization and urbanization: The changing financial ecology of urban infrastructure in the UK. Reg. Stud. Reg. Sci. 2019, 6, 496–511. [Google Scholar] [CrossRef]
- Shannon, M.; Otsuki, K.; Zoomers, A.; Kaag, M. Sustainable Urbanization on Occupied Land? The politics of infrastructure development and resettlement in Beira city, Mozambique. Sustainability 2018, 10, 3123. [Google Scholar] [CrossRef]
- Tang, Y.; Xu, J.; Zhang, X. China’s investment and rate of return on capital revisited. J. Asian Econ. 2017, 49, 12–25. [Google Scholar] [CrossRef]
- Guo, S.; Shi, Y. Infrastructure investment in China: A model of local government choice under land financing. J. Asian Econ. 2018, 56, 24–35. [Google Scholar] [CrossRef]
- Cai, Z.; Liu, Q.; Cao, S. Real estate supports rapid development of China’s urbanization. Land Use Policy 2020, 95, 104582. [Google Scholar] [CrossRef]
- Gao, X.; Zhang, A.; Sun, Z. How regional economic integration influence on urban land use efficiency? A case study of Wuhan metropolitan area, China. Land Use Policy 2020, 90, 104329. [Google Scholar] [CrossRef]
- Wu, Y.; Heerink, N. Foreign direct investment, fiscal decentralization and land conflicts in China. China Econ. Rev. 2016, 38, 92–107. [Google Scholar] [CrossRef]
- Vongpraseuth, T.; Choi, C.G. Globalization, foreign direct investment, and urban growth management: Policies and conflicts in Vientiane, Laos. Land Use Policy 2015, 42, 790–799. [Google Scholar] [CrossRef]
- Lin, B.; Benjamin, I.N. Causal relationships between energy consumption, foreign direct investment and economic growth for MINT: Evidence from panel dynamic ordinary least square models. J. Clean Prod. 2018, 197, 708–720. [Google Scholar] [CrossRef]
- Ning, L.; Wang, F.; Li, J. Urban innovation, regional externalities of foreign direct investment and industrial agglomeration: Evidence from Chinese cities. Res. Policy 2016, 45, 830–843. [Google Scholar] [CrossRef]
- Yuan, F.; Wei, Y.D.; Xiao, W. Land marketization, fiscal decentralization, and the dynamics of urban land prices in transitional China. Land Use Policy 2019, 89, 104208. [Google Scholar] [CrossRef]
- Cao, Y.; Chen, J.; Zhang, Q. Housing investment in urban China. J. Comp. Econ. 2018, 46, 212–247. [Google Scholar] [CrossRef]
- Hafez, R.M. New cities between sustainability and real estate investment: A case study of New Cairo city. HBRC J. 2017, 13, 89–97. [Google Scholar] [CrossRef]
- Mavridis, S.C.; Vatalis, K.I. Investment in Construction and Economic Growth in Greece. Procedia Econ. Financ. 2015, 24, 386–394. [Google Scholar] [CrossRef][Green Version]
- Kim, N.S.; Yook, D. Enhancing the economic benefit assessment of roadway investment through the application of value of time by trip length. Transp. Policy 2018, 68, 28–36. [Google Scholar] [CrossRef]
- Chen, Z.; Xue, J.; Rose, A.Z.; Haynes, K.E. The impact of high-speed rail investment on economic and environmental change in China: A dynamic CGE analysis. Transp. Res. Part A Policy Pract. 2016, 92, 232–245. [Google Scholar] [CrossRef]
- Maparu, T.S.; Mazumder, T.N. Investigating causality between transport infrastructure and urbanization: A state-level study of India (1991–2011). Transp. Policy 2020. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, S.; Wang, T.; Dai, X.; Baninla, Y.; Nakatani, J.; Moriguchi, Y. Urbanization impacts on greenhouse gas (GHG) emissions of the water infrastructure in China: Trade-offs among sustainable development goals (SDGs). J. Clean. Prod. 2019, 232, 474–486. [Google Scholar] [CrossRef]
- Zeng, C.; Song, Y.; Cai, D.; Hu, P.; Cui, H.; Yang, J.; Zhang, H. Exploration on the spatial spillover effect of infrastructure network on urbanization: A case study in Wuhan urban agglomeration. Sustain. Cities Soc. 2019, 47, 101476. [Google Scholar] [CrossRef]
- Fang, G.; Wang, Q.; Tian, L. Green development of Yangtze River Delta in China under Population-Resources-Environment-Development-Satisfaction perspective. Sci. Total Environ. 2020, 727, 138710. [Google Scholar] [CrossRef] [PubMed]
- Kahouli, B. The short and long run causality relationship among economic growth, energy consumption and financial development: Evidence from South Mediterranean Countries (SMCs). Energy Econ. 2017, 68, 19–30. [Google Scholar] [CrossRef]
- Ahmed, Z.; Zafar, M.W.; Ali, S. Linking urbanization, human capital, and the ecological footprint in G7 countries: An empirical analysis. Sustain. Cities Soc. 2020, 55, 102064. [Google Scholar] [CrossRef]
- Xu, J.; Song, J.; Li, B.; Liu, D.; Wei, D.; Cao, X. Do settlements isolation and land use changes affect poverty? Evidence from a mountainous province of China. J. Rural Stud. 2020, 76, 163–172. [Google Scholar] [CrossRef]
- Xu, S.-C.; Miao, Y.-M.; Gao, C.; Long, R.-Y.; Chen, H.; Zhao, B.; Wang, S.-X. Regional differences in impacts of economic growth and urbanization on air pollutants in China based on provincial panel estimation. J. Clean. Prod. 2019, 208, 340–352. [Google Scholar] [CrossRef]
- Lan, F.; Gong, X.; Da, H.; Wen, H. How do population inflow and social infrastructure affect urban vitality? Evidence from 35 large-and medium-sized cities in China. Cities 2020, 100, 102454. [Google Scholar] [CrossRef]
- Kennedy, C.; Zhong, M.; Corfee-Morlot, J. Infrastructure for China’s Ecologically Balanced Civilization††Note: This paper is not intended to represent views endorsed by the OECD nor by its member countries. Engineering 2016, 2, 414–425. [Google Scholar] [CrossRef]
- Ferrer, A.L.C.; Thomé, A.M.T.; Scavarda, A.J. Sustainable urban infrastructure: A review. Resour. Conserv. Recycl. 2018, 128, 360–372. [Google Scholar] [CrossRef]
- Davies, C.; Lafortezza, R. Urban green infrastructure in Europe: Is greenspace planning and policy compliant? Land Use Policy 2017, 69, 93–101. [Google Scholar] [CrossRef]
- Kis-Katos, K.; Sjahrir, B.S. The impact of fiscal and political decentralization on local public investment in Indonesia. J. Comp. Econ. 2017, 45, 344–365. [Google Scholar] [CrossRef]
- Liu, N.; Liu, C.; Xia, Y.; Da, B. Examining the coordination between urbanization and eco-environment using coupling and spatial analyses: A case study in China. Ecol. Indic. 2018, 93, 1163–1175. [Google Scholar] [CrossRef]
- Pobric, A.; Robinson, G.M. Recent urban development and gentrification in post-Dayton Sarajevo, Bosnia and Herzegovina. Cities 2019, 89, 281–295. [Google Scholar] [CrossRef]
- Huang, H.; Dennis Wei, Y. Spatial inequality of foreign direct investment in China: Institutional change, agglomeration economies, and market access. Appl. Geogr. 2016, 69, 99–111. [Google Scholar] [CrossRef]
- Zhong, T.; Zhang, X.; Huang, X.; Liu, F. Blessing or curse? Impact of land finance on rural public infrastructure development. Land Use Policy 2019, 85, 130–141. [Google Scholar] [CrossRef]
- Gao, X.; Nakatani, J.; Zhang, Q.; Huang, B.; Wang, T.; Moriguchi, Y. Dynamic material flow and stock analysis of residential buildings by integrating rural–urban land transition: A case of Shanghai. J. Clean. Prod. 2020, 253, 119941. [Google Scholar] [CrossRef]
- Wesołowska, J. Urban Infrastructure Facilities as an Essential Public Investment for Sustainable Cities—Indispensable but Unwelcome Objects of Social Conflicts. Case Study of Warsaw, Poland. Transp. Res. Procedia 2016, 16, 553–565. [Google Scholar] [CrossRef][Green Version]
- Shanghai Municipal People’s Government. Shanghai Statistical Yearbook. 1990–2020; Shanghai Statistical Publishing House: Shanghai, China, 2020. [Google Scholar]
- United Nations. World Urbanization Prospects, the 2014 Revision; United Nations: New York, NY, USA, 2015. [Google Scholar]
- Dickey, D.A.; Fuller, W.A. Likelihood ratio statistics for autoregressive time series with a unit root. Econom. J. Econom. Soc. 1981, 49, 1057. [Google Scholar] [CrossRef]
- Dickey, D.A.; Fuller, W.A. Distribution of the estimators for autoregressive time series with a unit root. J. Am. Stat. Assoc. 1979, 74, 427–431. [Google Scholar]
- Maddala, G.S.; Kim, I.M. Unit Roots Cointegration and Structural Change: Issues in Unit Root Testing; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Hubrich, K.; Lütkepohl, H.; Saikkonen, P. A review of systemscointegration tests. Econom. Rev. 2001, 20, 247–318. [Google Scholar] [CrossRef]
- Wang, Q.; Su, M.; Li, R.; Ponce, P. The effects of energy prices, urbanization and economic growth on energy consumption per capita in 186 countries. J. Clean. Prod. 2019, 225, 1017–1032. [Google Scholar] [CrossRef]
- Sims, C. Macroeconomics and Reality. Econometrica 1980, 48, 1–48. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Athanasopoulos, G. Forecasting: Principles and Practice; OTexts: Melbourne, Australia, 2018; pp. 89–102. [Google Scholar]
- Xu, J.-W.; Moon, S. Stochastic Forecast of Construction Cost Index Using a Cointegrated Vector Autoregression Model. J. Manag. Eng. 2013, 29, 10–18. [Google Scholar] [CrossRef]
- Pesaran, B. Working with Microfit 4: Interactive Econometric Analysis; Oxford University Press: Oxford, UK, 1997. [Google Scholar]
- Liew, V.K.-S. Which lag length selection criteria should we employ? Econ. Bull. 2004, 3, 1–9. [Google Scholar]
- Gutierrez, C.E.C.; Souza, R.C.; Guillén, O.T.D.C. Selection of Optimal Lag Length in Cointegrated VAR Models with Weak Form of Common Cyclical Features. Braz. Rev. Econ. 2009, 29, 59–78. [Google Scholar] [CrossRef]
- Liu, Q.; Wang, S.; Zhang, W.; Li, J.; Zhao, Y.; Li, W. China’s municipal public infrastructure: Estimating construction levels and investment efficiency using the entropy method and a DEA model. Habitat. Int. 2017, 64, 59–70. [Google Scholar] [CrossRef]
- Guarini, M.R.; Morano, P.; Sica, F. Eco-system Services and Integrated Urban Planning. A Multi-criteria Assessment Framework for Ecosystem Urban Forestry Projects. In Values and Functions for Future Cities; Springer: Berlin/Heidelberg, Germany, 2020; pp. 201–216. [Google Scholar]
| Trace Test | Maximum Eigenvalue Test | |||||||
|---|---|---|---|---|---|---|---|---|
| No. of CE(s) | Eigenvalue | Statistic | Critical Value | Prob. ** | Eigenvalue | Statistic | Critical Value | Prob. ** |
| LNUR and LNCPI, LNREI, LNFI | ||||||||
| None * | 0.7678 | 59.0405 | 40.1749 | 0.0002 | 0.7678 | 37.9662 | 24.1592 | 0.0004 |
| At most 1 | 0.3335 | 21.0744 | 24.2760 | 0.1202 | 0.3335 | 10.5505 | 17.7973 | 0.4289 |
| At most 2 | 0.3078 | 10.5239 | 12.3209 | 0.0982 | 0.3078 | 9.5664 | 11.2248 | 0.0965 |
| At most 3 | 0.0362 | 0.9575 | 4.1299 | 0.3799 | 0.0362 | 0.9575 | 4.1299 | 0.3799 |
| LNUR and LNTI | ||||||||
| None * | 0.5069 | 19.6435 | 12.3209 | 0.0025 | 0.5069 | 18.3839 | 11.2248 | 0.0024 |
| At most 1 | 0.0473 | 1.2596 | 4.1299 | 0.3056 | 0.0473 | 1.2596 | 4.1299 | 0.3056 |
| Lag | LR | FPE | AIC | SC | HQ |
|---|---|---|---|---|---|
| 1 | / | / | / | / | / |
| 2 | ) | / | / | ) | / |
| 3 | / | ) | / | / | / |
| 4 | / | / | ) | / | ) |
| 5 | / | / | / | / | / |
| 6 | / | / | / | / | / |
| 7 | / | / | / | / | / |
| 8 | / | / | ) | / | ) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, Y.; Wang, C.; Chen, C.; Ding, K.; Zeng, W. Total Investment in Fixed Assets and the Later Stage of Urbanization: A Case Study of Shanghai. Sustainability 2021, 13, 3661. https://doi.org/10.3390/su13073661
Luo Y, Wang C, Chen C, Ding K, Zeng W. Total Investment in Fixed Assets and the Later Stage of Urbanization: A Case Study of Shanghai. Sustainability. 2021; 13(7):3661. https://doi.org/10.3390/su13073661
Chicago/Turabian StyleLuo, Yulong, Can Wang, Chen Chen, Kangle Ding, and Weiliang Zeng. 2021. "Total Investment in Fixed Assets and the Later Stage of Urbanization: A Case Study of Shanghai" Sustainability 13, no. 7: 3661. https://doi.org/10.3390/su13073661
APA StyleLuo, Y., Wang, C., Chen, C., Ding, K., & Zeng, W. (2021). Total Investment in Fixed Assets and the Later Stage of Urbanization: A Case Study of Shanghai. Sustainability, 13(7), 3661. https://doi.org/10.3390/su13073661