1. Introduction
Electric Vehicles (EVs) are a promising solution to resolve the greenhouse emission issue as well as the fossil fuels scarcity problem in the future. Even though the demand for EVs is expected to increase in the next few years, it is still constrained by many factors including gasoline prices, battery costs, and the availability of Charging Station (CS) infrastructure. On the other hand, investors are willing to invest in CS infrastructure if and only if enough number of consumers are available in the network.
To address the problem above, also called the “chicken-egg problem”, many design parameters related to the available CS in the EV transportation network were studied in the literature [
1,
2,
3]. Such parameters need to be involved to determine the best Electric Vehicle Charging Station (EVCS) infrastructure. These parameters include: location, level, and size and capacity of the available CSs as discussed below:
In this paper, both budget and route-related constraints are considered. A Markov-chain based model is proposed to study the relation among the demand on CS, the size and the capacity of the CS, and the quality of service represented by the mean length of the queue in the CS. In addition, a CS infrastructure design is presented. The infrastructure is based on the net profit estimated by the proposed model and under both route and budget constraints using a metaheuristic Grey Wolf Optimization (GWO) algorithm.
The rest of this paper is organized as follows: First, a literature review on EVCSs’ allocation algorithms and infrastructure planning is introduced. Second, the proposed methodology is presented including the stochastic modeling approach, a brief overview of the GWO algorithm, and the implementation of EVCSs’ allocation as an optimization problem using GWO. Third, a simulation on the proposed model is demonstrated and experimental results are examined. Then, work significance and limitations are discussed. Finally, conclusions, future work, and recommendations are drawn.
2. Literature Review
Many approaches have been proposed to address the optimization problem of allocating EVCSs. Proposed models in the literature can be categorized into flow-capturing models and node-serving models.
In flow-capturing models, the demand is represented by vehicle flow in any route. CSs need to be allocated in the route between the origin and the destination. Mainly, the optimization problem in flow-capturing is formulated as a Mixed Integer Programming Problem (MIP), where the objective is to maximize the EV flow in all available routes within the EV transport network, and the constraints are either route- or demand-related constraints or both. The model was first proposed by Kuby and Lim [
11] and named flow-refueling location model (FRLM) [
12]. FLRM extends flow-intercepting model [
13,
14] which aims at maximizing the traffic flow given the number of facilities. However, instead of allocating a single refueling station, FLRM can allocate multiple stations based on demand and maximum allowable travel distance [
12,
15]. Since then, several mathematical models for FLRM were proposed [
1,
12,
15,
16]. Nevertheless, flow-capturing models still suffer from several limitations such as: (I) inflexibility: it is very hard to capture all information needed to simulate a realistic EV network, (II) high-complexity: the complexity of the model increases when the size of the EV network, the available tours, and/or the number of available CSs increase, and (III) centrality: the model does not address the problem of decentralized networks.
On the other hand, node-serving models aim at maximizing EVCS coverage by either maximizing the demand or minimizing the travel distance for specific refueling locations (nodes). Liu [
17] proposed an algorithm to deploy the three levels of CSs in an EV network. The algorithm was developed based on demand in each area and aimed at minimizing the separation distance between CS nodes [
6]. Shi and Zheng [
18] proposed another approach where fuzzy c-mean clustering method was used to cover EV charging demands in each cluster [
19]. Node-serving models showed great performance in solving EVCS allocation in urban areas, where many constraints are needed to be defined and uncertain/different demand levels exist for each node in the EV network. However, EV network should be modeled carefully so that all constraints are stated, and a feasible yet realistic solution is applied.
To solve EVCS allocation, mathematical programming models were primarily used in the literature. However, for such models, when the number of constraints and/or decision variables increases, the computational complexity increases. Hence, finding an optimal solution becomes challenging. On the other hand, metaheuristic algorithms are used to find global (near-optimal) solution with less computational effort. For this reason, metaheuristic algorithms show higher flexibility when it comes to simulating realistic scenarios in EV network. For instance, Vazifeh et al. [
20] defined the optimization problem of EVCS allocation as a non-deterministic polynomial-time hard (NP-Hard) problem [
21]. To solve a NP-Hard problem, the total area was partitioned into small square cells. The optimization problem was solved using Genetic Algorithm (GA). In addition to GA, swarm-intelligence metaheuristic algorithms were also used in a number of studies in the literature such as the work by Rahman et al. [
22], and Vasant et al. [
23] who used Gravitational Search Algorithm (GSA) and Particle swarm Optimization (PSO) to implement a CS infrastructure considering energy prices and battery capacity constraints [
24,
25].
To estimate the demand for EVCS, big data and surveys were mainly used [
4,
6,
8,
21]. The problem with the existing methods is that demand uncertainty is not captured. For this reason, Markov-chain theory was applied in a few studies to stochastically model the arrival rate of EVs at a CS [
9,
11,
26,
27]. For instance, a death-and-birth process model was proposed by Farkas and Prikler [
26]. A mathematical model for the average waiting rate and the mean queue length was calculated based on the steady-state probabilities. Birth-and-death rates are represented by the arrival rate of EVs and the charging rate, respectively.
To summarize the above discussion, EVCS allocation is a challenging problem and is extremely crucial to the EV industry. Although flow-capturing models are the most popular solutions proposed in literature. These models suffer from inflexibility, high-complexity, and centrality. On the other hand, node-serving models such as the models proposed by Vazifeh et al. [
20], Rahman et al. [
22], and Vasant et al. [
23] showed better flexibility and were able to simulate realistic scenarios for an EV network. However, none of these models captured the uncertainty of EV demand. Estimating EV demand has been studied using different methods in the literature. The demand uncertainty is captured using Markov-chain model. However, none of the proposed models to estimate demand uncertainty using Markov-chain were utilized in allocating EVCS. In this paper, we combine the Markov-chain theory with node-serving approach to allocate EVCS.
First, Markov-chain model is proposed to provide a relation between the demand and the desired number of sockets per CS, as well as the desired number of CSs in an urban area to maintain the best quality of service. Then, the work of Farkas and Prikler [
26] was extended by considering the balking parameters; EVs will enter with a probability α in the case when the served EVs in the CSs equals the total number of charging slots.
Secondly, a node-serving model to allocate the best CS locations was developed. A Grey Wolf Optimizer (GWO) was utilized to find the best set of CSs from all available locations. The set of CSs were selected under routing constraints. The Markov-chain model was used to estimate the net profit of the selected set of CSs at each time iteration and is applied to the GWO as an objective function. The network was optimized by selecting the best CS locations for the EVCS infrastructure that provide the maximum estimated profit under predefined routing constraints.
The proposed algorithm is different from related work in that a Markov-chain model is combined with a metaheuristic algorithm to capture realistic scenarios of CS demands, costs, quality of service, and the corresponding profit. GWO is used to solve the EVCS allocation problem. Compared to other metaheuristic algorithms such as GA and PSO, GWO is considered as one of the fastest and the most efficient metaheuristic algorithms for the reason of using three solutions at the convergence to achieve better global solution [
28]. Finally, both budget and routing constraints are also considered including the cost of building a CS, waiting time at the CS, available routes between CSs, and the maximum distance an EV can go after a full charge. The worst-case scenario was considered for EV distance range with battery capacity set to 20 kWh and adding the consumption caused by traffic, weather, and using radio.
Contributions are summarized below:
- (I)
The proposed algorithm simulates the stochastic behavior of EVCS infrastructure including demand and cost uncertainty using Markov-chain processes.
- (II)
The parameters affecting the CS quality of service and the achieved profit of EV network were investigated using birth-and-death model and sensitivity analysis.
- (III)
GWO is proposed to optimize the NP-hard allocation problem. GWO is known for lower complexity and higher flexibility compared to other solutions proposed in the literature to address the EVCS infrastructure problem.
- (IV)
Both budget and routing constraints are considered in the optimization model.
- (V)
Unlike FLRM, state of charge (SOC) uncertainty is included in the proposed model.
Sustainability can be achieved using the proposed model by gradually implementing the network in multiple phases according to current demand. Therefore, both EV consumers and CS investors are satisfied.
3. System Model
This section provides a detailed description of the proposed Markov-chain-based model of EVCS, an overview of GWO algorithm, and EVCS allocation using GWO.
3.1. Markov-Chain of EV Charging Station
Queuing in CS can be modeled as a birth-and-death process, where the birth rate is the arrival rate of EVs to the CS, the death rate is the charging rate, and the state represents the number of EVs at the CS at time .
The arrival time of EV to the CS is assumed to follow a Poisson process with λ rate, and the charging rate is following exponential process with µ rate [
17,
26]. CS has c sockets available for EVs, and a maximum capacity of N vehicles. The model is also modified to be a reneging model in which the EV driver will enter the CS with probability α if (s)he found the CS full at arrival time. Hence, the Markov-chain is modeled as in
Figure 1.
The steady-state probabilities are evaluated as below, where
is the probability that there will be exactly k EVs at the CS at a time [
29]:
It can be concluded that the steady-state probability
can be obtained from the following formula:
Hence, the steady-state probability of state 0 can be calculated as follows:
The average number of EV drivers in the CS (
):
Average amount of time the EV driver spends in the CS is (
) which follows Little’s low:
where
is the average arrival rate of entering EV drivers considering only actual arrivals:
The average number of customers waiting in queue is (
):
Average amount of time the EV driver spends in the queue is (
) which follows Little’s low:
Expected net profit (
):
where
is the operating cost of the CS per minute and
is the profit per a single EV.
3.2. Grey Wolf Optimization (GWO)
GWO is one of the swarm intelligence optimization algorithms. The basic concept of metaheuristic algorithms is to generate high-quality solutions based on an initial random population of possible solutions and a fitness function (or objective function). The generation is inspired by natural systems behaviors and performed until a termination condition has been reached.
The basic idea of the metaheuristic swarm intelligence GWO algorithm is to simulate the hunting procedure done by grey wolves in the wildlife [
30]. Basically, four types of wolves are simulated: alpha wolves (
, beta wolves (
, gamma wolves (
and omega wolves (
ordered from the strongest to the weakest. To obtain a new solution, the best three solutions represent the first three types of wolves respectively cooperating in hunting the prey and achieving a better solution.
The social hierarchy, tracking, encircling, and attacking prey by grey wolf are simulated and mathematically modeled using GWO. It can be obtained by considering the best solution as , second-best solution as , third-best solution as , and the rest of the solutions as .
Encircling prey is modeled as below [
30]:
where
is the current iteration,
and
are coefficient vectors,
is the position vector of the prey, and
is the position vector of a grey wolf.
The coefficient vectors
and
are obtained from the equations below:
where
and
are random values uniformly distributed between 0 and 1, and
is a linearly decreasing coefficient from 2 to 0.
For hunting, alpha wolves (
are leading the rest of wolves. While beta and sigma (
) wolves are also participating the hunting process. The first three solutions are always saved and used for forming the new solution.
where:
The new position (solution) is formed by combining the three best positions:
It can be observed that the new solution is positioned in a random place within the circle of the three top solutions: alpha (, beta (), and gamma (). In other words, the three top solutions determine the new solution position.
3.3. GWO for EV Charging Station Allocation
Assume that the possible CS locations are given with all the needed information about demand in each area (represented by the arrival rate of EV drivers), the cost for locating a CS in each location (
$ per minute), and a specific available size per each CS. GWO initialize a population of random solutions. Each solution includes a subset of the candidate CSs available for the desired infrastructure. First, each solution in the population is evaluated using a fitness function. The fitness function calculates the achieved profit when using the selected subset of CSs based on the Markov-chain process with a pre-known arrival rate and operating cost for each CS. In addition, the total number of selected CSs is added to the objective function to minimize the number of selected CSs. Then, a new group of solutions (positions) are generated based on the method explained in the previous section and then evaluated using the fitness function. The procedure is repeated until meeting stopping criteria, which, in our case, is the maximum number of iterations. Finally, the best solution (subset of CSs selected) is studied under routing constraints. In other words, the EV is guaranteed to accomplish a complete route between selected CSs. This is done by using different techniques: (I) Calculating the distance between CSs. The distance between each CS and the closest one should be less than or equal to half the maximum distance an EV can go with a full charge without recharge. This is a valid assumption in the routing problem and has been used in FRLM and other routing models to address EV routing problem in the literature [
12,
13,
14,
15,
16,
19,
22,
31]. The assumption is based on allocating CSs in the middle of the EV origin to distention O-D path. The worst-case scenario was considered in terms of EV driving distance to address urban area traffic, weather, and using radio; (II) Capturing the uncertainty of State of Charge (SOC). The uncertainty is added to the charging rate (
) when the model is implemented.
The proposed algorithm is shown in Equations (29)–(33); the objective function (fitness) aims at maximizing the profit while minimizing the total number of selected CSs. Where
is the net profit after implementing the EVCS network,
is the total number of selected CSs,
is the total number of potential CS locations, and
are weights (priority ratios). The first constraint evaluates the net profit following Equation (16) where
and
are the arrival rate, steady-state probability, and the operating cost per minute at CS
, respectively. Second and third constraints evaluate the steady-state probability at CS
. Where
and
represent the capacity and size of CS
, respectively.
represents the uncertainty of SOC and is a random variable. The fourth constraint ensures that the driving distance between any two selected CSs in the network (
) to be less than half the distance the EV can go (
). The last two constraints guarantee that the subset of the selected CSs (
) is part of the potential CS location set (
), and that both sets are integers representing the CS id. It is worth mentioning that the set of selected CSs
at any time represents the position (solution) formed by GWO
and represents the decision variable.
4. Experimental Results
To simulate the proposed model, python 2.7 [
32] is used with Bokeh package for visualization [
18]. The following parameters are considered in the proposed mathematical model. These parameters have been used and estimated by Farkas and Prikler [
26]:
: Number of parking slots (including sockets) = maximum allowable number of EVs in the CS (Maximum Capacity) = EVs being served + EVs waiting in the queue
: Number of charging sockets
µ: Charging rate (service rate) (1/min)
λ: EV arrival rate to the CS (1/min)
α: The entering probability when the CS is full (0.3 for all experiments).
It is worth mentioning that the birth-and-death model is following the queuing theory, the M/M/c (in complete Kendall’s notation) queue [
33]. This is a queue with Poisson arrivals, and
servers with exponentially distributed service times with
places in the queue. When the customer/EV driver is served by a slot
, the slot
is considered busy, otherwise,
is considered idle (waiting for a new customer).
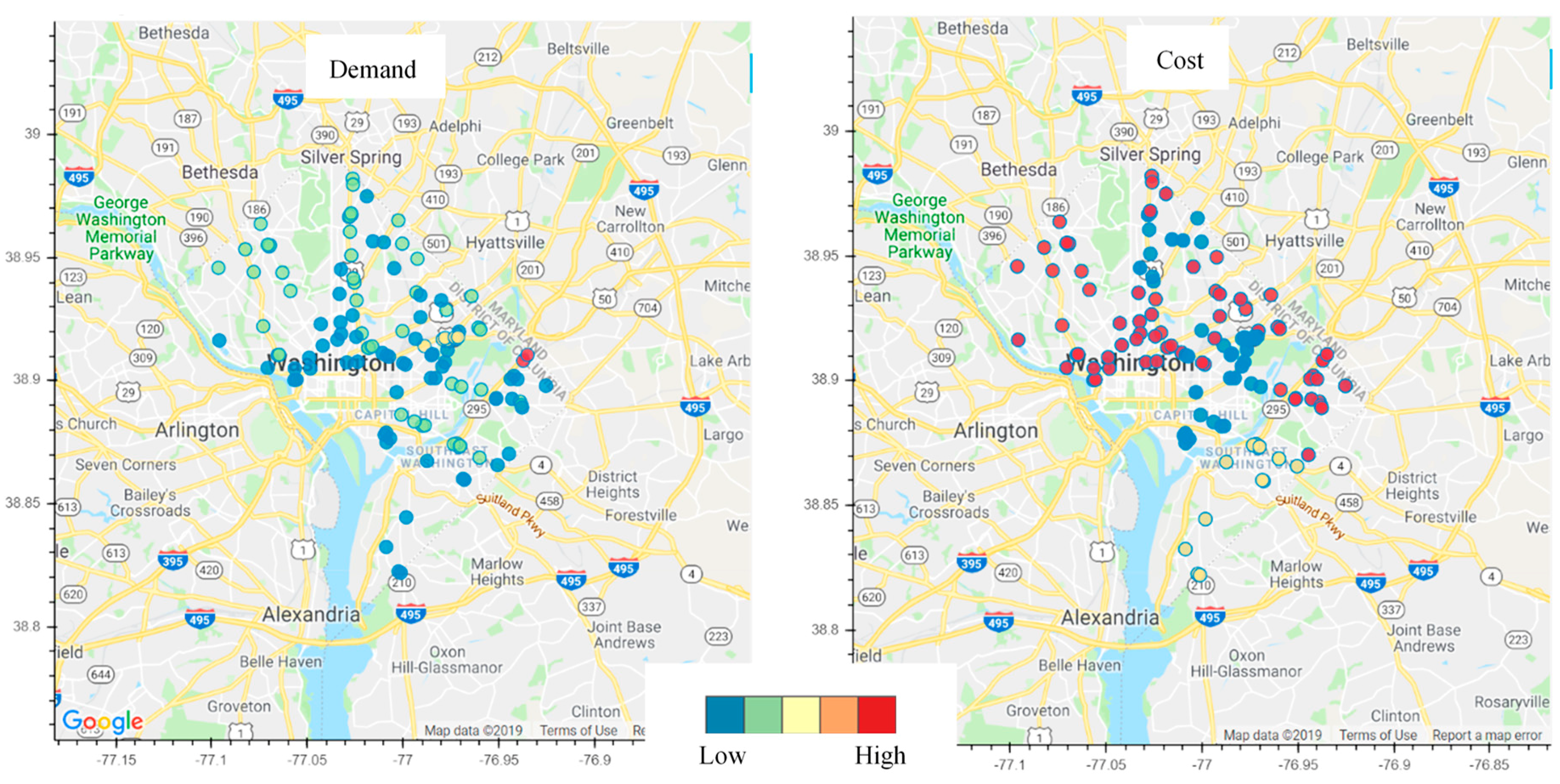
As an illustrative example, the algorithm is performed on Washington D.C. transportation network. The possible locations of CSs were assumed to be the refueling station locations in the city. The data of refueling station locations were extracted from Socrata [
34], while the routing driving distance (in meters) between different locations was evaluated based on Google API [
35]. Strictly speaking, the driving distance from station A to station B is not the same driving distance from station B to A. Finally, costs and rates at each CSs were estimated based on (
District of Columbia Open Data [
9]; Smith and Castellano [
33]; Davis et al. [
8]) as follows. Cost is proportional to Average Standardized Land Price per Square Foot in D.C. [
23]. Installation and electricity costs of charging stations were added to the estimated cost of land based on Smith and Castellano [
33] who estimated annual electricity and installation costs to be
$686/yr and
$1270/yr for Level 2, respectively, and
$1128 and
$5100 for Level 3, respectively. Finally, the arrival rate is estimated to be proportional to the Annual Average Daily Traffic (AADT) in D.C. [
36].
Figure 2 illustrates demand and cost distribution based on the available data. It can be observed that D.C. highway towards Maryland have the highest traffic compared to other areas. On the other hand, costs are considered higher around downtown areas.
Two types of experiments are held. First, the algorithm is performed under the assumption that SOC level is 0.5 (constant). This assumption was considered in most FRLM-based approaches [
9,
12,
13,
14,
15,
16,
19,
22]. Then, the algorithm is performed under SOC level uncertainty [
20].
Parameters used in the experiment are described in
Table 1.
Table 1a shows GWO parameters. Solutions of GWO are represented by bit vectors (continuous version). Each bit in the vector corresponds to a CS in the network. When the bit (rate) is greater than 0.5, the CS is selected. Otherwise, the CS is neglected.
There are limited locations to build CSs. Hence, the capacity of the CS and the number of available sockets will also be limited. Furthermore, the number of EVs will be growing exponentially and expected to be very small at the first stage of implementing the EVCS infrastructure [
22]. Hence, the arrival rate in the first stages is expected to be low.
4.1. Sensitivity Analysis
To study the effect of the assumptions on the network model, the model was tested while varying the independent variables α, , c, N, and λ. All statistical analyses have been performed using Minitab 18 under 95% confidence interval (CI) for difference. In other words, samples are considered significantly different if the p-value is less than 0.05.
4.1.1. Single Charging Station
Table 1b summarizes the parameter settings for a CS built in a refueling station in an urban area [
9,
26,
38,
39]. The maximum CS capacity of the CS (N) is 10 EVs, the number of sockets available for charging (c) ranges between 1 and 5, the arrival rate of EVs (λ) equals one EV every 60 min to one EV every 10 min, and the service rate (µ) is based on charging levels. For instance, for CS level 1, charging may last for 2 h. Hence, the service rate is 1/120 (1/min). The entering probability (α) is kept to 0.3. This means that the probability of an EV to enter a CS, if it arrives at the station when it is full (N cars are currently in the station), is 30%.
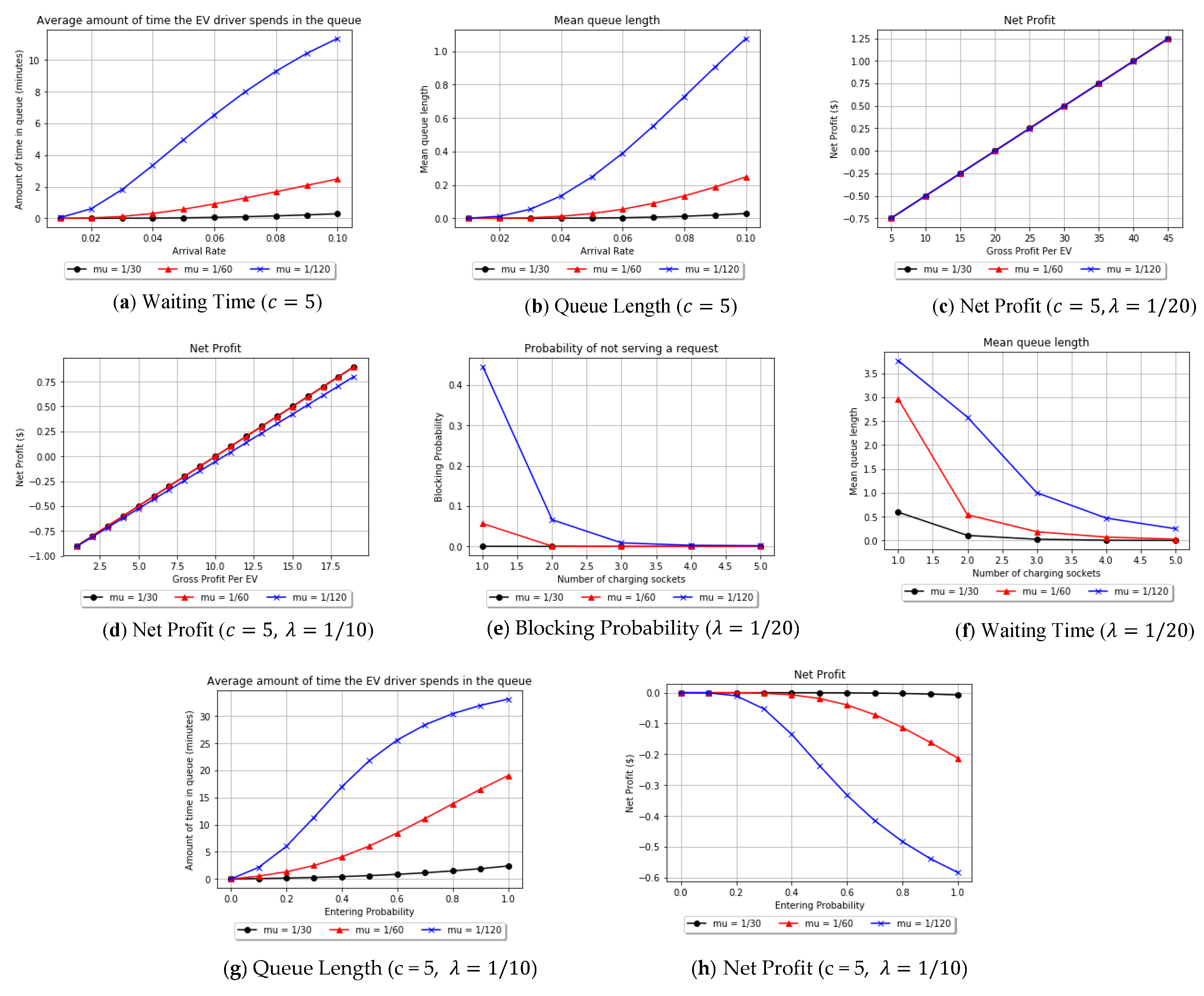
Level 1 (service time 120 min), Level 2 (service time 60 min), and Level 3 (service time 30 min) chargers are compared in
Figure 3. It can be observed that when the arrival rate is low, all charging levels will provide similar performance including blocking rate, waiting time, and the number of vehicles in the queue. Whereas, the performance differs when the arrival rate increase and/or the number of sockets minimized. Additionally, an investigation on the best pricing is held for two different arrival rate scenarios (
Figure 3c,d). The operating cost per minute is assumed to be 1
$/min [
39]. On the other hand, to achieve positive net profit, the gross profit per EV should be greater than
$10, and
$20 for high and for low arrival rates, respectively. The effect of number of sockets (c) were studied (
Figure 3e,f). When the number of sockets in the CS increases, the arriving EVs will have higher possibility to find an available slot to charge. The waiting time decreases. Hence, the blocking rate decreases. Finally, the entering probability effect was investigated (
Figure 3h,i). The higher the probability the EV enters the CS, the higher the queue length (
Figure 3h). Whereas, since the arrival rate is higher than the charging rate for Levels 1 and 2, and when the entering probability is high, the arriving EVs leave when they find the CS capacity is full. The possibility of serving new customers reduces. Hence, the net profit decreases (
Figure 3i). It is worth mentioning that, for the sake of comparison between the three levels, the operating cost was assumed to be equal for all charging levels in this experiment, while the actual operating cost of Level 3 is supposed to be higher than that for Level 2. This assumption is relaxed for the rest of the paper.
4.1.2. Multiple Charging Stations
In the previous section, the effect of independent variables on the performance of a single charging station with birth-and-death Markov model was investigated. Similarly, sensitivity analyses are applied on the proposed network model applied to Washington D.C. network in high arrival rate (
Table 1c). It is worth mentioning that the GWO model is a metaheuristic algorithm, which means that the solution is a global solution which might slightly change every time the algorithm is executed depending on the search population and the starting position. For this reason, the model was performed twenty-five times and statistical analysis was applied to evaluate the significance based on ANOVA (summarized in
Table 2a). Overall results represent the average output of the twenty-five model performances.
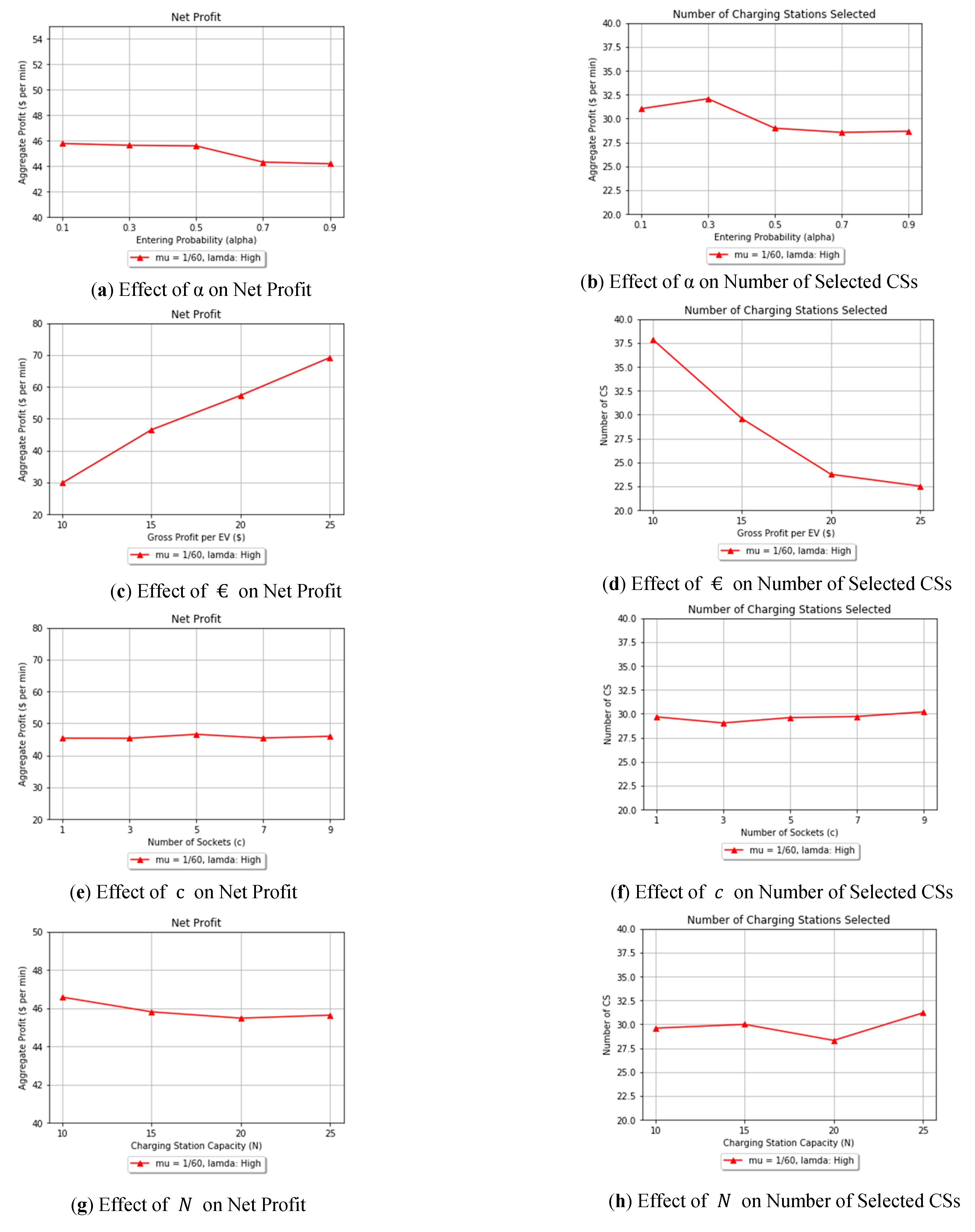
First, the effect of varying the entering probability is studied, statistically.
Figure 4a,b show that varying α does not show significant effect on the net profit nor number of selected charging stations. However, as discussed in
Section 4.1.1., the possibility of having CSs full is higher, and the possibility of serving new customers reduces. Hence, the net profit decreases. On the other hand, when the entering probability is high, more EVs are expected to enter the CS.
Figure 4c,d show how gross profit per EV (
) significantly affect both the net profit and the number of selected CSs. When the gross profit per EV increases, the net profit increases. As a result, the number of charging stations needed to obtain the desired positive net profit decreases.
Number of slots (c) and CS capacity (N) are studied in
Figure 4e–h. Results show that the model is flexible to be adjusted to overcome the lower capacity in CSs by slightly increasing the number of charging stations selected.
Finally, µ and λ effect on the proposed model are examined in
Figure 5 and
Figure 6 and
Table 2b. At the first stages of infrastructure planning, the arrival rate is expected to be as low as one EV per 8 h. In this experiment, the arrival rate was set to be in the range of one EV per 12.5 min for first stages (low arrival rate), and in the range of one EV per 2.5 min (high arrival rate) for later stages when the EV number in the network increases. In both stages, the arrival rate is set to be proportional to AADT as discussed earlier in this section.
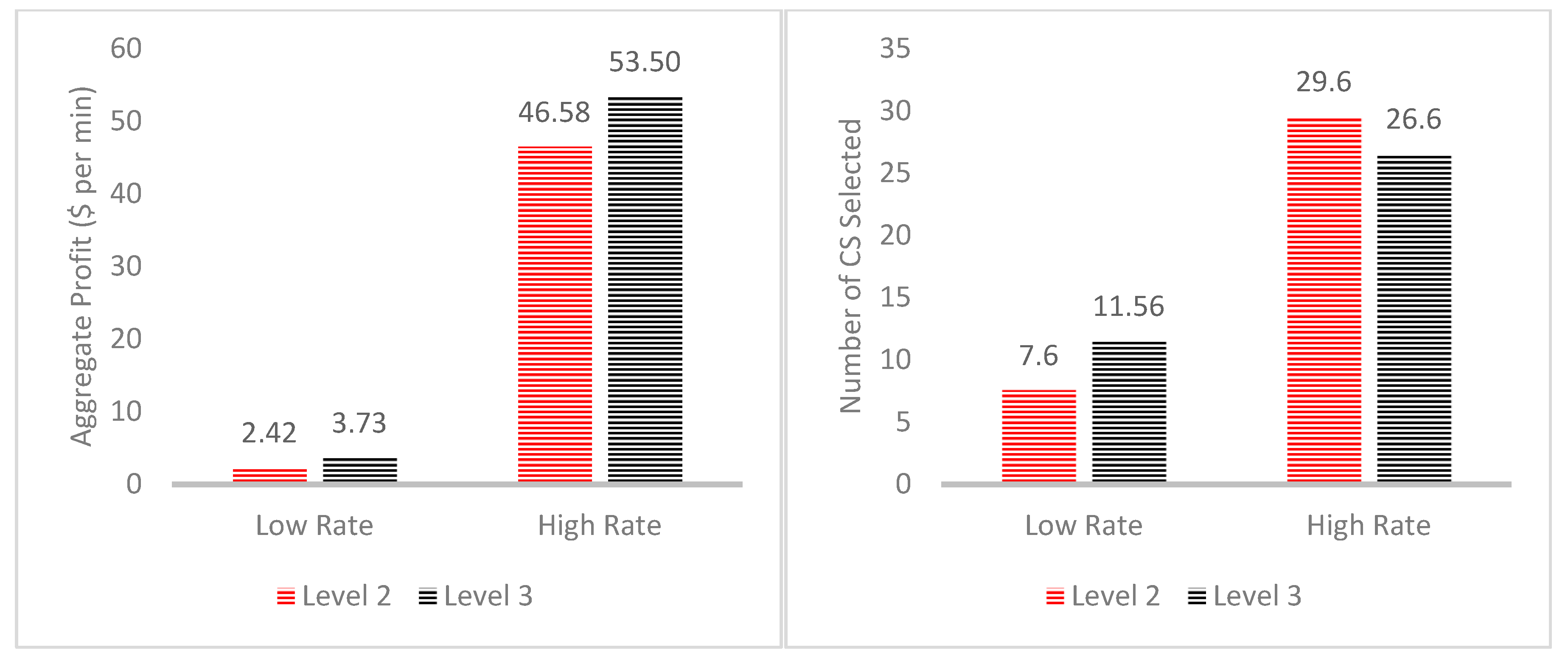
At first stages, and assuming SOC level to be half-full, and comparing the implementation of a network of only Level 2 chargers (µ = 1/60), and a network of only Level 3 chargers (µ = 1/30), the average number of selected CSs is 7.6, and 11.56 out of 151 total available locations at Washington D.C., respectively. The aggregate net profit is
$2.43 and
$3.73 per minute for Level 2 and 3, respectively. According to the sensitivity analysis presented in
Table 2b, the effect of charger level is significant (
p-value < 0.05). It can be concluded that slow chargers can achieve better performance with respect to the number of CSs selected and comparable net profit when installed in the first infrastructure implementation stages (
Figure 5 and
Table 2b).
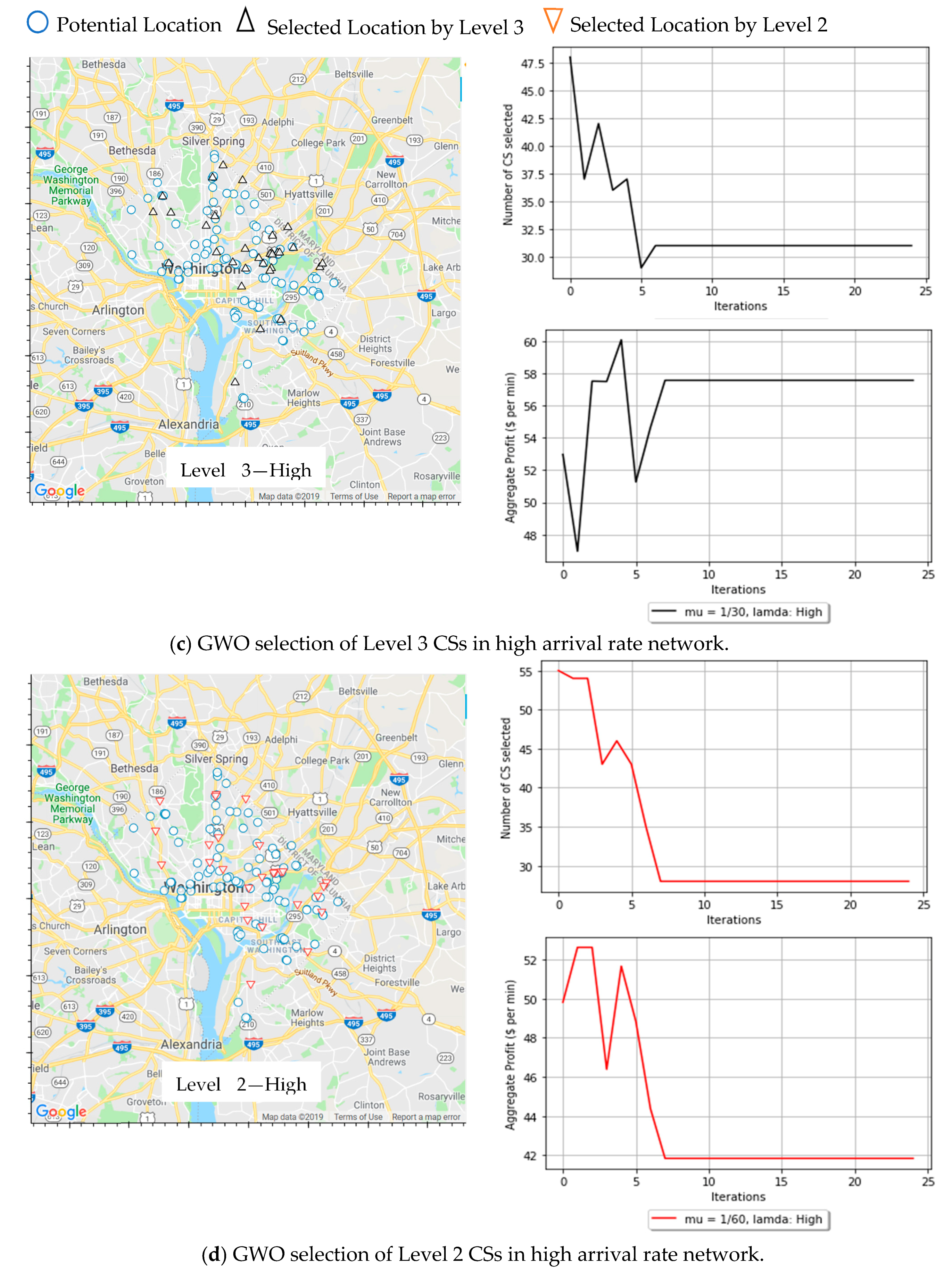
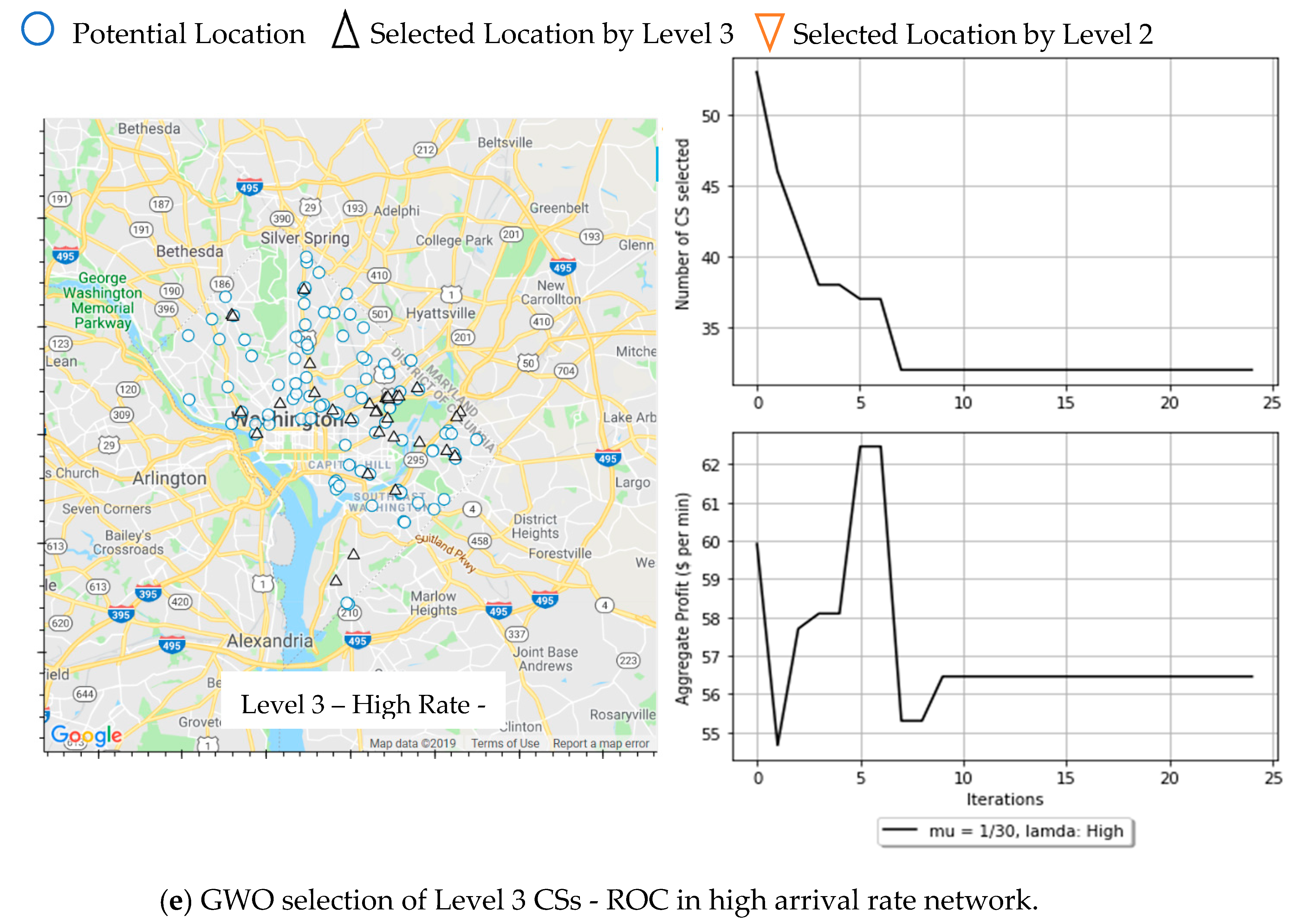
On the other hand, when the network grows and the number of EVs increases in the network, the fast (Level 3) chargers achieve higher net profit than the slow (Level 2) chargers with $53.50 compared to $46.58. The average selected number of CSs is 26.6, and 29.6 for Level 3, and Level 2, respectively.
Uncertain SOC level is investigated in
Figure 6. For Level 3 chargers and high arrival rate, the average number of CSs selected is around 26.6 for both models (assuming fixed SOC and uncertain SOC). However, the net profit achieved by uncertain SOC model is
$61.03 compared to
$53.50 achieved by assuming a half-full SOC model. Which, in turn, shows that uncertain SOC level might affect the selection of the best CS location and the estimated net profit, while the model and CS level performances remain the same at the same arrival rate according to
t-test shown in
Table 2b (
p-value > 0.05).
4.2. CS Allocation Using GWO
Finally, to validate GWO performance, both selected CS locations and the convergence are illustrated in
Figure 7. The convergence of GWO is plotted for both profit and number of CS selected for all previous scenarios. The proposed GWO is a multi-objective algorithm that counts for both the number of selected CSs, and the net profit. The fitness function (Equation (29)) value is a standardized ratio that combines a weighted value of both objective metrics, where the weights for the number of CS, and profit were 0.1, and 0.9, respectively.
In the equation above, higher weight is given to net profit because the installation costs of CS are included. This means that the more the CSs selected, the higher the installation costs, and the lower the achieved net profit. Hence, net profit also depends on the number of selected CSs. Nevertheless, these weights can be tuned based on the infrastructure design priorities. It can be observed from the figure that the number of selected CSs will be reduced until the achieved net profit is maximized. The best solution is the one that balances both the number of CSs and the net profit as shown in the figure. Additionally, it can be shown from
Figure 7 that mostly CSs at higher demand rates and lower costs are the ones that will mostly be selected. From the figure, selected CS locations do not reflect demand. The locations are selected based on the combination of demand, cost, and travel distance. According to the model, the travel distance constraint is still achieved if the demand is low and can be covered by a CS that is built away from the downtown area. The model avoids selecting a location within that area due to high installation costs.
6. Conclusions
A stochastic model for charging stations of electric vehicles is proposed. The model is based on birth-and-death Markov-chain process where the arrival rate of EVs is the birth rate, and the charging rate is the death rate. When the number of EVs in the CS is greater than the number of sockets available, then the EV drivers enter the CS with probability α. The Markov-chain model is used to estimate the expected net profit and is applied as an objective function to the GWO to select the best CSlocations out of all possible locations. The proposed algorithm was applied to Washington D.C.’s transportation infrastructure, where fueling stations are suggested to be the candidate locations of CSs, and the distance between target locations was calculated based on driving distance.
The model can simulate realistic scenarios and can provide accurate estimation of the net profit. To achieve the best planning for the EVCS infrastructure, slow CSs of Level 2 need to be installed in the areas with low arrival rates of network implementation, and fast CSs (Level 3) can be used to achieve higher profit in later stages and/or high demand areas in the early stages.
For future work, the algorithm can be improved by considering other factors such as the chicken-egg problem, which can be addressed by performing the model in a multi-period manner by increasing the demand gradually. Further improvement can be achieved by considering different types and sizes of charging stations including the charging rate for each type along with SOC level uncertainty. Finally, demand variation effect on pricing can be investigated to maximize the net profit of EVCS.