Revisiting the Spatial Autoregressive Exponential Model for Counts and Other Nonnegative Variables, with Application to the Knowledge Production Function
Abstract
1. Introduction
2. The SAR-E Regression
2.1. Model Specification and Partial Effects
2.2. Estimation
- Run a PPML regression of on and and calculate the predicted values .
- Run a PPML regression of on and .
3. Simulation Study
3.1. Simulation Design
3.2. Monte Carlo Results
4. Empirical Application
4.1. Data and Variables
4.2. Exploratory Spatial Analysis
4.3. Estimation Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| β1-SAR-Poisson 1stStep-ML—W1 | β1-SAR-Poisson 1stStep-OLS—W1 | β1-Aspatial Poisson ML—W1 | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Rho/n | 100 | 250 | 500 | 750 | 1000 | 100 | 250 | 500 | 750 | 1000 | 100 | 250 | 500 | 750 | 1000 |
| 0.0 | −0.0028 | −0.0011 | −0.0007 | 0.0000 | 0.0000 | −0.0011 | −0.0010 | −0.0006 | −0.0003 | −0.0003 | 0.0003 | −0.0004 | −0.0005 | 0.0000 | 0.0000 |
| 0.2 | −0.0013 | 0.0000 | −0.0007 | 0.0001 | −0.0004 | −0.0047 | −0.0041 | −0.0044 | 0.0040 | −0.0036 | 0.0311 | 0.0312 | 0.0312 | 0.0310 | 0.0308 |
| 0.4 | −0.0006 | 0.0000 | −0.0006 | 0.0002 | 0.0002 | −0.0032 | −0.0047 | −0.0046 | −0.0044 | −0.0046 | 0.0891 | 0.0868 | 0.0872 | 0.0872 | 0.0870 |
| 0.6 | 0.0003 | 0.0007 | 0.0015 | 0.0012 | 0.0015 | −0.0013 | −0.0019 | −0.0020 | −0.0022 | −0.0020 | 0.2021 | 0.1979 | 0.1988 | 0.1969 | 0.1971 |
| 0.8 | 0.0049 | 0.0046 | 0.0040 | 0.0032 | 0.0043 | 0.0021 | 0.0014 | 0.0017 | 0.0005 | 0.0004 | 0.4957 | 0.4846 | 0.4886 | 0.4771 | 0.4861 |
| β2-SAR-Poisson 1stStep-ML—W1 | β2-SAR-Poisson 1stStep-OLS—W1 | β2-Aspatial Poisson ML—W1 | |||||||||||||
| Rho/n | 100 | 250 | 500 | 750 | 1000 | 100 | 250 | 500 | 750 | 1000 | 100 | 250 | 500 | 750 | 1000 |
| 0.0 | −0.0062 | −0.0028 | 0.0026 | 0.0004 | 0.0003 | −0.0105 | −0.0021 | −0.0010 | −0.0015 | −0.0015 | −0.0064 | −0.0004 | −0.0003 | −0.0004 | −0.0007 |
| 0.2 | −0.0016 | 0.0012 | 0.0014 | −0.0004 | 0.0003 | −0.0132 | −0.0118 | −0.0156 | −0.0138 | −0.0130 | 0.1018 | 0.1035 | 0.1028 | 0.1027 | 0.1036 |
| 0.4 | 0.0024 | 0.0009 | 0.0031 | −0.0036 | 0.0043 | −0.0143 | −0.0182 | −0.0188 | −0.0191 | −0.0179 | 0.2737 | 0.2768 | 0.2760 | 0.2789 | 0.2799 |
| 0.6 | 0.0017 | 0.0023 | 0.0040 | −0.0001 | 0.0027 | −0.0052 | −0.0051 | −0.0097 | −0.0094 | −0.0098 | 0.6201 | 0.6327 | 0.6391 | 0.6363 | 0.6383 |
| 0.8 | −0.0015 | −0.0022 | −0.0058 | 0.0077 | −0.0078 | 0.0072 | 0.0066 | 0.0065 | 0.0017 | 0.0017 | 1.7530 | 1.7635 | 1.7964 | 1.8182 | 1.8423 |
| Rho-SAR-Poisson 1stStep-ML—W1 | Rho-SAR-Poisson 1stStep-OLS—W1 | ||||||||||||||
| Rho/n | 100 | 250 | 500 | 750 | 1000 | 100 | 250 | 500 | 750 | 1000 | |||||
| 0.0 | 0.0042 | 0.0015 | 0.0005 | −0.0012 | −0.0008 | 0.0037 | 0.0018 | −0.0003 | 0.0018 | 0.0014 | |||||
| 0.2 | 0.0012 | −0.0025 | 0.0006 | −0.0003 | 0.0003 | 0.0079 | 0.0105 | 0.0149 | 0.0131 | 0.0119 | |||||
| 0.4 | −0.0036 | −0.0014 | −0.0012 | −0.0023 | −0.0027 | 0.0169 | 0.0234 | 0.0246 | 0.0247 | 0.0249 | |||||
| 0.6 | −0.0002 | −0.0004 | −0.0018 | −0.0016 | −0.0010 | 0.0160 | 0.0181 | 0.0204 | 0.0208 | 0.0209 | |||||
| 0.8 | 0.0047 | 0.0039 | 0.0048 | 0.0050 | 0.0050 | 0.0018 | 0.0034 | 0.0042 | 0.0061 | 0.0082 | |||||
| β1-SAR-Poisson 1stStep-ML—W1 | β1-SAR-Poisson 1stStep-OLS—W1 | β1-Aspatial Poisson ML—W1 | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Rho/n | 100 | 250 | 500 | 750 | 1000 | 100 | 250 | 500 | 750 | 1000 | 100 | 250 | 500 | 750 | 1000 |
| 0.0 | 0.0242 | 0.0154 | 0.0102 | 0.0083 | 0.0069 | 0.0270 | 0.0163 | 0.0117 | 0.0090 | 0.0077 | 0.0171 | 0.0174 | 0.0122 | 0.0099 | 0.0084 |
| 0.2 | 0.0251 | 0.0152 | 0.0107 | 0.0087 | 0.0071 | 0.0271 | 0.0165 | 0.0119 | 0.0092 | 0.0083 | 0.0424 | 0.0353 | 0.0330 | 0.0321 | 0.0316 |
| 0.4 | 0.0223 | 0.0137 | 0.0102 | 0.0077 | 0.0070 | 0.0228 | 0.0141 | 0.0106 | 0.0089 | 0.0080 | 0.0946 | 0.0893 | 0.0885 | 0.0880 | 0.0877 |
| 0.6 | 0.0176 | 0.0106 | 0.0080 | 0.0065 | 0.0061 | 0.0181 | 0.0113 | 0.0079 | 0.0065 | 0.0056 | 0.2122 | 0.2027 | 0.2017 | 0.1989 | 0.1987 |
| 0.8 | 0.0161 | 0.0134 | 0.0124 | 0.0113 | 0.0106 | 0.0174 | 0.0155 | 0.0123 | 0.0120 | 0.0118 | 0.5380 | 0.5063 | 0.5029 | 0.4887 | 0.4954 |
| β2-SAR-Poisson 1stStep-ML—W1 | β2-SAR-Poisson 1stStep-OLS—W1 | β2-Aspatial Poisson ML—W1 | |||||||||||||
| Rho/n | 100 | 250 | 500 | 750 | 1000 | 100 | 250 | 500 | 750 | 1000 | 100 | 250 | 500 | 750 | 1000 |
| 0.0 | 0.1034 | 0.0649 | 0.0454 | 0.0357 | 0.0314 | 0.1085 | 0.0648 | 0.0495 | 0.0382 | 0.0330 | 0.0716 | 0.0752 | 0.0564 | 0.0449 | 0.0382 |
| 0.2 | 0.0912 | 0.0567 | 0.0401 | 0.0333 | 0.0287 | 0.0999 | 0.0631 | 0.0437 | 0.0357 | 0.0316 | 0.1588 | 0.1263 | 0.1132 | 0.1089 | 0.1089 |
| 0.4 | 0.0811 | 0.0486 | 0.0353 | 0.0300 | 0.0261 | 0.0849 | 0.0531 | 0.0411 | 0.0354 | 0.0309 | 0.2967 | 0.2854 | 0.2800 | 0.2819 | 0.2821 |
| 0.6 | 0.0606 | 0.0395 | 0.0305 | 0.0277 | 0.0238 | 0.0643 | 0.0403 | 0.0292 | 0.0242 | 0.0215 | 0.6483 | 0.6454 | 0.6465 | 0.6423 | 0.6432 |
| 0.8 | 0.0602 | 0.0548 | 0.0558 | 0.0502 | 0.0476 | 0.0589 | 0.0487 | 0.0427 | 0.0404 | 0.0428 | 1.9053 | 1.8426 | 1.8515 | 1.8604 | 1.8784 |
| Rho-SAR-Poisson 1stStep-ML—W1 | Rho-SAR-Poisson 1stStep-OLS—W1 | ||||||||||||||
| Rho/n | 100 | 250 | 500 | 750 | 1000 | 100 | 250 | 500 | 750 | 1000 | |||||
| 0.0 | 0.1112 | 0.0676 | 0.0474 | 0.0383 | 0.0320 | 0.1191 | 0.0734 | 0.0532 | 0.0398 | 0.0357 | |||||
| 0.2 | 0.0792 | 0.0483 | 0.0330 | 0.0276 | 0.0239 | 0.0873 | 0.0542 | 0.0395 | 0.0318 | 0.0279 | |||||
| 0.4 | 0.0512 | 0.0289 | 0.0214 | 0.0173 | 0.0149 | 0.0560 | 0.0390 | 0.0332 | 0.0307 | 0.0294 | |||||
| 0.6 | 0.0237 | 0.0148 | 0.0122 | 0.0110 | 0.0097 | 0.0311 | 0.0244 | 0.0237 | 0.0230 | 0.0224 | |||||
| 0.8 | 0.0142 | 0.0118 | 0.0106 | 0.0097 | 0.0094 | 0.0152 | 0.0146 | 0.0131 | 0.0137 | 0.0162 | |||||
| β1-SAR-Poisson 1stStep-ML—W2 | β1-SAR-Poisson 1stStep-OLS—W2 | β1-Aspatial Poisson ML—W2 | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Rho/n | 100 | 250 | 500 | 750 | 1000 | 100 | 250 | 500 | 750 | 1000 | 100 | 250 | 500 | 750 | 1000 |
| 0.0 | −0.0006 | −0.0010 | 0.0001 | −0.0001 | 0.0003 | −0.0001 | −0.0010 | 0.0001 | −0.0002 | 0.0002 | −0.0008 | −0.0004 | 0.0001 | 0.0000 | 0.0001 |
| 0.2 | −0.0017 | −0.0002 | −0.0001 | −0.0005 | −0.0004 | −0.0019 | −0.0007 | −0.0004 | −0.0006 | −0.0005 | 0.0290 | 0.0291 | 0.0285 | 0.0285 | 0.0286 |
| 0.4 | 0.0003 | 0.0002 | −0.0006 | 0.0003 | −0.0002 | −0.0007 | −0.0002 | −0.0008 | 0.0001 | −0.0003 | 0.0769 | 0.0761 | 0.0754 | 0.0750 | 0.0740 |
| 0.6 | 0.0012 | −0.0005 | −0.0003 | 0.0001 | −0.0003 | 0.0008 | −0.0004 | −0.0002 | 0.0002 | −0.0001 | 0.1711 | 0.1662 | 0.1609 | 0.1609 | 0.1592 |
| 0.8 | 0.0025 | −0.0015 | −0.0016 | −0.0017 | −0.0015 | 0.0003 | 0.0002 | 0.0000 | 0.0000 | 0.0001 | 0.4010 | 0.3873 | 0.3743 | 0.3630 | 0.3577 |
| β2-SAR-Poisson 1stStep-ML—W2 | β2-SAR-Poisson 1stStep-OLS—W2 | β2- Aspatial Poisson ML—W2 | |||||||||||||
| Rho/n | 100 | 250 | 500 | 750 | 1000 | 100 | 250 | 500 | 750 | 1000 | 100 | 250 | 500 | 750 | 1000 |
| 0.0 | −0.0012 | 0.0010 | −0.0027 | 0.0005 | −0.0004 | −0.0005 | 0.0010 | −0.0029 | −0.0009 | −0.0005 | −0.0785 | −0.0014 | −0.0011 | 0.0004 | −0.0005 |
| 0.2 | −0.0038 | −0.0021 | −0.0011 | −0.0003 | 0.0001 | −0.0058 | −0.0035 | −0.0019 | −0.0003 | −0.0003 | −0.0520 | 0.0991 | 0.0998 | 0.1022 | 0.1009 |
| 0.4 | 0.0031 | 0.0020 | −0.0003 | −0.0003 | 0.0008 | −0.0006 | −0.0002 | −0.0012 | −0.0003 | 0.0002 | −0.0219 | 0.2671 | 0.2663 | 0.2682 | 0.2670 |
| 0.6 | 0.0045 | 0.0018 | 0.0013 | −0.0007 | 0.0005 | −0.0007 | 0.0010 | 0.0015 | 0.0009 | 0.0008 | 0.0143 | 0.5905 | 0.6000 | 0.6034 | 0.6027 |
| 0.8 | 0.0397 | 0.0172 | 0.0109 | −0.0069 | 0.0081 | 0.0015 | 0.0006 | −0.0001 | 0.0000 | 0.0004 | 0.0364 | 1.6308 | 1.6558 | 1.6638 | 1.6922 |
| Rho-SAR-Poisson 1stStep-ML—W2 | Rho-SAR-Poisson 1stStep-OLS—W2 | ||||||||||||||
| Rho/n | 100 | 250 | 500 | 750 | 1000 | 100 | 250 | 500 | 750 | 1000 | |||||
| 0.0 | −0.0152 | −0.0020 | 0.0001 | −0.0010 | −0.0017 | −0.0082 | 0.0007 | 0.0018 | 0.0010 | −0.0006 | |||||
| 0.2 | −0.0033 | 0.0006 | 0.0007 | 0.0009 | 0.0015 | −0.0122 | −0.0108 | −0.0115 | −0.0121 | −0.0119 | |||||
| 0.4 | −0.0038 | −0.0009 | 0.0024 | 0.0002 | 0.0007 | −0.0064 | −0.0030 | 0.0000 | −0.0026 | −0.0016 | |||||
| 0.6 | 0.0124 | 0.0072 | 0.0040 | 0.0021 | 0.0026 | 0.0126 | 0.0144 | 0.0152 | 0.0152 | 0.0154 | |||||
| 0.8 | 0.0501 | 0.0341 | 0.0236 | 0.0166 | 0.0143 | 0.0047 | 0.0044 | 0.0045 | 0.0045 | 0.0043 | |||||
| β1-SAR-Poisson 1stStep-ML—W2 | β1-SAR-Poisson 1stStep-OLS—W2 | β1-Aspatial Poisson ML—W2 | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Rho/n | 100 | 250 | 500 | 750 | 1000 | 100 | 250 | 500 | 750 | 1000 | 100 | 250 | 500 | 750 | 1000 |
| 0.0 | 0.0387 | 0.0232 | 0.0165 | 0.0142 | 0.0114 | 0.0402 | 0.0236 | 0.0167 | 0.0143 | 0.0114 | 0.0276 | 0.0178 | 0.0120 | 0.0095 | 0.0082 |
| 0.2 | 0.0363 | 0.0207 | 0.0151 | 0.0121 | 0.0110 | 0.0360 | 0.0207 | 0.0151 | 0.0121 | 0.0110 | 0.0386 | 0.0327 | 0.0300 | 0.0296 | 0.0294 |
| 0.4 | 0.0304 | 0.0187 | 0.0136 | 0.0103 | 0.0088 | 0.0300 | 0.0186 | 0.0136 | 0.0103 | 0.0088 | 0.0820 | 0.0781 | 0.0763 | 0.0757 | 0.0745 |
| 0.6 | 0.0241 | 0.0134 | 0.0093 | 0.0076 | 0.0066 | 0.0233 | 0.0134 | 0.0093 | 0.0076 | 0.0065 | 0.1784 | 0.1694 | 0.1625 | 0.1621 | 0.1603 |
| 0.8 | 0.0305 | 0.0156 | 0.0123 | 0.0102 | 0.0092 | 0.0100 | 0.0056 | 0.0038 | 0.0031 | 0.0026 | 0.4256 | 0.4019 | 0.3816 | 0.3692 | 0.3626 |
| β2-SAR-Poisson 1stStep-ML—W2 | β2-SAR-Poisson 1stStep-OLS—W2 | β2-Aspatial Poisson ML—W2 | |||||||||||||
| Rho/n | 100 | 250 | 500 | 750 | 1000 | 100 | 250 | 500 | 750 | 1000 | 100 | 250 | 500 | 750 | 1000 |
| 0.0 | 0.1487 | 0.0914 | 0.0669 | 0.0541 | 0.0488 | 0.1520 | 0.0924 | 0.0674 | 0.0543 | 0.0489 | 0.1224 | 0.0797 | 0.0551 | 0.0436 | 0.0394 |
| 0.2 | 0.1368 | 0.0843 | 0.0624 | 0.0495 | 0.0421 | 0.1376 | 0.0845 | 0.0625 | 0.0496 | 0.0422 | 0.1512 | 0.1238 | 0.1109 | 0.1095 | 0.1075 |
| 0.4 | 0.1182 | 0.0758 | 0.0515 | 0.0412 | 0.0362 | 0.1186 | 0.0761 | 0.0515 | 0.0411 | 0.0361 | 0.2866 | 0.2732 | 0.2714 | 0.2691 | 0.2709 |
| 0.6 | 0.0902 | 0.0527 | 0.0387 | 0.0302 | 0.0274 | 0.0894 | 0.0529 | 0.0385 | 0.0300 | 0.0273 | 0.6054 | 0.6064 | 0.6061 | 0.6050 | 0.6043 |
| 0.8 | 0.1310 | 0.0613 | 0.0402 | 0.0270 | 0.0277 | 0.0376 | 0.0216 | 0.0156 | 0.0126 | 0.0105 | 1.6870 | 1.6898 | 1.6781 | 1.7039 | 1.7125 |
| Rho-SAR-Poisson 1stStep-ML—W2 | Rho-SAR-Poisson 1stStep-OLS—W2 | ||||||||||||||
| Rho/n | 100 | 250 | 500 | 750 | 1000 | 100 | 250 | 500 | 750 | 1000 | |||||
| 0.0 | 0.2196 | 0.1283 | 0.0934 | 0.0803 | 0.0687 | −0.0082 | 0.0007 | 0.0018 | 0.0010 | −0.0006 | |||||
| 0.2 | 0.1419 | 0.0860 | 0.0636 | 0.0484 | 0.0420 | −0.0122 | −0.0108 | −0.0115 | −0.0121 | −0.0119 | |||||
| 0.4 | 0.0814 | 0.0513 | 0.0360 | 0.0287 | 0.0245 | −0.0064 | −0.0030 | 0.0000 | −0.0026 | −0.0016 | |||||
| 0.6 | 0.0571 | 0.0377 | 0.0264 | 0.0187 | 0.0157 | 0.0126 | 0.0144 | 0.0152 | 0.0152 | 0.0154 | |||||
| 0.8 | 0.0840 | 0.0493 | 0.0290 | 0.0276 | 0.0245 | 0.0047 | 0.0044 | 0.0045 | 0.0045 | 0.0043 | |||||
| β1-SAR-Poisson 1stStep-ML—W3 | β1-SAR-Poisson 1stStep-OLS—W3 | β1-Aspatial Poisson ML—W3 | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Rho/n | 100 | 250 | 500 | 750 | 1000 | 100 | 250 | 500 | 750 | 1000 | 100 | 250 | 500 | 750 | 1000 |
| 0.0 | −0.0013 | −0.0009 | −0.0006 | 0.0000 | 0.0000 | −0.0015 | −0.0004 | −0.0002 | −0.0007 | 0.0002 | −0.0008 | −0.0004 | −0.0004 | 0.0000 | 0.0001 |
| 0.2 | −0.0002 | −0.0003 | 0.0001 | −0.0003 | 0.0002 | −0.0068 | −0.0057 | −0.0049 | −0.0051 | −0.0049 | 0.0334 | 0.0320 | 0.0328 | 0.0327 | 0.0327 |
| 0.4 | 0.0018 | 0.0031 | 0.0030 | 0.0033 | 0.0031 | −0.0074 | −0.0067 | −0.0061 | −0.0066 | −0.0059 | 0.0945 | 0.0955 | 0.0961 | 0.0950 | 0.0954 |
| 0.6 | 0.0053 | 0.0055 | 0.0049 | 0.0045 | 0.0076 | −0.0043 | −0.0036 | −0.0040 | −0.0047 | −0.0041 | 0.2162 | 0.2243 | 0.2249 | 0.2249 | 0.2227 |
| 0.8 | 0.0333 | 0.0256 | 0.0271 | 0.0269 | 0.0258 | 0.0024 | 0.0008 | 0.0008 | −0.0021 | −0.0002 | 0.5565 | 0.5744 | 0.5710 | 0.5781 | 0.5701 |
| β2-SAR-Poisson 1stStep-ML—W3 | β2-SAR-Poisson 1stStep-OLS—W3 | β2-Aspatial Poisson ML—W3 | |||||||||||||
| Rho/n | 100 | 250 | 500 | 750 | 1000 | 100 | 250 | 500 | 750 | 1000 | 100 | 250 | 500 | 750 | 1000 |
| 0.0 | −0.0016 | −0.0020 | 0.0028 | −0.0006 | 0.0001 | −0.0069 | −0.0032 | −0.0038 | −0.0011 | −0.0013 | −0.0014 | −0.0011 | 0.0034 | −0.0005 | 0.0000 |
| 0.2 | 0.0020 | 0.0014 | 0.0053 | 0.0043 | 0.0041 | −0.0173 | −0.0166 | −0.0191 | −0.0190 | −0.0184 | 0.1017 | 0.1032 | 0.1052 | 0.1047 | 0.1046 |
| 0.4 | 0.0175 | 0.0206 | 0.0198 | 0.0221 | 0.0212 | −0.0227 | −0.0236 | −0.0241 | −0.0259 | −0.0267 | 0.2822 | 0.2859 | 0.2864 | 0.2869 | 0.2874 |
| 0.6 | 0.0382 | 0.0308 | 0.0296 | 0.0263 | 0.0248 | −0.0144 | −0.0147 | −0.0169 | −0.0191 | −0.0196 | 0.6469 | 0.6572 | 0.6612 | 0.6640 | 0.6653 |
| 0.8 | 0.0978 | 0.0919 | 0.0982 | 0.0490 | 0.0311 | 0.0067 | 0.0086 | −0.0031 | −0.0136 | −0.0153 | 1.8195 | 1.9117 | 1.9474 | 1.9597 | 1.9623 |
| Rho-SAR-Poisson 1stStep-ML—W3 | Rho-SAR-Poisson 1stStep-OLS—W3 | ||||||||||||||
| Rho/n | 100 | 250 | 500 | 750 | 1000 | 100 | 250 | 500 | 750 | 1000 | |||||
| 0.0 | 0.0006 | 0.0000 | 0.0002 | −0.0013 | −0.0002 | 0.0043 | 0.0006 | 0.0018 | 0.0015 | −0.0005 | |||||
| 0.2 | −0.0008 | 0.0015 | −0.0006 | 0.0007 | 0.0002 | 0.0193 | 0.0199 | 0.0215 | 0.0227 | 0.0219 | |||||
| 0.4 | −0.0050 | −0.0086 | −0.0081 | −0.0088 | −0.0090 | 0.0303 | 0.0329 | 0.0336 | 0.0358 | 0.0346 | |||||
| 0.6 | 0.0002 | −0.0041 | −0.0048 | −0.0059 | −0.0114 | 0.0236 | 0.0247 | 0.0275 | 0.0296 | 0.0288 | |||||
| 0.8 | 0.0118 | 0.0060 | 0.0003 | −0.0034 | −0.0015 | 0.0114 | 0.0112 | 0.0158 | 0.0239 | 0.0231 | |||||
| β1-SAR-Poisson 1stStep-ML—W3 | β1-SAR-Poisson 1stStep-OLS—W3 | β1-Aspatial Poisson ML—W3 | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Rho/n | 100 | 250 | 500 | 750 | 1000 | 100 | 250 | 500 | 750 | 1000 | 100 | 250 | 500 | 750 | 1000 |
| 0.0 | 0.0315 | 0.0198 | 0.0134 | 0.0109 | 0.0090 | 0.0358 | 0.0212 | 0.0148 | 0.0119 | 0.0100 | 0.0276 | 0.0178 | 0.0119 | 0.0095 | 0.0082 |
| 0.2 | 0.0326 | 0.0198 | 0.0133 | 0.0117 | 0.0099 | 0.0356 | 0.0212 | 0.0147 | 0.0118 | 0.0109 | 0.0427 | 0.0367 | 0.0345 | 0.0339 | 0.0336 |
| 0.4 | 0.0316 | 0.0197 | 0.0139 | 0.0118 | 0.0107 | 0.0324 | 0.0199 | 0.0144 | 0.0119 | 0.0106 | 0.1015 | 0.0983 | 0.0976 | 0.0959 | 0.0962 |
| 0.6 | 0.0271 | 0.0174 | 0.0125 | 0.0103 | 0.0134 | 0.0266 | 0.0160 | 0.0119 | 0.0104 | 0.0087 | 0.2288 | 0.2300 | 0.2284 | 0.2275 | 0.2246 |
| 0.8 | 0.0655 | 0.0502 | 0.0472 | 0.0455 | 0.0439 | 0.0494 | 0.0361 | 0.0327 | 0.0344 | 0.0324 | 0.6065 | 0.6061 | 0.5963 | 0.5972 | 0.5870 |
| β2-SAR-Poisson 1stStep-ML—W3 | β2-SAR-Poisson 1stStep-OLS—W3 | β2-Aspatial Poisson ML—W3 | |||||||||||||
| Rho/n | 100 | 250 | 500 | 750 | 1000 | 100 | 250 | 500 | 750 | 1000 | 100 | 250 | 500 | 750 | 1000 |
| 0.0 | 0.1356 | 0.0855 | 0.0592 | 0.0474 | 0.0413 | 0.1408 | 0.0865 | 0.0648 | 0.0509 | 0.0433 | 0.1224 | 0.0797 | 0.0540 | 0.0436 | 0.0394 |
| 0.2 | 0.1226 | 0.0759 | 0.0525 | 0.0437 | 0.0398 | 0.1295 | 0.0801 | 0.0573 | 0.0458 | 0.0423 | 0.1544 | 0.1242 | 0.1146 | 0.1126 | 0.1109 |
| 0.4 | 0.1143 | 0.0788 | 0.0645 | 0.0619 | 0.0558 | 0.1152 | 0.0718 | 0.0521 | 0.0456 | 0.0425 | 0.3083 | 0.2969 | 0.2915 | 0.2902 | 0.2899 |
| 0.6 | 0.1184 | 0.0851 | 0.0721 | 0.0582 | 0.0311 | 0.0898 | 0.0571 | 0.0394 | 0.0360 | 0.0341 | 0.6891 | 0.6764 | 0.6717 | 0.6715 | 0.6705 |
| 0.8 | 0.2134 | 0.1867 | 0.1864 | 0.1999 | 0.1949 | 0.1701 | 0.1297 | 0.1155 | 0.1217 | 0.1164 | 2.0317 | 2.0655 | 2.1007 | 2.0681 | 2.0419 |
| Rho-SAR-Poisson 1stStep-ML—W3 | Rho-SAR-Poisson 1stStep-OLS—W3 | ||||||||||||||
| Rho/n | 100 | 250 | 500 | 750 | 1000 | 100 | 250 | 500 | 750 | 1000 | |||||
| 0.0 | 0.1272 | 0.0784 | 0.0547 | 0.0436 | 0.0368 | 0.1414 | 0.0885 | 0.0621 | 0.0478 | 0.0441 | |||||
| 0.2 | 0.0983 | 0.0554 | 0.0380 | 0.0320 | 0.0274 | 0.1116 | 0.0647 | 0.0482 | 0.0400 | 0.0368 | |||||
| 0.4 | 0.0641 | 0.0377 | 0.0294 | 0.0268 | 0.0244 | 0.0717 | 0.0501 | 0.0419 | 0.0404 | 0.0382 | |||||
| 0.6 | 0.0440 | 0.0308 | 0.0254 | 0.0203 | 0.0248 | 0.0422 | 0.0324 | 0.0308 | 0.0322 | 0.0307 | |||||
| 0.8 | 0.0774 | 0.0542 | 0.0431 | 0.0417 | 0.0416 | 0.0429 | 0.036563 | 0.0342 | 0.0400 | 0.0387 | |||||
| β1-SAR-Poisson 1stStep-ML—W1 | β1-SAR-Poisson 1stStep-OLS—W1 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Rho/n | 100 | 250 | 500 | 750 | 1000 | 100 | 250 | 500 | 750 | 1000 |
| 0.0 | −0.0123 | −0.0068 | −0.0035 | −0.0022 | −0.0031 | −0.0077 | −0.0056 | −0.0062 | −0.0018 | −0.0028 |
| 0.2 | −0.0024 | −0.0021 | 0.0001 | 0.0003 | 0.0008 | 0.0044 | 0.0032 | 0.0056 | 0.0066 | 0.0068 |
| 0.4 | −0.0024 | −0.0016 | −0.0009 | −0.0004 | 0.0004 | 0.0077 | 0.0086 | 0.0102 | 0.0104 | 0.0113 |
| 0.6 | −0.0029 | −0.0009 | −0.0033 | −0.0019 | −0.0008 | 0.0086 | 0.0121 | 0.0107 | 0.0126 | 0.0136 |
| 0.8 | −0.0093 | −0.0164 | −0.0191 | −0.0220 | −0.0226 | 0.0097 | 0.0089 | 0.0100 | 0.0107 | 0.0097 |
| β2-SAR-Poisson 1stStep-ML—W1 | β2-SAR-Poisson 1stStep-OLS—W1 | |||||||||
| Rho/n | 100 | 250 | 500 | 750 | 1000 | 100 | 250 | 500 | 750 | 1000 |
| 0.0 | −0.0205 | −0.0086 | −0.0054 | −0.0020 | −0.0030 | −0.0187 | −0.0094 | −0.0031 | −0.0021 | −0.0038 |
| 0.2 | −0.0123 | −0.0024 | −0.0039 | −0.0028 | −0.0011 | −0.0364 | −0.0302 | −0.0326 | −0.0303 | −0.0289 |
| 0.4 | −0.0073 | 0.0012 | −0.0009 | 0.0018 | 0.0017 | −0.0583 | −0.0553 | −0.0573 | −0.0554 | −0.0564 |
| 0.6 | 0.0036 | 0.0033 | −0.0014 | 0.0022 | 0.0021 | −0.0694 | −0.0757 | −0.0789 | −0.0795 | −0.0788 |
| 0.8 | 0.0013 | 0.0045 | 0.0016 | −0.0018 | 0.0001 | −0.0532 | −0.0631 | −0.0686 | −0.0789 | −0.0778 |
| Rho-SAR-Poisson 1stStep-ML—W1 | Rho-SAR-Poisson 1stStep-OLS—W1 | |||||||||
| Rho/n | 100 | 250 | 500 | 750 | 1000 | 100 | 250 | 500 | 750 | 1000 |
| 0.0 | 0.0264 | 0.0079 | 0.0035 | 0.0021 | 0.0045 | 0.0206 | 0.0124 | 0.0071 | 0.0029 | 0.0063 |
| 0.2 | −0.0012 | −0.0032 | 0.0034 | 0.0028 | 0.0001 | −0.0056 | 0.0035 | 0.0094 | 0.0066 | 0.0051 |
| 0.4 | 0.0073 | 0.0052 | 0.0075 | 0.0062 | 0.0050 | 0.0204 | 0.0365 | 0.0419 | 0.0428 | 0.0435 |
| 0.6 | 0.0173 | 0.0088 | 0.0106 | 0.0081 | 0.0060 | 0.0586 | 0.0807 | 0.0868 | 0.0893 | 0.0895 |
| 0.8 | 0.0400 | 0.0306 | 0.0323 | 0.0329 | 0.0314 | 0.0555 | 0.0766 | 0.0837 | 0.0926 | 0.0920 |
| β1-SAR-Poisson 1stStep-ML—W1 | β1-SAR-Poisson 1stStep-OLS—W1 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Rho/n | 100 | 250 | 500 | 750 | 1000 | 100 | 250 | 500 | 750 | 1000 |
| 0.0 | 0.1142 | 0.0703 | 0.0477 | 0.0399 | 0.0359 | 0.1140 | 0.0702 | 0.0472 | 0.0395 | 0.0353 |
| 0.2 | 0.1068 | 0.0700 | 0.0477 | 0.0404 | 0.0348 | 0.1043 | 0.0663 | 0.0462 | 0.0391 | 0.0340 |
| 0.4 | 0.1103 | 0.0666 | 0.0462 | 0.0394 | 0.0325 | 0.1051 | 0.0636 | 0.0996 | 0.0824 | 0.0324 |
| 0.6 | 0.0950 | 0.0604 | 0.0408 | 0.0326 | 0.0302 | 0.0910 | 0.0586 | 0.0396 | 0.0333 | 0.0320 |
| 0.8 | 0.0763 | 0.0487 | 0.0408 | 0.0385 | 0.0373 | 0.0707 | 0.0462 | 0.0332 | 0.0291 | 0.0263 |
| β2-SAR-Poisson 1stStep-ML—W1 | β2-SAR-Poisson 1stStep-OLS—W1 | |||||||||
| Rho/n | 100 | 250 | 500 | 750 | 1000 | 100 | 250 | 500 | 750 | 1000 |
| 0.0 | 0.1740 | 0.1077 | 0.0767 | 0.0637 | 0.0536 | 0.2156 | 0.1323 | 0.0948 | 0.0771 | 0.0659 |
| 0.2 | 0.1635 | 0.1042 | 0.0727 | 0.0617 | 0.0520 | 0.2057 | 0.1274 | 0.0920 | 0.0794 | 0.0681 |
| 0.4 | 0.1638 | 0.1003 | 0.0720 | 0.0573 | 0.0498 | 0.2003 | 0.1274 | 0.0449 | 0.0385 | 0.0769 |
| 0.6 | 0.1548 | 0.0956 | 0.0695 | 0.0586 | 0.0476 | 0.1822 | 0.1257 | 0.1042 | 0.0958 | 0.0892 |
| 0.8 | 0.1548 | 0.1073 | 0.1017 | 0.0969 | 0.0900 | 0.1582 | 0.1117 | 0.0959 | 0.0962 | 0.0900 |
| Rho-SAR-Poisson 1stStep-ML—W1 | Rho-SAR-Poisson 1stStep-OLS—W1 | |||||||||
| Rho/n | 100 | 250 | 500 | 750 | 1000 | 100 | 250 | 500 | 750 | 1000 |
| 0.0 | 0.3733 | 0.2327 | 0.1647 | 0.1259 | 0.1109 | 0.4042 | 0.2554 | 0.1768 | 0.1393 | 0.1236 |
| 0.2 | 0.2934 | 0.1744 | 0.1175 | 0.1017 | 0.0818 | 0.3358 | 0.1986 | 0.1342 | 0.1173 | 0.0986 |
| 0.4 | 0.2205 | 0.1202 | 0.0830 | 0.0675 | 0.0575 | 0.2615 | 0.1477 | 0.1102 | 0.0904 | 0.0795 |
| 0.6 | 0.1368 | 0.0733 | 0.0510 | 0.0423 | 0.0357 | 0.1610 | 0.1142 | 0.0999 | 0.0968 | 0.0948 |
| 0.8 | 0.0873 | 0.0517 | 0.0451 | 0.0443 | 0.0417 | 0.1109 | 0.0927 | 0.0926 | 0.0998 | 0.0974 |
| β1-SAR-Poisson 1stStep-ML—W2 | β1-SAR-Poisson 1stStep-OLS—W2 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Rho/n | 100 | 250 | 500 | 750 | 1000 | 100 | 250 | 500 | 750 | 1000 |
| 0.0 | −0.0123 | −0.0024 | −0.0026 | −0.0002 | −0.0015 | −0.0064 | −0.0010 | −0.0022 | 0.0016 | −0.0013 |
| 0.2 | −0.0040 | −0.0032 | 0.0005 | −0.0001 | 0.0007 | −0.0016 | −0.0023 | −0.0043 | 0.0002 | 0.0008 |
| 0.4 | −0.0042 | 0.0027 | −0.0006 | −0.0008 | 0.0006 | −0.0033 | 0.0034 | −0.0002 | −0.0006 | 0.0008 |
| 0.6 | −0.0016 | 0.0016 | 0.0002 | 0.0009 | 0.0005 | −0.0014 | 0.0020 | 0.0003 | 0.0009 | 0.0005 |
| 0.8 | 0.0001 | 0.0049 | 0.0029 | 0.0013 | 0.0005 | −0.0007 | 0.0012 | 0.0013 | −0.0005 | −0.0007 |
| β2-SAR-Poisson 1stStep-ML—W2 | β2-SAR-Poisson 1stStep-OLS—W2 | |||||||||
| Rho/n | 100 | 250 | 500 | 750 | 1000 | 100 | 250 | 500 | 750 | 1000 |
| 0.0 | −0.0205 | −0.0105 | −0.0039 | −0.0002 | −0.0039 | −0.0101 | −0.0040 | −0.0026 | 0.0002 | −0.0034 |
| 0.2 | −0.0122 | −0.0033 | −0.0042 | 0.0030 | −0.0031 | −0.0088 | −0.0045 | 0.0009 | 0.0025 | −0.0038 |
| 0.4 | −0.0128 | −0.0010 | −0.0044 | 0.0011 | −0.0026 | −0.0116 | −0.0055 | −0.0058 | −0.0005 | −0.0036 |
| 0.6 | −0.0010 | −0.0026 | −0.0007 | −0.0009 | 0.0013 | −0.0064 | −0.0063 | −0.0018 | −0.0018 | 0.0004 |
| 0.8 | −0.0030 | −0.0034 | −0.0002 | −0.0011 | −0.0009 | −0.0024 | −0.0001 | 0.0024 | 0.0014 | 0.0006 |
| Rho-SAR-Poisson 1stStep-ML—W2 | Rho-SAR-Poisson 1stStep-OLS—W2 | |||||||||
| Rho/n | 100 | 250 | 500 | 750 | 1000 | 100 | 250 | 500 | 750 | 1000 |
| 0.0 | 0.0264 | −0.0183 | −0.0201 | −0.0258 | −0.0070 | −0.0024 | −0.0045 | 0.0007 | −0.0084 | 0.0027 |
| 0.2 | 0.0155 | −0.0226 | −0.0082 | −0.0167 | −0.0048 | −0.0681 | −0.0597 | −0.0580 | −0.0656 | −0.0571 |
| 0.4 | 0.0100 | −0.0100 | 0.0002 | −0.0058 | 0.0005 | −0.0904 | −0.0728 | −0.0654 | −0.0701 | −0.0653 |
| 0.6 | 0.0071 | 0.0018 | 0.0012 | 0.0023 | −0.0018 | −0.0497 | −0.0225 | −0.0170 | −0.0142 | −0.0152 |
| 0.8 | 0.0150 | 0.0136 | 0.0056 | 0.0066 | 0.0044 | 0.0135 | 0.0472 | 0.0570 | 0.0597 | 0.0620 |
| β1-SAR-Poisson 1stStep-ML—W2 | β1-SAR-Poisson 1stStep-OLS—W2 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Rho/n | 100 | 250 | 500 | 750 | 1000 | 100 | 250 | 500 | 750 | 1000 |
| 0.0 | 0.1142 | 0.0709 | 0.0503 | 0.0418 | 0.0353 | 0.1117 | 0.0717 | 0.0504 | 0.0421 | 0.0354 |
| 0.2 | 0.1113 | 0.0656 | 0.0472 | 0.0395 | 0.0337 | 0.1116 | 0.0657 | 0.0473 | 0.0397 | 0.0337 |
| 0.4 | 0.1072 | 0.0668 | 0.0445 | 0.0393 | 0.0330 | 0.1063 | 0.0666 | 0.0444 | 0.0390 | 0.0330 |
| 0.6 | 0.0970 | 0.0594 | 0.0407 | 0.0345 | 0.0309 | 0.0964 | 0.0591 | 0.0406 | 0.0343 | 0.0308 |
| 0.8 | 0.0774 | 0.0457 | 0.0308 | 0.0242 | 0.0214 | 0.0770 | 0.0441 | 0.0306 | 0.0241 | 0.0213 |
| β2-SAR-Poisson 1stStep-ML—W2 | β2-SAR-Poisson 1stStep-OLS—W2 | |||||||||
| Rho/n | 100 | 250 | 500 | 750 | 1000 | 100 | 250 | 500 | 750 | 1000 |
| 0.0 | 0.1740 | 0.1337 | 0.0986 | 0.0834 | 0.0710 | 0.2279 | 0.1466 | 0.1007 | 0.0854 | 0.0723 |
| 0.2 | 0.2144 | 0.1343 | 0.0949 | 0.0797 | 0.0690 | 0.2264 | 0.1397 | 0.0962 | 0.0811 | 0.0698 |
| 0.4 | 0.2003 | 0.1293 | 0.0908 | 0.0753 | 0.0660 | 0.2143 | 0.1322 | 0.0915 | 0.0758 | 0.0661 |
| 0.6 | 0.1901 | 0.1190 | 0.0861 | 0.0670 | 0.0612 | 0.1950 | 0.1185 | 0.0854 | 0.0671 | 0.0612 |
| 0.8 | 0.1522 | 0.0970 | 0.0624 | 0.0518 | 0.0443 | 0.1542 | 0.0901 | 0.0621 | 0.0518 | 0.0442 |
| Rho-SAR-Poisson 1stStep-ML—W2 | Rho-SAR-Poisson 1stStep-OLS—W2 | |||||||||
| Rho/n | 100 | 250 | 500 | 750 | 1000 | 100 | 250 | 500 | 750 | 1000 |
| 0.0 | 0.3733 | 0.4956 | 0.3579 | 0.3020 | 0.2538 | 0.4872 | 0.3062 | 0.2027 | 0.1741 | 0.1505 |
| 0.2 | 0.3981 | 0.3621 | 0.2393 | 0.2000 | 0.1718 | 0.4180 | 0.2643 | 0.1808 | 0.1573 | 0.1370 |
| 0.4 | 0.4164 | 0.2356 | 0.1561 | 0.1264 | 0.1106 | 0.3929 | 0.2239 | 0.1568 | 0.1347 | 0.1222 |
| 0.6 | 0.3435 | 0.1368 | 0.0897 | 0.0667 | 0.0619 | 0.2933 | 0.1541 | 0.1102 | 0.0852 | 0.0786 |
| 0.8 | 0.1594 | 0.0571 | 0.0338 | 0.0294 | 0.0250 | 0.2220 | 0.0781 | 0.0662 | 0.0643 | 0.0650 |
Appendix B. Countries in the Sample
| Pat | R&D_B | R&D_G | R&D_U | Pers_B | Pers_G | Pers_U | Educ | Pop | GDP | Mort | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Pat | 1.000 | ||||||||||
| R&D_B | 0.717 | 1.000 | |||||||||
| R&D_G | 0.301 | 0.438 | 1.000 | ||||||||
| R&D_U | 0.390 | 0.533 | 0.510 | 1.000 | |||||||
| Pers_B | 0.474 | 0.601 | 0.332 | 0.211 | 1.000 | ||||||
| Pers_G | 0.153 | 0.215 | 0.591 | 0.117 | 0.622 | 1.000 | |||||
| Pers_U | 0.164 | 0.286 | 0.329 | 0.261 | 0.746 | 0.674 | 1.000 | ||||
| Educ | 0.263 | 0.450 | 0.408 | 0.440 | 0.296 | 0.253 | 0.355 | 1.000 | |||
| Pop | 0.056 | 0.082 | 0.119 | −0.088 | 0.663 | 0.651 | 0.775 | 0.010 | 1.000 | ||
| GDP | 0.573 | 0.639 | 0.519 | 0.642 | 0.368 | 0.148 | 0.226 | 0.559 | −0.043 | 1.000 | |
| Mort | −0.285 | −0.248 | −0.176 | −0.266 | −0.141 | −0.017 | −0.099 | −0.275 | 0.082 | −0.466 | 1.000 |

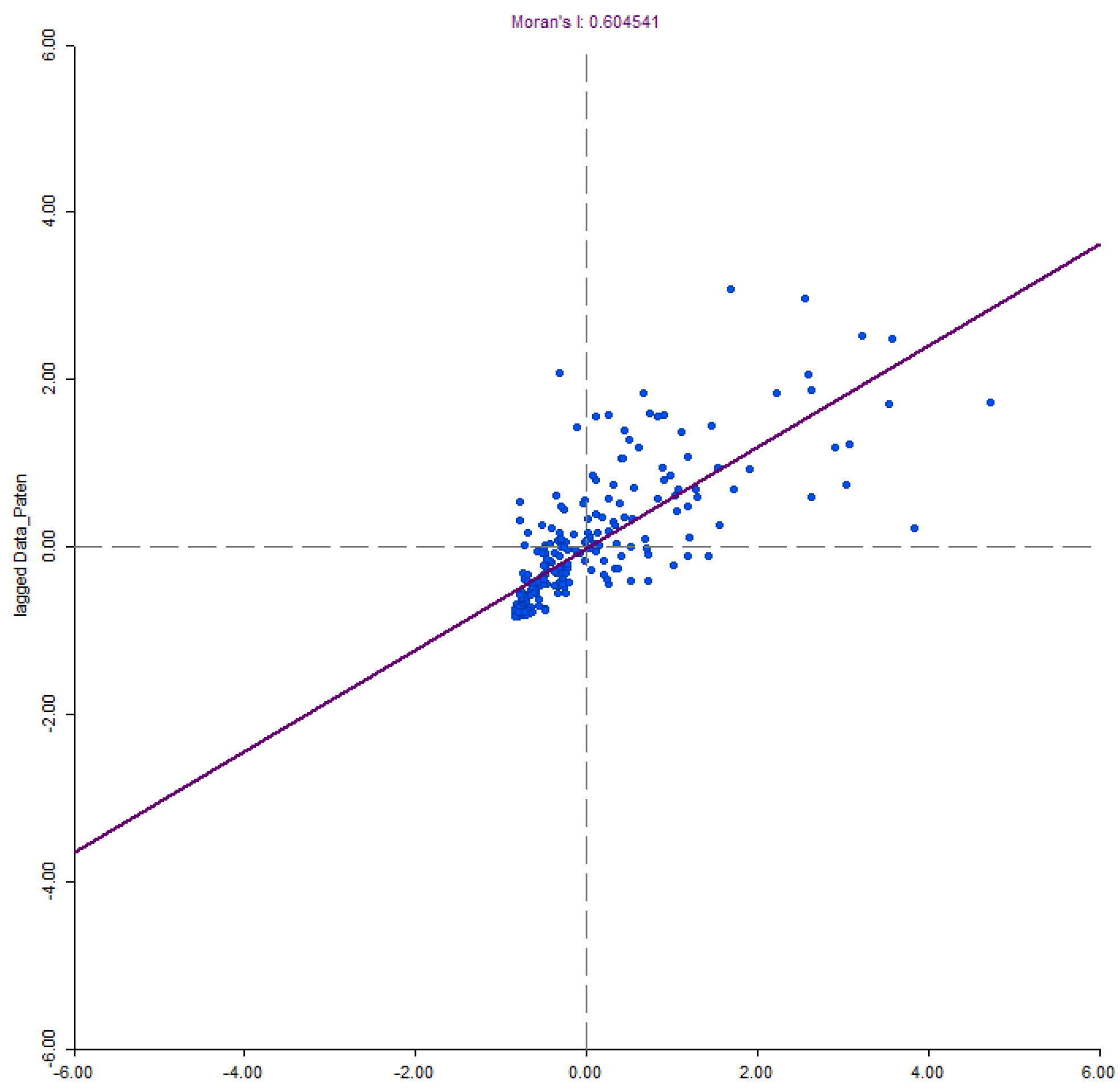
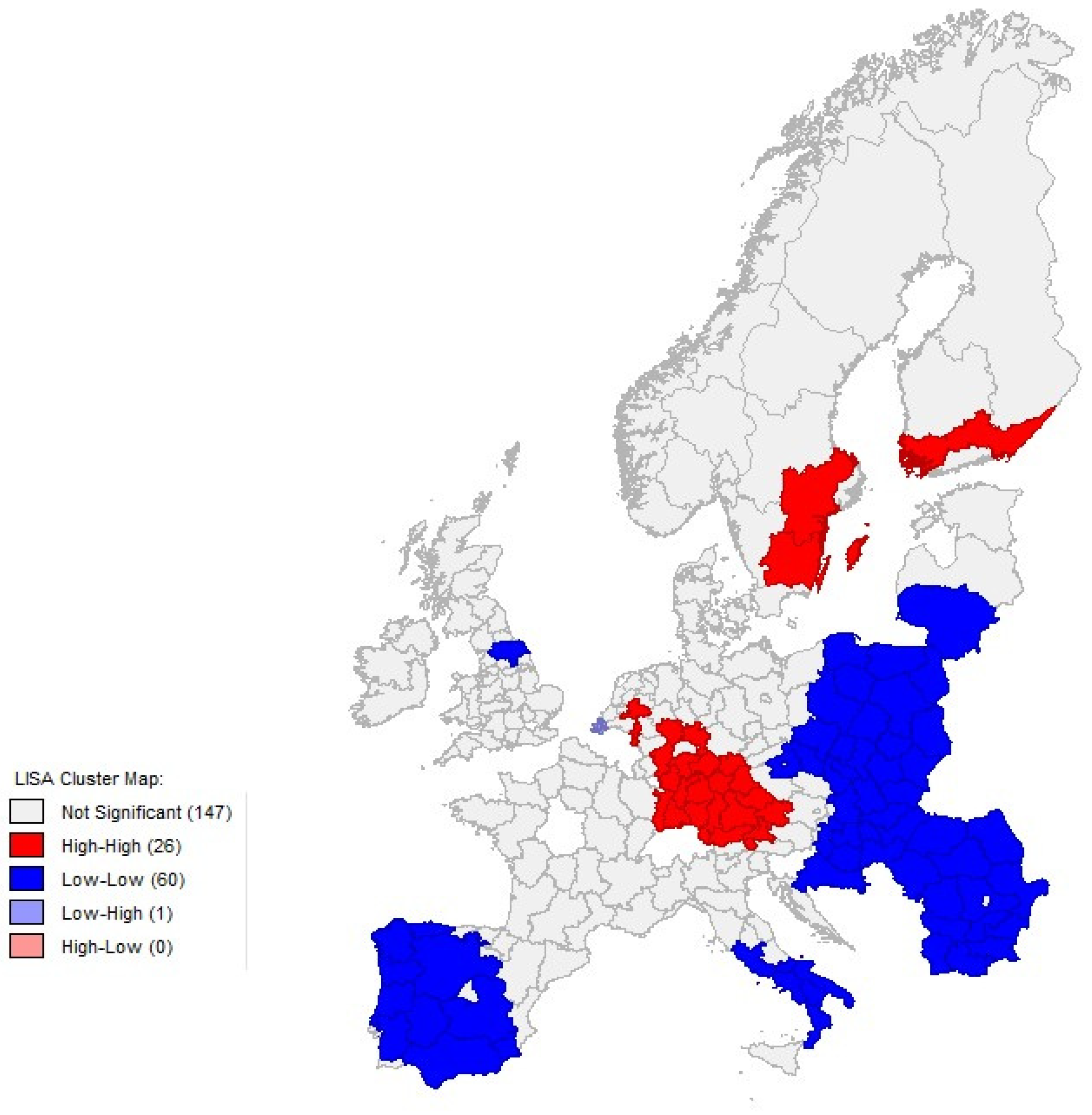
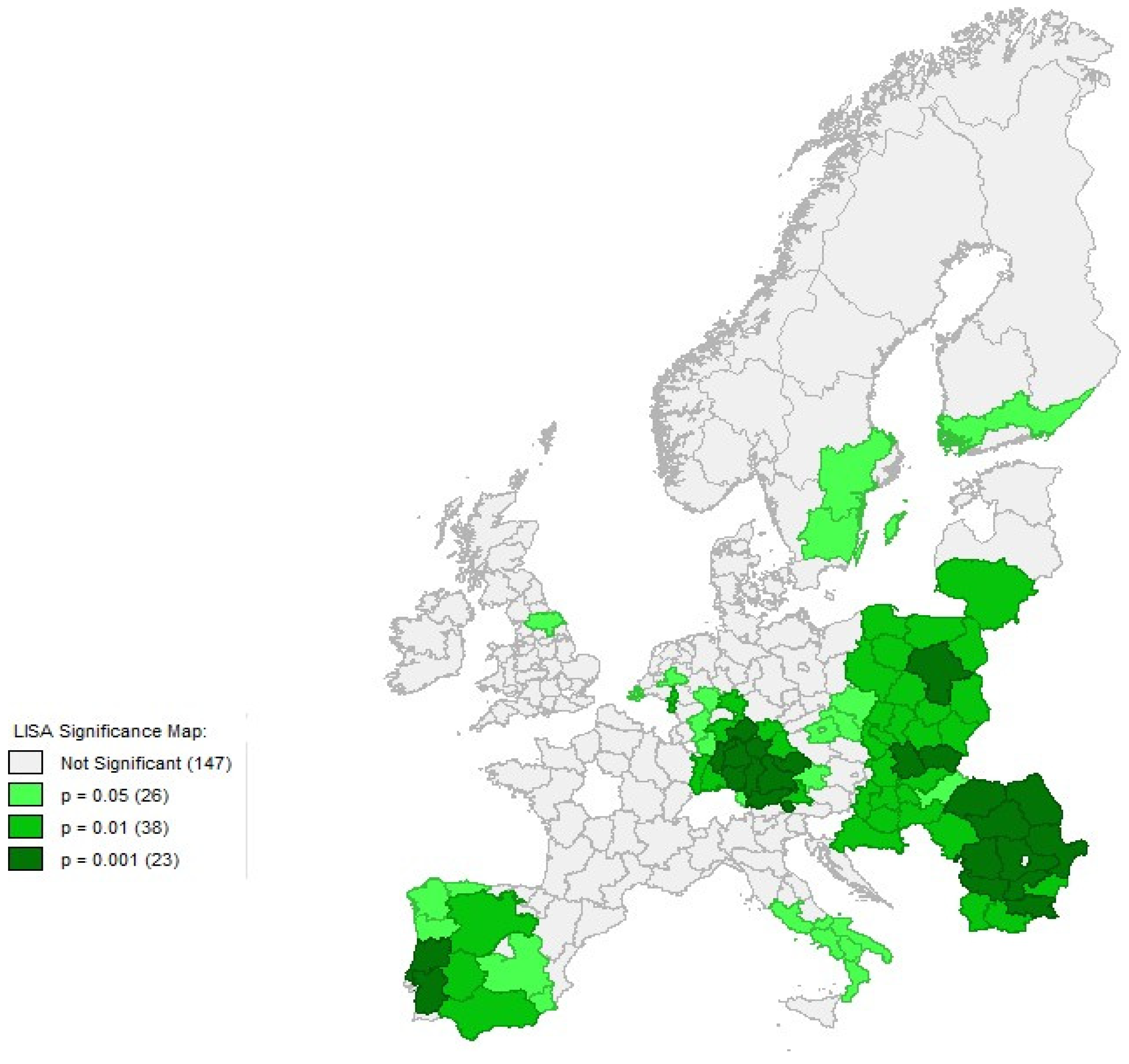
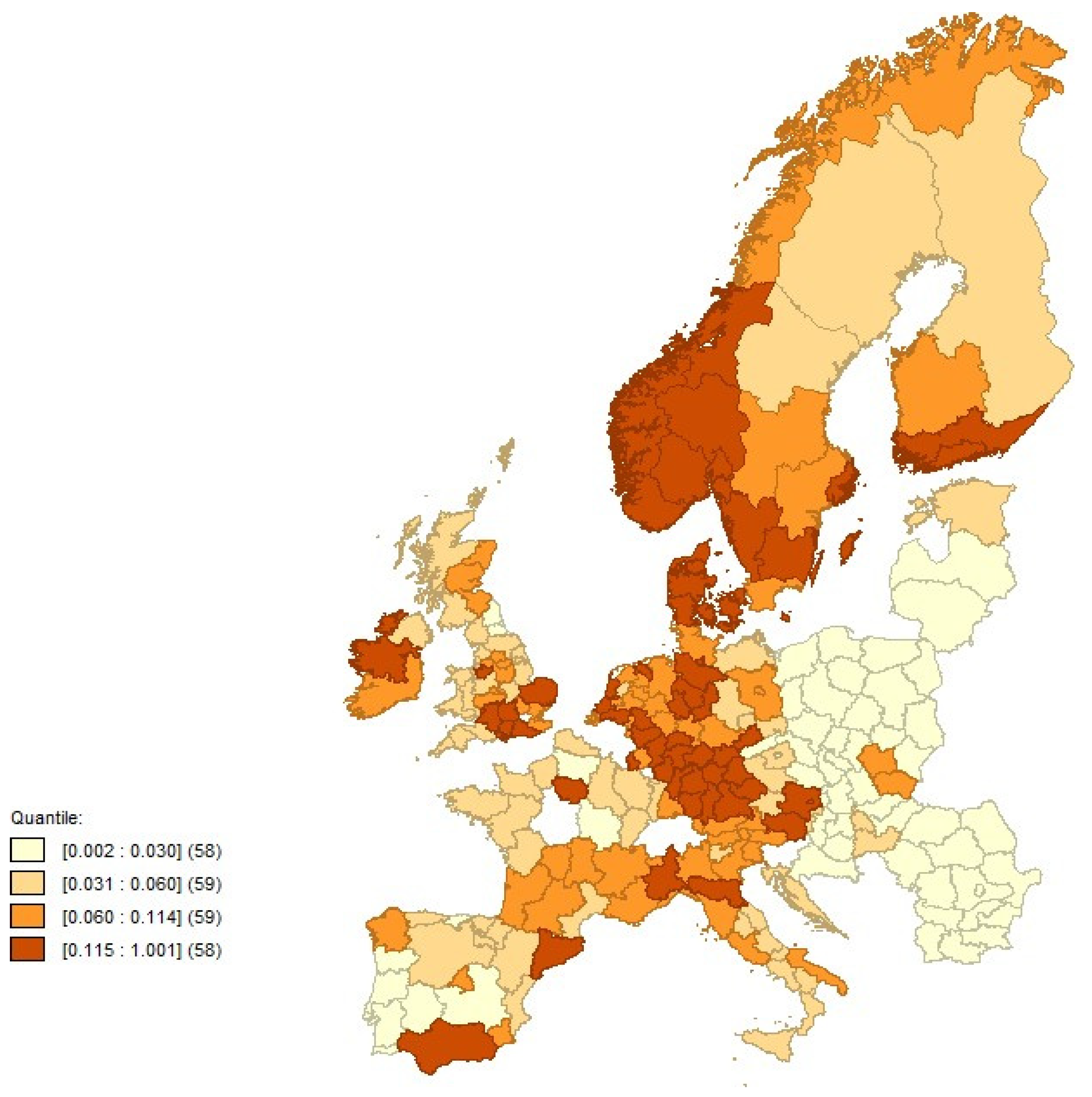

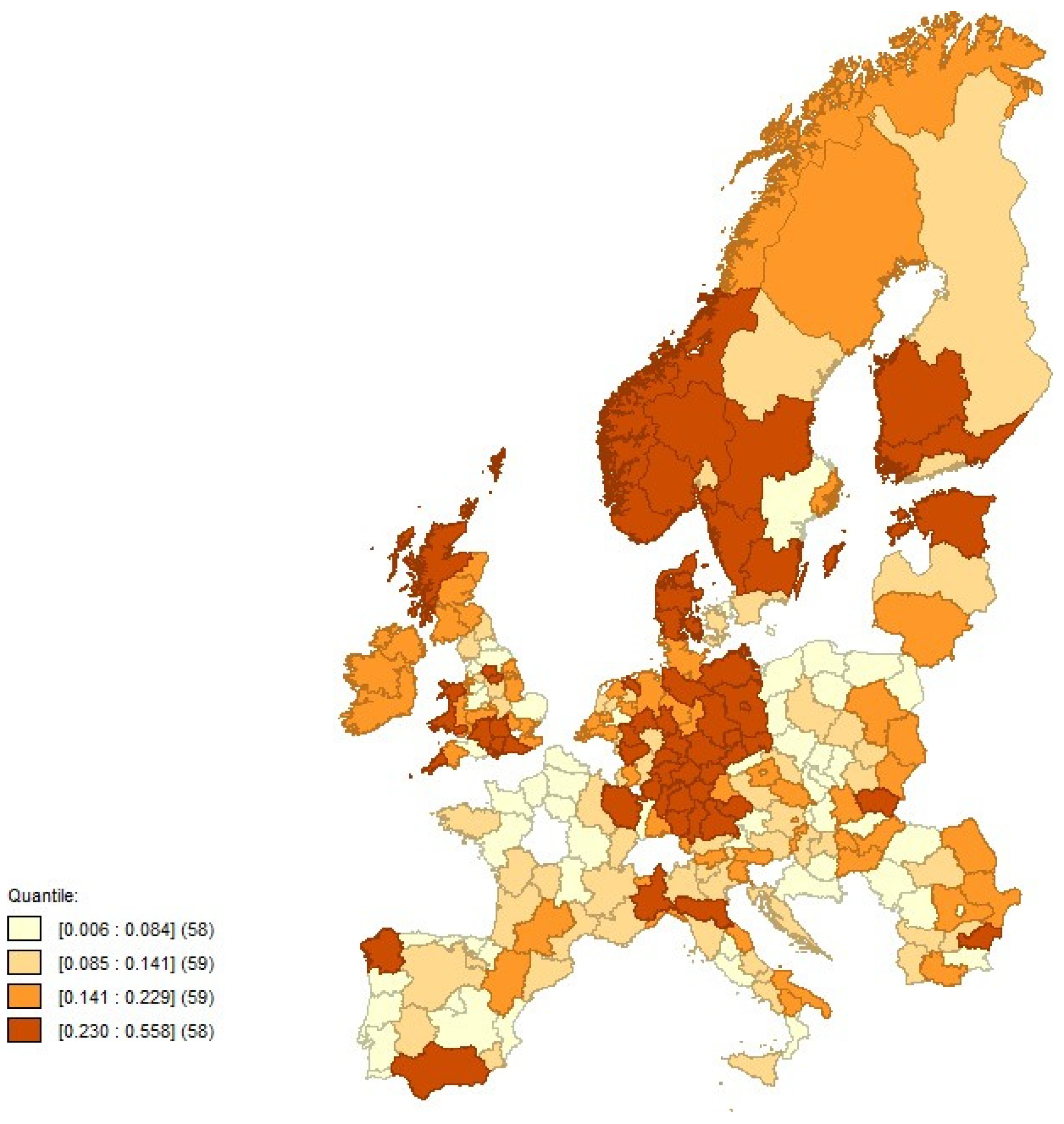
References
- Alamá-Sabater, L.; Márquez-Ramos, L.; Navarro-Azorín, J.M.; Suárez-Burguet, C. A two-methodology comparison study of a spatial gravity model in the context of interregional trade flows. Appl. Econ. 2015, 47, 1481–1493. [Google Scholar] [CrossRef]
- Fu, Y.; Gabriel, S.A. Labor migration, human capital agglomeration and regional development in China. Reg. Sci. Urban Econ. 2012, 42, 473–484. [Google Scholar] [CrossRef]
- Miguélez, E.; Moreno, R. Research Networks and Inventors’ Mobility as Drivers of Innovation: Evidence from Eu-rope. Reg. Stud. 2013, 47, 1668–1685. [Google Scholar] [CrossRef]
- Silva, J.M.C.S.; Tenreyro, S. The log of gravity. Rev. Econ. Stat. 2003, 88, 641–658. [Google Scholar] [CrossRef]
- Elhorst, J.P. Applied spatial econometrics: Raising the bar. Spat. Econ. Anal. 2010, 5, 9–28. [Google Scholar] [CrossRef]
- Anselin, L. Spatial externalities, spatial multipliers, and spatial econometrics. Int. Reg. Sci. Rev. 2003, 26, 153–166. [Google Scholar] [CrossRef]
- Lesage, J.P.; Chih, Y.-Y. Interpreting heterogeneous coefficient spatial autoregressive panel models. Econ. Lett. 2016, 142, 1–5. [Google Scholar] [CrossRef]
- Anselin, L. Thirty years of spatial econometrics. Pap. Reg. Sci. 2010, 89, 3–25. [Google Scholar] [CrossRef]
- Besag, J. Spatial interaction and the statistical analysis of lattice systems. J. R. Stat. Soc. Ser. B Stat. Methodol. 1974, 36, 192–225. [Google Scholar] [CrossRef]
- Kaiser, M.S.; Cressie, N. Modeling Poisson variables with positive spatial dependence. Stat. Probab. Lett. 1997, 35, 423–432. [Google Scholar] [CrossRef]
- Griffith, D. A Spatial Filtering Specification for the Auto-Poisson Model. Stat. Probab. Lett. 2002, 58, 245–251. [Google Scholar] [CrossRef]
- Lambert, D.M.; Brown, J.P.; Florax, R.J. A two-step estimator for a spatial lag model of counts: Theory, small sample performance and an application. Reg. Sci. Urban Econ. 2010, 40, 241–252. [Google Scholar] [CrossRef]
- Sengupta, A.; Cressie, N. Empirical Hierarchical Modelling for Count Data using the Spatial Random Effects Model. Spat. Econ. Anal. 2013, 8, 389–418. [Google Scholar] [CrossRef]
- Czado, C.; Schabenberger, H.; Erhardt, V. Non nested model selection for spatial count regression models with applica-tion to health insurance. Stat. Pap. 2014, 55, 455–476. [Google Scholar] [CrossRef]
- LeSage, J.P.; Fischer, M.M.; Scherngell, T. Knowledge spillovers across Europe: Evidence from a Poisson spatial inter-action model with spatial. Pap. Reg. Sci. 2007, 86, 393–421. [Google Scholar] [CrossRef]
- Glaser, S. A Review of Spatial Econometric Models for Count Data (No. 19-2017); Hohenheim Discussion Papers in Business, Economics and Social Sciences; Universität Hohenheim, Fakultät Wirtschafts- und Sozialwissenschaften: Stuttgart, Germany, 2017. [Google Scholar]
- Autant-Bernard, C.; LeSage, J. Quantifying knowledge spillovers using spatial econometric tools. J. Reg. Sci. 2011, 51, 471–496. [Google Scholar] [CrossRef]
- Gourieroux, C.; Monfort, A.; Trognon, A. Pseudo maximum likelihood methods: Applications to Poisson models. Econometrica 1984, 52, 701. [Google Scholar] [CrossRef]
- StataCorp LLC. Stata Statistical Software: Release 16; StataCorp LLC: College Station, TX, USA, 2019. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2020. [Google Scholar]
- Kelejian, H.H.; Prucha, I.R. HAC estimation in a spatial framework. J. Econ. 2007, 140, 131–154. [Google Scholar] [CrossRef]
- Klier, T.; McMillen, D.P. Clustering of auto supplier plants in the United States: Generalized method of moments spa-tial logit for large samples. J. Bus. Econ. Stat. 2008, 26, 460–471. [Google Scholar] [CrossRef]
- Fingleton, B.; Le Gallo, J. Estimating spatial models with endogenous variables, a spatial lag and spatially dependent disturbances: Finite sample properties*. Pap. Reg. Sci. 2008, 87, 319–339. [Google Scholar] [CrossRef]
- Santos, L.S.; Proença, I. The inversion of the spatial lag operator in binary choice models: Fast computation and a closed formula approximation. Reg. Sci. Urban Econ. 2019, 76, 74–102. [Google Scholar] [CrossRef]
- Billé, A.G. Computational Issues in the Estima tion of the Spatial Probit Model: A Comparison of Various Estimators. Rev. Reg. Stud. 2013, 43, 131–154. [Google Scholar]
- Anselin, L.; Le Gallo, J. Interpolation of air quality measures in hedonic house price models: Spatial aspects. Spat. Econ. Anal. 2006, 1, 31–52. [Google Scholar] [CrossRef]
- Buesa, M.; Heijis, S.; Baumert, T. The determinants of regional innovation in Europe: A combined factorial and a re-gression knowledge production function approach. Res. Policy 2010, 39, 722–735. [Google Scholar] [CrossRef]
- Acs, Z.J.; Anselin, L.; Varga, A. Patents and innovation counts as measures of regional production of new knowledge. Res. Policy 2002, 31, 1069–1085. [Google Scholar] [CrossRef]
- QGIS Development Team. QGIS Geographic Information System. Open Source Geospatial Foundation Project. 2020. Available online: https://www.qgis.org/en/site/ (accessed on 20 January 2021).
- Anselin, L.; Syabri, I.; Kho, Y. GeoDa: An Introduction to Spatial Data Analysis. Geogr. Anal. 2006, 38, 5–22. [Google Scholar] [CrossRef]
- Griliches, Z. Issues in assessing the contribution of research and development to productivity growth. Bell J. Econ. 1979, 10, 92. [Google Scholar] [CrossRef]
- Krammer, S.M. Drivers of national innovation in transition: Evidence from a panel of Eastern European countries. Res. Policy 2009, 38, 845–860. [Google Scholar] [CrossRef]
- Ferreira, V.; Godinho, M.M. The determinants of innovation. In Dynamics of Knowledge Intensive Entrepreneurship: Business Strategy and Public Policy; Routledge: London, UK, 2015; p. 304. [Google Scholar]
- Zhang, F.; Wang, Y.; Liu, W. Science and Technology Resource Allocation, Spatial Association, and Regional Innova-tion. Sustainability 2020, 12, 694. [Google Scholar] [CrossRef]
- Autant-Bernard, C. Science and knowledge flows: Evidence from the French case. Res. Policy 2001, 30, 1069–1078. [Google Scholar] [CrossRef]
- Farrar, D.E.; Glauber, R.R. Multicollinearity in regression analysis: The problem revisited. Rev. Econ. Stat. 1967, 49, 92. [Google Scholar] [CrossRef]
- Furková, A. Spatial spillovers and European Union regional innovation activities. Cent. Eur. J. Oper. Res. 2019, 27, 815–834. [Google Scholar] [CrossRef]
| Variables | Abbrev. | Unit | Expected Outcome |
|---|---|---|---|
| The number of patents registered (dependent variable) | Pat | Unit per million inhabitants | − |
| Intramural Expenditure on R&D by private business | R&D_B | Euros per inhabitant | + |
| Intramural Expenditure on R&D by the government | R&D_G | Euros per inhabitant | Ambiguous |
| Intramural Expenditure on R&D by universities | R&D_U | Euros per inhabitant | Ambiguous |
| Total R&D personnel and researchers in private business (no. of full-time workers) | Pers_B | - | + |
| Total R&D personnel and researchers in the government (no. of full-time workers) | Pers_G | - | Ambiguous |
| Total R&D personnel and researchers in universities (no. of full-time workers) | Pers_U | - | Ambiguous |
| % Population aged 25–64 with Bachelor’s degree | Educ | Percentage | + |
| Population | Pop | Number of inhabitants | − |
| GDP per capita | GDP | Thousand euros per capita | + |
| Tuberculosis mortality | Mort | Rate per 100,000 inhabitants | − |
| Variables | N | Mean | Std Dev | Min | Max |
|---|---|---|---|---|---|
| Pat | 234 | 89.171 | 106.045 | 0.000 | 590 |
| R&D_B | 234 | 318.248 | 382.444 | 0.000 | 2441.700 |
| R&D_G | 234 | 59.819 | 87.684 | 0.000 | 480.600 |
| R&D_U | 234 | 135.917 | 152.388 | 0.000 | 891.700 |
| Pers_B | 234 | 5744.342 | 9291.554 | 0.000 | 97,982.000 |
| Pers_G | 234 | 1467.979 | 2628.740 | 0.000 | 17,934.000 |
| Pers_U | 234 | 3294.923 | 3558.347 | 0.000 | 34,836.000 |
| Educ | 234 | 27.334 | 8.700 | 11.200 | 50.100 |
| Pop | 234 | 1,982,780.5 | 1,563,839.6 | 126,620.0 | 11,898,502.0 |
| GDP | 234 | 26.922 | 13.874 | 3.561 | 84.047 |
| Mort | 234 | 1.009 | 1.375 | 0.100 | 8.800 |
| SAR-PPML 1stStep-ML | SAR-PPML 1stStep-OLS | |||
|---|---|---|---|---|
| Variable | Coefficients | Bootstrap SE | Coefficients | Bootstrap SE |
| 6.81 × 10−1 *** | 0.06838 | 6.19 × 10−1 *** | 0.07821 | |
| R&D_B | 8.91 × 10−4 *** | 0.00034 | 9.18 × 10−4 *** | 0.00035 |
| R&D_G | −2.15 × 10−3 * | 0.00130 | −2.01 × 10−3 | 0.00157 |
| R&D_U | −3.21 × 10−4 | 0.00079 | −5.85 × 10−4 | 0.00083 |
| Pers_B | −1.33 × 10−5 | 0.00003 | −1.59 × 10−5 | 0.00003 |
| Pers_G | 2.75 × 10−5 | 0.00006 | 3.43 × 10−5 | 0.00006 |
| Pers_U | 5.07 × 10−5 | 0.00005 | 1.86 × 10−5 | 0.00005 |
| Educ | 2.58 × 10−4 | 0.01165 | 7.55 × 10−5 | 0.01279 |
| Pop | −3.21 × 10−9 | 9.62 × 10−8 | 6.10 × 10−8 | 1.14 × 10−7 |
| GDP | 3.81 × 10−2 *** | 0.01003 | 4.42 × 10−2 *** | 0.01127 |
| Mort | −1.95 × 10−1 ** | 0.09624 | −6.72 × 10−2 | 0.09071 |
| Log Likelihood | −6557.154 | −7704.048 | ||
| N | 234 | 234 | ||
| SAR-PPML 1stStep-ML | SAR-PPML 1stStep-OLS | |||||
|---|---|---|---|---|---|---|
| Variable | Direct | ASpill-in | ASpill-out | Direct | ASpill-in | ASpill-out |
| R&D_B | 0.0934 | 0.1743 | 0.1683 | 0.0878 | 0.1126 | 0.1093 |
| R&D_G | −0.2250 | −0.4200 | −0.4054 | −0.1921 | −0.2464 | −0.2391 |
| R&D_U | −0.0336 | −0.0628 | −0.0606 | −0.0560 | −0.0718 | −0.0697 |
| Pers_B | −0.0014 | −0.0026 | −0.0025 | −0.0015 | −0.0020 | −0.0019 |
| Pers_G | 0.0029 | 0.0054 | 0.0052 | 0.0033 | 0.0042 | 0.0041 |
| Pers_U | 0.0053 | 0.0099 | 0.0096 | 0.0018 | 0.0023 | 0.0022 |
| Educ | 0.0270 | 0.0504 | 0.0487 | 0.7221 | 0.9258 | 0.8984 |
| Pop | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| GDP | 3.9933 | 7.4536 | 7.1953 | 4.2288 | 5.4222 | 5.2617 |
| Mort | −20.4060 | −38.0886 | −36.7686 | −6.4270 | −8.2409 | −7.9969 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Proença, I.; Glórias, L. Revisiting the Spatial Autoregressive Exponential Model for Counts and Other Nonnegative Variables, with Application to the Knowledge Production Function. Sustainability 2021, 13, 2843. https://doi.org/10.3390/su13052843
Proença I, Glórias L. Revisiting the Spatial Autoregressive Exponential Model for Counts and Other Nonnegative Variables, with Application to the Knowledge Production Function. Sustainability. 2021; 13(5):2843. https://doi.org/10.3390/su13052843
Chicago/Turabian StyleProença, Isabel, and Ludgero Glórias. 2021. "Revisiting the Spatial Autoregressive Exponential Model for Counts and Other Nonnegative Variables, with Application to the Knowledge Production Function" Sustainability 13, no. 5: 2843. https://doi.org/10.3390/su13052843
APA StyleProença, I., & Glórias, L. (2021). Revisiting the Spatial Autoregressive Exponential Model for Counts and Other Nonnegative Variables, with Application to the Knowledge Production Function. Sustainability, 13(5), 2843. https://doi.org/10.3390/su13052843







