Abstract
This paper analyses the relationship between Nitrous Oxide emissions, agricultural land use, and economic growth in Pakistan. Agriculture largely contributes to Nitrous Oxide emissions. Hence, models of agriculture induced Nitrous Oxide emissions are estimated in addition to models of total Nitrous Oxide emissions. Estimated models accommodate more flexible forms of relationship between economic growth and emissions than those of the widely adopted models in testing the Environmental Kuznets Curve. The Auto-Regressive Distributed Lag (ARDL) bounds testing approach to co-integration and the vector error correction model approach is applied to test the Environmental Kuznets’s Curve hypothesis for Pakistan and to detect the directions of causality among variables using the time series data for the period 1971 to 2012. Results indicate that an N-shaped rather than an inverted U-shaped relationship exists in the case of Pakistan. The tipping values for total Nitrous Oxide emissions and agriculturally induced Nitrous Oxide emissions indicate that Pakistan passes through a phase of increasing environmental degradation. Increases in agricultural land use and per capita energy use will increase the level of Nitrous Oxide emissions. However, controlling Nitrous Oxide emissions from agricultural land use and per capita, energy use without adversely affecting economic development will be a serious policy challenge for Pakistan.
1. Introduction
The emissions of Greenhouse Gases (GHG) such as Carbon Dioxide (CO2), Sulphur Dioxide (SO2), and Nitrous Oxide (N2O) have increased significantly in agrarian economies through the extensive adoption of highly intensive production systems in livestock and crop farming [1]. Among these gasses, the N2O is currently the leading ozone-depleting element as chlorofluorocarbon (CFC) emissions have been virtually eliminated [2]. According to a recent report (see Table 1) by the United States Environmental Protection Agency (US-EPA), N2O has more than 300 times stronger warming effect than that of CO2 [3]. Agriculture is the major source of N2O emissions and anthropogenic sources account for about 70% of agriculturally induced N2O [4]. About 63% of agriculturally induced N2O emissions come from the direct use of soils according to Tian et al. [5]. Compared to CO2 emissions, the gasses such as N2O less likely to spread beyond the borders and have serious long-term consequences on human health and welfare [6]. By 2100, the total N2O emissions from the production of chemical fertilisers are estimated to be four times the present levels of emissions [7,8]. Therefore, agricultural economies like Pakistan should be more concerned about N2O emissions especially during the phases of rapid economic expansion. The relationship between N2O emissions and economic growth needs to be investigated to help design agricultural policies that strike a sustainable balance between economic growth and the environment [9,10]. However, the link between N2O emissions and economic growth remains a considerably less researched subject, in particular, in the context of developing countries.

Table 1.
Global Warming Potentials of Green House Gases Compared to CO2.
The economic development of Pakistan depends heavily on agriculture which accounts for 19.5% of gross domestic product (GDP), and employs 42.3% of the labour force. The industrial sector, fast-growing value-added industries in particular, depends heavily on agriculture for raw material and critical inputs [11,12]. It also plays a central role in export earnings, food security, and poverty reduction.
The main objective of this study is to examine the relationship between N2O emissions and economic growth and determine whether the relationship follows an Environmental Kuznets Curve (EKC) in Pakistan. This is achieved by estimating models of total and agriculturally induced N2O emissions which are derived from the basic model of EKC. The estimated models relate total and agriculturally induced N2O emissions to economic growth (GDP), agricultural land used (ALU), energy used (ENU), and exports (EXP). The ARDL bounds testing approach which is preferable for short samples is employed to capture the short-run and long-run dynamics of the models [13]. The outcomes of the study are expected to help formulate environmentally friendly policies for sustainable economic development [14,15,16]. The rationale for this study rests on at least two important facts. First, the number of studies on the nexus between N2O emissions and economic growth is significantly less compared to the studies on CO2 and economic growth. In particular, there is a dearth of country-specific studies on the subject. The fact that the N2O emissions are relatively more concentrated and less likely to cross borders, highlights the importance of country-specific studies for effective policymaking in different countries [17,18,19]. The recent study by Duodu [20] confirms that N2O emissions are a local pollutant that is mostly produced from agricultural activities; fertiliser use, and agricultural soils. The reason is that N2O emissions are not majorly by-products of industrial activities. “It also stems from the use of fertilisers and general agricultural activities. Since developing countries are more agrarian and their economic activities may lead to an increase in N2O emissions” (p. 32). This study also highlights that the N2O emissions have been neglected in previous studies and policy debate and confirmed that there is no evidence for the Pollution Haven Hypothesis (PHH) for N2O emissions in the case of Sub-Saharan African (SSA) countries which are mostly the developing countries while PHH is confirmed for the CO2 emissions which indicates that comparing the results for Organisation for Economic Co-operation and Development (OECD) and SSA countries, the results also show that trade makes SSA countries relatively dirtier because of the global externality of CO2 emissions. Similarly, US-EPA [3] shows concern over the devastating effect of N2O emissions on the environment which is more damaging to the ozone layer which also highlights the importance to study the N2O emissions.
Second, Pakistan is fast approaching a state where environmental degradation will be a serious policy challenge mainly for reasons such as the dominance of the agricultural sector and the development of energy projects currently underway. In Pakistan, the agricultural sector is expected to remain a major leading sector of economic growth with a potential for substantial increases in N2O emissions in the future while the energy projects being established under the China Pakistan economic corridor (CPEC) are coal run and bound to contribute to the rising levels of GHG emissions. The government has expressed a strong commitment to combat climate change and meet GHG reduction targets which can only be realised through a comprehensive understanding of the factors responsible for GHG emissions in the country. Nonetheless, to the best of the authors’ knowledge, there has been no previous study that examined the link between N2O emissions, agricultural land used, and economic growth in Pakistan.
The rest of the paper is organised as follows. Section 2 presents an analysis of observed trends in the total and agriculturally induced N2O emissions and their determinants. Section 3 presents a brief literature review of previous studies on EKC. A description of the model, data, and methodology is presented in Section 4. Section 5 presents an analysis of the estimated results. Conclusions and policy implications are provided in the last section.
2. N2O Emissions in Pakistan
Pakistan is primarily an agrarian economy that has experienced a noticeable increase in the level of N2O emissions over time. Figure 1 shows that, in per capita terms, the total and agriculturally induced N2O emissions have followed similar trends in Pakistan. Both variables show rising trends between 1971 and 1985, and a decline in 1986 caused by an increase in the cost of production due to an increase in fertiliser prices which is the main cause of a decrease in the N2O emissions. After the fifth five-year plan (1978–1983), the government of Pakistan reduced the subsidy for fertiliser and the share of fertiliser in the overall agriculture GDP declined from 5.7 to 3.6% in the sixth five-year plan (1983–1988) which is caused by a sharp decline in the public sector investment in the agriculture sector which leads to a decline in overall agriculture activity, which further affects the agriculture share in development outlay which substantially decline from 20 (1978–1983) to 16% (1983–1988) [21]. On the other hand, data shows a significant increase in population growth in the same period [22]. This is also another reason for a decline in the N2O emissions in this period as we take the data in per capita N2O emissions. However, after which the agriculturally induced N2O emissions per capita remain relatively unchanged. The increased modernisation in the agricultural sector by new technologies and the growth of the shares of industry and services sectors in GDP may have been mainly responsible for these trends.
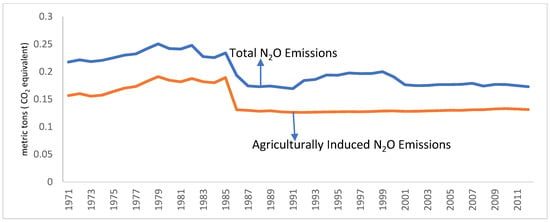
Figure 1.
Total and Agriculturally Induced N2O Emissions (per capita) in Pakistan. Source: World Development Indicators (WDI).
However, the levels of N2O emissions in Pakistan are relatively higher than international standards. The data for the year 2012 shows that Pakistan per capita N2O emissions is 0.27 thousand metric tons (CO2 equivalent) which is much higher than the neighbouring counties like India have a per capita N2O emissions is 0.19 thousand metric tons (CO2 equivalent) in the same year while Bangladesh is 0.18, Afghanistan is 0.23, Maldives is 0.08, and Sri Lanka is 0.14 thousand metric tons (CO2 equivalent) per capita [23].
The high level of N2O emissions has several consequences. It creates smog that paralyzes routine life in Pakistan during the winter season by reducing visibility to a few meters and costs significantly to the economy. Further, it can cause serious damages to the ambient atmosphere by creating various nitrate compounds [24]. Many thermal power plants in Pakistan add to the level of N2O, as these are run by coal. Industrial furnaces produce a temperature higher than 1700 °C, due to which the nitrogen (N2) and oxygen (O2) react with each other and form N2O [25]. Combustion of oil mainly visible in vehicular transportation is the second-largest producer of N2O emissions. Apart from industrial sources, residential areas also contribute to the rise in N2O emissions through the level of humidity, improper usage of burners, and heights of buildings. Vehicular congestion, a result of the ever-growing population in Pakistan, generates traffic fumes and causes N2O emissions in residential areas [26]. According to Relwani et al. [27] and Himmel and DeWerth [28], the high tipping yellow flame produced by cooking also contributes to N2O emissions in residential areas. The tall buildings do not directly add to the level of N2O emissions, yet they resist ventilation and sunlight in the neighbourhood that increases the usage of air-conditioning systems [29].
Figure 2 shows the linear and positive relationship between per capita income and per capita energy used in Pakistan in general over the years. Since 2007 this trend has slightly changed, and per capita energy use shows a decline while per capita income continues to grow. Figure 3 shows an upward trend in exports of Pakistan while agricultural land used shows a consistent decline which implies that exports do not depend significantly on agricultural land use. The increasing share of industrial and services sectors in Pakistan’s economy can help understand this trend.
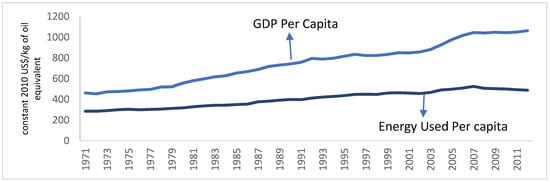
Figure 2.
GDP and Energy Used (per capita) in Pakistan. Source: World Development Indicators (WDI).

Figure 3.
Agricultural Land Used per Capita and Exports as a percentage of GDP in Pakistan. Source: World Development Indicators (WDI).
3. Literature Review
The Environmental Kuznets Curve (EKC), since its’ introduction by Grossman and Kruger [30], provided a framework in which the link between environmental degradation and economic growth can be explored. Environmental pollution has become a central area of research in the face of rapid economic growth and an increase in the emission of GHG globally during the last few decades. As a consequence, the EKC concept has become a discrete research subject and stimulated a large number of empirical and theoretical literature [19,31,32]. The EKC gained popularity among academia, researchers, and policymakers due to its important implications for economic development, particularly for developing countries. It has also influenced the policies and priorities of the International Monetary Fund (IMF) and World Bank which is evident from their prescriptions for pro-growth policies [33]. Nevertheless, the EKC has been under criticism for incompleteness in the context of sustainable development [34,35,36]. The validity of EKC has been tested for several countries and regions using different methods of estimation and various variables for environmental degradation [17,19,37,38]. These studies can be divided into three groups according to the environmental degradation indicators used. The first group uses the level of carbon dioxide (CO2) emissions [39,40,41,42]. These studies usually focus on developed countries or where growth has been significant. The second group relates to Sulphur dioxide (SO2) to income per capita [43,44]. The third group verifies EKC through nitrous oxide (N2O) [13,17,45]. However, only a small number of studies focused on N2O emissions. In this study, we focus on the N2O emissions, and a brief account of studies that use N2O emissions or the total GHG emissions as a dependent variable is given in Table 2.

Table 2.
Previous Empirical Studies on EKC using N2O and total Greenhouse Gases.
As the information in Table 2 shows, only a very small number of studies have focussed on N2O emissions. Most of them employed the linear or quadratic specifications of the equation representing the basic EKC model. Overall, these studies produced mixed results that highlight the importance of conducting case-specific studies using more flexible forms of the relationship between N2O emissions and economic growth.
4. Model Specification, Data, and Methodology
The models estimated in this study are derived from the following simple model of EKC:
where N2O is the total nitrous oxide emissions (metric tons of CO2 equivalent) per capita, GDP is gross domestic product per capita, α0 is the constant term, α1 and α2 are the slope coefficients, and t indicates the period in years, while εt is a white-noise error term. All the model variables are expressed in natural logarithmic form. The total N2O per capita accounts for the emissions from livestock management, industrial activities, and agricultural biomass burning. While agricultural N2O accounts for the emissions produce from “fertiliser use (synthetic and animal manure), animal waste management, agricultural waste burning (nonenergy, on-site), and savannah burning” according to the World Development Indicators WDI (2019). The signs of the estimated coefficients are expected to be positive for α1 and negative for α2 if the EKC relationship holds. Earlier studies have used various functional forms in estimating the relationship between economic growth and environmental degradation [55,56,57]. The most commonly used functional forms are linear, quadratic, and cubic. As described by Perman and Stern [58], various shapes and forms of EKC could be observed, depending on the measure of environmental degradation. Van Alistine and Neumayer [59] estimated a cubic function on the basis that a second turning point may be observed. Yang et al. [56] and Zhang [60] estimated both quadratic and cubic specifications, obtaining results of robust support for both specifications. This study examines the plausibility of linear, quadratic, and cubic specifications without suggesting a priori specification, however, it relies on both quadratic and cubic specifications for obtaining robust results following Yang et al. [56]. The cubic form of the Equation (1) can be written as follows:
With the inclusion of three additional explanatory variables, namely agricultural land used (ALU), exports (Exp), and energy use (ENU) the augmented specifications of Equations (1) and (2) can be obtained. These are giving by Equations (3) and (4) below.
The agricultural land used affects the N2O emissions positively especially in developing countries where farmers use large amounts of fertilisers in the crops production processes which represent a significant source of N2O emissions. Exports may not affect N2O emissions (Kearsley and Riddel, [61]), but can be related to EKC according to the (PHH) [62]. The PHH asserts that developed countries have stricter environmental regulations and adopt clean technologies, whereas the more pollutant production processes take place in developing countries where the transfer of pollution occurs, instead of mitigation, across regions [17]. Energy consumption leads to environmental degradation as it is positively linked with greenhouse gas emissions [63,64,65]. This may be true in the case of Pakistan, where the contribution of non-renewable energy sources to total energy is more than 90 percent.
In estimating the models, the inverted U-shaped EKC can be obtained by imposing the coefficient restrictions that α1 > 0 and α2 < 0 on Equation (3). An N-shaped curve can be obtained by imposing coefficient restrictions that β1 > 0, β2 < 0 and β3 > 0 on Equation (4). All possible shapes of the relationship between N2O and GDP which depend upon the signs of the estimated coefficients of the linear, quadratic, and cubic models are stated in Table 3.

Table 3.
Possible Shapes of the Relationship between N2O and GDP.
To detect the shape of the relationship in Pakistan, each of the quadratic and cubic models (Equations (3) and (4)), is estimated separately for total and agriculturally induced N2O emissions. The annual time series data over the period from 1971 to 2012 on GDP per capita (constant 2010 US dollars), total N2O emissions per capita, agriculturally induced N2O emissions per capita, agricultural land used per capita, energy use (kg of oil equivalent) per capita, and exports of goods and services as percent of GDP are used. The source of the data is WDI-2019 [22]. This is the latest data (1971–2012) available in the WDI for N2O emissions for Pakistan which is a data constraint in this study and can be extended when the new data are available.
Following Pesaran et al. [67], this study applies the ARDL bounds testing approach to cointegration. This approach has two advantages over other traditional techniques such as Engle and Granger [68]; Johansen and Juselius [69] and Phillips and Hansen [70]. First, it is equally applicable when every variable is not integrated of order one. Second, when applied to small samples it remains more efficient [13]. However, it crashes if the variables are I(2) processes [71]. The structural break unit root tests developed by Zivot and Andrews [72] are applied to test the stationarity properties of the variables. These tests, which can identify an unknown structural breakpoint in the time series, are relatively more reliable than Augmented Dicky Fuller (ADF) and Philips Perron (PP) tests in the presence of structural breaks [73].
The bounds test, an F-test, is applied on the Equations (3) and (4) to test the co-integration under the null hypotheses given below,
Equation (3): H0: α1 = α2 = α3 = α4 = α5 = 0
Equation (4): H0: β1 = β2 = β3 = β4 = β5 = β6 = 0
The alternative hypothesis is that at least one of the αi ≠ 0 or βi ≠ 0. Given the small sample of the study, this paper uses the critical bounds developed by Narayan [74] as the critical values generated by Pesaran et al. [67] are biased downward. Once a cointegration relationship is established, Equations (3) and (4) are estimated to capture the long-run dynamics [75]. After obtaining the long-run estimates, the turning point(s) can be determined by equating the first derivative of Equations (3) and (4) with respect to GDP to 0, such as, for Equation (3),
Similarly, we can find two turning points for the cubic model. The Error Correction Term (ECT) shows the speed of adjustment which indicates how quickly the variables converge to the long-run equilibrium following a one-time shock in the model. So, the condition for the convergence is that the coefficient of ECT should be negative and statistically significant with a magnitude that is less than or equal to one. To capture the short-run dynamics, following the error correction model is estimated for Equation (3).
Similarly, for Equation (4),
The diagnostic tests developed by Brown et al. [76] are applied to verify the stability of the estimated model parameters. The causality tests based on the Vector Error Correction Model (VECM) as suggested by Granger [77] are used to investigate the causal relationships. The VECM model is as follows:
where the speed of adjustment toward equilibrium is measured by the vector π which represents the mean-reversion mechanism of the VECM. Under the VECM two types of Granger causality relationships exist as suggested by Granger [77]. The long-run causality can be determined by the statistical significance of ECTt−1 using a t-test and the short-run causality can be tested by the statistical significance of ECTt−1 using the Wald-test [64]. It is worth noting here that the parametric methodology used in the paper at hand has few limitations as Parametric models may lead to model misspecification [78] and are applicable when the relationship between regressor and regressand is known [79]. Parametric approaches are unable to estimate the relationship between the variables especially in the context of climate change literature [80]. Furthermore, like many empirical studies on ecology, this research may face the problem of multicollinearity i.e., correlation of independent variables with each other. This research is further confined due to the use of ARDL is currently the most advanced nonlinear autoregressive distributed lag (NARDL) is more common in literature as they can capture the short-run and long-run non-linearities and asymmetries by introducing positive and negative partial sum decompositions of the independent variables [81].
5. Empirical Results and Discussion
Descriptive statistics for the variables are presented in Table 4. In terms of the standard deviation, GDP is relatively more volatile than N2O emissions, and the N2O emissions, both total and agriculturally induced, have the smallest volatility of all the variables.

Table 4.
Descriptive Statistics.
Results of the Zivot Andrew Structural Break unit root tests are reported in Table 5. The computed test statistics (T-stat) for the first differences of all the variables indicate that all the model variables are integrated of order one, i.e., I(1), at a 1% level of significance as required by the ARDL bounds approach [82].

Table 5.
Zivot Andrew Structural Break Unit Root Test.
Following Lütkepohl [83], Akaike information criterion (AIC) is used to select an optimal lag length for the ARDL bounds test of co-integration, the results of which are reported in Table 6. The computed F-statistics reported for each model surpass the corresponding lower and upper critical bounds, rejecting the null hypothesis of no cointegration at the 5% level of significance.

Table 6.
Bounds Testing to Cointegration—ARDL.
The long-run results for the models of total and agriculturally induced N2O emissions are reported in Table 7, along with the results of a selection of diagnostic tests that are performed for detecting serial correlation, autoregressive conditional heteroscedasticity, normality, and specification bias. The diagnostic test results reveal that all the long-run models are correctly specified except the quadratic specification for agriculturally induced N2O emissions. They also reveal that errors are normally distributed, and no heteroscedasticity or autocorrelation is found in the cubic specifications.

Table 7.
Long-run Results.
All the estimated coefficients of GDP variables are significant in the cubic specification and insignificant in the quadratic specification at the 5% level of significance. These results stand in favour of an N-shaped relationship in which N2O emissions initially follow a traditional EKC up to a certain level of GDP per capita beyond which N2O emissions once again increase with economic growth. Similar findings are reported by Allard et al. [84] for lower middle income and high-income countries, and Paudel et al. [85] for Latin American countries, on the nexus between CO2 emissions and economic growth.
The coefficient of the agricultural land used is positive and significant in all specifications except the quadratic model of the agriculturally induced N2O emissions. This result is consistent with the findings of Boluk and Mert [86] and Zambrano-Monserrate et al. [87,88,89]. This finding implies that the reduction in N2O emissions in Pakistan requires careful management of the extent, as well as the methods and processes of agricultural land use. The per capita energy use is positively related to N2O emissions in all the specifications. This result is consistent with the finding of Tiwari et al. [65] and Shahbaz et al. [63] which explored the link between energy consumption and CO2 emissions. For Pakistan, where non-renewable energy sources account for 90 percent of total energy, the policy implication from this result is that directing more resources to renewable energy projects is necessary to protect the environment. Such as Pakistan is a petroleum-producing country and this could be one of the drivers of the GHGs emissions which provides a common ground for the assessment of the factors influencing environmental pollution [90].
The coefficient of exports remains negative in all the specifications but significant only in the quadratic specification of the agriculturally induced N2O emissions. Overall, this result reveals that the PHH does not hold in the case of Pakistan. This may also indicate that the resources and processes in export production, in general, are non-polluting in terms of N2O emissions. This finding is consistent with the study of Duodu [20] which also confirmed that for N2O emissions, PHH does not hold for the Sub-Saharan African countries, it also confirms by the view of OECD [91] which states that stringent environmental laws have no detrimental impact on exports.
Based on the estimated results, this study finds that the relationship between GDP per capita and N2O emissions in Pakistan follows an N-type curve rather than an inverted U-shaped curve as depicted in Figure 4 and Figure 5. Similar relationships have been found by Zhang [60], Binder and Neumayer [92], Canas, et al. [93], and De Bruyn and Opschoor [94] between GDP per capita and other indicators of GHG emissions.
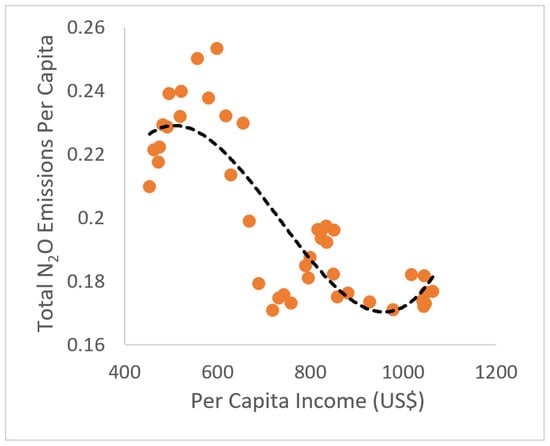
Figure 4.
Total N2O Emissions and per Capita Income Relationship in Pakistan.
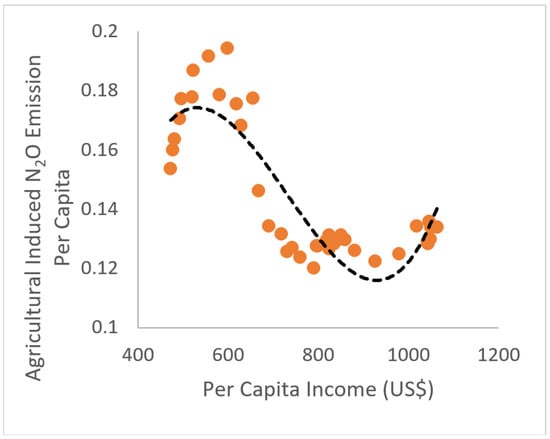
Figure 5.
Agricultural Induced N2O Emissions and Income Relationship in Pakistan.
The tipping points estimated from the cubic model are $502 and $1002 for total N2O emissions, and $511 and $1007 for the agriculturally induced N2O emissions. The tipping points of $1002 and $1007 are the threshold levels of GDP per capita beyond which increases in GDP per capita lead to increases in N2O emissions. The two threshold levels are not much different showing a similar pattern of relationships between N2O emissions and GDP per capita.
The estimated short-run results are reported in Table 8. The estimated coefficients for the changes in GDP and the squared GDP have the expected signs in all the specifications. The estimated coefficients of the error correction term (ECTt−1) is negative and significant at a 1% level in all the specifications. The coefficient shows the speed of adjustment to reinstate the equilibrium in the dynamic model, that is, the effect of a shock will be corrected by ranging from 42.8 to 51.8% within a year in all specifications. Nevertheless, the short run and the long run results are similar in that there is no evidence for an inverted U-shaped EKC.

Table 8.
Short-run Results.
For effective forecasting and policymaking, the stability of the parameters is important. As suggested by Pesaran et al. [67], the stability of the estimated parameters of ECM is tested using the Cumulative Sum (CUSUM) and Cumulative Sum of Squares (CUSUMSQ) of recursive residuals developed by Brown et al. [76]. The CUSUM test is based on the recursive residuals. According to the CUSUM test, if we detect any systematic subsequent movements in the values of the estimated intercept coefficients signalling a possible structural instability in the parameters. The estimated results by the CUSUM test confirmed that the intercept term is stable over time for both models which confirms that there is no breakpoint in the data, and we cannot reject the chosen specification throughout the sample period. While the CUSUMSQ test shows the instability in the variance of the regression error and based on the sum of squared recursive residuals that means if we want to detect random movements that do not necessarily come from a structural change in coefficients is stable over time. The estimated results show that there is no random movement in the estimated coefficients and all the model coefficients are stable over time. The plots of these tests are depicted in Figure 6, which confirms the stability of coefficients as the test statistics lie within the critical bounds of 5%.

Figure 6.
Plots of CUSUM and CUSUMSQ for the estimated ECM for the Cubic Model.
The results of the long run and short-run Granger causality tests are reported in Table 9 and Table 10 for the cubic specifications of the models for total and agriculturally induced N2O emissions.

Table 9.
Granger Causality test for Total N2O Emissions.

Table 10.
Granger Causality Test for Agricultural Induced N2O Emissions.
In the case of total N2O emissions, the results provide strong evidence for a long-run bidirectional causality for the three variables: N2O emissions, real GDP per capita, and exports. The bidirectional causality between N2O emissions and economic growth assert that on the one hand economic growth pattern in Pakistan may lead to a change in the pattern of the N2O emissions, while on the other hand, N2O emissions impact the economic growth which leads to a favourable way for the sustainable development in Pakistan. However, Pakistan has not yet reached a state of sustainable development and at present passes through the increasing phase of environmental degradation. However, formulating policies to reduce N2O emissions without seriously affecting economic growth would be a daunting task given the strong positive relationship between N2O emissions and economic growth at present. It is more likely a chance that in developing countries like Pakistan, the government has been less concerned to reduce its volume to boost the economic growth in the country and the N2O emissions are off the table in the policy agenda.
In the short run, a unidirectional causality running from N2O emissions to economic growth is evident. For the other variables, the empirical results show evidence for a bidirectional causality between agricultural land used and economic growth while exports and energy used to have no evidence of causality either way to economic growth. Evidence for unidirectional causality is also found from exports to the energy used.
In the case of agriculturally induced N2O emissions, the evidence supports a bidirectional causality for the three variables: N2O emissions, agricultural land use, and energy use per capita in the long run. In the short term, the results show no evidence for causality running from N2O emissions to economic growth. For the other variables, the empirical results show evidence for a unidirectional causality from agricultural land used and exports to economic growth while the energy used has a unidirectional causality from economic growth to energy used. Evidence of bidirectional causality is found for agricultural land used and the energy used. The causality relation detected based on these results are summarised in Table 11 above.

Table 11.
The direction of the Granger Causality Test for both Specifications.
6. Conclusions and Policy Implications
In this study, the link between N2O emissions and economic growth in Pakistan is investigated using models of total and agriculturally induced N2O emissions. The empirical models of N2O emissions are derived from the basic model of EKC by incorporating agricultural land used, exports, and energy used as explanatory variables, in addition to GDP. The models are estimated using the ARDL bounds tests approach of co-integration and the data for the period 1971 to 2012. The estimated results from quadratic and cubic specifications are analysed to determine if the link between N2O emissions and economic growth conforms to the inverted U-shape of EKC or an N-shaped relationship.
The study finds that the N2O emissions and economic growth in Pakistan follow an N-shaped relationship rather than an inverted U-shaped relationship. This is true for both the total and agriculturally induced N2O emissions. The tipping values of GDP per capita are $502 and $1002 for total N2O emissions and $511 and $1007 for agriculturally induced N2O emissions. These tipping values lie within the sample which implies that Pakistan has not yet reached a state of sustainable development and at present passes through the increasing phase of environmental degradation. The results further imply that the government environmental protection policies adopted according to the Kyoto Protocol have not effectively reduced N2O emissions in Pakistan. Therefore, a binding agreement of all levels of government is of paramount importance for effective control of N2O emissions in Pakistan. However, formulating policies to reduce N2O emissions without seriously affecting economic growth would be a daunting task given the strong positive relationship between N2O emissions and economic growth at present.
Apart from economic growth the increases in the agricultural land used and energy use have been responsible for rising levels of N2O emissions in Pakistan. To control N2O emissions, the agriculture sector needs to focus on more environmentally friendly methods and practices such as encouraging organic farming than the traditional ways of farming that extensively use organic and inorganic fertilisers as suggested by Husnain et al. [95]. The result that the increased energy use leads to environmental degradation at present highlights the importance of redirecting resources towards renewable energy projects for environmental protection in the future. The results show no strong relationship between exports and N2O emissions which implies that exports may not be seriously threatened by government actions to drastically reduce N2O emissions.
Author Contributions
A.H., Conceptual framework, data analysis, and investigation, methodology, software, validation, visualisation, writing—original draft preparation, M.I.u.H., analysed and interpreted the results, writing, F.S., literature review, and review and editing the final draft, W.R., supervision and writing—review and editing. All authors read and approved the final manuscript.
Funding
No source of funding available for this research.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The datasets used and/or analysed during the current study are available from the World Bank Dataset, World Development Indicators https://databank.worldbank.org/reports.aspx?source=2&series=SH.UHC.NOP1.ZG# (accessed on 23 December 2019).
Conflicts of Interest
The authors declare that they have no competing interests.
References
- Henseler, M.; Dechow, R. Simulation of regional nitrous oxide emissions from German agricultural mineral soils: A linkage between an agro-economic model and an empirical emission model. Agric. Syst. 2014, 124, 70–82. [Google Scholar] [CrossRef]
- Ravishankara, A.R.; Daniel, J.S.; Portmann, R.W. Nitrous Oxide (N2O): The Dominant Ozone-Depleting Substance Emitted in the 21st Century. Science 2009, 326, 123–125. [Google Scholar] [CrossRef]
- United States Environmental Protection Agency (EPA). Climate Change Indicators in the United States, 4th ed.; United States Environmental Protection Agency: Crystal City, VA, USA, 2016.
- Smith, K.A.; Mosier, A.R.; Crutzen, P.J.; Winiwarter, W. The role of N2O derived from biofuels, and from agriculture in general, in Earth’s climate. Phil. Trans. R. Soc. 2012, 367, 1169–1174. [Google Scholar] [CrossRef] [PubMed]
- Tian, H.; Lu, C.; Ciais, P.; Michalak, A.M.; Canadell, J.G.; Saikawa, E.; Huntzinger, D.N.; Gurney, K.R.; Sitch, S.; Zhang, B.; et al. The terrestrial biosphere as a net source of greenhouse gases to the atmosphere. Nature 2016, 531, 225–228. [Google Scholar] [CrossRef]
- Lacheheb, M.; Rahim, A.S.A.; Sirag, A. Economic Growth and Carbon Dioxide Emissions: Investigating the Environ-mental Kuznets Curve Hypothesis in Algeria. Int. J. Energy Econ. Policy 2016, 5, 1125–1132. [Google Scholar]
- Kroeze, C.; Dumont, E.; Seitzinger, S.P. New estimates of global emissions of N2O from rivers and estuaries. Environ. Sci. 2005, 2, 159–165. [Google Scholar] [CrossRef]
- Mosier, A.R.; Zhu, Z.L. Changes in patterns of fertilizer nitrogen use in Asia and its consequences for N2O emissions from agricultural systems. Nutr. Cycl. Agroecosyst. 2000, 57, 107–117. [Google Scholar] [CrossRef]
- Aziz, N.; Sharif, A.; Raza, A.; Rong, K. Revisiting the role of forestry, agriculture, and renewable energy in testing envi-ronment Kuznets curve in Pakistan: Evidence from Quantile ARDL approach. Env. Sci. Pollut. Res. 2020, 27, 10115–10128. [Google Scholar] [CrossRef]
- Narayan, P.K.; Narayan, S. Carbon dioxide emissions and economic growth: Panel data evidence from developing countries. Energy Policy 2010, 38, 661–666. [Google Scholar] [CrossRef]
- GOP. Economic Survey of Pakistan; Ministry of Finance, Government of Pakistan (GOP): Islamabad, Pakistan, 2017.
- Bakhsh, K.; Rose, S.; Ali, M.F.; Ahmad, N.; Shahbaz, M. Economic growth, CO2 emissions, renewable waste and FDI relation in Pakistan: New evidences from 3SLS. J. Environ. Manag. 2017, 196, 627–632. [Google Scholar] [CrossRef]
- Zambrono-Monserrate, M.A.; Fernandez, M.A. An environmental Kuznets curve for N2O emissions in Germany: An ARDL approach. UN Sustain. Dev. J. 2017, 41, 119–127. [Google Scholar] [CrossRef]
- Destek, M.A.; Ulucak, R.; Dogan, E. Analyzing the environmental Kuznets curve for the EU countries: The role of ecological footprint. Environ. Sci. Pollut. Res. 2018, 25, 29387–29396. [Google Scholar] [CrossRef]
- Fernandez, M.; Daigneault, A. The Paris Agreement and its impact on cattle and food sectors of New Zealand. N. Z. J. Agric. Res. 2016, 59, 436–443. [Google Scholar] [CrossRef]
- Fernandez, M.; Daigneault, A. Emissions trading and the economic impact of the Paris agreement on New Zealand. Compend. Cuad. Econ. Adm. 2016, 3, 16–26. [Google Scholar]
- Haider, A.; Bashir, A.; Husnain, M.I.U. Impact of agricultural land use and economic growth on nitrous oxide emissions: Evidence from developed and developing countries. Sci. Total. Environ. 2020, 741, 140421. [Google Scholar] [CrossRef]
- Ang, J.B. Economic development, pollutant emissions and energy consumption in Malaysia. J. Policy Model. 2008, 30, 271–278. [Google Scholar] [CrossRef]
- Husnain, M.I.U.; Haider, A.; Khan, M.A. Does the environmental Kuznets curve reliably explain a developmental issue? Environ. Sci. Pollut. Res. 2021, 28, 11469–11485. [Google Scholar] [CrossRef] [PubMed]
- Duodu, A. Is Trade Bad for the Environment? Decomposing the Impact of Trade on Environmental Quality. Master’s Thesis, School of Economics and Management, Lund University, Lund, Sweden, 2018. [Google Scholar]
- Burki, A.A.; Iqbal, N. Review of Agricultural Pricing Policies in Pakistan: The Choice for a Just Price. Asia Pac. Dev. J. 1994, 1, 91–105. [Google Scholar]
- World Bank World Development Indicators. The World Bank Group A to Z 2016; World Bank World: Washington, DC, USA, 2015; p. 192c. [Google Scholar]
- Our World in Data. Available online: https://ourworldindata.org/greenhouse-gas-emissions#per-capita-nitrous-oxide-emissions-how-much-does-the-average-person-emit (accessed on 10 February 2021).
- Sinha, A.; Bhattacharya, J. Environmental Kuznets curve estimation for NO2 emission: A case of Indian cities. Ecol. Indic. 2016, 67, 1–11. [Google Scholar] [CrossRef]
- Zeldovich, Y.B. The oxidation of nitrogen in combustion and explosions. Acta Physicochim. URSS 1946, 21, 577–628. [Google Scholar]
- Bhaduri, S. Vehicular growth and air quality at major traffic intersection points in Kolkata city: An efficient intervention strategy. SIJ Trans. Adv. Space Res. Earth Explor. 2013, 1, 19–25. [Google Scholar]
- Relwani, S.M.; Moschandreas, D.J.; Billick, I.H. Effects of Operational Factors on Pollutant Emission Rates from Residential Gas Appliances. J. Air Pollut. Control. Assoc. 1986, 36, 1233–1237. [Google Scholar] [CrossRef] [PubMed]
- Himmel, R.L.; de Werth, D.W. Evaluation of the Pollutant Emissions from Gas-Fired Ranges. Project EP-1-23-Analysis of Flue Products from Gas-Fired Appliances; Report No. 1492; American Gas Association Laboratories: Cleveland, OH, USA, 1974. [Google Scholar]
- Lau, S.S. The Physical Environment of Tall Residential Buildings: The Case of Hong Kong. In High-Rise Living in Asian Cities; Yuen, B., Yeh, A.G.O., Eds.; Springer: Amsterdam, The Netherlands, 2011; pp. 25–47. [Google Scholar]
- Grossman, G.M.; Krueger, A.B. Environmental Impacts of a North. American Free Trade Agreement; National Bureau of Economic Research: Cambridge, MA, USA, 1991. [Google Scholar]
- Jebli, M.B.; Youssef, S.B.; Ozturk, I. Testing the environmental Kuznets curve hypothesis: The role of renewable and non-renewable energy consumption and trade in OECD countries. Ecol. Indic. 2016, 60, 824–831. [Google Scholar] [CrossRef]
- Tutulmaz, O. Environmental Kuznets Curve time series application for Turkey: Why controversial results exist for similar models? Renew. Sustain. Energy Rev. 2015, 50, 73–81. [Google Scholar] [CrossRef]
- Gill, A.R.; Viswanathan, K.K.; Hassan, S. The Environmental Kuznets Curve (EKC) and the environmental problem of the day. Renew. Sustain. Energy Rev. 2018, 81, 1636–1642. [Google Scholar] [CrossRef]
- Farhani, S.; Mrizak, S.; Chaibi, A.; Rault, C. The environmental Kuznets curve and sustainability: A panel data analysis. Energy Policy 2014, 71, 189–198. [Google Scholar] [CrossRef]
- Kaika, D.; Zarvas, E. The environmental Kuznets (EKC) theory-Part A: Concept, causes, and the CO2 emission case. Energy Policy 2013, 62, 1392–1402. [Google Scholar] [CrossRef]
- Kaika, D.; Zarvas, E. The environmental Kuznets (EKC) theory-Part B: Critical issues. Energy Policy 2013, 62, 1403–1411. [Google Scholar] [CrossRef]
- Al-Mulali, U.; Saboori, B.; Ozturk, I. Investigating the environmental Kuznets curve hypothesis in Vietnam. Energy Policy 2015, 76, 123–131. [Google Scholar] [CrossRef]
- Lin, S.; Wang, S.; Marinova, D.; Zhao, D.; Hong, J. Impacts of urbanization and real economic development on CO2 emissions in non-high-income countries: Empirical research based on the extended STIRPAT model. J. Clean. Prod. 2017, 166, 952–966. [Google Scholar] [CrossRef]
- Liu, X.; Bae, J. Urbanization and industrialization impact of CO2 emissions in China. J. Clean. Prod. 2018, 172, 178–186. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, S.; Bae, J. The impact of renewable energy and agriculture on carbon dioxide emissions: Investigating the en-vironmental Kuznets curve in four selected ASEAN countries. J. Clean. Prod. 2017, 164, 1239–1247. [Google Scholar] [CrossRef]
- Dogan, E.; Turkekul, B. CO2 emissions, real output, energy consumption, trade, urbanization and financial development: Testing the EKC hypothesis for the USA. Environ. Sci. Pollut. Res. 2016, 23, 1203–1213. [Google Scholar] [CrossRef] [PubMed]
- Shahbaz, M.; Sinha, A. Environmental Kuznets curve for CO2 emissions: A literature survey. J. Econ. Stud. 2019, 46, 106–168. [Google Scholar] [CrossRef]
- Wang, Y.; Han, R.; Kubota, J. Is there an Environmental Kuznets Curve for SO2 emissions? A semi-parametric panel data analysis for China. Renew. Sustain. Energy Rev. 2016, 54, 1182–1188. [Google Scholar] [CrossRef]
- Taguchi, H. The environmental Kuznets curve in Asia: The case of sulfur and carbon emissions. Asia-Pac. Dev. J. 2012, 19, 77–92. [Google Scholar] [CrossRef]
- Cho, C.-H.; Chu, Y.-P.; Yang, H.-Y. An Environment Kuznets Curve for GHG Emissions: A Panel Cointegration Analysis. Energy Sources Part. B Econ. Plan. Policy 2013, 9, 120–129. [Google Scholar] [CrossRef]
- Och, M. Empirical Investigation of the Environmental Kuznets Curve Hypothesis for Nitrous Oxide Emissions for Mongolia. Int. J. Energy Econ. Policy 2017, 7, 117–128. [Google Scholar]
- Wang, S.; Yang, F.; Wang, X.; Song, J. A Microeconomics Explanation of the Environmental Kuznets Curve (EKC) and an Empirical Investigation. Pol. J. Environ. Stud. 2017, 26, 1757–1764. [Google Scholar] [CrossRef]
- Nassani, A.A.; Aldakhil, A.M.; Abro, M.M.Q.; Zaman, K. Environmental Kuznets curve among BRICS countries: Spot lightening finance, transport, energy and growth factors. J. Clean. Prod. 2017, 154, 474–487. [Google Scholar] [CrossRef]
- Fujii, H.; Managi, S. Economic development and multiple air pollutant emissions from the industrial sector. Environ. Sci. Pollut. Res. 2016, 23, 2802–2812. [Google Scholar] [CrossRef]
- Luo, Y.; Chen, H.; Zhu, Q.; Peng, C.; Yang, G.; Yang, Y.; Zhang, Y. Relationship between Air Pollutants and Economic Development of the Provincial Capital Cities in China during the Past Decade. PLoS ONE 2014, 9, e104013. [Google Scholar] [CrossRef] [PubMed]
- Kubicová, J. Testing greenhouse gasses in Slovakia for environmental Kuznets curve and pollution haven hypothesis. J. Int. Stud. 2014, 7, 161–177. [Google Scholar] [CrossRef] [PubMed]
- Tamang, P. Re-examining the Environmental Kuznets Curve: Evidence from Time Series. Financ. Quant. Anal. 2013, 1, 30–42. [Google Scholar] [CrossRef]
- Mazzanti, M.; Montini, A.; Zoboli, R. Environmental Kuznets Curves for Greenhouse Gas emissions. Evidence from Italy using National Accounts Matrix including Environmental Accounts and provincial panel data. Int. J. Glob. Environ. Issues 2008, 8, 392. [Google Scholar] [CrossRef]
- Roca, J.; Padilla, E.; Farré, M.; Galletto, V. Economic growth and atmospheric pollution in Spain: Discussing the environmental Kuznets curve hypothesis. Ecol. Econ. 2001, 39, 85–99. [Google Scholar] [CrossRef]
- Shafik, N.; Bandyopadhyay, S. Economic Growth and Environmental Quality: Time Series and Cross-Country Evidence; BackGround Paper for the World Development Report; The World Bank: Washington, DC, USA, 1992. [Google Scholar]
- Yang, H.; He, J.; Chen, S. The fragility of the Environmental Kuznets Curve: Revisiting the hypothesis with Chinese data via an “Extreme Bound Analysis”. Ecol. Econ. 2015, 109, 41–58. [Google Scholar] [CrossRef]
- Moosa, I.A. The econometrics of the environmental Kuznets curve: An illustration using Australian CO2 emissions. Appl. Econ. 2017, 49, 4927–4945. [Google Scholar] [CrossRef]
- Perman, R.; Stern, D.I. Evidence from panel unit root and cointegration tests that the Environmental Kuznets Curve does not exist. Aust. J. Agric. Resour. Econ. 2003, 47, 325–347. [Google Scholar] [CrossRef]
- Van Alistine, J.; Neumayer, E. The Environmental Kuznets Curve. In Handbook on Trade and the Environment 2010; Gallagher, K.P., Ed.; Edward Elgar Publishing: Cheltenham, UK, 2010. [Google Scholar]
- Zhang, J. Delivering Environmentally Sustainable Economic Growth: The Case of China; Working Paper; Asia Society: New York, NY, USA, 2012. [Google Scholar]
- Kearsley, A.; Riddel, M. A further inquiry into the Pollution Haven Hypothesis and the Environmental Kuznets Curve. Ecol. Econ. 2010, 69, 905–919. [Google Scholar] [CrossRef]
- Cole, M.A. Trade, the pollution haven hypothesis and the environmental Kuznets curve: Examining the linkages. Ecol. Econ. 2004, 48, 71–81. [Google Scholar] [CrossRef]
- Shahbaz, M.; Hye, Q.M.A.; Tiwari, A.K.; Leitão, N.C. Economic growth, energy consumption, financial development, international trade and CO2 emissions in Indonesia. Renew. Sustain. Energy Rev. 2013, 25, 109–121. [Google Scholar] [CrossRef]
- Shahbaz, M.; Khraief, N.; Uddin, G.S.; Ozturk, I. Environmental Kuznets curve in an open economy: A bounds testing and causality analysis for Tunisia. Renew. Sustain. Energy Rev. 2014, 34, 325–336. [Google Scholar] [CrossRef]
- Tiwari, A.K.; Shahbaz, M.; Hye, Q.M.A. The environmental Kuznets curve and the role of coal consumption in India: Cointe-gration and causality analysis in an open economy. Renew Sustain. Energy Rev. 2013, 18, 519–527. [Google Scholar] [CrossRef]
- Dinda, S. Environmental Kuznets Curve Hypothesis: A Survey. Ecol. Econ. 2004, 49, 431–455. [Google Scholar] [CrossRef]
- Pesaran, M.H.; Shin, Y.; Smithc, R.J. Bounds testing approaches to the analysis of level relationships. J. Appl. Econ. 2001, 16, 289–326. [Google Scholar] [CrossRef]
- Engle, R.F.; Granger, C.W.J. Co-Integration and Error Correction: Representation, Estimation, and Testing. Econometrica 1987, 55, 251. [Google Scholar] [CrossRef]
- Johansen, S.; Juselius, K. Maximum likelihood estimation and inference on cointegration with applications to the demand for money. Oxf. Bull. Econ. Stat. 2009, 52, 169–210. [Google Scholar] [CrossRef]
- Phillips, P.C.B.; Hansen, B.E. Statistical Inference in Instrumental Variables Regression with I(1) Processes. Rev. Econ. Stud. 1990, 57, 99–125. [Google Scholar] [CrossRef]
- Sadik-Zada, E.R.; Loewenstein, W.; Hasanli, Y. Production linkages and dynamic fiscal employment effects of the extractive industries: Input-output and nonlinear ARDL analyses of Azerbaijani economy. Miner. Econ. 2021, 34, 3–18. [Google Scholar] [CrossRef]
- Zivot, E.; Andrews, D.W. Further evidence on the great crash, the oil-price shock, and the unit-root hypothesis. J. Bus. Econ. Stat. 1992, 10, 251–270. [Google Scholar]
- Baum, C.F. A review of Stata 8.1 and its time series capabilities. Int. J. Forecast. 2004, 20, 151–161. [Google Scholar] [CrossRef]
- Narayan, P.K. The saving and investment nexus for China: Evidence from cointegration tests. Appl. Econ. 2005, 37, 1979–1990. [Google Scholar] [CrossRef]
- Bouznit, M.; Pablo-Romero, M.D.P. CO2 emission and economic growth in Algeria. Energy Policy 2016, 96, 93–104. [Google Scholar] [CrossRef]
- Brown, R.L.; Durbin, J.; Evans, J.M. Techniques for Testing the Constancy of Regression Relationships Over Time. J. R. Stat. Soc. Ser. B 1975, 37, 149–163. [Google Scholar] [CrossRef]
- Granger, C.W.J. Investigating Causal Relations by Econometric Models and Cross-spectral Methods. Econometrica 1969, 37, 424. [Google Scholar] [CrossRef]
- Hsiao, C. Panel Data Analysis—Advantages and Challenges. SSRN Electron. J. 2006, 16, 1–22. [Google Scholar] [CrossRef]
- Sadik-Zada, E.R.; Loewenstein, W. Drivers of CO2-Emissions in Fossil Fuel Abundant Settings: (Pooled) Mean Group and Nonparametric Panel Analyses. Energies 2020, 13, 3956. [Google Scholar] [CrossRef]
- Gao, J.; Hawthorne, K. Semiparametric estimation and testing of the trend of temperature series. Econ. J. 2006, 9, 332–355. [Google Scholar] [CrossRef]
- Shin, Y.; Yu, B.; Greenwood-Nimmo, M. Modelling Asymmetric Cointegration and Dynamic Multipliers in a Nonlinear ARDL Framework. In Festschrift in Honor of Peter Schmidt; Sickles, R., Horrace, W., Eds.; Springer: New York, NY, USA, 2014. [Google Scholar]
- Balaguer, J.; Cantavella, M. Estimating the environmental Kuznets curve for Spain by considering fuel oil prices (1874–2011). Ecol. Indic. 2016, 60, 853–859. [Google Scholar] [CrossRef]
- Lütkepohl, H. Structural vector autoregressive analysis for cointegrated variables. Allg. Stat. Arch. 2006, 90, 75–88. [Google Scholar] [CrossRef]
- Allard, A.; Takman, J.; Uddin, G.S.; Ahmed, A. The N-shaped environmental Kuznets curve: An empirical evaluation using a panel quantile regression approach. Environ. Sci. Pollut. Res. 2017, 25, 5848–5861. [Google Scholar] [CrossRef]
- Paudel, K.P.; Schafer, M.J. The Environmental Kuznets Curve Under a New Framework: The Role of Social Capital in Water Pollution. Environ. Resour. Econ. 2009, 42, 265–278. [Google Scholar] [CrossRef]
- Bölük, G.; Mert, M. The renewable energy, growth and environmental Kuznets curve in Turkey: An ARDL approach. Renew. Sustain. Energy Rev. 2015, 52, 587–595. [Google Scholar] [CrossRef]
- Zambrano-Monserrate, M.A.; García-Albán, F.F.; Henk-Vera, K.A. Bounds testing approach to analyze the existence of an Environmental Kuznets Curve in Ecuador. Int. J. Energy Econ. Policy 2016, 6, 159–166. [Google Scholar]
- Zambrano-Monserrate, M.A.; Valverde-Bajana, I.; Aguilar-Bohorquez, J.; Mendoza-Jimenez, M.J. Relationship between eco-nomic growth and environmental degradation: Is there evidence of an Environmental Kuznets Curve for Brazil? Int. J. Energy Econ. Policy 2016, 6, 208–216. [Google Scholar]
- Zambrano-Monserrate, M.A.; Troccoly-Quiroz, A.; Pacheco-Borja, M.J. Testing the environmental Kuznets Curve hypothesis in Iceland: 1960–2010. Rev. Econ. Rosario 2016, 19, 5–28. [Google Scholar] [CrossRef]
- Sadik-Zada, E.R.; Gatto, A. The puzzle of greenhouse gas footprints of oil abundance. Socio-Econ. Plan. Sci. 2020, 100936. [Google Scholar] [CrossRef]
- OECD. Data on Pakistan, 2016. Available online: https://www.oecd.org/ (accessed on 6 June 2020).
- Binder, S.; Neumayer, E. Environmental pressure group strength and air pollution: An empirical analysis. Ecol. Econ. 2005, 55, 527–538. [Google Scholar] [CrossRef]
- Canas, Â.; Ferrão, P.; Conceição, P. A new environmental Kuznets curve? Relationship between direct material input and income per capita: Evidence from industrialised countries. Ecol. Econ. 2003, 46, 217–229. [Google Scholar] [CrossRef]
- De Bruyn, S.; Opschoor, J. Developments in the throughput-income relationship: Theoretical and empirical observations. Ecol. Econ. 1997, 20, 255–268. [Google Scholar] [CrossRef]
- Husnain, M.I.U.; Khan, M.; Mahmood, H.Z. An assessment of public and private benefits of organic farming in Pakistan. J. Anim. Plant Sci. 2017, 27, 996–1004. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).