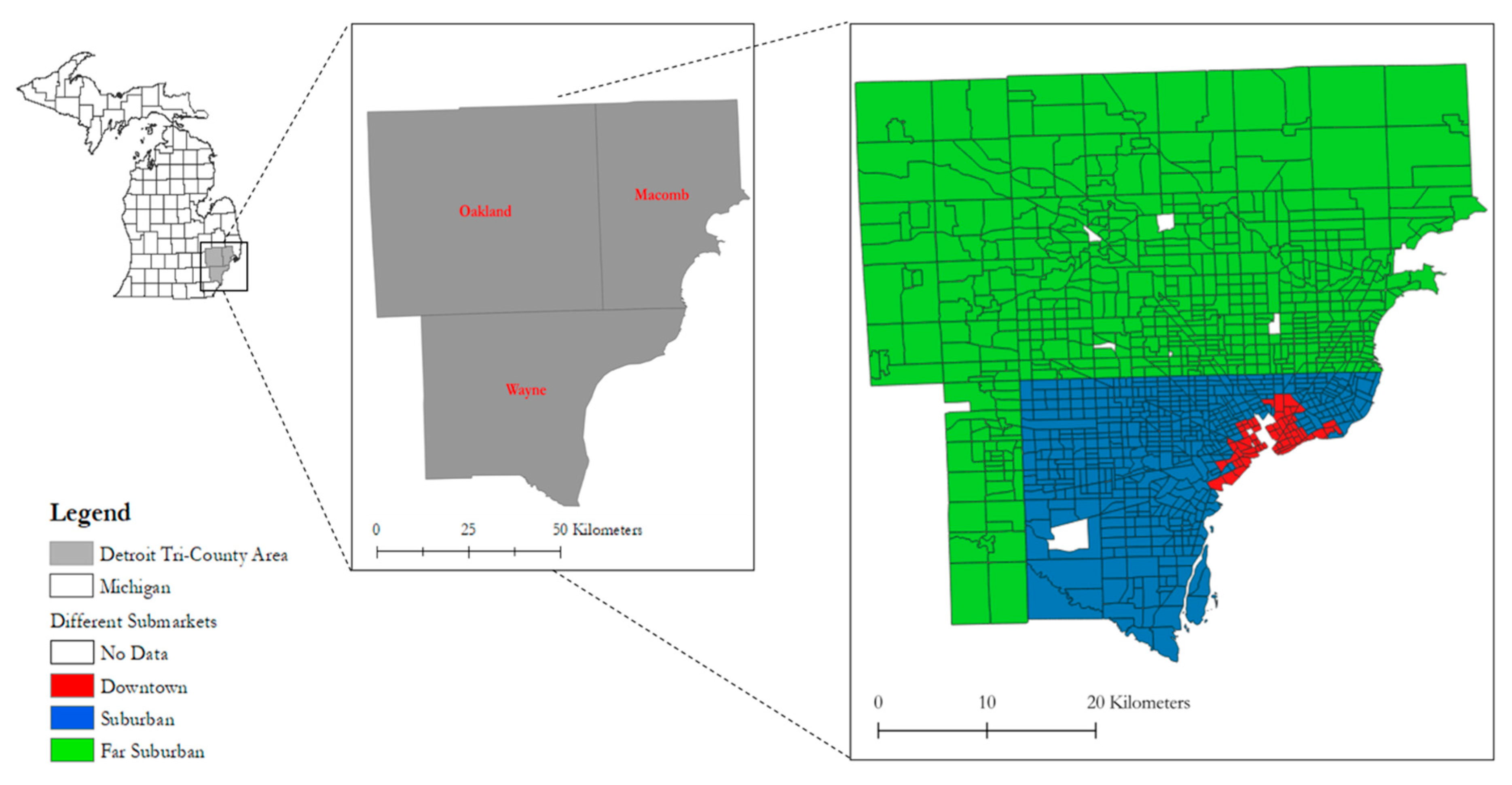
1. Introduction
For the first time in human history, more people are living in urban areas (4.2 billion people or 55% of the world’s population) and this is expected to grow in the coming decades [
1]. While the world’s urban population continues to grow, this growth is not equal [
2]. Some cities are actually shrinking, and the list of shrinking cities expands every year and currently includes: Leipzig in Germany; Urumqi in China; and Detroit in the United States [
3,
4,
5]. The causes of urban shrinkage have been the source of much debate but can be broadly attributed to a combination of factors related to deindustrialization, suburbanization (i.e., urban sprawl) and demographic withdrawal (see: [
6,
7,
8]). It has also been noted that urban shrinkage poses a significant challenge to urban sustainability from the urban planning, development and management point of view due to declining populations and changes in land use [
9].
The challenges brought by shrinking cities, especially in and around the traditional downtown core of the city results in many problems such as population loss, economic depression (due to loss in tax revenue), a growth in vacant properties and the contraction of the land and housing markets. From a more general perspective, cities that focus too much on one branch of the economy are often not regarded as sustainable, as such cities are more vulnerable if the specific industry that they rely on declines [
10] (as was the case for Detroit and its reliance on the manufacturing industry). Hence, a decline of a specific industry will cause people to lose their jobs and unemployment rates to rise. Residents in such cities may therefore leave their current location in order to find employment opportunities in other areas. Such employment mobility results in a large number of properties in shrinking cities to be left vacant as the population in a city declines. Significant amounts of vacant land and abandoned properties across an entire urban area are one of the key characteristics of a shrinking city [
11]. Not only do these vacant (abandoned) properties potentially result in higher rates of crime [
12], but they also impact the local economy and contract the local housing market [
13]. For example, local governments collect less property tax revenue due to the vacant properties, and therefore have less money to allocate to public safety and infrastructure, which in turn potentially accelerates population decline. In other words, the economic decline may worsen and the vacant properties may lead to the oversupply of stock within local housing markets. Therefore, it is rational to expect house prices to decrease and, if the population continues to decline, the local housing market may contract or collapse completely [
14].
Numerous factors including regional housing market trends, job suburbanization, deindustrialization, downturns in the economy, increasing unemployment rates and population loss account for the causes of shrinking cities and the consequent contraction of the housing market at the macro-level [
14,
15,
16]. For example, in Detroit, the continued suburbanization of jobs has driven people from downtown areas. More generally speaking, deindustrialization and the loss of manufacturing, construction, and retail has accounted for 60 percent of job losses in the 100 largest United States metro areas over the last few decades [
15]. People working in such sectors become unemployed and seek employment elsewhere [
8]. The motivation of this paper is to explore the housing market in a shrinking city from the micro-level interactions, specifically based on individuals’ preferences and trading interactions. Therefore, an agent-based model is utilized as a tool to simulate and analyze a shrinking city’s housing market. Specifically, we explore how urban shrinkage emerges at the macro-level through the simulation of housing trades at the individual level. In the remainder of the paper,
Section 2 introduces the study area and provides a literature review with respect to housing and land markets from an agent-based modeling perspective.
Section 3 outlines our model, while
Section 4 presents the results of our simulation experiments. Finally,
Section 5 concludes the paper and discusses areas of future study.
4. Results
Before detailing the results of the model, we first want to discuss our efforts for verification. Here we refer to verification as the process of checking if the model matches its design [
45]. In this study, verification of the model was performed by conducting code walkthroughs, visual debugging [
67] and a series of control variates experiments to ensure the model was working as designed [
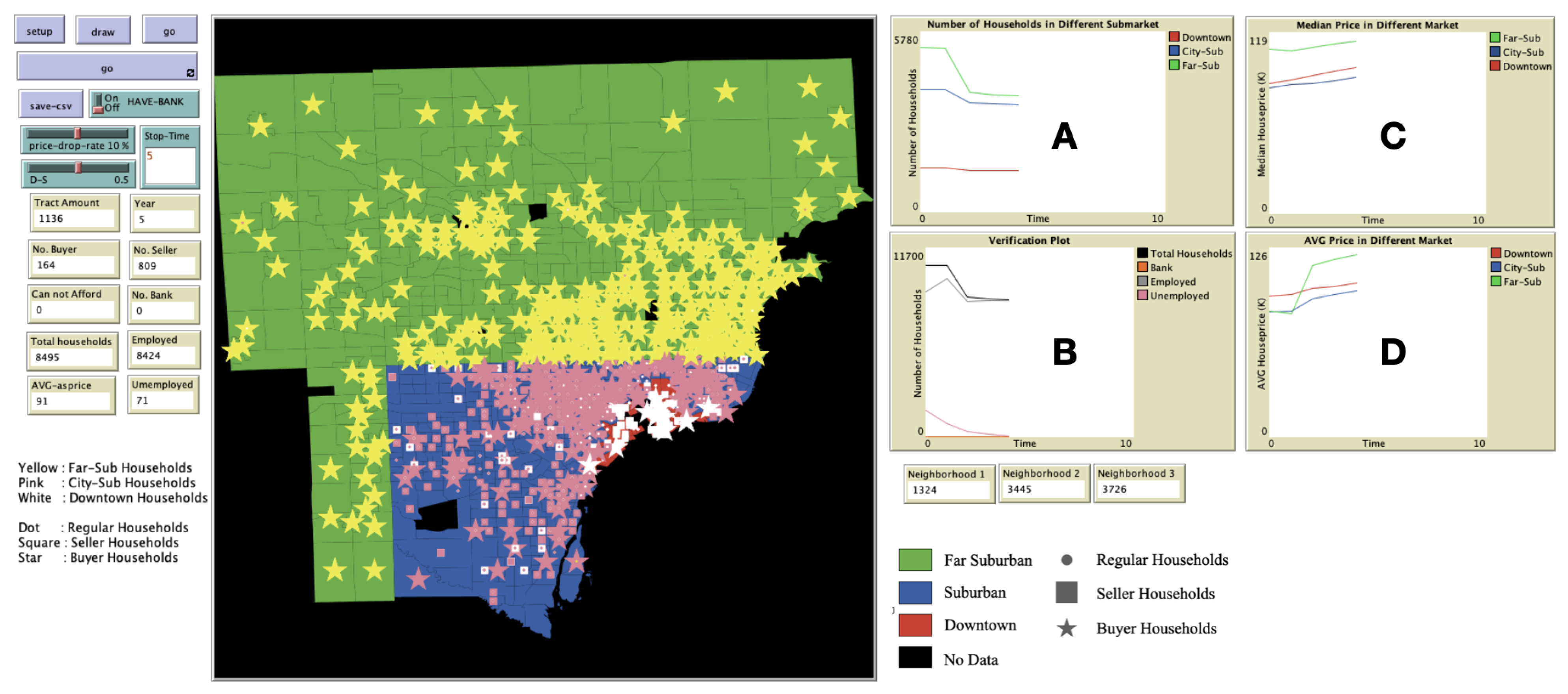
68]. These tests ensured that we made no logical errors in the translation of the model into code, and that there were no programming errors. Visual debugging can be carried via the model interface when the model is running.
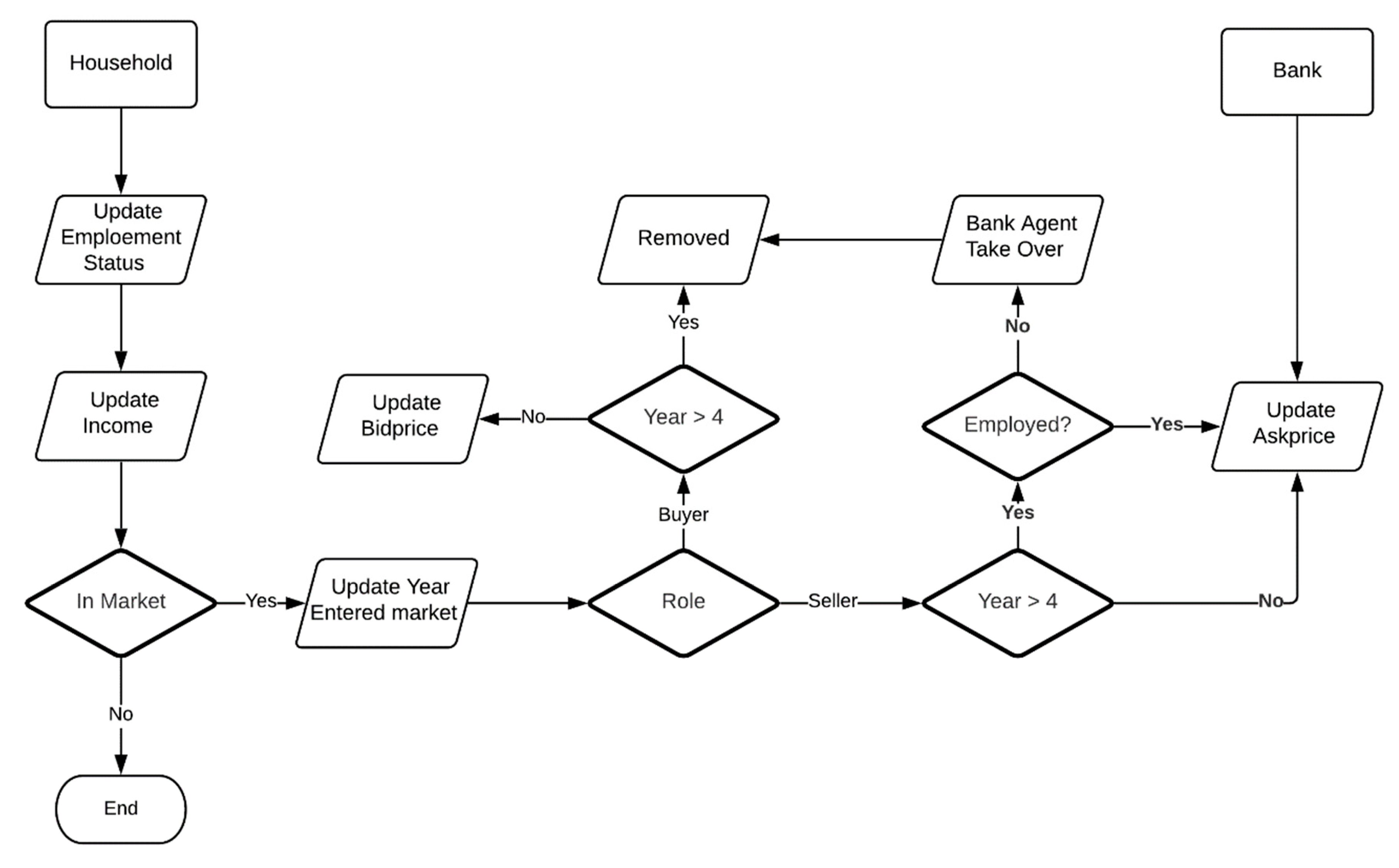
Figure 2 not only introduces the model interface, but also shows an example of visual debugging during a model run. For individual households, we use various shapes and sizes to distinguish different roles and status during a simulation. For example, a dot represents a regular household, a square represents a seller household and a star represents a buyer household, and the size differences of stars indicate the difference statuses of buyers during the trade. A larger star represents a buyer who has successfully completed a house purchase. Other than visual verification at the micro-level as discussed above, four plots (e.g., plot A, B, C, D) are used for macro-level visual verification as shown in
Figure 2. Plot A captures the change in the number of households during the simulation. Plot B outputs some generic results (e.g., total household number, number of bank agents), but the main purpose of this plot is to show that the households’ employment statuses are updating (i.e., changing) over the simulation, which was discussed in
Section 3.4.2. As for Plots C and D, they show the median and average house prices during the simulation. With these plots updating during the simulation, we can ensure that the model does not have programming errors that stop the simulation instantly, but further experiments were needed to test the impacts of the input parameters, which it is not possible to capture through visual debugging alone and we turn to this next.
As discussed in
Section 3.3.1, three input parameters were used in the model: (1) D-S; (2) HAVE-BANK?; (3) Price-Drop-Rate. To test these three input parameters, a series of control experiments were carried out for verification purposes. For instance, when verifying D-S, we only modified the value of D-S and kept the other two parameters set to default values as shown in
Table 2. Each experiment was run 50 times and, in what follows, we describe only the average results.
To verify D-S (see
Section 3.3.1), one does not need to run the model, as D-S is only used when the model is being initialized to set the number of buyers and sellers. Therefore we tested various D-S values (e.g., 0.1, 0.5 and 0.9) and noted its outcome with respect to number of buyers and sellers. Various D-S values stand for different demand and supply scenarios, which will be discussed further below. As shown in
Table 4, the model is able to generate different numbers of buyers and sellers by modifying the value of D-S. As for the other two parameters (i.e., price-drop-rate and HAVE-BANK?), because they are used during the simulation, the following verification experiments were undertaken.
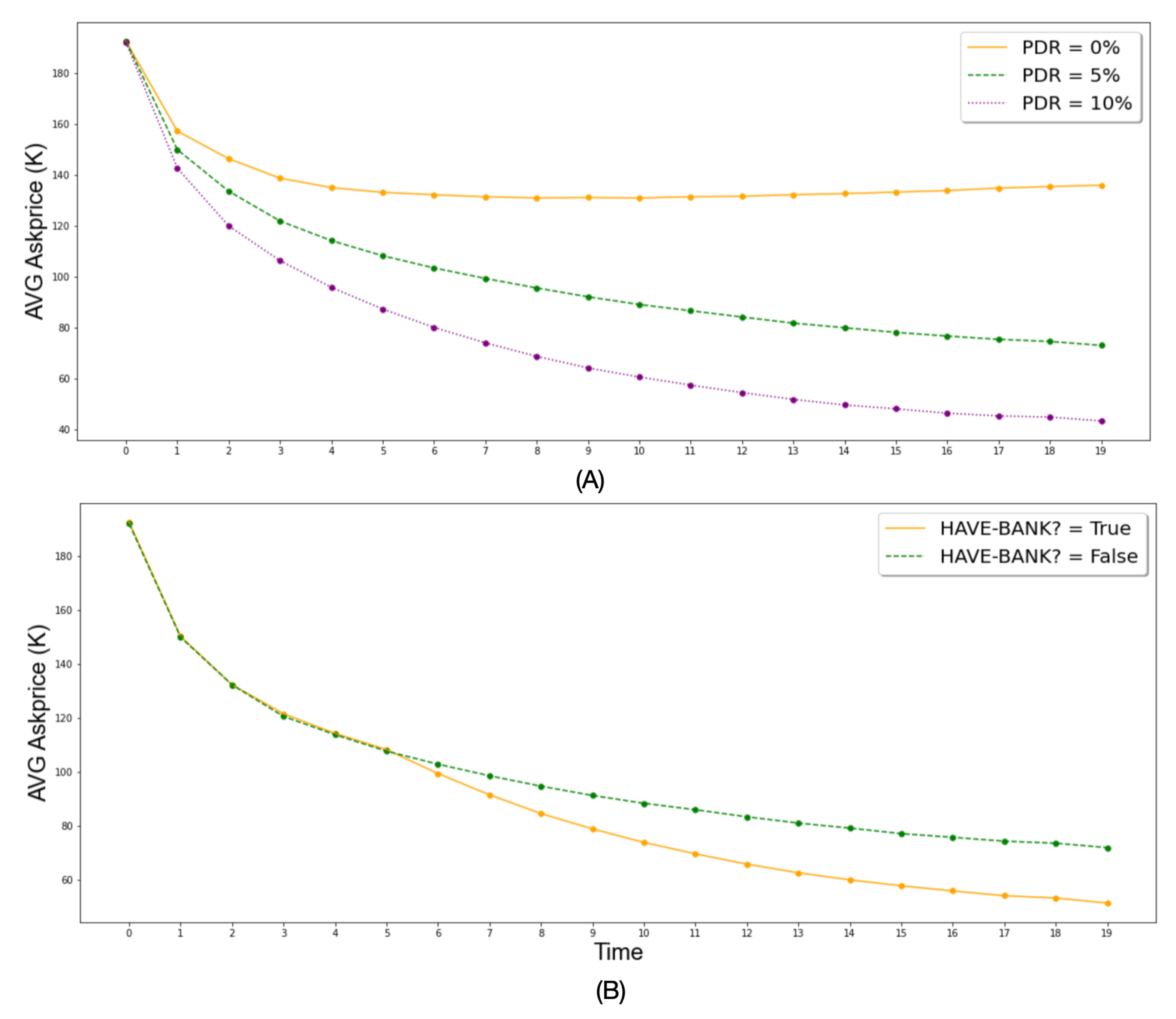
To test price-drop-rate, we carried a series of extreme value tests by setting the parameter to 0, 5, and 10 which represents how much of a percentage of the ask-price will be decreased in each time step if the house is not sold. In this experiment, the bank agent is not added (i.e., HAVE-BANK is False), our rationale for this is that the purpose here is simply to test the impacts of Price-Drop-Rate on ask-price. Hence, by capturing the average ask-price changes over the course of a simulation one gains sufficient evidence for this stage of verification. As
Figure 8A shows, when increasing the value of Price-Drop-Rate, the average ask-price decreases more, which indicates that the Price-Drop-Rate parameter does have an impact on the average ask-price and this parameter works as intended.
Moving to the verification of HAVE-BANK?, as discussed in
Section 3.3.1, HAVE-BANK? allows the model to add a bank agent. Unlike that of regular sellers, bank agents’ ask-price drop rate is doubled (seen
Section 3.4.2). Hence, we assume that with the increasing number of bank owned properties, the average ask-prices may decrease more than those in a scenario where there is no bank agent. In
Table 5, we capture 805 bank owned proprieties by the end of the simulation, which indicates HAVE-BANK? is capable of adding a bank agent when the need arises.
Figure 8B shows that the average ask-price drops with the increasing number of properties owned by the bank agent, and the average ask-price is lower compared to the no bank scenario. This suggests that the bank agent is added properly by the model. After carrying out these tests, we feel confident that the model behaves as it is intended and matches its design and thus is verified.
Now, turning to model results and validation, we refer to validation as the process ensuring the model aligns to the real world, specifically how the model can capture basic market behavior as it potentially relates to urban shrinkage. In order to do this we present three simulation scenarios of different demand and supply conditions for a period of 20 (year) time steps. We ran each scenario 50 times and, in what follows, we describe only the average results. We chose 20 years as this will cover the years of 1990, 2000 and 2010, which we have census data for, which in turn can be used to validate the model. To control for demand and supply, we only changed the D-S parameter in the model and kept all other parameters at their default values (e.g.,
Table 2). Three different scenarios were simulated to explore how different demand and supply conditions impact on median and average house prices in the different sub-markets: (1) equal demand and supply; (2) demand exceeds supply; (3) supply exceeds demand.
Table 6 shows the final median and average house prices in each sub-market for different D-S settings, which are the same values described in
Section 4.
Building on
Table 6,
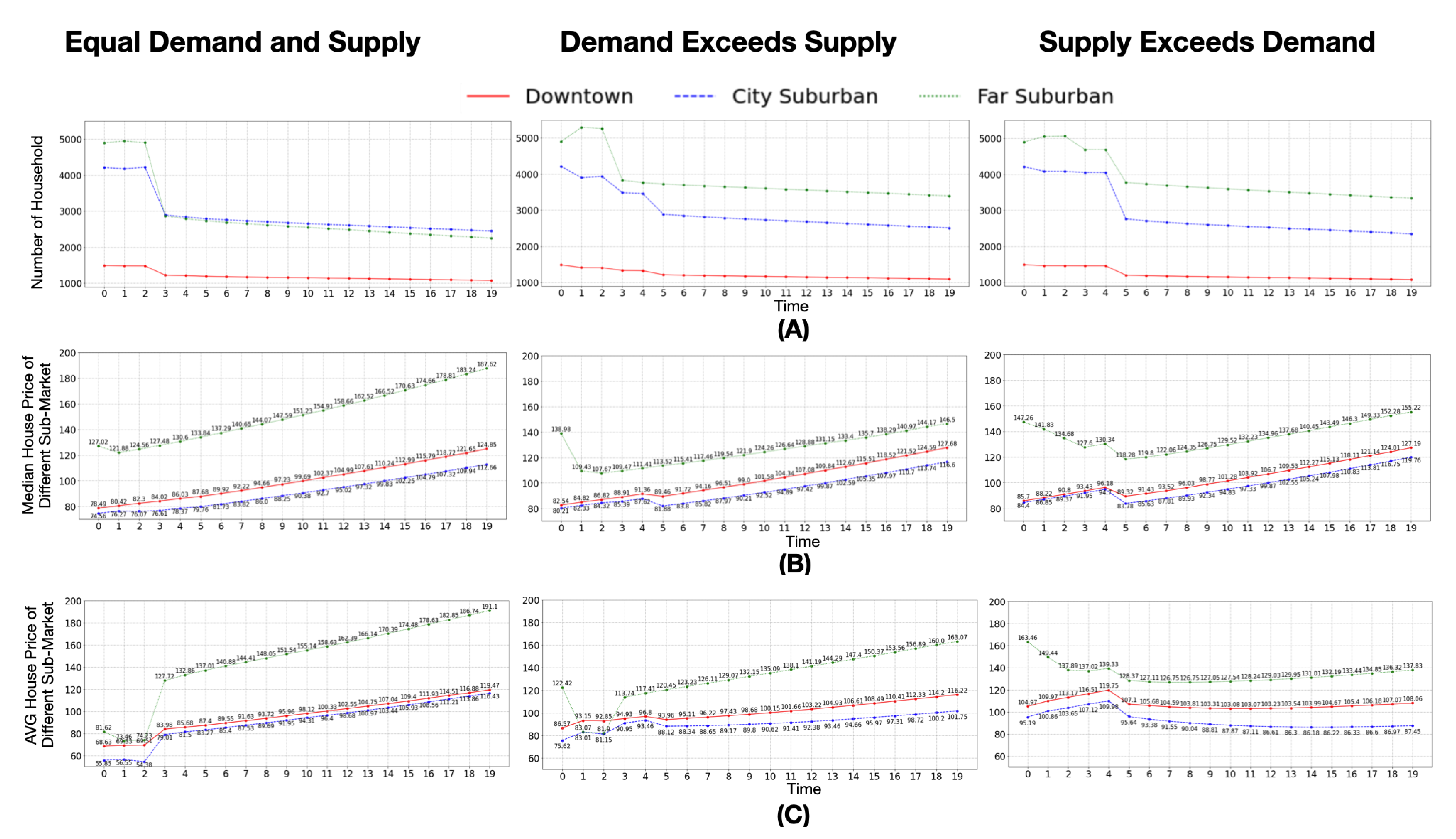
Figure 9A shows the three scenarios with respect to the number of households in each sub-market. As
Figure 9A shows, the overall trend of household numbers in all the three scenarios are decreasing, which can be considered as population loss in a shrinking city. However, one can see that around time step 5, there is a drop in the number of households. This drop is due to the bank agent entering the simulation and taking over sellers’ houses which were unsold (as discussed in
Section 3.4.2).
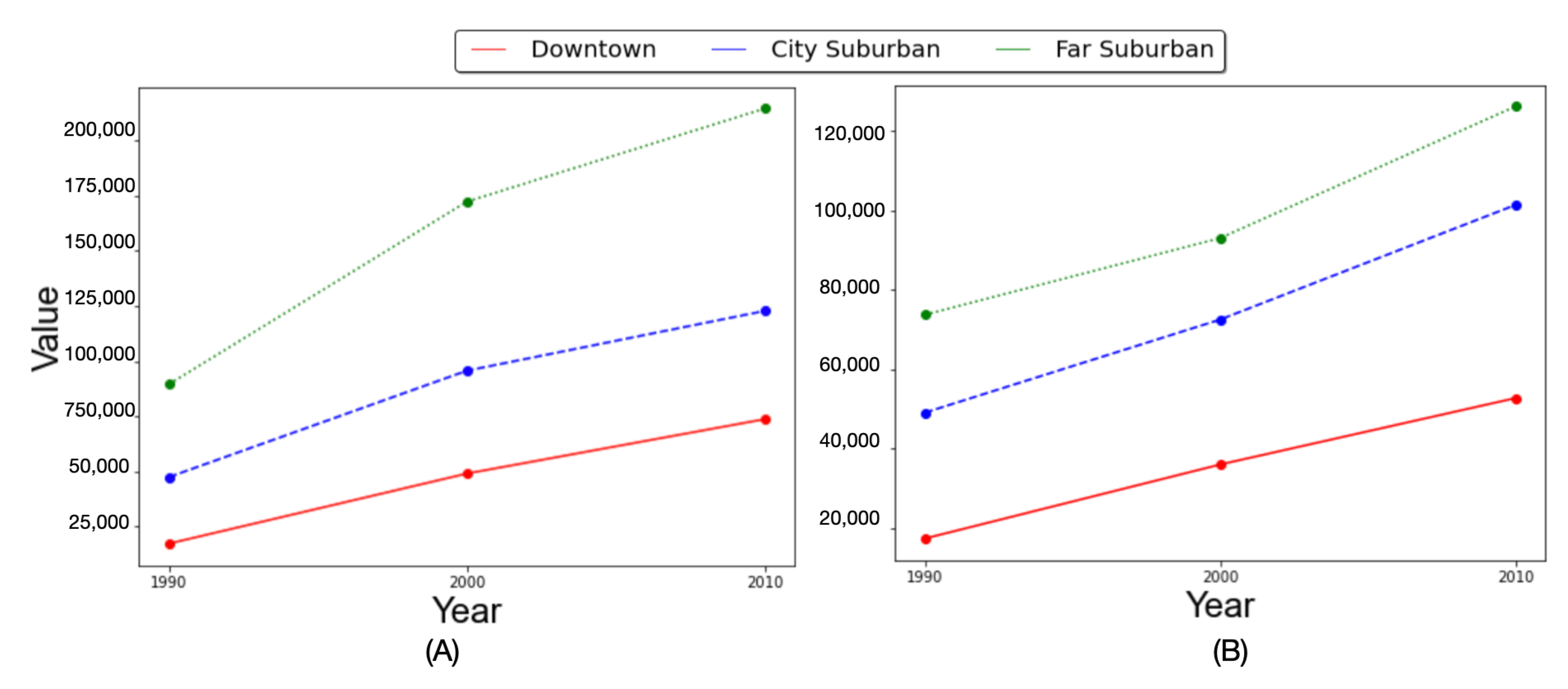
Figure 9B,C demonstrates how median and average house prices change over the simulation scenarios. The results indicate that among all three simulation scenarios, the median and average house prices in different sub-markets turn out to be increasing. This is due to inflation, which is included in our model (as discussed in
Section 3.4.3). The simulated increasing house price trends are similar to those of the empirical data which was shown in
Figure 9.
If the demand exceeds supply scenarios, although all buyers are attempting to find sellers and complete trades (i.e., buy a house), due to insufficient sellers generated at initialization of the model, the number of relocating households is the lowest among all scenarios. However, as shown in
Table 6, the model captures the highest median house price in the far suburban sub-market (which is approximately 60% more than that of downtown), which is due to the sellers flooding this area as discussed in
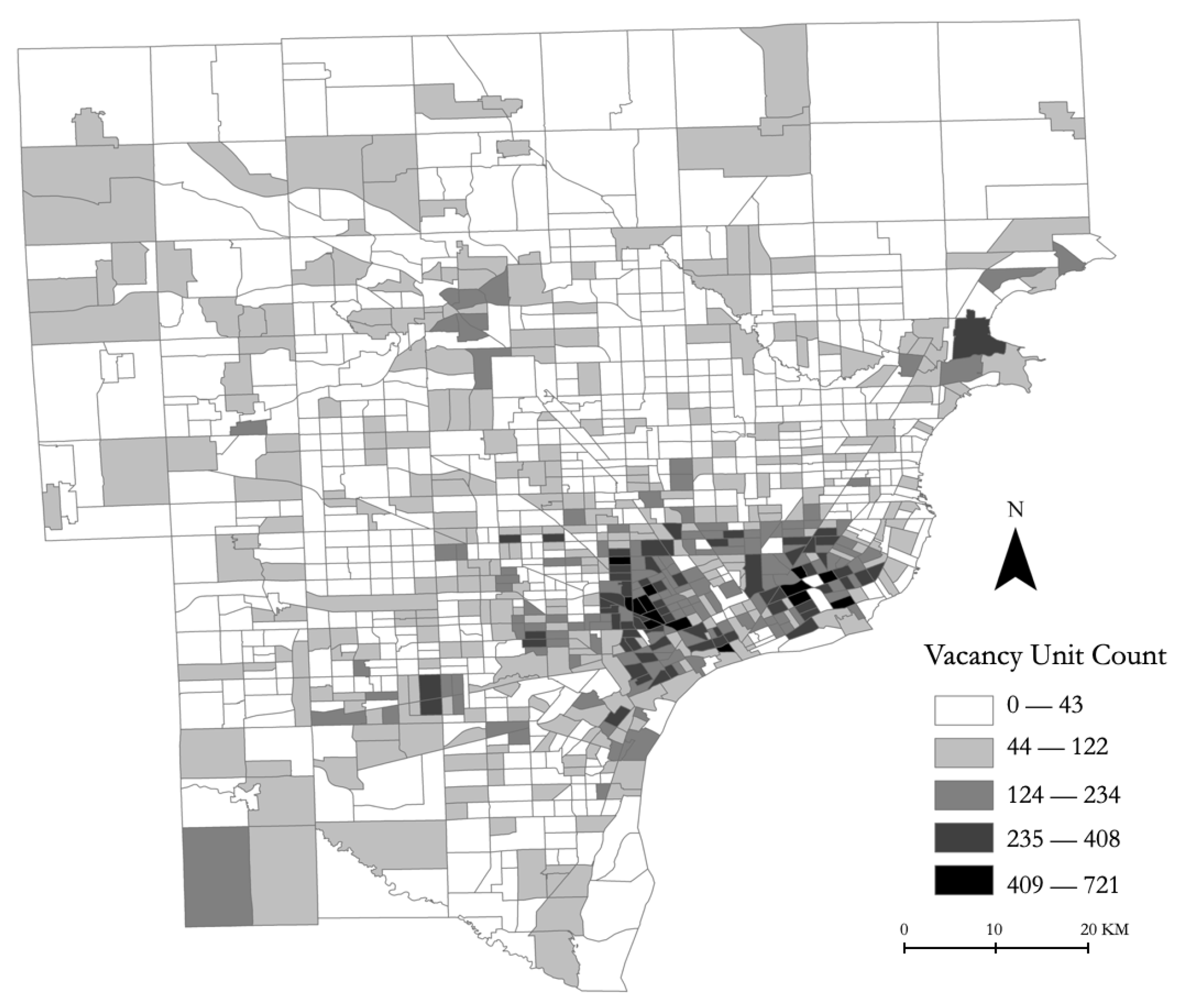
Section 3.4.1 and is similar to what one sees in the “real world” (i.e.,
Figure 7). This suggests the model captures the correct market behavior.
While in the demand equals supply scenario, due to a relatively balanced market, we witness the most household relocations being captured, along with lowest median house prices in suburban and far suburban sub-markets (i.e., suburban: 116.60; far suburban: 146.50). However, the median house price in the downtown sub-market is not the lowest among all scenarios (i.e., 127.68). This result might sound counter-intuitive because one would expect the lowest median house price in the supply exceeds demand scenario, however, the average house price for all three sub-markets in this scenario is in the middle of all the scenarios which suggests there are nuances in how one should record and report the results of the model. One reason for this result could be because all buyers have preferences for purchasing houses in far suburban and suburban (as discussed in
Section 3.4.1), which leads to a relatively competitive market. In addition, all sub-markets’ average house prices are the lowest among all scenarios.
By discussing the results above from the three scenarios, hopefully it is clear to the reader that our model captures urban shrinkage from the aspect of decreasing numbers of households in the downtown sub-market. Also, similar to empirical data as shown in
Figure 7, even without inflation, house prices are still increasing even in a well-known shrinking city and our model captures similar trends in the three scenarios (as shown in
Figure 9). To some extent one could consider such results as level 2 validation in terms of the Axtell and Epstein [
69] schema of classification of model validation, in the sense we can attain quantitative agreements of emerging macro-structures (e.g., declining number of households and increasing house prices) from the bottom-up. We illustrate this in
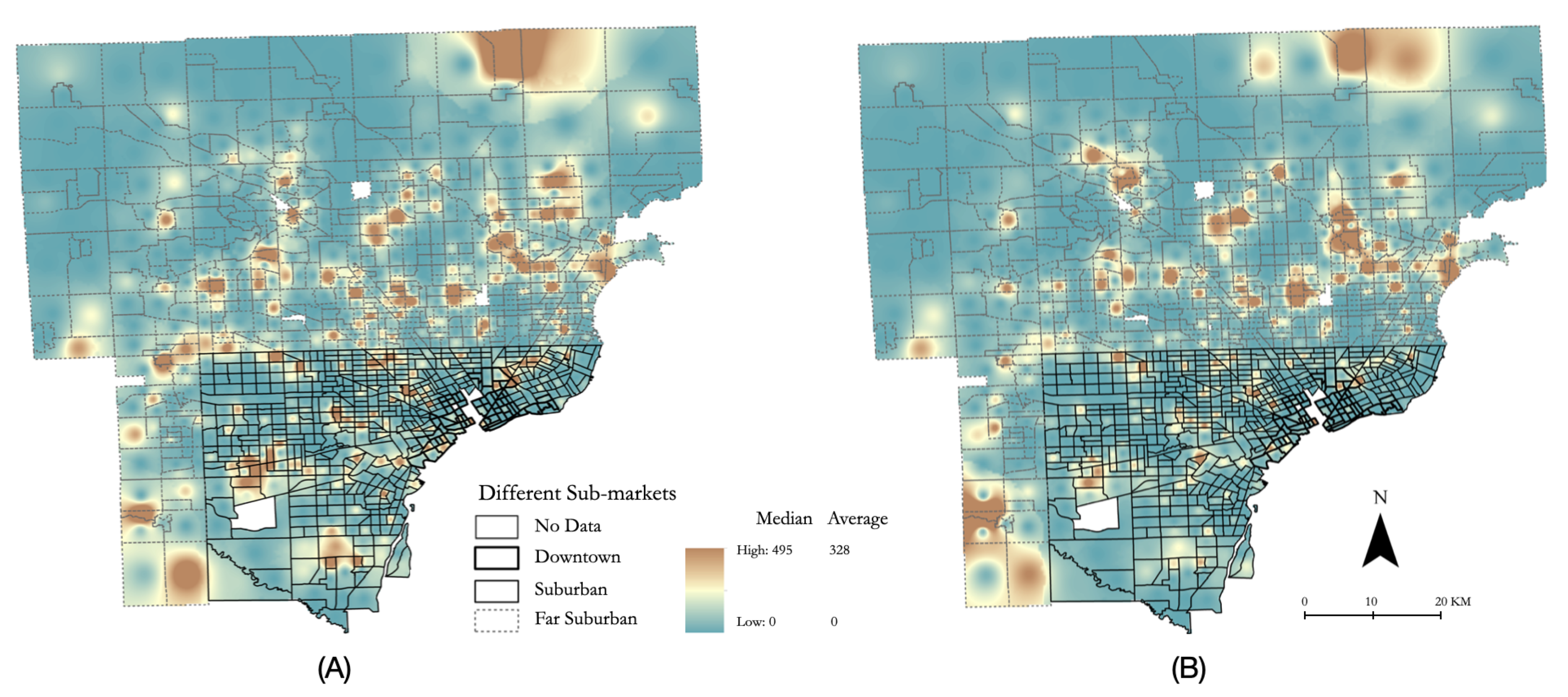
Figure 10 which shows the resulting house prices from the demand equals supply scenario. More specifically,
Figure 10A illustrates a heat map of each census tract’s median house price at the end of the simulation, while
Figure 10B displays the heat map of the average house price. According to these heat maps, high median and average house prices are mainly captured in far suburban sub-markets.
5. Conclusions and Discussion
While we are witnessing a global growth of the urban population, which raises concerns about urban sustainability (e.g., [
9,
70,
71]), not all cities are growing (
Section 1). Some, like Detroit, are actually shrinking, which has drawn a lot of discussion from the research and practice communities globally as it causes population loss, economic decline and a growth in crime due to vacant properties and housing market contraction (e.g., [
7,
13,
14,
72]). However, few efforts have been made to explore this phenomenon from a modeling and simulation domain. This paper significantly adds to this nascent field of inquiry by specifically capturing how the buying and selling of houses can lead to urban shrinkage from the bottom-up through a case study of the Detroit Tri-County area. Results from this model (i.e.,
Section 4) have implications concerning urban shrinkage. For example, we show how household decline in an area could potentially lead to less tax revenue and therefore limits a city’s ability to provide services, which in turn can lead to more urban decline as discussed in
Section 1. Although the simulated median and average house prices are showing an upward trend, which seems inconsistent with the intuitive results of a contracting housing market (i.e., the decreasing of house prices), this was due to the inflation over the simulated years (see
Section 3.4.3 and
Section 4).
While our model can capture urban shrinkage, like all models there are limitations and there is always room for improvement. One area of improvement could be to extend the model to represent more types of housing stock (e.g., apartments, single family homes, etc.) which could be sourced from the American Community Survey or local government property records along with home sales data. We chose not to go this route here as the purpose of the model was to act as a prototype to explore how urban shrinkage might emerge from the bottom-up through the interactions of buying and selling houses. Another area of further work could be to better characterize new incoming populations. In the current model we did not introduce new households based on their heterogeneous financial and demographic backgrounds due to data limitations (i.e., the census data is not continuous between 2000 and 2010). As a result of this, the final simulated household numbers may be lower than the empirical data. With this being said, the declining trend in the number of households for the whole study area is captured successfully by the model, which aligns with the empirical data. One way to better capture new households entering the study area is to use techniques from synthetic population generation such as those seen in dynamic micro-simulation models (e.g., [
73]). This would potentially allow us to better capture how changes in demographics impact on residents’ ability to stay in an area and their preferences for certain types of neighborhoods, but that is beyond the scope of this current paper as this would be a large undertaking and most agent-based models like the ones cited in
Section 2 only look at one aspect (i.e., subsystem) such as the land market rather than the entire urban system itself [
45].
Building upon this idea, the model presented in this paper only explored the buying and selling of properties; however, as we noted in the introduction (
Section 1), urban shrinkage is a complex issue and we do not specifically model the economic environment comprehensively (rather we simply consider inflation as only an aspect of the economic environment). This simulation could be improved by incorporating time series data with respect to the economy such as unemployment rates or economic growth. Alternatively one could couple this model with a more macro economic model to account for such factors (e.g., [
74,
75]). Other than incorporating more data into the simulation, the model could capture more nuanced residential dynamics if the time step was deceased from a year to, say, monthly. This would allow for a slower incremental price dropping of house values if they remained unsold. It would also be interesting to experiment with multiple space-time scales in order to explore the equifinality of urban shrinkage at different temporal and spatial scales (e.g., [
76]). Another area of work, especially with respect to urban sustainability, would be to explore what it would take to stop urban shrinkage, or how neighborhoods go from declining to growing, such as through gentrification. Gentrification in Detroit has been discussed in the literature (e.g., [
77,
78,
79]). Hence, another direction to extend the model would be to explore gentrification in Detroit through modeling and simulation. Similar to urban shrinkage, there is a growing body of models (e.g., [
39,
40,
80]) that show promise for capturing such phenomena. Moving the focus point from Detroit to other metropolitan areas, we believe the model presented here could be generalized across metropolitan areas by integrating more data and adding new types of agents (e.g., investors whose behaviors are different from households and banks). This is one reason we provide the code and the data to the model (see
Section 3), to allow other researchers to extend and explore the model as they see fit. Even with these limitations and areas of further work we believe this paper has demonstrated how agent-based modeling integrated with geo-spatial data provides a promising method for exploring urban shrinkage and, if developed further, potentially offers a means to test policies to alleviate this issue.