1. Introduction
A sculpture exhibition hall is an exhibition space for all types of sculptures. Such exhibits impose unique requirements for their three-dimensional perception, as their exhibition effect depends significantly on the quality of the architectural light environment design. Owing to the inevitable connection between the natural light environment and the design of a museum’s exhibition hall, the exhibition space for different exhibits imposes different daylighting requirements based on the characteristics of the exhibits. During the design process, one should first understand the relationship between the daylighting design methods and the museum’s natural light [
1] to yield a reasonable daylighting design based on the actual light environment. Through the daylighting design of a museum exhibition hall, one can not only reduce the energy consumption of electric lighting to achieve energy saving, but can also enhance the visual comfort of the audience [
2,
3]. To achieve such an effect, an accurate prediction of the daylighting effect and effectiveness at the beginning of the design is necessary. For example, Zhao et al. [
4] evaluated the effect of 22 different design parameters on indoor daylighting to improve user exercise experience in a gymnasium, with the consideration that daylighting can effectively conserve energy. With the constraints of illuminance level and its uniformity, effects owing to factors such as date, latitude, window position, glass transmittance, building height and depth, and window size on daylighting were simulated; it was discovered that the high transmittance of the glass resulted in high brightness contrast between the shadow and irradiation area, giving rise to low
UD in the lighting area, and window size was directly related to daylighting. Therefore, the daylighting of side windows was affected the most by the glass transmittance, building height, and depth. For skylights with different sizes, the most influential factors were glass transmittance and building height. In the study, a simplified formula was obtained through linear regression, enabling architects to rapidly calculate the required window size in the preliminary design stage.
Electric lighting is adopted in many new museum exhibition halls, since the ultraviolet and infrared radiation in natural light is much higher than that of the electric light source. If direct solar light enters the exhibition room without treatment, it will not only cause the indoor temperature to rise and produce direct glare, but will also likely damage and age the sculpture exhibits due to the photochemical action from the ultraviolet (UV) and radiant heating effect of infrared (IR) [
5,
6]. To reduce the damage to exhibits from light sources and to maintain visual quality, Durmus et al. [
7,
8,
9] optimized the spectral power distribution (SPD) of seven narrow-band light-emitting diodes (LEDs) using a multi-target genetic algorithm to reduce light absorption and energy consumption. With respect to spatial and spectral optimization for visual restoration, Vázquez et al. [
10] developed a point-by-point light projection system which achieves the goals of reducing damage to the artwork and saving energy. Furthermore, the projection of light on an exhibit allows us to modify the appearance of the object in a virtual and reversible way [
9,
11]. In museums, this optical technology is suitable for the restoration of cultural heritage, art displays and even educational projects.
On the other hand, natural light is superior to electric light in color rendering, light efficiency and psychological influence. If natural light can be used reasonably, it can not only reflect the original appearance of exhibits, but also create vivid space atmosphere and reduce lighting energy consumption. Natural light, therefore, is indispensable for the exhibition of sculptures. The three-dimensional sense of sculpture exhibits may be obtained, as the indoor color rendering index (CRI) of the electric light which can restore exhibits authentic color be compensated by introducing daylighting. Pinilla [
12] believes that natural light represents not only the rational use of ecological and sustainable energy, but also an inherent artistic aspect of sculpture exhibits, as daylight and seasonal variations were component of the exhibits’ artistic effect. Under the consideration of the exhibits’ protection, Luengo [
13] indicated that the lighting environment of the exhibits should fully respect the historical creation background of the exhibits, so as to accurately convey the artistic effect of the exhibits. For the museums with combination of electric light and natural light, del Hoyo-Meléndez et al. [
14] have progressively and systematically investigated the importance of natural light distribution in museum buildings, which use both electric and natural lighting. Viani et al. [
15] exploited an intelligent lighting system to balance the illumination of daylighting and electric light sources, and to adjust the illumination of electric lighting in real time after monitoring the illumination of daylight through sensors, attenuating the museum’s energy consumption.
However, the natural daylighting design of a museum is complicated. Natural light is highly dynamic and varies significantly with time, place, and weather conditions, which all generate different intensities and directions of the light incidences on the sculptures, resulting in different glare factors, uniformity, and visitor’s experiences, rendering it difficult for designers to consider. Meanwhile, the design of natural daylighting must be combined with the form, lighting and shading of buildings, necessitating complex influencing factors. If an architect designs based on only experience or conventional analysis methods, not only will a significant amount of time be incurred, but also the resulting quantification will be difficult; therefore, the expected and final environmental lighting effects will deviate significantly [
14]. In addition, the adoption of natural light has been controversial because it is difficult to accurately control the amount of daylighting as well as evaluate the daylighting effect accurately. Generally, when an architect is engaged in the daylighting design of a museum exhibition hall, the first consideration is the effect of the window position on daylighting. Luo et al. [
16] demonstrated that for the same window size, the daylighting factor (
DF) of a skylight is better than that of a side window, but the illuminance uniformity is poor. It is more appropriate to adopt a mixed daylighting method combining side windows and skylights for museum buildings with large dimensions. Perez et al. [
17] reported that for large-dimensioned museum buildings, the indoor lighting effect improved as the height of the window increased. Kim et al. [
18] investigated the daylighting effect of museum skylights and discovered that saw-tooth skylights presented favorable daylighting effects.
A daylighting design based on light environment quality can ensure a pleasant and healthy viewing experience for visitors. As large-sized windows for daylight in museum buildings generally result in direct glare in the visual field, reasonably sized windows for daylight must be adjusted to ensure light comfort in the exhibition hall and reduce the effects of glare in specific areas [
19]. Acosta et al. [
20] discovered through actual measurements that the
DF of an indoor area was positively correlated with the surface area of glasses other than windows in the surroundings. Therefore, improper design or lack of effective methods for controlling natural light might result in excessively high illuminance and poor uniformity of daylighting (
UD) at certain areas of the indoor space, resulting in both direct and reflected glare in the viewers’ visual field and hence degrading people’s viewing experience. Moreover, it has been demonstrated that various factors affect visual discomfort caused by glare, which change constantly with time [
21]. Among them, the various types of glare are dominant factors affecting the light environment quality in museum exhibition halls, and it is an existing problem that is difficult to overcome. Because severe glare problems occur in museum buildings, quantitative analysis methods should be used to objectively analyze and optimize the light environment. Huang et al. [
22,
23] optimized the pattern and components of daylighting by simulating the light environment of a museum exhibition space and systematically analyzed the daylighting parameters.
When introducing natural light into a sculpture exhibition hall, factors such as the protection of sculpture exhibits, viewing experience of the audience, and creation of light environment should be considered comprehensively [
24]. When creating a light environment, the daylighting quality should be improved by reducing glare using quantitative and experimental methods to accurately predict glare and minimize the effects of glare when viewing exhibits [
25]. Furthermore, the parameters of light composition, such as correlated color temperature (CCT), CRI, and SPD can be ameliorated by the proper introduction of daylight. This article proposes a reasonable daylighting design for an exhibition space based on the specific characteristics of sculpture exhibits to create a favorable light environment. To avoid the improper design of the light environment for a sculpture exhibition hall, reasons of glare caused by daylighting were analyzed, and factors affecting the daylighting quality of the sculpture exhibition hall were investigated. Then, the effects of the spectral composition parameters and factors (like CCT, CRI, SPD, UV, and IR) on the indoor light quality is also discussed. Therefore, the daylighting design of a sculpture exhibition hall was optimized from the perspective of adjusting daylighting parameters.
2. Display Modes and Daylighting Pattern
Sculptures are static, visible, and tangible three-dimensional objects. Whereas Western sculptures include primarily various types of stone and bronze carvings, Chinese traditional sculptures include primarily stone, wood, bone, bronze, and root carvings. As sculptures imply certain cultural characteristics are often presented in different forms, the theme, cultural background, structural characteristics, and composition materials of sculptures must be analyzed comprehensively to clarify the salient points conveyed by the sculpture before performing the daylighting design of the sculptures. Because sculptures are generally insensitive to light, the introduction of light must not only provide a certain degree of illumination on the surface of the sculptures, thereby ensuring the presentation of details, but also highlight the texture and shadow of the sculptures to express their three-dimensional shapes. Sculpture exhibition halls often adopt top daylighting (diffused light), side daylighting (directional light), or a combination of both. The introduction of daylight must complement the characteristics of the indoor lighting, since the color, texture, and detail of sculpture depends enormously on the parameters of indoor lighting, such as CCT, CRI, SPD.
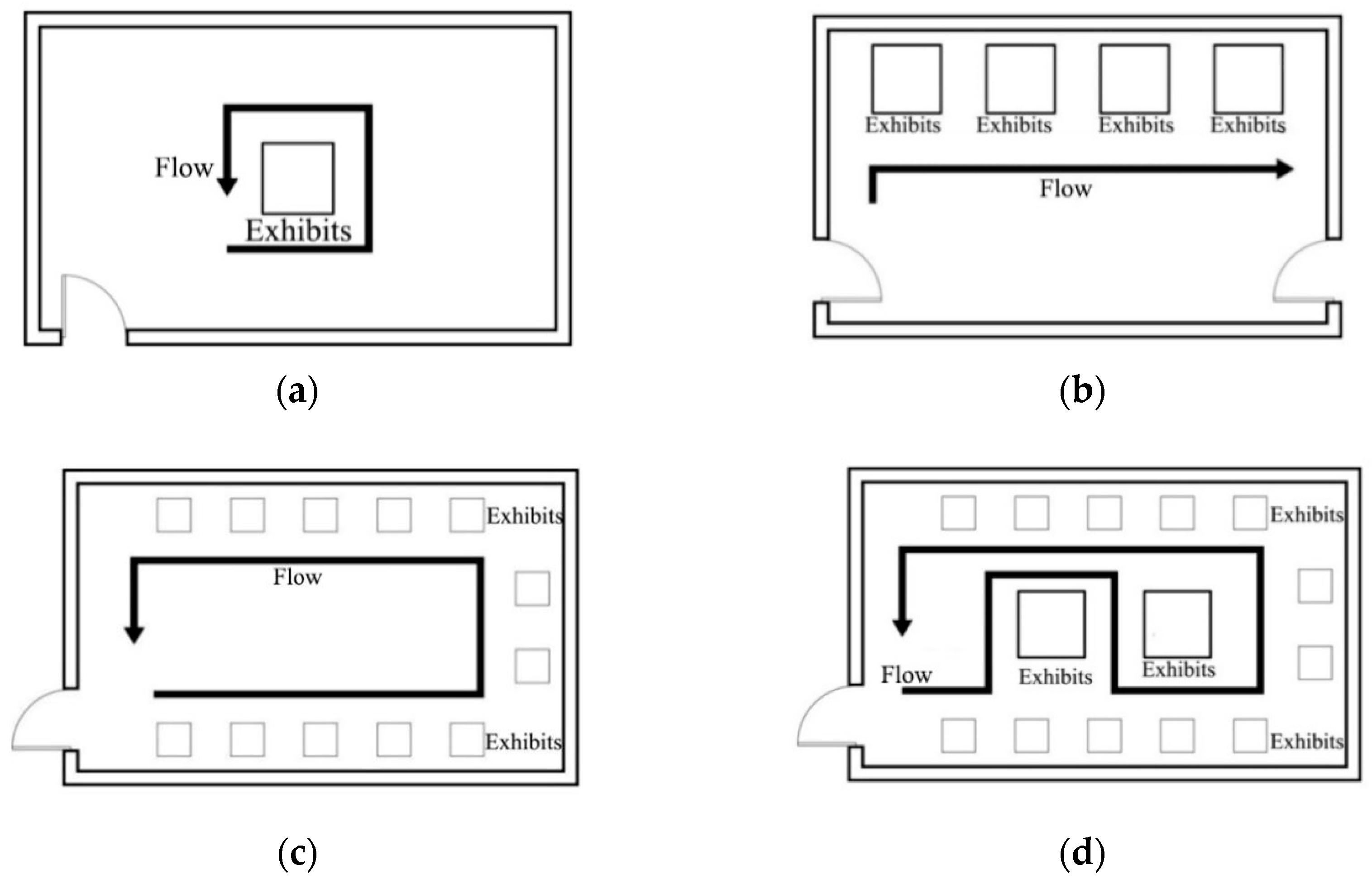
The display modes primarily include independent, single-line, multiline, and mixed displays. The main display modes and corresponding daylighting patterns of the sculpture exhibition hall are shown in
Table 1.
In general, the daylighting environment of the sculpture exhibition hall is primarily composed of natural and electric lights. Natural daylighting affects daylighting level and illuminance uniformity on indoor sculptures.
2.1. Display Modes
The display modes of sculptures in an exhibition hall are primarily independent, single-line, multiline, and mixed displays.
Independent display refers to the installation of a single large sculpture or multiple small sculpture exhibits in a centralized form in the center of an exhibition hall. In such an arrangement, all surfaces of the exhibits can be viewed from 0° to 360° around the exhibits. The independent display layout and viewing flow are shown in
Figure 1a.
- 2.
Single-line display
Single-line display refers to the arrangement of sculptures with similar size in a straight line, generally along one side wall of a room. The viewing flow is consistent along the direction of the showcase, and only a certain characteristic surface of the sculptures is generally exhibited to the visitors. The single-line display layout and viewing flow are shown in
Figure 1b.
- 3.
Multiline display
A multiline display can be regarded as an extension of the single-line display. The sculpture exhibits are arranged in two parallel lines or arranged along three side walls. The viewing flow is along the side walls; usually, only the front and part of the flanks of the sculptures can be viewed. The display layout and viewing flow are shown in
Figure 1c.
- 4.
Mixed display
Mixed display is a combination of independent and multiline displays. Large or symbolic sculpture exhibits are placed at the center of the exhibition hall to highlight the theme. Simultaneously, relatively minor exhibits are arranged along the surrounding walls to form a linear display layout. The spatial relationship between the exhibits is relatively free. The display layout and viewing flow are shown in
Figure 1d.
2.2. Daylighting Pattern
Top daylighting is a typical form of daylighting in sculpture exhibition halls. The window for daylighting is generally set on the roof of a hall. Light enters from the skylight and either directly illuminates or is incident on the surface of the sculpture after being refracted or diffused through the daylighting opening. Top daylighting can be further categorized into centralized and decentralized top daylighting.
Centralized top daylighting can produce strong luminance contrast, creating key areas that are illuminated for visual focus. Most museums use this kind of daylighting pattern (
Figure 2a,b). Decentralized top daylighting can flexibly disperse openings, resulting in overall bright light effect and relatively uniform indoor daylighting. In the Guangzhou Art Museum, a cone-shaped daylighting component comprising a number of scattered daylighting holes is installed above a statue exhibit (
Figure 2c). External light enters the exhibition space through these holes and is directed to the statue from different angles. The crisscrossed light forms multiple shades, providing a strong visual effect and expresses the artistic connotation of the statue.
- 2.
Side daylighting
Side daylighting is a typical daylighting pattern in sculpture exhibition halls as well. In this scheme, side window or high side windows are used, and the daylighting openings are generally set on a single-sided exterior wall. The light from the side windows has a clear directionality. The use of side daylighting in a sculpture exhibition hall can render a rich shading effect from the sculptures, hence enhancing the three-dimensional shape of the sculptures.
The medieval exhibition hall of the Metropolitan Museum of Art in the US adopts single-sided daylighting with high side windows and suspended downlights for lighting, resulting in a clear luminance contrast and hence more vivid medieval knight statues (
Figure 3a). The sculpture exhibition area of Guangzhou Art Museum uses side windows (floor-to-ceiling windows) extensively for daylighting such that the exhibition area is bright overall with high uniformity. The sculptures are placed beside the side windows to create a strong shading effect for viewing. Simultaneously, curtains are used to block a significant amount of direct light to increase the softness of light and avoid glare when viewing (
Figure 3b).
- 3.
Top and side daylighting
The daylighting pattern that combines both top and side daylighting typically adopts distributed flat skylights on the top. While considering uniform daylighting in the room, the directional illumination from the side windows is used to highlight the three-dimensionality of the sculpture exhibits. The sculpture exhibition space of Guangxi Art Museum adopts the combined daylighting pattern. The top daylighting adopts a distributed arrangement in a strip to provide uniform ambient brightness in the room. Simultaneously, side windows are used extensively in a large area, and the sculptures are placed next to these side windows to create a rich three-dimensional effect from the light and shadows for the sculptures (
Figure 4a). Some exhibition spaces use the entire ceiling or surfaces composed of densely distributed openings and strips for daylighting. For example, the Metropolitan Museum of Art in the US uses large-scale side windows and flat skylights to create a scenario where the sculpture exhibits are placed entirely under the sun without being excessively dazzling (
Figure 4b). Because stone sculptures are insensitive to light, the exhibition hall shown in
Figure 5 also uses skylight strips (one kind of the flat skylight) to introduce natural light which transmits through the diffusing glass and develops diffused light diffuses to display details of the Buddhist statues. In the exhibition hall space, the diffused light provided by the large-scale daylighting opening renders the illumination of the exhibition space more uniform.
3. Daylight Parameters
The
DF is one of the most used parameters in building daylighting design, energy saving, and indoor visual comfort evaluation. It is expressed as
where
is the illuminance at a certain point indoor under an overcast sky, expressed in lx;
is the illuminance at a certain point outdoor without obstruction under an overcast sky, expressed in lx. There is a direct linear relationship between environmental illumination and daylighting factor. According to “Museum Architectural Design Standard” JGJ 66-2015,
DF ≥ 2% for side window lighting and
DF ≥ 1% for skylight lighting in sculpture exhibition hall [
26].
The uniformity of daylighting (
UD) is an important parameter for measuring the spatial distribution of illuminance; it is defined as:
where
DFmin is the minimum
DF on the plane;
DFave is the average
DF on the plane, expressed in lx. Uneven illumination distribution can cause fatigue of human eyes, reduce visual acuity, and impair viewing experience. According to JGJ 66-2015,
UD should be exceeded 0.7 under the skylight, but there is no
UD requirement for side window [
26].
Luminance Lθ refers to the luminous intensity per unit projection area, expressed in cd/m2, and is given:
Acosθ is the projection area of a light source in the line of sight, m2; Iθ refers to the luminous intensity of a light source in line of sight, cd.
Luminance contrast
C refers to ratio of luminance difference between target and background in visual field and background luminance, and is expressed:
Lt is the target luminance, cd/m2; Lb is the background luminance, cd/m2; ΔL is the luminance difference between target and background in field of vision, cd/m2.
An excessively high luminance contrast can cause discomfort and disfunction to the human eyes. Glare is defined as annoyance and discomfort caused by excessive luminance or luminance contrast in the visual field. Hopkinson [
27] investigated the glare produced by large-scale light sources (primarily natural light through windows) and proposed the daylight glare index (
DGI), expressed as follows:
where
Ls is the luminance of the glare source, expressed in cd/m
2;
Lb is the luminance of the background, expressed in cd/m
2;
ωs is the solid angle formed by the glare source to the observer’s eyes, expressed as
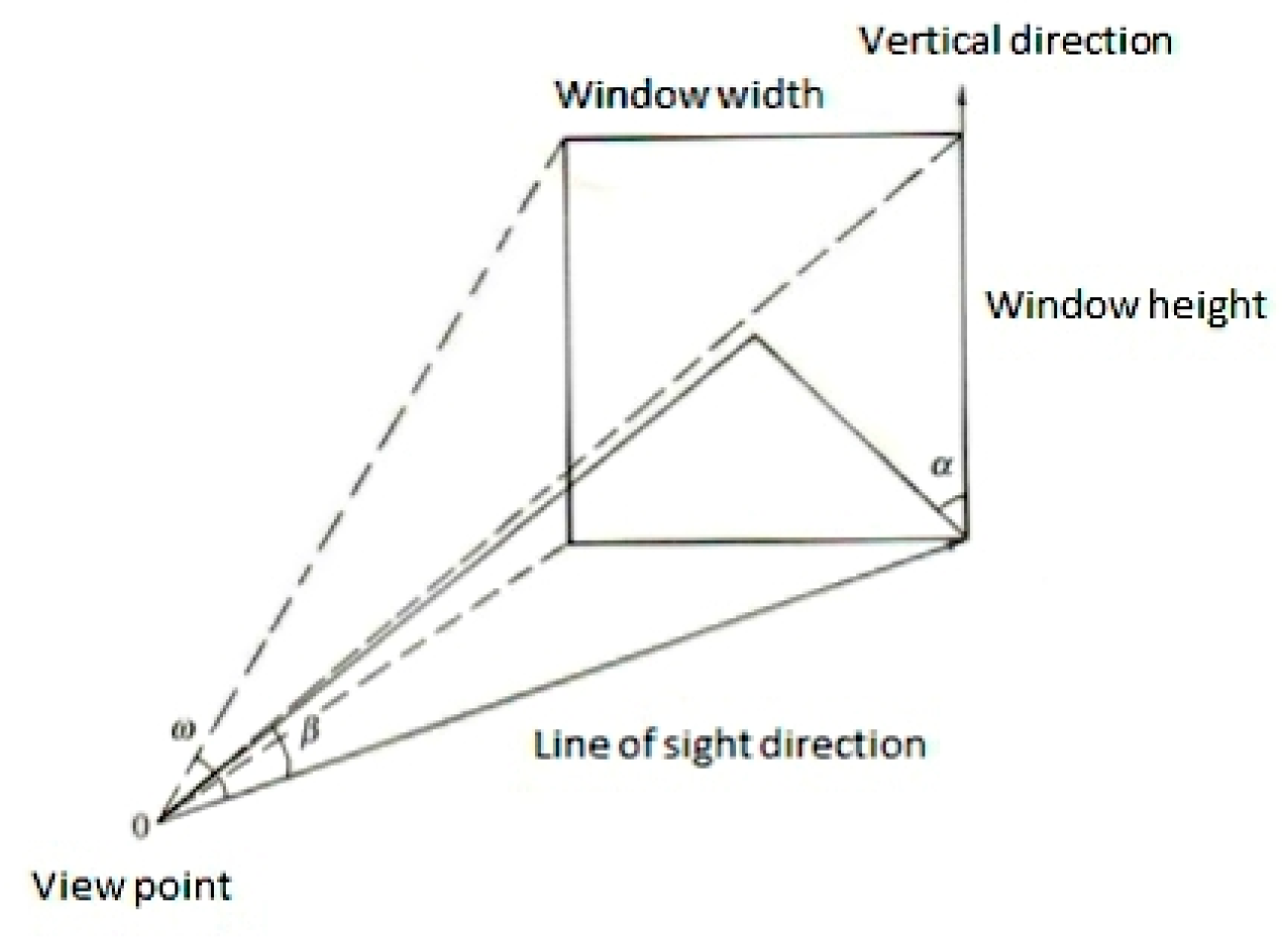
where
a and
b are the width and height of the window, respectively;
d is the distance from the observation point to the center of the window, as shown in
Figure 6. Ω
s refers to the solid angle corrected by considering the Guth position of the glare source, i.e.,
Here,
P is the Guth position index, expressed as
where
α is the angle between the diagonal and the normal direction of the window;
β is the angle between the line connecting the observer’s eye and the center of the window and the direction of the line of sight (see
Figure 6).
Furthermore, Nazzal [
24] proposed a different expression for the
DGI of natural daylighting, as follows:
where
Lexterior is the exterior luminance from direct sunlight, diffuse light from the sky, and light reflected from the ground and outer surfaces of objects;
Ladaptation is the adaptation luminance, i.e., the luminance from the surrounding environment including that reflected from the inner surfaces;
Lwindow is the luminance of the window, i.e., the average vertical brightness of the window,
ωN is the solid angle subtended by the window to the point of observation, sr; Ω
pN is the corrected solid angle subtended by the window, sr.
5. Optimization and Discussion
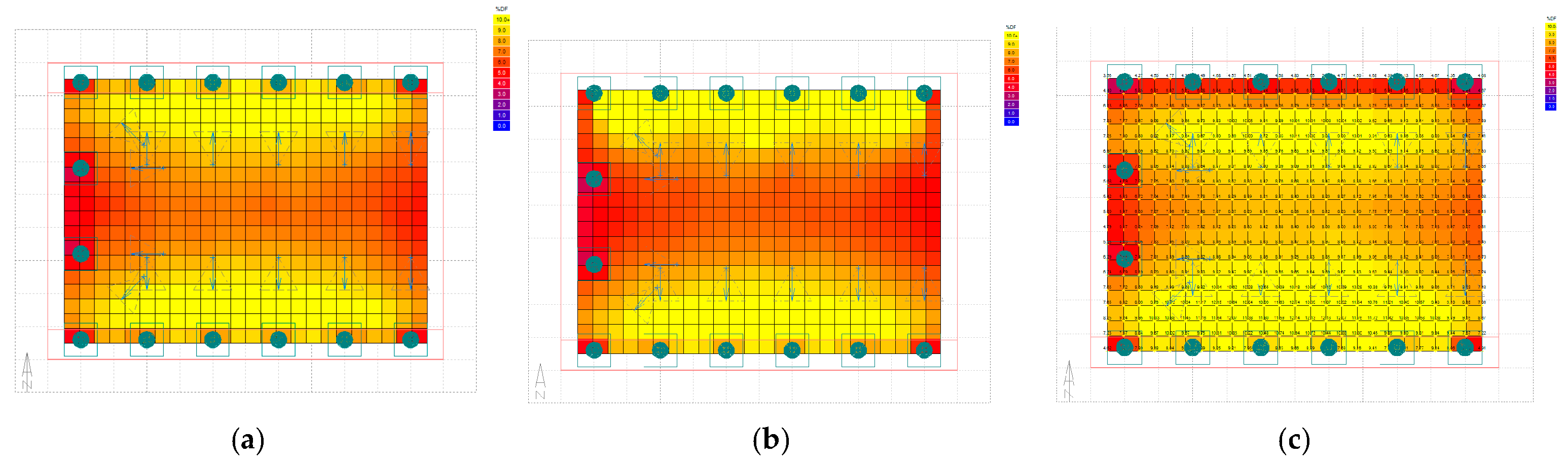
Because the disadvantage of the daylighting pattern of flat skylights with high side windows is the fact that the illuminance in the central area of the exhibition hall is slightly lower, the illuminance of this area should be increased to improve the uniformity of the viewing space.
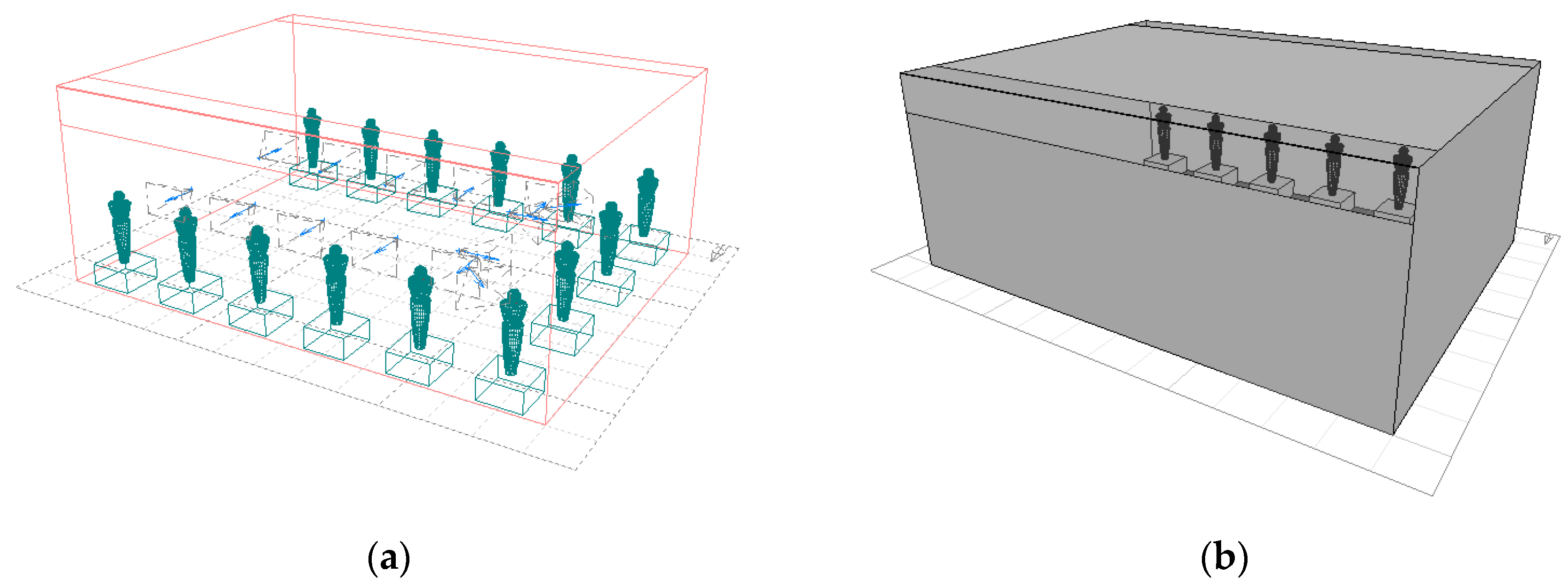
In the optimized scheme, the high side window installed on the north wall of the exhibition hall in the original scheme is maintained in size but folded in half such that it becomes a L-shaped component, where half of it remains as the high side window, and the other half becomes a flat skylight (see
Figure 11a). In other words, the original high side window is changed into a combination of flat skylights with high side window. The optimized exhibition hall model is shown in
Figure 11b.
Table 5 and
Table 6 show that, by changing the high side window into a combination of flat skylights and high side windows, the uniformity of daylighting in the viewing space improved but the overall uniformity decreased. This occurred because the optimized scheme increased the amount of indoor daylighting, thereby increasing the average indoor
DF; however, the lowest daylighting level was observed in the shadow created by the sculptures and remained unchanged, resulting in a decline in the overall uniformity of daylighting of the entire exhibition hall. Therefore, the combination of flat skylights and high side windows exploits the high daylighting efficiency of the flat skylights and simultaneously suppresses the strong directionality of light entering through the side window to a certain extent. Consequently, the illuminance in the center of the exhibition hall increased, and its uniformity improved.
Variations in the uniformity and glare before and after optimization were analyzed.
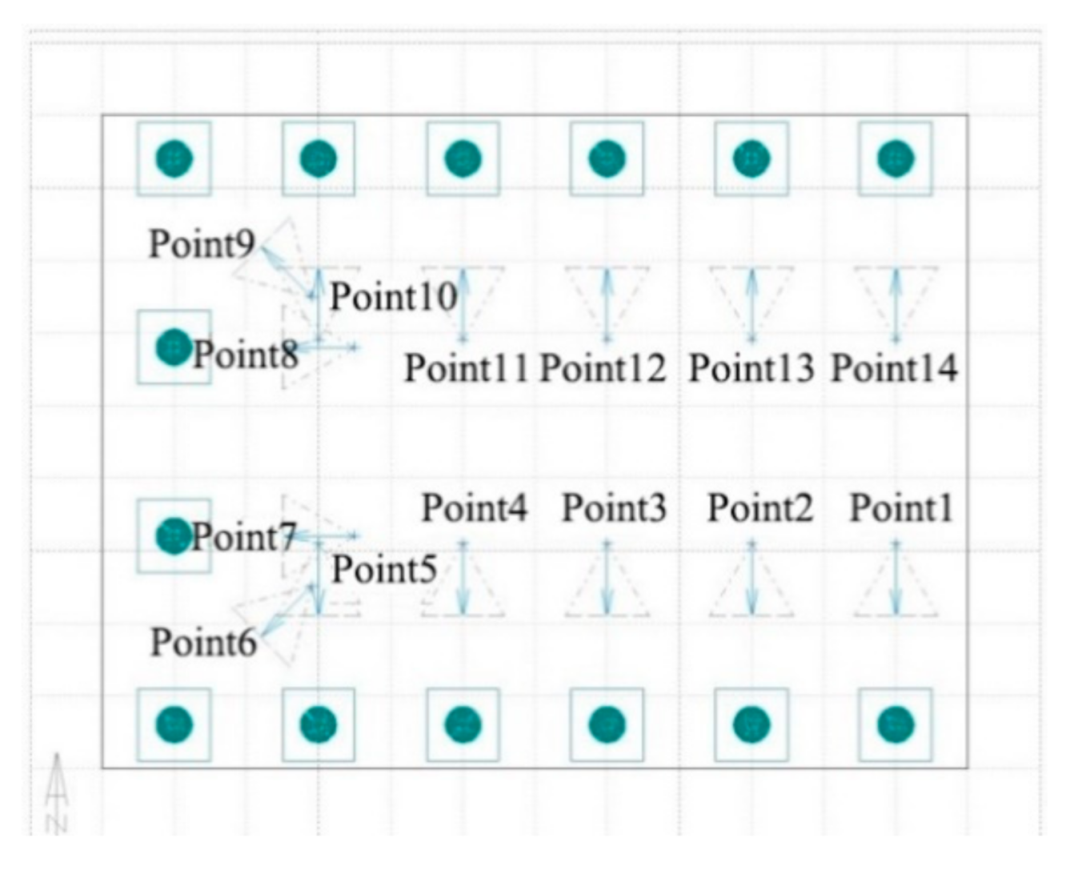
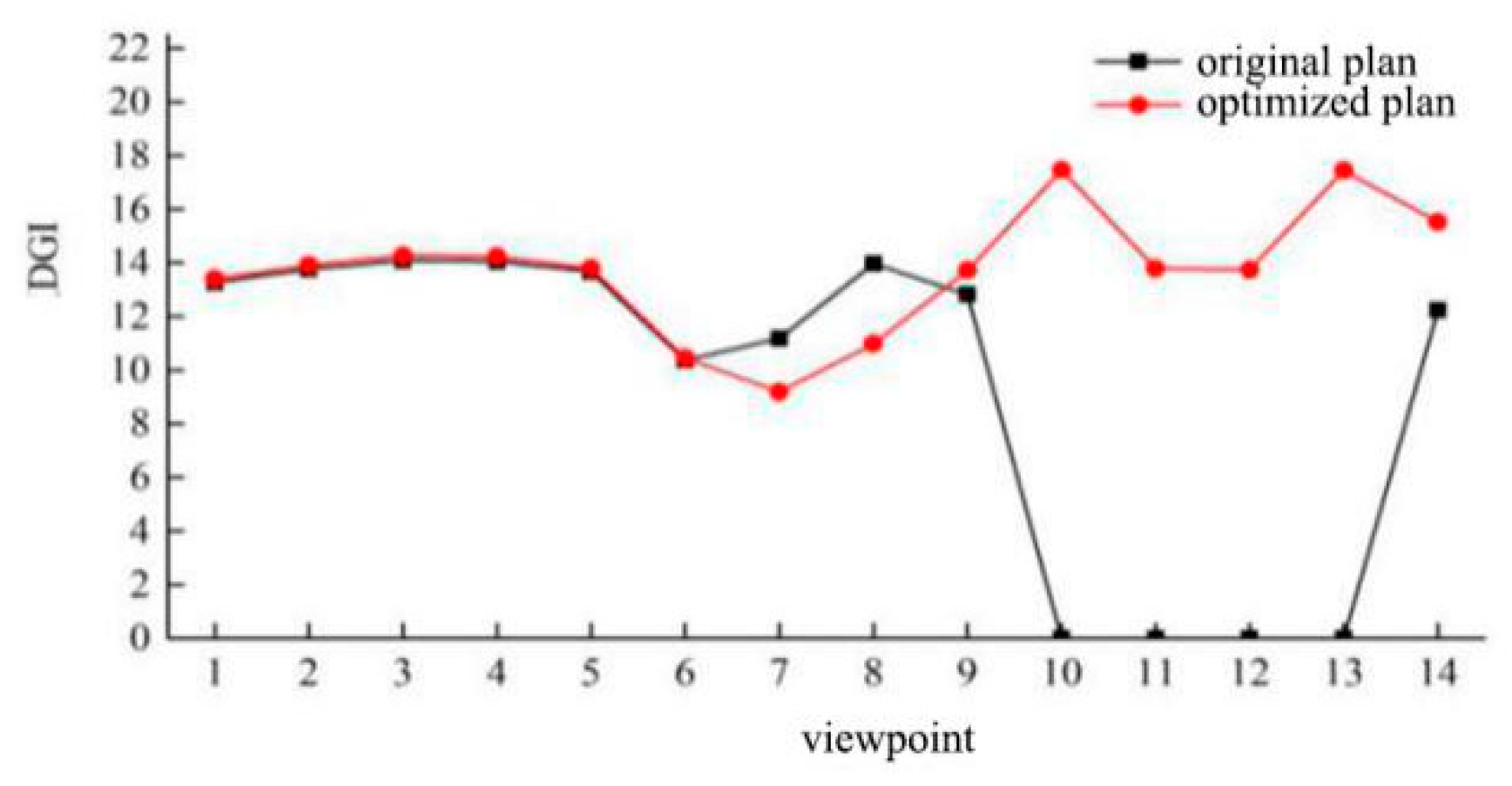
Figure 12 shows comparisons of
DGIs, respectively, of the original and optimized schemes.
Figure 12 shows that after adopting the optimized scheme, the
DGI at viewpoints 1–9 did not change significantly, i.e., the visual experience was relatively consistent with the original scheme before the visitors entered the side where the high side window was located. The
DGI value at viewpoints 10–14 increased, whereas the
DGI values at viewpoints 10 and 13 reached approximately 17.45, which was still below the threshold for glare. Compared with the original daylighting scheme, the optimized high side window reduced in size, causing an increase in the
DGI at some viewpoints; however, it was still within the allowable glare range. The
DGI curve tended to be flat, and the consistency in visual experience improved.
In summary, with a multiline display layout, when the daylighting scheme of flat skylights with high side windows was adopted, by changing one of the high side windows into a L-shaped window comprising a flat skylight and a high side window, better uniformity of daylighting was achieved. In addition, the DGI curve was relatively flat, resulting in a relatively consistent visual experience during viewing.
The overall uniformity for the flat skylights and the flat skylights with side windows was poor, with the center of the exhibition hall being relatively dark. Therefore, it is necessary to apply electric light sources to this central area, increase ambient lighting, or adopt other measures to increase the illumination to improve the overall illuminance uniformity. In addition, when the viewpoint was on the side of the side window, the sculpture exhibits were facing away from the light source; hence, appropriate directional light sources should be added to provide local lighting to increase the luminance of the exhibits.
6. Conclusions
As the concepts of green ideology, environmental protection and healthy building become increasingly popular, more attention will be directed toward natural daylighting in museum design. The daylighting conditions of sculpture exhibition halls were analyzed herein, where the exhibition space was summarized and classified. Subsequently, the exhibition space was modeled and simulated to calculate the daylighting parameters, such as the DF, UD, luminance distribution, and DGI of the natural lighting environment with different daylighting schemes. After comparing and analyzing the daylighting quality of various exhibition halls, the sculpture exhibition hall with multiline display was presented as an example. It was discovered that the flat skylights with high side windows yielded the most ideal DF, UD, and DGI. This shows that the daylighting scenario of flat skylights with high side windows was conducive to the display of sculpture exhibits. The significance of this daylighting pattern is that for museum buildings with a long span, large-sized side windows are necessary for daylighting. However, the introduction of skylights can effectively reduce the size demand for side windows while maintaining the same daylighting quality. However, for flat skylights with high side windows, the luminance in the central area of the exhibition hall was still relatively low. Hence, it is necessary to further propose a corresponding daylighting optimization strategy for the exhibition space, while retaining the size of the high side windows. One of the high side windows was folded in half to form a flat skylight and a high side window half of its original size. This can effectively increase the illuminance in the central area of the exhibition hall without increasing the size of windows for daylighting, while improving the luminance uniformity of the viewing space.
In the daylighting design of sculpture exhibition space in a museum, the following factors can be considered to further control the daylighting quality: (1) the usage of window-shades, grille, curtains or other obstructions to prevent direct light from entering the exhibition hall; at the same time, the illumination of natural light can be controlled; (2) more UV and IR from natural light can lead to photochemical reactions and radiant heating effects, which can cause the sculpture exhibits to fade and accelerate the material aging, etc. The application of electric lighting can be used to minimize the effect of changes in sky lights on displays [
3,
29,
30]. Based on the characteristics of sculpture exhibits, display layouts, and building environments, a targeted daylighting design was proposed herein to provide a suitable natural light environment for an exhibition space.
The textures and colors of sculptures depend largely on the spectral composition of the light they receive, and electric lighting can compensate for the absence of that part of the visible shortwave light that influences the light reflected by the sculptures that enters our eyes due to filtration of window glass. Accordingly, daylighting design should be incorporated with the indoor electric lighting scheme to reflect the perfect vision of sculptures. Through optimization, a suitable daylighting pattern was obtained that can assist architects in using natural light reasonably to express the characteristics of sculptures for daylighting design, while creating a comfortable light environment in the sculpture exhibition space.