Adaptive-Hybrid Harmony Search Algorithm for Multi-Constrained Optimum Eco-Design of Reinforced Concrete Retaining Walls
Abstract
1. Introduction
2. Employed Metaheuristic Algorithms
2.1. Genetic Algorithm (GA)
2.2. Differential Evolution (DE)
2.3. Particle Swarm Optimization (PSO)
2.4. Artificial Bee Colony (ABC) Algorithm
2.5. Firefly Algorithm (FA)
- Fireflies are hermaphrodites and attract the other ones to themselves in every condition.
- Brighter kth firefly attracts the jth firefly which is a less bright one, because attractiveness (β) increases as long as brightness (I) increases. But kth firefly continues to fly randomly in the case that a less bright one is not found than itself (for minimization problems) (Equation (10)).
- The brightness of fireflies is determined by the objective function. Therefore, the brightness of kth firefly (I(xk)) at an x position is proportional with objective function (f (xk)).
2.6. Teaching–Learning-Based Optimization (TLBO)
2.7. Grey Wolf Optimization (GWO)
2.8. Flower Pollination Algorithm (FPA)
2.9. Jaya Algorithm (JA)
2.10. Harmony Search (HS)
2.11. Adaptive Harmony Search (AHS)
2.12. Adaptive-Hybrid Harmony Search (AHHS)
3. Investigation and Optimization of Reinforced Concrete (RC) Retaining Walls
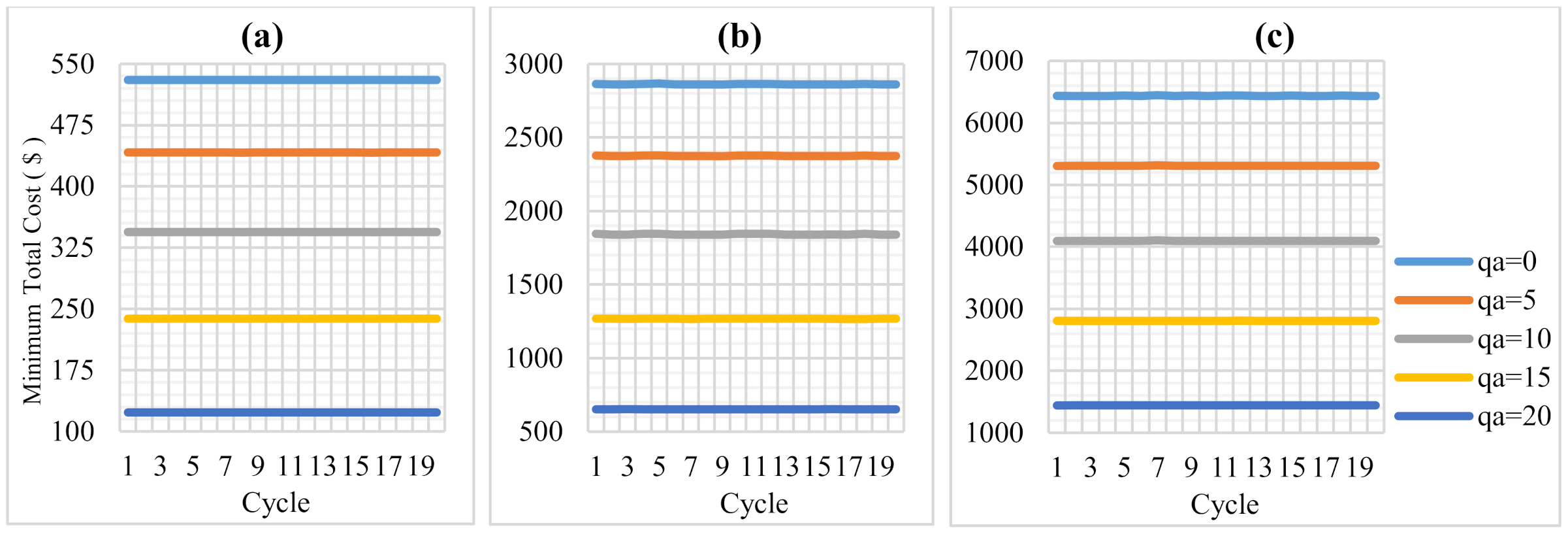
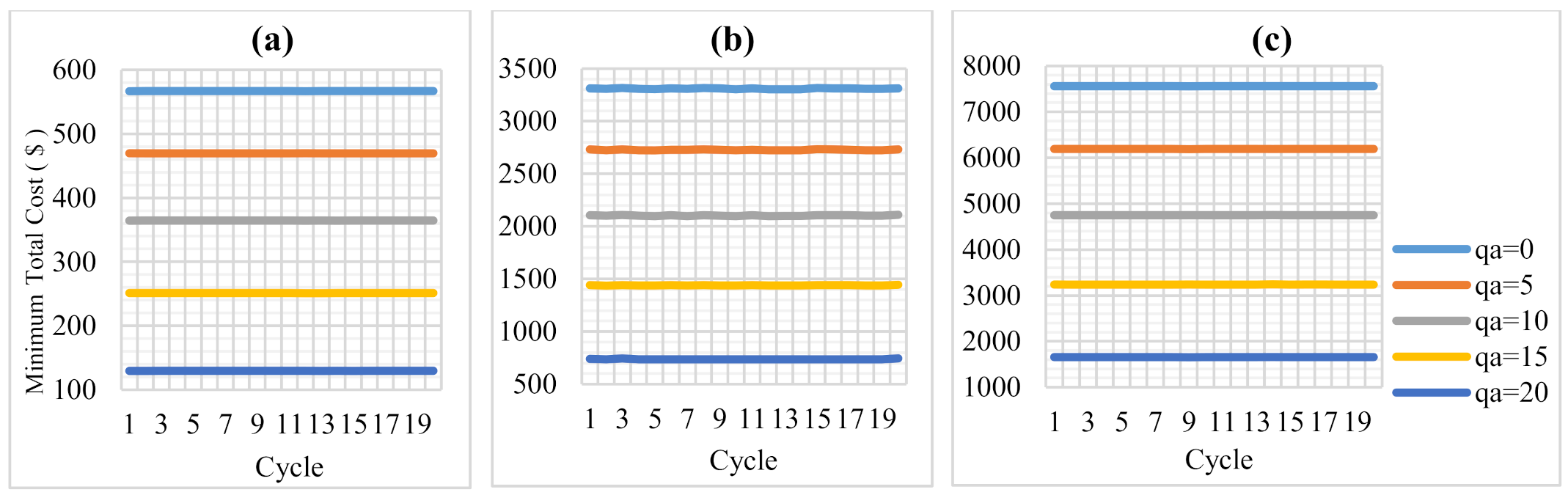
3.1. Optimization for T-Shaped Wall Designs via Multiple Cycles (Case 1)
3.2. Optimization for Wall Designs via Multiple Cycles for H = 10 m (Case 2)
3.3. Best Population and Iteration Numbers for Optimization Processes (Case 3)
3.4. Optimum Analysis for Different Wall Structure Variations with Multiple Cycles (Case 4)
4. Conclusions
4.1. Case 1
4.2. Case 2
4.3. Case 3
4.4. Case 4
4.5. General Advantages of AHHS
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Saribas, A.; Erbatur, F. Optimization and sensitivity of retaining structures. J. Geotech. Eng. 1996, 122, 649–656. [Google Scholar] [CrossRef]
- Çakır, T. Influence of wall flexibility on dynamic response of cantilever retaining walls. Struct. Eng. Mech. 2014, 49, 1–22. [Google Scholar] [CrossRef]
- Goldberg, D.E. Genetic algorithms in search. In Optimization and Machine Learning; Addison Wesley: Boston, MA, USA, 1989. [Google Scholar]
- Holland, J.H. Adaptation in Natural and Artificial Systems; University of Michigan Press: Ann Arbor, MI, USA, 1975. [Google Scholar]
- Kennedy, J.; Eberhart, R.C. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks No. IV, Perth, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Erol, O.K.; Eksin, I. A new optimization method: Big bang–big crunch. Adv. Eng. Softw. 2006, 37, 106–111. [Google Scholar] [CrossRef]
- Geem, Z.W.; Kim, J.H.; Loganathan, G.V. A new heuristic optimization algorithm: Harmony search. Simulation 2001, 76, 60–68. [Google Scholar] [CrossRef]
- Yang, X.S. Firefly algorithms for multimodal optimization. In Stochastic Algorithms: Foundations and Applications; Springer: Berlin/Heidelberg, Germany, 2009; pp. 169–178. [Google Scholar]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Mahjoubi, S.; Barhemat, R.; Bao, Y. Optimal placement of triaxial accelerometers using hypotrochoid spiral optimization algorithm for automated monitoring of high-rise buildings. Autom. Constr. 2020, 118, 103273. [Google Scholar] [CrossRef]
- Rhomberg, E.J.; Street, W.M. Optimal design of retaining walls. J. Struct. Div. 1981, 107, 992–1002. [Google Scholar] [CrossRef]
- Ceranic, B.; Fryer, C.; Baines, R.W. An application of simulated annealing to the optimum design of reinforced concrete retaining structures. Comput. Struct. 2001, 79, 1569–1581. [Google Scholar] [CrossRef]
- Yepes, V.; Alcala, J.; Perea, C.; Gonzalez-Vidosa, F. A parametric study of optimum earth-retaining walls by simulated annealing. Eng. Struct. 2008, 30, 821–830. [Google Scholar] [CrossRef]
- Ahmadi-Nedushan, B.; Varaee, H. Optimal Design of Reinforced Concrete Retaining Walls using a Swarm Intelligence Technique. In Proceedings of the First International Conference on Soft Computing Technology in Civil, Structural and Environmental Engineering, Stirlingshire, UK, 1–4 September 2009. [Google Scholar]
- Kaveh, A.; Abadi, A.S.M. Harmony search based algorithms for the optimum cost design of reinforced concrete cantilever retaining walls. Int. J. Civ. Eng. 2011, 9, 1–8. [Google Scholar]
- Ghazavi, M.; Salavati, V. Sensitivity analysis and design of reinforced concrete cantilever retaining walls using bacterial foraging optimization algorithm. In Proceedings of the 3rd International Symposium on Geotechnical Safety and Risk (ISGSR), München, Germany, 2–3 June 2011; pp. 307–314. [Google Scholar]
- Camp, C.V.; Akin, A. Design of Retaining Walls Using Big Bang-Big Crunch Optimization. J. Struct. Eng. ASCE 2012, 138, 438–448. [Google Scholar] [CrossRef]
- Kaveh, A.; Kalateh-Ahani, M.; Fahimi-Farzam, M. Constructability optimal design of reinforced concrete retaining walls using a multi-objective genetic algorithm. Struct. Eng. Mech. 2013, 47, 227–245. [Google Scholar] [CrossRef]
- Khajehzadeh, M.; Taha, M.R.; Eslami, M. Efficient gravitational search algorithm for optimum design of retaining walls. Struct. Eng. Mech. 2013, 45, 111–127. [Google Scholar] [CrossRef]
- Sheikholeslami, R.; Gholipour Khalili, B.; Zahrai, S.M. Optimum Cost Design of Reinforced Concrete Retaining Walls Using Hybrid Firefly Algorithm. Int. J. Eng. Technol. 2014, 6, 465–470. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Kashani, A.R.; Roke, D.A.; Mousavi, M. Optimization of retaining wall design using recent swarm intelligence techniques. Eng. Struct. 2015, 103, 72–84. [Google Scholar] [CrossRef]
- Kaveh, A.; Soleimani, N. CBO and DPSO for optimum design of reinforced concrete cantilever retaining walls. Asian J. Civ. Eng. 2015, 16, 751–774. [Google Scholar]
- Sheikholeslami, R.; Khalili, B.G.; Sadollah, A.; Kim, J. Optimization of reinforced concrete retaining walls via hybrid firefly algorithm with upper bound strategy. KSCE J. Civ. Eng. 2016, 20, 2428–2438. [Google Scholar] [CrossRef]
- Aydogdu, I. Cost optimization of reinforced concrete cantilever retaining walls under seismic loading using a biogeography-based optimization algorithm with Levy flights. Eng. Optim. 2017, 49, 381–400. [Google Scholar] [CrossRef]
- Mergos, P.E.; Mantoglou, F. Optimum design of reinforced concrete retaining wall with the flower pollination algorithm. Struct. Multidiscip. Optim. 2019. [Google Scholar] [CrossRef]
- Kalemci, E.N.; İkizler, S.B.; Dede, T.; Angın, Z. Design of reinforced concrete cantilever retaining wall using Grey wolf optimization algorithm. In Structures; Elsevier: Amsterdam, The Netherlands, 2020; Volume 23, pp. 245–253. [Google Scholar]
- Öztürk, H.T.; Dede, T.; Türker, E. Optimum design of reinforced concrete counterfort retaining walls using TLBO, Jaya algorithm. In Structures; Elsevier: Amsterdam, The Netherlands, 2020; Volume 25, pp. 285–296. [Google Scholar]
- Aral, S.; Yılmaz, N.; Bekdaş, G.; Nigdeli, S.M. Jaya Optimization for the Design of Cantilever Retaining Walls with Toe Projection Restriction. In Proceedings of the International Conference on Harmony Search Algorithm, Istanbul, Turkey, 16–17 July 2020; Springer: Singapore, 2020; pp. 197–206. [Google Scholar]
- Yılmaz, N.; Aral, S.; Nigdeli, S.M.; Bekdaş, G. Optimum Design of Reinforced Concrete Retaining Walls Under Static and Dynamic Loads Using Jaya Algorithm. In Proceedings of the International Conference on Harmony Search Algorithm, Istanbul, Turkey, 16–17 July 2020; Springer: Singapore, 2020; pp. 187–196. [Google Scholar]
- Murty, K.G. Optimization Models for Decision Making: Volume 1; University of Michigan: Ann Arbor, MI, USA, 2003; Available online: http://www-personal.umich.edu/~murty/books/opti_model/ (accessed on 2 July 2018).
- Sivanandam, S.N.; Deepa, S.N. Genetic Algorithms. In Introduction to Genetic Algorithms; Springer: Berlin/Heidelberg, Germany, 2008; pp. 29–51. [Google Scholar]
- Storn, R.; Price, K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Jones, M.T. Artificial Intelligence: A Systems Approach; Infinity Science Press LLC: Hingham, MA, USA, 2008; ISBN 9788131804049. [Google Scholar]
- Koziel, S.; Yang, X.S. (Eds.) Computational Optimization, Methods and Algorithms (Volume 356); Springer: Berlin/Heidelberg, Germany, 2011; ISBN 978-3-642-20858-4. [Google Scholar]
- Keskintürk, T. Diferansiyel gelişim algoritması. İstanbul Ticaret Üniversitesi Fen Bilimleri Dergisi 2006, 5, 85–99. [Google Scholar]
- Rao, S.S. Engineering Optimization Theory and Practice, 4th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2009; ISBN 978-0-470-18352-6. [Google Scholar]
- Shi, Y.; Eberhart, R.C. Empirical study of particle swarm optimization. In Proceedings of the 1999 Congress on Evolutionary Computation-CEC99, (Cat. No. 99TH8406). Washington, DC, USA, 6–9 July 1999. [Google Scholar]
- Bai, Q. Analysis of particle swarm optimization algorithm. Comput. Inf. Sci. 2010, 3, 180. [Google Scholar] [CrossRef]
- Karaboga, D. An Idea Based on Honeybee Swarm for Numerical Optimization; Technical Report TR06; Department of Computer Engineering, Engineering Faculty, Erciyes University: Kayseri, Turkey, 2005; Volume 200, pp. 1–10. [Google Scholar]
- Karaboga, D.; Basturk, B. Artificial Bee Colony (ABC) Optimization Algorithm for Solving Constrained Optimization Problems. In Proceedings of the International Fuzzy Systems Association World Congress, Cancun, Mexico, 18–21 June 2007; Springer: Berlin/Heidelberg, Germany, 2007; pp. 789–798. [Google Scholar]
- Karaboga, D.; Basturk, B. On the performance of artificial bee colony (ABC) algorithm. Appl. Soft Comput. 2008, 8, 687–697. [Google Scholar] [CrossRef]
- Singh, A. An artificial bee colony algorithm for the leaf-constrained minimum spanning tree problem. Appl. Soft Comput. 2009, 9, 625–631. [Google Scholar] [CrossRef]
- Yang, X.S.; Bekdaş, G.; Nigdeli, S.M. (Eds.) Metaheuristics and Optimization in Civil Engineering; Springer: Cham, Switzerland, 2016; ISBN 9783319262451. [Google Scholar]
- Rao, R.V.; Savsani, V.J.; Vakharia, D.P. Teaching–learning-based optimization: A novel method for constrained mechanical design optimization problems. Comput.-Aided Des. 2011, 43, 303–315. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Faris, H.; Aljarah, I.; Al-Betar, M.A.; Mirjalili, S. Grey wolf optimizer: A review of recent variants and applications. Neural Comput. Appl. 2018, 30, 413–435. [Google Scholar] [CrossRef]
- Şahin, İ.; Dörterler, M.; Gökçe, H. Optimum design of compression spring according to minimum volume using grey wolf optimization method. Gazi J. Eng. Sci. 2017, 3, 21–27. [Google Scholar]
- Yang, X.S. Flower pollination algorithm for global optimization. In Proceedings of the International Conference on Unconventional Computing and Natural Computation, Orléans, France, 3–7 September 2012; Springer: Berlin/Heidelberg, Germany, 2012; pp. 240–249. [Google Scholar]
- Rao, R. Jaya: A simple and new optimization algorithm for solving constrained and unconstrained optimization problems. Int. J. Ind. Eng. Comput. 2016, 7, 19–34. [Google Scholar]
- Rao, R.V.; Rai, D.P.; Ramkumar, J.; Balic, J. A new multi-objective Jaya algorithm for optimization of modern machining processes. Adv. Prod. Eng. Manag. 2016, 11, 271–286. [Google Scholar] [CrossRef][Green Version]
- Du, D.C.; Vinh, H.H.; Trung, V.D.; Hong Quyen, N.T.; Trung, N.T. Efficiency of Jaya algorithm for solving the optimization-based structural damage identification problem based on a hybrid objective function. Eng. Optim. 2018, 50, 1233–1251. [Google Scholar] [CrossRef]
- Zhang, T.; Geem, Z.W. Review of harmony search with respect to algorithm structure. Swarm Evol. Comput. 2019, 48, 31–43. [Google Scholar] [CrossRef]
- Geem, Z.W. State-of-the-art in the structure of harmony search algorithm. In Recent Advances in Harmony Search Algorithm; Springer: Berlin/Heidelberg, Germany, 2010; pp. 1–10. [Google Scholar]
- Rankine, W. On the stability of loose earth. Philos. Trans. R. Soc. Lond. 1857, 147. [Google Scholar] [CrossRef]
- ACI 318: Building Code Requirements for Structural Concrete and Commentary; ACI Committee: Geneva, Switzerland, 2014.
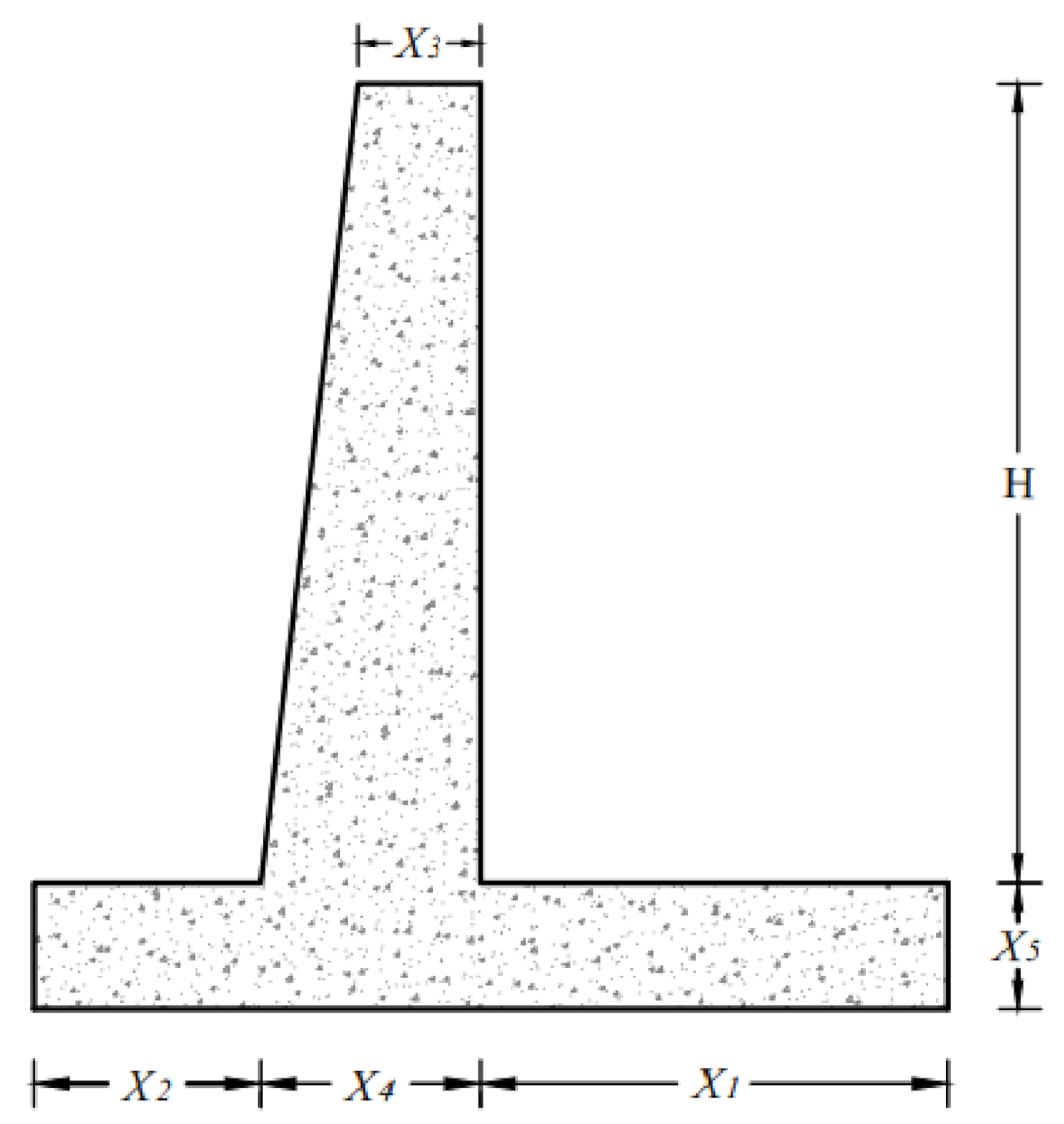

| Definition | Symbol | Limit/Value | Unit | |
|---|---|---|---|---|
| Design Variables | Heel slab/back encasement width of retaining wall | X1 | 0–10 | M |
| Toe slab/front encasement width of retaining wall | X2 | 0–3 | M | |
| Upper part width of cantilever/stem of wall | X3 | 0.2–3 | M | |
| Bottom part width of cantilever/stem of wall | X4 | 0.3–3 | M | |
| The thickness of the bottom slab of the retaining wall | X5 | 0.3–3 | M | |
| Design Constants | Difference between the top elevation of bottom-slab with soil in behind of wall (active zone)/stem height | H | 6 | M |
| Weight per unit of volume of back soil of wall (active zone) | γz | 18 | kN/m3 | |
| Surcharge load in the active zone (on the top elevation of soil) | qa | 10 | kN/m2 | |
| The angle of internal friction of back soil of wall | Φ | 30° | ||
| Allowable bearing value of soil | qsafety | 300 | kN/m2 | |
| The thickness of granular backfill | tb | 0.5 | M | |
| Coefficient of soil reaction | Ksoil | 200 | MN | |
| Compressive strength of concrete at 28 days | fc’ | 25 | MPa | |
| Tensile strength of steel reinforcement | fy | 420 | MPa | |
| The elasticity modulus of concrete | Ec | 31,000 | MPa | |
| The elasticity modulus of steel | Es | 200,000 | MPa | |
| Weight per unit of volume for concrete | γc | 25 | kN/m3 | |
| Weight per unit of volume for steel | γs | 7.85 | t/m3 | |
| Width of wall bottom slab | b | 1000 | Mm | |
| Concrete unit cost | Cc | 50 | $/m3 | |
| Steel unit cost | Cs | 700 | $/ton |
| Description | Constraints |
|---|---|
| Safety for overturning stability | g1(X): FoSot,design ≥ FoSot |
| Safety for sliding | g2(X): FoSs,design ≥ FoSs |
| Safety for bearing capacity | g3(X): FoSbc,design ≥ FoSbc |
| Minimum bearing stress (qmin) | g4(X): qmin ≥ 0 |
| Flexural strength capacities of critical sections (Md) | g5–7(X): Md ≥ Mu |
| Shear strength capacities of critical sections (Vd) | g8–10(X): Vd ≥ Vu |
| Minimum reinforcement areas of critical sections (Asmin) | g11–13(X): As ≥ Asmin |
| Maximum reinforcement areas of critical sections (Asmax) | g14–16(X): As ≤ Asmax |
| Load Coefficients in ACI Regulation | Symbol | Value |
|---|---|---|
| The coefficient for load increment | Cl | 1.7 |
| Reduction coefficient for section bending moment capacity for tension-controlled design | FiM | 0.9 |
| Reduction coefficient for section shear load capacity | FiV | 0.75 |
| Constant load coefficient | GK | 0.9 |
| Live load coefficient | QK | 1.6 |
| Horizontal load coefficient | HK | 1.6 |
| Safety coefficient for overturning | Osafety | 1.5 |
| Safety coefficient for slipping | Ssafety | 1.5 |
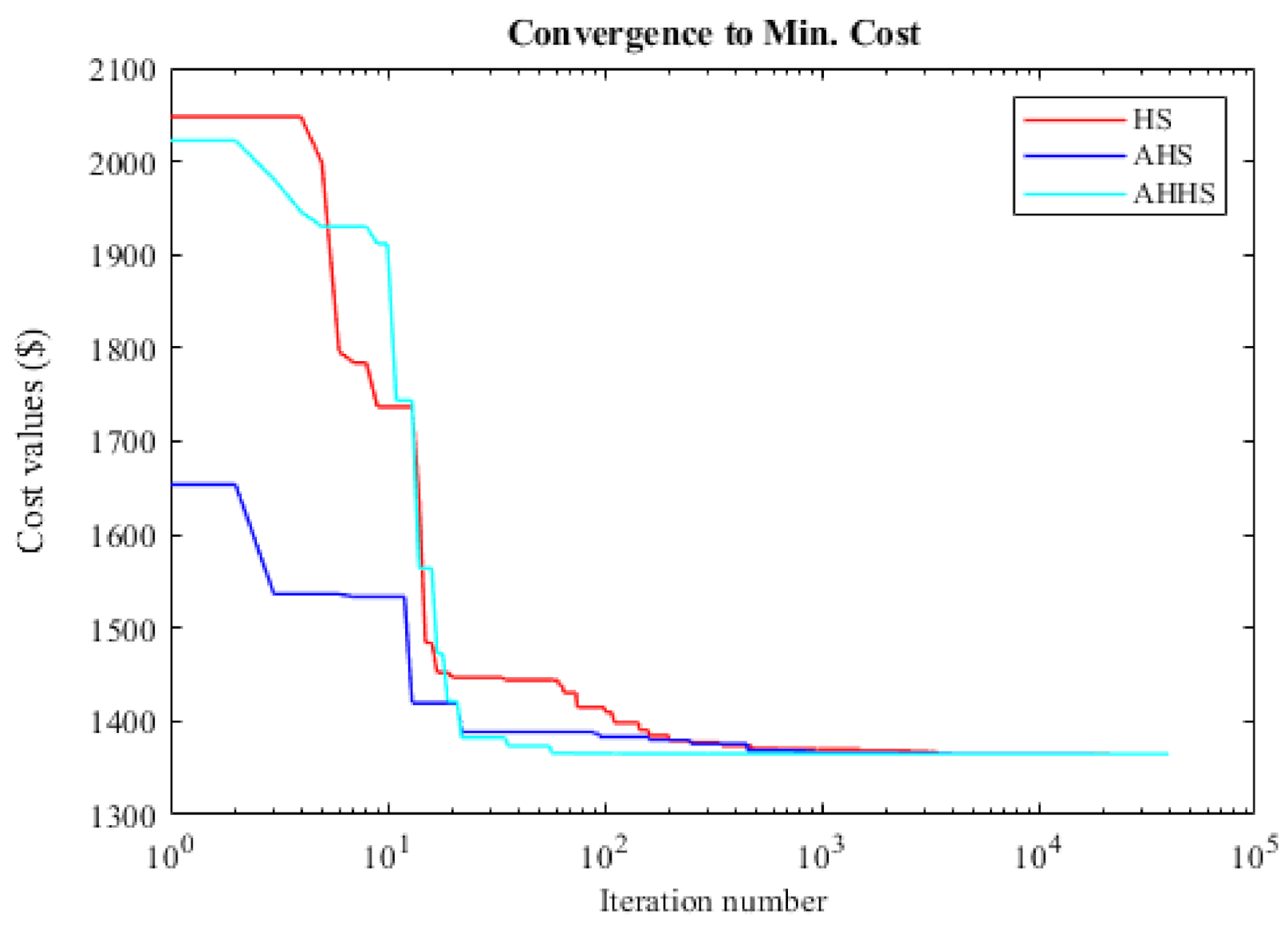
| Algorithm | X1 | X2 | X3 | X4 | X5 | Min. Cost | Ave. Cost | Standard Dev. |
|---|---|---|---|---|---|---|---|---|
| GA | 4.1257 | 0.0003 | 0.2003 | 0.6212 | 0.4274 | 428.2421 | 449.3181 | 36.9566 |
| DE | 4.1323 | 0.0000 | 0.2000 | 0.6098 | 0.4267 | 428.1139 | 433.3653 | 11.4300 |
| PSO | 4.1322 | 0.0000 | 0.2000 | 0.6099 | 0.4267 | 428.1139 | 449.2315 | 40.6569 |
| HS | 4.1197 | 0.0000 | 0.2000 | 0.6222 | 0.4160 | 428.2851 | 429.2780 | 0.6148 |
| FA | 4.1292 | 0.0000 | 0.2000 | 0.6145 | 0.4266 | 428.1238 | 428.1696 | 0.0294 |
| ABC | 4.1315 | 0.0000 | 0.2000 | 0.6135 | 0.4299 | 428.1452 | 431.0378 | 3.5220 |
| TLBO | 4.1323 | 0.0000 | 0.2000 | 0.6099 | 0.4267 | 428.1139 | 428.1139 | 5.0000 × 10−7 |
| FPA | 4.1323 | 0.0000 | 0.2000 | 0.6099 | 0.4267 | 428.1139 | 429.2931 | 2.1345 |
| GWO | 4.0584 | 0.9320 | 0.2000 | 0.6012 | 0.3800 | 435.1009 | 448.5719 | 9.1413 |
| JA | 4.1323 | 0.0000 | 0.2000 | 0.6099 | 0.4267 | 428.1139 | 428.1139 | 1.2000 × 10−7 |
| Algorithm | X1 | X2 | X3 | X4 | X5 | Min. Cost | Ave. Cost | Standard Dev. | HMCR | PAR |
|---|---|---|---|---|---|---|---|---|---|---|
| HS | 4.1308 | 0.0000 | 0.2000 | 0.6078 | 0.4192 | 428.2027 | 429.8543 | 2.0568 | 0.5 | 0.1 |
| 4.1309 | 0.0000 | 0.2000 | 0.6134 | 0.4245 | 428.2236 | 428.7516 | 1.1862 | 0.1 | 0.1 | |
| 4.1381 | 0.0002 | 0.2000 | 0.6037 | 0.4292 | 428.1761 | 430.0087 | 2.2499 | rand( ) | rand( ) | |
| AHS | 4.1308 | 0.0000 | 0.2000 | 0.6118 | 0.4264 | 428.1151 | 428.2852 | 0.9061 | 0.5 | 0.1 |
| 4.1354 | 0.0001 | 0.2000 | 0.6053 | 0.4270 | 428.1151 | 428.2852 | 0.9211 | 0.1 | 0.1 | |
| 4.1321 | 0.0000 | 0.2000 | 0.6100 | 0.4266 | 428.1139 | 429.4559 | 2.2556 | rand( ) | rand( ) | |
| AHHS | 4.1322 | 0.0000 | 0.2000 | 0.6098 | 0.4266 | 428.1139 | 428.1139 | 1.7512 × 10−5 | 0.5 | 0.1 |
| 4.1323 | 0.0000 | 0.2000 | 0.6098 | 0.4267 | 428.1139 | 428.1143 | 2.5401 × 10−4 | 0.1 | 0.1 | |
| 4.1323 | 0.0000 | 0.2000 | 0.6098 | 0.4267 | 428.1139 | 428.1139 | 2.1047 × 10−5 | rand( ) | rand( ) |
| Algorithm | X1 | X2 | X3 | X4 | X5 | Min. Cost | Ave. Cost | Standard Dev. |
|---|---|---|---|---|---|---|---|---|
| GA | 6.3330 | 1.4884 | 0.2000 | 1.3872 | 0.7068 | 1365.3200 | 1376.4551 | 32.4525 |
| DE | 6.3479 | 1.4916 | 0.2000 | 1.3657 | 0.7086 | 1365.2365 | 1419.9082 | 1.0055 × 102 |
| PSO | 6.3484 | 1.4914 | 0.2000 | 1.3656 | 0.7086 | 1365.2388 | 1458.7287 | 1.4244 × 104 |
| HS | 6.3210 | 1.4771 | 0.2000 | 1.4072 | 0.7038 | 1365.7077 | 1366.2693 | 0.4286 |
| FA | 6.3471 | 1.4737 | 0.2000 | 1.3672 | 0.7029 | 1365.3144 | 1365.3999 | 0.0561 |
| ABC | 6.3534 | 1.4937 | 0.2000 | 1.3584 | 0.7100 | 1365.2989 | 1366.2121 | 1.6558 |
| TLBO | 6.3481 | 1.4916 | 0.2000 | 1.3655 | 0.7086 | 1365.2365 | 1365.2365 | 2.4953 × 10−5 |
| FPA | 6.3483 | 1.4919 | 0.2000 | 1.3651 | 0.7087 | 1365.2365 | 1366.4543 | 3.8868 |
| GWO | 6.3525 | 1.4440 | 0.2000 | 1.3619 | 0.6999 | 1365.7193 | 1376.5011 | 6.6415 |
| JA | 6.3479 | 1.4916 | 0.2000 | 1.3657 | 0.7086 | 1365.2365 | 1365.2366 | 6.7456 × 10−5 |
| Algorithm | X1 | X2 | X3 | X4 | X5 | Min. Cost | Ave. Cost | Standard Dev. | HMCR | FW |
|---|---|---|---|---|---|---|---|---|---|---|
| HS | 6.3480 | 1.4918 | 0.2000 | 1.3657 | 0.7086 | 1365.2417 | 1365.3211 | 0.0509 | rand( ) | |
| AHS | 6.3479 | 1.4908 | 0.2000 | 1.3657 | 0.7083 | 1365.2371 | 1365.2478 | 0.0081 | ||
| AHHS | 6.3481 | 1.4914 | 0.2000 | 1.3654 | 0.7085 | 1365.2365 | 1365.2369 | 2.3466 × 10−4 | ||
| Algorithm | X1 | X2 | X3 | X4 | X5 | Min. Cost | Ave. Cost | Standard Dev. | Iter. Num. | Pop. Num. |
|---|---|---|---|---|---|---|---|---|---|---|
| GA | 4.1304 | 0.0046 | 0.2001 | 0.6106 | 0.4240 | 428.2186 | 428.6384 | 0.3440 | 2995 | 15 |
| DE | 4.1323 | 0.0000 | 0.2000 | 0.6098 | 0.4267 | 428.1139 | 428.1139 | 0.0000 | 1997 | 30 |
| PSO | 4.1324 | 0.0000 | 0.2000 | 0.6096 | 0.4267 | 428.1140 | 699.2741 | 732.5740 | 3993 | 30 |
| HS | 4.1356 | 0.0000 | 0.2000 | 0.6110 | 0.4271 | 428.3122 | 432.0160 | 1.8713 | 4991 | 25 |
| FA | 4.1331 | 0.0000 | 0.2000 | 0.6078 | 0.4254 | 428.1195 | 428.4955 | 0.1738 | 1498 | 30 |
| ABC | 4.1393 | 0.0000 | 0.2000 | 0.5998 | 0.4269 | 428.1525 | 428.7319 | 0.6954 | 3494 | 30 |
| TLBO | 4.1323 | 0.0000 | 0.2000 | 0.6098 | 0.4267 | 428.1139 | 428.1139 | 1.200 × 10−5 | 4991 | 25 |
| FPA | 4.1323 | 0.0000 | 0.2000 | 0.6099 | 0.4267 | 428.1139 | 428.1139 | 0.0000 | 3993 | 30 |
| GWO | 4.0961 | 0.3437 | 0.2000 | 0.6020 | 0.3762 | 434.2075 | 457.4451 | 9.1502 | 2496 | 30 |
| JA | 4.1323 | 0.0000 | 0.2000 | 0.6099 | 0.4267 | 428.1139 | 428.1139 | 5.000 × 10−6 | 4492 | 25 |
| Algorithm | X1 | X2 | X3 | X4 | X5 | Min. Cost | Ave. Cost | Standard Dev. | Iter. Num. | Pop. Num. | HMCR | PAR |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| HS | 4.1281 | 0.0000 | 0.2000 | 0.6164 | 0.4265 | 428.1428 | 428.4236 | 0.1856 | 2995 | 25 | rand( ) | |
| AHS | 4.1326 | 0.0000 | 0.2000 | 0.6094 | 0.4267 | 428.1143 | 428.1207 | 0.0055 | 4492 | 25 | ||
| AHHS | 4.1323 | 0.0000 | 0.2000 | 0.6097 | 0.4267 | 428.1139 | 428.1139 | 7.600 × 10−6 | 4492 | 10 | ||
| Symbol | Ranges | Increment | Unit |
|---|---|---|---|
| H | 3–10 | 1 | M |
| γz | 16–22 | 1 | kN/m3 |
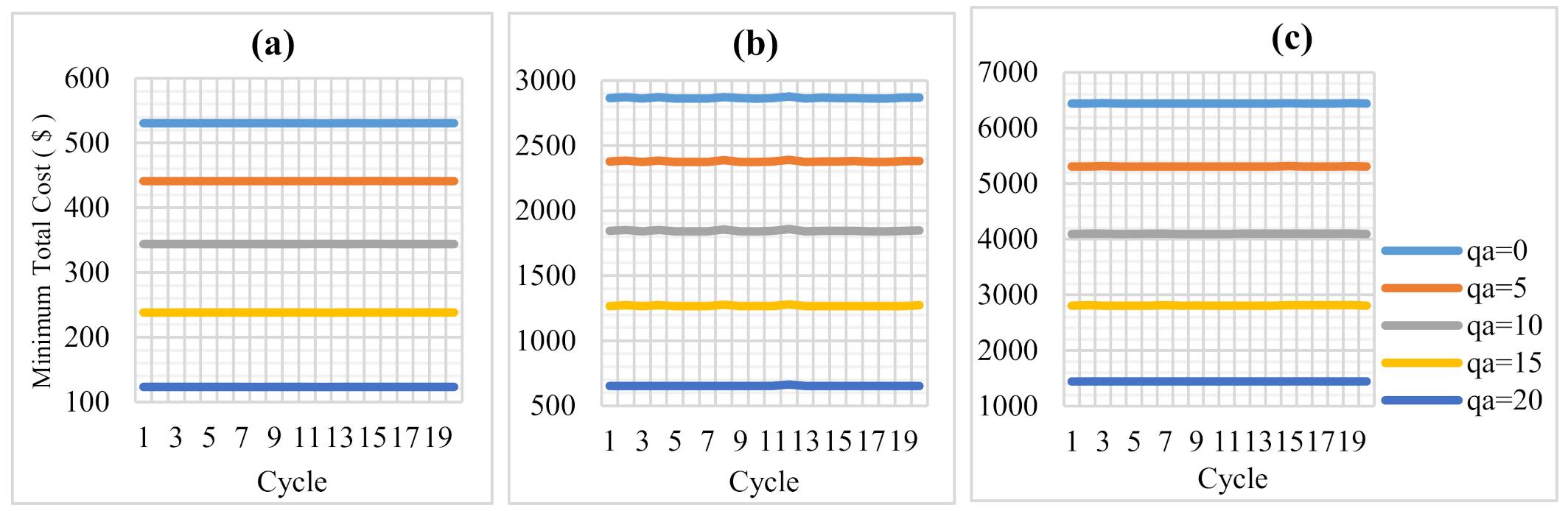
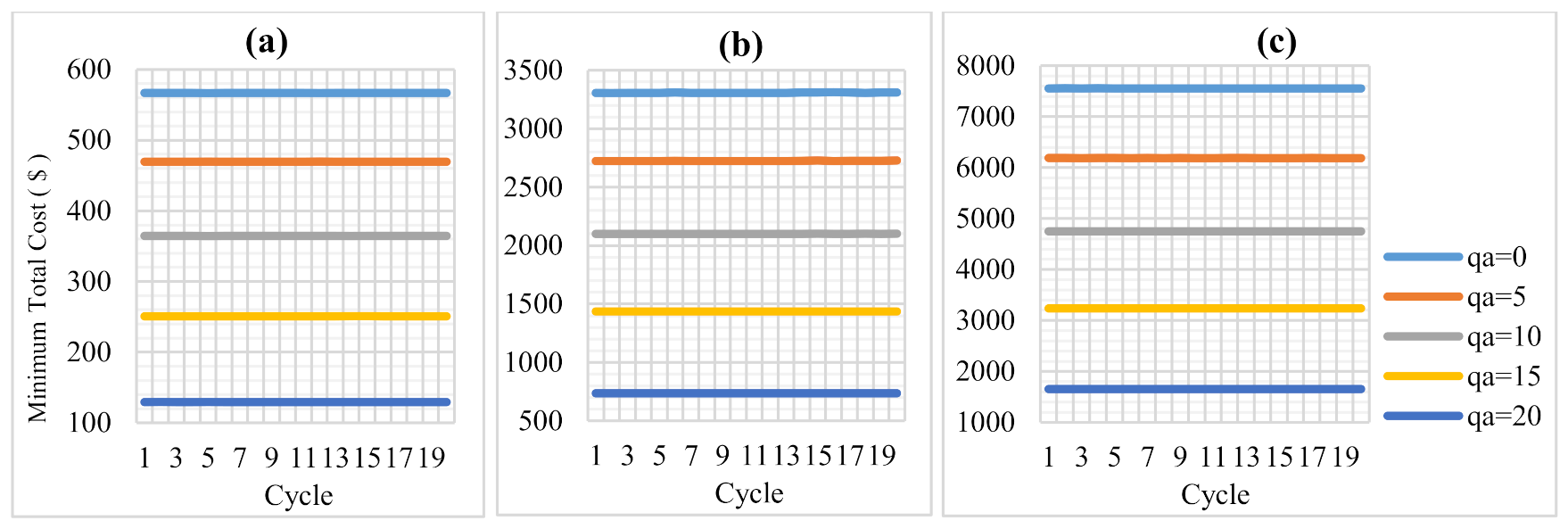
| qa | 0–20 | 5 | kN/m2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yücel, M.; Kayabekir, A.E.; Bekdaş, G.; Nigdeli, S.M.; Kim, S.; Geem, Z.W. Adaptive-Hybrid Harmony Search Algorithm for Multi-Constrained Optimum Eco-Design of Reinforced Concrete Retaining Walls. Sustainability 2021, 13, 1639. https://doi.org/10.3390/su13041639
Yücel M, Kayabekir AE, Bekdaş G, Nigdeli SM, Kim S, Geem ZW. Adaptive-Hybrid Harmony Search Algorithm for Multi-Constrained Optimum Eco-Design of Reinforced Concrete Retaining Walls. Sustainability. 2021; 13(4):1639. https://doi.org/10.3390/su13041639
Chicago/Turabian StyleYücel, Melda, Aylin Ece Kayabekir, Gebrail Bekdaş, Sinan Melih Nigdeli, Sanghun Kim, and Zong Woo Geem. 2021. "Adaptive-Hybrid Harmony Search Algorithm for Multi-Constrained Optimum Eco-Design of Reinforced Concrete Retaining Walls" Sustainability 13, no. 4: 1639. https://doi.org/10.3390/su13041639
APA StyleYücel, M., Kayabekir, A. E., Bekdaş, G., Nigdeli, S. M., Kim, S., & Geem, Z. W. (2021). Adaptive-Hybrid Harmony Search Algorithm for Multi-Constrained Optimum Eco-Design of Reinforced Concrete Retaining Walls. Sustainability, 13(4), 1639. https://doi.org/10.3390/su13041639








