The Inland Container Transportation Problem with Separation Mode Considering Carbon Dioxide Emissions
Abstract
1. Introduction
2. Literature Review
2.1. The ICT Problem
2.2. Vehicle Routing Problem with Separation Mode
2.3. Carbon Emission Minimization in Container Transportation Problem
3. Problem Description
3.1. Assumptions
- (1)
- Each tractor can only combine with one semi-trailer with/without container simultaneously.
- (2)
- Without considering the incompatible condition for tractors and semi-trailers.
- (3)
- Semi-trailers and empty containers are inexhaustible.
- (4)
- The tractors have different emission coefficients for driving status and waiting status.
- (5)
- The travel speed and emission coefficient are constant and identical for different vehicle state, i.e., single tractor, tractor with semi-trailer, tractor with semi-trailer and empty container, and tractor with semi-trailer and full container.
3.2. Parameters and Variables
3.3. Objective Function and Constraints
4. Optimisation Methodology
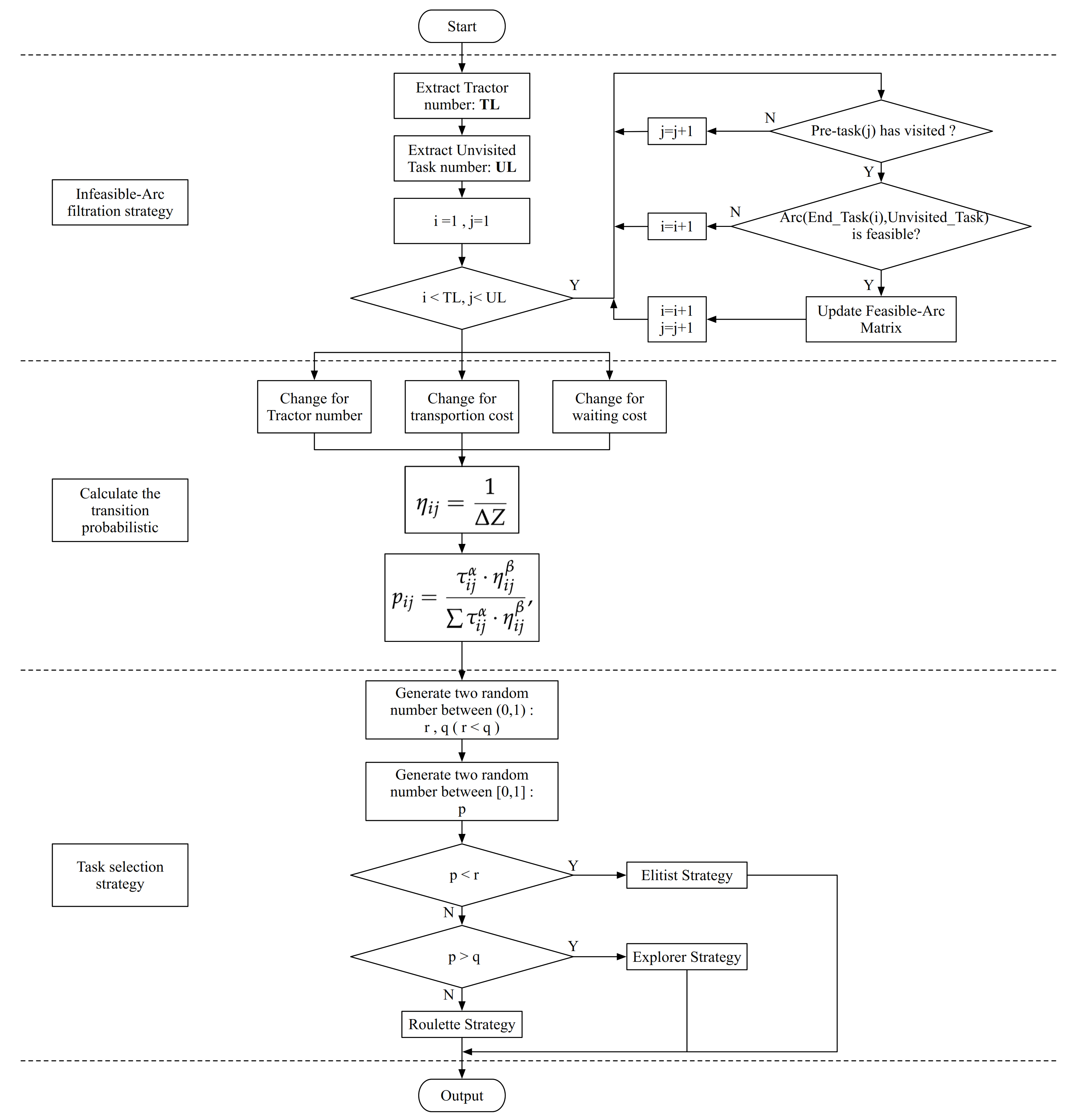
4.1. Ant path Encoding and Constructive Procedure
| Algorithm 1: Framework of Infeasible-Arc filtration strategy. |
| INPUT: Currently solution encoding for tractors. |
| OUTPUT: Feasible-Arc Martix. |
| 1. Extract the tractor number as . |
| 2. Extract Unvisited tasks number as . |
| 3. Build a null matrices as |
| 4. for i = 1: |
| 5. for j = 1: |
| 6. if the Pre-task of task j has been visited. |
| 7. if After insert task j, tractor j had plenty of time for return trip. |
| 8. Assignment to Optional-arc Matrix . |
| 9. end |
| 10. end |
| 10. end |
| 10. end |
- Elitist Strategy: select the arc with a maximum transition probabilistic .
- Explorer Strategy: select one stochastic arc in a feasible-arc matrix.
- Roulette Strategy: the classical in existing ACO, where the probability for each arc corresponds to its transition probabilistic .
4.2. Solution Decoding Rule and Pheromone Update Strategy
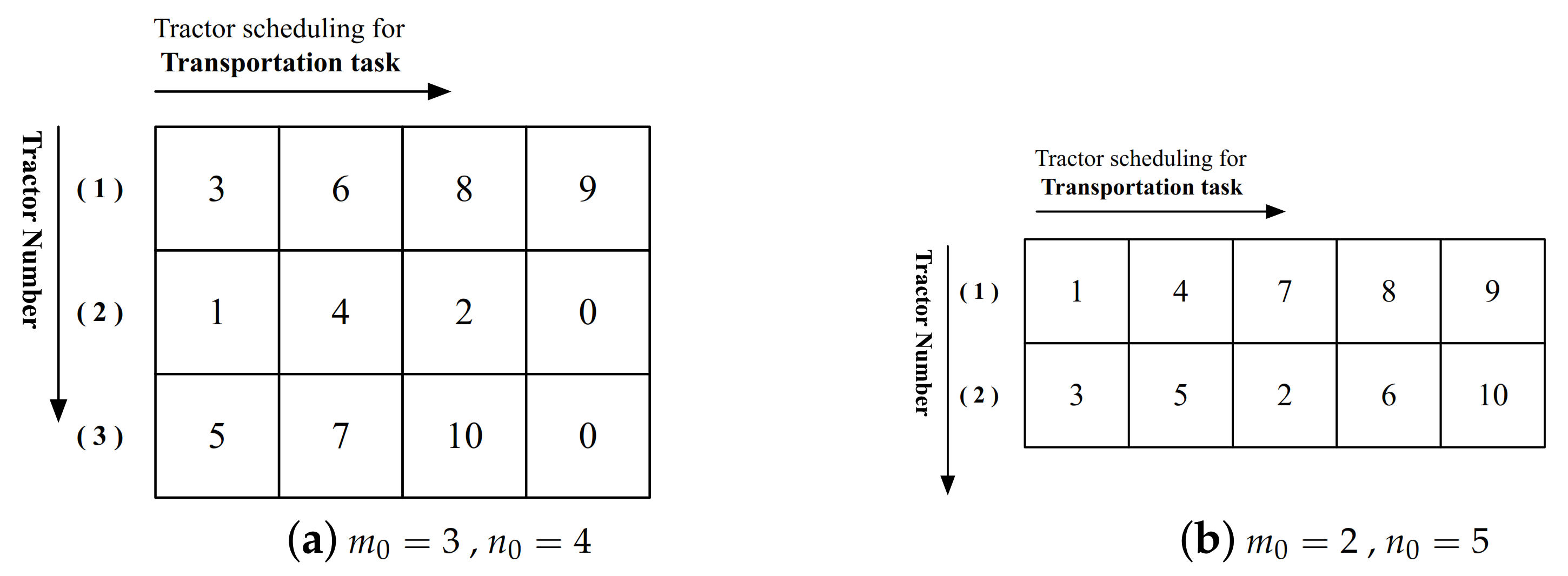
- Step 1. Choose a Two-dimensional variable matrix solution.
- Step 2. Randomly select one row of this encoding. If all numbers are zero, Repeat this Step; else extract all the non-zero task number in sequence. One typical selection of tractor route in this Step is Figure 1a is “1-4-2”, for example.
- Step 3. Determine the sub-sequence of tractor route. For the example in Step 2, the sub-sequence are “0–1”, “1–4”, “4–2”, “2–0”.
- Step 4. If the objective value of this ant less than the current best solution, adopt Max–Min Ant System (MMAS) updating strategy, which only elitist ant have survived and update pheromone of sub-sequence (the pheromone update amount is , where denotes total variation for each decision step of ant and equals to objective function value of our model, and Q is pheromone update value); or else, update the whole sub-sequence pheromone of each ant.
- Step 5. Repeat Steps 2–4 until all of the tractor route in Step 1 has updated pheromone.
5. Computational Experiments
5.1. Instances Generation
5.2. Small-Scale Instances
5.3. Large-Scale Instances
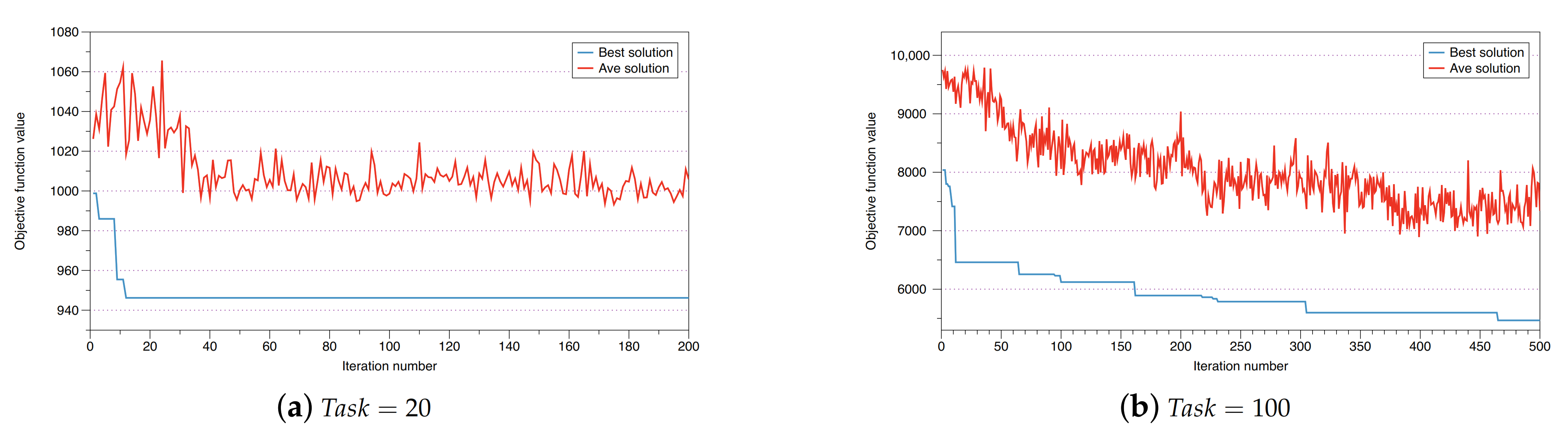
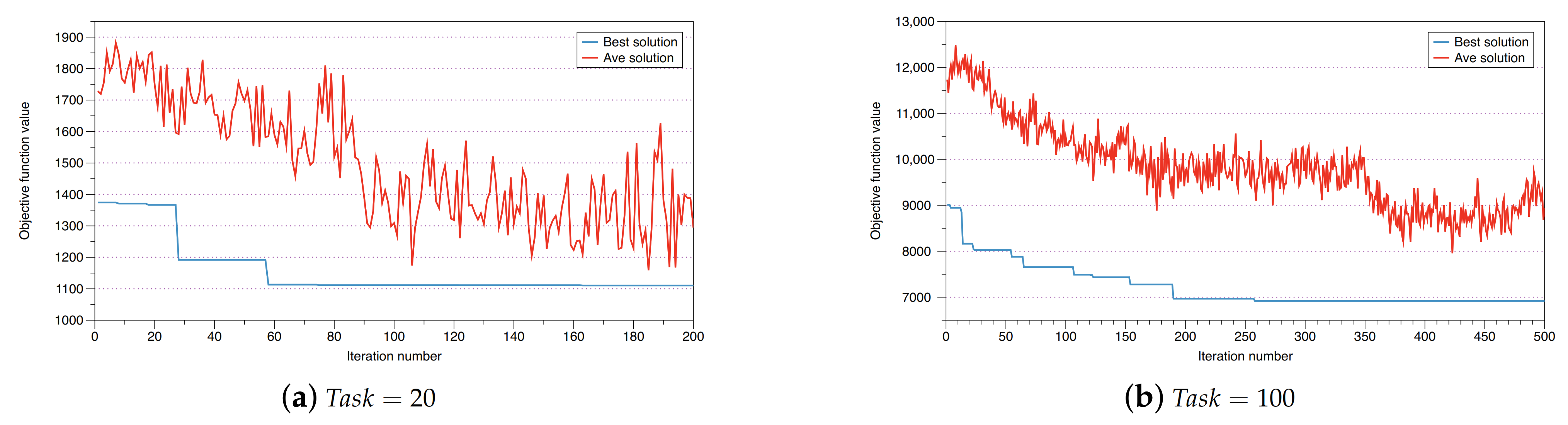
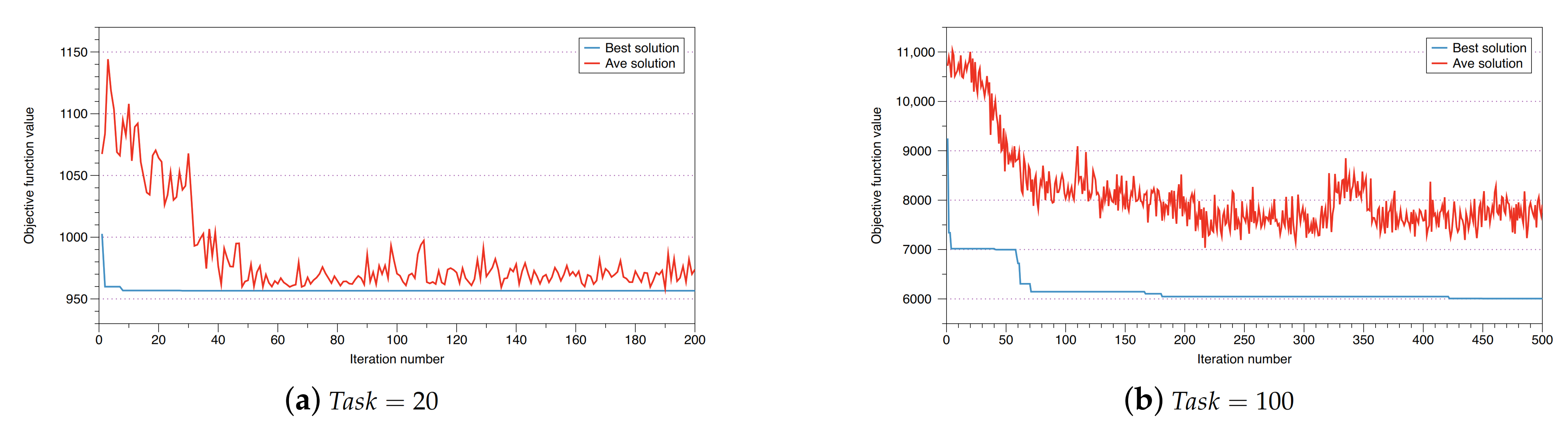
5.4. Performance Analysis of the Customized ACO
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, H.; Lu, Y.; Zhang, J.; Wang, T. Trends in road freight transportation carbon dioxide emissions and policies in China. Energy Policy 2013, 57, 99–106. [Google Scholar] [CrossRef]
- Demir, E.E.; Burgholzer, W.; Hrušovský, M.; Arıkan, E.; Jammernegg, W.; Van Woensel, T.T. A green intermodal service network design problem with travel time uncertainty. Transp. Res. Part B Methodol. 2016, 93, 789–807. [Google Scholar] [CrossRef]
- Shi, X.; Zhang, Y.; Voss, S. Actions applied by Chinese shipping companies under greenhouse gas emissions trading scheme. Int. J. Shipp. Transp. Logist. 2013, 5, 463–484. [Google Scholar] [CrossRef]
- Huang, Z.; Shi, X.; Wu, J.; Hu, H.; Zhao, J. Optimal annual net income of a containership using CO2 reduction measures under a marine emissions trading scheme. Transp. Lett. 2015, 7, 24–34. [Google Scholar] [CrossRef]
- Huang, Z.; Shi, X.; Wu, J.; Hu, H.; Zhao, J. How Will the Marine Emissions Trading Scheme Influence the Profit and CO2 Emissions of a Containership. In International Conference on Computational Logistics; Springer: Berlin/Heidelberg, Germany, 2013; pp. 45–57. [Google Scholar]
- Li, H. Effects of the Drop-and-Pull Transportation Mode on Mitigation of Carbon Dioxide Emissions based on the System Dynamics Model. J. Syst. 2016, 25, 514–526. [Google Scholar]
- Olivo, A.; Zuddas, P.; Di Francesco, M.; Manca, A. An operational model for empty container management. Marit. Econ. Logist. 2005, 7, 199–222. [Google Scholar] [CrossRef]
- Zhang, R.; Yun, W.Y.; Moon, I. A reactive tabu search algorithm for the multi-depot container truck transportation problem. Transp. Res. Part Logist. Transp. Rev. 2009, 45, 904–914. [Google Scholar]
- Zhang, R.; Yun, W.Y.; Kopfer, H. Heuristic-based truck scheduling for inland container transportation. OR Spectr. 2010, 32, 787–808. [Google Scholar] [CrossRef]
- Fang, L.; Xiaoning, S.; Hao, H. Analysis of Influencing Factors and Location Prediction of Dry Port Based on Logit Model. J. Chongqing Jiaotong Univ. 2012, 5, 31. [Google Scholar]
- Li, F.; Shi, X.; Hu, H. Location selection of dry port based on AP clustering-the case of southwest China. J. Syst. Manag. Sci. 2011, 1, 255–260. [Google Scholar]
- Zhang, G.; Smilowitz, K.; Erera, A. Dynamic planning for urban drayage operations. Transp. Res. Part E Logist. Transp. Rev. 2011, 47, 764–777. [Google Scholar] [CrossRef]
- Zhang, R.; Yun, W.Y.; Kopfer, H. Multi-size container transportation by truck: Modeling and optimization. Flex. Serv. Manuf. J. 2015, 27, 403–430. [Google Scholar] [CrossRef]
- Zhang, R.; Zhao, H.; Moon, I. Range-based truck-state transition modeling method for foldable container drayage services. Transp. Res. Part E Logist. Transp. Rev. 2018, 118, 225–239. [Google Scholar] [CrossRef]
- Zhang, R.; Huang, C.; Wang, J. A novel mathematical model and a large neighborhood search algorithm for container drayage operations with multi-resource constraints. Comput. Ind. Eng. 2020, 139, 106–143. [Google Scholar] [CrossRef]
- Funke, J.; Kopfer, H. A model for a multi-size inland container transportation problem. Transp. Res. Part E Logist. Transp. Rev. 2016, 89, 70–85. [Google Scholar] [CrossRef]
- van Riessen, B.; Negenborn, R.R.; Dekker, R. Real-time container transport planning with decision trees based on offline obtained optimal solutions. Decis. Support Syst. 2016, 89, 1–16. [Google Scholar] [CrossRef]
- Li, K.X.; Park, T.J.; Lee, P.T.W.; McLaughlin, H.; Shi, W. Container transport network for sustainable development in South Korea. Sustainability 2018, 10, 3575. [Google Scholar] [CrossRef]
- Fazi, S.; Roodbergen, K.J. Effects of demurrage and detention regimes on dry-port-based inland container transport. Transp. Res. Part C Emerg. Technol. 2018, 89, 1–18. [Google Scholar] [CrossRef]
- Huang, D.; Zhao, G. A Shared Container Transportation Mode in the Yangtze River. Sustainability 2019, 11, 2886. [Google Scholar]
- Shi, X.; Vanelslander, T. Design and evaluation of transportation networks: constructing transportation networks from perspectives of service integration, infrastructure investment and information system implementation. Netnomics 2010, 11, 1–4. [Google Scholar] [CrossRef][Green Version]
- Sterzik, S.; Kopfer, H.; Yun, W.Y. Reducing hinterland transportation costs through container sharing. Flex. Serv. Manuf. J. 2015, 27, 382–402. [Google Scholar] [CrossRef]
- Song, Y.; Zhang, J.; Liang, Z.; Ye, C. An exact algorithm for the container drayage problem under a separation modes. Transp. Res. Part E Logist. Transp. Rev. 2017, 106, 231–254. [Google Scholar] [CrossRef]
- Shan, W.; Peng, Z.; Liu, J.; Yao, B.; Yu, B. An exact algorithm for inland container transportation network design. Transp. Res. Part B Methodol. 2020, 135, 41–82. [Google Scholar] [CrossRef]
- Daham, H.A.; Yang, X.; Warnes, M.K. An efficient mixed integer programming model for pairing containers in inland transportation based on the assignment of orders. J. Oper. Res. Soc. 2017, 68, 678–694. [Google Scholar] [CrossRef]
- Li, H.; Lv, T.; Li, Y. The tractor and semitrailer routing problem with many-to-many demand considering carbon dioxide emissions. Transp. Res. Part D Transp. Environ. 2015, 34, 68–82. [Google Scholar] [CrossRef]
- Sterzik, S.; Kopfer, H. A tabu search heuristic for the inland container transportation problem. Comput. Oper. Res. 2013, 40, 953–962. [Google Scholar] [CrossRef]
- Ji, S.; Luo, R. A hybrid estimation of distribution algorithm for multi-objective multi-sourcing intermodal transportation network design problem considering carbon emissions. Sustainability 2017, 9, 1133. [Google Scholar]
- Vidović, M.; Popović, D.; Ratković, B.; Radivojevic, G. Generalized mixed integer and VNS heuristic approach to solving the multisize containers drayage problem. Int. Trans. Oper. Res. 2017, 24, 583–614. [Google Scholar] [CrossRef]
- Chao, I.M. A tabu search method for the truck and trailer routing problem. Comput. Oper. Res. 2002, 29, 33–51. [Google Scholar] [CrossRef]
- Tan, K.C.; Chew, Y.H.; Lee, L.H. A hybrid multi-objective evolutionary algorithm for solving truck and trailer vehicle routing problems. Eur. J. Oper. Res. 2006, 172, 855–885. [Google Scholar] [CrossRef]
- Lin, S.W.; Vincent, F.Y.; Chou, S.Y. Solving the truck and trailer routing problem based on a simulated annealing heuristic. Comput. Oper. Res. 2009, 36, 1683–1692. [Google Scholar] [CrossRef]
- Villegas, J.G.; Prins, C.; Prodhon, C.; Medaglia, A.L.; Velasco, N. A GRASP with evolutionary path relinking for the truck and trailer routing problem. Comput. Oper. Res. 2011, 38, 1319–1334. [Google Scholar] [CrossRef]
- Villegas, J.G.; Prins, C.; Prodhon, C.; Medaglia, A.L.; Velasco, N. A matheuristic for the truck and trailer routing problem. Eur. J. Oper. Res. 2013, 230, 231–244. [Google Scholar] [CrossRef]
- Lu, Y.; Lang, M.; Yu, X.; Li, S. A Sustainable Multimodal Transport System: The Two-Echelon Location-Routing Problem with Consolidation in the Euro—China Expressway. Sustainability 2019, 11, 5486. [Google Scholar] [CrossRef]
- Yang, Z.H.; Yang, G.M.; Xu, Q.; Guo, S.J.; Jin, Z.H. Optimization on tractor-and-trailer transportation scheduling with uncertain empty-trailer tasks. J. Traffic Transp. Eng. 2016, 16, 103–111. [Google Scholar]
- Xue, Z.; Lin, W.-H.; Miao, L.; Zhang, C. Local container drayage problem with tractor and trailer operating in separable mode. Flex. Serv. Manuf. J. 2015, 27, 431–450. [Google Scholar] [CrossRef]
- Xue, Z.; Zhang, C.; Lin, W.-H.; Miao, L.; Yang, P. A tabu search heuristic for the local container drayage problem under a new operation mode. Transp. Res. Part E Logist. Transp. Rev. 2014, 62, 136–150. [Google Scholar] [CrossRef]
- Caballini, C.; Sacone, S.; Saeednia, M. Cooperation among truck carriers in seaport containerized transportation. Transp. Res. Part E Logist. Transp. Rev. 2016, 93, 38–56. [Google Scholar] [CrossRef]
- Sun, Q.; Sun, J.; Jin, Z.; Sun, S. Mode selection of tractor-and-semitrailer swap transport for ro-ro shipping under land-sea combined transportation. Marit. Policy Manag. 2019, 46, 995–1010. [Google Scholar] [CrossRef]
- Liao, C.-H.; Tseng, P.-H.; Cullinane, K.; Lu, C.-S. The impact of an emerging port on the carbon dioxide emissions of inland container transport: An empirical study of Taipei port. Energy Policy 2010, 38, 5251–5257. [Google Scholar] [CrossRef]
- Jaehun, S. A carbon emission evaluation model for a container terminal. J. Clean. Prod. 2018, 186, 526–533. [Google Scholar]
- Hung, G.S. The impact of foldable ocean containers on back haul shippers and carbon emissions. Transp. Res. Part D Transp. Environ. 2019, 67, 514–527. [Google Scholar]
- Hoen, K.M.R.; Tan, T.; Fransoo, J.C.; Van Houtum, G.J. Effect of carbon emission regulations on transport mode selection under stochastic demand. Flex. Serv. Manuf. J. 2014, 26, 170–195. [Google Scholar] [CrossRef]
- Fan, H.; Ren, X.; Guo, Z.; Li, Y. Truck Scheduling Problem Considering Carbon Emissions under Truck Appointment System. Sustainability 2019, 11, 6256. [Google Scholar] [CrossRef]
- Li, L.; Zhang, X. Integrated optimization of railway freight operation planning and pricing based on carbon emission reduction policies. J. Clean. Prod. 2020, 263, 121316. [Google Scholar] [CrossRef]
- Yin, C.; Ke, Y.; Yan, Y.; Lu, Y.; Xu, X. Operation Plan of China Railway Express at Inland Railway Container Center Station. Int. J. Transp. Sci. Technol. 2020, 9, 249–262. [Google Scholar] [CrossRef]
- Thai, P.H.; Lee, H. Developing a green route model for dry port selection in Vietnam. Asian J. Shipp. Logist. 2019, 35, 96–107. [Google Scholar]
- Tsao, Y.-C.; Linh, V.T. Seaport-dry port network design considering multimodal transport and carbon emissions. J. Clean. Prod. 2018, 199, 481–492. [Google Scholar] [CrossRef]
- Qiu, X.; Lam, J.S.L. The value of sharing inland transportation services in a dry port system. Transp. Sci. 2018, 52, 835–849. [Google Scholar] [CrossRef]
- Yuvraj, G.; Abad, P. An ant colony system (ACS) for vehicle routing problem with simultaneous delivery and pickup. Comput. Oper. Res. 2009, 36, 3215–3223. [Google Scholar]
- Xu, S.; Liu, Y.; Chen, M. Optimisation of partial collaborative transportation scheduling in supply chain management with 3PL using ACO. Expert Syst. Appl. 2017, 71, 173–191. [Google Scholar] [CrossRef]
- Solomon, M.M. Algorithms for the vehicle routing and scheduling problems with time window constraints. Oper. Res. 1987, 35, 254–265. [Google Scholar] [CrossRef]

| - | Drive to full container yard | Drive to the Receiver location | Drive to empty container yard Pickup empty container Drive to the Shipper location | Drive to the Shipper location | |
| Back to trailer depot | Drive to the trailer depot Pull on a trailer Drive to full container yard | Drive to the Receiver location | Drive to the trailer depot Pull on a trailer Drive to empty container yard Pickup empty container Drive to the Shipper location | Drive to the Shipper location | |
| Drive to empty container yard Drop the empty container solely Back to trailer depot | Drive to empty container yard Drop the empty container solely Drive to full container yard | Drive to empty container yard Drop the empty container solely Drive to the trailer depot Drop off a trailer Drive to the Receiver location | Drive to the Shipper location | Drive to empty container yard Drop the empty container solely Drive to the trailer depot Drop off a trailer Drive to the Shipper location | |
| Back to trailer depot | Drive to the trailer depot Pull on a trailer Drive to full container yard | Drive to the Receiver location | Drive to the trailer depot Pull on a trailer Drive to empty container yard Pickup empty container Drive to the Shipper location | Drive to the Shipper location | |
| Back to trailer depot | Stay at heavy container yard | Drive to the trailer depot Drop off a trailer Drive to the Receiver location | Drive to empty container yard Pickup empty container Drive to the Shipper location | Drive to the trailer depot Drop off a trailer Drive to the Shipper location |
| Dst. | Scale | Task | Commercial Solver | Improved ACO | (%) | (%) | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| CPU | CPU | |||||||||
| C | 4-C | 1/1/1/1 | 332.721 | 0.17 | 332.721 | 332.721 | 332.721 | 0.52 | 0 | 0 |
| 6-C | 1/1/2/2 | 331.183 | 0.34 | 331.183 | 331.183 | 331.183 | 0.73 | 0 | 0 | |
| 6-C | 2/2/1/1 | 331.265 | 0.40 | 331.265 | 331.265 | 331.265 | 0.78 | 0 | 0 | |
| 8-C | 1/1/3/3 | 354.255 | 6.99 | 354.255 | 354.255 | 354.255 | 1.50 | 0 | 0 | |
| 8-C | 2/2/2/2 | 351.938 | 9.51 | 351.938 | 351.938 | 351.938 | 1.53 | 0 | 0 | |
| 10-C | 2/2/3/3 | 452.071 | 421.67 | 452.071 | 454.403 | 453.006 | 2.08 | 0 | 0.21 | |
| 12-C | 3/3/3/3 | 830.999 | 3600 | 746.601 | 789.913 | 776.838 | 5.31 | 10.16 | 4.05 | |
| 16-C | 4/4/4/4 | 1032.308 | 3600 | 780.542 | 846.301 | 811.051 | 5.66 | 24.39 | 3.91 | |
| R | 4-R | 1/1/1/1 | 342.529 | 0.40 | 342.529 | 342.529 | 342.529 | 0.55 | 0.00 | 0.00 |
| 6-R | 1/1/2/2 | 300.000 | 0.52 | 300.000 | 300.000 | 300.000 | 0.84 | 0.00 | 0.00 | |
| 6-R | 2/2/1/1 | 309.252 | 0.63 | 309.252 | 309.252 | 309.252 | 0.85 | 0.00 | 0.00 | |
| 8-R | 1/1/3/3 | 316.540 | 7.36 | 316.540 | 316.540 | 316.540 | 1.05 | 0.00 | 0.00 | |
| 8-R | 2/2/2/2 | 331.790 | 12.34 | 331.790 | 331.790 | 331.790 | 1.26 | 0.00 | 0.00 | |
| 10-R | 2/2/3/3 | 453.292 | 661.11 | 453.292 | 503.865 | 495.169 | 2.76 | 0.00 | 9.24 | |
| 12-R | 3/3/3/3 | 774.703 | 3600 | 686.196 | 732.741 | 719.969 | 4.89 | 11.42 | 4.92 | |
| 16-R | 4/4/4/4 | 1154.970 | 3600 | 765.292 | 823.932 | 804.578 | 7.40 | 33.74 | 5.13 | |
| RC | 4-RC | 1/1/1/1 | 322.275 | 0.31 | 322.275 | 322.275 | 322.275 | 0.59 | 0.00 | 0.00 |
| 6-RC | 1/1/2/2 | 360.371 | 0.55 | 360.371 | 360.371 | 360.371 | 0.84 | 0.00 | 0.00 | |
| 6-RC | 2/2/1/1 | 357.678 | 0.41 | 357.678 | 357.678 | 357.678 | 0.93 | 0.00 | 0.00 | |
| 8-RC | 1/1/3/3 | 355.796 | 9.45 | 355.796 | 355.796 | 355.796 | 1.09 | 0.00 | 0.00 | |
| 8-RC | 2/2/2/2 | 397.043 | 6.55 | 397.043 | 397.043 | 397.043 | 1.26 | 0.00 | 0.00 | |
| 10-RC | 2/2/3/3 | 821.319 | 242.93 | 723.373 | 776.307 | 766.909 | 1.41 | 11.93 | 6.02 | |
| 12-RC | 3/3/3/3 | 854.553 | 3600 | 717.856 | 803.346 | 766.660 | 5.27 | 16.00 | 6.80 | |
| 16-RC | 4/4/4/4 | 979.120 | 3600 | 752.427 | 835.855 | 790.760 | 8.60 | 23.15 | 5.09 | |
| Average | 18.68 | 5.13 | ||||||||
| No. | Scale | Stay-With Mode | Separation Mode | (%) | (%) | (%) | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| CPU | CPU | |||||||||
| 1 | 20-R | 1129.815 | 1143.228 | 10.19 | 940.749 | 947.871 | 11.55 | 16.73 | −1.19 | −0.757 |
| 2 | 30-R | 1205.287 | 1256.424 | 12.50 | 1110.288 | 1151.889 | 32.67 | 7.88 | −4.24 | −3.747 |
| 3 | 30-R | 1718.442 | 1794.912 | 20.64 | 1372.741 | 1427.110 | 27.58 | 20.12 | −4.45 | −3.961 |
| 4 | 30-R | 1721.429 | 1805.311 | 21.42 | 1414.490 | 1469.680 | 32.19 | 17.83 | −4.87 | −3.902 |
| 5 | 40-R | 2300.307 | 2469.760 | 103.43 | 1955.706 | 2062.820 | 136.39 | 14.98 | −7.37 | −5.477 |
| 6 | 60-R | 3512.034 | 4106.269 | 426.39 | 3038.304 | 3277.800 | 524.04 | 13.49 | −16.92 | −7.883 |
| 7 | 80-R | 4994.781 | 6006.973 | 662.64 | 4241.813 | 4850.220 | 923.31 | 15.08 | −20.26 | −14.343 |
| 8 | 100-R | 6526.592 | 8207.964 | 1178.31 | 5458.694 | 6293.559 | 2091.55 | 16.36 | −25.76 | −15.294 |
| 9 | 120-R | 8843.383 | 10,717.706 | 2222.92 | 6920.267 | 8411.912 | 3170.94 | 21.75 | −21.19 | −21.555 |
| 10 | 160-R | 11,324.120 | 15,363.589 | 4609.23 | 9016.639 | 11,991.371 | 7939.20 | 20.38 | −35.67 | −32.992 |
| 11 | 200-R | 16,598.903 | 23,704.445 | 10,346.77 | 11,994.986 | 18,404.399 | 14,680.57 | 27.74 | −42.81 | −53.434 |
| Ave | 17.48 | −16.79 | −14.85 | |||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, W.; Jin, Z.; Huang, Y.; Xu, S. The Inland Container Transportation Problem with Separation Mode Considering Carbon Dioxide Emissions. Sustainability 2021, 13, 1573. https://doi.org/10.3390/su13031573
He W, Jin Z, Huang Y, Xu S. The Inland Container Transportation Problem with Separation Mode Considering Carbon Dioxide Emissions. Sustainability. 2021; 13(3):1573. https://doi.org/10.3390/su13031573
Chicago/Turabian StyleHe, Wenqing, Zhihong Jin, Ying Huang, and Shida Xu. 2021. "The Inland Container Transportation Problem with Separation Mode Considering Carbon Dioxide Emissions" Sustainability 13, no. 3: 1573. https://doi.org/10.3390/su13031573
APA StyleHe, W., Jin, Z., Huang, Y., & Xu, S. (2021). The Inland Container Transportation Problem with Separation Mode Considering Carbon Dioxide Emissions. Sustainability, 13(3), 1573. https://doi.org/10.3390/su13031573







