Assessment Urban Transport Service and Pythagorean Fuzzy Sets CODAS Method: A Case of Study of Ciudad Juárez

Abstract

The purpose of this research article is to provide a comprehensive method of evaluation for public transportation. In this sense, this study considers transport lines that offer in Ciudad Juárez, Chihuahua. Hence, this study presents a description of the public transport system as part of the literature review. Likewise, the document describes an appropriate model based on the more outstanding publications about urban mobility and public transportation for passengers. Nevertheless, it is based on the Pythagorean Fuzzy combinative distance-based assessment (CODAS) to analyze and evaluate the alternatives through criteria that define general performance. Thus, the integration of these methods provides an adequate methodology for decision-making concerning urban planning and mobility to detect and improve the performance of criteria not considered within sustainable urban mobility plans. Results show how the applied approach can work as a powerful tool for the appraisal of the transport service. Finally, the results give relevant information to the local authority of the transport management of Ciudad Juarez to do improvements focused on the user.

1. Introduction

The tendency in the search for problems of transportation and urban mobility solutions, as well as in urban planning and geographic information systems (GIS), has increased worldwide, especially when talking about public passenger transportation, because there is an area of opportunity to implement public politics in cities with high population density. In other words, it is necessary to make objective and impartial decisions, that is, with a technical approach that helps to cover all the relevant aspects that affect quality.

As an example, we have several studies about sustainable mobility where we can see that mobility was reduced everywhere during the COVID-19 pandemic; bike-sharing also has a high impact during this pandemic in Thessaloniki, Greece, where cite evaluated the perception of the people about this transport mode using questionnaires; the results concluded that most people still feel vulnerable, however, i.e. most people travel by private car (50.5%), they do not usually use protection if it is not necessary and still travel by private car, but the people that use the bike-sharing system think that it is a good transport mode after COVID-19 [1]. Furthermore, in [2], a case study based in Poland was developed, where the bike-sharing system is an element of analysis in four different points, with data based on the operator to analyze the functioning of the system in Warsaw, which were georeferenced with a GIS’ software, then questionnaires were used to analyze the level of satisfaction with the Liker scale with a 4.5 of average rating. The analysis has been set up to 0.743 of Cronbach’s alpha coefficient.

Other case studies presented by [3] focused on the park and ride parking type, which is a good model to have a public transportation integration and sustainable service; this case study developed in Poland included the data base of the users and how used the service is, to motivate the citizen to use public transport. In a similar way, Politis et al. [4] with the bike-sharing systems were the principals factors by the users to use this services—the cost and the time travel. Furthermore, Ibrahim et al. [5] developed research to explain the intentions of the users to use the bus-based park-and-ride facilities in Putrajaya, Malaysia, and with the objective of increase, the number of service users through integration with public transport modes.

In multicriteria decision methods (MCDM), there are some applications in real life; in [6], some methods were used to assess the road freight transport companies based on the opinions of eight experts to weight the criteria keys (key drivers and financial drivers) in the order of importance. The conclusions of the case of study were that the MCDM does not need historical data to develop the numerical case; Rank 4 was attained by X4 company using complex proportional assessment (COPRAS), technique for order of preference by similarity to ideal solution (TOPSIS), evaluation based on distance from average solution (EDAS), and preference ranking organization method for enrichment of evaluations (PROMETHEE); with this application, we can see that MCDM helps to detect the most important drivers in the company. On the other hand, in [7], AHP method allows assessing passenger demand of the Amman urban transport system in Jordan, where service quality and price elements were considered, as well as the service offered to users, including the environmental aspects and tractability; that is, a total of 143 criteria decision were evaluated by 100 evaluators from different ages and social layers between April and May 2018. The results show that transport quality was first in level 1, safety of travel in level 2 and frequency of lines in level 3. The view of the users helps to making decisions about urban transportation.

However, the greatest obstacle that has arisen is the integration of qualitative information within the projects, with a large number of criteria to assess the quality of the service provided by a public transportation system usually obtained through opinions and interpretations of the users and experts—this is why the contribution of multicriteria decision methods to reduce the bias and improve information analysis is highlighted. One of the most important sets is the Pythagorean Fuzzy set (PFS), which better models uncertainty and is considered a new generation of Fuzzy sets (FS), as well as intuitionistic Fuzzy sets (IFS) [8], as part of the MCDM. Similarly, these fuzzy sets have generated hybridizations with some MCDM, as is the example of the MOORA method with IFS [9], which for the transportation area and urban mobility allows hierarching the route alternatives and detecting the route with the best characteristics for given criteria [10]. Thus, the assumptions of rating criteria according to the opinion in linguistic terms of experts in the subject were followed by a mathematical analysis in some matrixes represented by fuzzy numbers to evaluate the alternatives and establish and hierarchical order [11]. In the past decade, new methods for assessing MCDM problems have emerged as a response to include some characteristics which the actual methods have not considered [12] as the combinative distance-based assessment (CODAS) method developed by [13], that has the goal of determining which is the best alternative based on the Euclidean distance as the primary measure and the Taxicab distance (or Manhattan) that is the secondary measure when the Euclidean distances are incomparable.

1.1. Multicriteria Decision Making

In the last three decades, multicriteria decision making (MCDM) has been taking on vital importance in mathematics problems and computational sciences. Their principal characteristic is their valuation as applied science, which has the objective of determining the value of something such as a product or service, using elements of comparison where a professional evaluates all the criteria for every alternative that is usually subjective and quantitative information [14]. Zavadskas et al. [15] presents two categories, see, with the classification of the methods of multicriteria decision: first, the multi-attribute decision making (MADM) used to resolve discrete problems, where the alternatives are predetermined and the professional evaluates (a priori) every criteria, and the multi-objective decision making (MODM) that is used to resolve continual problems where the alternatives are not predetermined and will have some continued solutions with respect to two or more criteria named Paretoś border, where the professionals participate a posteriori [16]. MCDM is usually used to obtain the best alternative to fully satisfy a range of indicators of performance [17] and are based on the criteria with best preferred aspects according to the objectives of every problem or project; these criteria are also considered in a process of evaluation. In general, the MCDM consists of assigning choice weights, analyzing via pair-wise ranking of the alternatives’ respect of a criterion and establishing the importance and preference criteria or alternatives in an evaluation’s matrix to homogenize, because in the multicriteria decision making, the information can be qualitative data too, therefore suggesting that the evaluation can be with an objective vision where the intuition of every decision maker $\left(professional\right)$ represents their experience in individual evaluation [10]. Moreover, it is described as the process of the evaluation and selection of the best alternative of the universe [18] because we can classify as necessary to reduce bias and expose the problem with precision.

Furthermore, there were different methods of multicriteria to solve problems of transport and urban mobility, also applied in urban planification and geographic information system (GIS) for selecting the best alternative in a project and to implement politics publics, because this is necessary to design indicators for monitoring it [19]. The principal MCDM is the analytic hierarchy process (AHP) [20], technique for order of preference by similarity to ideal solution (TOPSIS) [21], analytic network process (ANP), [22]; multicriteria optimization and compromise solution (VIKOR, ViseKriterijumsa Optimizacija i Kompromisno Resenje) [23]; preference ranking organization method for enrichment of evaluations (PROMETHEE) [24]; elimination and choice expressing reality (ELECTRE) [25]; and multi-objective optimization on the basis of the ratio analysis (MOORA) introduced by [11], among other relevant methods.

Thus, Keshavarz-Ghorabaee et al. [13] was the first to develop the combinative distance-based assessment (CODAS) method based on crisp sets, or ordinal information to the assessment some alternatives. This method is based on the combination of the Euclidean distance as the primary unit and the Taxicab (or Hamming) distance as the secondary unit to compared between them respect to the negative-ideal point; Ghorabaee applied CODAS method to select a industrial robot using criteria of its operation. Furthermore, Ghorabaee et al. [26] used linguistic variables and trapezoidal fuzzy numbers to extend the CODAS to evaluate market segmentation; the results were compared with the ranking of Fuzzy EDAS and Fuzzy TOPSIS methods for the same problem. Panchal et al. [27] proposed an integration of the multi-criteria decision making to solve problems about maintenances for the industrial process; therefore, to calculate the weights of criteria and subcriteria, the geometric mean (GM) method is used, then the weights calculated are include in the proposed method to rank the alternatives of the strategy maintenance.

Thereby, Badi and Abdulshahed [28] applied CODAS methods using crisp sets in a case study of supplier selection for a steelmaking company in Libya. They used sensibility analysis to measure the validity and stability of this method. Some time after, Boltürk [29] developed an integration of the CODAS method using Pythagorean Fuzzy sets and applied the proposal to select a supplier in a manufacturing firm. Peng and Garg [30] introduced an application with WDBA to select the optimum alternative with CODAS method; the principal characteristic that provided WDBA is to compare the shortest distance with the negative-ideal solution. Badi et al. [31] developed a problem to select the best location to install a desalination plant using the geographic information of Libya as criteria. Dahooei et al. [32] evaluated model of business intelligence for enterprise system; the model consists of Fuzzy numbers to calculate criteria weights and to evaluate alternatives with intuitionistic Fuzzy logic with interval values.

Pamučar et al. [33] used the pairwise to determine the importance level of the criteria and then the method integrate CODAS crisp to select wave energy technology as a case of study. IVIF-CODAS method was used by [34] to select sustainable material in construction projects with incomplete weight information; Roy developed a sensibility analysis to validate IVIF-CODAS changing weights of criteria, reaching a high degree of stability. Yalcin and Yapıcı Pehlivan [35] developed a case study for personnel selection with linguistic terms of uncertainty (hesitant Fuzzy linguistic term sets, HFLTS); in a similar case of application using this information type, [36] appraised organizational and technological into Industry 4.0.

In a different view of application, Ijadi Maghsoodi et al. [37] used SWARA as a tool to calculate criteria weights and CODAS under crisp sets to select material for dam construction based on the technical specifications (chemical and physics) of each alternative. Buyukozkan and Göçer [38] is highly recognized to developed and worked with multi-criteria decision making; they developed a model of decision making based on CODAS under intuitionistic Fuzzy to determine and prioritize strategies of SCL (smart city logistic). Laha and Biswas [39] assess the performance of bank institutions using entropy method to calculate weights criteria and CODAS to assess the stability and level of performance. Moreover, Ouhibi and Moalla proposed multiple classification and categories under incremental positions for central profiles and limits used to compared the distances of the CODAS method. Karaşan et al. [40] work with a method to select the best alternative to install wind generation plants.

Using the best and worst (BWM) method, Ijadi Maghsoodi et al. [41] evaluated the weights of the criteria and the linguistic variables with 2-tuple interval values. To select computer system to work in the cloud according to the criteria of availability, reliability, security, maintenance, among others [42] developed a special application using interval-valued intuitionistic Fuzzy CODAS for multi-attribute decision-making method in Tehran. In another order of ideas, Flores-Ruvalcaba et al. [12] performed a comparison of MOORA with CODAS methods under Pythagorean Fuzzy sets to show the benefits and disadvantages between this methods. Flores Ruvalcaba found that the weight of the criteria in CODAS method just considers necessary one expert to apply the method through linguistic terms does not have a step for calculate the contribution of the stakeholders, these stakeholders are named decision makers (DM) in MCDM. Zhou et al. [43] developed an interesting model of aggregation with Pythagorean Fuzzy sets with CODAS and pure linguistic information, with application to financial strategies of multi-national companies.

1.2. Weights of the Criteria and Decision Makers

The contributions of criteria in multi-criteria decision making is expressed through the integration of the DM’s opinions. Perez et al. [9] use the intuitionistic Fuzzy weighted average (IFWA) for rating the kth DM, then [44] change the information type using Pythagorean Fuzzy set (PFS) instead of intuitionics Fuzzy set (IFS), therefore they used the same configuration, named as Fuzzy weighted arithmetic Pythagorean, that is based on the geometry like Pythagorean Fuzzy weighted arithmetic averaging (PFWAA) operator, this operator can be used with PFS, because it is an extension of IFS [45] and can provide better certainty to reduce uncertainty.

Entropy is another method that works on a predefined decision matrix of criteria. The concept of entropy has two sides; first, when the concept refers to a measure of a certain property of a system like a temperature; second, when the concept is subjective and can be used as a tool to build models [46]. This method can be combined with MCDM to evaluate alternatives through the weight of the criteria because all criteria do not have the same degree of importance in decision-making in real life. The entropy method of the set of normalized outcomes of the jth criterion is given by the degree of diversity of the information.

The Criteria for Public Transportation

The criteria for public transportation are based in their contribution of the operation’s performance and the quality of the service. Moreover, the COVID-19 pandemic that first appeared in Wuhan, China in December 2019 [47], then covered Mexico in March 2020, influences service and operation due to the interaction of different masses of people inside buses throughout the day, because COVID-19 is highly deadly and and contagious through contact with body fluids [48]. Thus, the risk conditions are increasing due to the lack of sanitation protocols, the use of face masks, and healthy distance between users as a minimum of 6 foot, as recommended by the World Health Organization (WHO) [49].

Finally, the proposal in this study is related to deal with the transport service assessment (TSA) via the MCDM method. Thus, the situation is to lead this transport assessment service (TSA) in order to do improvement focused on users. In this sense, we design an algorithm to do this appraisal step by step. In this mode, the authorities responsible for managing the transport service can be guided during analysis about TSA.

2. Basic Concepts of Pythagorean Fuzzy Set

In this section, we described some basic concepts of PFSs, introduced by Yager, and explained as follows.

A Pythagorean Fuzzy set gives the characteristic of the membership and non-membership degrees that must be equal or less than 1, and that is the principal difference with intuitionistic Fuzzy sets (IFS) introduced by Atanassoc in 1986, because in IFS, the contribution or membership and non-membership degrees in general is more than 1.

Definition 1.

Let a set X be a universe of discourse. A PFS P is represented as the next form equation: $\tilde{P}=\left\{\left.⟨x,P\left({\mu }_P\left(x\right),{\nu }_P\left(x\right)\right.⟩\right)|xϵX\right\}$ Here ${\mu }_{P\left(x\right)}$ and ${\nu }_{P\left(x\right)}\in X\to \left[0,1\right]$ depict the degree of membership and non-membership function of the fuzzy set P; ${\mu }_{P\left(x\right)}ϵ\left[0,1\right]$ depict the membership degree of $xϵXinP$. For all PFS, the next condition is necessary:

$${\left({\mu }_P\left(x\right)\right)}^2+{\left({\nu }_P\left(x\right)\right)}^2\le 1$$

(1)

Moreover, the degree of hesitancy that is called indeterminacy grade or Pythagorean index degree, ${\pi }_P\left(y\right)$, of x in P can be calculate as follows:

$${\pi }_P\left(y\right)=\sqrt{1-\left({\left({\mu }_P\left(x\right)\right)}^2+{\left({\nu }_P\left(x\right)\right)}^2\right)}$$

(2)

where ${\left({\mu }_P\left(x\right)\right)}^2+{\left({\nu }_P\left(x\right)\right)}^2\le 1$ is for each $xϵX$.

Definition 2.

Consider two PFNs [43] as $\widetilde{P_1}=\left\{\left.⟨x,P_1\left({\mu }_{P1}\left(x\right),{\nu }_{P1}\left(x\right)\right.⟩\right)x\in X\right\}$ and $\widetilde{P_2}=\left\{\left.⟨x,P_1\left({\mu }_{P2}\left(x\right),{\nu }_{P2}\left(x\right)\right.⟩\right)xϵX\right\}$ the following basic operations are valid:

$${\tilde{P}}_i=\left({\mu }_{Pi},{\nu }_{Pi}\right),$$

(3)

$${\tilde{P}}_1\oplus {\tilde{P}}_2=\sqrt{1-\left(1-{\mu }_{P1}^2\right)\left(1-{\mu }_{P2}^2\right)},\left({\nu }_{P1}·{\nu }_{P2}\right)$$

(4)

$${\tilde{P}}_1\otimes {\tilde{P}}_2={\mu }_{P1}·{\mu }_{P2},\sqrt{1-\left(1-{\nu }_{P1}^2\right)\left(1-{\nu }_{P2}^2\right)·}$$

(5)

$$\lambda \tilde{P}=P\left(\sqrt{1-{\left(1-{\mu }_P^2\right)}^{\lambda }},{\left({\nu }_P\right)}^{\lambda }\right),\lambda \ge 0and\lambda \in R$$

(6)

3. The Proposed Methodology

This section describes the method proposed for CODAS with multi-criteria decision-making and Pythagorean Fuzzy sets, following the methodology show in Figure 1.

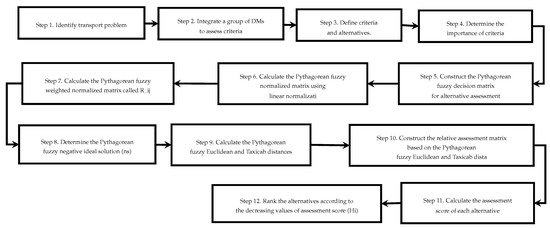
Figure 1. Pythagorean Fuzzy (PF)- combinative distance-based assessment (CODAS) Methodology (Source: The authors).

In addition, the major contribution is the way of calculating the Pythagorean Fuzzy weight of criteria and the contribution of the expertise of the decision makers (DMs) for evaluating every alternative; also it can see how to select the best threshold parameter “$\tau$” to analyze the distances Euclidean and Taxicab for two alternatives in the next steps.

Step 1. Identify transport problem.

In this sequence, the problem is identified using the scenes, context and the information to be collected. In this sense, the problem can be attacked with enough background in order to have complete data about it.

Step 2. Define criteria and alternatives.

Decision criteria are the group of criteria that can describe the best way of performance of an alternative. The alternatives of set $A_i$ with i = 1, 2, …, m each of them evaluated for decision criteria of set $C_j$ with j = 1, 2,..., n.

Step 3. Integrate a group of DMs to assess each criteria.

Where DMs = ${DM}_1$, ${DM}_2$, …, ${DM}_k$, …, ${DM}_l$ is a set of decision makers. The expertise for each DM is established using linguistic terms expressed by Pythagorean Fuzzy numbers shown in Table 1. The overall contribution of every decision maker defined as ${DM}_k=\left\{{\pi }_k,{\nu }_k,{\pi }_k\right\}$ with the corresponding weight of kth DM is calculated using the concept proposed by Boran [44]:

$${\lambda }_k=\frac{\left({\mu }_k+{\pi }_k\left(\frac{{\mu }_k}{{\mu }_k+{\pi }_k}\right)\right)}{{\sum }_{k=1}^l\left({\mu }_k+{\pi }_k\left(\frac{{\mu }_k}{{\mu }_k+{\pi }_k}\right)\right)}$$

(7)

where ${\sum }_{k=1}^l{\lambda }_k=1$.

Table 1. Pythagorean Fuzzy Numbers of the criteria and decision makers (DMs).

Linguistic Terms	$\mathit{\mu }$	$\mathit{\nu }$	$\mathit{\pi }$
Apprentice (Ap )/Very Unimportant (VU)	0.10	0.90	0.42
Learner (Lr)/Unimportant (U)	0.35	0.60	0.72
Capable (Cp )/Medium (M)	0.50	0.45	0.74
Skillful (S) /Important (I)	0.75	0.40	0.53
Dominant (D)/Very Important (VI)	0.90	0.10	0.42

Step 4. Determine the importance of criteria. Using the linguistic terms expressed by pythagorean fuzzy numbers shown in Table 1, the group of DMs analyzes the criteria that describe all alternatives, then all DMs give an evaluation for each criterion to be considered and determine what is the contribution of each one to the problem.

Construct the matrix of assessments for each criterion by kth DMs.

$${\tilde{w}}_j=PFWA=\left({{\tilde{w}}_j}^{\left(1\right)},{{\tilde{w}}_j}^{\left(2\right)},\dots ,{{\tilde{w}}_j}^{\left(k\right)}\right)$$

(8)

$${\tilde{w}}_j={\lambda }_1·{{\tilde{w}}_j}^{\left(1\right)}\oplus {{\lambda }_2·{\tilde{w}}_j}^{\left(2\right)}\oplus \dots \oplus {\lambda }_k·{{\tilde{w}}_j}^{\left(k\right)}$$

(9)

$${\tilde{w}}_j=\left(\sqrt{1-\prod _{j=1}^l{\left(1-{\mu }_{ij}^2\right)}^{{\lambda }_k}},\prod _{j=1}^l{\left({\nu }_{ij}\right)}^{{\lambda }_k}\right)$$

(10)

$${\tilde{w}}_j=\frac{\left({\mu }_k+{\pi }_k\left(\frac{{\mu }_k}{{\mu }_k+{\pi }_k}\right)\right)}{{\sum }_{k=1}^l\left({\mu }_k+{\pi }_k\left(\frac{{\mu }_k}{{\mu }_k+{\pi }_k}\right)\right)}$$

(11)

Step 5. Construct the Pythagorean Fuzzy decision matrix for alternative assessment. The individual opinion of DMs in linguistic terms is transformed using the linguistic variables of the Table 2, then all opinions of each DM are included in an aggregated Pythagorean Fuzzy decision matrix (APFDM) as follows:

Table 2. Pythagorean Fuzzy Numbers of the alternatives.

Linguistic Terms	$\mathit{\mu }$	$\mathit{\nu }$	$\mathit{\pi }$
Extremenly Low (EL)	0.10	0.99	0.10
Very Low (VL)	0.10	0.97	0.22
Low (L)	0.25	0.92	0.30
Medium Low (ML)	0.40	0.87	0.29
Medium (M)	0.50	0.80	0.33
Medium High (MH)	0.60	0.71	0.37
High (H)	0.70	0.60	0.39
Very High (VH)	0.80	0.44	0.41
Extremenly High (EH)	1.00	0.00	0.00

Where ${\tilde{x}}_{ij}\ge 0$ and ${\tilde{x}}_{ij}=\left({\mu }_P,{\nu }_P\right)$ and $0\le {\left({\mu }_P\left(x\right)\right)}^2+{\left({\nu }_P\left(x\right)\right)}^2\le 1$

$${\tilde{x}}_{ij}=APFDM\left({{\tilde{x}}_{ij}}^{\left(1\right)},{{\tilde{x}}_{ij}}^{\left(2\right)},\dots ,{{\tilde{x}}_{ij}}^{\left(k\right)}\right)$$

(12)

$${\tilde{x}}_{ij}={\lambda }_1·{{\tilde{x}}_{ij}}^{\left(1\right)}\oplus {{\lambda }_2·{\tilde{x}}_{ij}}^{\left(2\right)}\oplus \dots \oplus {\lambda }_k·{{\tilde{x}}_{ij}}^{\left(k\right)}$$

(13)

$${\tilde{x}}_{ij}=\left(\sqrt{1-\prod _{j=1}^l{\left(1-{\mu }_{ij}^2\right)}^{{\lambda }_k}},\prod _{j=1}^l{\left({\nu }_{ij}\right)}^{{\lambda }_k}\right)$$

(14)

Then, the APFDM is defined as:

$$\tilde{X}={\left[x_{ij}\right]}_{m.n}=\left[\begin{array}{cccc}{\tilde{x}}_{11}& {\tilde{x}}_{12}& \cdots & {\tilde{x}}_{1n}\\ {\tilde{x}}_{21}& {\tilde{x}}_{22}& \cdots & {\tilde{x}}_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ {\tilde{x}}_{m1}& x_{m2}& \cdots & {\tilde{x}}_{mn}\end{array}\right]$$

(15)

Step 6. Calculate the Pythagorean fuzzy normalized matrix using linear normalization. Using Equations (16) and (17) this step is developed as following.

$${{\eta }_{\mu }}_{ij}=\frac{{\tilde{x}}_{ij}}{{max}_i{\tilde{x}}_{ij}},{{\eta }_{\nu }}_{ij}=\frac{{min}_i{\tilde{x}}_{ij}}{{\tilde{x}}_{ij}}ifj\in N_b$$

(16)

$${{\eta }_{\mu }}_{ij}=\frac{{min}_i{\tilde{x}}_{ij}}{x_{ij}},{{\eta }_{\nu }}_{ij}=\frac{{\tilde{x}}_{ij}}{{max}_i{x}_{ij}}ifj\in N_c$$

(17)

where $N_b$ and $N_c$ represent the sets of benefit and cost criteria, respectively.

Step 7. Calculate the Pythagorean Fuzzy weighted normalized matrix called ${\overline{R}}_{ij}$

$${\tilde{R}}_{ij}=\left\{{\tilde{r}}_{ij}\right\}={\tilde{w}}_j\otimes {\tilde{x}}_{ij}$$

(18)

$${\tilde{R}}_{ij}=\left\{⟨x,\sqrt{1-{\left({\mu }_{x_i}^2\left(x\right)\right)}^{w_j}},\prod _{j=1}^l{\left({\nu }_{x_i}\left(x\right)\right)}^{w_j}⟩xϵX\right\}$$

(19)

$$\tilde{R}={\left[x_{ij}\right]}_{m.n}=\left[\begin{array}{cccc}{\tilde{x}}_{11}& {\tilde{x}}_{12}& \cdots & {\tilde{x}}_{1n}\\ {\tilde{x}}_{21}& {\tilde{x}}_{22}& \cdots & {\tilde{x}}_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ {\tilde{x}}_{m1}& x_{m2}& \cdots & {\tilde{x}}_{mn}\end{array}\right]$$

(20)

Step 8. Determine the Pythagorean Fuzzy negative ideal solution $\widetilde{ns}$. Using the following equations $\widetilde{ns}$ is obtained following:

$$\widetilde{ns}={\left[{\widetilde{ns}}_j\right]}_{1xm}$$

(21)

$$\underset{i}{max}{\overline{r}}_{{\mu }_{ij}},\underset{i}{min}{\overline{r}}_{{\nu }_{ij}}ifj\in N_b$$

(22)

$$\underset{i}{min}{\overline{r}}_{{\nu }_{ij}},\underset{i}{max}{\overline{r}}_{{\mu }_{ij}}ifj\in N_b$$

(23)

Step 9. Calculate the Pythagorean Fuzzy Euclidean and Taxicab distances. Using alternatives from the negative ideal solution as the following equations:

$$E_i=\sqrt{\sum _{j=1}^m{\left({\overline{u}}_{{\mu }_{i}j}-{\overline{ns}}_{{\mu }_{i}j}\right)}^2+{\left({\tilde{u}}_{{\nu }_{i}j}-{\overline{ns}}_{{\nu }_{i}j}\right)}^2}$$

(24)

$$T_i=\sum _{j=1}^m\left|\left({\overline{u}}_{{\mu }_{i}j}-{\overline{ns}}_{{\mu }_{i}j}\right)+\left({\overline{u}}_{{\nu }_{i}j}-{\overline{ns}}_{{\nu }_{i}j}\right)\right|$$

(25)

Step 10. Construct the relative assessment matrix based on the Pythagorean Fuzzy Euclidean and Taxicab distances. These steps are given in the following equations:

$$R_a={\left[h_{ik}\right]}_{nxn}$$

(26)

$$h_{ik}=\left(E_i-E_k\right)+\left(\psi \left(E_i-E_k\right)\times \left(T_i-T_k\right)\right)$$

(27)

where $kϵ\left\{1,2,\cdots ,n\right\}$ and c denotes a threshold function to recognize the equality of the Euclidean distances of two alternatives, as given in the following equation:

$$\psi \left(x\right)=\left\{\begin{array}{ccc}1& if& \left|x\right|\ge \tau \\ 0& if& \left|x\right|<\tau \end{array}\right.$$

(28)

If the difference between Euclidean distances of two alternatives is less than, these two alternatives are also compared by the Taxicab distance.

Step 11. Calculate the assessment score of each alternative. In order to obtain the score, Equation (29) is used to determine it:

$$H_i=\sum _{k=1}^n{h}_{ik}$$

(29)

Step 12. Rank the alternatives according to the decreasing values of assessment score $\left(H_i\right)$. The alternative with the highest $H_i$ is the best alternative among the alternatives.

4. Numerical Case

In this section, a numerical real life case is used. The steps are as follows:

Stpep 1. Identify transport problem. This illustrative case belongs to an assessment of public transportation system in Ciudad Juárez, in which several criteria described the principal characteristics that must have a good service to the users.

Step 2. Define criteria and alternatives. Table 3 contains the criteria and their explanation—it is very important consider the type of criteria—this means that some criteria are of cost (minimum values are ideal) and another are of benefit (high values are ideal). In order to explain what the alternatives assessment in this proposal are, the modal distribution of public transportation system is in Ciudad Juárez. Here, alternatives assessment in this proposal is described as follows in Table 4:

Table 3. The decision criteria.

Criteria	Reference
Average travel time, Convenience, Security, Reliability, Flexibility, Precision, Operational risk, Quality of service, Energy consumption, Available, Accessibility	[50]
Timeliness, Average travel time, Convenience, Intramodality, Security, cost, System coverage, Service timetable, Reliability, Velocity, Comfortable, Available, Mobility impact	[17]
Frequency, Security, Cost, Comfortable and Accessibility	[51]
Timeliness, Average travel time, Cost, System coverage	[24]
Cost, Occupancy, Comfortable, Accessibility, Information	[52]
Visual information of COVID-19 of mask, Training protocols of COVID-19, identify safe seats	[49]

Table 4. Alternatives of public transportation.

Line	Ramal	Status	Alternatives
1-A	Paseo de la Victoria (Express)	In service	R1
1-A	Morelos	In service	R2
1-A	Unitec	In service	R3
1-A	Tradicional	In service	R4
1-B	Talamas (Express)	In service	R5
Universitaria	Universitaria	In service	R6

Step 3. Integrate a group of DMs to assess criteria.

Integrate a group of DMs to assess the group of decision criteria representative of the alternatives is shown in Table 5.

Table 5. The contribution of every Decision Maker.

Decision Maker	1	2
Linguistic Term	D	Ap
PF number	{$0.90$, $0.10$, $0.42$}	{$0.10$, $0.90$, $0.42$}

Step 4. Determine the importance of criteria.

The importance of criteria is shown in Table 6.

Table 6. Criteria of public transportation.

Criteria	Description	Type	DM1	DM2	${\mathit{\mu }}_{\mathit{k}}$	${\mathit{\nu }}_{\mathit{k}}$	${\mathit{\pi }}_{\mathit{k}}$	W(${\mathit{\lambda }}_{\mathit{j}}$)
C1	Frequency	Benefit	VI	I	0.8908	0.1149	0.4397	0.0453
C2	Timeliness	Benefit	I	M	0.7337	0.4047	0.5458	0.0384
C3	Average travel time	Cost	VI	I	0.8908	0.1149	0.4397	0.0453
C4	Convenience	Benefit	I	M	0.7337	0.4047	0.5458	0.0384
C5	Intramodality	Benefit	M	VI	0.5884	0.3872	0.7098	0.0360
C6	Security	Benefit	VI	M	0.8843	0.1162	0.4522	0.0454
C7	Cost	Cost	VI	VI	0.9000	0.1000	0.4243	0.0453
C8	System coverage	Benefit	M	M	0.5000	0.4500	0.7399	0.0315
C9	Service timetable	Benefit	M	M	0.5000	0.4500	0.7399	0.0315
C10	Reliability	Benefit	VI	VI	0.9000	0.1000	0.4243	0.0453
C11	Velocity	Cost	VI	VI	0.9000	0.1000	0.4243	0.0453
C12	Occupancy	Benefit	I	I	0.7500	0.4000	0.5268	0.0387
C13	Flexibility	Benefit	M	M	0.5000	0.4500	0.7399	0.0315
C14	Precision	Benefit	M	M	0.5000	0.4500	0.7399	0.0315
C15	operational risk	Cost	VI	VI	0.9000	0.1000	0.4243	0.0453
C16	Comfortable	Benefit	I	I	0.7500	0.4000	0.5268	0.0387
C17	Quality of service	Benefit	I	I	0.7500	0.4000	0.5268	0.0387
C18	Energy consumption	Benefit	VI	VI	0.9000	0.1000	0.4243	0.0453
C19	Mobility impact	Benefit	VI	VI	0.9000	0.1000	0.4243	0.0453
C20	Available	Benefit	M	M	0.5000	0.4500	0.7399	0.0315
C21	Accessibility	Benefit	VI	VI	0.9000	0.1000	0.4243	0.0453
C22	Information in stations	Benefit	M	M	0.5000	0.4500	0.7399	0.0315
C23	Visual information on buses	Benefit	I	M	0.7337	0.4047	0.5458	0.0384
C24	Protocols of COVID-19	Benefit	VI	I	0.8908	0.1149	0.4397	0.0453
C25	Identify safe seats and place	Benefit	VI	M	0.8843	0.1162	0.4522	0.0454

Step 5. Construct the Pythagorean Fuzzy decision matrix for alternatives assessment.

To calculate the aggregated pythagorean fuzzy decision matrix that which is in Table 7 using Linguistic Terms.

Table 7. The evaluations of criteria for each alternative.

Criteria	R1	R2	R3	R4	R5	R6	R1	R2	R3	R4	R5	R6
C1	H	MH	MH	M	MH	VH	M	MH	H	H	MH	VH
C2	VL	L	L	L	VL	VL	M	ML	L	M	VL	M
C3	ML	M	ML	M	H	VH	L	M	VH	MH	H	VH
C4	MH	M	M	MH	MH	H	H	M	M	M	ML	MH
C5	M	MH	MH	M	L	L	ML	MH	M	M	L	M
C6	M	MH	H	ML	MH	ML	M	MH	H	ML	MH	ML
C7	H	H	H	H	H	ML	H	H	H	H	H	ML
C8	M	H	MH	MH	ML	M	M	H	H	M	ML	M
C9	M	ML	M	MH	ML	L	M	M	M	M	ML	L
C10	ML	M	MH	ML	ML	H	ML	M	MH	ML	ML	H
C11	L	H	M	MH	M	M	MH	H	MH	MH	VH	VH
C12	MH	M	M	L	MH	H	H	M	M	L	H	VH
C13	MH	L	VL	VL	VL	L	H	L	VL	M	L	L
C14	MH	H	M	MH	ML	L	MH	MH	M	H	ML	L
C15	VH	M	M	M	ML	MH	VH	M	H	M	M	H
C16	ML	M	ML	M	L	L	M	M	MH	M	L	M
C17	M	MH	M	ML	ML	ML	MH	MH	ML	M	MH	MH
C18	ML	MH	M	M	ML	M	ML	MH	M	M	ML	M
C19	H	H	H	H	MH	MH	MH	H	H	H	MH	MH
C20	ML	M	ML	H	ML	H	ML	M	ML	M	M	H
C21	L	MH	ML	MH	VL	L	M	MH	M	MH	VL	M
C22	VL	M	MH	ML	VH	VH	VL	M	M	ML	M	M
C23	ML	ML	ML	ML	L	M	ML	M	ML	M	M	M
C24	MH	M	M	ML	ML	MH	M	ML	ML	ML	ML	M
C25	EL	L	ML	L	L	VL	VL	M	L	L	L	VL

Table 4 describes the meanings of $R1,\cdots ,R6$, which represent alternatives involved in this study. Table 2 describes the alternatives assessment using the ID of the linguistic terms.

Step 6. Calculate the Pythagorean fuzzy normalized matrix using linear normalization.

The Pythagorean Fuzzy normalized matrix using linear normalization is depicted in Table 8.

Table 8. Pythagorean Fuzzy Normalized Matrix.

(a)
Alternative	C1		C2		C3		C4		C5		C6		C7		C8		C9
	$\mathbf{\mu }$	$\mathbf{\nu }$	$\mathbf{\mu }$	$\mathbf{\nu }$	$\mathbf{\mu }$	$\mathbf{\nu }$	$\mathbf{\mu }$	$\mathbf{\nu }$	$\mathbf{\mu }$	$\mathbf{\nu }$	$\mathbf{\mu }$	$\mathbf{\nu }$	$\mathbf{\mu }$	$\mathbf{\nu }$	$\mathbf{\mu }$	$\mathbf{\nu }$	$\mathbf{\mu }$	$\mathbf{\nu }$
R1	$0.857$	$0.713$	$0.668$	$0.953$	$1.000$	$1.000$	$0.885$	$0.874$	$0.819$	$0.880$	$0.714$	$0.750$	$0.571$	$0.690$	$0.714$	$0.750$	$0.845$	$0.898$
R2	$0.750$	$0.620$	$0.935$	$0.992$	$0.776$	$0.914$	$0.723$	$0.763$	$1.000$	$1.000$	$0.857$	$0.845$	$0.571$	$0.690$	$1.000$	$1.000$	$0.696$	$0.833$
R3	$0.765$	$0.630$	$0.867$	$0.986$	$0.813$	$0.929$	$0.723$	$0.763$	$0.986$	$0.988$	$1.000$	$1.000$	$0.571$	$0.690$	$0.874$	$0.859$	$0.845$	$0.898$
R4	$0.660$	$0.566$	$1.000$	$1.000$	$0.759$	$0.904$	$0.855$	$0.849$	$0.833$	$0.888$	$0.571$	$0.690$	$0.571$	$0.690$	$0.845$	$0.835$	$1.000$	$1.000$
R5	$0.750$	$0.620$	$0.347$	$0.935$	$0.555$	$0.686$	$0.846$	$0.842$	$0.417$	$0.772$	$0.857$	$0.845$	$0.571$	$0.690$	$0.571$	$0.690$	$0.676$	$0.826$
R6	$1.000$	$1.000$	$0.668$	$0.953$	$0.485$	$0.503$	$1.000$	$1.000$	$0.481$	$0.783$	$0.571$	$0.690$	$1.000$	$1.000$	$0.714$	$0.750$	$0.423$	$0.781$
(b)
Alternative	C10		C11		C12		C13		C14		C15		C16		C17		C18
	$\mathbf{\mu }$	$\mathbf{\nu }$	$\mathbf{\mu }$	$\mathbf{\nu }$	$\mathbf{\mu }$	$\mathbf{\nu }$	$\mathbf{\mu }$	$\mathbf{\nu }$	$\mathbf{\mu }$	$\mathbf{\nu }$	$\mathbf{\mu }$	$\mathbf{\nu }$	$\mathbf{\mu }$	$\mathbf{\nu }$	$\mathbf{\mu }$	$\mathbf{\nu }$	$\mathbf{\mu }$	$\mathbf{\nu }$
R1	0.571	0.690	1.000	1.000	0.859	0.833	1.000	1.000	0.868	0.859	0.515	0.510	0.823	0.927	0.853	0.898	0.667	0.816
R2	0.714	0.750	0.446	0.669	0.702	0.727	0.409	0.759	1.000	1.000	0.823	0.927	1.000	1.000	1.000	1.000	1.000	1.000
R3	0.857	0.845	0.611	0.882	0.702	0.727	0.163	0.720	0.723	0.763	0.780	0.901	0.854	0.938	0.819	0.880	0.833	0.888
R4	0.571	0.690	0.521	0.792	0.351	0.632	0.315	0.734	0.885	0.874	0.823	0.927	1.000	1.000	0.686	0.823	0.833	0.888
R5	0.571	0.690	0.568	0.841	0.859	0.833	0.203	0.724	0.578	0.701	1.000	1.000	0.500	0.870	0.712	0.833	0.667	0.816
R6	1.000	1.000	0.568	0.841	1.000	1.000	0.409	0.759	0.361	0.663	0.673	0.809	0.577	0.882	0.712	0.833	0.833	0.888
(c)
Alternative	C19		C20		C21		C22		C23		C24		C25
	$\mathbf{\mu }$	$\mathbf{\nu }$	$\mathbf{\mu }$	$\mathbf{\nu }$	$\mathbf{\mu }$	$\mathbf{\nu }$	$\mathbf{\mu }$	$\mathbf{\nu }$	$\mathbf{\mu }$	$\mathbf{\nu }$	$\mathbf{\mu }$	$\mathbf{\nu }$	$\mathbf{\mu }$	$\mathbf{\nu }$
R1	0.988	0.983	0.571	0.690	0.481	0.783	0.128	0.482	0.800	0.920	1.000	1.000	0.258	0.886
R2	1.000	1.000	0.714	0.750	1.000	1.000	0.639	0.584	0.823	0.927	0.831	0.891	0.743	0.964
R3	1.000	1.000	0.571	0.690	0.686	0.823	0.756	0.650	0.800	0.920	0.831	0.891	1.000	1.000
R4	1.000	1.000	0.979	0.972	1.000	1.000	0.511	0.537	0.823	0.927	0.676	0.826	0.644	0.951
R5	0.857	0.845	0.588	0.695	0.167	0.732	1.000	1.000	0.577	0.882	0.676	0.826	0.644	0.951
R6	0.857	0.845	1.000	1.000	0.481	0.783	1.000	1.000	1.000	1.000	1.000	1.000	0.258	0.902

Step 7. Calculate the Pythagorean Fuzzy weighted normalized matrix called ${\tilde{R}}_{ij}$. In this mode, the respective matrix ${\tilde{R}}_{ij}$ is presented in Table 9.

Table 9. Pythagorean Fuzzy weighted normalized matrix.

(a)
Criteria Alternative	C1		C2		C3		C4		C5		C6		C7		C8		C9
	$\mathbf{\mu }$	$\mathbf{\nu }$	$\mathbf{\mu }$	$\mathbf{\nu }$	$\mathbf{\mu }$	$\mathbf{\nu }$	$\mathbf{\mu }$	$\mathbf{\nu }$	$\mathbf{\mu }$	$\mathbf{\nu }$	$\mathbf{\mu }$	$\mathbf{\nu }$	$\mathbf{\mu }$	$\mathbf{\nu }$	$\mathbf{\mu }$	$\mathbf{\nu }$	$\mathbf{\mu }$	$\mathbf{\nu }$
R1	0.241	0.985	0.150	0.998	1.000	1.000	0.239	0.995	0.198	0.995	0.179	0.987	0.133	0.983	0.149	0.991	0.197	0.997
R2	0.192	0.979	0.277	1.000	0.202	0.996	0.167	0.990	1.000	1.000	0.242	0.992	0.133	0.983	1.000	1.000	0.144	0.994
R3	0.198	0.979	0.228	0.999	0.218	0.997	0.167	0.990	0.347	1.000	1.000	1.000	0.133	0.983	0.211	0.995	0.197	0.997
R4	0.160	0.975	1.000	1.000	0.195	0.995	0.222	0.994	0.204	0.996	0.133	0.983	0.133	0.983	0.196	0.994	1.000	1.000
R5	0.192	0.979	0.070	0.997	0.128	0.983	0.217	0.993	0.083	0.991	0.242	0.992	0.133	0.983	0.111	0.988	0.138	0.994
R6	1.000	1.000	0.150	0.998	0.110	0.969	1.000	1.000	0.097	0.991	0.133	0.983	1.000	1.000	0.149	0.991	0.079	0.992
(b)
Criteria Alternative	C10		C11		C12		C13		C14		C15		C16		C17		C18
	$\mathbf{\mu }$	$\mathbf{\nu }$	$\mathbf{\mu }$	$\mathbf{\nu }$	$\mathbf{\mu }$	$\mathbf{\nu }$	$\mathbf{\mu }$	$\mathbf{\nu }$	$\mathbf{\mu }$	$\mathbf{\nu }$	$\mathbf{\mu }$	$\mathbf{\nu }$	$\mathbf{\mu }$	$\mathbf{\nu }$	$\mathbf{\mu }$	$\mathbf{\nu }$	$\mathbf{\mu }$	$\mathbf{\nu }$
R1	0.133	0.983	1.000	1.000	0.225	0.993	1.000	1.000	0.207	0.995	0.118	0.970	0.207	0.997	0.221	0.996	0.162	0.991
R2	0.178	0.987	0.100	0.982	0.161	0.988	0.076	0.991	1.000	1.000	0.224	0.997	1.000	1.000	1.000	1.000	1.000	1.000
R3	0.242	0.992	0.145	0.994	0.161	0.988	0.029	0.990	0.152	0.992	0.204	0.995	0.222	0.998	0.205	0.995	0.229	0.995
R4	0.133	0.983	0.119	0.989	0.071	0.982	0.057	0.990	0.217	0.996	0.224	0.997	1.000	1.000	0.156	0.992	0.229	0.995
R5	0.133	0.983	0.132	0.992	0.225	0.993	0.036	0.990	0.113	0.989	1.000	1.000	0.105	0.995	0.164	0.993	0.162	0.991
R6	1.000	1.000	0.132	0.992	1.000	1.000	0.076	0.991	0.066	0.987	0.164	0.990	0.125	0.995	0.164	0.993	0.229	0.995
(c)
Criteria Alternative	C19		C20		C21		C22		C23		C24		C25
	$\mathbf{\mu }$	$\mathbf{\nu }$	$\mathbf{\mu }$	$\mathbf{\nu }$	$\mathbf{\mu }$	$\mathbf{\nu }$	$\mathbf{\mu }$	$\mathbf{\nu }$	$\mathbf{\mu }$	$\mathbf{\nu }$	$\mathbf{\mu }$	$\mathbf{\nu }$	$\mathbf{\mu }$	$\mathbf{\nu }$
R1	0.395	0.999	0.111	0.988	0.109	0.989	0.023	0.977	0.196	0.997	1.000	1.000	0.056	0.994
R2	1.000	1.000	0.149	0.991	1.000	1.000	0.128	0.983	0.206	0.997	0.227	0.995	0.189	0.998
R3	1.000	1.000	0.111	0.988	0.169	0.991	0.162	0.987	0.196	0.997	0.227	0.995	1.000	1.000
R4	1.000	1.000	0.309	0.999	1.000	1.000	0.097	0.981	0.206	0.997	0.165	0.991	0.155	0.998
R5	0.242	0.992	0.115	0.989	0.036	0.986	1.000	1.000	0.124	0.995	0.165	0.991	0.155	0.998
R6	0.242	0.992	1.000	1.000	0.109	0.989	1.000	1.000	1.000	1.000	1.000	1.000	0.056	0.995

Step 8. Determine the Pythagorean Fuzzy negative ideal solution (ns).

Then, using Equations (21)–(24), the Pythagorean Fuzzy negative ideal solution is displayed in Table 10.

Table 10. Pythagorean Fuzzy Negative Ideal Solution.

(a)

Criteria

C1

C2

C3

C4

C5

C6

C7

C8

C9

$\mathbf{\mu }$

$\mathbf{\nu }$

$\mathbf{\mu }$

$\mathbf{\nu }$

$\mathbf{\mu }$

$\mathbf{\nu }$

$\mathbf{\mu }$

$\mathbf{\nu }$

$\mathbf{\mu }$

$\mathbf{\nu }$

$\mathbf{\mu }$

$\mathbf{\nu }$

$\mathbf{\mu }$

$\mathbf{\nu }$

$\mathbf{\mu }$

$\mathbf{\nu }$

$\mathbf{\mu }$

$\mathbf{\nu }$

ns

1.000

0.975

1.000

0.997

0.110

1.000

1.000

0.990

1.000

0.991

1.000

0.983

0.133

1.000

1.000

0.988

1.000

0.992

(b)

Criteria

C10

C11

C12

C13

C14

C15

C16

C17

C18

$\mathbf{\mu }$

$\mathbf{\nu }$

$\mathbf{\mu }$

$\mathbf{\nu }$

$\mathbf{\mu }$

$\mathbf{\nu }$

$\mathbf{\mu }$

$\mathbf{\nu }$

$\mathbf{\mu }$

$\mathbf{\nu }$

$\mathbf{\mu }$

$\mathbf{\nu }$

$\mathbf{\mu }$

$\mathbf{\nu }$

$\mathbf{\mu }$

$\mathbf{\nu }$

$\mathbf{\mu }$

$\mathbf{\nu }$

ns

1.000

0.983

0.100

1.000

1.000

0.982

1.000

0.990

1.000

0.987

0.118

1.000

1.000

0.995

1.000

0.992

1.000

0.991

(c)

Criteria

C19

C20

C21

C22

C23

C24

C25

$\mathbf{\mu }$

$\mathbf{\nu }$

$\mathbf{\mu }$

$\mathbf{\nu }$

$\mathbf{\mu }$

$\mathbf{\nu }$

$\mathbf{\mu }$

$\mathbf{\nu }$

$\mathbf{\mu }$

$\mathbf{\nu }$

$\mathbf{\mu }$

$\mathbf{\nu }$

$\mathbf{\mu }$

$\mathbf{\nu }$

ns

1.000

0.992

1.000

0.988

1.000

0.986

1.000

0.977

1.000

0.995

1.000

0.991

1.000

0.994

Step 9. Calculate the Pythagorean Fuzzy Euclidean and Taxicab distances. Then, using Equations (24) and (25), the Pythagorean Fuzzy Euclidean and Taxicab distances are described in Table 11 and Table 12. We decide to use Table 5 to explain the meanings of $(R1,\cdots ,R6)$ which represent alternatives involved in this study.

Table 11. Pythagorean fuzzy Euclidean distance.

(a)
	C1	C2	C3	C4	C5	C6	C7	C8	C9
R1	0.576	0.723	0.792	0.580	0.643	0.675	0.000	0.724	0.645
R2	0.653	0.523	0.009	0.693	0.000	0.575	0.000	0.000	0.733
R3	0.644	0.596	0.012	0.693	0.427	0.000	0.000	0.623	0.645
R4	0.706	0.000	0.007	0.606	0.633	0.751	0.000	0.646	0.000
R5	0.653	0.865	0.001	0.613	0.842	0.575	0.000	0.790	0.743
R6	0.001	0.723	0.001	0.000	0.815	0.751	0.751	0.724	0.849
(b)
	C10	C11	C12	C13	C14	C15	C16	C17	C18
R1	0.751	0.810	0.601	0.000	0.628	0.001	0.629	0.606	0.702
R2	0.675	0.000	0.704	0.854	0.000	0.011	0.000	0.000	0.000
R3	0.575	0.002	0.704	0.942	0.720	0.007	0.605	0.632	0.595
R4	0.751	0.000	0.863	0.889	0.614	0.011	0.000	0.712	0.595
R5	0.751	0.001	0.601	0.929	0.787	0.778	0.801	0.698	0.702
R6	0.000	0.001	0.000	0.854	0.872	0.002	0.766	0.698	0.595
(c)
	C19	C20	C21	C22	C23	C24	C25
R1	0.367	0.790	0.794	0.955	0.646	0.000	0.892
R2	0.000	0.724	0.000	0.761	0.630	0.597	0.657
R3	0.000	0.790	0.691	0.702	0.646	0.597	0.000
R4	0.000	0.477	0.000	0.815	0.630	0.697	0.714
R5	0.575	0.783	0.930	0.001	0.767	0.697	0.714
R6	0.575	0.000	0.794	0.001	0.000	0.000	0.892

Table 12. Pythagorean fuzzy Taxicab distance.

(a)
	C1	C2	C3	C4	C5	C6	C7	C8	C9
R1	0.748	0.850	0.890	0.756	0.797	0.818	0.017	0.848	0.799
R2	0.804	0.721	0.088	0.833	0.009	0.749	0.017	0.012	0.854
R3	0.798	0.770	0.105	0.833	0.644	0.017	0.017	0.782	0.799
R4	0.840	0.003	0.081	0.774	0.791	0.867	0.017	0.798	0.008
R5	0.804	0.930	0.002	0.779	0.917	0.749	0.017	0.889	0.860
R6	0.025	0.850	0.031	0.010	0.903	0.867	0.867	0.848	0.921
(b)
	C10	C11	C12	C13	C14	C15	C16	C17	C18
R1	0.867	0.900	0.765	0.010	0.785	0.030	0.790	0.775	0.838
R2	0.818	0.018	0.834	0.923	0.013	0.103	0.005	0.008	0.009
R3	0.749	0.039	0.834	0.971	0.844	0.082	0.775	0.792	0.767
R4	0.867	0.009	0.929	0.942	0.775	0.103	0.005	0.844	0.767
R5	0.867	0.024	0.765	0.964	0.885	0.882	0.895	0.835	0.838
R6	0.017	0.024	0.018	0.923	0.934	0.037	0.875	0.835	0.767
(b)
	C19	C20	C21	C22	C23	C24	C25
R1	0.599	0.889	0.888	0.977	0.802	0.009	0.944
R2	0.008	0.848	0.014	0.866	0.792	0.769	0.807
R3	0.008	0.889	0.826	0.829	0.802	0.769	0.006
R4	0.008	0.680	0.014	0.899	0.792	0.835	0.842
R5	0.758	0.885	0.964	0.023	0.876	0.835	0.842
R6	0.758	0.012	0.888	0.023	0.005	0.009	0.943

Step 10. Construct the relative assessment matrix based on the Pythagorean Fuzzy Euclidean and Taxicab distances.

To construct the relative assessment matrix based on the Pythagorean Fuzzy Euclidean and Taxicab distances, the Equations (26) and (27) are utilized and the information is presented in Table 13.

Table 13. Pythagorean fuzzy relative appraisal.

Route	R1	R2	R3	R4	R5	R6
R1	0.000	0.845	0.370	0.478	−0.137	0.546
R2	−0.845	0.000	−0.476	−0.368	−0.982	−0.299
R3	−0.370	0.476	0.000	0.108	−0.507	0.176
R4	−0.478	0.368	−0.108	0.000	−0.615	0.068
R5	0.137	0.982	0.507	0.615	0.000	0.683
R6	−0.546	0.299	−0.176	−0.068	−0.683	0.000

Step 11. Calculate the assessment score of each alternative.

In order to determine the assessment score of each alternative, the Equation (29) is used. Then, Table 14 depicts the results.

Table 14. Assessment score and rank.

Route	${\mathit{H}}_{\mathit{i}}$	RANK
R1	2.101	2
R2	−2.970	6
R3	−0.116	3
R4	−0.765	4
R5	2.925	1
R6	−1.175	5

Step 12. Rank the alternatives according to the decreasing values of assessment score $\left(H_i\right)$. Finally, the ranking of the alternative is represented as: $R5\succ R1\succ R3\succ R4\succ R6\succ R2$.

Where, $\mathbf{R}\mathbf{5}$ depicts the best option due it obtaining the higher value from score $\left(H_i\right)$. This information can be used in order to prepare a pool of plans and strategies to do improvements of the transport service focused on the users.

5. Comparative Analysis

In order to evaluate our proposal, some variations were carried out in the decision makers’ contribution, with different threshold functions, as suggests [13]. This sensitivity analysis is performed to determine the consistency of the changes of the alternatives for three different variation, as shown in Figure 2.

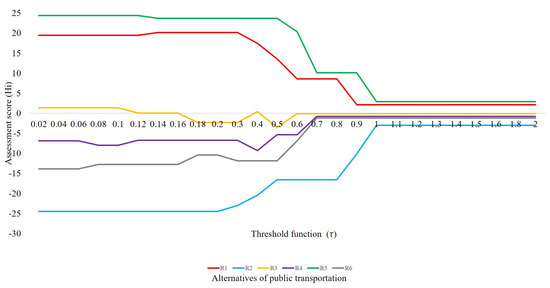
Figure 2. Sensitivity analysis of threshold function (Source: The authors).

Subsequently, the correlation analysis of the results of the sensitivity analysis is observed in Table 15, where there is a high correlation between the alternatives; for example, the alternative R1 has a high correlation (more than 90%) with R2, R4, R5 and R6, also as shown in Figure 2, R3 is observed with low correlation (0.0107), because there is a distance with R1.

Table 15. Correlation analysis.

	Row 1	Row 2	Row 3	Row 4	Row 5	Row 6
R1	1
R2	−0.9718	1
R3	0.0107	−0.0476	1
R4	−0.9430	0.8985	−0.0652	1
R5	0.9628	−0.9665	−0.0251	−0.9569	1
R6	−0.9573	0.9080	−0.0651	0.9680	−0.9622	1

Comparative Method

Different methods were compared with the proposed method of Pythagorean Fuzzy CODAS to observe how much the influence of the Taxicab and Euclidean distance and the threshold function respect with PF-MOORA [44], PF-TOPSIS [53] and PF-CODAS are, and they are proposed with a variant with entropy to criteria weights [54].

6. Conclusions

Nowadays, the MCDM method is a prominent field reported in the literature. In this mode, this study proposes an integrated method under Pythagorean Fuzzy with CODAS technique that includes a method to determine the criteria weights based on the expertise of the decision makers to the problem of the public transportation system. As shown, the contributions of the decision makers can change the results of public transportation routes $\left(ramales\right)$ that need attention. This method integrates the individual contribution weight of each DM and this experience is related to the evaluation of each expert on the weight of each criteria. As well as the experience contributing to the evaluation of the criteria for each public transportation route (the alternatives). The proposed method has a good correlation with other Pythagorean methods, as shown in Table 16 and Figure 3.

Table 16. Comparison with other methods.

	PF-CODAS Entropy	PF-MOORA	PF-TOPSIS
PF-MOORA	$-0.486$
PF-TOPSIS	$-0.829$	$0.714$
PF-CODAS propose	$1.000$	$-0.486$	$-0.829$

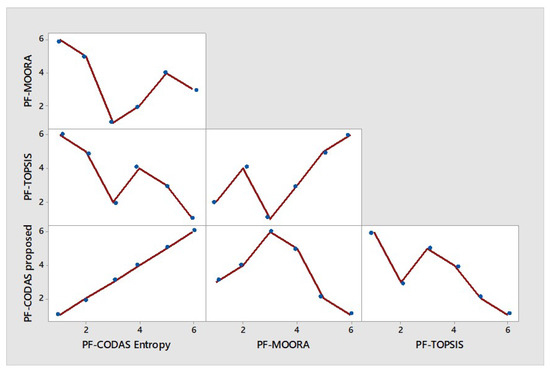
Figure 3. Comparison methods (Source: The authors).

Specifically, this study shows the attention to the criteria in Table 3 and detects this proposed method, which is the priority alternative, Table 14 helps transport authorities and the operators to improve the quality of the service because the improvement in transport operation directly affects the social impact of real users, attracts potential users and improves the perception of the citizen about the local transportation service. Ciudad Juárez has 29 lines distributed in 119 routes (ramales), therefore, it is complex to determine which is the critical route considering all criteria that describe the operational services with impact in users. In that sense, the numerical case shows the appraisal for 6 routes that have the service area in common and part of their route is similar, the results showed that the best alternative assessment was R5, line 1-B: Talamas (Express), and the worst alternative was R2, 1-A: Morelos. Therefore, it is recommended to prioritize the alternative R2 for implementing actions and transport policy.

The method developed will be proposed to local authorities for its implementation to be considered, in order to verify areas of opportunity. In the future, it is recommended to include computational programs to reduce mathematical development time, as well as to integrate GIS programs to use referenced databases during the implantation.