Experimental Study on Local Scour Depth around Monopile Foundation in Combined Waves and Current
Abstract
:1. Introduction
2. Existing Design Methods for Local Scour Depth
3. Experimental Verification
3.1. Experiments Arrangement
3.2. Experimental Results and Analysis
3.2.1. Verification of Main Influencing Factors
3.2.2. Verification of Local Scour Depth
4. Prediction Equation in Combined Waves and Current
4.1. Dimensional Analyses
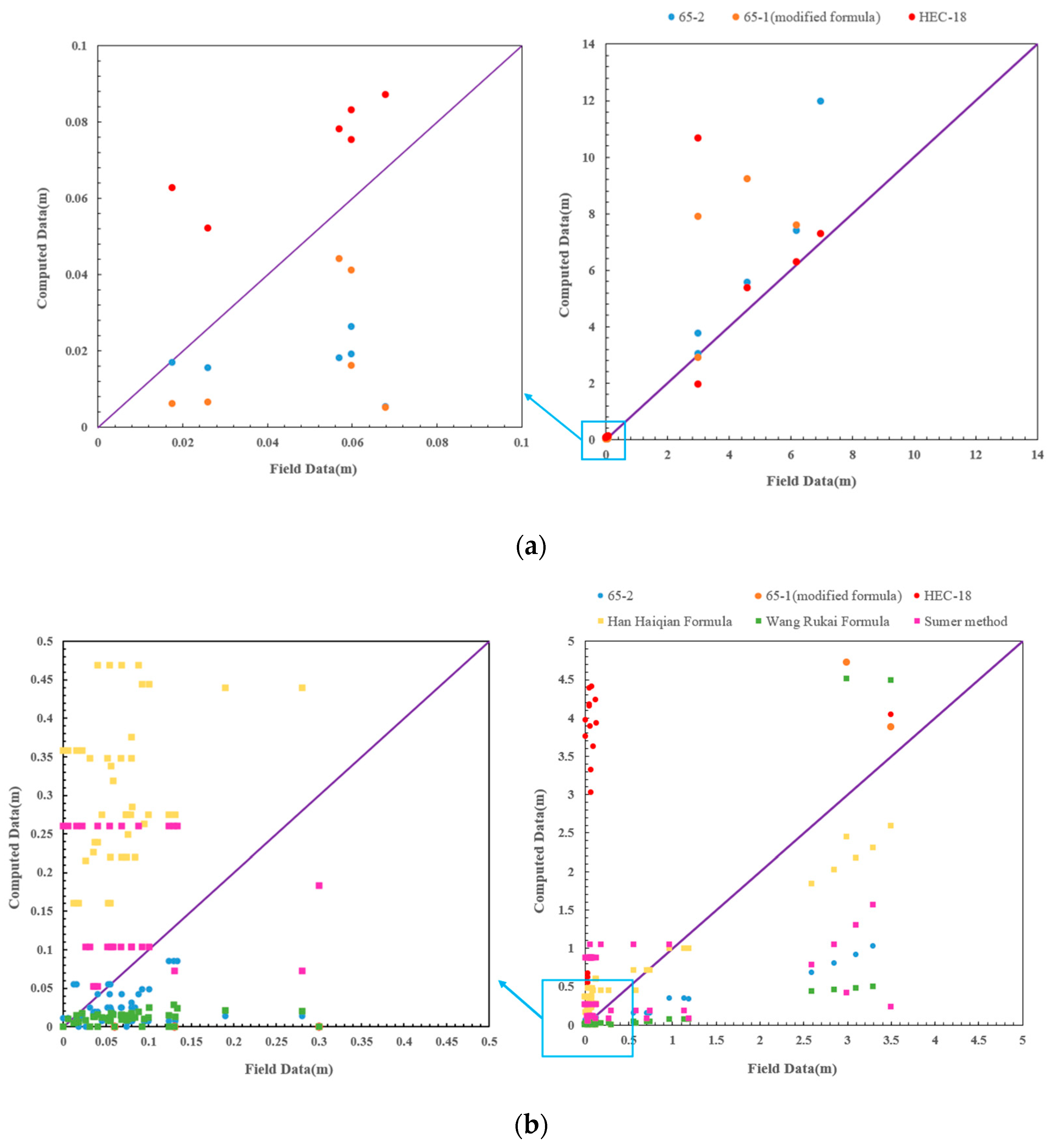
4.2. Verification of New Predication Formula
4.3. Discussions
5. Conclusions
- (1)
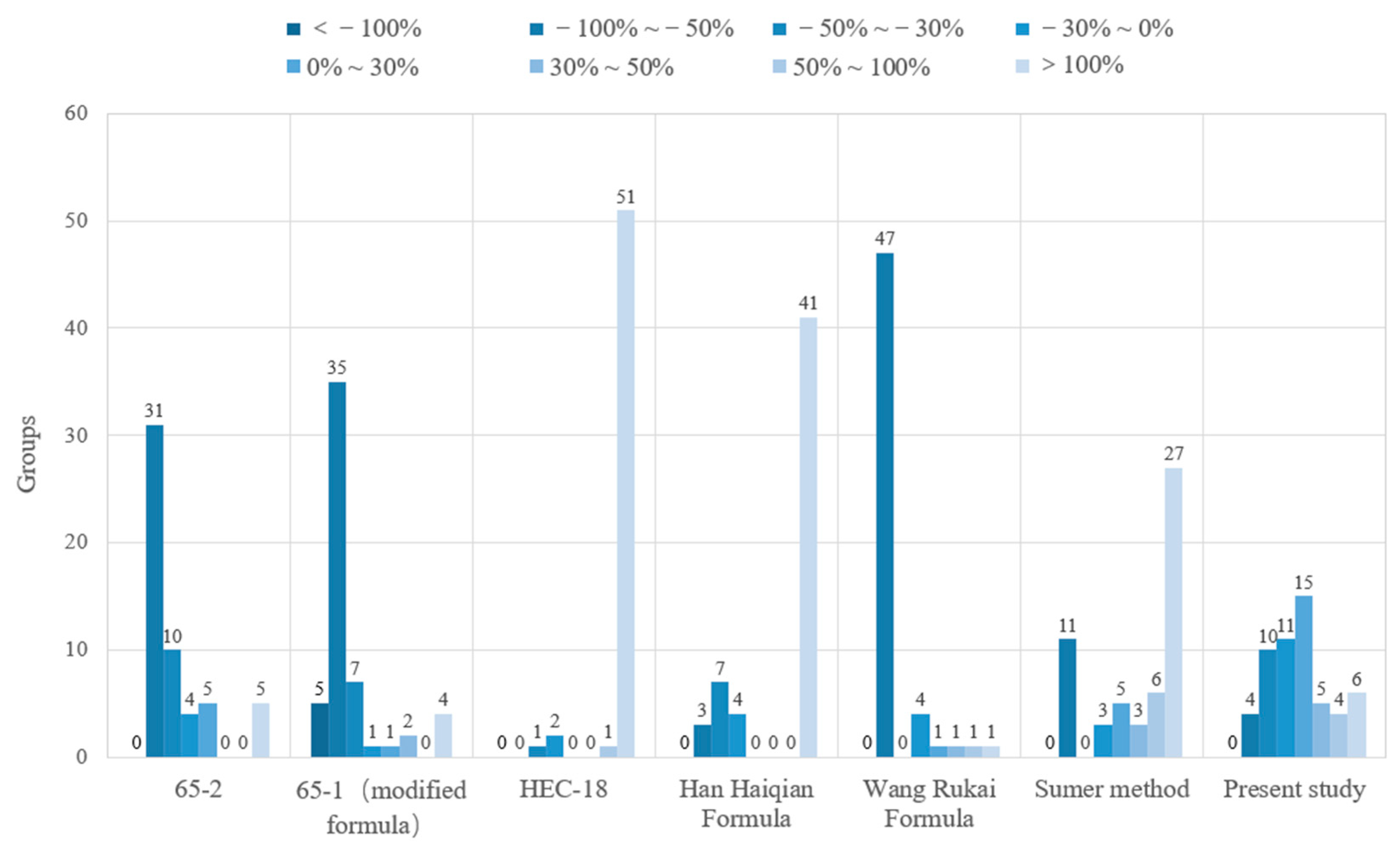
- For the prediction of the local scour depth of bridge piers, Formula 65-2, 65-1 (modified formula) and HEC-18 equation have similar computed results, and the Formula 65-2 is the most stable and reliable.
- (2)
- The local scour depth around monopile foundation in combined waves and current is important in the field of coastal and offshore engineering, but it has not been sufficiently studied. The design methods above cannot assess the maximum scour depth accurately in all instances. The Han Haiqian formula focuses on estimating the maximum local scour depth at foundation of sea/bay-crossing bridges in tidal currents. The Wang Rukai formula takes waves into account, but this equation requires more parameters than other methods, which means it may be not convenient when used at the design stage. The Sumer method has a simple calculation process, but it may underestimate the scour depth due to waves combined with strong currents. The mean relative errors of Formula 65-2, 65-1 (modified formula), HEC-18, Han Haiqian Formula, Wang Rukai Formula and Sumer method proposed herein are 74.7%, 82.5%, 966.5%, 490.1%, 76.8% and 425.9%, respectively.
- (3)
- Considering to the principle of dimensional analysis, experimental phenomena, and the main influencing factors of the local scour depth of a monopile, a new equation for predicting the equilibrium scour depth of a monopile under the action of combined waves and current is proposed. The mean relative error between the predicted value of the formula and the measured value in this paper is 49.1%, which is significantly smaller than other formulas.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Smith, D.W. Why do bridges fail. In Civil Engineering-ASCE; American Society of Civil Engineers: New York, NY, USA, 1977; Volume 47, pp. 58–62. [Google Scholar]
- Zu, M. Panel of Experts: Flooding Caused the Bridge to Collapse. Available online: http://dzb.scdaily.cn/2013/08/03/20130803620303904128.htm (accessed on 3 August 2013).
- Du, F. Research on the Geological Causes of ShengLi Well Workover Platform III Overturning Accident. Master’s Thesis, Ocean University of China, Qingdao, China, 2013. [Google Scholar]
- Liang, F.; Wang, C.; Huang, M.; Wang, Y. Experimental observations and evaluations of formulae for local scour at pile groups in steady currents. Mar. Georesources Geotechnol. 2015, 35, 245–255. [Google Scholar] [CrossRef]
- Ahmad, N.; Melville, B.W.; Mohammad, T.; Suif, Z. Evaluation of pier-scour predictions for wide piers using field data. Int. J. Geomate 2018, 14, 140–145. [Google Scholar] [CrossRef]
- Qi, W.-G.; Gao, F.-P. Physical modeling of local scour development around a large-diameter monopile in combined waves and current. Coast. Eng. 2014, 83, 72–81. [Google Scholar] [CrossRef] [Green Version]
- Ni, Z.; Wang, M.; Zhang, X. Local scour of composite piers under action of tidal current. Hydro-Sci. Eng. 2013, 2, 45–51. [Google Scholar]
- Sumer, B.M.; Fredsoe, J. Flow around a cylinder in steady current. In Hydrodynamics around Cylindrical Structures; World Scientific Publ Co Pte Ltd.: Singapore, 2006; Volume 26, pp. 1–35. [Google Scholar]
- Sheppard, D.M.; Miller, W. Live-Bed Local Pier Scour Experiments. J. Hydraul. Eng. 2006, 132, 635–642. [Google Scholar] [CrossRef] [Green Version]
- Chen, G.; Zuo, Q.; Huang, H. Local scour around large-scale cylinder under wave action. Ocean Eng. 2004, 22, 46. [Google Scholar]
- Rambabu, M.; Rao, S.; Sundar, V. Current-induced scour around a vertical pile in cohesive soil. Ocean Eng. 2003, 30, 893–920. [Google Scholar] [CrossRef]
- Oliveto, G.; Hager, W.H. Temporal Evolution of Clear-Water Pier and Abutment Scour. J. Hydraul. Eng. 2002, 128, 811–820. [Google Scholar] [CrossRef]
- Sumer, B.M.; Fredsøe, J. Scour around Pile in Combined Waves and Current. J. Hydraul. Eng. 2001, 127, 403–411. [Google Scholar] [CrossRef]
- Bayram, A.; Larson, M. Analysis of Scour around a Group of Vertical Piles in the Field. J. Waterw. Port. Coast. Ocean Eng. 2000, 126, 215–220. [Google Scholar] [CrossRef]
- Sumer, B.M.; Fredsøe, J.; Christiansen, N. Scour Around Vertical Pile in Waves. J. Waterw. Port. Coast. Ocean Eng. 1992, 118, 15–31. [Google Scholar] [CrossRef]
- Sumer, B.M.; Fredsøe, J. Scour below Pipelines in Waves. J. Waterw. Port. Coast. Ocean Eng. 1990, 116, 307–323. [Google Scholar] [CrossRef]
- Melville, B.W. Live-bed scour at bridge piers. J. Hydraul. Eng. 1984, 110, 1234–1247. [Google Scholar] [CrossRef]
- Melville, B. Local Scour at Bridge Sites. Ph.D. Thesis, The University of Auckland, Auckland, New Zealand, 1975. [Google Scholar]
- Laursen, E.M. Scour at Bridge Crossings. J. Hydraul. Div. 1960, 86, 39–54. [Google Scholar] [CrossRef]
- Melville, B.W.; Sutherland, A.J. Design method for local scour at bridge piers. J. Hydraul. Eng. 1988, 114, 1210–1226. [Google Scholar] [CrossRef]
- Valela, C.; Rennie, C.D.; Nistor, I. Improved bridge pier collar for reducing scour. Int. J. Sediment Res. 2021, 37, 37–46. [Google Scholar] [CrossRef]
- Chiew, Y.M. Scour Protection at Bridge Piers. J. Hydraul. Eng. 1992, 118, 1260–1269. [Google Scholar] [CrossRef]
- Rahman, M.M.; Haque, M.A. Local scour estimation bridge site: Modification and application of lacey formula. Int. J. Sediment Res. 2003, 18, 3–4. [Google Scholar]
- Pandey, M.; Sharma, P.K.; Ahmad, Z.; Singh, U.K. Evaluation of existing equations for temporal scour depth around circular bridge piers. Environ. Fluid Mech. 2017, 17, 981–995. [Google Scholar] [CrossRef]
- Moreno, M.; Maia, R.; Couto, L. Prediction of Equilibrium Local Scour Depth at Complex Bridge Piers. J. Hydraul. Eng. 2016, 142, 04016045. [Google Scholar] [CrossRef]
- MTPRC (Ministry of Transport of the People’s Republic of China). Hydrological Specifications for Survey and Design of Highway Engineering. In Industry Standard-Transportation; JTG C30-2015; MTPRC: Beijing, China, 2015. [Google Scholar]
- LRFD Bridge. Design Specifications; American Association of State Highway and Transportation Officials: Washington, DC, USA, 2012. [Google Scholar]
- NEAPRC (National Energy Administration of the People’s Republic of China). Code for Design of Wind Turbine Foundations for Offshore Wind Power Projects; NB/T 10105-2018; NEAPRC: Beijing, China, 2018. [Google Scholar]
- Du, S.; Dai, G.; Gao, L.; Wan, Z.; Zhu, M. Prediction of local scour depth at offshore wind turbine monopile foundation in combined waves and current. J. Southeast Univ. Nat. Sci. Ed. 2020, 50, 616–622. [Google Scholar]
- DNV (Det Norske Veritas). Support Structures for Wind Turbines; DNVGL-ST-0126; DNV: Bærum, Norway, 2018. [Google Scholar]
- Lei, T.; Ren, J.; Tao, H.; Jing, H. Review on calculation methods for local scour of pier foundations. J. Sediment Res. 2020, 45, 61–68. [Google Scholar]
- Pan, D.; Li, J.; Zhou, C.; Wang, J. Study on local scour characteristics of wind power pile foundation in offshore wind farm in Zhanjiang. Coast. Eng. 2020, 39, 271–278. [Google Scholar]
- Wang, W.; Yang, J.; Li, R. Calculation of local scour around wind turbine’s pile of offshore wind farm. J. Waterw. Harb. 2012, 33, 57–60. [Google Scholar]
- Wang, S.; Mou, L.; Wei, K.; Qin, L.; Xiang, Q. Experimental study on local scour of cylindrical pier under different hydraulic conditions. J. Disaster Prev. Mitig. Eng. 2020, 40, 425–431. [Google Scholar]
- Yang, Y.L.; Qi, M.L.; Wang, X.; Li, J.Z. Experimental study of scour around pile groups in steady flows. Ocean Eng. 2020, 195, 12. [Google Scholar] [CrossRef]
- Zhu, Z.; Yu, P. Comparative study between chinese code and us code on calculation of local scour depth around bridge piers. China J. Highw. Transp. 2016, 29, 36–43. [Google Scholar]
- Gautam, S.; Dutta, D.; Bihs, H.; Afzal, M.S. Three-dimensional Computational Fluid Dynamics modelling of scour around a single pile due to combined action of the waves and current using Level-Set method. Coast. Eng. 2021, 170, 104002. [Google Scholar] [CrossRef]
- Han, H.; Chen, Y.; Sun, Z. Estimation of Maximum Local Scour Depths at Multiple Piles of Sea/Bay-crossing Bridges. KSCE J. Civ. Eng. 2018, 23, 567–575. [Google Scholar] [CrossRef]
- Dai, G.; Gao, L.; Chen, X.; Wan, Z.; Zhu, M.; Du, S. A Calculation Model of the Equilibrium Scour Depth for Monopile Foundations under Waves and Currents. Arab. J. Sci. Eng. 2021, 46, 5023–5029. [Google Scholar] [CrossRef]


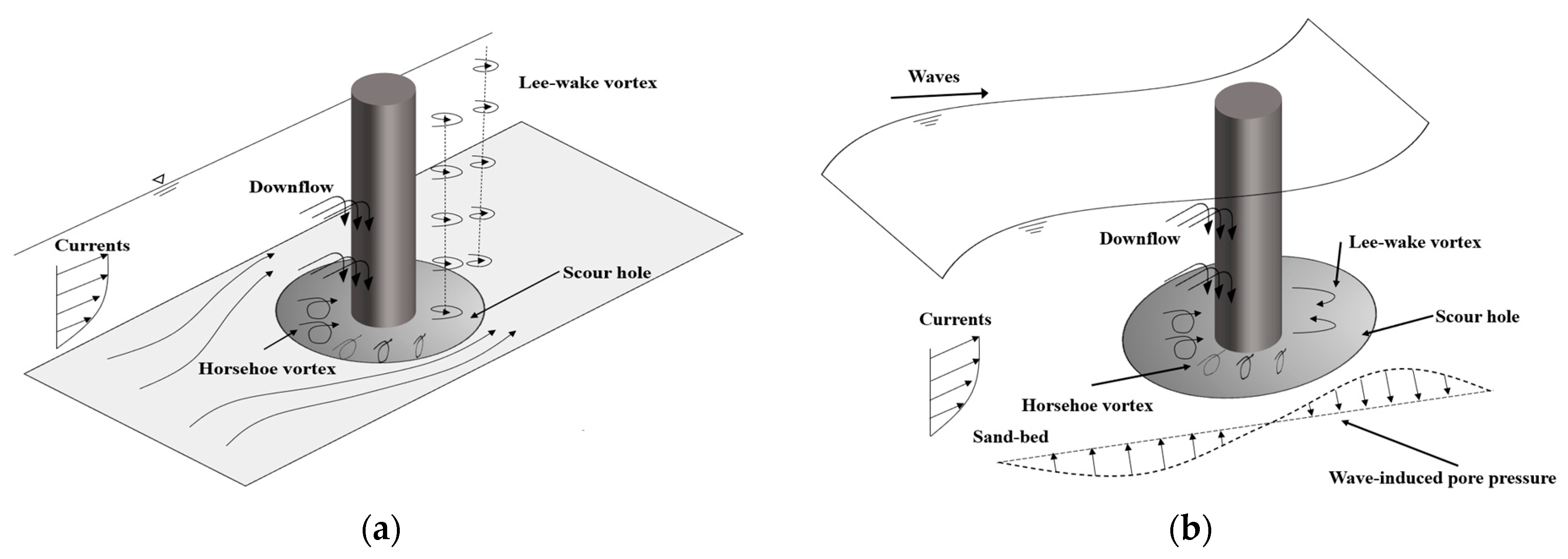

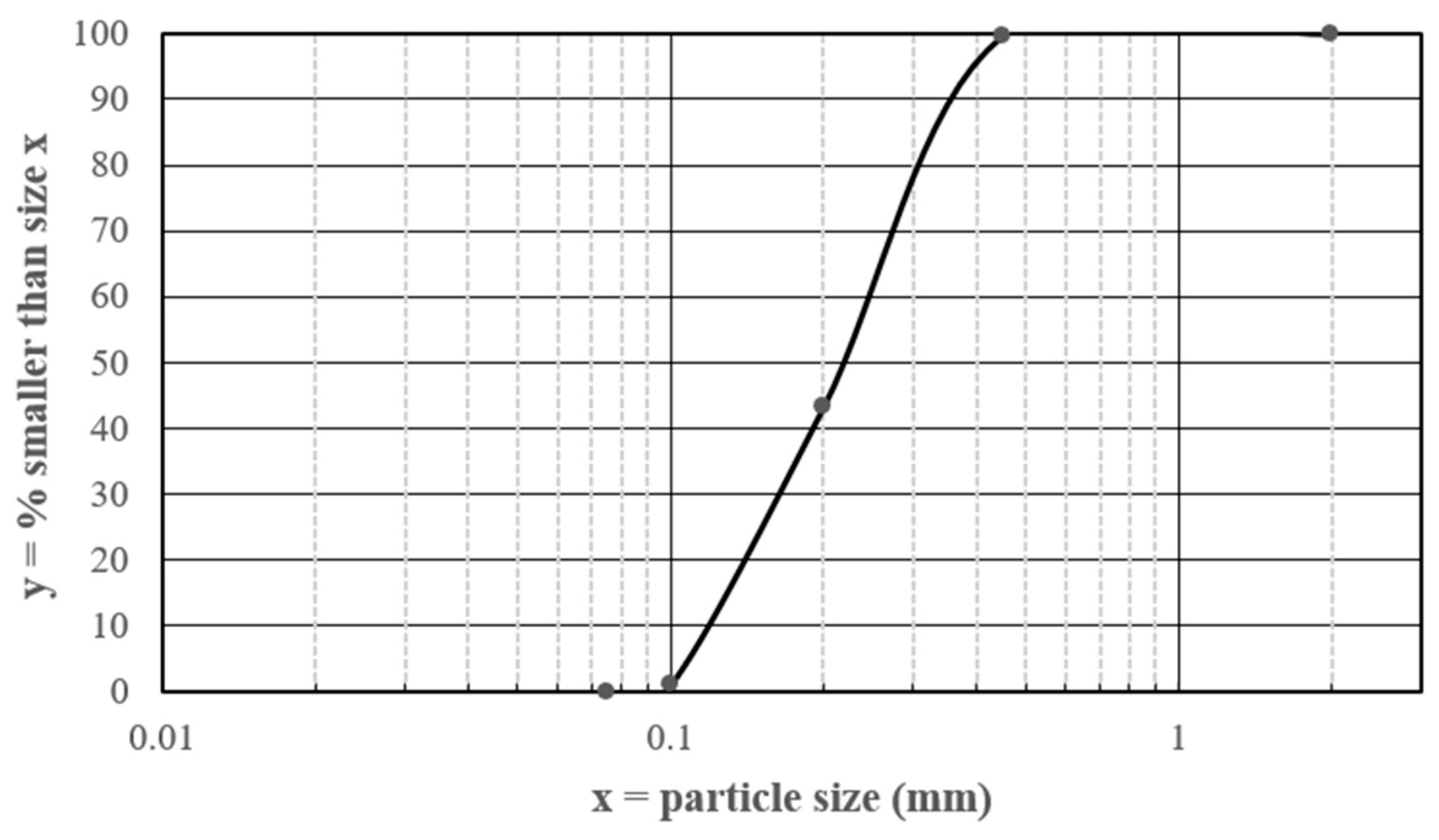


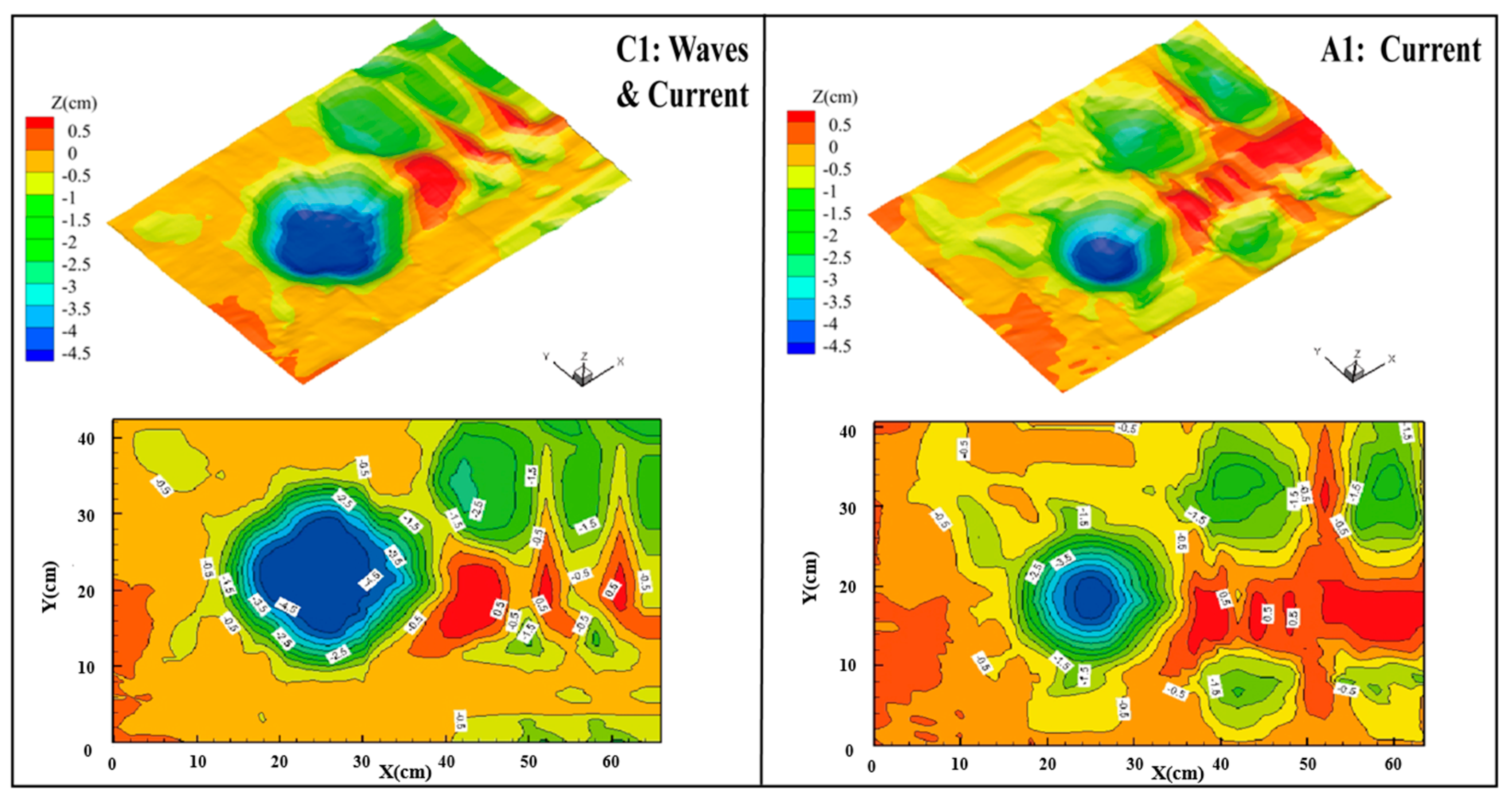
| Codes | Equations | Design Specifications | Notes |
|---|---|---|---|
| 65-2 | is given by ; | Hydrological Specifications for Survey and Design of Highway Engineering (JTG C30-2015) [26] | 1. Based on field and experiment data collected in China [29] 2. Performed well in the following decades 3. Dimensional disharmony 4. The expression is valid for both live-bed and clear water |
| 65-1 (modified formula) | Hydrological Specifications for Survey and Design of Highway Engineering (JTG C30-2015) [26] | 1. Based on field and experiment data collected in China 2. Performed well in the following decades 3. Dimensional disharmony [29] 4. The expression is valid for both live-bed and clear water 5. Makes up for the insufficiency of the large calculation value of the 65-2 type pair in predicting the local scour depth around the pier and the river bed in the foundations such as large boulders and pebbles | |
| HEC-18 | is given by | American Association of State Highway and Transportation Officials (AASHTO LRFD) [27] | 1. Based on field and experiment data collected in USA 2. Include the coefficients for the effect of bed forms, size of bed materials, and wide piers 3. Dimensionally consistent 4. The expression is valid for both live-bed and clear water |
| Han Haiqian Formula | is given by | Chinese Code for Design of Wind Turbine Foundations for Offshore Wind Power Projects (NB/T 10105-2018) [28] | 1. Based on field and experiment data collected in China under tidal current 2. Include the coefficients for the effect of arrangement form |
| Wang Rukai Formula | where is given by | Chinese Code for Design of Wind Turbine Foundations for Offshore Wind Power Projects (NB/T 10105-2018) [28] | 1. Comprehensive considerations 2. Complicated calculation |
| Sumer method | Chinese Code for Design of Wind Turbine Foundations for Offshore Wind Power Projects (NB/T 10105-2018) [28] & The DVN GL standard for Support structures for wind turbines (DNVGL-ST-0126-2018) [30] | 1. The expression is valid for live-bed conditions 2. For steady current, which implies KC→∞, it appears from this expression that S/D→1.3 3. For waves it appears that for KC < 6, no scour hole is formed. The physical explanation for this is that no horseshoe vortex develops for KC < 6 |
| Group | Hydraulic Condition | Model | Pile Diameter (m) | Water Depth (m) | Flow Velocity (m/s) | Wave Height (m) | Wave Period (s) |
|---|---|---|---|---|---|---|---|
| A1 | Steady current | Column | 0.04 | 0.3 | 0.25 | ||
| A2 | Steady current | Column | 0.04 | 0.4 | 0.225 | ||
| A3 | Steady current | Column | 0.04 | 0.4 | 0.25 | ||
| C1 | Waves & current | Column | 0.04 | 0.4 | 0.225 | 0.06 | 1 |
| C2 | Waves & current | Column | 0.04 | 0.4 | 0.225 | 0.08 | 1 |
| C3 | Waves & current | Column | 0.04 | 0.3 | 0.225 | 0.06 | 1 |
| Group | Measured Depth | 65-2 Formula | 65-1 Modified Formula | HEC-18 | Han Haiqian Formula | Wang Rukai Formula | Sumer Method |
|---|---|---|---|---|---|---|---|
| A1 | 4.1 | 2.29 | 3.42 | 56 | - | - | - |
| A2 | 3.5 | 1.80 | 2.02 | 62 | - | - | - |
| A3 | 3.7 | 2.19 | 3.95 | 70 | - | - | - |
| C1 | 3.7 | 1.90 | 2.02 | 54 | 24 | 1.34 | 5.20 |
| C2 | 4.0 | 1.80 | 2.02 | 62 | 24 | 1.54 | 5.20 |
| C3 | 3.5 | 1.90 | 2.41 | 67 | 23 | 1.29 | 5.20 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Zhang, B.; Shen, C.; Fu, X.; Li, W. Experimental Study on Local Scour Depth around Monopile Foundation in Combined Waves and Current. Sustainability 2021, 13, 13614. https://doi.org/10.3390/su132413614
Li J, Zhang B, Shen C, Fu X, Li W. Experimental Study on Local Scour Depth around Monopile Foundation in Combined Waves and Current. Sustainability. 2021; 13(24):13614. https://doi.org/10.3390/su132413614
Chicago/Turabian StyleLi, Junhan, Bin Zhang, Chao Shen, Xiaoli Fu, and Weichao Li. 2021. "Experimental Study on Local Scour Depth around Monopile Foundation in Combined Waves and Current" Sustainability 13, no. 24: 13614. https://doi.org/10.3390/su132413614
APA StyleLi, J., Zhang, B., Shen, C., Fu, X., & Li, W. (2021). Experimental Study on Local Scour Depth around Monopile Foundation in Combined Waves and Current. Sustainability, 13(24), 13614. https://doi.org/10.3390/su132413614






