Abstract
Currently, manufacturers seek to provide customized and sustainable products, requiring flexible manufacturing systems and advanced production management to cope with customization complexity and improve environmental performance. The reconfigurable manufacturing system (RMS) is expected to provide cost-effective customization in high responsiveness. However, reconfiguration optimization to produce sustainable mass-customized products in RMS is a complex problem requiring multi-criteria decision making. It is related to three problems, process planning, scheduling, and layout optimization, which should be integrated to optimize the RMS performance. This paper aims at integrating the above three problems and developing an effective approach to solving them concurrently. It formulates a multi-objective mathematical model simultaneously optimizing process planning, job-shop scheduling, and open-field layout problem to improve RMS sustainability. The penalty for product tardiness, the total manufacturing cost, the hazardous waste, and the greenhouse gases emissions are minimized. Economic and environmental indicators are defined to modify the Pareto efficiency when searching the Pareto-optimal solutions. Exact Pareto-optimal solutions are obtained by brute-force search and compared with those of the non-environmental indicator model. NSGA-III is adopted to obtain the approximate Pareto-optimal solutions in high effectiveness and efficiency. A small numerical example is applied to validate the mathematical model and resolution methods.
1. Introduction
Customers today require unique personalized products as well as sustainable ones. Companies on the other hand want to improve their environmental impact while surviving in today’s environment characterized by highly variable and uncertain demand. Low-carbon product family design is an excellent idea to deal with the diverse needs of customers and the pressure from government policy for environmental protection [1]. Sustainable manufacturing is useful in minimizing material and energy wastage as well as improving machine utilization and process productivity coupled with higher customer satisfaction [2]. Companies seek to be flexible with cost-efficiency and more sustainable. The reconfigurable manufacturing system (RMS) is recognized as one of the most advantageous next-generation manufacturing systems allowing flexibility not only in producing a variety of parts but also in changing the system itself, which could facilitate the ever-quicker introduction of new products caused by the current customer-driven market and the increased awareness of environmental issues [3]. Mass customization (MC) has become a vital manufacturing strategy to meet agility and high responsiveness for most companies in view of current levels of market globalization, rapid technological innovations, and intense competition [4]. MC can lead to better environmental performance [5]. Since RMS is designed to perform different operations on various products grouped in families according to their operational requirements [6], it is beneficial to employ RMS to provide MC. However, the complexity of planning and scheduling in this scenario is progressively raised, especially if the layout switching is jointly considered. Effective methods to generate the best layout arrangements are significant to improve business profit and customer satisfaction as well as to promote environmental protection and the achievement of MC with RMS in practice.
The work aims to formulate the integrated process planning, scheduling, and layout problem as well as to propose a suitable method to produce multiple mass-customized products in RMS with minimum tardiness penalty, total cost, and amount of pollutants.
The significance of the work is first in simultaneously studying open-field layout reconfiguration with process planning and job-shop scheduling for MC in RMS. Rare studies optimize environmental objective simultaneously with makespan and cost for the integrated problem. Moreover, this study sensibly devises the Pareto-optimal solutions sorting principle in two steps by the economic and environmental indicators converted from the proposed multi-objectives.
The main contributions of this paper are:
- including the environmental sustainability for this integrated production management problem in RMS, which is limited in previous research;
- modifying the Pareto efficiency by combining the characteristics of this problem to get a reasonable number of Pareto-optimal solutions for decision makers; and
- surveying the appropriate parameters to design a decent heuristic approach in order to solve this problem effectively and efficiently.
The rest of this paper is organized as follows: the literature review is presented in Section 2; assumptions, notations, and the mathematical model to formulate the problem in detail are introduced in Section 3; a numerical case to validate the mathematical model, the modified Pareto efficiency, the exact Pareto-optimal solutions obtained by brute-force search to this small case, and comparison with the exact Pareto-optimal solutions for no environmental indicator model are presented in Section 4; the approximate Pareto-optimal solutions obtained from a reference-point-based many-objective evolutionary algorithm following NSGA-II framework, NSGA-III [7], is explained in Section 5, along with the parameter tuning to prove the effectivity and efficiency of this approach; conclusions and future research directions are summarized in Section 6.
2. Literature Review
Previous studies principally treat process planning, scheduling, and layout design for MC in RMS as detaching themes. Mathematical programming and heuristics are often used to solve these problems. Research to integrate them is very limited. The works on sustainability in RMS are few. The issue is not sufficiently treated. As scheduling correlates deeply with RMS layout, operation sequence, and configuration to produce mass-customized products, the comprehensive investigation is more likely to reach the global optimum with minimum cost, time, and environmental impact.
The selection of a machine and its configuration is the primary task to determine the process planning for distinct product features in RMS. Early research extensively investigated the development of an optimal process plan for diverse parts composing a singular product or given order. Bensmaine [8] proposed an adapted NSGA-II-based approach minimizing the total cost and the total time by the selection of candidate reconfigurable machines among available sets, which then will be used to carry out a certain product with specific characteristics. Hasan [9] designed an algorithm to find the exact global optimum of configuration and order execution sequence associated with the selected configuration in RMS for the maximum benefit.
Some studies select the optimal process planning from the existing operation sequence, or feasible triples consisting of the machine, configuration, and tool indices for each operation. Musharavati [10] exploited simulated annealing algorithm with auxiliary knowledge to minimize multiple parts’ production cost in multistage parallel reconfigurable manufacturing lines. Touzout [11] addressed the single-product multi-unit process planning problem to minimize the total cost, total completion time, and machine exploitation in RMS where three hybrid heuristics were proposed and compared.
Scheduling is responsible for unfolding a plan into detailed resource assignments and sequences [12]. Valente [13] outlined an Integrated Scheduling Architecture supporting the static and dynamic scheduling execution of control tasks in reconfigurable production systems. Prasad [14] used Shannon entropy to calculate weights of criteria and multi-attribute range evaluation to calculate the uncertainty of decision variables into the uncertainty of ranking for products scheduling in RMS. Mahmoodjanloo [15] dealt with an extension of a flexible job-shop scheduling problem containing reconfigurable machine tools with configuration-dependent reconfiguration time to minimize makespan.
With the drawbacks involving unbalanced resource utilization, infeasible and unrealistic process plans and uncoordinated and isolated optimization when process planning and scheduling are treated as separate entities, more and more researchers combine these two topics into a single cohesive unit [16]. Dou [17] established a multi-objective mixed-integer programming model in a reconfigurable flow line to minimize total cost and tardiness in view of the close coupling between configuration generation and scheduling. Morganti et al. [18] engaged the operation-triplet process planning and scheduling for multiple parts with defect frequencies in RMS.
The flexibility in RMS provides the capacity to produce several products in the same system with layout reconfiguration, whereas operations sequence or precedence, space for reconfiguration, unproductive time, departments or machines size and shape, machine capacity, stationary facilities, non-overlapping departments and empty spaces are constraints for adjustment with minimal effort [19]. Haddou et al. presented several works to advance this research subject. In 2017, they introduced a multi-objective approach that assessed the evolution and layout transition efforts between products of a product family in RMS design [20]. In 2018, they put forward an exhaustive search-based heuristic to ensure that the best layout respects both the constraints imposed by the generated process plan and those depicting the available location in the shop floor where machines are going to be placed [21]. In 2019, Haddou, Benderbal, and Benyoucef [22] incorporated AMOSA with the above exhaustive search-based heuristic for the RMS layout design infra performance metrics.
The delays originating from layout reconfiguration will influence the optimal planning and scheduling. Hence, it is important to simultaneously optimize the three problems. The difficulty is that each problem already exhibits its own computational complexity, which escalates the total degree of difficulty to resolve the unified problem. Gao [23] built a linear mathematical model to minimize the tardiness penalty for job-shop scheduling and open-field layout in RMS. Campos [24] settled the instance selection problem for a modular mass-customized product via a 0–1 nonlinear integer programming concerning machine reconfiguration and layout allocation in RMS. Ghanei [25] presented a mixed-integer programming model to minimize the total cost of energy consumption, layout reconfiguration, and part transportation between machines during the multi-period planning and scheduling problem.
The complexity of reconfiguration, product variation, and development processes necessitate the use of tools to improve the eco-friendliness of RMS, for which Kurniadi [26] suggested a multi-disciplinary green bill of material with an additional multi-disciplinary feature to minimize emissions and hazardous materials during product development and manage product information across multiple disciplines during the reconfiguration process. Touzout et al. [27] propounded a hybrid multi-objective approach that consolidates the strengths of the multi-objective integer linear programming and the evolutionary algorithm AMOSA to tackle the process plan problem in RMS with a criterion of GHG emissions. At the same time, a comparative study of this method with two other hybrid-meta-heuristics was carried out to solve the sustainable single-product multi-unit process plan generation in RMS, and these approaches were inspired by a microscopical study of optimal Pareto front solutions [28]. Khezri [29] conducted the process planning for a single unit of a product in RMS with the goal of minimizing the amount of wasted hazardous which consists of hazardous liquid waste and GHG, the total production cost, and the total production time. Lamy [30] examined the impact of reconfigurable machine tools on schedules in the context of a multiple path shop floor subject to variations in power supply.
In conclusion, simultaneously optimizing process planning, scheduling, and layout under environmental sustainability for several mass-customized products in RMS is a research gap. It is worthwhile to formulate the united problem and develop theory and techniques for the purpose of the green and intelligent industry.
3. Problem Formulation
This paper complies with the rules of FJSP and dynamic open-field layout problem with process planning to decide the optimal machine location, the operation sequence of each part, machine, and configuration to perform each operation, and processing time of each operation to yield a number of mass-customized products composed of several parts belonging to some part variants in an RMS.
A job indicates the complete procedure to produce a part. Whether belonging to the same product or not, jobs producing parts belonging to the exact part variant have identical parameters to perform the same operation, but the executing machine and configuration might differ. An unfinished part is termed a WIP. Assumptions and notations about products, part variants, jobs, WIP, operations, machines, and configurations are stated hereafter.
3.1. Assumptions
The model is based on the following assumptions:
- Parameters about a WIP’s transportation time, cost, energy consumption, and holding cost are only dependent on the type of part variant this WIP belongs to;
- Parameters about an operation’s processing time, processing cost, processing energy consumption, hazardous waste, setup time, setup cost, and setup energy consumption are dependent on the type of part variant the corresponding WIP belongs to, the kind of this operation, the executing machine, and the configuration;
- Parameters about reconfiguration time, cost, and energy consumption on a machine depend on the former configuration and the latter configuration;
- Energy consumed from different activities is quantified with the same unit, which can be added directly to estimate the amount of GHG emissions;
- Parts and the final mass-customized products are qualified without any defect during production in RMS;
- All machines are idle without configurations and setups at the beginning of the task to produce a given number of mass-customized products; and
- All the raw materials and handling devices are available.
3.2. Notations
Sets, indices, parameters, and decision variables of the model are described as follows:
3.2.1. Sets and Indices
, Set of products;
, Indices of products, , ;
, Set of part variants;
, Indices of part variants, , ;
, Set of jobs belonging to part variant in product ; if there is no job belonging to part variant in product ;
, Indices of jobs, , ;
, Set of operations;
, Indices of operations, , ;
, Set of operations to process part variant ;
, Set of operations precedent to operation when processing part variant ; if there is no operation precedent to operation ;
, Indices of positions in the operation sequence of jobs, , ;
, Indices of positions in the processing sequence on machines, , ;
, Set of machines;
, Indices of machines, , ;
, Set of configurations on machine ;
, Indices of configurations, , .
3.2.2. Parameters
To deliver every mass-customized product on time, the production of all the parts that make up every mass-customized product should be finished before the due date. In case some product is delayed, the manufacturer will receive a penalty to bear the customer’s loss. The tardiness penalty depends on customers and the tardiness duration. Different values of the tardiness penalty parameters in unit time imply the patience of distinct customers.
, Due date of product ;
, Tardiness penalty of product per time unit;
An RMS could process various part variants experiencing similar operations in a part family. Based on the above assumptions, parameters about transporting a WIP between two consecutive operations performed on different machines and holding them when the subsequent machine is occupied differ by disparate part variants. Operation precedence is considered in processing part variants. Operations could be performed on alternative machines with optional configurations.
, 1 if operation is feasible on machine with configuration ; 0 otherwise;
, Transport time of a WIP belonging to part variant per distance unit;
, Transport cost of a WIP belonging to part variant per distance unit;
, Energy consumption for transporting a WIP belonging to part variant per distance unit;
, Holding cost of a WIP belonging to part variant per time unit;
An operation indicates a procedure shaping parts with a specific feature in structure or creating a particular function. Identical operations have different setup and processing parameters values for different part variants. They also differ by executing machines with selective configurations.
, Processing time of operation for a WIP belonging to part variant on machine with configuration ;
, Processing cost of operation for a WIP belonging to part variant on machine with configuration ;
, Energy consumption of performing operation for a WIP belonging to part variant on machine with configuration ;
, Hazardous waste discharged from performing operation for a WIP belonging to part variant on machine with configuration ;
, Setup time of operation for a WIP belonging to part variant on machine with configuration ;
, Setup cost of operation for a WIP belonging to part variant on machine with configuration ;
, Energy consumption of setup operation for a WIP belonging to part variant on machine with configuration ;
System reconfiguration enables machines’ position change from the initial layout to the optimal one for a production task. Machine reconfiguration enables machines to perform diverse operations with abundant reconfigurable manufacturing tools.
, Boundary of the workshop on the X-coordinate;
, Boundary of the workshop on the Y-coordinate;
, Time for moving machine in distance unit;
, Cost for moving machine in distance unit;
, Energy consumption for moving machine in distance unit;
, Initial position of machine on the X-coordinate;
, Initial position of machine on the Y-coordinate;
, Security distance of machine on the X-coordinate;
, Security distance of machine on the Y-coordinate;
The layout reconfiguration occurs at the beginning of the production period. All machines are freely placed in a rectangular plant of length and width . Every machine has a security distance on the X and Y coordinate apiece. For machine , the minimum acceptable interspaces between the location of machine and others on the X and Y coordinate are defined as the security distance and .
, Reconfiguration time from configuration to configuration on machine , if , ;
, Reconfiguration cost from configuration to configuration on machine , if , ;
, Energy consumption of reconfiguration from configuration to configuration on machine , if , ;
Hazardous waste could result in severe soil contamination and marine pollution, threatening the survival of humans and other creatures. Increase of GHG concentrations in the atmosphere causes frequent extreme weather and climate change globally. For these, limits of the average hazardous waste and GHG emissions per time unit are adopted in this problem formulation for appraising the sustainability level of production optimization. The limit of the average hazardous waste per time unit is estimated from the boundary of the hazardous waste for the manufacturer in a year or a certain duration. The limit of the average GHG emissions per time unit is estimated as above. Referring to the common method of GHG emissions measurement in the related literature, the amount of GHG emissions is derived from converting the total amount of energy consumption with a designated factor.
, Limit of the average hazardous waste per time unit;
, Emission factor for energy consumption;
, Limit of the average GHG emissions per time unit.
3.2.3. Independent Decision Variables
, Position of machine on the X-coordinate;
, Position of machine on the Y-coordinate;
, Operation processed at position in the operation sequence of job belonging to part variant in product ;
, Machine to perform operation at position in the operation sequence of job belonging to part variant in product ;
, Configuration on machine to perform operation at position in the operation sequence of job belonging to part variant in product ;
, Beginning time to perform operation at position in the operation sequence of job belonging to part variant in product .
3.2.4. Auxiliary Decision Variables
, Completion time of operation at position in the operation sequence of job belonging to part variant in product ;
, Tardiness of product ;
, Beginning time to perform operation at position in the processing sequence on machine ;
, Product of the performed operation at position in the processing sequence on machine ;
, Part variant of the performed operation at position in the processing sequence on machine ;
, Job of the performed operation at position in the processing sequence on machine ;
, Position of the performed operation at position in the processing sequence on machine ;
, Distance between machine and machine on the X-coordinate;
, Distance between machine and machine on the Y-coordinate.
3.3. Mathematical Model
The aim of this work is to bring forward a constructive mathematical method to take on an MC order fabricated in an RMS-equipped factory and find a resolution to gain the optimum value of the above decision variables for reduced loss of delay, total cost, and harm to the environment. The problem is formulated as a mixed-integer nonlinear programming model (MINLP). The objective functions and constraints are expressed hereafter. Abbreviations in the mathematical model are listed in Table 1.

Table 1.
Abbreviations (authors’ own study).
3.3.1. Objective Functions
There are three objectives in this mathematical model, to minimize:
- The total penalty of tardiness for all the delayed products accomplished after the due date;
- The total cost including the total setup cost, the total processing cost, the total WIP transport cost, the total WIP holding cost, the total machine reconfiguration cost, and the total layout reconfiguration cost; and
- The value of the environment indicator defined as the aggregate of the normalized hazardous waste item (the ratio of the total amount of hazardous waste and the allowed amount of hazardous waste) and the normalized GHG emissions item (the ratio of the total amount of GHG emissions and the allowed amount of GHG emissions).
Essentially, the above objective functions optimize the production scheme for manifold mass-customized products in RMS for time, cost, and environmental impact. The completion time of every mass-customized product is weighted by customer-based priority in the first objective function. In addition, energy consumption is taken into account through GHG emissions. All the variables in the objective functions are defined in the constraints below.
3.3.2. Constraints
The following equations present the constraints to define the feasible solutions:
Constraint (4) defines the completion time of an operation in the operation sequence of one part’s process plan. Constraint (5) gives the definition of a product’s tardiness. Constraints (6)–(8) show the idea to obtain the auxiliary decision variables about jobs and operations in the processing order on machines. When all the independent variables of operation beginning times are decided, the processing orders on machines are also determined. The information about ordered jobs and operations on machines is crucial because machine reconfiguration and setup activities depend on the selected configurations to perform two consecutive operations and types of jobs processed. Constraint (6) finds the first operation on each machine. Constraint (7) rechecks and reformulates the remaining operations processed in order on machines. Constraint (8) acquires the corresponding jobs of operations in the processing order on machines. Constraint (9) calculates the distance on the X and Y coordinate between any two machines. Constraints (10)–(15) calculate the total setup cost, the total processing cost, the total WIP transport cost, the total WIP holding cost, the total machine reconfiguration cost, and the total layout reconfiguration cost separately. Constraint (16) calculates the total amount of hazardous waste. The total amount of consumed energy times factor to calculate the total amount of GHG emissions in Constraint (17). Constraint (18) implies the total amount of consumed energy comprising the total energy consumed from the setup, processing, WIP transport, machine reconfiguration, and layout reconfiguration activities. Constraints (19)–(23) calculate the total energy consumed from the activities mentioned above separately. Constraint (24) fixes the allowed amount of hazardous waste by multiplying the completion time of the entire production period with the limit of the average hazardous waste per time unit. Constraint (25) fixes the allowed amount of GHG emissions similarly to how the allowed amount of hazardous waste is fixed. Constraint (26) determines the completion time of the entire production period. Constraints (27) and (28) restrict a feasible solution subject to the hazardous waste and GHG emissions limit. Constraint (29) ensures that the selected machine and configuration are able to perform the corresponding operation. Constraint (30) states that the beginning time of an operation is no earlier than the sum of the completion time of any higher precedence operation and the WIP transport time between these two operations. Constraint (31) signifies that the first operation on each machine should be performed after setup. Constraint (32) claims no setup and reconfiguration between two consecutive and identical operations processing two WIPs belonging to the same part variant and performed on a machine with the same configuration. Otherwise, the setup time and reconfiguration time should be deliberated, as said in constraint (33). Constraint (34) declares non-overlapping between any two machines on the X or Y coordinate. Constraints (35)–(39) define the domain of the independent decision variables.
4. Numerical Experiment
This problem is NP-hard because the proved NP-hard FJSP is adopted. A small example is exercised to validate the model. The general Pareto efficiency is modified to reduce the optimal solutions in the Pareto front, inasmuch as multi-objective optimization will probably have redundant solutions to confuse decision-makers. Based on that, the exact Pareto-optimal solutions are obtained by brute-force search.
As depicted in Figure 1, there are two products in this small numerical example, each composed of an individual part belonging to a particular part variant. The due date and the tardiness penalty per time unit for each product are given in this figure. In addition, parameters about a WIP transport time, transport cost, transport energy consumption, and holding time belonging to each part variant are displayed in this figure.
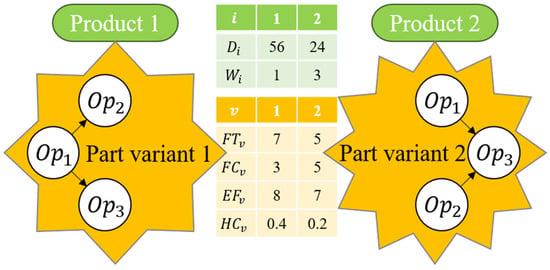
Figure 1.
Parameters about products and part variants in the numerical example (authors’ own study).
The average hazardous waste and GHG emissions limit per time unit ( and ) are designated to 1 and 7. The factor to appraise the GHG emissions by the amount of energy consumption () is set to 2.
The initial layout in the open-field workshop is illustrated in Figure 2. The security distance of each machine, together with the layout reconfiguration cost and energy consumption parameters, are marked in this figure too. Figure 3 presents the reconfirmation time, cost, and energy consumption parameters between different configurations on each machine.
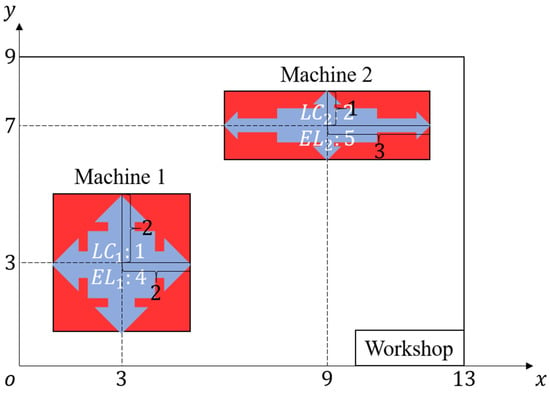
Figure 2.
Initial layout in the open-field workshop (authors’ own study).
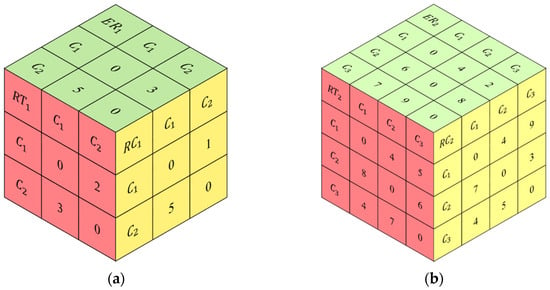
Figure 3.
Reconfiguration time, cost, and energy consumption: (a) on machine 1; (b) on machine 2 (author’s own study).
Parameters about processing time, processing cost, processing energy consumption, hazardous waste, setup time, setup cost, and setup energy consumption on a certain machine with a certain configuration to produce a part belonging to each part variant are presented in Figure 4.
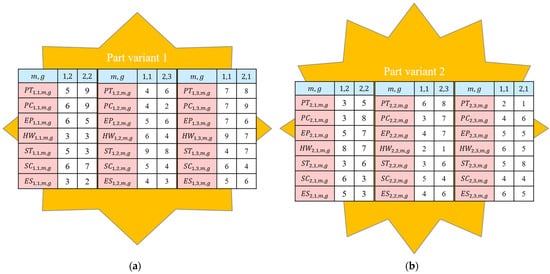
Figure 4.
Processing and setup parameters to produce a part belong to: (a) part variant 1; (b) part variant 2 (authors’ own study).
4.1. Modified Pareto Efficiency
For a three-objective minimizing mathematical model, two solutions sorted by the general Pareto efficiency have twenty-seven kinds of relationship ( since there are three kinds of relationship comparing the values of an objective function for two solutions and there are three objective functions). As illustrated in Figure 5, solution and solution in the Pareto front are non-dominated to each other, entailing that the values of their first objective function ( and ), second objective function ( and ), and third objective function ( and ) match one of the thirteen conditions. The general Pareto efficiency brings about numerous Pareto-optimal solutions in the Pareto front, also giving rise to excess approximate Pareto-optimal solutions during approximate optimization searching. Seeing that the number of feasible solutions in the solution space will not change by the sorting methods, a strict Pareto efficiency narrows the Pareto front and decreases the collected Pareto-optimal solutions.
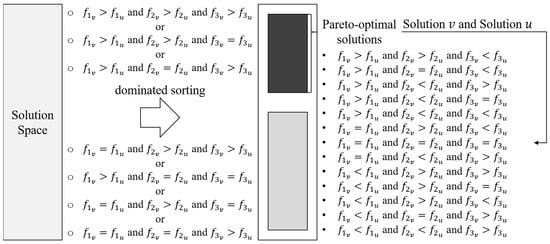
Figure 5.
General Pareto efficiency (author’s own study).
Owing to the fact that the first objective function and second objective function are quantified in currency, the sum of these two objectives () could be interpreted as the economic indicator. As illustrated in Figure 6, if is set as the first objective function and is set as the second objective function to formulate a bi-objective model directly, the Pareto front of this bi-objective model is close to that of the above three-objective model, when solutions are sorted by the general Pareto efficiency.
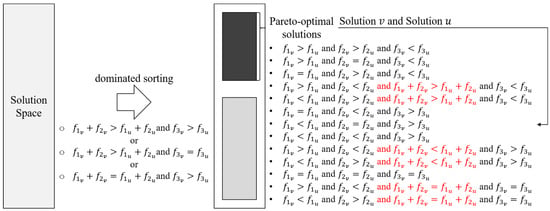
Figure 6.
General Pareto efficiency (authors’ own study).
This paper proposes a modified Pareto efficiency lowering the probability of a solution becoming non-dominated. As shown in Figure 7, it is divided into two steps. In the first step, solutions are sorted by the values of the first objective function and the second objective function. In the second step, all the non-dominated solutions from the previous step are further sorted by the economic indicator and the environment indicator (). As a result, the relationship between solution and solution in the Pareto front sorted by the modified Pareto efficiency falls into the reduced five conditions illustrated at the top of Figure 7.
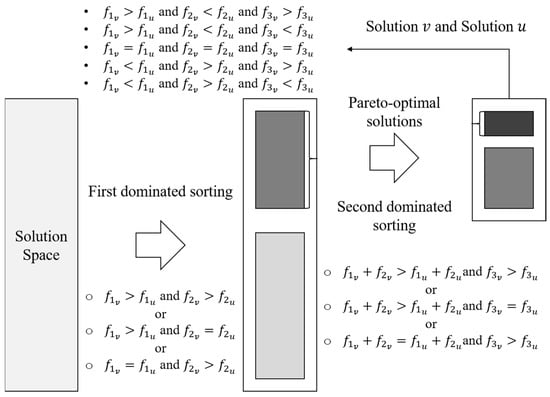
Figure 7.
Modified Pareto efficiency (authors’ own study).
4.2. Exact Pareto-Optimal Solutions Obtained from Brute-Force Search
There are three exact Pareto-optimal solutions obtained from brute-force search to this small numerical example. Table 2 lists the values of the three objectives in each solution. From this table, two solutions have the same values for all objective functions.

Table 2.
The values of the multi-objective functions in the exact Pareto-optimal solutions for the small numerical example (authors’ own study).
Table 3 displays the optimal layout in each exact Pareto-optimal solution. In fact, it is the same as the initial layout, reflecting that layout reconfiguration is the inferior strategy to arrange optimal production management.

Table 3.
The optimal layout in the exact Pareto-optimal solutions for the small numerical example (authors’ own study).
Table 4 gives the optimum beginning time to produce every part in the optimal operation sequence on the best machine with the selected configuration. We can observe that every job is implemented throughout one machine in each solution, which makes it seem that machine reconfiguration is superior to the WIP transport for this small numerical example.

Table 4.
The optimal production scheme in the exact Pareto-optimal solutions for the small numerical example (authors’ own study).
4.3. Comparison with Exact Pareto-Optimal Solutions for No Environmental Indicator Model
There are seven exact Pareto-optimal solutions for the model without the third objective function and the relevant parameters in this problem formulation. The values of the two objective functions, the optimal layout, and the optimal process planning and scheduling arrangement in each solution are in Table 5, Table 6 and Table 7.

Table 5.
The values of the multi-objective functions in the exact Pareto-optimal solutions for no environmental indicator model (authors’ own study).

Table 6.
The optimal layout in the exact Pareto-optimal solutions for no environmental indicator model (authors’ own study).

Table 7.
The optimal production scheme in the exact Pareto-optimal solutions for no environmental indicator model (authors’ own study).
Compared with the exact Pareto-optimal solutions in Section 4.2, there are four solutions eliminated by the environmental indicators. Moreover, these four solutions would be removed as well if all the above solutions are just sorted by the economic indicator. Thus, considering environmental sustainability has a positive impact on the optimization of mass-customized production management in RMS. The modified Pareto efficiency is advanced in gathering economically profitable and environmentally friendly solutions.
5. Approximate Optimization
The approximate Pareto-optimal solutions are obtained from NSGA-III, an algorithm advantaged in finding a well-converged and well-diversified set of points for multi—even many—objective optimization problems [7]. Without any preference information, the reference points are generated on the three three-dimensional unit simplex. The total number of the reference points () in this three-objective problem is defined by the division parameter for each objective axis ():
The decision variables about machine positions and the beginning time of each process in the operation sequence of every job are encoded with continuous values. Decision variables about the selected operation, machine, and configuration corresponding to each process in the operation sequence of every job are encoded with integer values. Since they are encoded with real values, there is no special decoding procedure. Selection, crossover, and mutation take place in order during each generation until the number of iterations comes to the generation limit.
The performance of NSGA-III is assessed by effectivity and efficiency. Based on the fact that this is a three objective minimization problem, and most of the approximate Pareto-optimal solutions are dominated by the exact Pareto-optimal solutions, or at best equal to the exact Pareto-optimal solutions, a metric () to assess the effectivity of NSGA-III for the numerical example is defined as the following equation:
In this equation, , , and are the mean values of the first, second, and third objective function in the exact Pareto-optimal solutions. , , and are the mean values of the first, second, and third objective function in the approximate Pareto-optimal solutions obtained by NSGA-III in a run.
The efficiency of NSGA-III to solve this problem is assessed by the computation time (). Small effectivity metric value and short computation time are preferred, representing high effectivity and efficiency.
In NSGA-III, the number of the reference points, mutation probability, and the generation limit stipulating the number of iterations in a run mainly influence the performance of this approach. Factor analysis is carried out in Minitab to check the dependency relating the effectiveness and efficiency of this approach with the three parameters stated above.
5.1. Approximate Pareto-Optimal Solutions Obtained from NSGA-III
Here are three approximate Pareto-optimal solutions obtained in a run by setting , mutation probability (0.05), and generation limit (2000). Hence, the number of the reference points is equal to six, twice the number of the exact Pareto-optimal solutions.
The objective values, optimal layout, and the optimal production scheme in these approximate Pareto-optimal solutions are displayed in Table 8, Table 9 and Table 10. For the optimal layout, only Machine 2’s position on the X-coordinate is changed compared with that in the exact Pareto-optimal solutions. The process plans for these solutions are almost the same as that of the exact Pareto-optimal solutions, while the scheduling is quite different as the beginning times of operations alter a lot.

Table 8.
The values of the multi-objective functions in the approximate Pareto-optimal solutions for the small numerical example (authors’ own study).

Table 9.
The optimal layout in the approximate Pareto-optimal solutions for the small numerical example (authors’ own study).

Table 10.
The optimal production scheme in the Exact Pareto-optimal solutions for the small numerical example (authors’ own study).
The computation time of the corresponding run is 7.828125 s, saving 99.6% of the computation time to obtain the exact Pareto-optimal solutions (2093.28125 s). The value of the effectivity metric is 0.256988154, which means the deviation of the mean value for three objective values is less than 26%.
The programming was conducted on a laptop computer powered by an Intel Core i7-7600U CPU (2.80 GHz) and 16 GB of RAM. Algorithms are programmed in PyCharm, the software of a Python Integrated Development Environment. The version used is 2021.2.2. Python 3.8 was configured as a project interpreter.
5.2. Parameter Tunning
There are two levels for each factor in factor analysis, as shown in Table 11. It requires eight runs necessary for a two-level full factorial design with three factors. The number of replicates for the corner points was three. Thus, there were 24 runs altogether in this factor analysis.

Table 11.
Two levels for each factor in factor analysis (authors’ own study).
The Pareto charts of standardized effects in Figure 8 reveal that the common factor of the number of the reference points, mutation probability, and generation limit is statistically significant to the effectivity of NSGA-III in solving this problem, yet the number of the reference points, generation limit, and the common factor of these two factors are statistically significant to the efficiency of NSGA-III in solving this problem.
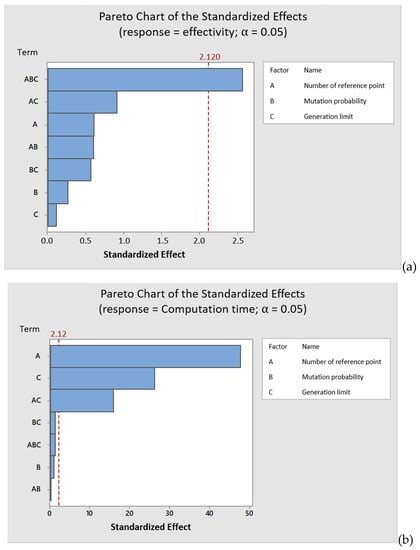
Figure 8.
Pareto charts of standardized effects about: (a) effectivity; (b) efficiency (authors’ own study).
The main effects plots in Figure 9 reveal that the number of the reference points and the mutation probability at a high level are obviously beneficial to improve the effectivity, the number of the reference points and the generation limit at a low level are evidently beneficial to improve the efficiency of this approach to solve the problem in this paper.
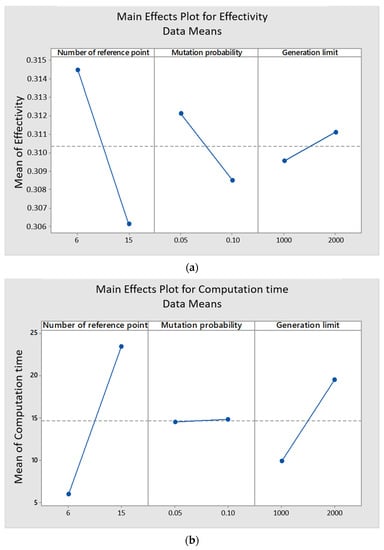
Figure 9.
Main effects plot about: (a) effectivity; (b) efficiency (authors’ own study).
6. Conclusions
This paper presented a multi-objective mathematical model to manage MC in RMS from the economic and environmental perspectives concurrently. Reconfiguration on machine and system levels are both taken into consideration. Decisions about process planning, job-shop scheduling, and open-field layout are simultaneously optimized in an MINLP model. The general Pareto efficiency is modified to sort solutions either in the solution space of exhaustive search or among the solutions obtained from iterations in the heuristics. Results comparing the exact Pareto-optimal of this problem and that of the non-environmental model certify the significance of considering environmental sustainability in the optimization of production management. Since this problem is NP-hard, NSGA-III is prospected to solve this problem in high efficiency. Limited by memory to obtain the exact Pareto-optimal solutions in brute-force search, this paper used a small numerical example to validate the mathematical model and the adopted approach. The dependency between the performance of this approach and the number of the reference points, mutation probability, and the generation limit is analyzed by two-level factor analysis. The results evidenced that NSGA-III with proper parameters is practical for finding the desired solutions timely for this sophisticated problem.
The limitation of this study is deficient validation with regard to the resolution. In addition to NSGA-III, other heuristics and combinatorial optimization algorithms for multi-objective mixed-integer nonlinear programming ought to be tried out. Supplemental numerical analysis for more problem instances of large scales should be done to test the performance of employed methods thoroughly. This work implicates the advantage of the eco-friendly standpoint in operation management and contributes to the fundamental understanding of layout integrated production planning for MC in RMS. It is applicable to intelligent discrete manufacturing in the context of Industry 4.0. The stochastic arrival of orders and investigation from the social pillar of sustainability could expand this model.
The state of the research illustrates that no continuous approaches for production planning and scheduling for reconfigurable manufacturing systems are available [31], while time-dependent energy prices are a consequence of replacing classical power plants with renewable energies in the course of sustainable power generation [32]. Therefore, developing novel strategies/algorithms that can be used in real-time to fulfill the efficiency requirement of operational decision-making in RMS is critical for future research [33]. Furthermore, dynamic environments complicate the model and run-time limits the application of mathematical optimization to this NP-hard problem [34]. New methodologies such as deep reinforcement learning should be explored to study the real-time optimization and collaborative control of RMS in intelligent manufacturing [35].
Author Contributions
Conceptualization, S.G., J.D. and J.L.D.; methodology, S.G., J.D. and J.L.D.; validation, S.G., J.D. and J.L.D.; formal analysis, S.G., J.D. and J.L.D.; investigation, S.G., J.D. and J.L.D.; resources, S.G., J.D. and J.L.D.; writing—original draft preparation, S.G.; writing—review and editing, J.D. and J.L.D.; visualization, S.G.; supervision, J.D. and J.L.D.; funding acquisition, J.D. and J.L.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by China Scholarship Council, grant number 201806280501. The APC was funded by Université de technologie de Compiègne.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors acknowledge the license support of Minitab software by Université de Technologie de Compiègne, Roberval (Mechanics, Energy and Electricity), Centre de Recherche Royallieu, CEDEX, CS 60319, 60203 Compiègne, France.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wang, Q.; Qi, P.; Li, S. A Concurrence Optimization Model for Low-Carbon Product Family Design and the Procurement Plan of Components under Uncertainty. Sustainability 2021, 13, 10764. [Google Scholar] [CrossRef]
- Rehman, A.U.; Mian, S.H.; Umer, U.; Usmani, Y.S. Strategic Outcome Using Fuzzy-AHP-Based Decision Approach for Sustainable Manufacturing. Sustainability 2019, 11, 6040. [Google Scholar] [CrossRef] [Green Version]
- Mehrabi, M.G.; Ulsoy, A.G.; Koren, Y. Reconfigurable manufacturing systems: Key to future manufacturing. J. Intell. Manuf. 2000, 11, 403–419. [Google Scholar] [CrossRef]
- da Silveira, G.J.; Borenstein, D.; Fogliatto, F. Mass customization: Literature review and research directions. Int. J. Prod. Econ. 2001, 72, 1–13. [Google Scholar] [CrossRef]
- Noël, C.; Meaude, M.; Daaboul, J. La customization de masse, est-elle une approche de production durable? In Proceedings of the 17ème colloque national S-mart AIP-PRIMECA, Université Polytechnique Hauts-de-France [UPHF], LAVAL VIRTUAL WORLD, Laval, France, 31 March–2 April 2021; p. hal-03296126. [Google Scholar]
- Bortolini, M.; Galizia, F.G.; Mora, C. Reconfigurable manufacturing systems: Literature review and research trend. J. Manuf. Syst. 2018, 49, 93–106. [Google Scholar] [CrossRef]
- Deb, K.; Jain, H. An Evolutionary Many-Objective Optimization Algorithm Using Reference-Point-Based Nondominated Sorting Approach, Part I: Solving Problems With Box Constraints. IEEE Trans. Evol. Comput. 2013, 18, 577–601. [Google Scholar] [CrossRef]
- Bensmaine, A.; Dahane, M.; Benyoucef, L. A non-dominated sorting genetic algorithm based approach for optimal machines selection in reconfigurable manufacturing environment. Comput. Ind. Eng. 2013, 66, 519–524. [Google Scholar] [CrossRef]
- Hasan, F.; Jain, P.K.; Kumar, D. Optimum configuration selection in Reconfigurable Manufacturing System involving multiple part families. OPSEARCH 2013, 51, 297–311. [Google Scholar] [CrossRef]
- Musharavati, F.; Hamouda, A. Simulated annealing with auxiliary knowledge for process planning optimization in reconfigurable manufacturing. Robot. Comput. Manuf. 2011, 28, 113–131. [Google Scholar] [CrossRef]
- Touzout, F.A.; Benyoucef, L. Multi-objective multi-unit process plan generation in a reconfigurable manufacturing environment: A comparative study of three hybrid metaheuristics. Int. J. Prod. Res. 2019, 57, 7520–7535. [Google Scholar] [CrossRef]
- Roshanaei, V.; Azab, A.; Elmaraghy, H. Mathematical modelling and a meta-heuristic for flexible job shop scheduling. Int. J. Prod. Res. 2013, 51, 6247–6274. [Google Scholar] [CrossRef]
- Valente, A.; De Simone, L.; Carpanzano, E.; Ferraris, F. A methodology for static and dynamic scheduling of automation tasks in reconfigurable production systems. CIRP J. Manuf. Sci. Technol. 2012, 5, 241–253. [Google Scholar] [CrossRef]
- Prasad, D.; Jayswal, S. Scheduling in reconfigurable manufacturing system for uncertainty in decision variables. Mater. Today Proc. 2018, 5, 18451–18458. [Google Scholar] [CrossRef]
- Mahmoodjanloo, M.; Tavakkoli-Moghaddam, R.; Baboli, A.; Bozorgi-Amiri, A. Flexible job shop scheduling problem with reconfigurable machine tools: An improved differential evolution algorithm. Appl. Soft Comput. 2020, 94, 106416. [Google Scholar] [CrossRef]
- Ausaf, M.F.; Gao, L.; Li, X. Optimization of multi-objective integrated process planning and scheduling problem using a priority based optimization algorithm. Front. Mech. Eng. 2015, 10, 392–404. [Google Scholar] [CrossRef]
- Dou, J.; Li, J.; Su, C. Bi-objective optimization of integrating configuration generation and scheduling for reconfigurable flow lines using NSGA-II. Int. J. Adv. Manuf. Technol. 2016, 86, 1945–1962. [Google Scholar] [CrossRef]
- Morganti, L.; Benderbal, H.H.; Benyoucef, L.; Bortolini, M.; Galizia, F.G. A New Process Quality-based Multi-objective Multi-part Approach for the Integrated Process Planning and Scheduling (IPPS) Problem in Reconfigurable Manufacturing Environment. IFAC-PapersOnLine 2020, 53, 10755–10760. [Google Scholar] [CrossRef]
- Maganha, I.; Silva, C. A Theoretical Background for the Reconfigurable Layout Problem. Procedia Manuf. 2017, 11, 2025–2033. [Google Scholar] [CrossRef]
- Haddou-Benderbal, H.; Dahane, M.; Benyoucef, L. Layout evolution effort for product family in Reconfigurable Manufacturing System design. IFAC-PapersOnLine 2017, 50, 10166–10171. [Google Scholar] [CrossRef]
- Benderbal, H.H.; Dahane, M.; Benyoucef, L. Exhaustive Search Based Heuristic for Solving Machine Layout Problem in Reconfigurable Manufacturing System Design. IFAC-PapersOnLine 2018, 51, 78–83. [Google Scholar] [CrossRef]
- Benderbal, H.H.; Benyoucef, L. A New Hybrid Approach for Machine Layout Design Under Family Product Evolution for Reconfigurable Manufacturing Systems. IFAC-PapersOnLine 2019, 52, 1379–1384. [Google Scholar] [CrossRef]
- Gao, S.; Daaboul, J.; Le Duigou, J. Layout and scheduling optimization problem for a reconfigurable manufacturing system. Int. J. Ind. Eng. Manag. 2021, 12, 165–177. [Google Scholar] [CrossRef]
- Sabioni, R.C.; Daaboul, J.; Le Duigou, J. Concurrent optimisation of modular product and Reconfigurable Manufacturing System configuration: A customer-oriented offer for mass customisation. Int. J. Prod. Res. 2021, 1–17. [Google Scholar] [CrossRef]
- Ghanei, S.; AlGeddawy, T. An Integrated Multi-Period Layout Planning and Scheduling Model for Sustainable Reconfigurable Manufacturing Systems. J. Adv. Manuf. Syst. 2020, 19, 31–64. [Google Scholar] [CrossRef]
- Kurniadi, K.A.; Ryu, K. Development of Multi-Disciplinary Green-BOM to Maintain Sustainability in Reconfigurable Manufacturing Systems. Sustainability 2021, 13, 9533. [Google Scholar] [CrossRef]
- Touzout, F.A.; Benyoucef, L.; Benderbal, H.H.; Dahane, M. A hybrid multi-objective based approach for sustainable process plan generation in a reconfigurable manufacturing environment. In Proceedings of the 2018 IEEE 16th International Conference on Industrial Informatics (INDIN), Porto, Portugal, 18–20 July 2018; pp. 343–348. [Google Scholar]
- Touzout, F.A.; Benyoucef, L. Sustainable multi-unit process plan generation in a reconfigurable manufacturing environment: A comparative study of three hybrid-meta-heuristics. In Proceedings of the 2018 IEEE 23rd International Conference on Emerging Technologies and Factory Automation (ETFA), Turin, Italy, 4–7 September 2018; Volume 1, pp. 661–668. [Google Scholar]
- Khezri, A.; Benderbal, H.H.; Benyoucef, L. A Sustainable Reconfigurable Manufacturing System Designing With Focus On Environmental Hazardous Wastes. In Proceedings of the 2019 24th IEEE International Conference on Emerging Technologies and Factory Automation (ETFA), Zaragoza, Spain, 10–13 September 2019; pp. 317–324. [Google Scholar]
- Lamy, D.; Schulz, J.; Zaeh, M.F. Energy-aware scheduling in reconfigurable multiple path shop floors. Procedia CIRP 2020, 93, 1007–1012. [Google Scholar] [CrossRef]
- Hees, A.; Reinhart, G. Approach for Production Planning in Reconfigurable Manufacturing Systems. Procedia CIRP 2015, 33, 70–75. [Google Scholar] [CrossRef]
- Johannes, C.; Wichmann, M.G.; Spengler, T.S. Energy-oriented production planning with time-dependent energy prices. Procedia CIRP 2019, 80, 245–250. [Google Scholar] [CrossRef]
- Koren, Y.; Gu, X.; Guo, W. Reconfigurable manufacturing systems: Principles, design, and future trends. Front. Mech. Eng. 2018, 13, 121–136. [Google Scholar] [CrossRef] [Green Version]
- Waschneck, B.; Reichstaller, A.; Belzner, L.; Altenmüller, T.; Bauernhansl, T.; Knapp, A.; Kyek, A. Optimization of global production scheduling with deep reinforcement learning. Procedia CIRP 2018, 72, 1264–1269. [Google Scholar] [CrossRef]
- Yang, S.; Xu, Z. Intelligent scheduling and reconfiguration via deep reinforcement learning in smart manufacturing. Int. J. Prod. Res. 2021, 1–18. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).