Multiple Analytical Models to Evaluate the Impact of Carbon Nanotubes on the Electrical Resistivity and Compressive Strength of the Cement Paste
Abstract
:1. Introduction
2. Research Significance
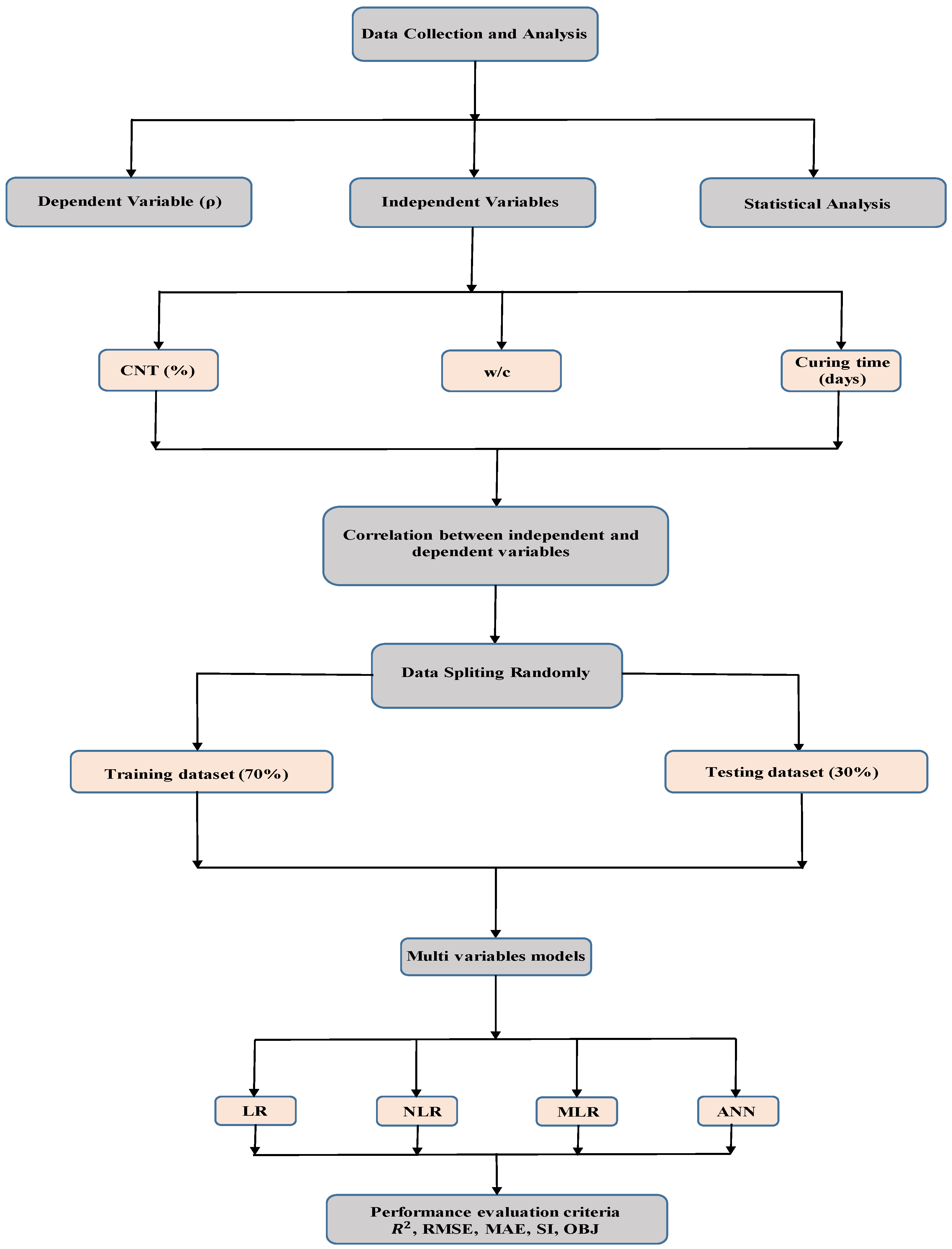
3. Methodology
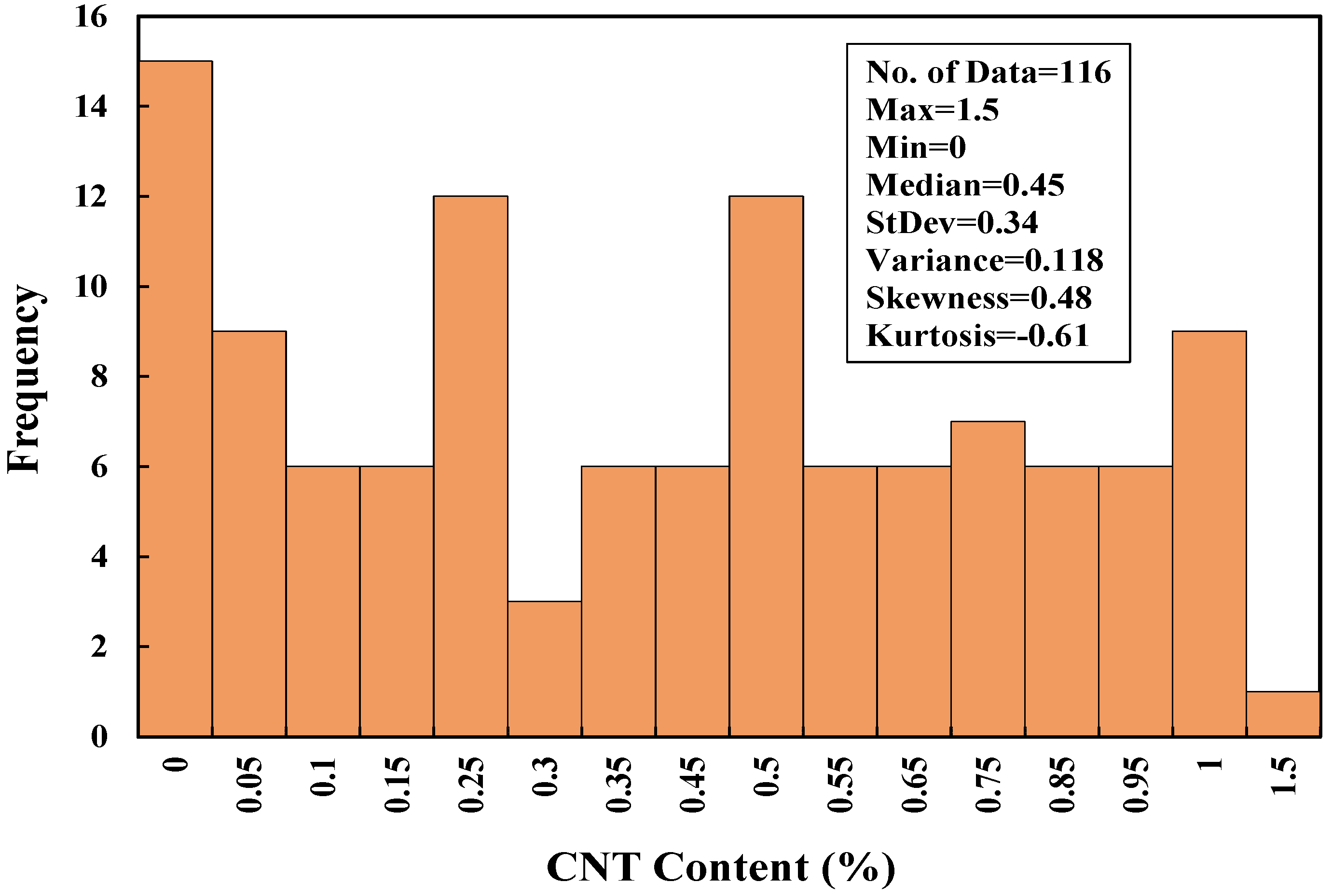
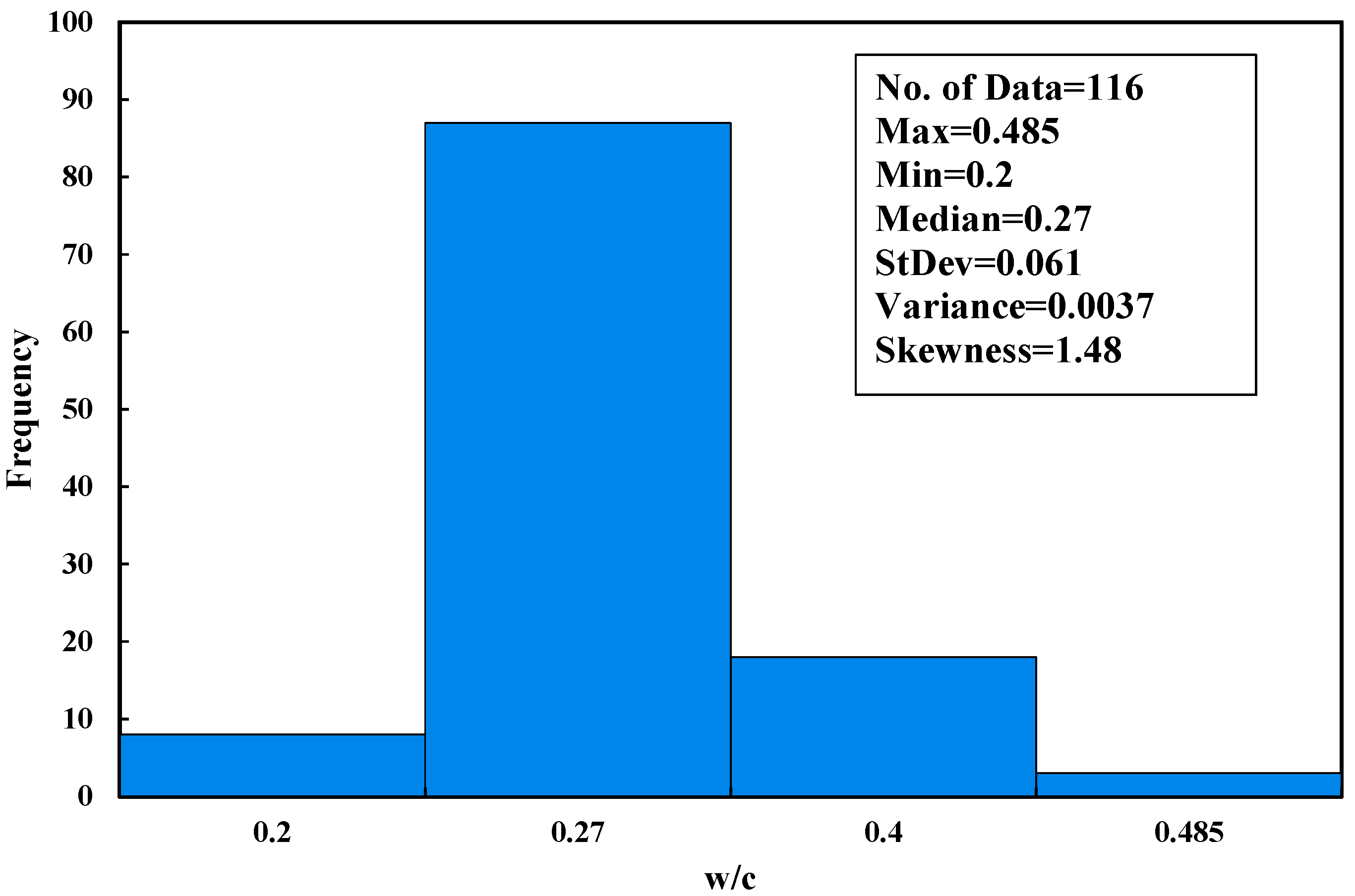
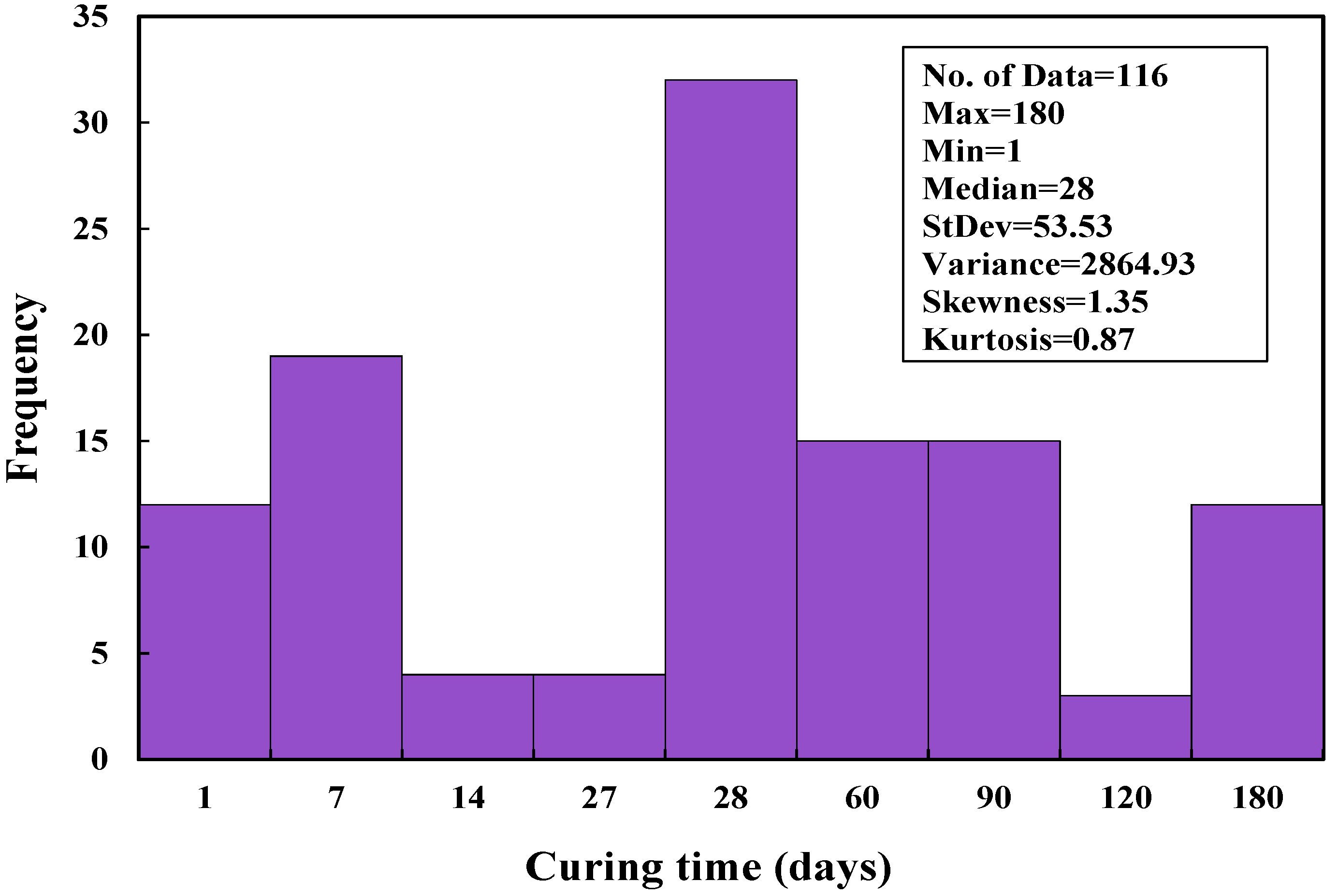
3.1. Statistical Evaluation
- (i)
- Carbon Nanotubes (CNTs)
- (ii)
- Water to Cement Ratio (w/c)
- (iii)
- Curing Time (t)
- (iv)
- Electrical Resistivity (ρ)
3.2. Modeling
3.2.1. Linear Regression Model
3.2.2. Multi Logistic Regression Model
3.2.3. Nonlinear Regression Model
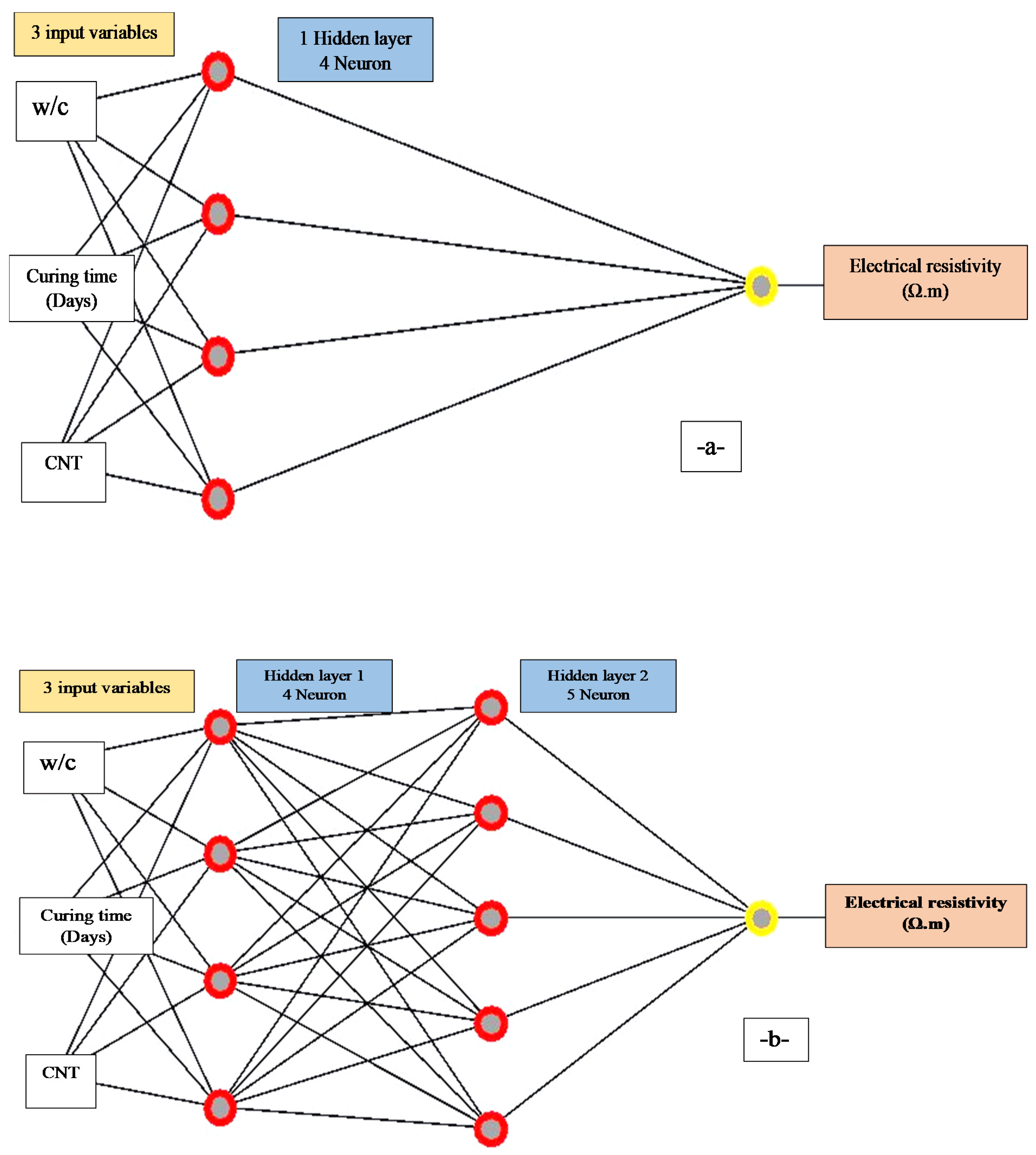
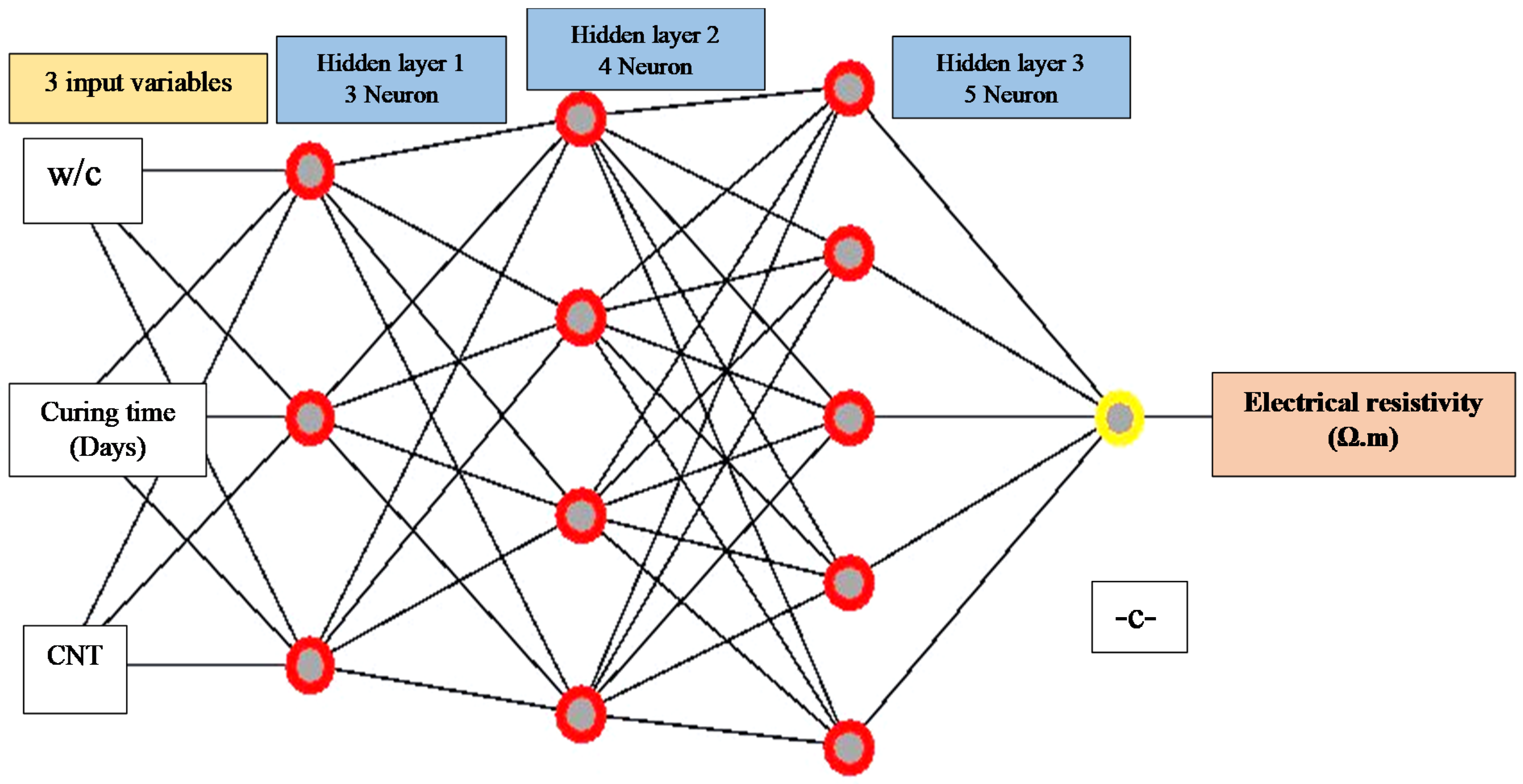
3.2.4. Artificial Neural Network
3.3. Assessment Criteria for Models
4. Analysis and Output
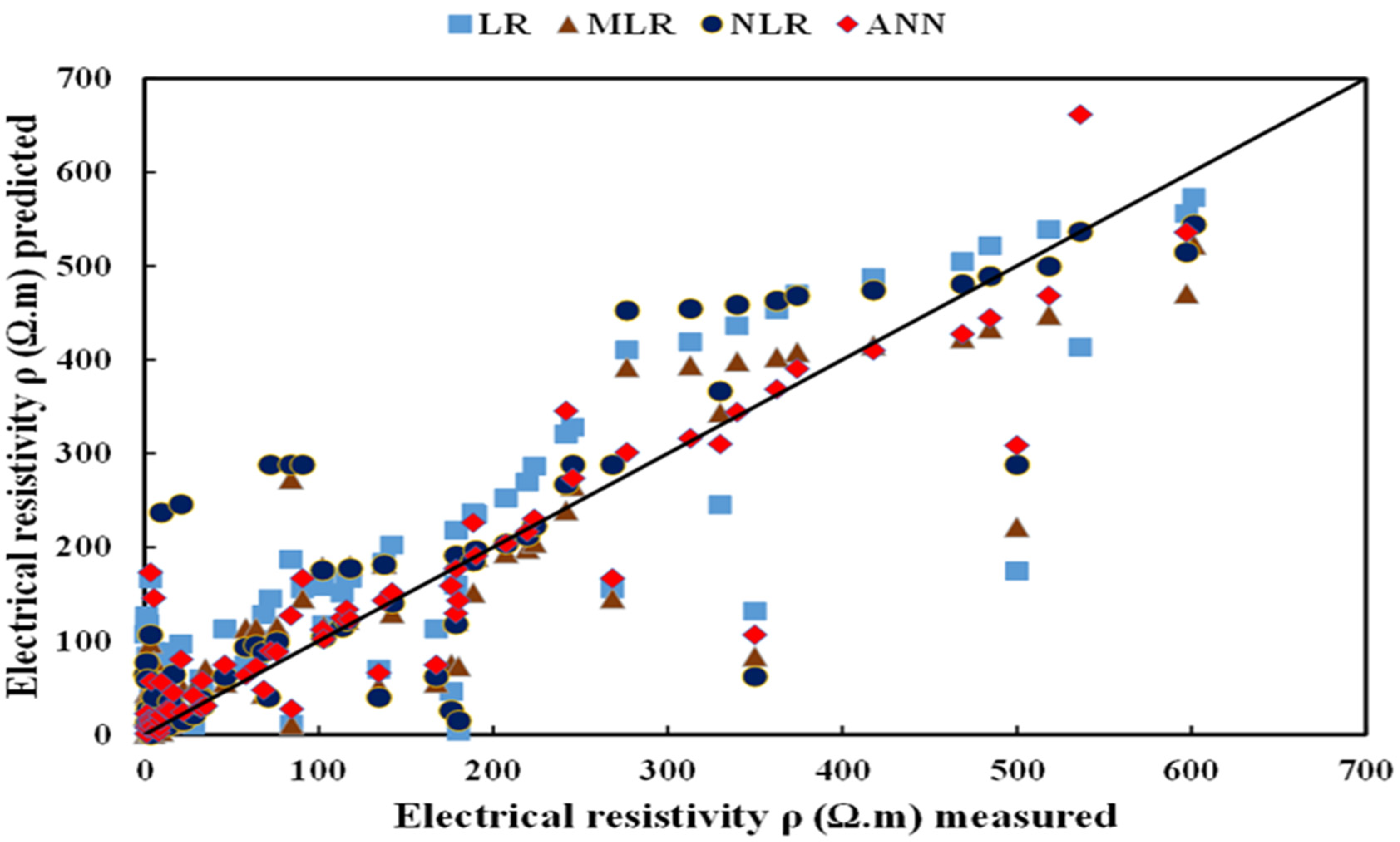
4.1. Predicted and Measured Electrical Resistivity Relationships
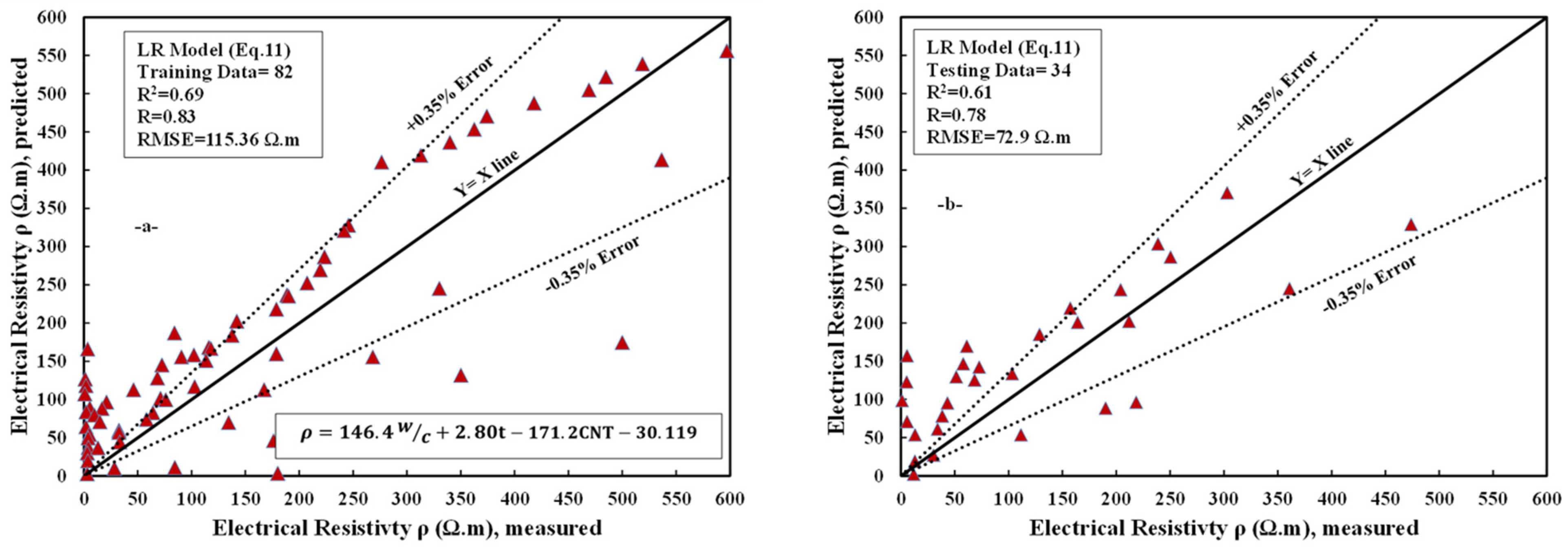
4.1.1. Linear Regression Model
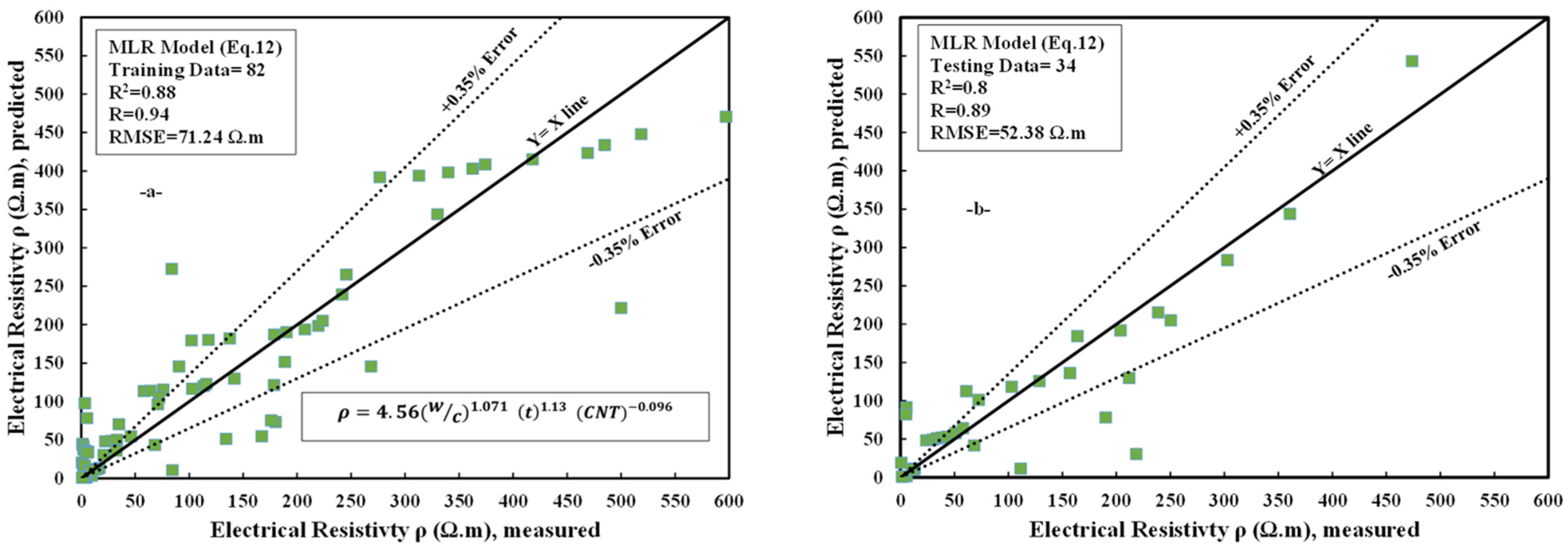
4.1.2. Multi Logistic Regression Model
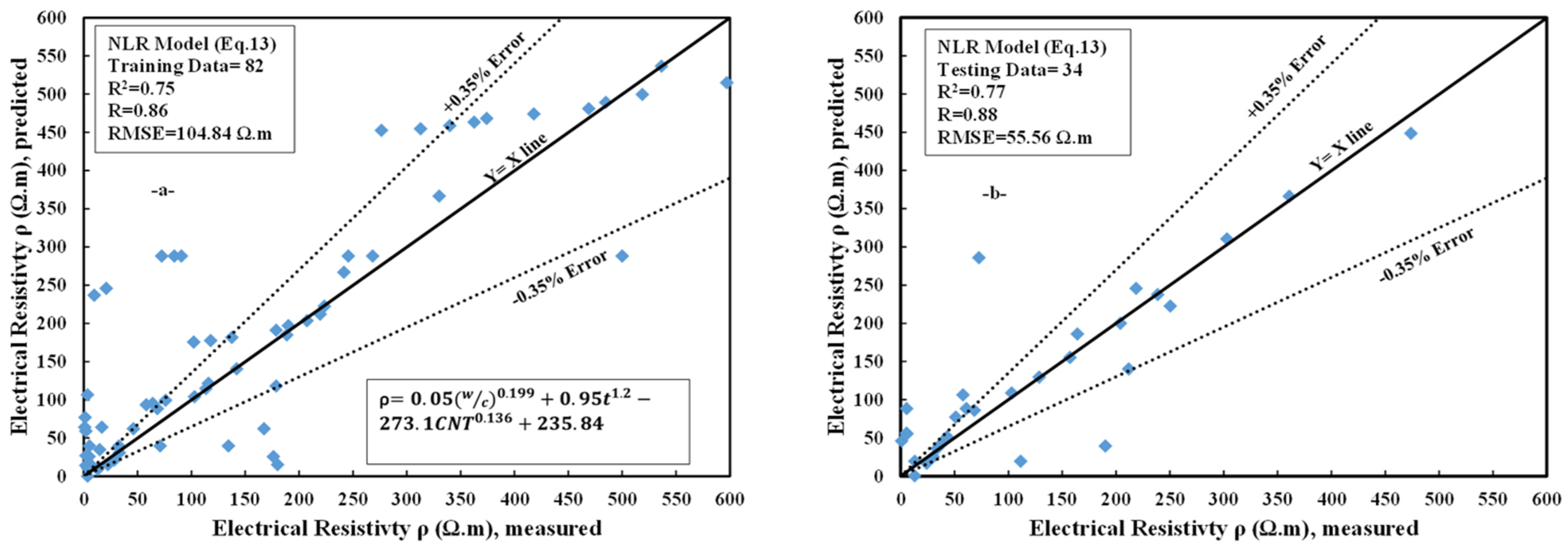
4.1.3. Nonlinear Regression Model
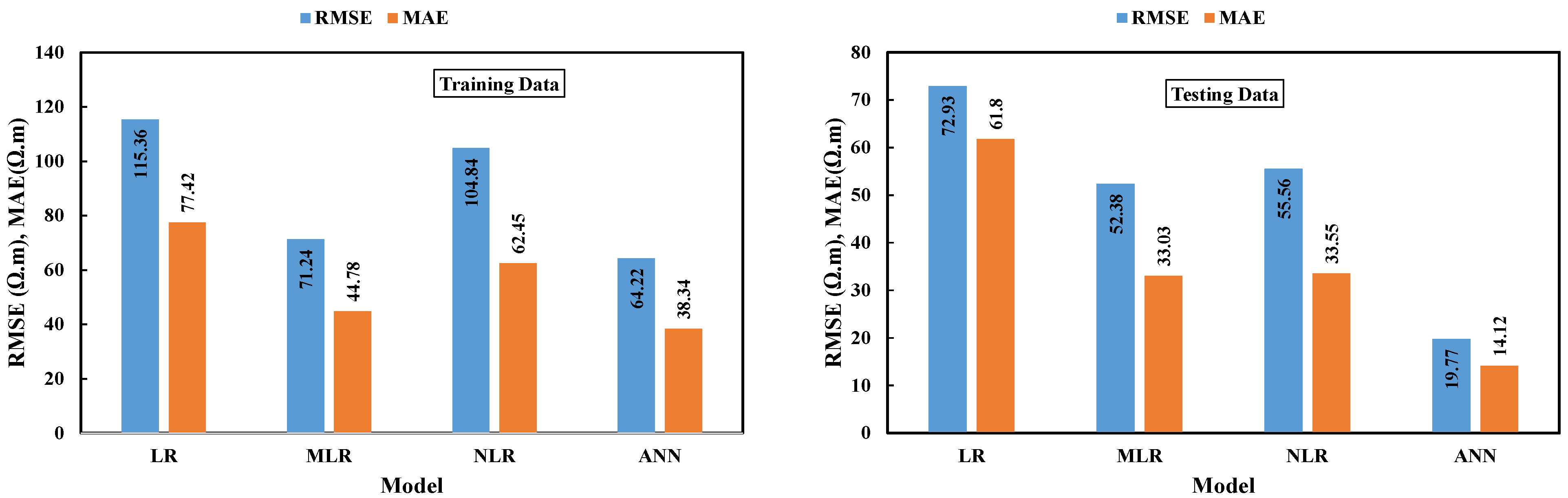
4.1.4. Artificial Neural Network Model
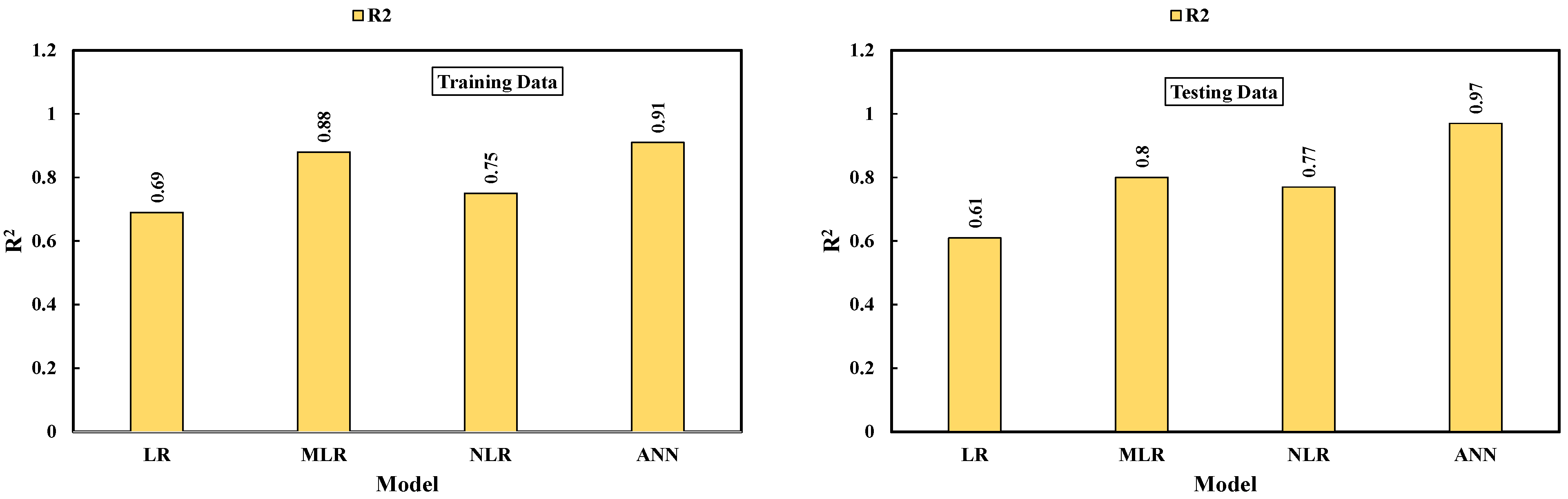
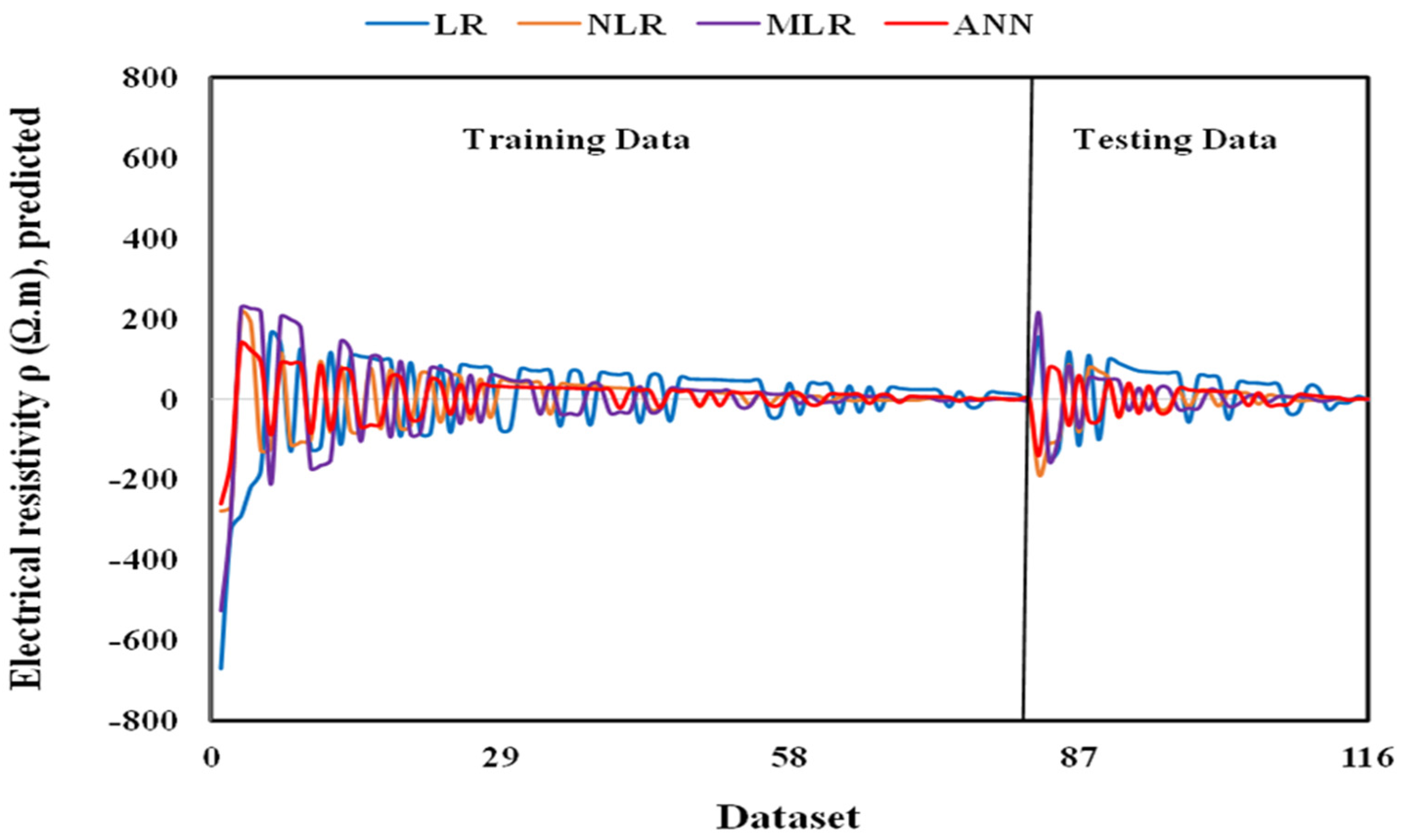
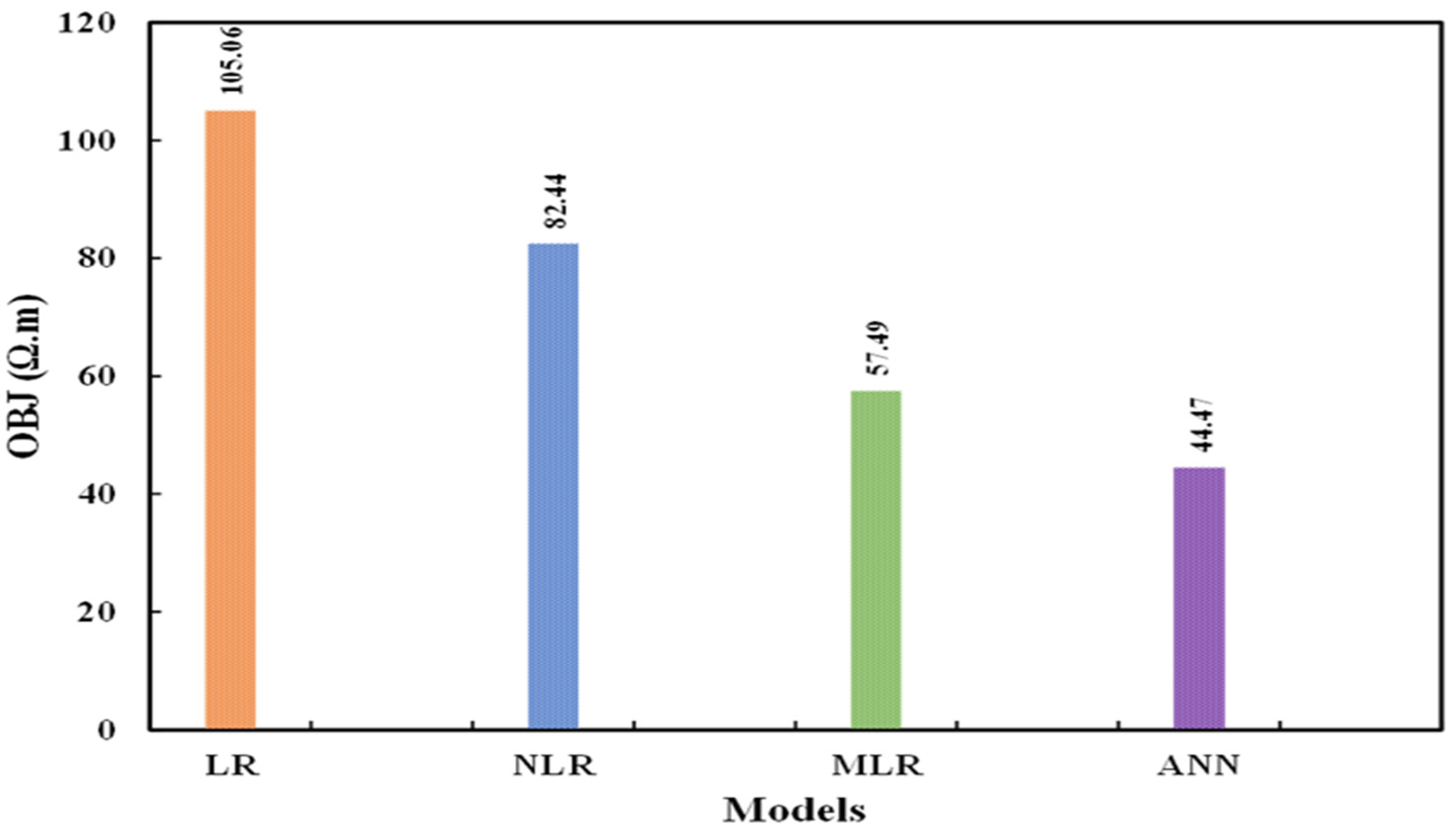
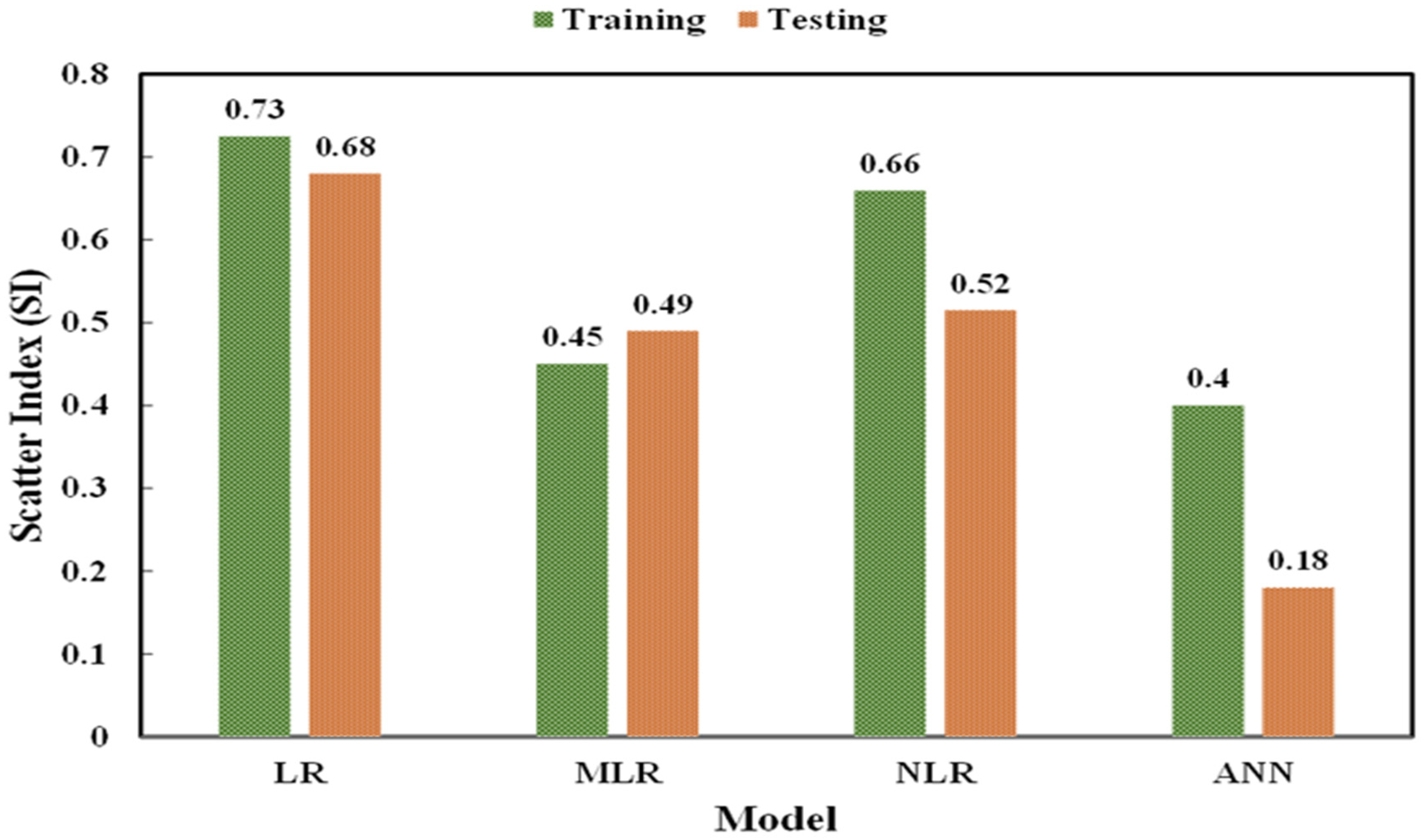
4.1.5. Comparison between Different Models
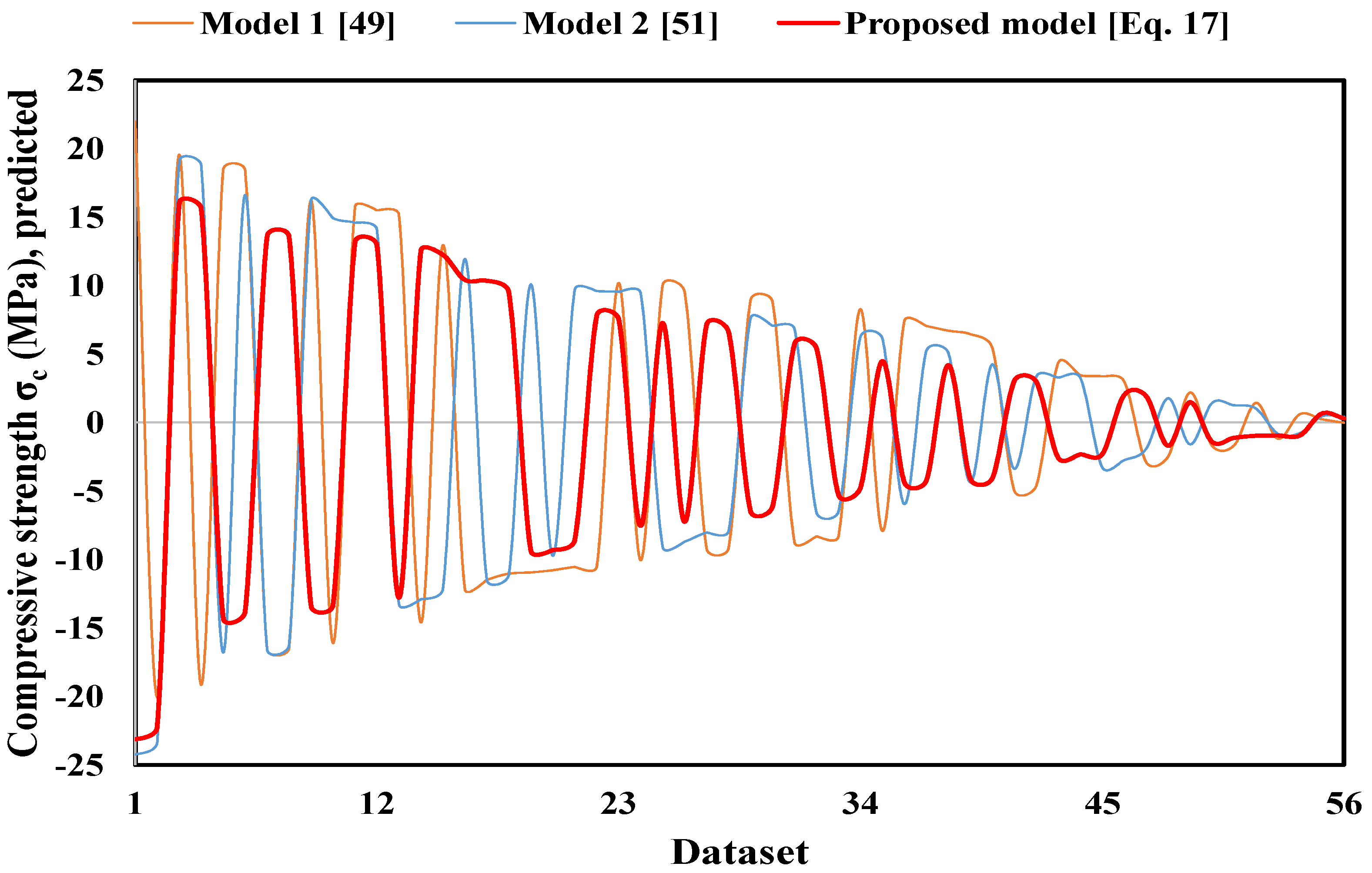
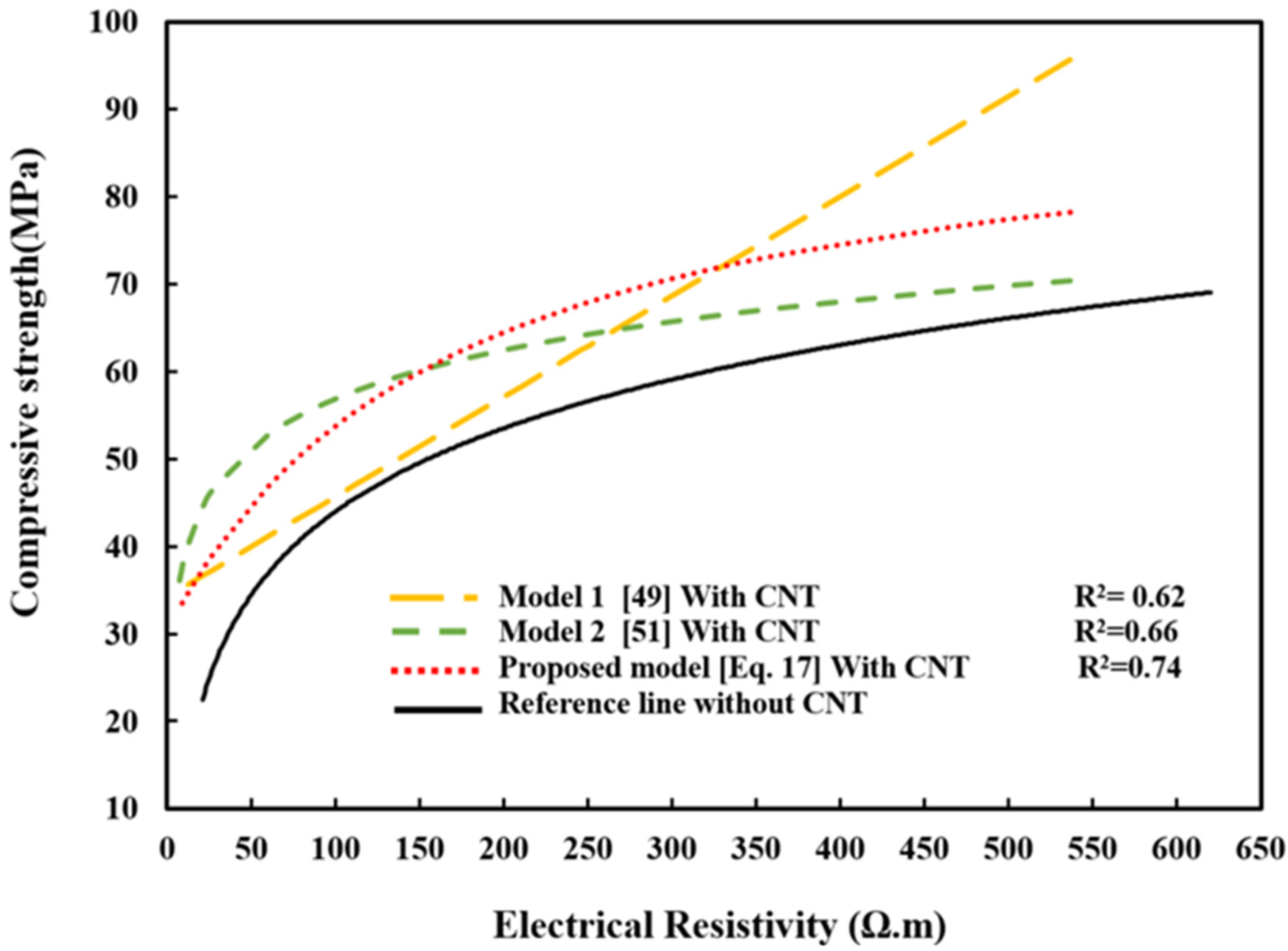
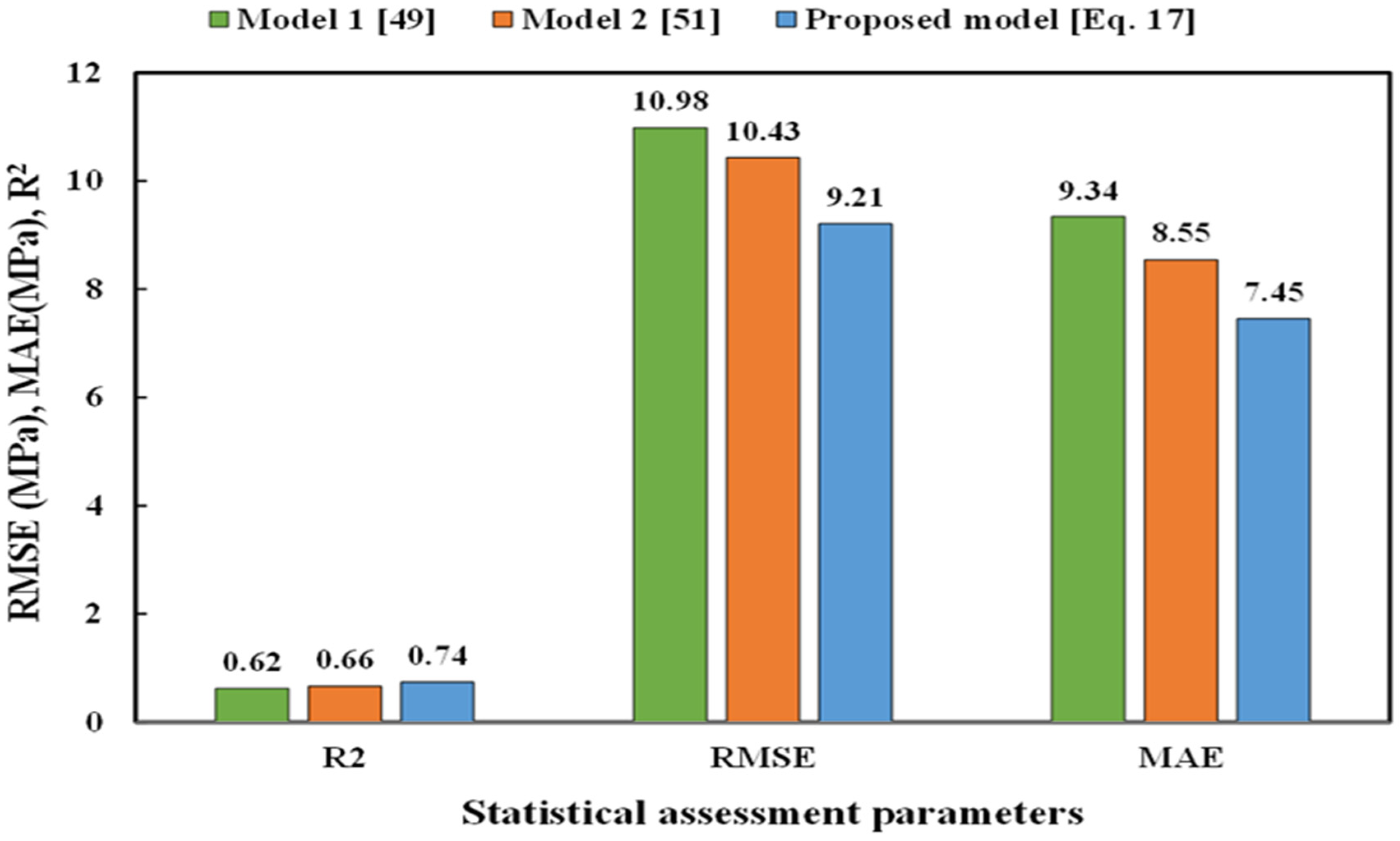
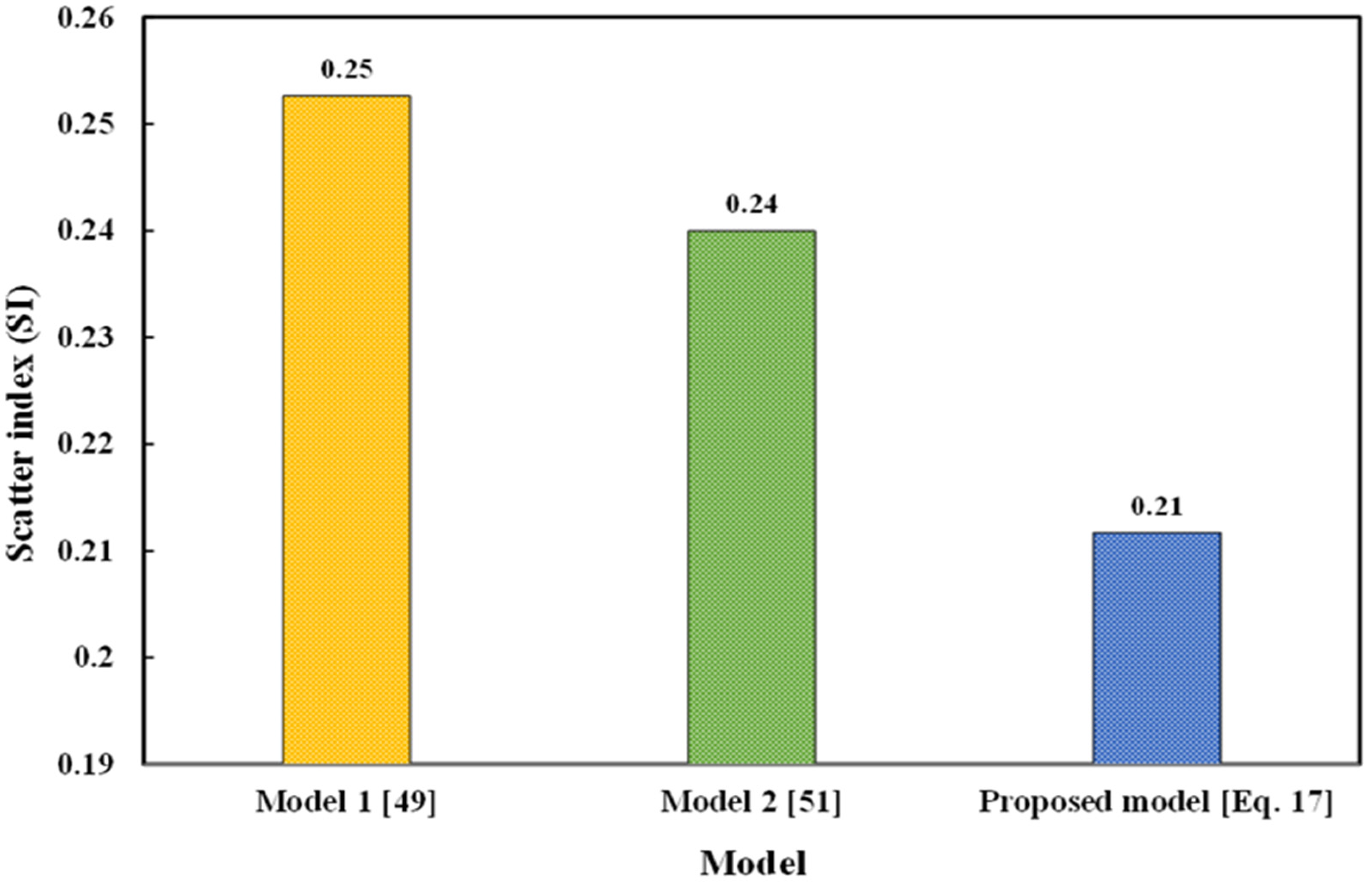
4.2. Correlation between Compressive Strength and Electrical Resistivity Based on the Proposed Model and Models from the Literature
5. Sensitivity Examination
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Effect of Carbon Nanotubes on Cement Paste Resistivity at Different w/c Ratios and Different Curing Age
| No. of Data | References | w/c | Curing Time (day) | CNT % | Electrical Resistivity (Ω.m) |
|---|---|---|---|---|---|
| 1 | [4] | 0.2 | 28 | 0 | 72.33 |
| 2 | 0.2 | 28 | 0.1 | 68.39 | |
| 3 | 0.2 | 28 | 0.5 | 32.54 | |
| 4 | 0.2 | 28 | 1 | 6.42 | |
| 5 | [28] | 0.2 | 27 | 0 | 72.53 |
| 6 | 0.2 | 27 | 0.1 | 68.39 | |
| 7 | 0.2 | 27 | 0.5 | 32.54 | |
| 8 | 0.2 | 27 | 1 | 6 | |
| 9 | [30] | 0.27 | 1 | 0 | 9.67 |
| 10 | 0.27 | 7 | 0 | 20.92 | |
| 11 | 0.27 | 28 | 0 | 90.65 | |
| 12 | 0.27 | 60 | 0 | 330 | |
| 13 | 0.27 | 90 | 0 | 620.22 | |
| 14 | 0.27 | 180 | 0 | 1252.23 | |
| 15 | 0.27 | 1 | 0.05 | 5.64 | |
| 16 | 0.27 | 7 | 0.05 | 16.75 | |
| 17 | 0.27 | 28 | 0.05 | 57.8 | |
| 18 | 0.27 | 60 | 0.05 | 188.57 | |
| 19 | 0.27 | 90 | 0.05 | 241.61 | |
| 20 | 0.27 | 180 | 0.05 | 601.56 | |
| 21 | 0.27 | 1 | 0.15 | 4.97 | |
| 22 | 0.27 | 7 | 0.15 | 14.78 | |
| 23 | 0.27 | 28 | 0.15 | 51.17 | |
| 24 | 0.27 | 60 | 0.15 | 157.14 | |
| 25 | 0.27 | 90 | 0.15 | 238.66 | |
| 26 | 0.27 | 180 | 0.15 | 597.14 | |
| 27 | 0.27 | 1 | 0.25 | 4.15 | |
| 28 | 0.27 | 7 | 0.25 | 13.01 | |
| 29 | 0.27 | 28 | 0.25 | 46.11 | |
| 30 | 0.27 | 60 | 0.25 | 141.92 | |
| 31 | 0.27 | 90 | 0.25 | 223.44 | |
| 32 | 0.27 | 180 | 0.25 | 518.57 | |
| 33 | 0.27 | 1 | 0.35 | 3.59 | |
| 34 | 0.27 | 7 | 0.35 | 12.95 | |
| 35 | 0.27 | 28 | 0.35 | 43.12 | |
| 36 | 0.27 | 60 | 0.35 | 128.66 | |
| 37 | 0.27 | 90 | 0.35 | 219.51 | |
| 38 | 0.27 | 180 | 0.35 | 484.69 | |
| 39 | 0.27 | 1 | 0.45 | 2.94 | |
| 40 | 0.27 | 7 | 0.45 | 12.87 | |
| 41 | 0.27 | 28 | 0.45 | 38.21 | |
| 42 | 0.27 | 60 | 0.45 | 115.89 | |
| 43 | 0.27 | 90 | 0.45 | 207.23 | |
| 44 | 0.27 | 180 | 0.45 | 468.97 | |
| 45 | 0.27 | 1 | 0.55 | 2.87 | |
| 46 | 0.27 | 7 | 0.55 | 11.79 | |
| 47 | 0.27 | 28 | 0.55 | 33.93 | |
| 48 | 0.27 | 60 | 0.55 | 113.44 | |
| 49 | 0.27 | 90 | 0.55 | 190.04 | |
| 50 | 0.27 | 180 | 0.55 | 417.9 | |
| 51 | 0.27 | 1 | 0.65 | 2.06 | |
| 52 | 0.27 | 7 | 0.65 | 10.7 | |
| 53 | 0.27 | 28 | 0.65 | 33.17 | |
| 54 | 0.27 | 60 | 0.65 | 103.13 | |
| 55 | 0.27 | 90 | 0.65 | 178.75 | |
| 56 | 0.27 | 180 | 0.65 | 374.2 | |
| 57 | 0.27 | 1 | 0.75 | 1.57 | |
| 58 | 0.27 | 7 | 0.75 | 9.7 | |
| 59 | 0.27 | 28 | 0.75 | 30.08 | |
| 60 | 0.27 | 60 | 0.75 | 102.83 | |
| 61 | 0.27 | 90 | 0.75 | 164.02 | |
| 62 | 0.27 | 180 | 0.75 | 362.41 | |
| 63 | 0.27 | 1 | 0.85 | 1.42 | |
| 64 | 0.27 | 7 | 0.85 | 9.3 | |
| 65 | 0.27 | 28 | 0.85 | 28.24 | |
| 66 | 0.27 | 60 | 0.85 | 75.97 | |
| 67 | 0.27 | 90 | 0.85 | 137.5 | |
| 68 | 0.27 | 180 | 0.85 | 339.82 | |
| 69 | 0.27 | 1 | 0.95 | 1.37 | |
| 70 | 0.27 | 7 | 0.95 | 8.72 | |
| 71 | 0.27 | 28 | 0.95 | 24.01 | |
| 72 | 0.27 | 60 | 0.95 | 64.13 | |
| 73 | 0.27 | 90 | 0.95 | 117.86 | |
| 74 | 0.27 | 180 | 0.95 | 312.81 | |
| 75 | 0.27 | 1 | 1 | 1.2 | |
| 76 | 0.27 | 7 | 1 | 8.23 | |
| 77 | 0.27 | 28 | 1 | 22.25 | |
| 78 | 0.27 | 60 | 1 | 58.19 | |
| 79 | 0.27 | 90 | 1 | 102.14 | |
| 80 | 0.27 | 180 | 1 | 276.47 | |
| 81 | [31] | 0.27 | 7 | 0 | 218.5 |
| 82 | 0.27 | 28 | 0 | 268.3 | |
| 83 | 0.27 | 60 | 0 | 360.8 | |
| 84 | 0.27 | 90 | 0 | 473.8 | |
| 85 | 0.27 | 120 | 0 | 536.4 | |
| 86 | 0.27 | 7 | 0.25 | 111.4 | |
| 87 | 0.27 | 28 | 0.25 | 167.3 | |
| 88 | 0.27 | 60 | 0.25 | 211.7 | |
| 89 | 0.27 | 90 | 0.25 | 250.4 | |
| 90 | 0.27 | 120 | 0.25 | 302.9 | |
| 91 | 0.27 | 7 | 0.5 | 84.5 | |
| 92 | 0.27 | 28 | 0.5 | 134.3 | |
| 93 | 0.27 | 60 | 0.5 | 178.6 | |
| 94 | 0.27 | 90 | 0.5 | 203.9 | |
| 95 | 0.27 | 120 | 0.5 | 245.6 | |
| 96 | [32] | 0.4 | 7 | 0.05 | 0.798 |
| 97 | 0.4 | 14 | 0.05 | 1.225 | |
| 98 | 0.4 | 28 | 0.05 | 3.46 | |
| 99 | 0.4 | 7 | 0.1 | 0.897 | |
| 100 | 0.4 | 14 | 0.1 | 1.84 | |
| 101 | 0.4 | 28 | 0.1 | 5.52 | |
| 102 | 0.4 | 7 | 0.3 | 1.9 | |
| 103 | 0.4 | 14 | 0.3 | 2.18 | |
| 104 | 0.4 | 28 | 0.3 | 5.22 | |
| 105 | 0.4 | 7 | 0.5 | 3.29 | |
| 106 | 0.4 | 14 | 0.5 | 3.9 | |
| 107 | 0.4 | 28 | 0.5 | 5.34 | |
| 108 | [33] | 0.485 | 28 | 0 | 84 |
| 109 | 0.485 | 28 | 0.1 | 61 | |
| 110 | 0.485 | 28 | 0.5 | 71 | |
| 111 | [36] | 0.4 | 28 | 0 | 500 |
| 112 | 0.4 | 28 | 0.25 | 350 | |
| 113 | 0.4 | 28 | 0.5 | 190 | |
| 114 | 0.4 | 28 | 0.75 | 176 | |
| 115 | 0.4 | 28 | 1 | 180 | |
| 116 | 0.4 | 28 | 1.5 | 35 | |
| Remarks | Ranged between 0.2–0.485 | varied between 1–180 (days) | Ranged between 0–1.5 (%) | varied between 0.798–1252.23 (Ω.m) |
| No. Data | References | Electrical Resistivity (Ω.m) | Compressive (MPa) |
|---|---|---|---|
| 1 | [32] | 536.4 | 73.7 |
| 2 | 473.8 | 70.1 | |
| 3 | 360.8 | 65.37 | |
| 4 | 302.9 | 76.85 | |
| 5 | 268.3 | 58.51 | |
| 6 | 250.4 | 72.125 | |
| 7 | 245.6 | 76.96 | |
| 8 | 211.7 | 69.425 | |
| 9 | 203.9 | 74.04 | |
| 10 | 196.48 | 68.22 | |
| 11 | 190.04 | 64.74 | |
| 12 | 178.6 | 71.225 | |
| 13 | 167.3 | 62.56 | |
| 14 | 134.3 | 65.71 | |
| 15 | 111.4 | 48.16 | |
| 16 | 105.978 | 56.88 | |
| 17 | 90.65 | 49.23 | |
| 18 | 84.5 | 52.21 | |
| 19 | [35] | 20.92 | 27.66 |
| 20 | 11.79 | 47.72 | |
| 21 | 1.57 | 32.2 | |
| 22 | 11.87 | 47.72 | |
| 23 | 33.93 | 59.53 | |
| 24 | 190.04 | 64.74 | |
| 25 | [33] | 84 | 31.7 |
| 26 | 61 | 33.8 | |
| 27 | 71 | 35.3 | |
| 28 | [53] | 2.09 | 18.73 |
| 29 | 8.29 | 45.95 | |
| 30 | 2.41 | 25.68 | |
| 31 | 5.27 | 36.49 | |
| 32 | 3.73 | 31.27 | |
| 33 | 1.79 | 14.86 | |
| 34 | [54] | 3.04 | 45.6 |
| 35 | 2.94 | 45.1 | |
| 36 | 2.88 | 44.6 | |
| 37 | 3.74 | 54.7 | |
| 38 | 3.74 | 53.8 | |
| 39 | 7.08 | 37.51 | |
| 40 | 7.06 | 25.48 | |
| 41 | 5.63 | 19.7 | |
| 42 | [55] | 71 | 35.3 |
| 43 | 61 | 33.8 | |
| 44 | 60.73 | 49.49 | |
| 45 | 28.04 | 37.19 | |
| 46 | [52] | 6.99 | 35.03 |
| 47 | 6.92 | 34.39 | |
| 48 | 6.81 | 31.99 | |
| 49 | 6.54 | 33.53 | |
| 50 | 6.45 | 30.6 | |
| 51 | 6.23 | 29.47 | |
| 52 | 6.18 | 24.9 | |
| 53 | 6.05 | 28.2 | |
| 54 | 5.98 | 26.62 | |
| 55 | 5.79 | 19.38 | |
| 56 | 5.71 | 21.92 | |
| Remarks | Electrical resistivity ranged between (1.57–536.4) Ω.m | Compressive strength varied between (14.86–76.86) MPa |
References
- Bartos, P.J. Nanotechnology in Construction: A Roadmap for Development, in Nanotechnology in Construction 3; Springer: Berlin/Heidelberg, Germany, 2009; pp. 15–26. Available online: https://link.springer.com/chapter/10.1007/978-3-642-00980-8_2 (accessed on 5 November 2021).
- Bentur, A.; Mindess, S. Fibre Reinforced Cementitious Composites. 2006. Available online: https://books.google.co.jp/books?hl=zh-CN&lr=&id=z0NZDwAAQBAJ&oi=fnd&pg=PP1&dq=Fibre+reinforced+cementitious+composites.&ots=bhtJopb-wN&sig=5v3vLY-bMBp8-nLtoQblgCO76fo#v=onepage&q=Fibre%20reinforced%20cementitious%20composites.&f=false (accessed on 5 November 2021).
- Dong, S.; Han, B.; Qu, J.; Li, Z.; Han, L.; Yu, X. Electrically conductive behaviors and mechanisms of short-cut super-fine stainless wire reinforced reactive powder concrete. Cem. Concr. Compos. 2016, 72, 48–65. [Google Scholar] [CrossRef] [Green Version]
- Jiang, S.; Zhou, D.; Zhang, L.; Ouyang, J.; Yu, X.; Cui, X.; Han, B. Comparison of compressive strength and electrical resistivity of cementitious composites with different nano-and micro-fillers. Arch. Civ. Mech. Eng. 2018, 18, 60–68. [Google Scholar] [CrossRef]
- Raki, L.; Beaudoin, J.; Alizadeh, R.; Makar, J.; Sato, T. Cement and concrete nanoscience and nanotechnology. Materials 2010, 3, 918–942. [Google Scholar] [CrossRef] [Green Version]
- Tuan, C.Y.; Yehia, S.A. Implementation of Conductive Concrete Overlay for Bridge Deck Deicing at Roca, Nebraska. 2004. Available online: https://digitalcommons.unomaha.edu/civilengfacproc/3/ (accessed on 5 November 2021).
- Zhang, L.; Han, B.; Ouyang, J.; Yu, X.; Sun, S.; Ou, J. Multifunctionality of cement based composite with electrostatic self-assembled CNT/NCB composite filler. Arch. Civ. Mech. Eng. 2017, 17, 354–364. [Google Scholar] [CrossRef]
- Han, B.; Ding, S.; Yu, X. Intrinsic self-sensing concrete and structures: A review. Measurement 2015, 59, 110–128. [Google Scholar] [CrossRef]
- Loh, K.J.; Gonzalez, J. Cementitious Composites Engineered with Embedded Carbon Nanotube Thin Films for Enhanced Sensing Performance. 2015. Available online: https://iopscience.iop.org/article/10.1088/1742-6596/628/1/012042/meta (accessed on 5 November 2021).
- Materazzi, A.L.; Ubertini, F.; D’Alessandro, A. Carbon nanotube cement-based transducers for dynamic sensing of strain. Cem. Concr. Compos. 2013, 37, 2–11. [Google Scholar] [CrossRef]
- Boschetti-de-Fierro, A.; Pardey, R.; Savino, V.; Müller, A.J. Piezoresistive behavior of epoxy matrix-carbon fiber composites with different reinforcement arrangements. J. Appl. Polym. Sci. 2009, 111, 2851–2858. [Google Scholar] [CrossRef]
- Chung, D. Cement reinforced with short carbon fibers: A multifunctional material. Compos. Part B: Eng. 2000, 31, 511–526. [Google Scholar] [CrossRef]
- Vipulanandan, C.; Prashanth, P. Impedance spectroscopy characterization of a piezoresistive structural polymer composite bulk sensor. J. Test. Eval. 2013, 41, 898–904. [Google Scholar] [CrossRef]
- Vipulanandan, C.; Sett, K. Development and characterization of piezoresistive smart structural materials. Eng. Constr. Oper. Challenging Environ. Earth Space 2004, 2004, 656–663. [Google Scholar]
- Vipulanandan, C.; Mohammed, A. Rheological properties of piezoresistive smart cement slurry modified with iron-oxide nanoparticles for oil-well applications. J. Test. Eval. 2017, 45, 2050–2060. [Google Scholar] [CrossRef]
- Ubertini, F.; Laflamme, S.; D’Alessandro, A. Smart cement paste with carbon nanotubes. In Innovative Developments of Advanced Multifunctional Nanocomposites in Civil and Structural Engineering; Elsevier: Amsterdam, The Netherlands, 2016; pp. 97–120. Available online: https://www.sciencedirect.com/science/article/pii/B9781782423263000063 (accessed on 5 November 2021).
- Vipulanandan, C.; Mohammed, A. Smart cement modified with iron oxide nanoparticles to enhance the piezoresistive behavior and compressive strength for oil well applications. Smart Mater. Struct. 2015, 24, 125020. [Google Scholar] [CrossRef]
- Zolotarev, A.A.; Lushin, I.A.; Charykov, A.N.; Semenov, N.K.; Namazbaev, I.V.; Keskinov, A.V.; Kritchenkov, A.S. Impact resistance of cement and gypsum plaster nanomodified by water-soluble fullerenols. Ind. Eng. Chem. Res. 2013, 52, 14583–14591. [Google Scholar] [CrossRef]
- Bawa, R.; Bawa, S.R.; Maebiuset, S.B.; Flynn, T.; Wei, C. Protecting new ideas and inventions in nanomedicine with patents. Nanomed. Nanotechnol. Biol. Med. 2005, 1, 150–158. [Google Scholar] [CrossRef] [PubMed]
- Rajabipour, F.; Weiss, J. Electrical conductivity of drying cement paste. Mater. Struct. 2007, 40, 1143–1160. [Google Scholar] [CrossRef]
- Chiarello, M.; Zinno, R. Electrical conductivity of self-monitoring CFRC. Cem. Concr. Compos. 2005, 27, 463–469. [Google Scholar] [CrossRef]
- Chen, B.; Liu, J.; Wu, K. Electrical responses of carbon fiber reinforced cementitious composites to monotonic and cyclic loading. Cem. Concr. Res. 2005, 35, 2183–2191. [Google Scholar] [CrossRef]
- Kim, G.M.; Yang, B.J.; Cho, K.J.; Kim, E.M.; Lee, H.K. Influences of CNT dispersion and pore characteristics on the electrical performance of cementitious composites. Compos. Struct. 2017, 164, 32–42. [Google Scholar] [CrossRef]
- Wen, S.; Chung, D.D.L. Partial replacement of carbon fiber by carbon black in multifunctional cement–matrix composites. Carbon 2007, 45, 505–513. [Google Scholar] [CrossRef]
- Chung, D.D.L. Piezoresistive Cement-Based Materials for Strain Sensing. J. Intell. Mater. Syst. Struct. 2016, 13, 599–609. [Google Scholar] [CrossRef]
- Gao, X.; Wang, H.; Li, S.; Lu, L.; Mo, Y. Piezoresistive effect of carbon nanofiber concrete exposed to different environmental conditions. Rev. Romana Mater.-Rom. J. Mater. 2015, 45, 341–347. [Google Scholar]
- Tumidajski, P.J. Electrical conductivity of Portland cement mortars. Cem. Concr. Res. 1996, 26, 529–534. [Google Scholar] [CrossRef]
- Hong, S.; Myung, S. A flexible approach to mobility. Nat. Nanotechnol. 2007, 2, 207–208. [Google Scholar] [CrossRef] [PubMed]
- Obitayo, W.; Liu, T. A review: Carbon nanotube-based piezoresistive strain sensors. J. Sens. 2012, 2012. [Google Scholar] [CrossRef] [Green Version]
- Sasmal, S.; Ravivarman, N.; Sindu, B.S.; Vigneshet, K. Electrical conductivity and piezo-resistive characteristics of CNT and CNF incorporated cementitious nanocomposites under static and dynamic loading. Compos. Part A Appl. Sci. Manuf. 2017, 100, 227–243. [Google Scholar] [CrossRef]
- Treacy, M.J.; Ebbesen, T.W.; Gibson, J.M. Exceptionally high Young’s modulus observed for individual carbon nanotubes. Nature 1996, 381, 678–680. [Google Scholar] [CrossRef]
- Siad, H.; Lachemi, M.; Sahmaran, M.; Mesbah, H.A.; Mesbah, K.A. Advanced engineered cementitious composites with combined self-sensing and self-healing functionalities. Constr. Build. Mater. 2018, 176, 313–322. [Google Scholar] [CrossRef]
- Konsta-Gdoutos, M.S.; Batis, G.; Danoglidis, P.A.; Zacharopoulou, A.K.; Zacharopoulou, E.K.; Falara, M.G.; Shah, S.P. Effect of CNT and CNF loading and count on the corrosion resistance, conductivity and mechanical properties of nanomodified OPC mortars. Constr. Build. Mater. 2017, 147, 48–57. [Google Scholar] [CrossRef]
- Zhang, W.; Ouyang, J.; Ruan, Y.; Zheng, Q.; Wang, J.; Yu, X.; Han, B. Effect of mix proportion and processing method on the mechanical and electrical properties of cementitious composites with nano/fiber fillers. Mater. Res. Express. 2018, 5, 015706. [Google Scholar] [CrossRef]
- Al-Dahawi, A.; Sarwary, M.H.; Öztürk, O.; Yıldırım, G.; Akın, A.; Şahmaran, M.; Lachemi, M. Electrical percolation threshold of cementitious composites possessing self-sensing functionality incorporating different carbon-based materials. Smart Mater. Struct. 2016, 25, 105005. [Google Scholar] [CrossRef]
- D’Alessandro, A.; Rallini, M.; Ubertini, F.; Materazzi, A.L.; Kenny, J.M. Investigations on scalable fabrication procedures for self-sensing carbon nanotube cement-matrix composites for SHM applications. Cem. Concr. Compos. 2016, 65, 200–213. [Google Scholar] [CrossRef]
- McCarter, W.J. Monitoring the influence of water and ionic ingress on cover-zone concrete subjected to repeated absorption. Cem. Concr. Aggreg. 1996, 18, 55–63. [Google Scholar]
- Vipulanandan, C.; Heidari, M.; Qu, Q.; Farzam, H.; Pappas, J.M. Behavior of Piezoresistive Smart Cement Contaminated with oil Based Drilling mud. In Offshore Technology Conference. 2014. Available online: https://onepetro.org/OTCONF/proceedings-abstract/14OTC/3-14OTC/D031S030R007/172097 (accessed on 5 November 2021).
- Wei, X.; Xiao, L.; Li, Z. Electrical measurement to assess hydration process and the porosity formation. J. Wuhan Univ. Technol.-Mater. Sci. Ed. 2008, 23, 761–766. [Google Scholar] [CrossRef]
- McCarter, W.J.; Starrs, G.; Chrisp, T.M. Electrical conductivity, diffusion, and permeability of Portland cement-based mortars. Cem. Concr. Res. 2000, 30, 1395–1400. [Google Scholar] [CrossRef]
- Vinotha, G.; Sundar, T.V.; Amuthalakshmi, D.; Vivek, M. Two new molecular preprocessing schemes for machine learning and their evaluation using some DT algorithms. AIP Conf. Proc. 2019, 2117. [Google Scholar] [CrossRef]
- Qadir, W.; Ghafor, K.; Mohammed, A. Characterizing and modeling the mechanical properties of the cement mortar modified with fly ash for various water-to-cement ratios and curing times. Adv. Civ. Eng. 2019, 2019. [Google Scholar] [CrossRef] [Green Version]
- Shariati, M.; Mafipour, M.S.; Ghahremani, B.; Azarhomayun, F.; Ahmadi, M.; Trung, N.T.; Shariati, A. A novel hybrid extreme learning machine–grey wolf optimizer (ELM-GWO) model to predict compressive strength of concrete with partial replacements for cement. Eng. Comput. 2020, 1–23. [Google Scholar] [CrossRef]
- FM Zain, M.; Abd, S.M. Multiple regression model for compressive strength prediction of high performance concrete. J. Appl. Sci. 2009, 9, 155–160. [Google Scholar] [CrossRef]
- Mohammed, A.; Mahmood, W.; Ghafor, K. TGA, rheological properties with maximum shear stress and compressive strength of cement-based grout modified with polycarboxylate polymers. Constr. Build. Mater. 2020, 235, 117534. [Google Scholar] [CrossRef]
- Sarwar, W.; Ghafor, K.; Mohammed, A. Modeling the rheological properties with shear stress limit and compressive strength of ordinary Portland cement modified with polymers. J. Build. Pathol. Rehabil. 2019, 4, 1–12. [Google Scholar] [CrossRef]
- Vipulanandan, C.; Mohammed, A.; Ganpatye, A. Smart cement performance enhancement with NanoAl 2 O 3 for real time monitoring applications using Vipulanandan models. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 30 April–3 May 2018. [Google Scholar]
- Mohammed, A.; Rafiqet, S.; Sihag, P.; Kurda, R.; Mahmood, W. Soft computing techniques: Systematic multiscale models to predict the compressive strength of HVFA concrete based on mix proportions and curing times. J. Build. Eng. 2020, 33, 101851. [Google Scholar] [CrossRef]
- Biglari, M.; Azami, A.S.; Kahidan, A.; Ghafari, E.; Ghasemi, M.A. Investigating the Effects of Cement Type and W/C Ratio on the Concrete Corrosion Using the Electrical Resistance Assessment Method. Civ. Eng. J. 2018, 4, 1897–1906. [Google Scholar] [CrossRef]
- Mohammed, A.; Rafiq, S.; Sihag, P.; Kurda, R.; Mahmood, W.; Mahmood, K.; Sarwar, W. ANN, M5P-tree and nonlinear regression approaches with statistical evaluations to predict the compressive strength of cement-based mortar modified with fly ash. J. Mater. Res. Technol. 2020, 9, 12416–12427. [Google Scholar] [CrossRef]
- Kekez, S.; Kubica, J. Application of Artificial Neural Networks for Prediction of Mechanical Properties of CNT/CNF Reinforced Concrete. Materials 2021, 14, 5637. [Google Scholar] [CrossRef]
- Hawreen, A.; Alexandre Bogas, J.; Guedes, M.; Pereira, M.F.C. Mechanical Characterization of Cement Pastes Reinforced with Pristine and Functionalized MWCNTs. In Materiais, XVIII Congresso da Sociedade Portuguesa de Materiais; University of Aveiro: Aveiro, Portugal, 2017; Available online: https://www.researchgate.net/publication/317348788_Mechanical_characterization_of_cement_pastes_reinforced_with_pristine_and_functionalized_multi-walled_carbon_nanotubes (accessed on 5 November 2021).
- Wei, X.; Tian, K.; Xiao, L. Prediction of compressive strength of Portland cement paste based on electrical resistivity measurement. Adv. Cem. Res. 2010, 22, 165–170. [Google Scholar] [CrossRef]
- Wei, X.; Xiao, L.; Li, Z. Prediction of standard compressive strength of cement by the electrical resistivity measurement. Constr. Build. Mater. 2012, 31, 341–346. [Google Scholar] [CrossRef]
- Dong, B.; Zhang, J.; Wang, Y.; Fang, G.; Liu, Y.; Xing, F. Evolutionary trace for early hydration of cement paste using electrical resistivity method. Constr. Build. Mater. 2016, 119, 16–20. [Google Scholar] [CrossRef]
- Mohsen, M.O.; Taha, R.; Taqa, A.A.; Shaat, A. Optimum carbon nanotubes’ content for improving flexural and compressive strength of cement paste. Constr. Build. Mater. 2017, 150, 395–403. [Google Scholar] [CrossRef]
- Kamal, M.; Safan, M.A.; Eltabey, M.; Zaki, E.I.S.; El-hassan, K.A. Compressive strength of Portland Cement Pastes and Mortars Containing Cu-Zn Nano-Ferrite. 2012. Available online: https://www.sid.ir/en/journal/ViewPaper.aspx?ID=262359 (accessed on 5 November 2021).
- Ferreira, R.M.; Jalali, S. NDT measurements for the prediction of 28-day compressive strength. NDT E Int. 2010, 43, 55–61. [Google Scholar] [CrossRef]
- Chi, L.; Wang, Z.; Lu, S.; Zhao, D.; Yao, Y. Development of mathematical models for predicting the compressive strength and hydration process using the EIS impedance of cementitious materials. Constr. Build. Mater. 2019, 208, 659–668. [Google Scholar] [CrossRef]
- Xiao, L.; Wei, X. Early age compressive strength of pastes by electrical resistivity method and maturity method. J. Wuhan Univ. Technol. Mater. Sci. Ed. 2011, 26, 983–989. [Google Scholar] [CrossRef]
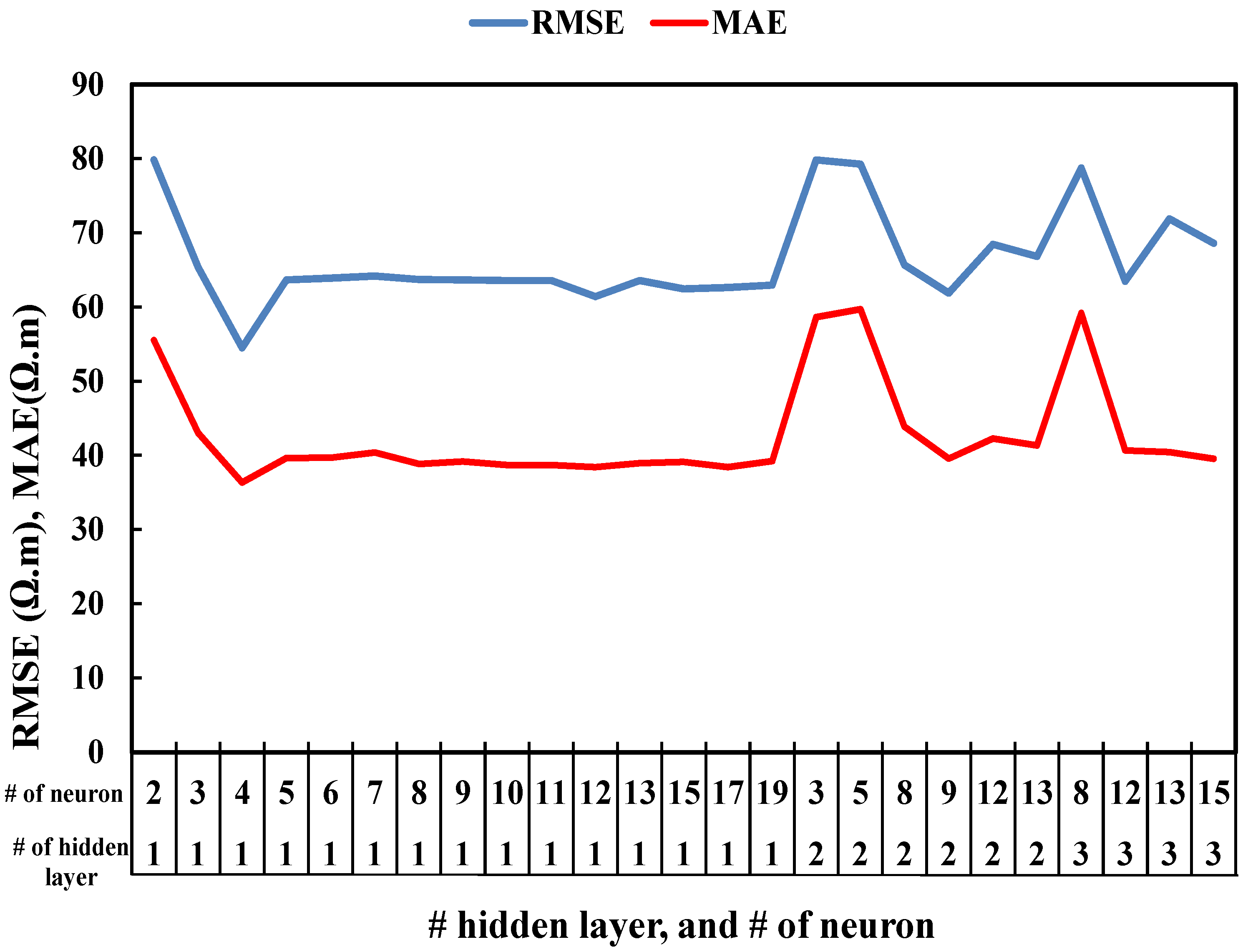

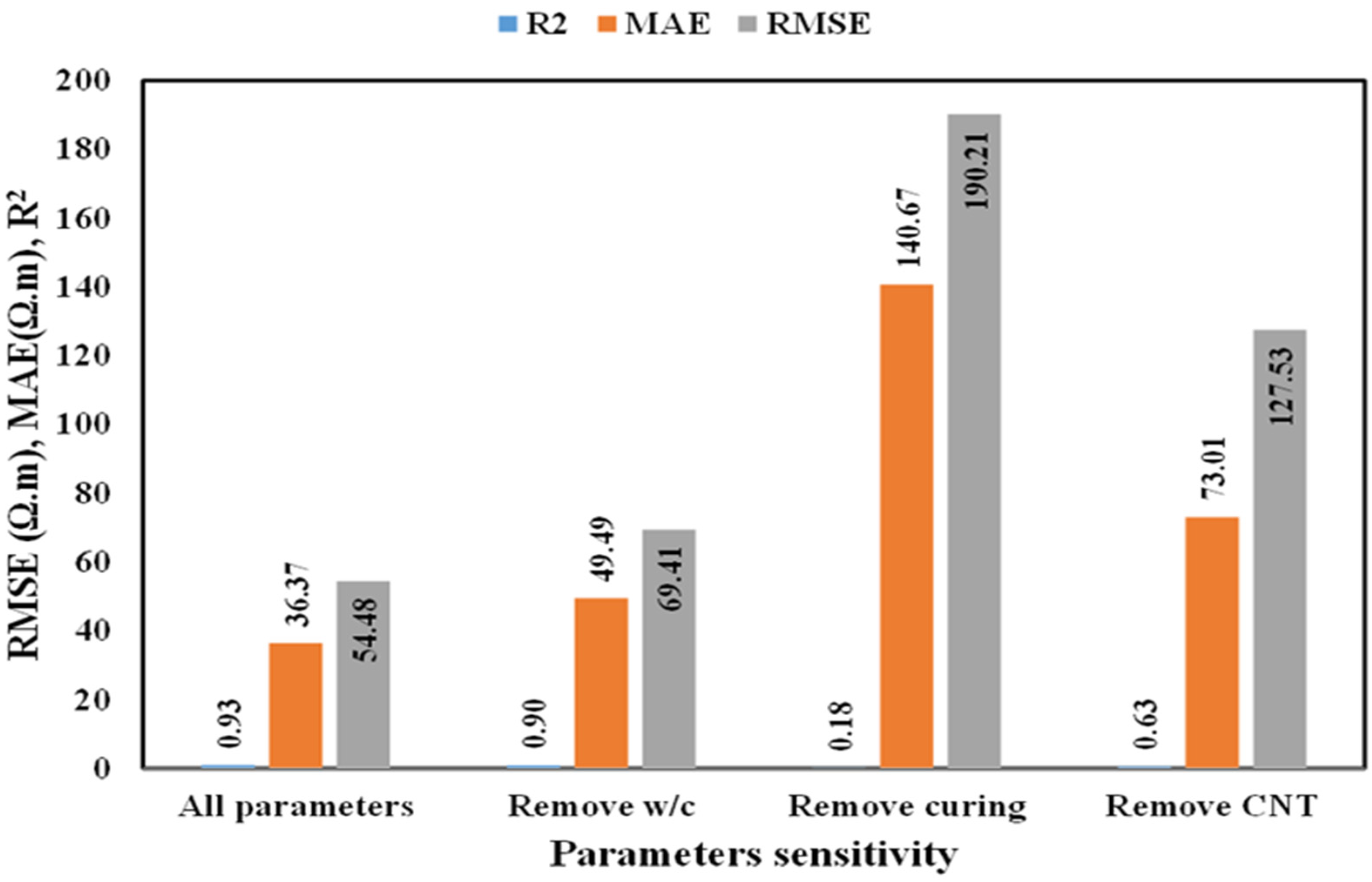
| Scen. No. | Input Combination | Removed Parameter | R2 | MAE (Ω.m) | RMSE (Ω.m) | Ranking |
|---|---|---|---|---|---|---|
| 1 | w/c, CNT, curing time | - | 0.93 | 36.37 | 54.48 | - |
| 2 | CNT, curing time | w/c | 0.89 | 49.49 | 69.41 | 3 |
| 3 | w/c, CNT | Curing time | 0.18 | 140.67 | 190.21 | 1 |
| 4 | w/c, curing time | CNT | 0.63 | 73.01 | 127.53 | 2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Piro, N.S.; Mohammed, A.S.; Hamad, S.M. Multiple Analytical Models to Evaluate the Impact of Carbon Nanotubes on the Electrical Resistivity and Compressive Strength of the Cement Paste. Sustainability 2021, 13, 12544. https://doi.org/10.3390/su132212544
Piro NS, Mohammed AS, Hamad SM. Multiple Analytical Models to Evaluate the Impact of Carbon Nanotubes on the Electrical Resistivity and Compressive Strength of the Cement Paste. Sustainability. 2021; 13(22):12544. https://doi.org/10.3390/su132212544
Chicago/Turabian StylePiro, Nzar Shakr, Ahmed Salih Mohammed, and Samir Mustafa Hamad. 2021. "Multiple Analytical Models to Evaluate the Impact of Carbon Nanotubes on the Electrical Resistivity and Compressive Strength of the Cement Paste" Sustainability 13, no. 22: 12544. https://doi.org/10.3390/su132212544
APA StylePiro, N. S., Mohammed, A. S., & Hamad, S. M. (2021). Multiple Analytical Models to Evaluate the Impact of Carbon Nanotubes on the Electrical Resistivity and Compressive Strength of the Cement Paste. Sustainability, 13(22), 12544. https://doi.org/10.3390/su132212544