Test-Retest Reliability of Unilateral Horizontal Drop Jump in Children

Abstract

Jumps are an indispensable activity for the development of coordination, muscle strength and power, especially in children. Positive effects of horizontal drop jump (HDJ) proved to be very important in improving individuals performance. HDJ presents a specific movement pattern that has similarities with running gait and take-off in different horizontal jumps. Influence and effect of implementating HDJ in children is yet to be determined. The aim of this research was to determine the test–retest reliability of the unilateral horizontal drop jump (UHDJ) in children of early school age (6–7 years). Participants (n = 31; 19 girls and 12 boys) were school-age children that regularly attended Physical Education classes (Girls: mean age 7.5 ± 0.3 years, mean height 127.1 ± 6.8 cm and mean weight 25.8 ± 5.2 kg; Boys: mean age 7.5 ± 0.2 years, mean height 127.5 ± 6.9 cm and mean weight 27.6 ± 7.1 kg). UHDJ was performed from an elevation of 30 cm relative to the platform with starting position 120 cm from the middle of the platform. A jump on the platform and a unilateral take-off in the distance were performed, followed by a bilateral landing on the mat. Intraclass correlation coefficient was used to determine the reliability between the two days of measurements. Test–retest reliability was calculated for all observed variables, and a good correlation was found between the performed measurements (ICC = 0.76–0.89). The α coefficient indicates good to excellent (0.86–0.94) internal consistency. These findings suggest the usefulness of applying a UHDJ in school-age children. Moreover, it can be used to identify children talented for sports, monitor the effects of training and discover and direct individuals towards suitable sports disciplines.

1. Introduction

Proper growth and development of children requires involvement in sports and daily physical activities [1]. These activities consist of different forms of running, jumping, and throwing [2]. Jumps are an indispensable activity for the development of coordination, muscle strength and power. The stretch-shortening cycle (SSC) is an integral part of jumps in which the cycles of stretching (eccentric phase) and shortening (concentric phase) of muscles alternate [3]. The development of plyometric contraction, i.e., the ability of the musculoskeletal system to make more use of the potentials to generate force, can be developed by applying drop jumps.

Rate of force development (RFD) and the maximum force (F_max) produced during the jump are indicators used to determine the strength of the take-off and the reactive force of the muscles (RSI) in the performance of drop jumps [4]. With the growth, i.e., aging, of adolescents (11–15 years old), the height of the jump progressively increases and the duration of contact with the ground (Cont_time) when performing different types of vertical jumps reduces [5,6]. Moreover, authors [5,6] point to the ability to effectively utilize nerve control and SSC potential. Full utilization of these potentials that accumulate during the eccentric phase is possible when the duration of contact with the ground does not exceed 200 ms [7]. Schmidtbleicher [8] suggests that all jumps, i.e., take-offs shorter than 250 ms belong to the fast SSC.

Drop jumps can be performed with single or double leg take-off and in vertical and horizontal directions. There are also two techniques for performing these jumps, with amortization and without amortization in the knee joint [9]. Studies [1,6,10,11] establish a positive interaction between jump height and contact time with a reactive strength index (RSI) in children and young athletes when performing the tasks of landing and vertical take-off from different heights. In contrast, insufficient attention is focused on defining parameters and the impact of the training program by applying a horizontal drop jump (HDJ), which has more similarities in its structure to activities dominated by horizontal movements (running, horizontal jumps). When observing correlation of vertical and horizontal jumps with sprint running over 10, 20 and 30 m, strongest correlation was determined in horizontal single leg jump, which is due to similar kinematic and dynamic structures with running gait [12]. Dobbs et al. [13] compared the peak and average forces of top athletes in the performance of vertical (Peak force = 4915 N; Mean force = 2749 N) and HDJ (Peak force = 1163 N; Mean force = 528) and concluded that significantly less force is manifested in the performance of a unilateral horizontal drop jump (UHDJ). Given the above, this motor structure can be applied in children and in the process of recovery after injury. Both types of jumps show a high association with running at 20 m, with a greater association found for HDJ [14]. Furthermore, in children there is moderate to large correlation between vertical explosive strength and sprint performance [15,16]. Moreover, the result of a landing with a horizontal take-off is significantly related to the results of running at 5, 10 and 25 m [17]. Before a UHDJ, the reliability for the jump distance (ICC = 0.95) and horizontal force (ICC = 0.96) were determined in adult athletes (22 ± 2.5 years) involved in multiple sports activities [18]. Dello Iacono et al. [19] stated that the activation potentials generated after a HDJ significantly affect the results of changing the direction and speed of running at 20 m. Simspon and Cronin [20] investigated whether a change in the distance of the starting position relative to the landing point influences the result of the jump distance and vertical and horizontal force. The results show that the change in distance (80%, 120%, 160% of the leg length) does not affect the stated variables.

Previous research has focused on the study of drop jumps in adults and top athletes, while an insufficient number has focused on the school and adolescent population. Additionally, there is lack of evidence connected to horizontal plane and unilateral jumps. Given the presented positive effects of HDJ and the similarity with the phase of the running step and the phase of take-off in the long jump, it is important to investigate in detail this element and its application in younger age groups. The aim of this research was to determine the test–retest reliability of the UHDJ in children of early school age conducted during two testing days.

2. Materials and Methods

2.1. Sample

The sample of participants (n = 31; 19 girls and 12 boys) consisted of school-age children (Girls: mean age 7.5 ± 0.3 years, mean height 127.1 ± 6.8 cm and mean weight 25.8 ± 5.2 kg; Boys: mean age 7.5 ± 0.2, mean height 127.5 ± 6.9 and mean weight 27.6 ± 7.1). Only the children who regularly attended Physical Education classes and did not have injuries of the lower extremities in the previous 6 months (information provided by PE teacher) were included in investigation. Prior to testing, participants were given detailed information on testing procedure, the benefits and potential risks of measurement. Moreover, they were asked to refrain from high-intensity exercises to avoid impact of fatigue and physical load on testing results.

2.2. Confirmation of the Ethics Committee

Prior to the research, the participants’ parents/guardians gave their consent for the implementation of measurements and the use of data. The research was approved by the Ethics committee of the Faculty of Kinesiology, University of Zagreb in accordance with the Declaration of Helsinki (Opinion No. 8/2021).

2.3. Instruments

For the purpose of measuring these variables, a platform for measuring the reaction forces of the ground (Quattro Jump 9290CD, Kistler, Switzerland) was used. The dimensions of the platform are 920 × 920 mm with a data collection speed of 500 Hz, and it is suitable for performing various types of jumps. Kinetic variables were analyzed in Quattro Jump software package v.1.1.1.4. The variable duration of contact with the ground was measured using an optical measuring instrument Optojump (Microgate, Bolzano, Italy). The device is one meter long and collects data at a speed of 1000 Hz. The data collected by this device were analyzed in the Optojump_next v.1.12.17.0 software package. Previous researches have justified the use of device to measure the parameters of vertical and horizontal drop jumps [17,18,21,22].

2.4. Measurement Protocol

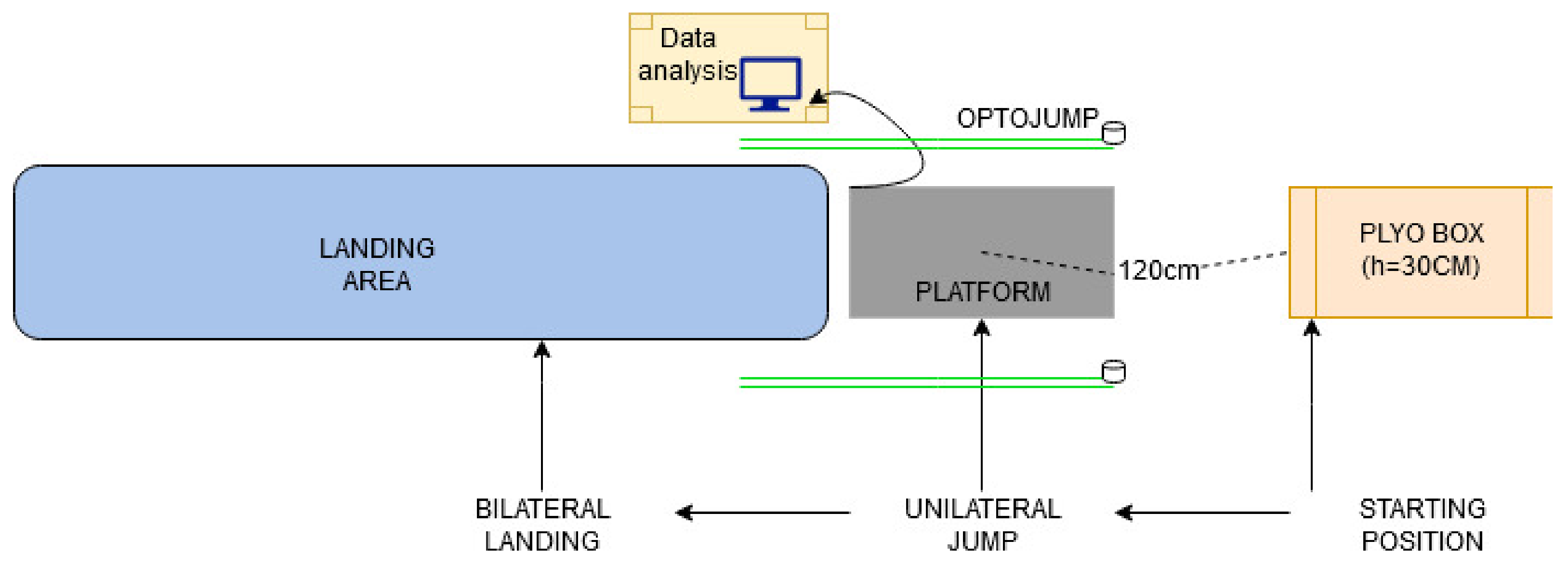
Testing procedure was conducted indoor in physical education gym during PE classes (from 2:00–4:00 p.m.). Prior to the start of the measurement, the participants performed a standardized 10 min warm-up consisting of continuous running; athletic running school exercises (low skip, high skip, straight leg bounds and butt kicks running); stretching of the articular systems and specific jumps (2 series of 10 repetitions of jumps from foot to foot) due to additional preparation and imitation of movement structures that are carried out in the research. The same protocol was repeated 3 days after the first test (Figure 1).

HDJ was performed from an elevation of 30 cm relative to the platform. Best jump performance for children was determined when jumping from 30 cm jump height [23]. The starting position is 120 cm from the middle of the platform. The participant is in a diagonal starting position in which the swinging leg is forward. A jump on the platform and a unilateral take-off in the distance are performed, followed by a bilateral landing on the mat (Figure 2). The instructions for the jump were to “take off as fast as possible and jump as far as possible.” UHDJ is performed with a take-off leg and 3 consecutive repetitions. The average values of the parameters of the performed jumps were used for further analysis.

2.5. Variables

The sample of variables consisted of kinetic and kinematic parameters: peak force in the concentric and eccentric take-off phase (Fmax_CON, Fmax_ECC); rate of force development in the concentric and eccentric take-off phase (RFDmax_CON, RFDmax_ECC); duration of contact with the ground (Cont_time).

2.6. Statistical Analysis

The collected data were processed using the statistical program Statistica 13.4. Basic descriptive statistical indicators (arithmetic mean, minimum, maximum, standard deviation) were calculated. The variance of the results was measured by the coefficient of variation (CV%). A reliability test (Intraclass Correlation Coefficients) was used to determine the reliability between the two days of measurements. An ICC value of less than 0.5 indicates low reliability, between 0.5 and 0.75 medium reliability, from 0.75 to 0.90 good reliability, and 0.90 and more excellent reliability [24]. Moreover, the Cronbach α coefficient was calculated for all variables [25] and the percentage change, i.e., difference between measurements (% Mean).

3. Results

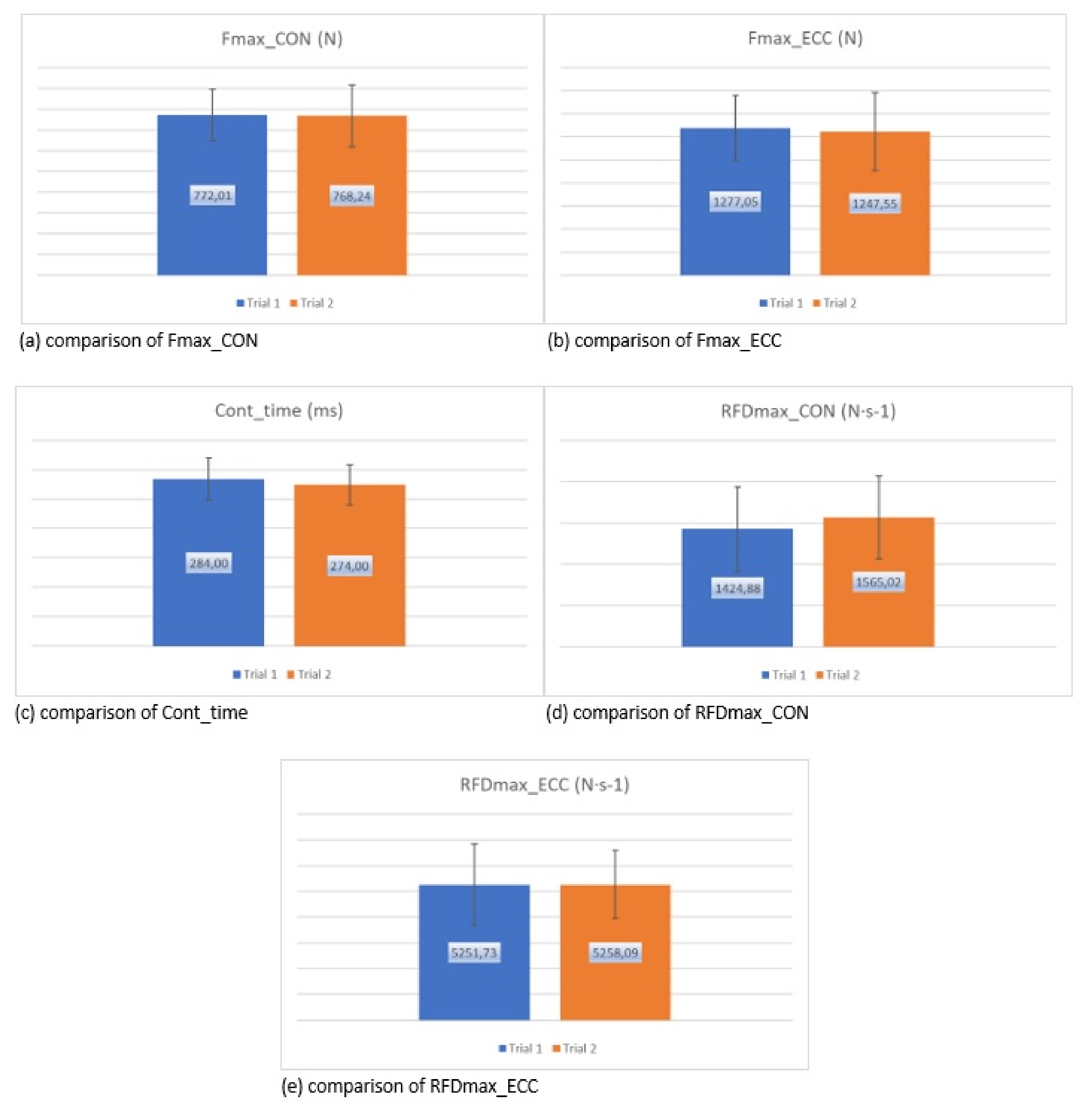
The results (

Table 1. Basic descriptive indicators of kinetic and kinematic parameters of UHDJ.

Variable	Trial	N	Mean	Min	Max	St.dev.
Fmax_CON (N)	1st	31	772.01	531.67	1026.00	123.42
	2nd	31	768.24	473.00	1094.67	149.41
Fmax_ECC (N)	1st	31	1277.05	791.33	1878.00	282.93
	2nd	31	1247.55	754.00	2028.00	337.06
Cont_time (ms)	1st	31	284.00	202.00	383.00	36.00
	2nd	31	274.00	215.00	384.00	34.00
RFDmax_CON (N·s−1)	1st	31	1424.88	787.35	2868.06	519.08
	2nd	31	1565.02	725.53	2526.57	503.42
RFDmax_ECC (N·s−1)	1st	31	5251.73	2637.33	8633.60	1577.49
	2nd	31	5258.09	2530.58	7885.26	1325.35

Legend: Fmax_CON—peak force in the concentric take-off phase, Fmax_ECC—peak force in the eccentric take-off phase, RFDmax_CON—force gradient in the concentric take-off phase, RFDmax_ECC—force gradient in the eccentric take-off phase; Cont_time—duration of take-off or contact with the ground; 1st/2nd—number of measurements; Mean—average value; Min—minimum value; Max—maximum value; St.dev—standard deviation.

and Figure 3) indicate higher average values of maximal forces during the eccentric take-off phase. In both Fmax variables, higher average forces were achieved in the first measurement. The highest achieved force was in the second measurement in the eccentric take-off phase (Fmax_ECC = 2028.00 N). Average results in the Cont_time variable ranged from 274–284 ms. The shortest take-off duration was 202 ms, while the longest was 384 ms. In the eccentric phase, maximum values (8633.60 N s⁻¹) were reached in the rate of force development variable during the first measurement. Moreover, the average values in the RFD_max variables were higher in the eccentric take-off phase. The lowest value of RFD was during the first measurement in the concentric take-off phase (725.53 N s⁻¹).

Test–retest reliability was calculated for all observed variables and a good correlation was found between the performed measurements (

Table 2. Test–retest reliability with correlation coefficient, coefficient of variation, percentage change of average values and standardized alpha values.

Variable	α	% Mean	CV%	ICC
Fmax_CON (N)	0.94	−0.49	17.65	0.89
Fmax_ECC (N)	0.92	−2.34	24.48	0.86
Cont_time (ms)	0.86	−3.58	12.67	0.76
RFDmax_CON (N·s−1)	0.89	9.84	34.25	0.80
RFDmax_ECC (N·s−1)	0.92	0.12	27.50	0.86

Legend: Fmax_CON—peak force in the concentric take-off phase, Fmax_ECC—peak force in the eccentric take-off phase, RFDmax_CON—force gradient in the concentric take-off phase, RFDmax_ECC—force gradient in the eccentric take-off phase; Cont_time—duration of take-off or contact with the ground; α—standardized value of alpha; % Mean—the percentage change in average values; CV%—coefficient of variation; ICC—correlation between measurements.

). The α coefficient indicates good to excellent (0.86–0.94) internal consistency.

In the variable FmaxCON, the highest correlation between the observed measurements was noticed (ICC = 0.89). Moreover, good reliability (ICC = 0.86) was obtained in the variables Fmax_ECC and RFDmax_ECC. The correlation coefficient for the RFDmax_CON variable is 0.80. Of all the observed parameters, the smallest correlation between the two measurements was obtained in the Cont_time variable (ICC = 0.76). Greatest percentage of change between measurements (9.84%) was determined in RFDmax_CON.

4. Discussion

Intensity of jumping exercise can be described with kinetic and kinematic parameters. Kinetic parameters observed in this study were F_max and RFD_max of eccentric and concentric phase after drop jump from 30 cm and unilateral take-off. Kinematic parameter used to describe duration of jump was Cont_time. This research aimed at defining test–retest reliability of UHDJ performed in two testing days. The observed parameters indicate a good correlation (ICC = 0.76–0.89) of the measured variables in children of school-age. According to the findings of Stalbom et al. [18], adult athletes, due to better movement control and motor performance and systematic training, have more reliable results (ICC = 0.75 to 0.96) and less variation between measurements (CV% = 6.5).

F_max variables showed satisfactory reliability in both the concentric and eccentric phase of jump. Eccentric phase of jump exhibited greater force than concentric (1277.05 vs. 772.01 N), which also affected greater change in % Mean (−2.34 vs.−0.49) and CV% (24.48 vs. 17.65). If converted to bodyweight (BW) and compared to authors [26], our Fmax results display greater values than children of age 11–14 years (Fmax_ECC = 3.98 bw vs. 4.86 bw; Fmax_CON = 2.57 bw vs. 2.96 bw).

The variable Cont_time has the lowest correlation between measurements (ICC = 0.76). In the second measurement, Cont_time lasted shorter on average (−3.58%). This trend of results (−1.43 to −5.58) was also determined when the test was performed from different landing distances [20]. Moreover, good reliability (ICC = 0.79) was obtained when performing a 40 cm HDJ in adult athletes with an average ground contact time of 370 ± 30 ms [27]. In relation to Cont_time in present study, authors [23] determined slower Cont_time in prepubertal girls and boys (Cont_time = 500.50 ms) when performing vertical drop jump from 30 cm height. Due to direction (vertical/horizontal) of drop jump, HDJ is more similar (when observing movement pattern and ground parameters) to running gait. Previous experience with knowledge and implementation of the test affected the shorter duration of contact with the ground during the second measurement. Presented data suggest how optimal drop height and length between starting position and platform enable children to perform UHDJ with good technique and to improve their performance over the time, similarly to adults.

The percentage change (% Mean) between the two measurements shows an increase in results of 9.84% in the variable RFDmax_CON, while in the eccentric take-off phase almost no changes are noticeable (% Mean = 0.12). Increase in RFDmax_CON relates to shorter contact time (−3.58%) which can be ascribed to better technical performance. For better understanding of concentric and eccentric part of the jump, Cont_time should be divided into this two phases. Results of Fmax_ECC variable reduced in 2nd measurement, on the contrary RFDmax_ECC variable improved slightly. This can partially be due to shorter contact time.

The coefficient of variability (CV% = 12.67 to 34.25) shows large variations between measurement results. Higher values of observed variation are conditioned by subjects’ age. No gender differences were determined. Meylan et al. [28], by observing the vertical and horizontal jump with preparation in young athletes, concluded that the reliability of the results is affected by the maturity of the athletes, especially during the eccentric phase of the jump.

It is necessary to consider that school children are not involved in top sports and high-intensity training, which certainly affects the results of this research. Additionally, it would be interesting to investigate gender differences and influence of maturity on mentioned parameters. While this research presented good test–retest reliability of UHDJ in children, extending of sample size and separating of Cont_time in ECC and CON phases would add to better understanding of observed UHDJ.

5. Conclusions

Drop jumps are an excellent exercise for developing jump-type explosive power. The kinetic and kinematic variables of HDJ in the children population has not been sufficiently researched, although it has been previously proven that, in a certain proportion, children can use the potentials of the musculoskeletal system. The movement structure of the UHDJ is like the specific unilateral jumps and the cycle of steps when running, either in sports or in children’s spontaneous playing. This research determined the test–retest reliability of the UHDJ in children of early school-age. Good reliability was found for all observed variables. These findings suggest the possibility of applying a UHDJ in this population. By applying this kind of jumping in practice, especially in sport training sessions, it is possible to identify deficiencies in the performance of specific elements and to monitor the effects of training. In physical education, it can help to identify children talented for sports and discover and direct individuals towards specific sports disciplines. Moreover, the presented methodology shows a simple and efficient way of conducting testing through which reliable parameters of take-off can be obtained. Moreover, through future research, it is necessary to focus on the differences in performance with the dominant and nondominant leg and to determine the relationship between the results of this test and the results in other tests of explosive power, speed and agility in young athletes.